Characterization of piezoelectric ceramics and 1-3 composites for high power transducers

Abstract

The high power characteristics of various piezoelectric ceramics and 1-3 composites were investigated. In contrast to “hard” Pb(Zr,Ti)O₃, modified (Bi_0.5Na_0.5)TiO₃ based ceramics were found to show a relatively linear electromechanical response under high drive conditions due to their high stability of mechanical quality factor. The effects of high drive field and duty cycle on the behavior of 1-3 composites were analyzed by varying active and passive components. Improved high power characteristics of 1-3 composites were achieved by selection of optimized composite components, with enhanced electromechanical efficiency and thermal stability under high drive conditions.

High power ultrasonic transducers are widely used in a variety of applications, such as medical therapeutic ultrasound, e.g., high intensity focused ultrasound (HIFU) and underwater sonar projectors. The goal of HIFU is to deliver focused, high intensity ultrasonic energy to the target area for the thermal ablation of diseased tissue, while the goal of underwater sonar projectors is to generate high acoustic pressure with broad bandwidth for the improvement in the detection range and the resolution of underwater imaging.^{1, 2, 3, 4} The performance improvement in high power ultrasonic transducers is, thus, related to the acoustic power handling capability of a piezoelectric transducer, such as enhanced power efficiency and reduced internal heating.

The acoustic power of a piezoelectric transducer is proportional to vibration velocity v₀, which is a function of piezoelectric material properties, specifically the product of electromechanical coupling factor k (or piezoelectric strain coefficient d) and mechanical quality factor Q_m, i.e., v₀ ∝ (k·Q_m or d·Q_m).^{5, 6, 7} Accordingly, the figure of merit of high power applications is the product of k and Q_m (or d·Q_m). High electromechanical coupling k allows for increased transducer bandwidth, while high Q_m reduces heat generation under high drive conditions.^{8, 9} Therefore, both high k and Q_m of piezoelectric materials are key for the high power performance of ultrasonic transducers.

Piezoelectric/polymer composites with 1-3 connectivity offer several advantages over monolithic piezoceramics, including higher electromechanical coupling and lower parasitic vibrations.^{10, 11} However, conventional 1-3 composites are limited for use in high power transducers, due to their inherently low Q_ms as a result of the passive matrix. This reduces the maximum drive field and consequently limits output power, as a result of increased mechanical loss and subsequent heat generation. One approach to solve this issue is the use of an appropriate passive material with low elastic loss and/or high thermal conductivity k_c, together with high Q_m piezoelectrics.¹²

In this letter, the high power characteristics of various piezoelectric ceramics (including Pb(Zr,Ti)O₃-PZT and (Bi_0.5Na_0.5)TiO₃–BNT based materials) and 1-3 composites were reported, with the emphasis on the influence of active and passive materials under high drive conditions.

The composites were fabricated using the conventional dice and fill method,¹³ where the final thicknesses of the composites were designed to be around 3.5–4.5 mm, which gives fundamental thickness resonance frequency being on the order of 350–450 kHz for PZT based composites and 500–600 kHz for BNT based composites. The piezoelectric materials used in this study were commercially available PZT ceramics (PZT5A, PZT4, and PZT8, Piezokinetics, Bellefonte, PA) and acceptor modified (Bi_0.5Na_0.5)TiO₃ based ceramics, (BNLKBT: 0.83Bi_0.5Na_0.5TiO₃-0.084Bi_0.5K_0.5TiO₃-0.056BaTiO₃-0.03Bi_0.5Li_0.5TiO₃).¹⁴ For the passive phase, various polymers were explored and selected based on the desired properties for high power composites- low elastic loss, low Young’s modulus, and high thermal conductivity. The selected polymers for this work are (I) Spurr resin (Polyscience, inc.), (II) Epotek 301 (Epoxy Technology, Inc.), (A) T7110 (Epoxy Technology, Inc.), and (B) Stycast 2850FT (Emerson & Cuming).

The dielectric and electromechanical properties of the prepared monolithic and composite samples were determined using an HP4194A impedance analyzer according to the IEEE Standard.¹⁵ In order to minimize clamping (loading) effects on the samples during measurements, lead wires were attached to the electrodes using silver epoxy. Polymer properties were obtained from the manufacturers’ datasheets and by ultrasonic measurements.¹² For high power measurements, the linear frequency modulation method was used,⁷ where high voltage waveform was generated by a National Instruments PXI-1033 connected to an M8 amplifier (Instruments, Inc., San Diego, CA). The vibration velocity was measured using a laser vibrometer (Polytec OFV-505 laser head and Polytec OFV-5000 laser controller). Current and vibration velocity from the samples were recorded using the PXI-1033 unit. The dynamic strain S was calculated according to the following equation:

$$S=\left(\frac{\pi }{2l}\right)\cdot \left(\frac{v}{\omega }\right),$$ (1)

where ω is angular resonant frequency, l is sample length (or composite thickness), and v is vibration velocity. For evaluation of duty cycle dependence of the vibration characteristics under isothermal conditions, a function generator (HP 33120A) with piezo linear amplifier (Piezo Systems EPA-104) was used to generate a high voltage waveform with different duty cycles. A variable input transformer (Instruments, Inc. VIT-13) and a laser vibrometer were connected to an oscilloscope (LeCroy LT-344) to monitor and measure the electrical and mechanical properties of the samples. During the measurements, the drive field and frequency were continually adjusted to maintain the fundamental resonance frequency under a 50 °C isothermal condition.

Table TABLE I. summarizes the measured small signal properties of piezoelectric materials using an impedance analyzer. Compared to hard PZT ceramics, BNLKBT ceramics generally exhibited lower piezoelectric response and coupling factors, but offered comparable Q_ms and higher coercive field. The higher coercive field is related to improved domain stability under high drive field, while high Q_m allows for improved acoustic power and thermal limitations. The properties of the various passive polymers are summarized in Table TABLE II.. Polymers (I) and (II) show low Young’s modulus Y_r, while polymers (A) and (B) exhibit high thermal conductivity. Low Y_r polymer matrix is preferred for 1-3 composite filler as it improves electromechanical coupling of composites.¹¹ In addition, polymer (I) shows low viscosity and attenuation coefficient, which reflect low elastic loss.^{16, 17} This may allow for better electromechanical performance of composites (I) under high drive operations.

TABLE I.

Electromechanical properties of acceptor modified BNLKBT and PZT longitudinal bars. Frequency constant, N₃₃ was determined under short-circuit condition (measured at 1V_rms).

	N33 (Hz m)	K33T	tanδ	k33	d33 (pC/N)	Qm	Ec/Ei (kV/cm)
BNLKBT	2180	600	0.007	0.46	110	800	35/3
PZT4	1520	1300	0.004	0.70	370	470	14/3
PZT8	1640	1000	0.002	0.63	240	1050	19/7
PZT5A	1500	2000	0.017	0.70	500	80	15/-

TABLE II.

Material parameters for various polymer materials, where ρ is density, V_L is longitudinal wave velocity, Y_r is Young’s modulus, η is viscosity, σ is Poisson ratio, k_c is thermal conductivity, and α_l is longitudinal attenuation coefficient. Note that the attenuation coefficients were determined at 10 MHz.

	ρ	VL	Yr	η		kc	αl
	(kg/m3)	(m/s)	(GPa)	(Poise)	σ	(W/m K)	(dB/m)
(I)	1135	2157	2.97	0.65	0.37	0.3	2360
(II)	1150	2740	5.06	1-2	0.35	0.2	4330
(A)	2164	2631	12.42	14-22	0.25	1.0	4120
(B)	2258	3130	16.26	2200	0.3	1.2	4740

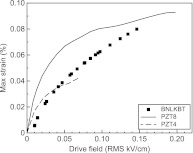
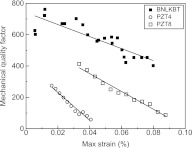
The comparison of the electromechanical response of monolithic PZTs and BNLKBT ceramics is shown in Fig. 1. PZT8 ceramics generally showed higher strain levels than PZT4 and BNLKBT ceramics for a given drive field. However, it is interesting to note that although PZT4 and PZT8 ceramics offered initially higher vibration velocities than BNLKBT ceramics, BNLKBT ceramics eventually achieved similar dynamic strain levels as hard PZT ceramics at high drive levels >0.15 kV/cm. The variation of Q_m for the various piezoelectric ceramics as a function of dynamic strain is demonstrated in Fig. 2. Although the Q_m of all the piezoelectrics decreased with increasing dynamic strain, the BNLKBT ceramics exhibited relatively stable Q_ms compared to hard PZT ceramics, resulting in improved high power performance, as shown in Fig. 1.

Figure 1.

Comparison of maximum dynamic strain of BNLKBT and hard PZT longitudinal bars as a function of ac drive field.

Figure 2.

Variations of Q_m for BNLKBT and hard PZT longitudinal bars as a function of maximum dynamic strain.

In contrast to various hard piezoceramics, the high power characteristics of 1-3 composites were dominated by the passive polymer phase, as evident in Table TABLE III..¹² It was observed that the composites containing low moduli polymers (I and II) possessed higher electromechanical properties, such as k_t and Q_m, when compared to the composites with high thermal conductivity polymers (A and B). However, it should be noted that high thermal conductivity polymer may improve high power performance of composites, offering efficient heat-sink outside of the composites.¹⁸

TABLE III.

Measured piezoelectric and electromechanical properties of various PZT8 1-3 composites with different polymers. d₃₃·Q_m is normalized to the value for PZT8 (B).

	ρ (kg/m3)	d33 (pC/N)	Qm	kt	f0·l (Hz m)	d33·Qm
PZT8 (I)	6140	200	320	0.62	1690	5.6
PZT8 (II)	5900	220	76	0.62	1651	1.5
PZT8 (A)	6060	200	45	0.6	1750	0.8
PZT8 (B)	6030	190	60	0.53	1730	1

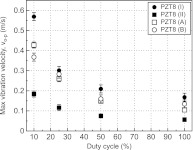
The effects of various polymers on vibration velocity and temperature rise were evaluated under high drive conditions, and the results are given in Fig. 3. Note that the symbol represents the measured vibration velocity of the composites when the thermal equilibrium of 50 °C was reached. The vibration velocities for tested samples were found to increase with decreasing duty cycle as a result of lower heat dissipation. Among the prepared composites, PZT8 (I) composites showed higher vibration velocities compared to others for a given duty cycle level, because of the low mechanical loss of PZT8 (I). At high duty cycles >20%, however, PZT8 (A) and PZT8 (B) showed similar levels of vibration velocity, possibly due to the high thermal conductivity of the polymers. On the contrary, the composites with high loss and low thermal conductivity polymer (II) exhibited low performance under high drive conditions, due to the rapid overheating at a relatively low drive field.

Figure 3.

Maximum vibration velocity, v_o-p (half peak-to-peak) of various PZT8 1-3 composites consisting of various polymer fillers as a function of duty cycle.

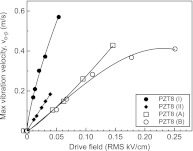
Fig. 4 shows the vibration velocity of various PZT8 composites as a function of drive field. The measurements were performed at 10% duty cycle, which allows for the determination of vibration velocity without temperature rise during the measurements. As expected, the level of vibration velocity was proportional to the d₃₃.Q_m of composites, exhibiting the highest dynamic strain levels for PZT8 (I) composites. PZT8 (A) and (B) composites showed similar levels of dynamic strain at low drive fields, but deviated from the linearity with increasing drive field. The maximum vibration velocity of both composites was on the order of 0.4 m/s, above which the temperature increased, >50 °C. It should be noted that PZT8 (II) initially showed higher vibration velocities compared to the composites with high thermal conductivity polymers, however, excessive heating occurred above 0.2 m/s.

Figure 4.

Comparison of vibration velocity, v_o-p of PZT8 composites as a function of ac drive field for various 1-3 composites at 10% duty cycle.

Among the four passive materials, polymer (I) was chosen as the passive material for high power composite transducers, due to its low elastic loss and Young’s modulus. Various piezoelectric composites (I) were fabricated in order to investigate the effect of piezoelectrics on high power performance. The small signal properties of various composites with polymer (I) are given in Table TABLE IV.. As can be observed, PZT8 (I) showed high figure of merit d₃₃.Q_m for high power applications, while BNLKBT (I) exhibited the lowest value.

TABLE IV.

Measured piezoelectric and electromechanical properties of BNLKBT and PZT based composites. d₃₃·Q_m is normalized to the value for BNLKBT (I).

	ρ (kg/m3)	d33 (pC/N)	Qm	kt	f0·l (Hz m)	d33·Qm
BNLKBT (I)	3880	110	150	0.46	2070	1
PZT4 (I)	5970	350	140	0.66	1540	3.0
PZT8 (I)	6140	190	320	0.62	1690	3.7
PZT5A (I)	6100	490	50	0.68	1410	1.5

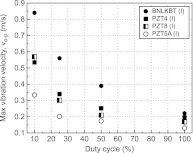
The vibration velocities for various composites (I) as a function of duty cycle are shown in Fig. 5. For comparison, the vibration velocity of PZT5A composites was also given. It was found that all tested composites showed similar levels of vibration velocity under continuous wave (cw) conditions (100% duty cycle). Of particular significance is that BNLKBT composites exhibited higher vibration velocities at low duty cycles (<50%). Considering that the BNLKBT ceramics have stable Q_m, as observed in Fig. 2, the higher vibration velocity of BNLKBT ceramics under low duty cycles is believed to be a consequence of higher stability of Q_m under high-level vibrations. As expected, PZT5A composites showed the lowest vibration velocity compared to others over the full range of investigated duty cycle, though possessing much higher piezoelectric coefficient, as listed in Table TABLE IV..

Figure 5.

Duty cycle dependence of vibration velocity, v_o-p for BNLKBT and PZT based composites.

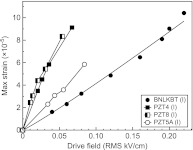
In order to further evaluate the effect of piezoelectric phase on the composite performance, the maximum dynamic strains of BNLKBT and PZT based composites as a function of drive field (at 10% duty cycle) are shown in Fig. 6. The BNLKBT composites exhibited lower dynamic strain for a given drive field when compared to PZT based composites, due to their lower small signal values of d₃₃.Q_m. However, the BNLKBT composites could be driven with higher fields while maintaining 50 °C isothermal condition, giving rise to higher dynamic strain than PZT based counterparts. The results are interesting because BNLKBT composites have the lowest figure of merit among the investigated composites, as shown in Table TABLE IV., which indicate that the high power performance of composites are not only related to the figure of merit d₃₃.Q_m of piezoelectrics, but also the high power stability of BNLKBT ceramics (stability of the Q_m and high coercive field).

Figure 6.

Comparison of maximum dynamic strain of BNLKBT and PZT based composites as a function of ac drive field at 10% duty cycle.

In conclusion, high power measurements of monolithic piezoelectrics revealed that although the overall electromechanical properties of BNLKBT were lower than those of hard PZT ceramics, the higher stability in Q_m under high drive conditions allowed for comparable dynamic strain to that of PZTs. For 1-3 composites, high power characteristics were strongly dependent on the type of polymer. The composites with low elastic modulus and low elastic loss polymer were found to possess high Q_m, while those with high thermal conductivity polymers improved the heat management under high duty cycles. In addition, BNLKBT composites were found to possess lower losses than PZT counterparts under high drive conditions due to the relatively stable Q_m of the monolithic ceramics, offered similar dynamic strains to those of PZT composites under high drive level, exhibiting potential candidates for high power transducer applications.