In vivo assessment of optimal b-value range for perfusion-insensitive apparent diffusion coefficient imaging

Abstract

Purpose: To assess the optimal b-values range for perfusion-insensitive apparent diffusion coefficient (ADC) imaging of abdominal organs using short-duration DW-MRI acquisitions with currently available ADC estimation methods.

Methods: DW-MRI data of 15 subjects were acquired with eight b-values in the range of 5–800 s/mm². The reference-standard, a perfusion insensitive, ADC value (ADC_IVIM), was computed using an intravoxel incoherent motion (IVIM) model with all acquired diffusion-weighted images. Simulated DW-MRI data was generated using an IVIM model with b-values in the range of 0–1200 s/mm². Monoexponential ADC estimates were calculated using: (1) Two-point estimator (ADC₂); (2) least squares three-point (ADC₃) estimator and; (3) Rician noise model estimator (ADC_R). The authors found the optimal b-values for perfusion-insensitive ADC calculations by minimizing the relative root mean square error (RRMS) between the ADC_IVIM and the monoexponential ADC values for each estimation method and organ.

Results: Low b-value = 300 s/mm² and high b-value = 1200 s/mm² minimized the RRMS between the estimated ADC and the reference-standard ADC_IVIM to less than 5% using the ADC₃ estimator. By considering only the in vivo DW-MRI data, the combination of low b-value = 270 s/mm² and high b-value of 800 s/mm² minimized the RRMS between the estimated ADC and the reference-standard ADC_IVIM to <7% using the ADC₃ estimator. For all estimators, the RRMS between the estimated ADC and the reference standard ADC correlated strongly with the perfusion-fraction parameter of the IVIM model (r = [0.78–0.83], p ≤ 0.003).

Conclusions: The perfusion compartment in DW-MRI signal decay correlates strongly with the RRMS in ADC estimates from short-duration DW-MRI. The impact of the perfusion compartment on ADC estimations depends, however, on the choice of b-values and estimation method utilized. Likewise, perfusion-related errors can be reduced to <7% by carefully selecting the b-values used for ADC calculations and method of estimation.

INTRODUCTION

Diffusion-weighted MRI (DW-MRI) is a noninvasive imaging technique sensitive to thermally driven motion of water molecules inside the body. This motion is usually represented with a monoexponential model with the apparent diffusion coefficient (ADC) as its parameter.¹The ADC plays an increasingly important role as a quantitative biomarker for many clinical applications including its ability to differentiate between benign and malignant lesions;² evaluate tumor aggressiveness;³ perform early assessment of tumor response-to-therapy;^{4, 5, 6} evaluate the extent of liver fibrosis;^{7, 8, 9} and assess the extent of Crohn's disease^{10, 11} as well as other diseases that are best evaluated with DW-MRI. Moreover, accurate estimates of ADC have been demonstrated as critical to diagnosing, evaluating, and monitoring these pathologies with precision.^{12, 13, 14}

Depending on the acquisition parameters, in vivo measurements of the DW-MRI signal decay and its associated ADC can reflect a slow diffusion component associated with the Brownian motion of water molecules combined with a fast diffusion component associated with the bulk motion of intravascular molecules in the tissue micro capillaries.^{15, 16} When using the monoexponential model, however, this combination may produce an overestimate of the ADC values.

While the more complex intravoxel incoherent motion (IVIM) model¹⁷ is able to separate the diffusion compartment from the micro capillaries’ blood flow; this technique requires long-duration acquisitions with multiple b-value DW-MRI to encompass the wide range of fast diffusion decay due to perfusion, and similarly, slow diffusion decay due to pure diffusion.¹⁸

Such extended imaging, however, is not always desirable or feasible in routine clinical imaging, as increased scan times needed to acquire multiple b-values may likewise prolong sedation or anesthesia, and may result in poor image quality due to motion artifact.¹⁶ Short-duration DW-MRI acquisitions capable of providing accurate, perfusion-insensitive, ADC estimates are therefore of broad clinical interest.

Yamada et al.,¹⁹ for example, suggest using intermediate and high b-values (e.g., 300 and 1100 s/mm², respectively) to approximate true diffusion using the monoexponential model while Padhani et al.²⁰ suggest using a lower b-value ≥ 100 s/mm² to obtain perfusion-insensitive ADC measurements. However, these studies are limited by the fact that neither performed a detailed quantitative analysis to identify optimal b-values. Although several papers have examined the choice of b-values for ADC calculations by evaluating the performance of the estimated ADC as a quantitative biomarker for various applications (usually for a specific pathology);^{12, 13, 14} these analyses may represent overfitting of the b-values to the clinical diagnostic question rather than to the pure diffusion measurements which are of interest. Moreover, the above-mentioned studies were limited to a specific ADC estimation method—most often the two-point estimator for two b-value images^{12, 21} or the least-squares estimator for more than two b-value images.^{12, 13, 14} Recently, several groups have shown that the accuracy of parameter estimates may be improved by using a Rician noise model to approximate the actual noise in diffusion-weighted MRI, though this approach may, at the same time, increase the variance of the estimates.^{22, 23, 24} Specifically, Walker-Samuel et al. have demonstrated that by maximizing a Rician likelihood function, body DW-MRI can produce ADC estimates that are more accurate (but with higher variance) than the least squares estimator, which implicitly assumes a Gaussian noise model.²⁵

In our experiment, we set out to quantitatively identify the range of b-values that provide ADC estimates of abdominal organs, less contamination from perfusion phenomena. We then compared our results to diffusion measurements from the IVIM model, specifically against the various ADC estimation methods in current clinical use.

MATERIALS AND METHODS

We carried out the study according to a protocol approved by our Institutional Review Board. MRI was retrospectively collected from 15 subjects [Nine males and six females with a mean age of 14.13 (range 7–24, std 4.09)] that underwent an abdominal MRI study between September 2010 and March 2011 due to suspected Crohn's disease. Abdominal organ findings in these subjects were normal.

MR imaging acquisition

The MRI imaging data of the abdomen was acquired using a 1.5 T unit (Magnetom Avanto, Siemens Medical Solutions, Erlangen, Germany) and a body-matrix coil and spine array coil for signal reception. The data were acquired with a free-breathing single-shot echo-planar imaging sequence using the following parameters: repetition time/echo time (TR/TE) = 6800/59 ms; SPAIR fat suppression; matrix size = 192 × 156; field of view = 300 × 260 mm; slice thickness/gap = 5 mm/0.5 mm; nominal diffusion time (Δ) = 25 ms; maximum gradient amplitude (G_max) = 2 G/cm; 40 axial slices; 8 b-values = 5,50,100,200,270,400,600,800 s/mm² with 1 average. To acquire four images at each b-value with an overall scan acquisition time of 4 min, a tetrahedral gradient scheme first proposed by Conturo et al.²⁶ was used. Next, trace-weighted diffusion images at each b-value were generated using geometric averages of the images acquired in each diffusion sensitization direction.²⁷

Quantitative MR image analysis

Reference-standard diffusion measurements

The IVIM model, first introduced by Le Bihan,¹⁷ accounts for both diffusion and perfusion effects on the signal decay

$$\begin{array}{c}\hfill s_i=s_0(f\exp (-b_i(D^{*}+D))+(1-f)\left(\exp (-b_{i}D)\right))\end{array}$$ (1)

where s_i is the observed signal with b-value:b_i; s₀ is the baseline signal (without any diffusion attenuation); f is the perfusion fraction; D* is the perfusion compartment; and D is the diffusion coefficient. We estimated the model parameters for each voxel, using eight b-value images that were acquired with the estimation method proposed by Freiman et al.²⁸ Finally, we defined the IVIM model D parameter, which represents the perfusion-insensitive diffusion compartment, as the reference standard ADC (ADC_IVIM) for all of our experiments.

Regions of interest annotation

Abdominal organs, including the liver, spleen, and kidneys, were entirely segmented using the semiautomatic ITK-SNAP software tool²⁹ to define the ROI for ADC calculations. The initial manual annotation and the semiautomatic segmentation were performed on the DW-MRI image with b-value = 5 s/mm².The kidneys were further separated into the cortex and medulla regions using graph min-cut segmentation³⁰ based on ADC_IVIM values derived from their respective diffusivity properties.³¹

Simulated data experiment

DW-MRI data were simulated from the estimated parametric maps at each voxel using Eq. 1 with b-values in the following ranges: 0–300 s/mm² with gaps of 25 s/mm², 400, and 600–1200 s/mm² with gaps of 25 s/mm².

Images were corrupted by Rician noise with each channel Gaussian noise of μ = 0 and σ = 8 representing the actual noise level observed in clinical DW-MRI.

Next, the commonly used monoexponential diffusion model¹

$$\begin{array}{c}\hfill s_i=s_0\exp (-b_i\mathrm{ADC})\end{array}$$ (2)

was fitted to the simulated images using the following three estimators:

1. Two b-values estimator (ADC₂):^{1, 32}

$$\begin{array}{c}\hfill \frac{\ln s_1-\ln s_2}{b_2-b_1}=\mathrm{ADC}\end{array}$$ (3)

where b₁, b₂ are the b-values used to acquire the signal s₁, s₂, and ADC is the unknown model parameter.

2. Least-squares estimator (ADC₃) with three b-value images:²⁵

$$\begin{array}{c}\hfill \left[s_0,\mathrm{ADC}\right]=\underset{s_0,\mathrm{ADC}}{\arg \min }\sum _{i=1}^N{\left(s_i-s_0\exp (-b_i\mathrm{ADC})\right)}^2,\end{array}$$ (4)

where b_i is the b-value used to acquire the signal s_i; N is the number of b-value images (three in our case); and s₀, ADC are the unknown model parameters. The singular value decomposition method was used to solve the derived linear system.

3. Maximum likelihood estimator with Rician noise model (ADC_R) with three b-value images.²⁵

$$\begin{array}{ccc}\hfill \left[s_0,\mathrm{ADC}\right]& =& \underset{\mathrm{ADC},s_0}{\arg \max }\sum _{i=1}^N\ln I_0\left(\frac{s_i\left(s_0\exp (-b_i\mathrm{ADC})\right)}{{\sigma }_{R_i}^2}\right)\hfill \\ & & -\sum _{i=1}^N\left(\frac{{\left(s_0\exp (-b_i\mathrm{ADC})\right)}^2}{2{\sigma }_{R_i}^2}\right),\hfill \end{array}$$ (5)

where I₀ is the modified Bessel function of the first kind with order zero.

Initial estimates of the model parameters were obtained with the least squares estimator Eq. 4. Noise variance was estimated using a predefined background region and Eq. 5 was maximized using the BOBYQA nonlinear optimization algorithm.³³ Both the values of the IVIM parameters and the ADC estimates were averaged over each organ. We aimed to find the b-values b_min and b_max that minimize the average relative root mean squared error (RRMS) between the ADC_IVIM and the ADC calculated with b_min and b_max over the J subjects

$$\begin{array}{ccc}& & \left[b_{\min },b_{\max }\right]\hfill \\ & & =\underset{b_{\min },b_{\max }}{\arg \min }\frac{1}{J}\sum _{j=1}^J\sqrt{100\times {\left(\frac{{\mathrm{ADC}}_{\mathrm{IVIM}}-\mathrm{ADC}(b_{\min },b_{\max })}{{\mathrm{ADC}}_{\mathrm{IVIM}}}\right)}^2}\hfill \end{array}$$ (6)

We found the b_min, b_max that minimize Eq. 6 by performing an exhaustive search over a lower b-value range of b_min = [0–300 s/mm²], and a b_max = [600–1200 s/mm²] with gaps of 25 s/mm². In turn, we determined the optimal combination of b-values that provide perfusion-insensitive ADC estimates from a minimum duration acquisition for each estimator (ADC₂, ADC₃, ADC_R) and organ. For the estimators that require three b-value images [Eqs. 4, 5], we used the additional b-value = 400s/mm² as the middle b-value. This simulation study also enabled us to evaluate the effect of b-value choice on ADC estimation for very high b-value images (>800 s/mm²) that were not part of the original clinical acquisition.

In vivo data experiment

Next, we fitted the monoexponential diffusion model [Eq. 2] to the acquired DW-MRI data using the three estimators described above [Eqs. 3, 4, 5]. Sets of b-value images (in pairs and triplets) covering the lower b-value range of 5–270 s/mm² and the higher b-value range of 600–800 s/mm² from the acquired DW-MRI data were used.

We found the b-values b_min and b_max that minimize the average relative root mean squared error over the J subjects between the ADC_IVIM and the ADC calculated with b_min and b_max [Eq. 6] by performing an exhaustive search over pairs of b_min and b_max from the acquired DW-MRI data for each estimator (ADC₂, ADC₃, ADC_R) and organ, respectively.

RESULTS

Table 1 depicts the summary statistics for the IVIM parameters and the ADC values calculated with b_min = 270 s/mm² and b_max = 800 s/mm² for each organ. The greatest difference between the ADC_IVIM and the estimated ADC using the monoexponential model was observed in the medulla of the kidney, which has the highest perfusion-fraction (f) value as compared to the other organs.

Table 1.

Summary statistics of IVIM and ADC values for each organ and ADC estimation method.

	F	D*a	D(ADCIVIM)a	ADC2a b, b	ADC3a b, b	ADCRa b, b
Liver	0.26 ± 0.04	27.4 ± 3.5	1.1 ± 0.1	1.1 ± 0.1	1.1 ± 0.1	1.1 ± 0.1
Kidney cortex	0.14 ± 0.03	22.2 ± 3.8	1.9 ± 0.1	1.9 ± 0.05	1.9 ± 0.1	1.9 ± 0.1
Kidney medulla	0.35 ± 0.07	22.2 ± 7.7	1.3 ± 0.1	1.5 ± 0.1	1.4 ± 0.1	1.5 ± 0.2
Spleen	0.14 ± 0.05	19.6 ± 4.2	0.9 ± 0.1	0.9 ± 0.1	0.9 ± 0.1	0.9 ± 0.1

¹Note: Data are means ± standard deviations.

^aData is in units of μm²/ms.

^bADC calculated with b_min = 270 s/mm² and b_max = 800 s/mm². For ADC₃ and ADC_R additional middle b-value = 400 s/mm² was used.

Figure 1 presents ADC maps calculated with the ADC₂ estimator using b_min of 0,100,200 s/mm² and b_max = 800 s/mm² along with their signal decay curves. As the b_min increases, the discrepancy between the ADC model and the slow-diffusion component of the signal decay decreases.

Figure 1.

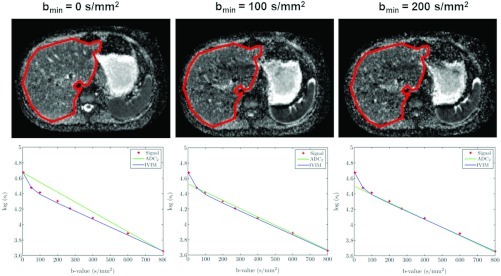
Representative ADC maps (first row) and liver (encircled) signal-decay plots (second row) organized according to the minimal b-value used to calculate the ADC. The ADC maps were calculated using the ADC₂ estimator with fixed b_max = 800 s/mm² and varying b_min. The discrepancy between the ADC₂ and the slow-diffusion component of the IVIM model (ADC_IVIM) decreases as the b_min increases.

Simulation experiments

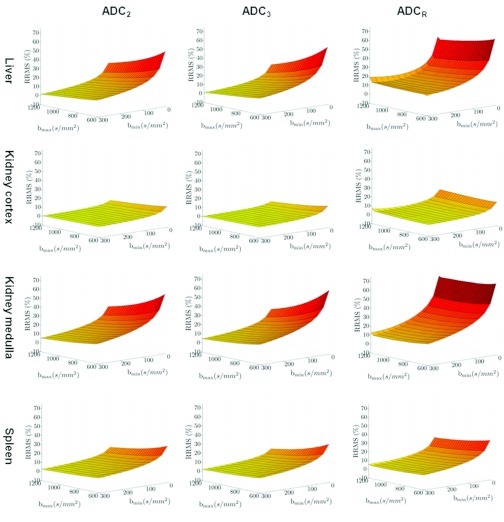
Figure 2 presents the RRMS surfaces as a function of b_min and b_max for each organ and estimator as calculated from the simulated DW-MRI data. The RRMS between ADC_IVIM and ADC₂, ADC₃, and ADC_R decreases as b_min increases. The effect of increasing the b_max also improves the RRMS. However, b_min has relatively greater influence. As hypothesized, the RRMS between ADC_IVIM and ADC₂, ADC₃, and ADC_R is greater in high perfusivity organs (i.e., the liver and the medulla of the kidney) than in low perfusivity organs (i.e., the cortex of the kidney and the spleen).

Figure 2.

The relative root mean squared error surface between the ADC estimates from the simulated DW-MRI data and the reference standard ADC_IVIM as a function of the b_min and b_max. The surfaces are organized according to the organ (rows) and the ADC estimator (columns).

Table 2 summarizes sets of b-values (in pairs and triplets) that minimize the RRMS between the reference standard ADC_IVIM and the ADC values. These b-value sets were calculated using the three estimators being evaluated for each organ along with their RRMS value. The minimal RRMS obtained using the ADC₃ estimator with b_min = 300 s/mm² and b_max = 1200 s/mm². The ADC_R estimator has the greatest discrepancy between the reference standard ADC_IVIM and the estimated ADC values.

Table 2.

Recommended pairs and triplets of b-values for each organ and ADC estimation method.

	ADC2		ADC3		ADCR
	b-values	RRMS %	b-values	RRMS %	b-values	RRMS %
Liver	300,1200	1.8	300,400,1200	1.5	300,400,1175	12.2
Kidney cortex	300,1200	0.6	300,400,1200	0.6	300,400,600	2.66
Kidney medulla	300,1200	5.4	300,400,1200	4.8	300,400,1075	10
Spleen	300,1175	2.6	300,400,1175	2.3	300,400,1175	4.7

To assess the contribution of the perfusion compartment in the DW-MRI signal decay to the inaccurate estimation of the ADC; we evaluated the correlation between the f values for each organ and patient, and the minimal RRMS obtained by each ADC estimator. Table 3 shows that for all estimators, the RRMS strongly correlates with the f values.

Table 3.

Correlation analysis between the fast-diffusion fraction (f) and the optimal RRMS obtained by the ADC estimators.

	r	P
ADC2	0.79	0.002
ADC3	0.78	0.003
ADCR	0.83	>0.001

In vivo experiments

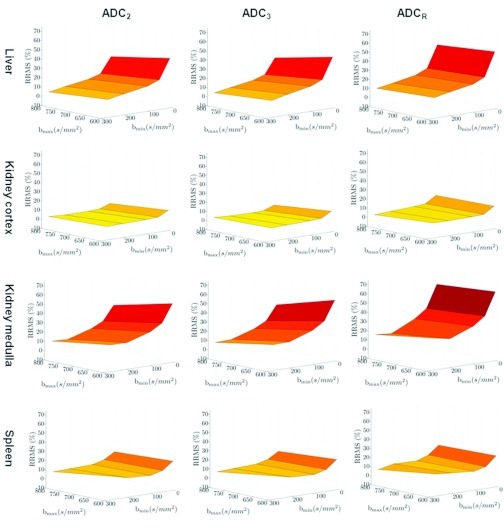
Figure 3 presents the RRMS surfaces as a function of b_min and b_max for each organ and estimator as calculated from the in vivo DW-MRI data. The RRMS between ADC_IVIM and ADC₂, ADC₃, and ADC_R decreases as b_min increases. The effect of increasing the b_max also improves the RRMS. However, b_min has relatively greater influence. As also seen in the simulation results, the RRMS between ADC_IVIM and ADC₂, ADC₃, and ADC_R is greater in high perfusivity organs (i.e., the liver and the medulla of the kidney) than in low perfusivity organs (i.e., the cortex of the kidney and the spleen).

Figure 3.

The relative root mean squared error surface between the ADC estimates from the in vivo DW-MRI data and the reference standard ADC_IVIM as a function of the b_min and b_max. The surfaces are organized according to the organ (rows) and the ADC estimator (columns).

Table 4 shows the sets of b-values (pairs and triplets) that minimize the RRMS between the reference standard ADC_IVIM and the ADC values calculated with the three estimators being evaluated for each organ along with their RRMS value. The minimal RRMS obtained using the ADC₃ estimator with b_min = 270 s/mm² and b_max = 800 s/mm².

Table 4.

Recommended pairs and triplets of b-values for each organ and ADC estimation method based on the in vivo data.

	ADC2		ADC3		ADCR
	b-values	RRMS %	b-values	RRMS %	b-values	RRMS %
Liver	270,800	3.5	270,400,800	3.1	270,400,800	9.1
Kidney cortex	200,800	1	100,400,800	1	270,400,800	1.8
Kidney medulla	200,800	8.6	270,400,800	6.8	200,400,800	13.4
Spleen	270,800	6.7	270,400,800	6.1	270,400,800	5.6

For all organs, the ADC₃ calculated with b_min = 270 s/mm² and b_max = 800 s/mm² provides a relatively accurate (i.e., RRMS error < 7%) estimation of the ADC.

DISCUSSION

Our study demonstrates the effect of the perfusion component in the DW-MRI signal decay on ADC measurements from short-duration DW-MRI acquisitions. While previous studies show the effect of the minimal b-value used for monoexponential ADC calculations due to the inclusion of perfusion-related signal decay;^{19, 31} the rigorous optimization of the b-values used in short-duration DW-MRI with available ADC estimators has not been previously explored.

Our simulation results suggest that perfusion-insensitive ADC measurements can be obtained by using short-duration DW-MRI with b_min = 300 s/mm² and b_max = 1200 s/mm². However, increasing the b_max to 1200 s/mm² may both reduce the signal-to-noise ratio in the DW-MRI image and create greater distortion because of the larger TE required. Our in vivo experiments show that by combining b_min = 270 s/mm² and b_max = 800 s/mm² we can obtain adequate perfusion-insensitive ADC measurements with short-duration DW-MRI without increasing the b_max beyond optimal levels. Our

findings also suggest that increases in b_min have a greater impact on the accuracy of ADC estimation than increases in b_max do. Moreover, our study shows a strong correlation between the error in perfusion-insensitive ADC estimation and the actual contribution of the fast-diffusion compartment to the DW-MRI signal decay. By comparing the errors in ADC estimations to the existing estimation methods, we were able to show that ADC_R (Ref. ²⁵) is more sensitive to perfusion effects than are ADC₂ (Refs. ^{1, 32}) and ADC₃ (Ref. ²⁵)_, respectively.

Our findings are of particular interest for detecting abdominal pathology in applications where a specific patient's ADC is compared to normative ADC values. Further, our data will aid in calibrating ADC estimates for assessing response-to-therapy, especially where ADC calculations have been performed in clinical practice using different ranges of b-values.

Our study had two significant limitations: First, to keep the imaging variables as constant and homogenous as possible, we performed all imaging experiments on the same 1.5 T system from a single vendor. This ideal scenario may not reflect the actual effect of the choice of b-values on DW-MRI data acquired with various field strengths or with systems from different vendors. Second, although our simulation experiments used very large and densely sampled ranges of b-values, we were forced, in part because of the in vivo nature of our second experiment, and in part because of scanning time limitations, to use a fixed, small set of b-values rather than exhaustively perform ADC calculations with all possible choices of b-values.

In conclusion, we have numerically identified the appropriate range of b-values that should be used in monoexponential ADC estimations relative to existing ADC estimation methods. By comparing monoexponential ADC estimates to perfusion-insensitive reference-standard ADC_IVIM for multiple organs, we have shown the feasibility of obtaining relatively accurate perfusion-insensitive ADC measurements using the monoexponential model with a fixed range of b-values for multiple organs using short-duration DW-MRI acquisition. In addition, we have identified the extent of errors in estimating ADC for each organ and likewise, have identified the best method for estimating a given choice of b-values.