Pair diffusion, hydrodynamic interactions, and available volume in dense fluids

Abstract

We calculate the pair diffusion coefficient D(r) as a function of the distance r between two hard sphere particles in a dense monodisperse fluid. The distance-dependent pair diffusion coefficient describes the hydrodynamic interactions between particles in a fluid that are central to theories of polymer and colloid dynamics. We determine D(r) from the propagators (Green's functions) of particle pairs obtained from molecular dynamics simulations. At distances exceeding ∼3 molecular diameters, the calculated pair diffusion coefficients are in excellent agreement with predictions from exact macroscopic hydrodynamic theory for large Brownian particles suspended in a solvent bath, as well as the Oseen approximation. However, the asymptotic 1/r distance dependence of D(r) associated with hydrodynamic effects emerges only after the pair distance dynamics has been followed for relatively long times, indicating non-negligible memory effects in the pair diffusion at short times. Deviations of the calculated D(r) from the hydrodynamic models at short distances r reflect the underlying many-body fluid structure, and are found to be correlated to differences in the local available volume. The procedure used here to determine the pair diffusion coefficients can also be used for single-particle diffusion in confinement with spherical symmetry.

INTRODUCTION

Pair diffusion features prominently in theories of reaction-diffusion dynamics¹ describing processes where reactant encounters are required, such as ligand binding and aggregation or fluorescence quenching. The hydrodynamic interactions quantified by the distance-dependent diffusion coefficient are also central to the theory and simulation of polymer dynamics, including protein folding simulations in implicit solvent, the hydrodynamic coupling in dense colloidal suspensions, and the function of nanomachines and bacterial flagella.^{2, 3} Pair diffusion therefore has attracted considerable attention from theoretical and simulation communities^{4, 5, 6, 7, 8, 9, 10, 11} in reflection of its fundamental and practical relevance, and as a means to test kinetic theory predictions. The studies of Haan,⁴ Posch, Vesely, and Steele,⁵ and Balucani et al.⁶ constitute early attempts to resolve at least average aspects of the position dependence of D(r) by simulation. Formidable challenges in both theory and simulations^{12, 13, 14, 15} have resulted in often contradictory results for this fundamental quantity.

Theoretically, the pair diffusion coefficient D(r) (with r the distance between two particles) has been attacked from two opposite directions, building up from kinetic theory¹² or projecting down from macroscopic hydrodynamics.^{2, 16} For D(r), kinetic theory had limited success at high fluid packing densities, largely because of the complexity of the molecular motions in dense fluids resulting from their many-body character. At the other extreme, details of the molecular structure of the solvent are ignored in estimates of the pair friction derived from macroscopic hydrodynamics, for instance, by using the Oseen or Rotne-Prager tensors.^{2, 16} Nevertheless, this approach has proved useful in studies of the dynamics of large and sufficiently distant pairs of colloidal particles in a solvent,¹⁷ where macroscopic hydrodynamics is expected to apply; but it is not immediately applicable when solute and solvent particles are of comparable size, for instance, in (aqueous) solutions of (bio)polymers.

Here, we determine the pair diffusion coefficient directly from the simulated many-body dynamics in a dense fluid. We focus on particles of the same size as the solvent molecules. This small-solute regime is of particular relevance because, on the one hand, it allows us to quantify hydrodynamic interactions relevant for molecular motions, including the dynamics of (bio)polymers in solution, and, on the other hand, it is far outside the regime where macroscopic hydrodynamics should be expected to apply.

The paper is outlined as follows. In Sec. 1, we describe the methodological details, including the theory to calculate the pair diffusion tensor, the algorithm used to determine the required Green's functions from simulation data, the simulation parameters, and the validation procedure. We validate our method by computing the pair diffusion coefficient for two spherical particles moving according to Brownian dynamics. In Sec. 2, we first present a comparison of Green's functions obtained from simulations against those predicted from our diffusion model, finding excellent agreement over 8 orders of magnitude. Then we examine the pair diffusion coefficients as a function of distance between two particles for several fluid packing fractions, and compare the simulation results to the predictions of macroscopic hydrodynamic theories. Finally, we show that the position-dependent pair diffusion coefficient is correlated to the local available volume. In the Appendix, we discuss the calculation of the angular pair diffusion coefficient.

METHODS

Theory

In the following, we present the theory to calculate the position-dependent pair diffusion tensor from simulation trajectory data. The diffusion tensor D of the vector r between two given particles in an isotropic and homogeneous fluid has spherical symmetry

$$\begin{array}{ccc}\hfill \mathbf{D}\left(\mathbf{r}\right)& =& D_{\perp }\left(r\right){\mathbf{e}}_r{\mathbf{e}}_r+D_{\parallel }\left(r\right)({\mathbf{e}}_{\theta }{\mathbf{e}}_{\theta }+{\mathbf{e}}_{\phi }{\mathbf{e}}_{\phi }),\hfill \end{array}$$ (1)

where r = |r| is the length of the pair vector; D_⊥(r) and D_∥(r) are the scalar diffusion coefficients in the radial and tangential directions, respectively; and e_r, e_θ, and e_φ are the orthonormal unit vectors of the spherical polar coordinate system, with e_r pointing in the radial direction, and e_θ and e_φ being tangential to longitudes and latitudes, respectively. The Smoluchowski (or Fokker-Planck) equation describing the diffusion of the pair vector then takes on the following form:

$$\begin{array}{ccc}\hfill {\partial }_{t}p& =& \mathrm{div}\left[\mathbf{D}\left(\mathbf{r}\right)e^{-\beta F}\mathrm{grad}\left(e^{\beta F}p\right)\right],\hfill \end{array}$$ (2)

where the Green's function p(r, θ, t|r ^′, θ₀ = 0, t = 0)sin θdθr²dr is the probability density for a pair vector starting at a distance r ^′ and azimuthal angle θ₀ = 0, without loss of generality because of the isotropic space (making the φ distribution uniform); F(r) = −k_BT ln g(r) is the distance-dependent free energy surface (or potential of mean force), with g(r) the pair correlation function of the two particles in the fluid; β = (k_BT)⁻¹ is the inverse temperature; ∂_t is the partial derivative with respect to time; and “div” and “grad” are the divergence and gradient operators in spherical polar coordinates, respectively.

In the following, we will use x = cos θ instead of θ and absorb the Jacobian r² of the spherical polar coordinates into the probability density. The diffusion equation 2 for the Green's function P(r, x, t|r ^′, 0) = r²p(r, cos ⁻¹(x), t|r ^′, 0, 0) in terms of these variables then becomes

$$\begin{array}{ccc}\hfill {\partial }_{t}P& =& {\partial }_r\left[D_{\perp }\left(r\right)(\beta V^{\prime }+{\partial }_r)P\right]\hfill \\ & & +\frac{D_{\parallel }\left(r\right)}{r^2}{\partial }_x\left[(1-x^2){\partial }_{x}P\right],\hfill \end{array}$$ (3)

where V(r) = F(r) − 2k_BTln r and V′ = dV(r)/dr. By integrating over x = cos θ, we obtain a diffusion equation for the Green's function in the radial direction alone, with the second term on the right hand side vanishing

$$\begin{array}{c}\hfill {\partial }_{t}G={\partial }_r\left[D_{\perp }\left(r\right)(\beta V^{\prime }G+{\partial }_{r}G)\right],\end{array}$$ (4)

where $G(r,t|r^{\prime },0)={\int }_{-1}^{1}dxP(r,x,t|r^{\prime },0)$ is the probability for the pair distance to be in (r, r + dr) at time t, starting from r ^′ at time 0. As a consequence, we can treat radial diffusion separately using standard one-dimensional diffusion, irrespective of the angular motion. In the Appendix, we outline an extension of the theory to the orientational diffusion of the pair distance vector.

Algorithm to determine pair diffusion coefficient

Here, we focus on the calculation of the position-dependence of the pair diffusion coefficient D(r) ≡ D_⊥(r), where we have dropped the subscript for notational simplicity. In our calculations of D(r), we face the dual challenges that it depends on the particle distance r, and that the pair dynamics becomes diffusive only at times at which the influence of the underlying free energy surface is already felt. We estimate this hydrodynamic time scale, t_H = σ²/ν, to be ∼0.7 in reduced units of time (see below) from the hard sphere (HS) kinematic viscosity¹⁸ ν at the lowest packing fraction (ϕ = 0.325) studied in this paper, with σ the hard sphere diameter. In our calculations, we use lag times that are larger than this hydrodynamic time scale. To disentangle the diffusive spread of the pair distance distribution from the drift of the mean position as a result of the underlying free energy surface, we use the propagator (or Green's function) G(r, t|r ^′, 0)dr.

In the following we outline the essence of the algorithm, with additional details presented in Ref. 19. In constructing a diffusion model, we assume that G satisfies the Smoluchowski diffusion equation 4, where the term within the brackets is the negative of the radial probability flux. A spatial discretization of the Smoluchowski equation 4,²⁰ results in a master equation that describes the pair dynamics as transitions between neighboring intervals along r. The particle-pair trajectories in the simulations are discretized by assigning pair distances into corresponding bins i along r, and then counting the numbers N_ji that a particular pair distance is in bin i at some time τ during the simulation, and in bin j later at time τ + Δt, irrespective of what happens at intermediate times, with Δt the lag time. For our long equilibrium trajectories, N_ji is symmetrized, N_ij = N_ji, consistent with microscopic time reversibility.

We then find pair diffusion coefficients D(r) and free energies F(r) that are consistent with the observed transitions between bins. For the discretized diffusion model with given D(r_i) and F(r_i), the path action (or likelihood) L can be be written as a product of Green's functions that are expressed in terms of a matrix exponential.¹⁹ To optimize the action and find the diffusion model most consistent with the observed N_ji, we infer D(r_i) and F(r_i) using a Bayesian approach,¹⁹ with uniform priors in ln D(r_i) and F(r_i) ensuring scale invariance in time and space.

In free diffusion, one typically fits a + 6D₀t (or, equivalently, 6D₀(t + τ)) to the mean-square displacement, with the constant a (or the time shift τ = a/6D₀) accounting for initial fast molecular motions. Here, we employ a similar procedure by optimizing also the time origin τ for transition counts N_ij collected at several different lag times Δt, 2Δt, …, kΔt = t, where t defines the “observation time.”

To validate the procedure, we first run Brownian dynamics simulations for two spherical particles of unit diameter freely diffusing with diffusion coefficient D₀ = 0.05 in a cubic box of length L = 12.5 under periodic boundary conditions and with reflecting boundary conditions at particle contact. The Brownian dynamics trajectories of the pair distance vector with diffusion coefficient 2D₀ are generated with a forward-Euler integrator, r(t + δt) = r(t) + (4D₀δt)^1/2g_t, with g_t uncorrelated Gaussian random numbers of zero mean and unit variance. If the particles overlap after the forward step, |r| < σ, we reflect the end point at the plane touching the sphere |r| = σ at the intersection with the line connecting r(t + δt) and r(t). This approximate correction would be exact for diffusion near a reflecting plane. By construction, in this case D(r) = 2D₀, which is indeed recovered by the procedure for distances r < L/2 (Fig. 1), nearly independent of grid size Δr. However, for r > L/2 and long lag times, the periodic boundary conditions cause artifacts because in the corners of the cubic simulation box the pair dynamics projected onto the minimum image distance depends not only on the length of the pair vector but also on its direction, counter to our assumption of a 1D diffusion equation.

Figure 1.

Pair diffusion coefficient D(r) for two freely diffusing Brownian particles of diameter 1 with periodic boundary conditions. Results for different grid sizes Δr = 0.004 (plus), 0.032 (cross), 0.024 (star), 0.016 (square) are compared to the exact value 2D₀ = 0.1 (horizontal line). The vertical solid line marks the contact distance r = 1. To assess artifacts from periodic boundary conditions, the vertical dashed lines mark distances r = L/2, $L/\sqrt{2}$, and $\sqrt{3}L/2$, where centered spheres touch the faces, edges, and corners of the cubic simulation box, respectively.

SIMULATIONS

To calculate D(r) for a particle pair in a dense fluid, we perform molecular dynamics (MD) simulations of HS fluids. In these simulations, particles follow linear trajectories between collisions. In a collision, the velocities of colliding particles are changed to conserve energy and momentum.²¹ To simplify the notation, dimensionless quantities will be used, obtained by appropriate combinations of a characteristic length (HS particle diameter σ) and time scale ($\sigma \sqrt{m\beta }$, where m is the particle mass). The packing fraction ϕ = πρ/6 is defined in terms of the particle density ρ. To construct the Green's functions, we performed MD simulations with N = 2000 identical HS particles. Periodic boundary conditions were applied in all directions. The average self-diffusivity D₀ was obtained by fitting the long-time (t ≫ 1) behavior of the average mean-squared displacements Δr² of the particles to the Einstein relation ⟨Δr²⟩ = 6D₀t. To minimize the system-size dependence,²² trajectories from simulations with N = 10000 particles were used to determine D₀, with remaining finite-size corrections of ≈1%.²³

RESULTS

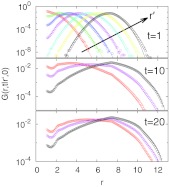
To test the applicability of the diffusion model, we compare its prediction for the dynamics of the pair distance to actual simulation data collected over a range of time scales. Figure 2 shows that diffusion quantitatively captures the pair dynamics in the fluid. The Green's functions G(r, t|r ^′, 0) from the diffusion model and the results of the MD simulation data are found to agree over 8 orders of magnitude. Even at the shortest observation time t = 1, we find that the Green's functions are only approximately Gaussian with position-dependent widths. The additional structure, particularly at contact (r = 1), would interfere with extracting accurate D(r) curves from the variance in the particle distances. At longer times, t = 10 and 20, the propagators deviate even more from the Gaussian form expected for free diffusion on a flat surface.

Figure 2.

Green's functions G(r, t|r ^′, 0) from simulations (symbols) and diffusion model (lines). G(r, t|r ^′, 0) is shown as a function of the pair distance r at packing fraction ϕ = 0.325. We use an observation time of t = 20 to obtain diffusion model parameters, combining results for lag times Δt = 1, 2, …, 20. The arrow in the top panel reflects increasing r ^′ = 1, 2, …, 7. Same color scheme is used for middle and bottom panels.

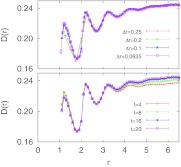
In Figure 3, we explore the effects of the spatial grid size Δr and the observation time t on the calculated pair diffusion coefficient. We find that for Δr ⩽ 0.1, grid size effects are negligible. Figure 3 (bottom) shows that the effect of changing the observation time t is negligible only for shorter distances r < 3. In contrast, for longer distances D(r) is almost flat at a short observation time t = 4 and does not show the asymptotic 1/r dependence expected from macroscopic hydrodynamic theory. However, the expected 1/r dependence is recovered for longer times t. This result implies that the hydrodynamic coupling at large distances is not instantaneous, such that a more accurate diffusion model would require the inclusion of memory effects in a frequency and position-dependent diffusion coefficient.²⁴ For t ⩾ 16, the predictions are essentially independent of t. In all following calculations, we thus use Δr = 0.1 and t = 20. We also note that the pair correlation function g(r) inferred from the Bayesian approach agrees very well with the direct estimate of g(r) (data not shown).

Figure 3.

Dependence of D(r) on diffusion model parameters. Pair diffusion coefficient D(r) versus distance r for a hard sphere fluid at packing fraction ϕ = 0.35 obtained for different (top) grid sizes Δr (with fixed observation time t = 20) and (bottom) observation times t (with fixed grid size Δr = 0.1). The lag time is Δt = 1 consistently.

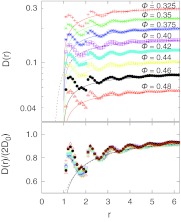
Having validated the procedure and diffusion model, we now examine the distance-dependent pair diffusion coefficients D(r) for different packing fractions ϕ. Figure 4 (top panel) shows D(r) for the HS fluid over a packing fraction range ϕ = 0.325 − 0.48 (symbols). Also shown are the predictions for D(r) from hydrodynamic theory for two spherical particles with slip boundary conditions,^{25, 26} as well as the widely used Oseen tensor correction² (for ϕ = 0.4; dashed line), which for the pair diffusion coefficient is D(r) = 2D₀ − k_BT/(2πηr) where η is the solvent shear viscosity, taken from Ref. 18. We find that both the exact hydrodynamic theory and the Oseen approximation (and similarly the Rotne-Prager tensor;² not shown) are remarkably accurate and quantitatively reproduce the large-r behavior. However, hydrodynamic predictions only qualitatively reproduce the observed decrease in D(r) near contact (r = 1) and lack any structure due to molecular correlations in the first- and second-shell around a particle.

Figure 4.

Pair diffusion for a hard-sphere fluid. (Top) Calculated pair diffusion coefficient D(r) versus distance r with increasing packing fraction ϕ (symbols). Lines are the predictions of hydrodynamic theory (see text). (Bottom) Normalized pair diffusion coefficient D(r)/2D₀, where D₀ is the self-diffusivity for a given ϕ. Symbols are our calculations, the thick line is the exact hydrodynamic theory,²⁵, ²⁶ and the dashed line is the Oseen approximation.

To characterize the effects of the molecular packing structure on the pair dynamics, we plot in Fig. 4 (bottom panel) the normalized pair diffusion coefficient D(r)/2D₀ for different packing fractions ϕ. As expected from macroscopic hydrodynamics, at large distances r the D(r)/2D₀ data collapse onto a single curve that is well represented by the hydrodynamic theory. Two important observations are: (i) D(r)/2D₀ is always less than 1, with pair diffusion slowed down by “hydrodynamic interactions.” (ii) D(r) rises sharply just outside distances of 1 and 2 particle diameters. A consequence of the sharp increase in D(r) at r = 2 is that at short times, particle pairs initially at a distance r ≈ 2 are more likely to separate farther than would be expected based on the gradient of the free energy F(r) alone.

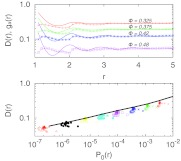
To gain further insight into the observed structure in D(r) and its relation to the static structure of the fluid, we plot in Figure 5 (top panel) both D(r) and the pair correlation function g(r). We find that there is some correlation between the structure in D(r) and g(r) except near the contact distance at r = 1 where these quantities are actually anti-correlated. Similar behavior was observed for a HS fluid confined between hard walls where the local density was found to be strongly correlated with the local diffusion coefficient except near the walls.²⁷ This behavior was found to be related to the physics of layer formation, with the available volume, as probed by the local test-particle insertion probability P₀, being largest in the locally dense regions of space.²⁸ A similar argument should hold in our case of a bulk HS fluid in which purely entropic excluded volume forces give rise to a structured g(r) profile to maximize the system entropy. The local insertion probability is given by P₀(r) = ρ(r)/ξ = ρg(r)/ξ, where the activity ξ = exp (βμ)/λ³ is spatially invariant for an equilibrium fluid, with μ the chemical potential and λ the thermal wavelength.

Figure 5.

Relation between fluid structure and dynamics. (Top) Pair diffusion coefficient D(r) (symbols connected by lines) and scaled pair correlation function g_a(r) = g(r)/a (lines) versus distance r where a is an arbitrary scaling factor used to match D(r) and g_a(r) at large r. (Bottom) D(r) as a function of the local fractional available volume P₀(r) (symbols; increasing packing fractions from right to left). The line is 2D₀ versus P₀ averaged over the entire system.

To test if D(r) is indeed related to P₀(r), we calculate ξ for the different packing fractions by utilizing grand canonical transition-matrix Monte Carlo simulations.²⁹ Figure 5 (bottom panel) shows D(r) versus P₀(r) for different ϕ. We find that the D(r) data approximately collapse onto a curve similar to the average bulk relationship (2D₀ versus P₀) that ignores any r dependence. Therefore, at least as a rough approximation, the local available volume can describe the pair diffusion in this case.

CONCLUDING REMARKS

The results of this paper shed light on the microscopic origins of the distance dependence of hydrodynamic interactions, in particular the role of particle packing and many-body motions consistent with Morrone, Li, and Berne.¹¹ Calculations of D(r) help establish a range of validity for the assumption of macroscopic hydrodynamics in the modeling of processes ranging from polymer dynamics to nanomachines, colloidal dynamics, and bacterial swimming. In practical applications, such as the calculation of diffusional encounter rates, the significant deviations between the calculated pair diffusion coefficients D(r) and the ideal (and widely used) assumption of $D\left(r\right)=2D_0=\mathit{const}.$ can result in substantial errors, with D(r) < 2D₀ consistently. At the least one should use a hydrodynamic theory, with both the exact theory and the Oseen tensor giving remarkably accurate results for hydrodynamic interactions at larger distances, and rough approximations in the regime dominated by molecular packing near contact.

APPENDIX: ANGULAR DIFFUSION COEFFICIENT

To treat the angular diffusion of pair distance vectors (or other vectors in an isotropic space), we notice that the second term on the right hand side of Eq. 3 corresponds to the angular momentum operator in quantum mechanics. We thus make the ansatz $P(r,x,t|r^{\prime },0)={\sum }_{l=0}^{\infty }{C}_l{P}_l\left(x\right)q_l(r,t|r^{\prime },0)$, where the P_l(x) are the Legendre polynomials of order l, and the coefficients C_l do not depend on t and r. With this ansatz, we obtain uncoupled one-dimensional evolution equations for each of the q_l (with l = 0, 1, …)

$${\partial }_t{q}_l={\partial }_r\left[D_{\perp }\left(r\right)(\beta V^{\prime }{q}_l+{\partial }_r{q}_l)\right]-\frac{D_{\parallel }\left(r\right)}{r^2}l(l+1)q_l.$$ (A1)

For l = 0, this expression is identical to Eq. 4; for l > 0, these are sink (or birth-death) equations for the q_l, with sink terms whose strength increases quadratically with l, and with D_∥(r)/r². That is, at long times only the distribution uniform in x survives (with P₀(x) = 1).

Expressed in terms of Dirac δ-functions, the initial condition for the Green's function is P(r, x, t = 0|r ^′, 0) = δ(r − r ^′)δ(1 − x) (where we chose the coordinate system such that the polar axis points in the direction of the pair distance vector at time zero), with normalization ${\int }_{-1}^{1}dx\int drP(r,x,t|r^{\prime },0)=1$. By using the orthogonality relations of the Legendre polynomials, ${\int }_{-1}^{1}dx{P}_l\left(x\right)P_m\left(x\right)=2{\delta }_{lm}/(2l+1)$ with δ_lm the Kronecker-δ, we obtain

$$\begin{array}{ccc}\hfill P(x,r,t|r^{\prime },0)& =& \sum _{l=0}^{\infty }\frac{2l+1}{2}{P}_l\left(x\right)q_l(r,t|r^{\prime },0),\hfill \end{array}$$ (A2)

where the q_l satisfy Eq. A1 with initial conditions q_l(r, 0|r ^′, 0) = δ(r − r ^′).

For the sake of completeness, we also sketch an algorithm to obtain the distance-dependent radial and angular diffusion coefficients D_⊥(r) and D_∥(r) from simulation data (or, equivalently, from experimental data, such as those obtained in colloidal-particle tracking experiments³⁰).

• 1.Use counts of transitions N_ji from bins i to j in the radial direction only (irrespective of the angular motion) as input in the algorithm¹⁹ described above to calculate the one-dimensional position-dependent diffusion coefficients D_⊥(r), and the potential of mean force V(r).
• 2.
  Determine counts N_{jα, i} for transitions from bin i in the radial direction to bin j, α in a two-dimensional histogram. Radial bins are indexed by j, and angular bins by α according to the cosine of the azimuthal angle,

  $$\begin{array}{ccc}\hfill x\left(t\right)& =& \cos \theta \left(t\right)=\frac{\mathbf{r}\left(t\right)·\mathbf{r}\left(0\right)}{\left|\mathbf{r}\right(t)\parallel \mathbf{r}(0\left)\right|}\hfill \end{array}$$ (A3)

  (with θ(0) = 0 and x(0) = 1 by definition of the coordinate system).
• 3.With D_⊥(r) and V(r) already determined in the first step, the Green's function Eq. A2 can be calculated for a given estimate of D_∥(r) from a spatially discretized version²⁰ of the sink equations, Eq. A1. With this Green's function, one can again use a Bayesian inference procedure (or maximum-likelihood method) to estimate the D_∥(r) (on lattice points halfway between the bin centers) that is most consistent with the observed transition counts N_{jα, i}.

Note that the infinite sum over l in Eq. A2 has to be truncated in practical calculations. Note further that the same algorithm can also be used to determine the diffusion coefficients of a single particle in confinement with spherical symmetry.