Abstract
A heterodimer consisting of two or more different kinds of proteins can display an enormous number of distinct molecular architectures. The conformational entropy is an essential ingredient in the Helmholtz free energy and, consequently, these heterodimers can have a very complex phase structure. Here, it is proposed that there is a state of proteins, in which the different components of a heterodimer exist in different phases. For this purpose, the structures in the protein data bank (PDB) have been analyzed, with radius of gyration as the order parameter. Two major classes of heterodimers with their protein components coexisting in different phases have been identified. An example is the PDB structure 3DXC. This is a transcriptionally active dimer. One of the components is an isoform of the intra-cellular domain of the Alzheimer-disease related amyloid precursor protein (AICD), and the other is a nuclear multidomain adaptor protein in the Fe65 family. It is concluded from the radius of gyration that neither of the two components in this dimer is in its own collapsed phase, corresponding to a biologically active protein. The UNRES energy function has been utilized to confirm that, if the two components are separated from each other, each of them collapses. The results presented in this work show that heterodimers whose protein components coexist in different phases, can have intriguing physical properties with potentially important biological consequences.
INTRODUCTION
Protein oligomers constitute the majority of functional units in living cells as, e.g., the mitochondrial complex III (Ref. 1) or complex I.2 The mutual interactions usually influence the structure of each of the components substantially. Natively-unfolded proteins,3 which attain a defined structure only when bound to a protein counterpart,4 are an extreme example. This process resembles the transition from a liquid to a solid phase. Furthermore, protein aggregation into large β-sheet fibrils can cause conformational diseases termed amyloidoses.5, 6 The carcinogenic outcome of aberrant expression of some proteins is also a result of a change of the pattern of the interactions with their partner proteins.7
The problem of protein oligomerization and aggregation has received great attention,8, 9, 10 starting from the very beginning of research on protein structure, and there now exists an enormous body of experimental11, 12, 13, 14 and theoretical15, 16, 17, 18 research on the subject. Different oligomers/aggregates are mainly treated from the point of view of the type of fold8, 9 or specific interactions that stabilize them,19, 20 rather than in terms of the identification of their universal, more quantitative features.
On the other hand, the thermodynamic and spectroscopic data of proteins in solution are often interpreted in terms of the two-state model, according to which the ensemble of protein molecules is a superposition of the folded and the unfolded phase.21 Thus, a protein in solution can be regarded as two coexistent phases, a concept quite familiar in polymer research. Protein heterodimers can thus be treated by the conventional mean-field Flory-Huggins theory,22, 23, 24, 25 which enables one to compute the fraction of each monomer in the collapsed (folded) phase. The conventional Flory-Huggins theory,22, 23 however, assumes that individual protein chains can be modeled in terms of random walks. But biologically active proteins are mainly in a collapsed phase. Moreover, the description in terms of volume fraction of the folded and the unfolded conformation cannot account for the difference in the stability of different protein segments. Thus, a mean-field approach22, 23 is not appropriate to describe individual proteins or protein oligomers at a detailed level.
The phase structure of a system in thermal equilibrium is determined by the minima of the thermodynamic Helmholtz free energy F, which is a sum of the internal energy U and the entropy S [Eq. 1]. For a protein, this general principle has been formulated by Anfinsen26 as the thermodynamic hypothesis, according to which the native structure of a protein is the global minimum of its Helmholtz free energy under physiological conditions.
| (1) |
The entropy is a measure of conformational complexity. In general, an increase in the volume of the conformational space also leads to an increased phase complexity.24, 27 Consequently, macromolecular complexes such as protein heterodimers should have a much richer phase structure than an ensemble of essentially structureless point-like molecules. Various factors can influence the volume of the available conformational space, such as protein architecture and the degree of polymerization. Even for a pair of two distinct proteins, the number of all possible conformations can be enormous.24, 27
In this work, the structures of protein heterodimers are analyzed in terms of coexisting polymer phases. Instead of a conventional description, based on the notions of collapsed or not collapsed states, a more refined analysis is performed. For this the dependence of the radius of gyration on chain length to distinguish different phases, which differ by chain compactness, is utilized as the order parameter. The statistics of oligomeric proteins in the protein data bank (PDB) (Ref. 28) is analyzed first and then, as a concrete example, focus is placed on the behavior of a dimer that originates from the transmembrane amyloid precursor protein (APP) by proteolytic cleavages.29, 30 The APP has several isoforms that can be present in many organs; however, its exact physiological function remains under debate.30, 31, 32 Full understanding of the proteolytic processing of APP is also lacking.30, 31, 32 But there appears to be two different pathways for proteolytic cleavage, a nonamyloidogenic, and an amyloidogenic one. The latter gives rise to the extracellular Aβ42 peptides that may be involved in Alzheimer's disease.30, 33 Both pathways also give rise to an isoform of the intracellular APP (AICD).34 In isolation, AICD is presumed to be an intrinsically unstructured protein.30, 31, 32 There are no structural data available in the protein data bank that could be used to elucidate its physical properties. But it can bind with the Fe65 family of nuclear multidomain adaptor proteins.30, 34, 35, 36, 37 Upon binding, AICD assumes a regular form that can be analyzed by x-ray crystallography. In the present article, the x-ray structure that is described in the PDB under the code 3DXC (Ref. 38) is treated. It is a complex of a 28-residue segment of AICD with Fe65, that has 130 residues. The closely related 3DXD and 3DXE complexes, also exist. These can be analyzed similarly and with similar conclusions. It is found that the 3DXC complex has very interesting physical properties that sets it apart from all but a very few protein complexes. This AICD/Fe65 complex is an example of an apparently previously unrecorded but seemingly systematic phenomenon in the context of protein research that is termed protein phase coexistence in this work: Like ice together with water, the two proteins in this complex are apparently in two different phases. An oligomer that displays this phenomenon of phase coexistence under physiological conditions is for sure an interesting object for future research. But since the AICD/Fe65 complex has the supplementary potential of being an important piece in the puzzle to understand Alzheimer's disease, there are many good reasons to investigate its physical properties.
This paper is organized as follows: In Subsection 2A, the use of the radius of gyration and its variation with the number of residues as a measure of compactness is reviewed. Subsections 2B, 2C, 2D develop the mathematical formalism to study the structure and dynamics of proteins: In Subsection 2B, it is explained how the Cα backbone can be described in terms of its virtual-bond and virtual-torsion angles. In Subsection 2C, the description of protein geometry in the collapsed phase in terms of a soliton solution of the discretized nonlinear Schrödinger equation (DNLS) is outlined. Finally, in Subsection 2D, the coarse-grained UNRES model39, 40, 41, 42 of polypeptide chains is described briefly. Use of this coarse-grained approach elongates the time scale by over three orders of magnitude with respect to all-atom simulations,43, 44 thus enabling us to observe significant conformational changes in comparatively short simulation time.
In Subsection 3A, oligomers in the PDB are analyzed. Two general classes of phase coexistent oligomers are identified. It is observed that the Alzheimer's disease related AICD/Fe65 dimer is an interesting example, with neither of the two component chains in the collapsed phase.
In Subsection 3B, the structure of AICD in the AICD/Fe65 dimer with PDB code 3DXC is analyzed on general grounds. It is shown that, despite being composed of two solitons of the DNLS equation, the AICD is in a linear rod-like phase. It is found that there are two natural positions for the first soliton, and it is suggested that this could lead to a genetic switch.
Finally, in Subsection 3C, Langevin dynamics simulations with the UNRES energy function39, 40, 41, 42 are used to confirm that, in isolation, both AICD and Fe65 of the 3DXC dimer collapse into the space-filling phase of biologically active proteins.
A brief overview of the results in Sec. 4 concludes the article.
METHODS
Radius of gyration as an order parameter
It has been known for a long time22, 23, 25 that a linear polymer chain such as a single-chain protein has a non-trivial phase structure that depends both on the chemical properties and on the temperature of the polymer-solvent system. In a good solvent environment, such as aqueous denaturating agents, the interactions between the polymer segments and the solvent molecules cause the polymer to expand and the polymer behaves like a self-avoiding random walk. In a poor solvent environment, such as water, the polymer-polymer self-interactions dominate, and the polymer collapses into a space-filling conformation. These two regimes are separated by the Θ-point, at which the polymer can be modeled by an ideal chain. Moreover, in the thermodynamical limit where the number N of amino-acid residues is very large, certain aspects of the phase structure become universal .45, 46, 47, 48 An example of a universal quantity is the compactness index ν. To define this quantity, the radius of gyration Rg (Refs. 22, 23, 24, 25) is introduced.
| (2) |
where ri are the coordinates of the atoms in the polymer. For a protein, for simplicity, may be restricted to run over the coordinates of only the backbone Cα atoms. The compactness index ν governs the large-N asymptotic form of Eq. 2. When the number N of amino-acid residues becomes very large, then49
| (3) |
where R0 is the form factor that characterizes the length scale (in ångstrøms) in the large-N limit, δ1, etc. are critical exponents, R1, etc. are the amplitudes; the terms with δ1, etc. and R1, etc., account for finite-size corrections. Besides the compactness index ν, the critical exponents δ1, etc., are universal quantities,49 but the amplitudes R0, R1, etc., are not universal.49
As a universal quantity, ν is independent of the detailed atomic structure. Different values of ν correspond to the different phases of the protein.22, 23, 24, 25, 27 The four mean-field values of ν are given by Eq. 422, 23, 24, 25, 27, 49, 50
| (4) |
Under physiological, i.e., poor solvent conditions, in which a single-chain protein collapses into the space-filling conformation,22, 23 the mean field exponent ν = 1/3. For an ordinary random-walk chain, the mean field value is ν = 1/2. This phase appears at the Θ-point22, 23 that separates the collapsed phase from the high-temperature self-avoiding random walk phase for which the Flory value ν = 3/5 is found. Finally, when ν = 1, the protein loses its inherently fractal structure and scales like a rigid rod.23, 51 Examples of polypeptide structures that can represent this phase are monotonic α-helices or polyproline II helices.
The mean-field values of the critical exponents ν, δ1, etc., in Eq. 3 are usually modified by fluctuations. For example, in the universality class of the self-avoiding random walk, the modified values are52, 53
| (5) |
A subsequent numerical Monte Carlo evaluation of the critical exponents of Eq. 5, gave very similar values,49
| (6) |
In the case of the collapsed phase where ν ≈ 1/3 the value of δ1 is not known to us. But from 5, 6 one can estimate that even in the case of a relatively short polypeptide chain, such as the 28-residue segment of AICD considered here, the finite-size correction to the radius of gyration can not be very large. With 6, one estimates that in the ν ≈ 1/3 phase when N = 28
| (7) |
Consequently, with , only the leading term needs to be retained, even for protein chains with not more than around 28 or so residues.
The pre-factor R0 and the finite-size correction coefficient R1 can, in principle, be computed for a protein. These factors contain all the effects of temperature and chemical microstructure, and all the atomic level details of the protein. Consequently, for a protein, relation, Eq. 3 becomes valuable only when the numerical value of R0 is either unique or can assume no more than a small number of clearly identifiable different values. It is found that this is indeed the case, i.e., for proteins, the values of R0 are very restricted, but different, for collapsed proteins and for proteins that are not in the collapsed phase. Moreover, it appears that, when N increases, the detailed amino acid structure of a protein becomes increasingly irrelevant in determining the value of the radius of gyration, i.e., for long protein chains, any inhomogeneity of the amino-acid sequence can be treated essentially as a finite size correction in Eq. 3.
In detailed studies of proteins, the radius of gyration has until now been utilized only sparsely.50, 54, 55, 56, 57 It appears to us that, commonly, the value of Rg has been viewed as nothing more than a rough measure, with a systematic change in its value indicating that protein collapse has taken place. In the present article, another point of view is presented. It is proposed that the seemingly quite small diversity in the values that R0 assumes for proteins, both in the collapsed and in the other available phases, suggests that Eq. 3 could assume a much wider rôle in protein research. The goal sought here is to scrutinize this potential usefulness of the radius of gyration as a quantitative order parameter. It is aimed to develop both ν and R0 here into practical tools to understand protein conformations and phase structure, not only for monomers but also for heterodimers.
Protein backbone geometry
We set the stage by explaining how protein geometry is described in terms of the Cα backbone. For this purpose, the positions ri of the backbone Cα atoms in Eq. 2 are utilized to introduce the unit tangent vectors
| (8) |
the unit binormal vectors
| (9) |
and the unit normal vectors
| (10) |
The orthogonal triplet () determines a frame at the positions of the backbone. The discrete virtual-bond angles and the discrete virtual-torsion angles are defined by Eqs. 11, 12, respectively.
| (11) |
| (12) |
with
| (13) |
A graphic definition of these angles, and all the other geometric quantities that are used in this paper, is given in Figure 1.
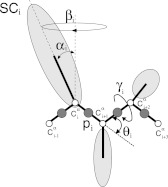
Figure 1.
Definitions of the variables of the UNRES model. The virtual-bond angle θi is determined by the three Cα carbons at sites i, i + 1, i + 2 and is defined as the angle between the virtual-bond vector and the virtual-bond vector [Eq. 11]. It should be noted that, for consistency with the notation of Sec. 2B, the angles θ used in this work are complements of the original angles θ, i.e., π − θ (see, e.g. Ref. 39). The Cα carbon atoms are represented by small open circles. The virtual-bond-dihedral angle γi it the angle between the two planes, determined by the Cα at sites (i, i + 1, i + 2) and (i + 1, i + 2, i + 3) [Eqs. 12, 13]. In addition, the UNRES energy function [Eqs. 32, 33, 34, 35] involves the following structure, shown in the Figure: The interaction sites are peptide-bond centers (p), and side-chain ellipsoids of different sizes (SC) attached to the corresponding α-carbons with different virtual-bond lengths bSC. The UNRES energy is also a function of the coordinates of the SC and p sites which are functions of (θ, γ, α, β) and also contains terms that depend explicitly on these angles.
Conversely, if the angles (θi, γi) are known, Eq. 14 can be used to construct the frame at position i + 1 iteratively from the frame at position i. Once all the frames are computed, the Cartesian coordinates of the entire Cα-trace can be calculated from Eq. 15.
| (14) |
| (15) |
where is the vector of the Cartesian coordinates of the kth Cα atom. With no loss of generality and can be set to point into the direction of the positive z-axis.
It should be noted that Eq. 15 does not involve the vectors and . Consequently, any linear combination of these two vectors can be selected in constructing the backbone. For this, the frame () is rotated by an angle Δi leaving intact,
| (16) |
where the tensor (T i)jk is defined by Eq. 17.
| (17) |
with
| (18) |
If the vectors n and b are combined into the complex vector
Equation 16 can be recast into Eq. 19.
| (19) |
A direct computation shows that the frame rotation of Eq. 16 induces the following transformations in Eq. 14,
| (20) |
| (21) |
In what follows, Eqs. 20, 21 are utilized to extend the fundamental range [0, π] of the virtual-bond angle θi into [−π, π] mod(2π), and the range of γi to [−π, π) mod(2π). This extension is compensated for in the fundamental range of θi by introducing the following transformation
| (22) |
It should be noted that regular protein secondary structures correspond to definite values of (θi, γi). For example, for the standard α-helix
| (23) |
and for the standard β-strand
| (24) |
with the angles in radians. All the other regular secondary structures such as 3/10 helices, left-handed helices, etc., can be described in a similar way.
For the protein backbone with all peptide groups in a planar trans conformation, the following can be set:
| (25) |
For the present purposes, deviations from the value of Eq. 25 are negligible even if the peptide bond involves proline,58 if only the trans peptide groups are considered. The excluded-volume (steric) constraint [Eq. 26] can also be imposed.
| (26) |
Soliton description of protein-backbone geometry
Despite the apparent complexity of interactions that are described by the various molecular dynamics force fields and realistic coarse-grained energy functions, collapsed proteins display a surprisingly small variety in their shapes. There seems to be a self-organizing principle at work, that strongly limits the diversity among the biologically active protein structures. This is also reflected in Figure 2a that the values of the a priori highly variable R0 in Eq. 3 are very restricted. Indeed, the presence of a universal self-organizing principle in protein folding is manifested in the PDB structures.28 For example, thus far the structural classification scheme SCOP (Ref. 59) has identified around 1.400 unique folds in the PDB while, in CATH,60 there are currently around 1.300 topologies. These numbers have remained largely unchanged during the last 3–4 years, suggesting that the number of different protein folds is quite limited, and probably most of them have already been found.59, 60, 61, 62 The success of SCOP and CATH and other approaches such as FSSP (Ref. 63) in classifying proteins confirms that proteins are built in a modular fashion, from a relatively small number of elemental components.
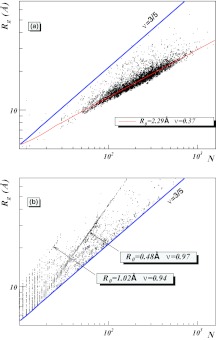
Figure 2.
(a) The (N, Rg) distribution of all individual single-chain PDB proteins with resolution less than 2.0 Å and with less than 30% homology. The lower line (ν = 0.37) describes mostly α-helical proteins and the top line is a ν = 3/5 Flory line. There are practically no single-chain proteins above the Flory line. (b) The (N, Rg) distribution for all multi-chain proteins from the current PDB that are above the Flory line. The two clusters given by equation 38, are clearly visible. The values of R0 and ν shown in the graphs were determined by linear regression.
In Ref. 64, it has been observed that the self-similar modular structure of proteins can be described mathematically in terms of a soliton solution65, 66 to a discrete version of the non-linear Schrödinger (DNLS) equation.67, 68, 69, 70 The original DNLS equation already shares a long history with protein research. It was introduced by Davydov67 who also showed that the equation supports a soliton solution. He proposed that the soliton explains how a localized deformation (and its energy excitation) propagates without dissipation along the α-helix. He also argued that a soliton that becomes trapped could evoke a deformation of the protein shape.
A soliton is the archetype structural self-organizer.65, 66 A soliton arises when non-linear interactions merge elementary constituents such as atoms into a localized collective excitation that is stable against small perturbations and cannot decay, unwrap, or disentangle. Solitons are extremely widely studied objects that can appear in many practical and theoretical scenarios. For example, solitons can be deployed for data transmission in transoceanic cables, for conducting electricity in organic polymers and describing chemical energy transportation in proteins.66 Many phenomena such as the formation of the morning glory cloud in the atmosphere, the Meissner effect in superconductivity and dislocations in liquid crystals65, 66 can be explained in terms of solitons. Solitons also model hadronic particles, cosmic strings, and magnetic monopoles in high energy physics.65
Following the justification in Ref. 71, a soliton, which is a solution to the equation of motion of the backbone Helmholtz free energy of Eq. 27 for the virtual-bond and virtual-torsion angles, is considered.
| (27) |
where θi is ith virtual-bond angle, γi is ith virtual-bond-dihedral (torsion) angle, and a, c, d, q, and m are parameters.64, 71, 72, 73, 74, 75, 76, 77 Equation 27 has been derived and motivated in detail in Refs. 64 and 71, 72, 73, 74, 75, 76, 77. Here it suffices to state that Eq. 27 can be shown to bethe long-distance limit that describes the full microscopic energy of a folded protein in the universal sense of Refs. 45, 46, 47, 48. As such, it does not explain the details of the (sub)atomic level mechanisms that give rise to protein folding.
The soliton solution is constructed by seeking the minimum of Eq. 27.64, 71, 75, 76 The necessary condition for the minimum is finding the zero of the gradient of F in the virtual-bond angles θ and in the virtual-bond dihedral angles γ. The solution of this problem is the solution of a system of 2N − 5 nonlinear equations in 2N − 5 unknowns (where N is the number of residues). In order to obtain this solution, the virtual-bond-dihedral angles γ are first expressed as functions of the virtual-bond angles θ, as given by Eq. 28.64, 71, 75, 76
| (28) |
with u = a/c and v = d/c. By inserting Eq. 28 into Eq. 27, the virtual-bond-dihedral angles γ are eliminated and a system of Eqs. 29 for the motion of the virtual-bond angles θ is obtained.
| (29) |
where θ0 = θN + 1 = 0 and
| (30) |
Here the familiar structure of the DNLS equation is recognized.67, 68 The only difference is in the first term on the right-hand side in Eq. 30. However, because this term contains θ in the denominator, its variation with θ is not that pronounced as the variation of the other two terms, which are proportional to the second and the fourth power of θ, respectively. Moreover, because |θ| > 1 radian for proteins, it turns out that the first term is small in value compared to the other terms.
The profile of the so-called dark soliton solution67, 68, 69, 70 to Eq. 29 can be constructed numerically by following the iterative procedure of Ref. 71. But its explicit form until now has not been found in terms of elementary functions. However, an excellent approximation is obtained by naively discretizing the continuum dark nonlinear Schrödinger equation (NLSE) soliton76
| (31) |
where s is a parameter that determines the center of the soliton. Equation 31, together with Eq. 28, represents a profile of θ and γ that is variable from site to site, as characterized by a loop in a protein. The μ1, 2 ∈ [0, π] are parameters, whose values are determined by the adjacent helices and strands. M1 and M2 constitute the integer parts of μ1, 2, and for simplicity M1 = M2 ≡ M is taken. To satisfy the monotonic character of the profile of Eq. 31, the experimental values of θi have to vary monotonically along the amino-acid sequence. Otherwise, a multiple of 2π is added to the experimental values. This does not affect the backbone geometry because θi′s are defined mod (2π). The integer M determines how many times θi covers its fundamental domain [−π, π) when the soliton is traversed once. It should be noted that negative values of θi are related to positive values of θi by Eq. 22. Finally, only σ1 and σ2 are intrinsically specific parameters for a given loop. But they specify only the length of the loop, not its shape which is determined by the functional form of Eq. 31 and, as in the case of μ1, 2, they are combinations of the parameters in Eq. 30.
The virtual-torsion angles γi, i = 1, 2, …, N − 3 are computed by substituting Eq. 31 into Eq. 28. Since there are only two independent parameters u and v in Eq. 28, the profile of γi is dependent entirely on θi, and on the structure of the adjacent regular secondary structures.
UNRES model of polypeptide chains
In the UNRES model,39, 40, 41, 42 a polypeptide chain is represented as a sequence of α-carbon atoms (Cαs) with attached side chains (SCs) and peptide groups positioned halfway between the consecutive Cαs. Only the side chains and the peptide groups are interaction sites, while the Cαs assist in geometry definition. The side chains are represented by ellipsoids of revolution, each with dimensions that characterize the amino acid in question. All definitions are summarized in the legend of Figure 1: The center of the ith side-chain ellipsoid is located a distance bSC(i) from the corresponding Cα, in the direction [αSC(i), βSC(i)] where αSC(i) and βSC(i) are the positional and torsional angles in a spherical coordinate system that is centered at the corresponding Cα. Among the dynamical variables that are not accounted for explicitly are the solvent degrees of freedom, the angles of rotation about side-chain bonds, the angles of rotation of the peptide groups about the Cα· · ·Cα virtual bonds etc. These are all included effectively, in the numerical values of the various parameters.
Schematically, the UNRES energy can be grouped into a sum of three terms,
| (32) |
E1 itself is a sum of three terms that involve only the backbone virtual-bond and virtual-torsion angles,
| (33) |
where f2(T) and f3(T) are temperature-dependent multipliers. The first term models virtual-bond-angle bending, the other two are torsional and double-torsional energies. Next,
| (34) |
These are terms that describe the following interactions, respectively: Side-chain-side-chain, side-chain-peptide, peptide-peptide, side-chain-local, and virtual-bond distortion. Finally,
| (35) |
is included. These two terms describe multi-body (correlation) interactions and the formation of disulfide bonds, respectively. The temperature-dependent multipliers are Bolzmann-like,
| (36) |
with T0 = 300K. The ws are the weights of the respective effective energy terms, which are determined by force-field calibration to reproduce the structure and folding thermodynamics of selected training protein(s). Langevin dynamics was implemented43, 44 with UNRES to study protein folding pathways; later,78, 79 the replica-exchange80 and multiplexed replica exchange81 algorithms were implemented to simulate ensembles of the proteins under study. In this work, the treatment is restricted to canonical Langevin simulations with the use of the force field calibrated with the 1GAB protein.40
RESULTS AND DISCUSSION
Phase co-existence in protein oligomers
We now proceed to inspect the phases of some protein oligomers, the structures of which are available from the PDB, in terms of the radius of gyration, with the compactness index ν in Eq. 3 as the order parameter. The possibility of a phase co-existence in oligomers is of particular interest.
The following line of arguments proposes that it does indeed make sense to employ Eq. 3 to study the phase structure of individual proteins: The data in SCOP (Ref. 59) and CATH (Ref. 60) and the results reported in Ref. 64 establish that most proteins have a self-similar structure over macromolecular distance scales. Since R0 is the only relevant length scale in the limit of long proteins, the large scale self-similarity implies that R0 can have only very restricted values. It is found that these different values are characteristics of the different fold types, such as mostly-α, mostly-βetc.
In Figure 2a, the radius of gyration Rg is plotted as a function of the number of residues for all those individual single-chain proteins in the PDB that have resolution less than 2.0 Å and sequence homology less than 30%. With a few exceptions, the values of Rg assemble around a line described by Eq. 3 with ν ≈ 1/3 for a collapsed protein. In Figure 2a, the line along which the mostly-α structures are clustered (that are dominant in the PDB data) is colored red. This line is given by
| (37) |
For the other subclasses such as α-and-β, mostly-β etc., the numerical values of R0 and ν are slightly different. In the limit N → ∞, it is expected that ν converges towards a unique value, while R0 may assume a small number of different values that are determined by the corresponding subclasses. Similar results were obtained by Dewey50 and by Dima and Thirumalai,56 see also Ref. 57.
It is notable that in the PDB data displayed in Figure 2a the non-linear, finite size corrections in Eq. 7 are not visible. This confirms that the numerical value of the coefficient R1 is small.
When the analysis is extended to include individual chains in protein oligomers, two clearly visible line-like clusters are found in the PDB that to our knowledge have not been reported previously. These two line-like clusters are identified in Figure 2b by using a clusterwise linear regression, as
| (38) |
In both clusters, the value of ν is very close to 1. Consequently these two clusters are in the same ν = 1 universality class, the slight difference in the values of ν being a finite size effect.82
The line-like cluster includes several membrane proteins and viral capsomers. An example of the latter is the HIV envelope glycoprotein with PDB code 1AIK. The cluster is populated mainly by collagen proteins like 2CUO in the PDB. In both clusters, mostly oligomers that consist of several similar or nearly similar subchains are found, and each subchain is located in the same cluster in Eq. 38. Apparently, the interactions between the different subchains override the effects of the poor solvent environment, preventing the individual subchains from collapsing into the ν ≈ 1/3 cluster.
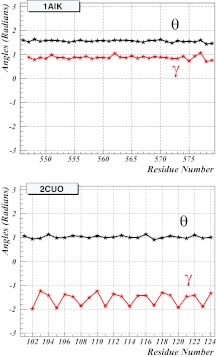
In Figure 3, the spectrum of the virtual-bond and virtual-torsion angles defined by Eqs. 11, 12, respectively, is shown as an example, for both 1AIK and 2CUO. The self-similar structure, which is consistent with a rigid rod-like geometry, is clearly visible in both spectra (i.e., the values of the virtual-bond angles θ and the virtual-bond-dihedral angles γ vary little along the sequence). It should be noted that, for 1AIK, the (θ, γ) spectrum coincides with that of the α-helix [Eq. 23]. For 2CUO, the virtual-bond angle has the β-strand value [Eq. 24], while the virtual-torsion angle repeats a pattern in which two values are in the vicinity around –1.4–1.5 radians, followed by one value which is about –2.0 radians. This corresponds to the Gly-Pro-X backbone structure which is characteristic of a collagen.
Figure 3.
The spectrum of the virtual-bond and virtual-torsion angles for 1AIK (top) and 2CUO (bottom), using PDB indexing. The black lines and symbols correspond to the virtual-bond angles θ and the red lines and symbols correspond to the virtual-bond dihedral angles γ, respectively.
Remarkably, it is found that there are also protein complexes in the clusters of Figure 2b that do not follow the structural patterns of membrane proteins, namely viral capsomers and collagens. In particular, a small number of hetero-oligomers that are composed of two or more proteins are identified, each on a different cluster defined by Eq. 3. Moreover, a number of dimers, in which one of the subchains is in the Θ-point cluster ν ≈ 1/2 with
| (39) |
while another subchain is in the cluster [Eq. 38] of Figure 2b, have been found here. To the extent that ν can be interpreted as an order parameter that characterizes different phases of a single polymer chain, the present observation suggests that these dimers are examples of proteins that display phase coexistence. As demonstrated by the emergence of two clearly visible separate line-like clusters in Figure 2b, with a sparsely populated intervening region, there is indeed a sharp cross-over transition between the different classes. The cross-over is reminiscent of a phase transition, in the thermodynamical limit.
Two different families of such phase coexistent heterodimers in the set of PDB data used here have been found. The first family consists of proteins whose multiple subchains are in different phases, and are stable only in oligomeric state. The PDB codes for the 11 proteins of this family are listed in Table 1. The second family consists of oligomers whose multiple subchains can also exist as stable proteins independently of each other. There are 16 different complexes in this data set and their PDB codes are listed in Table 2.
Table 1.
First class of phase co-existent heterodimers. Single proteins but with multiple subchains that are in different phases.
| 1WDC | 1G72 | 1GOT | 1HTR | 1LTS | 2FP7 |
| 2RIV | 3ABK | 3ARC | 3CX5 | 3DBO |
Table 2.
Second class of phase co-existent heterodimers; more than one protein with subchains in different phases.
| 1L2W | 1JDH | 1TH1 | 2F8X |
| 2EPV | 2PRR | 2BFX | 2D7C |
| 2VGO | 2K8F | 2QKH | 3EGG |
| 3HTU | 3HPW | 3IXS | 3DXC |
In each of these phase coexistent proteins, there is a difference in the lengths of the subchains. The subchains in the ν ≈ 1 cluster are systematically shorter than the subchains in the ν ≈ 1/2 cluster, reflecting the respective loss of conformational entropy in complex formation.
It is possible that there are also heterodimers with other combinations of phase coexistence. For example one long subchain component could remain in the collapsed ν ≈ 1/3 phase while a more restrained short subchain is in one of the phases with ν ≈ 1/2, ν ≈ 3/5, or ν ≈ 1. However, no clear examples of these patterns are found in the present PDB data.
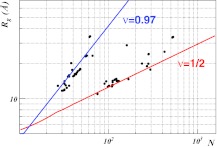
In Figure 4, the distribution of the individual subchains in the second class of phase coexistent complexes in the (N, Rg) plane is shown. The figure clearly displays how the longer subchains are located around the ν ≈ 1/2 cluster while the shorter chains are located on the cluster in Eq. 38.83, 84
Figure 4.
The distribution of individual chains on the (N, Rg) plane in the second class of phase coexistent hetero-oligomers found here. The data clearly accumulate around the top line that describes the cluster and the bottom line, the latter describing a Θ-point cluster with best-fit values R0 = 1.234 and ν = 0.508.
From a biological point of view, there are two notable hetero-oligomers in this second class. They are 2K8F and 3DXC (with the identical structures 3DXD, 3DXE). The first is the “molecular interpreter”85 p300 in the cluster and the tumor suppressing protein p53 in the ν ≈ 1/2 cluster. The second is the Alzheimer disease related AICD/Fe65 complex30, 34, 35, 36, 37 with the 28-residue AICD in the cluster and the Fe65 with 130 residues in the ν ≈ 1/2 cluster. In Sec. 3A the apparently exceptional physical properties of the AICD/Fe65 complex 3DXC are considered.
Structure of AICD in the AICD/Fe65 dimer
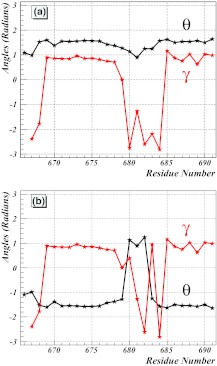
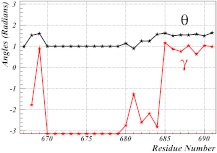
The structure of the shorter AICD subchain of the AICD/Fe65 dimer is analyzed here in detail. Its crystal structure is shown in Figure 5. The spectrum of the virtual-bond and virtual-torsion angles that describe its backbone are first inspected. The Cα coordinates in the PDB structure 3DXC, in combination with Eqs. 8, 9, 10, 11, 12, are used to arrive at a (θi, γi) profile that is displayed in Figure 6a. The AICD is located in the cluster with ν ≈ 1. However, in contrast to the spectra in Figure 3, its (θi, γi) profile does not display any self-similar structure. Instead, there appears to be a highly irregular behavior, in particular in γi, between the sites 678–685. In order to examine this behavior, the transformation defined by Eq. 22 is implemented to arrive at the profile shown in Figure 6b. The profile for θ suggests that it can be considered as two successive hyperbolic-tangent-like profiles such as Eq. 31, i.e., as two consecutive solitons. This figure reveals that AICD appears to consist of a pair of two very closely located loops which are both preceded and followed by α-helices.
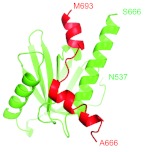
Figure 5.
Cartoon representation of the experimental structure of the AICD/Fe65 complex (PDB: 3DXC). Green: The Fe65 (longer) chain. Red: The AICD (shorter) chain. The first and the last residues of each chain are marked. Residue numbers have been taken from the 3DXC structure.
Figure 6.
(a) The spectrum of backbone virtual-bond angles θi (black line) and virtual-torsion angles γi (red line) for the AICD component of 3DXC (chain B). (b) The same spectrum after application of the transformation of Eq. 22 to reveal the soliton structure. The sites are indexed with residue numbers from the PDB.
The (θi, γi) profile in Figure 6b is reminiscent of the soliton profiles that have been studied extensively in Ref. 64. There, the DNLS soliton is shown to describe the modular building blocks of folded proteins that are in the ν ≈ 1/3 universality class. It is found that over 92% of the PDB proteins can be modeled in terms of the soliton profile [Eqs. 31, 28] that has been introduced in Ref. 71, in terms of no more than 200 different sets of numerical parameters. Consequently, a question arises as to whether the (θi, γi) profile that appears in Figure 6b could also be described in terms of the parameters of the DNLS soliton.
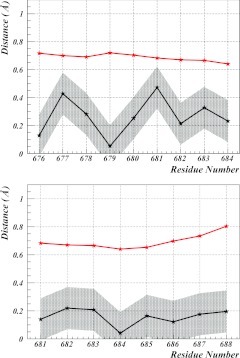
For protein 3DXC, it is found that the profile of each of the two loops in Figure 6b can be described by using the Ansatz given by Eqs. 31, 28. The parameter values are listed in Table 3. The corresponding (θi, γi) profiles computed from these equations describe the first loop at sites 676–683 (in terms of PDB indexing) with RMSD precision of 0.29 Å and the second loop at sites 681–688 with RMSD precision of 0.17 Å (see Figure 7). Both of these precisions are substantially below the Debye-Waller fluctuation distances that can be computed from the experimental B-factors in the PDB data by using Eq. 40.
| (40) |
Table 3.
Parameter values for the two solitons implied in Figure 6b. For virtual-bond angles, Eq. 31 is used. For virtual-torsion angles Eq. 28 is used. It should be noted that the values of both θ and γ in these two equations are defined mod (2π). The large values of M enable us to describe the irregular structures in Figure 6b. These irregularities are due entirely to multi-valuedness of the angular variables.
| loop |
||
|---|---|---|
| Parameters of equation 31 | 676–683 | 681–688 |
| μ1 + 2πN | 51.517 | 39.274 |
| μ2 + 2πN | 51.766 | 38.617 |
| σ1 | 2.984 | 3.327 |
| σ2 | 2.983 | 3.347 |
| s | 679.91 | 682.17 |
| u × 10−4 | 345.9832942 | 0.4445445 |
| v × 104 | −1.6625 | −6.3344 |
| number of matches | 177 | 896 |
Figure 7.
The two solitons of 3DXC. Residues are indexed with the numbers from the PDB structure. The black line denotes the residue-wise difference between the coordinates computed from the soliton and those computed from the PDB conformation. The red line denotes the Debye-Waller (one standard deviation) fluctuation distance, computed from the B-factors in the PDB. The grey area describes the estimated 0.15 Å zero-point fluctuation distance around the solitons.
Consequently, there is a very high quality description of the backbone in terms of two DNLS solitons. In Figure 7, it is shown how the soliton structures compare to the 3DXC backbone and experimental Debye-Waller fluctuations around it.
In Table 3, the number of times each of the two loops in 3DXC appears in the PDB are listed. From these, any two loops are identified whenever the mutual RMSD distance falls below 0.5 Å. This represents a typical value of the fluctuation distance in very high resolution x-ray structures. It should be noted that the Debye-Waller fluctuation distances for every site in the two loop regions of 3DXC are all above 0.65 Å (Figure 7).
The analysis of 3DXC establishes that it is composed of two solitons that are both abundant in the ν ≈ 1/3 cluster of collapsed proteins. In particular, there is nothing, either in the regular secondary structures or in the loop regions of the AICD component in the 3DXC complex, that is a priori unusual for a collapsed protein in the ν ≈ 1/3 phase. Nevertheless, this particular protein chain is located in the cluster that describes linear rod-like ν ≈ 1 structures. No such single-chain protein has been found in the PDB above the ν = 3/5 Flory line in Figure 2. It is proposed that the reason for this exceptional structure of AICD is a peculiarity of the phase co-existence identified in Figure 4. The mutual interaction between the AICD and Fe65 in the complex is so strong, that it overcomes the poor solvent effect and prevents AICD from collapsing into the ν ≈ 1/3 phase.
According to Davydov,67 a soliton is a localized carrier of energy and propagates without dissipation along an α-helix. This propagation evokes a deformation in the shape of the protein. If the soliton becomes trapped along the chain, it causes a change in the shape of the protein.67 The soliton pair along AICD is preceded by a long α-helix, and there is a proline at site 669. Since proline is an effective initiator of a loop in an isolated protein, the propagation of the first soliton along the α-helix until it becomes trapped by Pro(669) is proposed. It should be noted that there is also another proline at site 685, and it initiates the second soliton in its place.
Since the compactness index ν can have only discrete values [Eq. 4], it can not change when the soliton propagates continuously as a localized deformation along the α-helix. In particular, when the two solitons that are apart from each other are continuously translated along the backbone by shifting the value of s in Eq. 31, a collapsed conformation with ν = 1/3 can never be reached. The AICD will remain in the ν ≈ 1 phase [see the discussion under Eq. 4 in Sec. 2A].
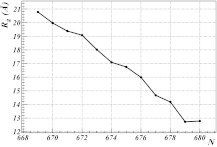
The explicit profile of the angles defined by Eqs. 11, 12 is used to investigate what takes place when the first soliton propagates along the backbone towards Pro(669). To propagate a soliton, the value of the parameter s in Eq. 31 is shifted. In Figure 8, it is shown how the radius of gyration Rg of the AICD depends on the position of the first soliton as it propagates towards Pro(669) while the second soliton remains fixed by Pro(685). The shape of the protein changes as the soliton propagates, and, in particular, the α-helix becomes converted into a β-strand by the soliton. The final (θi, γi) soliton profile is displayed in Figure 9. In Figure 10, the three-dimensional shapes for both the initial PDB conformation and the conformation in which the first soliton has propagated to site 669 are compared.
Figure 8.
The evolution of the radius of gyration for AICD in 3DXC (chain B), during the propagation of the first soliton from site 680 towards the proline at site 669; see also Figure 6b.
Figure 9.
The (θi, γi) profile of the 3DXC (chain B) after propagation of the first soliton onto the proline at site 669. See Figure 6 for the initial spectrum. The black lines and symbols correspond to the virtual-bond angles θ and the red lines and symbols correspond to the virtual-bond dihedral angles γ, respectively.
Figure 10.
The cartoon pictures of AICD. On the left, the PDB conformation corresponding to the (θ, γ) spectrum in Figure 6b and, on the right, the conformation corresponding to the spectrum in Figure 9.
It is found that Rg increases monotonically as the first soliton propagates. When it reaches the position where it becomes locked into Pro(669), the Rg value of the AICD has relocated itself from the cluster to the cluster. Since there are no other known ν ≈ 1 clusters in the PDB, it is proposed that these are the only two possible trapped conformations that AICD can have in the phase coexistent complex with Fe65.
It is proposed that the presence of two natural but alternative soliton locations in AICD could give rise to a genetic switch, with potentially interesting biological consequences that deserve to be investigated. This should be particularly interesting, since AICD is a product and Fe65 is a participant in the proteolytic cleavage processing of amyloid precursor protein (APP) into Aβ42 that relates to Alzheimer's disease.30, 34, 35, 36, 37, 38 It is interesting how the biological function of the AICD/Fe65 complex could be influenced by the soliton position, when the dimer translocates to the nucleus and participates in gene transcription. It is proposed that the two possible AICD conformations corresponding to the two clusters and might have quite different biological properties.
Collapse simulations of isolated AICD and Fe65
It is expected that, in isolation and under physiological conditions, the two possible ν ≈ 1 conformations of the AICD in 3DXC are unstable because they are not located in the cluster of ν ≈ 1/3 which corresponds to compact monomeric proteins in Figure 2. Indeed, no single-chain protein has been found in the PDB which is located above the ν = 3/5 Flory line in Figure 2. On the other hand, the two solitons that are the modular building blocks of AICD in 3DXC, are both abundant among the collapsed ν ≈ 1/3 proteins. Consequently, there are good reasons to expect that, in isolation, the AICD chain becomes subject to a phase transition-like changeover that takes it into the collapsed ν ≈ 1/3 cluster. Because there are no monomers in the PDB with compactness index ν ≈ 1/2, it can also be expected that Fe65 is similarly unstable in isolation, and becomes subject to a transition to the ν ≈ 1/3 cluster.
On general grounds, it can be expected that AICD can collapse along various pathways. For example, there could be a process in which the two solitons first annihilate each other and a new soliton structure is formed to bring about the phase transition from ν ≈ 1 to ν ≈ 1/3. Alternatively, there could be formation of a new soliton pair near Pro(669), with the ensuing collapse to ν ≈ 1/3. Other alternatives also exist; for example, the first soliton could become locked by Pro(669) and the relatively long β-strand could then buckle to form a new soliton pair, separated, e.g., by a β-turn. It is proposed here that detailed experiments should be designed to determine the structural properties of AICD under physiologically relevant conditions.
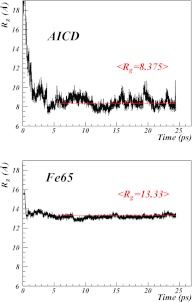
In order to better understand what takes place both in AICD and in Fe65 when they become removed from each other, canonical Langevin-dynamics simulations of isolated AICD and Fe65, respectively, have been performed using the UNRES force field [Eq. 32], starting from the conformations that AICD and Fe65 have in the 3DXC (heterodimer) experimental structure. The plots of the radius of gyration [computed from Eq. 2] vs. simulation time are shown in Figure 11 for both AICD and Fe65.
Figure 11.
Plots of the time evolution of the radius of gyration of isolated AICD (top) and isolated Fe65 (bottom) during Langevin molecular dynamics simulation with UNRES.
It should be noted that, in a living cell, such a separation between AICD and Fe65 may take place, for example, when the dimer becomes translocated to the nucleus. Because of a relation between the AICD/Fe65 complex and the amyloid precursor protein and the ensuing Alzheimer-disease-causing Aβ42, the separation of the two subchains from each other could somehow relate to Alzheimer's disease which makes the present UNRES investigation particularly interesting.
For both separate AICD and Fe65, a rapid cross-over transition in the value of the radius of gyration, followed by a stabilization in the collapsed form is found. This transition is suggestive of a phase transition, from a non-compact form that is present in the heterodimer to a globular compact form.
For AICD, the mean value of the radius of gyration converges to
| (41) |
and for Fe65
| (42) |
These are both very close to the collapsed ν = 1/3 values of the mostly-α cluster [Eq. 37] that are
| (43) |
It should be noted that, as stated in the discussion following Eq. 37, the difference between the clusters for mostly-α and other types of collapsed proteins is minuscule.
The remarkable observation in our simulations is that, for both AICD and Fe65, the final values of the radius of gyration fluctuate relatively strongly (Fig. 11). It is proposed here that this reflects the experimental observation that both proteins are unstructured,3 when they are in isolation and under in vivo conditions.
SUMMARY
In summary, by analyzing PDB structures, it has been found that physiologically relevant protein oligomers can display a behavior reminiscent of phase coexistence, in which the various subchains are in different phases. In particular, a family of dimers, for which one of the two subchains is in the same phase with a linear rod-like structure while the other is in the phase of a fully flexible chain, has been found. However, despite the apparent phase coexistence, both chains display the soliton structure that is characteristic of a single chain protein that is in the biologically active collapsed phase. It appears that the mutual interaction between the chains is so strong that it can overcome the effects of a poor solvent.
It has been proposed here that, if the two subchains are detached, they collapse. To confirm this, as an example, a detailed analysis of the potentially Alzheimer-disease related AICD/Fe65 complex has been carried out. It has been found that the AICD subchain can be described in terms of a two-soliton state at a very high precision, that exceeds the accuracy of experimental data as characterized by the B-factors. The soliton propagation along an α-helix of AICD has also been inspected, and it is proposed that this could give rise to a genetic-switch mechanism with potentially interesting biological consequences. Simulations using the UNRES energy function have been performed, and have confirmed that, in isolation, both AICD and Fe65 are indeed unstable and amenable to a transition, akin to a phase collapse, into a folded conformation. From a consideration of the results presented here, it is proposed that the analysis of protein complexes that display phase coexistence should be an interesting and biologically relevant challenge for future theoretical and experimental investigations.
ACKNOWLEDGMENTS
This work was supported by grants from the National Institutes of Health (Grant No. GM-14312), the National Science Foundation (Grant No. MCB10-19767), the Polish Ministry of Science and Higher Education (Grant No. DS 8372-4-0138-12), and a CNRS PEPS collaboration grant. Computational resources were provided by (a) Argonne Leadership Computing Facility at Argonne National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-06CH11357, (b) the National Science Foundation (http://www.nics.tennessee.edu/), and by the National Science Foundation through TeraGrid resources provided by the Pittsburgh Supercomputing Center (c) the Informatics Center of the Metropolitan Academic Network (IC MAN) in Gdańsk, (d) our 624-processor Beowulf cluster at Baker Laboratory of Chemistry, Cornell University, and (e) our 184-processor Beowulf cluster at the Faculty of Chemistry, University of Gdańsk.
References
- Crofts A. R., Annu. Rev. Physiol. 66, 689 (2004). 10.1146/annurev.physiol.66.032102.150251 [DOI] [PubMed] [Google Scholar]
- Althoff T., Mills D. J., Popot J.-L., and Kuehlbrandt W., EMBO J. 30, 4652 (2011). 10.1038/emboj.2011.324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dyson H. J. and Wright P. E., Nat. Rev. Mol. Cell Biol. 6, 197 (2005). 10.1038/nrm1589 [DOI] [PubMed] [Google Scholar]
- Uversky V. N., Chem. Soc. Rev. 40, 1623 (2011). 10.1039/c0cs00057d [DOI] [PubMed] [Google Scholar]
- Maters C. L., Simms G., Weinman N. A., Multhaup G., McDonald B. L., and Beyreuther K., Proc. Natl. Acad. Sci. U.S.A. 82, 4245 (1985). 10.1073/pnas.82.12.4245 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selkoe D., Neuron 6, 487 (1991). 10.1016/0896-6273(91)90052-2 [DOI] [PubMed] [Google Scholar]
- Garner A. L., Curr. Topics Med. Chem. 11, 258 (2011). 10.2174/156802611794072614 [DOI] [PubMed] [Google Scholar]
- Jones S. and Thornton J. M., Prog. Biophys. Mol. Biol. 63, 31 (1995). 10.1016/0079-6107(94)00008-W [DOI] [PubMed] [Google Scholar]
- Jones S. and Thornton J. M., Proc. Natl. Acad. Sci. U.S.A. 93, 13 (1996). 10.1073/pnas.93.1.13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheraga H. A., Biophys. Chem. 112, 117 (2004). 10.1016/j.bpc.2004.07.011 [DOI] [PubMed] [Google Scholar]
- Marintchev A., Frueh D., and Wagner G., Methods Enzymol. 130, 283 (2007). 10.1016/S0076-6879(07)30012-8 [DOI] [PubMed] [Google Scholar]
- Chen Y., Johnson J., McDonald P., Wu B., and Mueller J. D., Methods Enzymol. 472, 345 (2010). 10.1016/S0076-6879(10)72026-7 [DOI] [PubMed] [Google Scholar]
- Gavin A.-C., Maeda K., and Kuehner S., Curr. Opin. Struct. Biol. 22, 42 (2011). 10.1016/j.copbio.2010.09.007 [DOI] [PubMed] [Google Scholar]
- Jessulat M., Pitre S., Gui Y., Hooshyar M., Omidi K., Samanfar B., Tan L. H., Alamgir M., Green J., Dehne F., and Golshani A., Expert Opinion on Drug Discovery 6, 921 (2011). 10.1517/17460441.2011.603722 [DOI] [PubMed] [Google Scholar]
- Smith G. R. and Sternberg M. J. E., Curr. Opin. Struct. Biol. 12, 28 (2002). 10.1016/S0959-440X(02)00285-3 [DOI] [PubMed] [Google Scholar]
- Janin J., Mol. Biosys. 6, 2351 (2010). 10.1039/c005060c [DOI] [PubMed] [Google Scholar]
- Rojas A., Liwo A., Browne D., and Scheraga H. A., J. Mol. Biol. 537, 404 (2010). 10.1021/jp065810x [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y., Liwo A., Weinstein H., and Scheraga H. A., J. Mol. Biol. 405, 298 (2011). 10.1016/j.jmb.2010.10.051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conte L. Lo, Chothia C., and Janin J., J. Mol. Biol. 285, 2177 (1999). 10.1006/jmbi.1998.2439 [DOI] [PubMed] [Google Scholar]
- Sheinermann F. B., Norel R., and Honig B., Curr. Opin. Struct. Biol. 10, 153 (2000). 10.1016/S0959-440X(00)00065-8 [DOI] [PubMed] [Google Scholar]
- Privalov P. L. and Khechinashvili N. N. J., J. Mol. Biol. 86, 665 (1974). 10.1016/0022-2836(74)90188-0 [DOI] [PubMed] [Google Scholar]
- Huggins M. L., J. Chem. Phys. 9, 440 (1941). 10.1063/1.1750930 [DOI] [Google Scholar]
- Flory P. J., J. Chem. Phys. 9, 660 (1941). 10.1063/1.1750971 [DOI] [Google Scholar]
- De Gennes P. G., Scaling Concepts in Polymer Physics (Cornell University Press, Ithaca, 1979). [Google Scholar]
- Schäfer L., Excluded Volume Effects in Polymer Solutions, as Explained by the Renormalization Group (Springer-Verlag, Berlin, 1999). [Google Scholar]
- Anfinsen C. B., Science 181, 223 (1973). 10.1126/science.181.4096.223 [DOI] [PubMed] [Google Scholar]
- Bates F. S., Science 251, 898 (1991). 10.1126/science.251.4996.898 [DOI] [PubMed] [Google Scholar]
- Berman H. M., Westbrook J., Feng Z., Gilliland G., Bhat T. N., Weissig H., Shindyalov I. N., and Bourne P. E., Nucleic Acids Res. 28, 235 (2000). 10.1093/nar/28.1.235 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardy J. and Selkoe D. J., Õs Disease: Science 297, 353 (2002). 10.1126/science.1072994 [DOI] [PubMed] [Google Scholar]
- Kristin T., Jacobsen K. T., and Iverfeldt Æ. K., Cell. Mol. Life Sci. 66, 2299 (2009). 10.1007/s00018-009-0020-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng H. and Koo E. H., Molec. Neurodeg. 1, 1 (2006). 10.1186/1750-1326-1-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robakis N. K., Neurobiol. Aging 32, 372 (2011). 10.1016/j.neurobiolaging.2010.05.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts S. B., Ripellino J. A., Ingalls K. M., Robakis N. K., and Felsenstein K. M., J. Biol. Chem. 269, 3111 (1994). [PubMed] [Google Scholar]
- Müller T., Meyer H. E., Egensperger R., and Marcus K., Prog. Neurobiol. 85, 393 (2008). 10.1016/j.pneurobio.2008.05.002 [DOI] [PubMed] [Google Scholar]
- Sabo S. L., Lanier L. M., Ikin A. F., Khorkova O., Sahasrabudhe S., Greengard P., and Buxbaum J. D., J. Biol. Chem. 274, 7952 (1999). 10.1074/jbc.274.12.7952 [DOI] [PubMed] [Google Scholar]
- McLoughlin D. M., Christopher C. J., and Miller C. C. J., J. Neurosci. Res. 86, 744 (2008). 10.1002/jnr.21532 [DOI] [PubMed] [Google Scholar]
- Mueller T., Loosse C., Schroetter A., Schnabel A., Helling S., Egensperger R., and Marcus K., Curr. Alz. Res. 8, 573 (2011). 10.2174/156720511796391827 [DOI] [PubMed] [Google Scholar]
- Radzimanowski J., Simon B., Sattler M., Beyreuther K., Sinning I., and Wild K., EMBO Rep. 9, 1134 (2008). 10.1038/embor.2008.188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liwo A., Czaplewski C., Pillardy J., and Scheraga H. A., J. Chem. Phys. 115, 2323 (2001). 10.1063/1.1383989 [DOI] [Google Scholar]
- Liwo A., Khalili M., Czaplewski C., Kalinowski S., Ołdziej S., Wachucik K., and Scheraga H. A., J. Phys. Chem. B 111, 260 (2007). 10.1021/jp065380a [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liwo A., Czaplewski C., Ołdziej S., Rojas A. V., Kaźmierkiewicz R., Makowski M., Murarka R. K., and Scheraga H. A., in Coarse-Graining of Condensed Phase and Biomolecular Systems, edited by Voth G. (CRC, 2008). [Google Scholar]
- Liwo A., Oldziej S., Czaplewski C., Kleinerman D. S., Blood P., and Scheraga H. A., J. Chem. Theory Comput. 6, 890 (2010). 10.1021/ct9004068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khalili M., Liwo A., Rakowski F., Grochowski P., and Scheraga H. A., J. Phys. Chem. B 109, 13758 (2005). 10.1021/jp058008o [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khalili M., Liwo A., Jagielska A., and Scheraga H. A., J. Phys. Chem. B 109, 13798 (2005). 10.1021/jp058007w [DOI] [PMC free article] [PubMed] [Google Scholar]
- Widom B., J. Chem. Phys. 43, 3892 (1965). 10.1063/1.1696617 [DOI] [Google Scholar]
- Kadanoff L. P., Phys. 2, 263 (1966). [Google Scholar]
- Wilson K. G., Phys. Rev. B 4, 3174 (1971). 10.1103/PhysRevB.4.3174 [DOI] [Google Scholar]
- Fisher M. E., Rev. Mod. Phys. 46, 597 (1974). 10.1103/RevModPhys.46.597 [DOI] [Google Scholar]
- Li B., Madras N., and Sokal A., J. Stat. Phys. 80, 661 (1995). 10.1007/BF02178552 [DOI] [Google Scholar]
- Dewey T. G., J. Chem. Phys. 98, 2250 (1993). 10.1063/1.464205 [DOI] [Google Scholar]
- Onsager L., Ann. N.Y. Acad. Sci. 51, 627 (1949). 10.1111/j.1749-6632.1949.tb27296.x [DOI] [Google Scholar]
- De Gennes P. G., Phys. Lett. 38A, 339 (1972). 10.1016/0375-9601(72)90149-1 [DOI] [Google Scholar]
- LeGuillou J. C. and Zinn-Justin J., Phys. Rev. B 21, 3976 (1980). 10.1103/PhysRevB.21.3976 [DOI] [Google Scholar]
- Camacho C. and Thirumalai D., Proc. Natl. Acad. Sci. U.S.A. 90, 6369 (1993). 10.1073/pnas.90.13.6369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thirumalai D. and Klimov D. K., Curr. Opin. Struct. Biol. 9, 197 (1999). 10.1016/S0959-440X(99)80028-1 [DOI] [PubMed] [Google Scholar]
- Dima R. I. and Thirumalai D., J. Phys. Chem. B 108, 6564 (2004). 10.1021/jp037128y [DOI] [Google Scholar]
- Hong L. and Lei J., J. Polym. Sci. B - Polym Phys. 47, 207 (2009). 10.1002/polb.21634 [DOI] [Google Scholar]
- Sieradzan A., Scheraga H. A., and Liwo A., J. Chem. Theory Comput. 8, 1334 (2012). 10.1021/ct2008439 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murzin A. G., Brenner S. E., Hubbard T., and Chothia C., J. Mol. Biol. 247, 536 (1995). 10.1016/S0022-2836(05)80134-2 [DOI] [PubMed] [Google Scholar]
- Greene L. H., Lewis T. E., Addou S., Cuff A., Dallman T., Dibley M., Redfern O., Pearl F., Nambudiry R., Reid A., Sillitoe I., Yeats C., Thornton J. M., and Orengo C. A., Nucl. Acids Res. 35, D291 (2007). 10.1093/nar/gkl959 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoang T. X., Trovato A., Seno F., Banavar J. R., and Maritan A., Proc. Natl. Acad. Sci. U.S.A. 101, 7960 (2004). 10.1073/pnas.0402525101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Hubner I. A., Arakaki A. K., Shakhnovich E., and Skolnick J., Proc. Natl. Acad. Sci. U.S.A. 103, 2605 (2006). 10.1073/pnas.0509379103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holm L., Ouzounis C., Sander C., Tuparev G., and Vriend G., Protein Sci. 1, 1691 (1992). 10.1002/pro.5560011217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krokhotin A., Niemi A. J., and Peng X., Phys. Rev. E 85, 031906 (2012). 10.1103/PhysRevE.85.031906 [DOI] [PubMed] [Google Scholar]
- Manton N. and Sutcliffe P., Topological Solitons (Cambridge University Press, Cambridge, 2004). [Google Scholar]
- Dauxois T. and Peyrard M., Physics of Solitons (Cambridge University Press, Cambridge, 2006). [Google Scholar]
- Davydov A. S., J. Theor. Biol. 66, 379 (1977). 10.1016/0022-5193(77)90178-3 [DOI] [PubMed] [Google Scholar]
- Faddeev L. D. and Takhtajan L. A., Hamiltonian Methods in the Theory of Solitons (Springer Verlag, Berlin, 1987). [Google Scholar]
- Scott A. C., Phys. Reps. 217, 1 (1992). 10.1016/0370-1573(92)90093-F [DOI] [Google Scholar]
- Kevrekidis P. G., The Discrete Nonlinear Schrödinger Equation: Mathematical Analysis, Numerical Computations and Physical Perspectives (Springer-Verlag, Berlin, 2009). [Google Scholar]
- Molkenthin N., Hu S., and Niemi A. J., Phys. Rev. Lett. 106, 078102 (2011). 10.1103/PhysRevLett.106.078102 [DOI] [PubMed] [Google Scholar]
- Niemi A. J., Phys. Rev. D 67, 106004 (2003). 10.1103/PhysRevD.67.106004 [DOI] [Google Scholar]
- Chernodub M., Hu S., and Niemi A. J., Phys. Rev. E 82, 011916 (2010). 10.1103/PhysRevE.82.011916 [DOI] [PubMed] [Google Scholar]
- Danielsson U., Lundgren M., and Niemi A. J., Phys. Rev. E 82, 021910 (2010). 10.1103/PhysRevE.82.021910 [DOI] [PubMed] [Google Scholar]
- Chernodub M., Lundgren M., and Niemi A. J., Phys. Rev. E 83, 011126 (2011). 10.1103/PhysRevE.83.011126 [DOI] [PubMed] [Google Scholar]
- Hu S., Krokhotin A., Niemi A. J., and Peng X., Phys. Rev. E 83, 041907 (2011). 10.1103/PhysRevE.83.041907 [DOI] [PubMed] [Google Scholar]
- Hu S., Lundgren M., and Niemi A. J., Phys. Rev. E 83, 061908 (2011). 10.1103/PhysRevE.83.061908 [DOI] [PubMed] [Google Scholar]
- Nanias M., Czaplewski C., and Scheraga H. A., J. Chem. Theor. Comput. 2, 513 (2006). 10.1021/ct050253o [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czaplewski C., Kalinowski S., Liwo A., and Scheraga H. A., J. Chem. Theor. Comput. 5, 627 (2009). 10.1021/ct800397z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansmann U. H. E., Chem. Phys. Lett. 281, 140 (1997). 10.1016/S0009-2614(97)01198-6 [DOI] [Google Scholar]
- Pandé V. S., Baker I., Chapman J., Elmer S., Khaliq S., Larson S. M., Rhee Y. M., Shirts M. R., Snow C. D., Sorin E. J., and Zagrovic B., Biopolymers 68, 91 (2003). 10.1002/bip.10219 [DOI] [PubMed] [Google Scholar]
- This is the universality class of one-dimensional rod-like structures. However, it should be noted that this observation does not imply that the structures are actually rods but means that a protein molecule is much less compact than the same protein when squeezed into a ball. Although the three principal axes of the moment of inertia or the anisotropy parameter characterize the shape of a protein better, Rg is a parameter that can be used to judge this behavior: if the system is viewed as an ellipsoid with the principal dimensions a, b, and c, then \documentclass[12pt]{minimal}\begin{document}$R_g = \sqrt{a^2+b^2+c^2}$\end{document}Rg=a2+b2+c2. Thus, if one of the axes is much longer than the other ones, it will make a large contribution to Rg. For rod-like chains Rg has the strongest dependence on chain length, as follows from Eqs. . From Eqs. it also follows that polymer (protein) chains can be classified based on the dependence of the radius of gyration on chain length; hence we find that the plot of Rg vs. chain length contains several line-like clusters (Figure ).
- This bears a similarity to the decreasing compactness of folded polypeptides after binding to a mica surface, found in molecular dynamics simulations.
- Starzyk A. and Cieplak P., J. Chem. Phys. 135, 235103 (2011). 10.1063/1.3665930 [DOI] [PubMed] [Google Scholar]
- Smith J. L., Freebern W. J., Collins I., De Siervi A., Montano I., Haggerty I. C. M., McNutt M. C., Butscher W. G., Dzekunova I., Petersen D. W., Kawasaki E., Merchant J. L., and Gardner K., Proc. Natl Acad. Sci. U.S.A. 101, 11554 (2004). 10.1073/pnas.0402156101 [DOI] [PMC free article] [PubMed] [Google Scholar]