1. Introduction
The acute (48-h) Daphnia toxicity test is the most common and resource efficient experiment currently being used by eco-toxicologist and regulators to develop water quality criteria for stressors in aquatic environments (O.E.C.D. 1984; U.S.E.P.A. 2002). This test is designed to assess the toxicity of individual stressors by exposing Daphnia to a range of concentrations and measuring percent mortality, a nonlinear response variable. The acute toxicity test, however, is not always environmentally relevant due to the fact that contaminants rarely exist as individual stressors in natural environments. In aquatic systems, for example, organisms are exposed to a multitude of natural and anthropogenic stressors that can have both individual and interactive effects (Schwarzenbach et al. 2006). The current methodology used by the environmental regulatory agency, U.S.E.P.A. and eco-toxicologists to studying the effects of multiple stressors in aquatic ecosystems is to run multiple single-stressor acute toxicity tests for each of the stressors that make up the mixture, then combine the individual effects using a mixture model (i.e. concentration additivity or effects-based independent action; Boedeker et al. 1993; U.S.E.P.A. 2002). While this technique has been criticized, alternatives to this method have also been shown to have significant limitations (Greco et al. 1992; Drescher and Boedeker 1995; Norwood et al. 2003; Jonkers et al. 2005). To our knowledge, no other modeling techniques are currently being applied by eco-toxicologist to assess the acute effects of multiple stressors on aquatic organisms. On the other hand, in recent years many experimental designs have been proposed to enhance the use of these current mixture models or avoid them all together.
Alternative techniques using linear based models have been and continue to be applied by eco-toxicologist using a variety of different experimental designs (e.g. factorial designs and central composite design). Although, these methods are adequate at studying the effects of single or binary stressors, they become unreliable when studying multiple stressors in greater than binary combinations. This is because these methods are inadequate at determining complex interactions, common among mixtures. Here we define complex interactions as the biological effects among stressors and chemical modifiers that are greater than or less than would be predicted from the sum of the effects of individual constituents (i.e. additive). We avoid the more commonly used terms antagonistic and synergistic to avoid confusion that has resulted from the lack of consistency in the use of these terms in ecotoxicology (see Loewe 1953; Drescher and Boedeker 1995; Folt et al. 1999). We propose an easy to use yet computationally challenging model combined with a simplified experimental method in order to adequately interpret the complex effects associated with multiple stressors in aquatic ecosystems. To achieve this goal we designed a model that incorporates much of the current statistical modeling theory, yet is modified to specifically address the needs associated with the field of eco-toxicology.
Looking outside ecotoxicology, the issue of modeling complex interactions has been extensively studied by statisticians. Here we discuss the most current statistical theory and models associated with mixture interactions and their limitations; however, a more thorough review of the statistical literature is presented in the Discussion (see section 4.1). To account for the complex interactions associated with mixtures, recent efforts have focused on the use of generalized linear models (GLMs), constructing experimental designs implementing optimal design strategies with a sequential approach (e.g. Dror and Steinberg 2006; 2008, see also review by Khuri et al. 2006). This technique is most commonly implemented using a Bayesian approach in combination with D-optimal design (Gotwalt et al. 2009). This method is a dramatic improvement compared to those discussed thus far; however, the Bayesian approach requires knowledge of the limits of the stressor concentrations and a priori parameter distributions that are often unknown to the investigators, and the D-optimality criterion is often less effective at producing statistically significant models than other optimal designs for our model. Alternatively, we propose using the A-optimal criterion with an adaptive design approach as more efficient, statistically robust, easy to use alternative method for eco-toxicologists studying the acute multiple stressors interactive effects. Our iterative, quadratic, multivariate, logistic model, hereafter referred to as adaptive iterative design (AID), was designed with the ultimate goal of improving water quality assessment by increasing efficiency and accurately quantifying complex interactions associated with mixtures. AID was developed to be adaptable to the number and type of mixture components, and addresses the current limitations associated with evaluating the effects of complex interactions often associated with multiple stressors in aquatic ecosystems. AID addresses these current limitations by: 1) substantially reducing the need for large amounts of a priori knowledge, 2) simplifying the experimental design for multiple stressor studies, in turn reducing the number of experimental units, and 3) providing a statistical method to quantify complex interactions of nonlinear response variables. Our more efficient, easy-to-use, yet statistically robust method for accurate quantification of complex interactions is achieved by the integration of an adaptive step-wise approach to determine the nonlinear response model associated with acute toxicity tests. To validate our methods, we examined the effects of five stressors in combination, known to have complex interactions.
2. Methods
2.1 Test Procedure
Validation of the AID program consisted of simultaneously exposing Daphnia pulex to three contaminants (cadmium-Cd, zinc-Zn, and arsenic-As), while varying two water chemistry parameters (pH and hardness) and measuring mortality rate as the response variable, in sequential acute toxicity tests. These five variables were selected because they commonly co-occur in polluted aquatic environments and interact, generating a variety of complex interactive effects (e.g. Balistrieri and Blank 2008; Barata et al. 1998; Canizares-Villanueva et al. 2000; Fleeger et al. 2007; Hare 1992; Heijerick et al. 2002; Komjarova and Blust 2008; Mothersill et al. 2007; Muyssen et al. 2006; Shaw et al. 2006; Sunda and Huntsman 1996; Wang et al. 1999; Xie et al. 2007). We followed standard procedures for acute (48-h) Daphnia toxicity tests, as laid out by the U.S.E.P.A. (2002), with slight modifications that are provided in Shaw et al. (2006); however, similar methodologies such as O.E.C.D. (1984) are also applicable. Details on culturing Daphnia prior to experimentation are previously described in Folt et al. (1999) and Shaw et al. (2006) and only modifications to these methods are described here. D. pulex were maintained in reconstituted nanopure water at a constant hardness of 100 mg CaCO3/L, pH of 7 (modified COMBO media; Kilham et al. 1998), and fed Ankistrodesmus falcatus daily at a rate of 75,000 cells/mL for over eight generations (~6 months) prior to testing. Each experimental replicate consisted of <24-h old neonates, taken from a single clutch between the 3rd and 5th brood, placed in a 120 mL glass Qorpak™ jar filled with 100 mL of test solution. Test solutions consisted of a combination of three metals (i.e. Cd, Zn, and As) and modified pH and hardness levels. Metal solutions were made from CdCl2, ZnCl2, or AsNaO2. Hardness was modified using Mg(NO3)2 and Ca(NO3)2, while pH was modified using either 1N HCl or 1N NaOH and maintained for the duration of the experiment by adding 0.75 g/L of the buffer MOPS, according to Heijerick et al. (2003). Daphnia were not fed during testing and mortality was determined after 48-h by examining individuals for lack of movement (U.S.E.P.A. 2002).
2.2 Quality Assurance
The iterative process used in the AID program required tests to be performed in succession. To determine uniformity throughout our experiment we: 1) monitored several chemical parameters (i.e. pH, hardness, temperature, dissolved oxygen, and metal concentration) at the beginning and end of each experiment, and 2) conducted multiple single-metal (i.e. Cd, As, or Zn) acute toxicity tests simultaneously throughout the iterative process to account for temporal variability. No significant change in chemical parameters was detected over the course of the experiments (data not shown). Additionally, mortality was less than 10% in the control treatments and no significant difference were found over the duration of the experiment in the single-metal acute toxicity tests (data not shown). Alternatively, one could use a randomized block design method to account for any temporal effects (Hinkelmann and Kempthorne 2008).
2.3 Development of AID
The development of AID was predicated on the unsuccessful attempts to determine the effects of these same five variables (i.e. Cd, Zn, As, pH, and hardness) on D. pulex, using a slightly modified version of Schoen’s (1996) Central Composite Design (CCD) and the Design of Experiment feature in JMP (version 5.0.1, SAS Institute Inc. 2005). The CCD method was designed to increase efficiency by reducing the number of experimental units, while still maintaining sufficient statistical power to determine interactive effects (Edginton et al. 2004). The experimental design utilizes a center point replicated three to six times and axial points around the center point that are not replicated (Schoen 1996). After each run of the CCD experiment we had to readjust the axial points and center point in an attempt to more fully characterize the response curve. Following six attempts and over 250 experimental units, even with all of our prior experience conducting multiple single-stressor acute toxicity tests on these same metals (see Shaw et al. 2006), we were still unable to reliably determine the center point (see Appendix A for complete data set and experimental concentrations tested). With over 70% of the responses in the non-linear portions of the response curve, at or approaching 0% or 100% mortality (Appendix A), it was clear that a new method for determining the response of multiple stressors was needed. Therefore, we developed our model to handle the complexity associated with nonlinear response variables, improve the estimates of model parameters, directly quantify interactive effects, and incorporate an iterative component to increase experimental efficiency while maintaining significant statistical power, in an easy to use, open access software program (i.e. R).
2.4 Analysis of AID
We advocate the modeling of mortality rate via GLM, namely, logistic regression (Demidenko 2004; McCulloch et al. 2001) as described here in detail. Take x as a stressor concentration, we model the probability of individual mortality within a certain time, for example the U.S.E.P.A. (2002) 48-h standard acute toxicity test, as the logit function:
| (1) |
where y = 1 is the mortality indicator (y = 1 died, y = 0 stayed alive), and α, β > 0 are unknown parameters to be determined from the data. As follows from this model, when concentrations increase the probability of dying increases and approaches 1. Function (1) models a probabilistic Bernoulli event. However, the interpretation of the parameters remains as the mortality probability of an individual organism.
The most popular dose response relationship used to test a single stressor is expressed via a power function as:
| (2) |
where m(x) is the mortality rate at dose concentration x, EC50 is the concentration which yields 50% mortality in the population, and β is the positive parameter that reflects the reaction of the mortality to increased dose. Although other dose response relationships have been used, such as probit and Weibull (Christensen and Chen 1985), the advantage of model (2) is that parameter EC50 is explicitly presented and can be used as the common baseline to specify the effect of toxicity. Following Berkson (1951), we advocate the logit dose response model in the form:
| (3) |
Technically speaking, models (2) and (3) are equivalent because we can represent:
so that (2) turns into (3) letting α = −β ln EC50. As a consequence, if the dose response relationship is estimated in the form (3), then EC50 = e−α/β.
There are several advantages of equation (3) over (2) when modeling the mortality rate as a function of single or multiple stressor concentrations. First, parameterization of (3) allows for a more convenient interpretation for parameter β using the language of odds ratio commonly used in biostatistics and epidemiology (Rosner 2000; Rothman et al. 2008). Given the stressor concentration x, we define the odds of dying as the ratio of the mortality probability to the probability of surviving as:
When concentration increases by Δx the relative increase of the odds, O(x), on the scale of the relative increase of the concentration, is measured as:
Setting Δx to zero, we obtain that the instanteneous change of the odd of dying is expressed in terms of the derivartive on the log scale as:
| (4) |
Thus, β can be interpreted as the increased odds of dying as a function of increase concentration. This interpretation is scale independent because the killing strength of the stressor is expressed on a relative scale. This allowed us to use β when making comparison of stressors even when measured on different scales.
Second, treating formula (4) as the population mortality rate, we used the theory of Generalized Linear Model (GLM) to estimate parameters α and β with logit (McCullagh and Nelder 1989). The use of GLM is advantageous because most statistical packages have built-in functions to estimate GLM models using maximum likelihood. In the statistical package R this can be done using the following one-line code:
where binomial indicates that the logit link is used by default. Here γ is the mortality indicator variable (γ =0 mean alive and γ =1 means dead). For example, if for a certain stressor concentration value x, three organisms die and seven are alive, γ =1 repeats three times, γ =0 repeats seven times and x repeats 10 times. If x includes zero values we recommend using the minimum detectable concentration, as well as values several thresholds below detection concentrations to evaluate the sensitivity of using below detection values rather than zero.
Third and perhaps the most important advantage of equation (3) is that the logistic regression approach can be easily generalized to multiple stressors. Here we expand the logistic regression to incorporate multiple stressors (details of this derivation can be found in Appendix B). The mortality of an individual as a function of the concentration of multiple stressors is modeled via function (1) and the survival of n organism(s) over a 48-h period. If p is the probability of an individual organism dying, the probability of m organisms dying is described by the binomial probability which is proportional to pm (1 − p)n−m. If N containers with the same initial number of organisms (n) are involved in the experiment, assuming that death of an organism is a function of a stressor concentration and does not depend on the death of others (i.e. density independent), we arrive at the log-likelihood function:
| (5) |
where yi is the proportion of organism that died within 48 hours, μ is the inverse link function, xi is the vector of stressor concentrations and β is the vector of coefficients and β′x =β1x1 + β2x2 + …. For example, in the case of logit function (1) we have μ(s) = es/(1 + es), where s = α + βx. Vector xi implies that different containers may have different concentrations, and more importantly, its components may contain quadratic or cross-product values of stressor concentration. Moreover, since scale coefficients are fixed, the variance of the intercept also does not change. Estimation of α and β parameters through the maximization of function (5), is programmed in many statistical packages (e.g. SAS, S-Plus, and R) as part of the GLM estimation. Several models (iterative and non-iterative) for dealing with mortality rate with multiple stressors have been suggested in the literature (see Christensen and Chen 1985; Dror and Steinberg 2006, 2008; Gotwalt et al. 2009; Hewlett and Plackett 1959; Woods et al. 2006). However, all these models are complex and require special, often expensive software. We reduced the complexity and the need for special software by designing model (5) to use GLM, a standard component of most statistical software packages.
2.5 Optimization of AID
In laboratory experiments we have control over individual stressor concentration. However, the process of determining what set of concentrations will improve the dose response relationship requires the choice of the optimality criterion (Pukelsheim, 1993). For those interested in a complete review of optimal designs in the framework of GLMs, we suggest the review by Khuri al. (2006) and Woods et al. (2006). Here we focus on the two major choices to be made before developing an optimal design: 1) the criterion by which optimal designs are judged, such as D- or A-criterion, and 2) at what parameter values the criterion design is evaluated. First, while the majority of authors have elected to use the D-optimal design (Gotwalt et al. 2009), we employ the A-optimal design, which minimizes the sum of variances of estimated parameters because it has a more appropriate statistical interpretation for our interests. Second, mainly two approaches exist on selection of parameter values where the design criterion is evaluated: a) the Bayesian approach, and b) the sequential (or adaptive) approach. Bayesian approach requires a priori distribution of parameters of GLM and therefore is somewhat subjective. Our approach utilizes a sequential-adaptive design because the parameter values are data driven and the optimal design is more flexible.
Several optimal designs, including A-design, under logistic regression have been studied by Mathew and Sinha (2001). Unfortunately, their solution does not admit a closed form and is computationally intensive. Therefore, we incorporated the A-optimal design into a simpler design, here after referred to as the Optimal Model (details of the mathematical derivation can be found in Appendix B) to create the critical iterative step associated with AID.
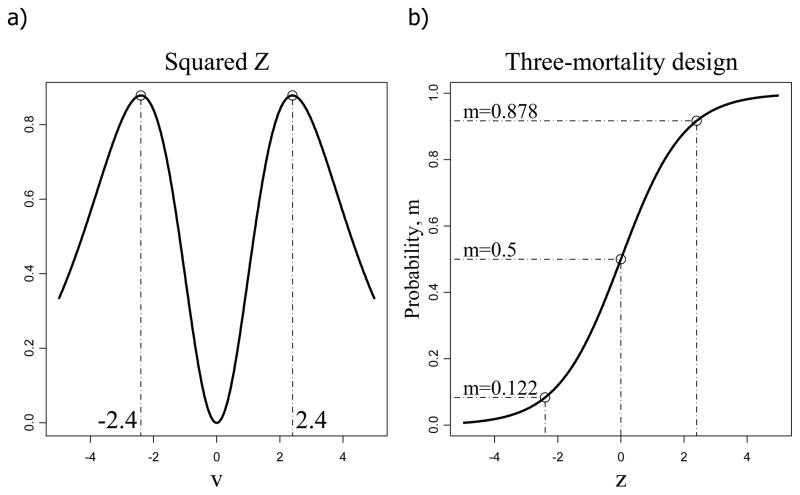
To develop the Optimal Model we first note that since the individual mortality is a binary event, minimum variance of the intercept in the logit dose response curve is achieved when the probability of dying is 1/2. Since the variance is m(1 − m), one needs to have m = 1/2 to achieve maximum precision, so that we start with EC50 concentration for each stressor. One could justify this choice as the optimal stressor concentration under the null hypothesis of zero stressor coefficients. Now we find two other optimal concentration levels to increase the robustness of our model by using a 3-point design, as discussed by Abdelbasit and Plackett (1983). Using α = −βln EC50 we rewrite α + β ln x as β ln(x/EC50) and letting u = ln(x/EC50) the mortality rate function simplifies to μ (u) = eβu/(1 + eβu). Next we reformulate the question on the Optimal Model as follows: what concentration(s) of the stressor provides maximum statistical significance of the slope coefficient, expressed as the Z-score, as the ratio of the maximum likelihood estimator to its standard error. To simplify the solution, we look for a symmetric design, as in Mathew and Sinha (2001). As shown in Figure 1a, the maximum Z-score for coefficient β is achieved when concentration levels satisfy the equation v = β ln(x/EC50) = ±2.4, which correspond to probabilities m = 0.122and m = 0.878, see Figure 1b. Therefore, the optimum stressor concentrations that maximizes the significance of the beta-coefficient (i.e. minimum p-value) with the logit model are those leading to the Optimal Model at the rates 0.122, 0.5, and 0.878 (Figure 1b).
Figure 1.
Optimal Design model with the logit model. The optimum concentrations have maximum Z-score for coefficient β at ±2.4 (a), which corresponds to mortality rates of 0.122 and 0.878 (b).
2.6 Implementation of AID
The AID process begins with estimating the parameters of the dose response curve using a minimal amount of data about the stressors of interest, individually or in combinations. This data can be collected from the literature or previous experimental acute toxicity data can be used. Next, the optimal design model is used to determine the next set of optimal stressor concentration values to be tested to better characterize the response curve. This iterative process continues until the model is stable, i.e. the next set of concentration values, determined by the optimal design, does not statistically improve the model’s goodness of fit. Once a stable model is in hand, thorough analysis of the individual and interactive effects can be conducted. To adequately convey the AID process, each of the steps mentioned above will be described below in greater detail.
Although, AID was developed to minimize the need for a priori knowledge, utilizing existing acute toxicity data (e.g. EC values) for each individual or combination of stressors of interest, will likely increase the efficiency of AID. For example, in this study we used data from the previous unsuccessful central composite design experiments (Appendix A) to develop the following multivariate logistic regression model, without interactions, building off the work of Carter et al. (1988):
where y is the proportion of organisms that die within 48 hours and pH, As, Cd and Zn are stressor concentrations. This basic model describes the effect of each of the stressors alone in terms of the beta-coefficient and the statistical significance of each stressor expressed in terms of the t-statistic (or p-value).
The next step expands the basic model to include the interactions for all possible combinations of the mixture variables. Here we determined what if any combination of stressors significantly contributed to the model (i.e. which interactive effects are greater or less than additive). Next, to determine the best model, the degree of uncertainty for each of the significant interaction terms was ranked based on the value and stability of the statistical coefficients, which in this case were t-values. Models were rejected if they included interaction terms with high residual deviance that resulted in one of the stressor terms, associated with the interaction, to be insignificant. Once the best model was determined the dose response data was then used to initiate the iterative process of the AID design (see Appendix B-multivariate logistic regression). The iterative step was designed to improve the characterization of the response curve by defining the new dose values to test, as shown in Table 1. These experiments were conducted until no considerable improvement of statistical significance of regression coefficients judged by t-statistics were found, at which point the model was deemed stable and ready to be used to investigate the individual and interactive effects of the mixture variables.
Table 1.
Experimental design of the two iterative steps including concentrations and response data:
| Date of Experiment | pH | Hardness | Cd (ug/L) | As (ug/L) | Zn (ug/L) | Mortality (Dead/Total) |
|---|---|---|---|---|---|---|
| 1st Iterative | 5 | 124 | 0 | 0 | 0 | 0.00 |
| 1st Iterative | 5 | 124 | 57 | 1000 | 1000 | 0.33 |
| 1st Iterative | 5 | 124 | 57 | 1000 | 1000 | 0.29 |
| 1st Iterative | 5 | 124 | 57 | 1000 | 1000 | 0.33 |
| 1st Iterative | 5 | 124 | 57 | 1000 | 1000 | 0.31 |
| 1st Iterative | 5 | 124 | 57 | 1000 | 1000 | 0.30 |
| 2nd Iterative | 5 | 300 | 0 | 0 | 0 | 0.00 |
| 2nd Iterative | 5 | 300 | 189 | 250 | 1298 | 0.16 |
| 2nd Iterative | 5 | 300 | 189 | 250 | 1298 | 0.16 |
| 2nd Iterative | 5 | 300 | 189 | 250 | 1298 | 0.09 |
| 2nd Iterative | 5 | 300 | 189 | 250 | 1298 | 0.13 |
| 2nd Iterative | 5 | 300 | 189 | 250 | 1298 | 0.11 |
3. Results
After just two iterations of AID identifying new concentration values (Table 1), the dose response model was deemed stable (i.e. the output matched model prediction). The stable AID determined model was then used to identify the individual and all possible combinations of the five components and there combined effects (i.e. greater and less than additive interactions) on Daphnia mortality. Interestingly, of all possible combinations only binary interactions (i.e. ln(As)*ln(Cd), ln(As)*ln(Zn), and ln(Cd)*ln(Zn)) were found to be significant (Table 2). Furthermore, the iterative step was proven effective in that the ln(As)*ln(Zn) interaction was not identified until after the two optimizing iterations of AID were conducted. However, not all significant interactions were selected for further study. More specifically, ln(As)*ln(Cd) was not considered even though a significant interaction was observed due to the fact that the As term alone was not significant (Table 2). Also, the ln(As)*ln(Zn) model was not selected for further study due to high variability and because this interaction had a low predictive power (i.e. t-value) compared to other models (Table 2). The model with the least uncertainty was the ln(Cd)*ln(Zn) model (Table 2) and therefore was deemed the Optimal Model.
Table 2.
Coefficients and (t-values) for each of the variables associated with the basic model and the three significant models identified by our model. No other binary models and those incorporating more than two factors were found to be significant.
| Models | ln(pH) | ln(Hardness) | ln(As) | ln(Cd) | ln(Zn) | Interaction | Deviance |
|---|---|---|---|---|---|---|---|
| Basic | 6.31 (4.52) | −1.04 (−3.51) | 0.53 (4.44) | 0.65 (3.67) | 0.40 (3.21) | 110.6 | |
| ln(As)*ln(Cd) | 6.40 (4.56) | −1.04 (−3.52) | −0.01 (−0.01) | −0.20 (−0.22) | 0.43 (3.31) | 0.12 (0.98) | 109.7 |
| ln(As)*ln(Zn) | 6.27 (4.47) | −1.04 (−3.50) | 1.25 (2.24) | 0.60 (3.37) | 1.25 (1.93) | −0.12 (−1.34) | 108.8 |
|
| |||||||
| ln(Cd)*ln(Zn) | 5.00 (3.32) | −1.00 (−3.16) | 0.25 (1.77) | 2.29 (5.91) | 1.59 (5.78) | −0.33 (−5.19) | 79.1 |
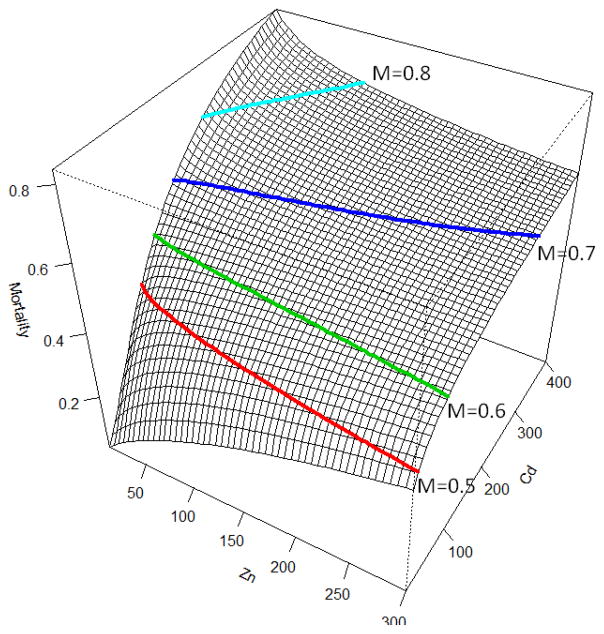
The coefficients of the Optimal Model (i.e. ln(Cd)*ln(Zn)) were used to identify the individual effects of the five mixture components on Daphnia mortality (Table 2). The positive t-values associated with pH, As, Cd and Zn suggests that Daphnia mortality increased as pH, As, Cd, or Zn increased (Table 2). On the other hand, an increase of hardness with its negative t-value is predicted to decrease Daphnia mortality in the presence of the other components (Table 2). The model also defines the direction and magnitude of the significant interactions (Table 2). For example, the t-value for the As*Cd interaction term was 0.98, which indicates a greater than additive effect when As and Cd are both present in the system (Table 2). The negative signs associated with t-values for the interactions of ln(As)*ln(Zn) and ln(Cd)*ln(Zn) indicate a significantly less than additive effect of these two metal combinations on Daphnia mortality. Furthermore, while both ln(As)*ln(Zn) and ln(Cd)*ln(Zn) exhibited less than additive effects, the interaction term for ln(Cd)*ln(Zn) is almost 4x greater than that of ln(As)*ln(Zn) (Table 2). The final model with three isomortality lines is depicted in Figure 2 as a surface function of Cd and Zn, while other all other components are kept constant (i.e. pH=6, hardness=100, As=100).
Figure 2.
Mortality surface as a function of Zn and Cd (pH=6, hardness=100, As=100) with four isomortality lines (Table 2). The less than additive effect between Zn and Cd is weak at higher mortality rates (isomortality lines nearly straight) and is stronger at low mortality rate (isomortality lines curve).
The coefficients of the ln(Cd)*ln(Zn) model were also used to predict the effects of each stressor on Daphnia mortality, at concentrations not specifically tested in this study. To demonstrate this we examined the effect increasing the concentrations of Cd, Zn, or As by 1% would have on Daphnia mortality. One percent was selected to show the sensitivity associated with this analysis. To calculate the effect of increasing the Cd concentration by 1%, while holding the Zn concentration at 2000 μg/L, we simply used the equation 2.29–0.33*ln(2000)=−0.21 from Table 2. In other words, the model predicts that a 1% increase in Cd concentration will result in a 0.21% decrease in mortality with Zn at 2000 μg/L. Similar calculations were also made for concentrations of Zn in combination with d. In this case, an increase of Zn concentration by 1% with Cd held at 200 μg/L, the model predicts Daphnia mortality will decrease by 0.16% (Table 2). In contrast, an increase in As concentration by 1%, in the presence of Zn at 2000 μg/L, is predicted to increase Daphnia mortality by 0.25% (Table 2). The well characterized response model created by the AID process allows for a nearly limitless examination of individual stressor concentrations. Furthermore, this same process can be used to predict the effects changes in stressor concentration levels have on significant interactions, as illustrated in the Discussion.
4. Discussion
4.1 Previous works and their limitations
Current experimental designs and analyses for assessing the effects of multiple stressor including interactive effects using acute toxicity tests, are constrained by one or more of the following limitations: 1) large, complex experimental designs to test more than a few stressors in combination, 2) significant amount of a priori knowledge required, and 3) inability to characterize complex interactions. These problems arise primarily because the response variable associated with acute toxicity tests, mortality, is nonlinear.
The most commonly used experimental design and analysis for acute toxicity testing is that of the full factorial accompanied by an analysis of variance (ANOVA). Since ANOVA assumes a continuous response and mortality is a binary response, a probit or logit transformation is typically used to linearize the response (Chen et al. 2004, 2008; De Schamphelaere and Janssen 2004; Edginton et al. 2004; Folt et al. 1999; Heijerick et al. 2003). This transformation technique is limited by its inability to incorporate response values of 0% or 100%, which are common in acute toxicity testing. The factorial design is a basic design which has been improved upon by methods such as the central composite design. However, the central composite design is limited by large, complex experimental designs that become impractical when examining higher order mixtures.
Although ANOVA combined with probit transformation is the most commonly used method for analyzing nonlinear endpoints associated with acute toxicity tests, there are other methods available such as LIFETEST in SAS and the chi-square test with 95% intervals. However, these too are limited in ways that make them inadequate for the study of the effects of multiple stressors. The survival analysis method is limited by the fact that interactions are not directly assessed, but instead inferred from multiple pair-wise comparisons among the different stressor treatments, and the interactive effects are not clearly defined or quantified (Chen et al. 2004, 2008; Folt et al. 1999). The chi-square test with 95% confidence intervals uses a probit transformation and predicts effects based on additive models (see Enserink et al. 1991; Greco et al. 1992; Shaw et al. 2006). The major limitation of this approach is the need for a substantial amount of a priori knowledge to characterize the response curve for even a single stressor, and the challenge is even greater to examine a multitude of stressors.
Mixture models are commonly used to address the issue that stressors co-occurring in nature. However, the lack of consensus on how to apply these models has only further complicated the issue of using linear models (Berenbaum 1989; Folt et al. 1999; Greco et al. 1992; Jonker et al. 2005; Norwood et al. 2003; Suzuki 1994; Vighi et al. 2003). The conflict over the use of mixture models has been substantiated by studies using both models on the same data set and showing conflicting results regarding the nature of chemical interactions (e.g. Konemann and Pieters 1996). The two most commonly used mixture models are concentration additivity and effects-based independent action, each of which has significant limitations as described in brief below; however, for a more thorough review on the subject see Drescher and Boedeker (1995) and the review by Norwood et al. (2003). The concentration additivity model is based on the assumption that individual contaminants in a mixture exhibit similar slopes in their response curves (i.e. modes of action; Groten et al. 2001; Loewe and Muischnek 1926). This assumption requires the use of identical slopes for the concentration-response curves of the individual components (Chen and Chiou 1995). In contrast, effects-based independent action models incorporate the effects of the individual contaminants to predict the overall toxicity of a mixture (Greco et al. 1992; Groten et al. 2001). Although no assumptions regarding toxic mechanisms (i.e. the slope of the response curve) of the individual toxicants are needed, a well-defined concentration response curve is required in order to establish effects concentrations.
A comparison of these two mixture models at ecologically relevant levels by Boedeker et al. (1993) revealed that the concentration additive model consistently predicted a higher combined effect than the independent action model. This suggests that the concentration additive model is the more conservative mixture model. To some this may justify the regulatory agency U.S.E.P.A.’s continued use of the concentration additive model to combine the results of the individual stressor acute toxicity tests when dealing with mixtures, as previously mentioned. However, this issue of which mixture model is the most appropriate to use, the concentration additive or the independent action, is far from resolved (Greco et al. 1992). Furthermore, neither mixture model is able to account for the complex (i.e. less than or greater than additive) effects of mixtures (Bury et al. 2002; Drescher and Boedeker 1995; Edginton et al. 2004; Heijerick et al. 2002; Norwood et al. 2003). The inability to accurately determine and quantify complex interactions known to occur in mixtures, prevents regulators from accurately accessing the effects of contaminants in our environment and therefore set proper water quality criteria. To address this issue we propose a novel model approach to ecotoxicology whose design is comparable to other previously described models found in the statistical literature, but never before applied to the field of ecotoxicology to identify and quantify complex interactive effects associated with mixtures.
4.2 Validity of AID
Current standard methods for assessing the effects of multiple stressors in aquatic environments employ very large and complex experimental designs that often require significant amounts of prior knowledge, and use complex statistical analyses for quantifying stressors effects, yet are still unable to quantify interaction terms. This presents a significant challenge for environmental toxicologists when assessing the overall toxicity of multiple contaminants on aquatic organisms, and for regulators when trying to develop water quality criteria that adequately protect the health of aquatic systems. We successfully developed a program that addresses these challenges. Our AID program identified the optimal model, accurately determined the direction, and quantified the magnitude of both individual and interactive effects. Additionally, we were able to use AID to extrapolate our findings to relevant concentrations of our mixture variables not tested directly. All this was accomplished with an easy to use program that minimizes the amount of a priori knowledge and experimental units, yet maintains the statistical power to accurately assess complex interactive effects.
4.3 Validation of AID
We validated our model by testing a combination of stressors and chemical modifiers known to interact in aquatic systems. Here we only discuss the significant interactions and those that did not conform to expectations. The most significant interaction determined by the AID program was the less than additive interaction of ln(Cd)*ln(Zn) on D. pulex mortality. This finding of less than additive interactive effects between Cd and Zn has been shown in previous studies, among them Shaw et al. (2006). In their study they attributed this interaction to the fact that Zn and Cd share a common uptake pathway and because Zn was always present in molar excess, Cd even at toxic levels was outcompeted for uptake (Shaw et al. 2006). Determination of Zn-Cd as the optimal model allowed for a closer examination into the fate of the five variables, both as individuals and in combinations.
The less than additive effects between Cd and Zn, enables us to compute a neutralizing value for these two metals using the coefficients of the ln(Cd)*ln(Zn) model. The neutralizing value is a concentration level at which any increases in the other metal will have no effect on Daphnia mortality. The Zn neutralizing value at which point mortality is not affected by increase of Cd levels, within the bounds of the concentrations tested is derived from the equation 2.29–0.33*ln(Zn)=0. This equation populated with values from Table 1, predicts that when Zn concentrations exceed 1000 μg/L any increase in Cd concentration will have no effect on Daphnia mortality within the concentration range tested (i.e. 40 – 260 μg/L). Using this same technique the neutralizing value for Cd is 122 μg/L, at which point Zn levels of 400 – 1000 μg/L are predicted to have no effect on mortality. Regulators may not find the calculation of neutralizing values helpful, since they often focus on non-lethal response variables. However, the AID process can easily be extended to population level endpoints, such as reproduction, making the ability to determine the neutralizing effects of multiple stressors of great interest to regulators.
In the analysis of all possible combinations of Cd, Zn, As, pH and hardness, we found that the inclusion of higher order interactions did not improve the model. Only the addition of certain binary interaction terms increased the predictability of the dose response compared to the basic model (Table 2). The power of binary combinations over higher order interaction terms has also been shown in a study examining the effects of multiple metal stressors in terrestrial systems (Jonker et al. 2005). This finding suggests that the numerous binary stressor studies common in the ecotoxicology literature may be instrumental in predicting the effects of the multitude of higher order mixtures common in our aquatic environments. However, further research on binary combinations and their roll in predicting higher order combinations of stressors is warranted to determine how often binary combinations successfully predict the dose response of mixtures, and why binary combinations are better predictors than higher order interaction terms.
Multiple stressor studies have historically relied on full factorial design, which is still being deemed as one of the better experimental design options for the study of multiple stressors (Jonker et al. 2005). However, as discussed earlier, this design is only practical when testing a small number of stressors due to the number of experimental replicates needed to test the effects of all possible stressor combinations. Alternative methods have been developed to address this limitation, such as the center point enhanced and the central composite design. Both of these methods reduce the number of experimental units and gain efficiency by using an incomplete factorial design, by which design points are set to maximize the range of interest (Baca and Threlkeld 2000; Heijerick et al. 2003; Edginton et al. 2004). Compensation for the loss of statistical power from an unbalanced experimental design comes from the use of more complex statistical analyses than that of the traditional ANOVA. While these methods have their limitations, as discussed earlier, a major difference between these methods and the method presented here is the required size of the experiment.
Here we compare our design to both the full factorial design and the more resource efficient of the modified factorial designs, the center point enhanced design. The full factorial design would require 243 experimental units, without replication. While, the center point enhanced design would require a minimum of 33 experimental units, assuming the minimum number of replicates for both the center point (3) and additional design point (1). This is truly a minimum because the center point enhanced design is dependent on how well the values put in characterize the response curve. In other words, if the stressors response curves or interactions are unknown, then it is highly likely to run through several iterations of the center point design. And you may still be unable to properly characterize the response curves associated with complex mixtures, because you are basically shooting in the dark. AID has no set requirement due to its iterative nature. Furthermore, the adaptive-iterative aspect of our design allows for our model to use the new data before determining the next set of concentrations to tests in order to best characterize the response curves. This is a more efficient and iterative approach than tradition designs currently being used to test multiple stressors.
AID also reduces the amount of prior knowledge required for the contaminants of interest, compared to the aforementioned methods, to initially parameterize the model. Toxicity values can be obtained, either from the primary literature or in our case from acute toxicity tests. The inclusion of the iterative process allows AID to 1) utilize non-linear acute toxicity data, 2) quantify the effects of multiple stressor interactions that are additive, less than additive or greater than additive, 3) quantify the magnitude and direction of these interactions, 4) more accurately detect significant interaction and 5) be more cost effective by reducing not only the number of experimental units per test, but even the number of tests required to fully characterize the complex dose-response curve associated with the effects of multiple stressors on a non-continuous response variable, such as mortality.
The AID approach was primarily developed for testing the acute effects of multiple stressors on aquatic organisms (i.e. mortality); however, it can also be used in combination with linear models and the analysis of continuous data sets to test for chronic effects such as reproduction and growth rate. In addition, it is flexible and can be applied to either concentration-response or other effects-based independent action approach, to significantly reduce the requirement of having a well-characterized response curves for each stressor. Finally, this iterative approach can utilize previously published single and multiple stressor acute toxicity data to improve existing models on contaminant toxicity. For these reasons we provide the R-code, in full, with instructions for using the AID program (see Appendix C). Our primary goal was to develop a method that simplifies the experimental design and analysis required for examining the effects of multiple stressors on aquatic organisms. However, our methods have the potential to be used in other ecosystems and with other endpoints. We hope our model promotes the study of interactive effects for the purposes of improving our understanding of how contaminants interact in highly variable environments. Moreover, we believe this novel approach allows for a more effective way to address the problem of managing contaminant mixtures in a regulatory framework.
Supplementary Material
Highlights.
The adaptive-iterative design (AID) examines nonlinear variable response to stressors.
AID reduces the amount of a priori knowledge and size of experimental design.
An easy to use R-code program to identify greater- and less-than additive effects.
Accurate determination of direction and magnitude of individual and interactive effects.
We report that binary interactions are the best predictors of higher order mixture effects.
Acknowledgments
The project described was supported by National Institute of Environmental Health Sciences (NIEHS) awards P42ES007373 through the Superfund Basic Research Program to CYC and CLF, and R01ES019324 through the Outstanding New Environmental Science program to JRS, and awards from the National Cancer Institute (NCI), CA130880 and U54CA151662 to ED. The content is solely the responsibility of the authors and does not necessarily represent the official views of NIEHS, NCI, or the National Institutes of Health. Support was also provided by the School of Public and Environmental Affairs at Indiana University and the Center for Environmental Health Sciences at Dartmouth College. We thank Anna Bowling for edits on drafts of this paper. The current manuscript was improved through the contributions of three anonymous reviewers. This work both benefits and contributes to the Daphnia Genomics Consortium.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abdelbasit KM, Plackett RL. Experimental Design for binary data. Journal of the American Statistical Association. 1983;78:90–98. [Google Scholar]
- Baca RM, Threlkeld ST. The effects of toxicants on planktonic systems an integrated approach using the analysis of size distributions. J Aquatic Ecosystem stress Recovery. 2000;8:95–105. [Google Scholar]
- Balistrieri LS, Blank RG. Dissolved and labile concentrations of Cd, Cu, Pb and Zn in the South Fork Coeur d’Alene River, Idaho: Comparisons among chemical equilibrium models and implications for biotic ligand models. Applied Geochemistry. 2008;23:3355–3371. [Google Scholar]
- Barata C, Baird DJ, Markich SJ. Influence of genetic and environmental factors on the tolerance of Daphnia magna Straus to essential and non-essential metals. Aquatic Toxicology. 1998;42:115–137. [Google Scholar]
- Berenbaum MC. What is synergy? Pharmacological Reviews. 1989;41:93–141. [PubMed] [Google Scholar]
- Berkson J. Why I prefer logits to probits. Biometrics. 1951;7:327–339. [Google Scholar]
- Boedeker W, Drescher K, Altenberger R, Faust M, Grimme LH. Combined effects of toxicants: The need and soundness of assessment approaches in ecotoxicology. The Science of the Total Environment. 1993;(Supplement):931–939. [Google Scholar]
- Bury NR, Shaw J, Glover C, Hogstrand C. Derivation of a toxicity-based model to predict how water chemistry influences silver toxicity to invertebrates. Comparative Biochemistry and Physiology C-Toxicology & Pharmacology. 2002;133:259–270. doi: 10.1016/s1532-0456(02)00096-0. [DOI] [PubMed] [Google Scholar]
- Canizares-Villanueva RO, Martinez-Jeronimo F, Espinosa-Chavez F. Acute toxicity to Daphnia magna of effluents containing Cd, Zn, and a mixture Cd-Zn, after metal removal by Chlorella vulgaris. Environmental Toxicology. 2000;15:160–164. [Google Scholar]
- Carter WH, Gennings C, Staniswalis JG, Campbell ED, White KL. A statistical approach to the construction and analysis of isobolograms. Journal of the American College of Toxicology. 1988;7:963–973. [Google Scholar]
- Chen CY, Chiou YS. Toxicity of binary-mixtures of organic-chemicals. Environmental Toxicology and Water Quality. 1995;10:97–106. [Google Scholar]
- Chen CY, Hathaway KM, Folt CL. Multiple stress effects of Vision (R) herbicide, pH, and food on zooplankton and larval amphibian species from forest wetlands. Environ Toxicol Chem. 2004;23:823–831. doi: 10.1897/03-108. [DOI] [PubMed] [Google Scholar]
- Chen CY, Hathaway KM, Thompson DG, Folt CL. Multiple stressor effects of herbicide, pH, and food on wetland zooplankton and a larval amphibian. Ecotoxicology and Environmental Safety. 2008;71:209–218. doi: 10.1016/j.ecoenv.2007.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christensen ER, Chen CY. A general noniterative multiple toxicity model including probit, logit, and Weibull transformations. Biometrics. 1985;41:711–725. [PubMed] [Google Scholar]
- Demidenko E. Theory and Applications. New York: Wiley; 2004. Mixed Models. [Google Scholar]
- De Schamphelaere KAC, Janssen CR. Effects of dissolved organic carbon concentration and source, pH, and water hardness on chronic toxicity of copper to Daphnia magna. Environ Toxicol Chem. 2004;23:1115–1122. doi: 10.1897/02-593. [DOI] [PubMed] [Google Scholar]
- Drescher K, Boedeker W. Assessment of the combined effects of substances: The relationship between concentration addition and independent action. Biometrics. 51:716–730. [Google Scholar]
- Dror HA, Steinberg DM. Robust experimental design for multivariate generalized linear models. Technometrics. 2006;48:520–529. [Google Scholar]
- Dror HA, Steinberg DM. Sequential experimental designs for generalized linear models. Journal of American Statistical Association. 2008;103:288–298. [Google Scholar]
- Edginton AN, Sheridan PM, Boermans HJ, Thompson DG, Holt JD, Stephenson GR. A comparison of two factorial designs, a complete 3×3 factorial and a central composite rotatable design, for use in binomial response experiments in aquatic toxicology. Archives of Environmental Contamination and Toxicology. 2004;46:216–223. doi: 10.1007/s00244-003-2176-9. [DOI] [PubMed] [Google Scholar]
- Enserink EL, Maasdiepeveen JL, Vanleeuwen CJ. Combined effects of metals-An ecotoxicological evaluation. Water Research. 1991;25:679–687. [Google Scholar]
- Fleeger JW, Gust KA, Marlborough SJ, Tita G. Mixtures of metals and polynuclear aromatic hydrocarbons elicit complex, nonadditive toxicological interactions in meiobenthic copepods. Environ Toxicol Chem. 2007;26:1677–1685. doi: 10.1897/06-397r.1. [DOI] [PubMed] [Google Scholar]
- Folt CL, Chen CY, Moore MV, Burnaford J. Synergism and antagonism among multiple stressors. Limnology and Oceanography. 1999;44:864–877. [Google Scholar]
- Gotwalt CM, Jones BA, Steinberg DM. Fast computation of desings robust to parameter uncertainty for nonlinear settings. Technometrics. 2009;51:88–95. [Google Scholar]
- Greco WR, Unkelbach HD, Poch G, Suhnel J, Kundi M, Boedeker W. Consensus on concepts and terminology for combined action assessment: The Saariselka agreement. Archives of Complex Environmental Studies. 1992;4:65–69. [Google Scholar]
- Groten JP, Feron VJ, Suhnel J. Toxicology of simple and complex mixtures. Trends in Pharmacological Sciences. 2001;22:316–322. doi: 10.1016/s0165-6147(00)01720-x. [DOI] [PubMed] [Google Scholar]
- Hare L. Aquatic insects and trace-metals-Bioavailability, bioaccumulation, and toxicity. Critical Reviews in Toxicology. 1992;22:327–369. doi: 10.3109/10408449209146312. [DOI] [PubMed] [Google Scholar]
- Heijerick DG, De Schamphelaere KAC, Janssen CR. Predicting acute zinc toxicity for Daphnia magna as a function of key water chemistry characteristics: Development and validation of a biotic ligand model. Environmental Toxicology and Chemistry. 2002;21:1309–1315. [PubMed] [Google Scholar]
- Heijerick DG, Janssen CR, De Coen WM. The combined effects of hardness, pH, and dissolved organic carbon on the chronic toxicity of Zn to D. magna: Development of a surface response model. Archives of Environmental Contamination and Toxicology. 2003;44:210–217. doi: 10.1007/s00244-002-2010-9. [DOI] [PubMed] [Google Scholar]
- Hewlett PS, Plackett RL. A unified theory for quantal responses to mixtures of drugs: Non-iterative action. Biometrics. 1959;15:591–610. [Google Scholar]
- Hinkelmann K, Kempthorne O. Design and Analysis of Experiments. 2. I and II. New York: Wiley; 2008. [Google Scholar]
- Jonker MJ, Svendsen C, Bedaux JJM, Bongers M, Kammenga JE. Significance testing of synergistic/antagonistic, dose level-dependent, or dose ratio-dependent effects in mixture dose-response analysis. Environ Toxicol Chem. 2005;24:2701–2713. doi: 10.1897/04-431r.1. [DOI] [PubMed] [Google Scholar]
- Khuri AI, Mukherjee B, Sinha BK, Ghosh M. Design issues of General Linear Models: A Review. Statistical Science. 2006;21:376–399. [Google Scholar]
- Kilham SS, Kreeger DA, Lynn SG, Goulden CE, Herrera L. COMBO: a defined freshwater culture medium for algae and zooplankton. Hydrobiologia. 1998;377:147–159. [Google Scholar]
- Komjarova I, Blust R. Multi-metal interactions between Cd, Cu, Ni, Pb and Zn in water flea Daphnia magna, a stable isotope experiment. Aquatic Toxicology. 2008;90:138–144. doi: 10.1016/j.aquatox.2008.08.007. [DOI] [PubMed] [Google Scholar]
- Konemann WH, Pieters MN. Confusion of concepts in mixture toxicology. Food and Chemical Toxicology. 1996;34:1025–1031. doi: 10.1016/s0278-6915(97)00070-7. [DOI] [PubMed] [Google Scholar]
- Loewe S. The problem of synergism and antagonism of combined drugs. Arzneim Forsch. 1953;3:285–290. [PubMed] [Google Scholar]
- Loewe S, Muischnek H. Effect of combinations: mathematical basis of the problem. Arch Exp Pathol Pharmacol. 1926;114:313–326. [Google Scholar]
- Mathew T, Sinha BK. Optimal designs for binary data under logistic regression. Journal of Statistical Planning and Inference. 2001;93:295–307. [Google Scholar]
- McCullagh P, Nelder JA. Generalized Linear Models. 2. New York: Chapman and Hall; 1989. [Google Scholar]
- McCulloch CE, Searle SR. Generalized, Linear and Mixed Models. New York: Wiley; 2001. [Google Scholar]
- Mothersill C, Salbu B, Heier LS, Teien HC, Denbeigh J, Oughton D, Rosseland BO, Seymour CB. Multiple stressor effects of radiation and metals in salmon (Salmo salar) Journal of Environmental Radioactivity. 2007;96:20–31. doi: 10.1016/j.jenvrad.2007.01.025. [DOI] [PubMed] [Google Scholar]
- Muyssen BTA, De Schamphelaere KAC, Janssen CR. Mechanisms of chronic waterborne Zn toxicity in Daphnia magna. Aquatic Toxicology. 2006;77:393–401. doi: 10.1016/j.aquatox.2006.01.006. [DOI] [PubMed] [Google Scholar]
- Norwood WP, Borgmann U, Dixon DG, Wallace A. Effects of Metal Mixtures on Aquatic Biota: A Review of Observations and Methods. Human and Ecological Risk Assessment. 2003;9:795–811. [Google Scholar]
- OECD. Guideline for testing of chemicals: Part 1- the 24hr EC50 acute immobilization test. 1984;202:1–3. [Google Scholar]
- Pukelsheim F. Optimal Design of Experiments. New York: Wiley; 1993. [Google Scholar]
- Rosner B. Fundamentals of Biostatistics. 5. Pacific Grove; Duxbury: 2000. [Google Scholar]
- Rothman KJ, Greenland S, Lash TL. Modern Epidemiology. 3. Philadelphia: Walters Kluwer; SAS Institute Inc; 2008. JMP version 5.0.1 2005. [Google Scholar]
- Schoen ED. Statistical designs in combination toxicology: a matter of choice. Food Chem Toxicol. 1996;34:1059–1065. doi: 10.1016/s0278-6915(97)00075-6. [DOI] [PubMed] [Google Scholar]
- Schwarzenbach RP, Escher BI, Fenner K, Hofstetter TB, Johnson CA, von Gunten U, Wehrli B. The challenge of micropollutants in aquatic systems. Science. 2006;313:1072–1077. doi: 10.1126/science.1127291. [DOI] [PubMed] [Google Scholar]
- Shaw JR, Dempsey TD, Chen CY, Hamilton JW, Folt CL. Comparative toxicity of cadmium, zinc, and mixtures of cadmium and zinc to daphnids. Environ Toxicol Chem. 2006;25:182–189. doi: 10.1897/05-243r.1. [DOI] [PubMed] [Google Scholar]
- Sunda WG, Huntsman SA. Antagonisms between cadmium and zinc toxicity and manganese limitation in a coastal diatom. Limnology and Oceanography. 1996;41:373–387. [Google Scholar]
- Suzuki T, Watanabe K, Kikkawa S, Nakagami H. Effect of crystallinity of microcrystalline cellulose on granulation in high-shear mixer. Chemical & Pharmaceutical Bulletin. 1994;42:2315–2319. [Google Scholar]
- U.S.E.P.A. Methods for Measuring the Acute Toxicity of Effluents and Receiving Waters to Freshwater and Marine Organisms, 5th addition. Washington, DC: U.S.E.P.A., Office of Water; 2002. p. 275. [Google Scholar]
- U S.E.P.A. Guidelines for the health risk assessment of chemical mixtures. Federal Register. 1986;51:3414–34025. [Google Scholar]
- Vighi M, Altenburger R, Arrhenius A, Backhaus T, Bodeker W, Blanck H, Consolaro F, Faust M, Finizio A, Froehner K, Gramatica P, Grimme LH, Gronvall F, Hamer V, Scholze M, Walter H. Water quality objectives for mixtures of toxic chemicals: problems and perspectives. Ecotoxicology and Environmental Safety. 2003;54:139–150. doi: 10.1016/s0147-6513(02)00047-7. [DOI] [PubMed] [Google Scholar]
- Wang WX, Fisher NS. Effects of calcium and metabolic inhibitors on trace element uptake in two marine bivalves. Journal of Experimental Marine Biology and Ecology. 1999;236:149–164. [Google Scholar]
- Woods DC, Lewis SM, Eccleston JA, Russell KG. Designs for generalized linear models with several variables and model uncertainty. Technometrics. 2006;48:284–292. [Google Scholar]
- Xie FL, Lampi MA, Dixon DG, Greenberg BM. Assessment of the toxicity of mixtures of nickel or cadmium with 9,10-phenanthrenequinone to Daphnia magna: Impact of a reactive oxygen-mediated mechanism with different redox-active metals. Environ Toxicol Chem. 2007;26:1425–1432. doi: 10.1897/06-224r.1. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.