Surface phonons, elastic response, and conformal invariance in twisted kagome lattices

Abstract

Model lattices consisting of balls connected by central-force springs provide much of our understanding of mechanical response and phonon structure of real materials. Their stability depends critically on their coordination number z. d-dimensional lattices with z = 2d are at the threshold of mechanical stability and are isostatic. Lattices with z < 2d exhibit zero-frequency “floppy” modes that provide avenues for lattice collapse. The physics of systems as diverse as architectural structures, network glasses, randomly packed spheres, and biopolymer networks is strongly influenced by a nearby isostatic lattice. We explore elasticity and phonons of a special class of two-dimensional isostatic lattices constructed by distorting the kagome lattice. We show that the phonon structure of these lattices, characterized by vanishing bulk moduli and thus negative Poisson ratios (equivalently, auxetic elasticity), depends sensitively on boundary conditions and on the nature of the kagome distortions. We construct lattices that under free boundary conditions exhibit surface floppy modes only or a combination of both surface and bulk floppy modes; and we show that bulk floppy modes present under free boundary conditions are also present under periodic boundary conditions but that surface modes are not. In the long-wavelength limit, the elastic theory of all these lattices is a conformally invariant field theory with holographic properties (characteristics of the bulk are encoded on the sample boundary), and the surface waves are Rayleigh waves. We discuss our results in relation to recent work on jammed systems. Our results highlight the importance of network architecture in determining floppy-mode structure.

Networks of balls and springs or frames of nodes connected by compressible struts provide realistic models for physical systems from bridges to condensed solids. Their elastic properties depend on their coordination number z—the average number of nodes each node is connected to. If z is small enough, the networks have deformation modes of zero energy—they are floppy (1–6). As z is increased, a critical value, z_c, is reached at which springs provide just enough constraints that the system has no zero-energy floppy modes (7) (or mechanisms, ref. 2, in the engineering literature), and the system is isostatic. For z > z_c, networks with appropriate geometry (see below) are rigid in the sense that they have no zero modes other than those associated with trivial rigid translations and rotations. If a network with z > z_c is homogeneously distributed in space, it can be viewed as an elastic solid whose long-wavelength mechanical properties are described by a continuum elastic energy with nonvanishing elastic moduli (7–11). The phenomenon of rigidity percolation (12, 13) whereby a sample spanning rigid cluster develops upon the addition of springs is one version of this floppy-to-rigid transition. The coordination numbers of whole classes of systems, including engineering structures (14, 15) (bridges and buildings), randomly packed spheres near jamming (10, 11, 16, 17), network glasses (7, 8), cristobalites (18), zeolites (19, 20), and biopolymer networks (21–24) are close enough to z_c that their elasticity and mode structure is strongly influenced by those of the isostatic lattice.

Though the isostatic point always separates rigid from floppy behavior, the properties of isostatic lattices are not universal; rather they depend on lattice architecture. Here we explore the unusual properties of a particular class of periodic isostatic lattices derived from the two-dimensional kagome lattice by rigidly rotating triangles through an angle α without changing bond lengths as shown in Fig. 1. The bulk modulus B of these lattices is rigorously zero for all α ≠ 0. As a result, their Poisson ratio acquires its limit value of -1; when stretched in one direction, they expand by an equal amount in the orthogonal direction: They are maximally auxetic (25–28). These modes represent collapse pathways (29, 30) of the kagome lattice. Modes of isostatic systems are generally very sensitive to boundary conditions (9, 31, 32), but the degree of sensitivity depends on the details of lattice structure. For reasons we will discuss more fully below, modes of the square lattice, which is isostatic, are in fact insensitive to changes from free boundary conditions (FBCs) to periodic boundary conditions (PBCs), whereas those of the undistorted kagome lattice are only mildly so. The modes of both, however, change significantly when rigid boundary conditions (RBCs) are applied. We show here that, in all families of the twisted kagome lattice, modes depend sensitively on whether FBCs, PCBs, or RBCs are applied: Finite lattices with free boundaries have floppy surface modes that are not present in their periodic or rigid spectrum or in that of finite undistorted kagome lattices. In the long-wavelength limit, the surface floppy modes, which are present in any 2d material with B = 0, reduce to surface Rayleigh waves (33) described by a conformally invariant energy whose analytic eigenfunctions are fully determined by boundary conditions. At shorter wavelengths, the surface waves become sensitive to lattice structure and remain confined to within a distance of the surface that diverges as the undistorted kagome lattice is approached. In the simplest twisted kagome lattice, all floppy modes are surface modes, but in more complicated lattices, including ones with uniaxial symmetry that we construct, there are both surface and bulk floppy modes.

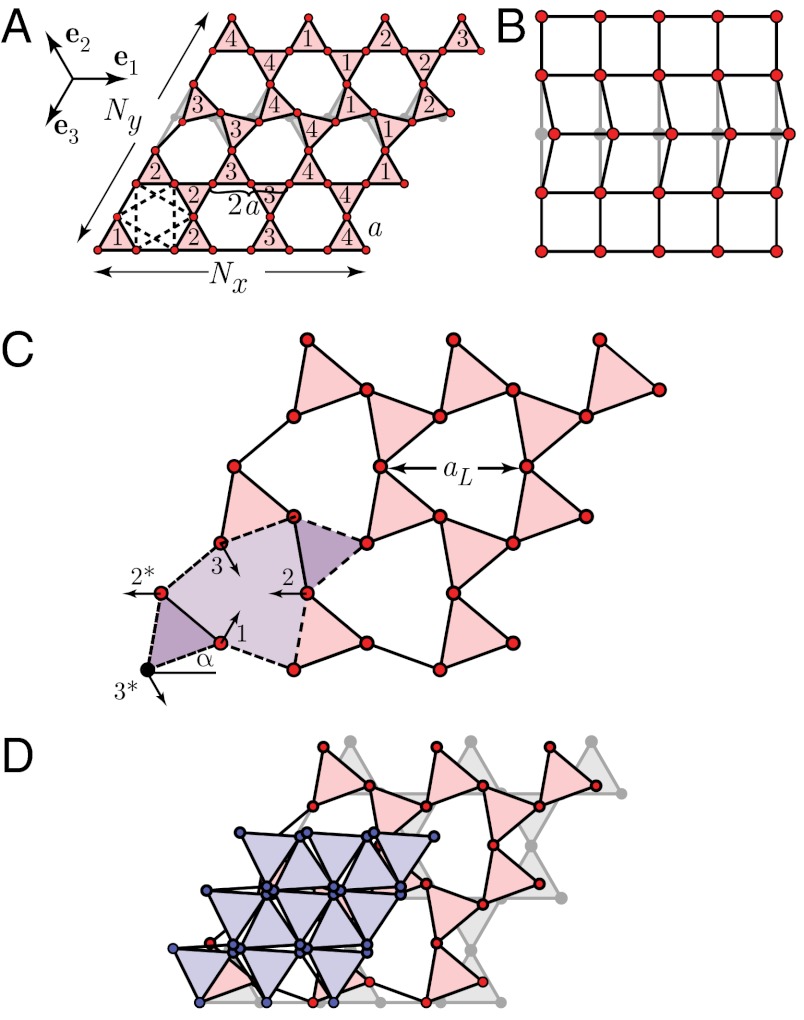
Fig. 1.

(A) Section of a kagome lattice with N_x = N_y = 4 and N_c = N_xN_y three-site unit cells. Nearest-neighbor bonds, occupied by harmonic springs, are of length a. The rotated row (second row from the top) represents a floppy mode. Next-nearest-neighbor bonds are shown as dotted lines in the lower left hexagon. The vectors e₁, e₂, and e₃ indicate symmetry directions of the lattice. The numbers in the triangles indicate those that twist together under PBCs in zero modes along the three symmetry direction. Note that there are only four of these modes. (B) Section of a square lattice depicting a floppy mode in which all sites along a line are displaced uniformly. (C) Twisted kagome lattice, with lattice constant a_L = 2a cos α, derived from the undistorted lattice by rigidly rotating triangles through an angle α. A unit cell, bounded by dashed lines, is shown in violet. Arrows depict site displacements for the zone-center (i.e., zero wavenumber) ϕ mode which has zero (nonzero) frequency under free (periodic) boundary conditions. Sites 1, 2, and 3 undergo no collective rotation about their center of mass, whereas sites 1, 2^∗, and 3^∗ do. (D) Superposed snapshots of the twisted lattice showing decreasing areas with increasing α.

Arguments due to Maxwell (1) provide a criterion for network stability: Networks in d dimensions consisting of N nodes, each connected with central-force springs to an average of z neighbors, have 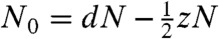zero-energy modes when z < 2d (in the absence of redundant bonds—see below). Of these, a number, N_tr, which depends on boundary conditions, are trivial rigid translations and rotations, and the remainder are floppy modes of internal structural rearrangement. Under FBCs and PBCs, N_tr equals d(d + 1)/2 and d, respectively. With increasing z, mechanical stability is reached at the isostatic point at which N₀ = N_tr. The Maxwell argument is a global one; it does not provide information about the nature of the floppy modes and does not distinguish between bulk or surface modes.

Kagome Zero Modes and Elasticity

The kagome lattice of central-force springs shown in Fig. 1A is one of many locally isostatic lattices, including the familiar square lattice in two dimensions (Fig. 1B) and the cubic and pyrochlore lattices in three dimensions, with exactly z = 2d nearest-neighbor (NN) bonds connected to each site not at a boundary. Under PBCs, there are no boundaries, and every site has exactly 2d neighbors. Finite, N-site sections of these lattices have surface sites with fewer than 2d neighbors and of order 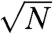zero modes. The free kagome lattice with N_x and N_y unit cells along its sides (Fig. 1A) has N = 3N_xN_y sites, N_B = 6N_xN_y - 2(N_x + N_y) + 1 bonds, and N₀ = 2(N_x + N_y) - 1 zero modes, all but three of which are floppy modes. These modes, depicted in Fig. 1A, consist of coordinated counterrotations of pairs of triangles along the symmetry axes e₁, e₂, and e₃ of the lattice. There are N_x modes associated with lines parallel to e₁, N_y associated with lines parallel to e₃, and N_x + N_y - 1 modes associated with lines parallel to e₂.

In spite of the large number of floppy modes in the kagome lattice, its longitudinal and shear Lamé coefficients, λ and μ, and its bulk modulus B = λ + μ are nonzero and proportional to the NN spring constant k: 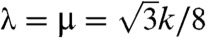and 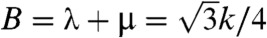. The zero modes of this lattice can be used to generate an infinite number of distorted lattices with unstretched springs and thus zero energy (30). We consider only periodic lattices, the simplest of which are the twisted kagome lattices obtained by rotating triangles of the kagome unit cell through an angle α as shown in Fig. 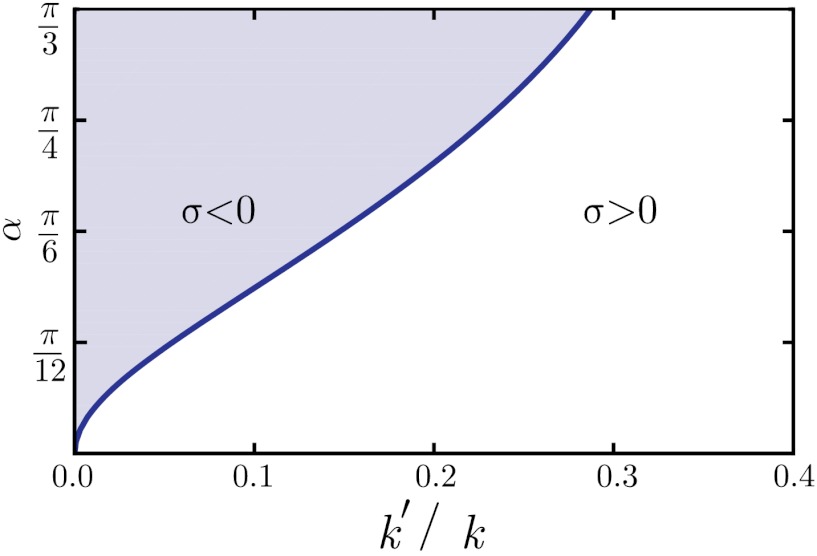1 C and D (30, 34). These lattices have C_3v rather than C_6v symmetry and, like the undistorted kagome lattice, three sites per unit cell. As Fig. 1D shows, the lattice constant of these lattices is a_L = 2a cos α, and their area A_α decreases as cos²α as α increases. The maximum value that α can achieve without bond crossings is π/3, so that the maximum relative area change is A_π/3/A₀ = 1/4. Because all springs maintain their rest length, there is no energy cost for changing α and, as a result, B is zero for every α ≠ 0, whereas the shear modulus 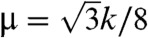remains nonzero and unchanged. Thus, the Poisson ratio σ = (B - μ)/(B + μ) attains its smallest possible value of -1. For any α ≠ 0, the addition of next-nearest-neighbor (NNN) springs, with spring constant k^′ (or of bending forces between springs) stabilizes zero-frequency modes and increases B and σ. Nevertheless, for sufficiently small k^′, σ remains negative. Fig. 2 shows the region in the k^′ - α plane with negative σ.

Fig. 2.

Phase diagram in the α - k^′ plane showing region with negative Poisson ratio σ.

Kagome Phonon Spectrum

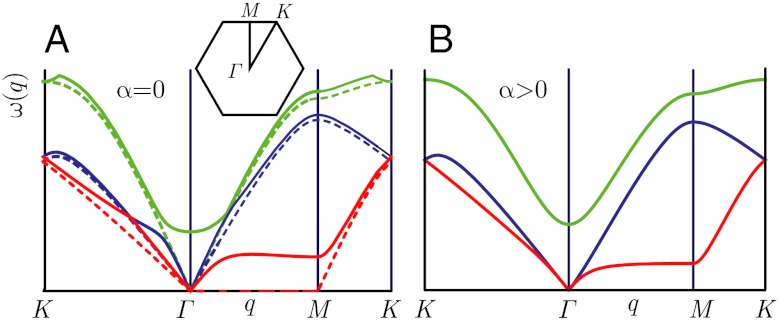
We now turn to the linearized phonon spectrum of the kagome and twisted kagome lattices subjected to PBCs. These conditions require displacements at opposite ends of the sample to be identical and thus prohibit distortions of the shape and size of the unit cell and rotations but not uniform translations, leaving two rather than three trivial zero modes. The spectrum (35) of the three lowest frequency modes along symmetry directions of the undistorted kagome lattice with and without NNN springs is shown in Fig. 3A. When k^′ = 0, there is a floppy mode for each wavenumber q ≠ 0 running along the entire length of the three symmetry-equivalent straight lines running from M to Γ to M in the Brillouin zone (see Fig. 3, Inset). When N_x = N_y, there are exactly N_x - 1 wavenumbers with q ≠ 0 along each of these lines for a total of 3(N_x - 1) floppy modes. In addition, there are three zero modes at q = 0 corresponding to two rigid translations and one floppy mode that changes unit cell area at second but not first order in displacements, yielding a total of 3N_x zero modes rather than the 4N_x - 1 modes expected from the Maxwell count under FBCs. This discrepancy is our first indication of the importance of boundary conditions. The addition of NNN springs endows the floppy modes at k^′ = 0 with a characteristic frequency 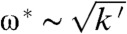and causes them to hybridize with the acoustic phonon modes (Fig. 3A) (35). The result is an isotropic phonon spectrum up to wavenumber 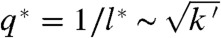and gaps at Γ and M of order ω^∗. Remarkably, at nonzero α and k^′ = 0, the mode structure is almost identical to that at α = 0 and k^′ > 0 with characteristic frequency 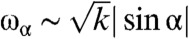and length l_α ∼ 1/ω_α. In other words, twisting the kagome lattice through an angle α has essentially the same effect on the spectrum as adding NNN springs with spring constant | sin α|²k. Thus, under PBCs, the twisted kagome lattice has no zero modes other than the trivial ones: It is “collectively” jammed in the language of refs. 32 and 36, but because it is not rigid with respect to changing the unit cell size, it is not strictly jammed.

Fig. 3.

(A) Phonon spectrum for the undistorted kagome lattice. Dashed lines depict frequencies at k^′ = 0 and full lines at k^′ > 0. The inset shows the Brillouin zone with symmetry points Γ, M, and K. Note the line of zero modes along ΓM when k^′ = 0, all of which develop nonzero frequencies for wavenumber q > 0 when k^′ > 0 reaching 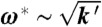on a plateau beginning at 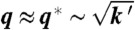defining a length scale l^∗ = 1/q^∗. (B) Phonon spectrum for α > 0 and k^′ = 0. The plateau along ΓM defines 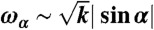and its onset at q_α ∼ ω_α defines a length l_α ∼ 1/| sin α|.

Mode Counting and States of Self-Stress

To understand the origin of the differences in the zero-mode count for different boundary conditions, we turn to an elegant formulation (2) of the Maxwell rule that takes into account the existence of redundant bonds (i.e., bonds whose removal does not increase the number of floppy modes; ref. 13) and states in which springs can be under states of self-stress (3–6). Consider a ring network in two dimensions shown in Fig. 4 with N = 4 nodes and N_b = 4 springs with three springs of length a and one spring of length b. The Maxwell count yields N₀ = 4 = 3 + 1 zero modes: two rigid translations, one rigid rotation, and one internal floppy mode—all of which are “finite-amplitude” modes with zero energy even for finite-amplitude displacements. When b = 3a, the Maxwell rule breaks down. In the zero-energy configuration, the long spring and the three short ones are colinear, and a prestressed state in which the b spring is under compression and the three a springs are under tension (or vice versa) but the total force on each node remains zero becomes possible. This is called a state of self-stress. The system still has three finite-amplitude zero modes corresponding to arbitrary rigid translations and rotations, but the finite-amplitude floppy mode has disappeared. In the absence of prestress, it is replaced by two “infinitesimal” floppy modes of displacements of the two internal nodes perpendicular of the now linear network. In the presence of prestress, these two modes have a frequency proportional to the square root of the tension in the springs. Thus, the system now has one state of self-stress and one extra zero mode in the absence of prestress, implying N₀ = 2N - N_B + S, where S is the number of states of self-stress.

Fig. 4.

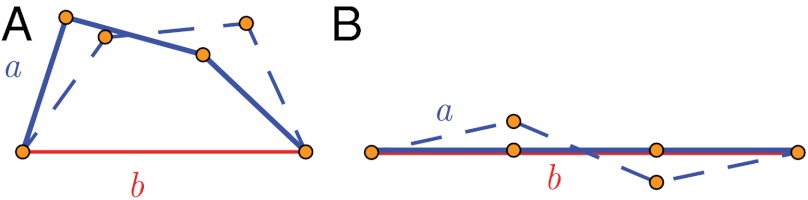
(A) Ring network with b > 3a showing internal floppy mode. (B) Ring-network with b = 3a showing one of the two infinitesimal modes.

This simple count is more generally valid, as can be shown with the aid of the equilibrium and compatibility matrices (2), denoted, respectively, as H and C ≡ H^T. H relates the vector t of N_B spring tensions to the vector f of dN forces at nodes via H·t = f, and C relates the vector d of dN node displacements to the vector e of N_B spring stretches via C·d = e. The dynamical matrix determining the phonon spectrum is D = kH·H^T. Vectors t₀ in the null space of H, (H·t₀ = 0), describe states of self-stress, whereas vectors d₀ in the null space of C represent displacements with no stretch e—i.e., modes of zero energy. Thus the null-space dimensions of H and C are, respectively, S and N₀. The rank-nullity theorem of linear algebra (37) states that the rank r of a matrix plus the dimension of its null space equals its column number. Because the rank of a matrix and its transpose are equal, the H and C matrices, respectively, yield the relations r + S = N_B and r + N₀ = dN, implying N₀ = dN - N_B + S. Under PBCs, locally isostatic lattices have z = 2d exactly, and the Maxwell rule yields N₀ = 0: There should be no zero modes at all. But we have just seen that both the square and undistorted kagome lattices under PBCs have of order 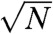zero modes as calculated from the dynamical matrix, which, because it is derived from a harmonic theory, does not distinguish between infinitesimal and finite-amplitude zero modes. Thus, in order for there to be zero modes, there must be states of self-stress, in fact, one state of self-stress for each zero mode.

In the square lattice under FBCs, N = N_xN_y and N_B = 2N_xN_y - N_x - N_y, there are no states of self-stress, and N₀ = N_x + N_y zero modes depicted in Fig. 1B. Under PBCs, the dimension of the null space of H is S = N_x + N_y, and there are also N₀ = S = N_x + N_y zero modes that are identical to those under FBCs. We have already seen that there are N₀ = 2(N_x + N_y) - 1 zero modes in the free undistorted kagome lattice. Direct evaluations (29) (see SI Text) of the dimension of the null spaces of H and C for the undistorted kagome lattice with PBCs yields S = N₀ = 3N_x when N_x = N_y. The zero modes under PBCs are identical to those under FBCs except that the 2N_x - 1 modes associated with lines parallel to e₂ under FBCs get reduced to N_x modes because of the identification of apposite sides of the lattice required by the PBCs, as shown in Fig. 1A. Thus the modes of both the square and kagome lattices do not depend strongly on whether FBCs or PBCs are applied. Under RBCs, however, the floppy modes of both disappear. The situation for the twisted kagome lattice is different. There are still 2(N_x + N_y) - 1 zero modes under FBCs, but there are only two states of self-stress under PBCs and thus only N₀ = S = 2 zero modes, as a direct evaluation of the null spaces of H and C verifies (SI Text), in agreement with the results obtained via direct evaluation of the eigenvalues of the dynamical matrix (35, 38). All of the floppy modes under FBCs have disappeared.

Effective Theory and Edge Modes

An effective long-wavelength energy E_eff for the low-energy acoustic phonons and nearly floppy distortions provides insight into the nature of the modes of the twisted kagome lattice. The variables in this theory are the vector displacement field u(x) of nodes at undistorted positions x and the scalar field ϕ(x) describing nearly floppy distortions within a unit cell. The detailed form of E_eff depends on which three lattice sites are assigned to a unit cell. Fig. 1C depicts the lattice distortion ϕ for the nearly floppy mode at Γ (with energy proportional to | sin α|²) along with a particular representation of a unit cell, consisting of a central asymmetric hexagon and two equilateral triangles, with eight sites on its boundary. If sites 1, 2, and 3 are assigned to the unit cell, then the distortion ϕ involves no rotations of these sites relative to their center of mass, and the harmonic limit of E_eff depends only on the symmetrized and linearized strain u_ij = (∂_iu_j + ∂_ju_i)/2 and on ϕ:

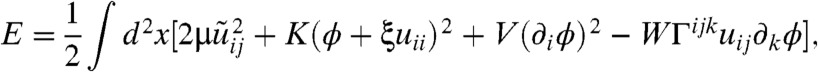[1]

where 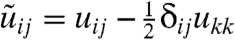is the symmetric-traceless stain tensor, 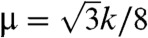, , 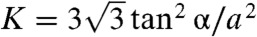, , 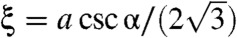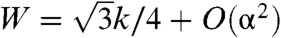and 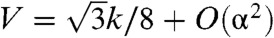. The last term in which Γ^ijk is a third-rank tensor, whose only nonvanishing components are Γ^xxx = -Γ^xyy = -Γ^yyx = -Γ^xyx = 1, is invariant under operations of the group C_6v but not under arbitrary rotations. The Kξϕu_ii term is the only one that reflects the C_3v (rather than C_6v) symmetry of the lattice. There are several comments to make about this energy. The gauge-like coupling in which the isotropic strain u_ii appears only in the combination (ϕ + ξu_ii)² guarantees that the bulk modulus vanishes: ϕ will simply relax to -ξu_ii to reduce to zero the energy of any state with nonvanishing u_ii. The coefficient K can be calculated directly from the observation that, under ϕ alone, the length of every spring changes by 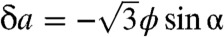, and this length change is reversed by a homogenous volume change u_ii = δA_α/A_α = -2δa/a. In the α → 0 limit, K → 0, and the energy reduces to that of an isotropic solid with bulk modulus 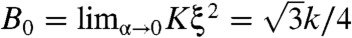if the V and W terms, which are higher order in gradients, are ignored. The W term gives rise to a term, singular in gradients of u, when ϕ is integrated out that is responsible for the deviations of the finite-wavenumber elastic energy from isotropy. At small α, the length scale l_α appears in several places in this energy: in the length ξ and in the ratios 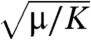, , 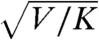and 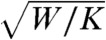. At length scales much larger than l_α, the V and W terms can be ignored, and ϕ relaxes to -ξu_ii, leaving only the shear elastic energy of an elastic solid proportional 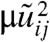. At length scales shorter than l_α, ϕ deviates from -ξu_ii and contributes significantly to the form of the energy spectrum. If 1, 2^∗, and 3^∗ in Fig. 1D are assigned to the unit cell, then ϕ involves rotations relative to the lattice axes, and the energy develops a Cosserat-like form (39, 40) that is a function of ϕ - a(∇ × u)_z/2 rather than ϕ.

The modes of our elastic energy in the long-wavelength limit (ql_α ≪ 1) are simply those of an elastic medium with B = 0. In this limit, there are transverse and longitudinal bulk sound modes with equal sound velocities 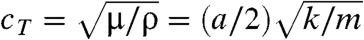and 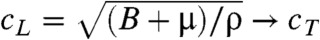, where m is the particle mass at each node and ρ is the mass density. In addition there are Rayleigh surface waves (33) in which there is a single decay length (rather than the two at B > 0), and displacements are proportional to e^-q_yy cos[q_xx] with q_y = q_x for a semiinfinite sample in the upper half-plane so that the penetration depth into the interior is 1/q_x. These waves have zero frequency in two dimensions when B = 0, and they do not appear in the spectrum with PBCs. Thus this simple continuum limit provides us with an explanation for the difference between the spectrum of the free and periodic twisted kagome lattices. Under FBCs, there are zero-frequency surface modes not present under PBCs.

Further insight into how boundary conditions affect spectrum follows from the observation that the continuum elastic theory with B = 0 depends only on 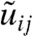. The metric tensor g_ij(x) of the distorted lattice is related to the strain u_ij(x) via the simple relation g_ij(x) = δ_ij + 2u_ij(x); and 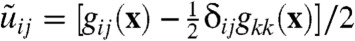, which is zero for g_ij = δ_ij, is invariant, and thus remains equal to zero, under conformal transformations that take the metric tensor from its reference form δ_ij to h(x)δ_ij for any continuous function h(x). The zero modes of the theory thus correspond simply to conformal transformations, which in two dimensions are best represented by the complex position and displacement variables z = x + iy and w(z) = u_x(z) + iu_y(z). All conformal transformations are described by an analytic displacement field w(z). Because, by Cauchy’s theorem, analytic functions in the interior of a domain are determined entirely by their values on the domain’s boundary (the “holographic” property; ref. 41), the zero modes of a given sample are simply those analytic functions that satisfy its boundary conditions. For example, a disc with fixed edges (u = 0) has no zero modes because the only analytic function satisfying this FBC is the trivial one w(z) = 0; but a disc with free edges (stress and thus strain equal to zero) has one zero mode for each of the analytic functions w(z) = a_nzⁿ for integer n≥0. The boundary conditions 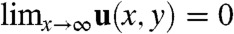and u(x,y) = u(x + L,y) on a semiinfinite cylinder with axis along x are satisfied by the function w(z) = e^iq_xz = e^iq_xxe^-q_xy when q_x = 2nπ/L, where n is an integer. This solution is identical to that for classical Rayleigh waves on the same cylinder. Like the Rayleigh theory, the conformal theory puts no restriction on the value of n (or equivalently q_x). Both theories break down, however, at 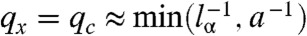, beyond which the full lattice theory, which yields a complex value of 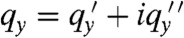, is needed.

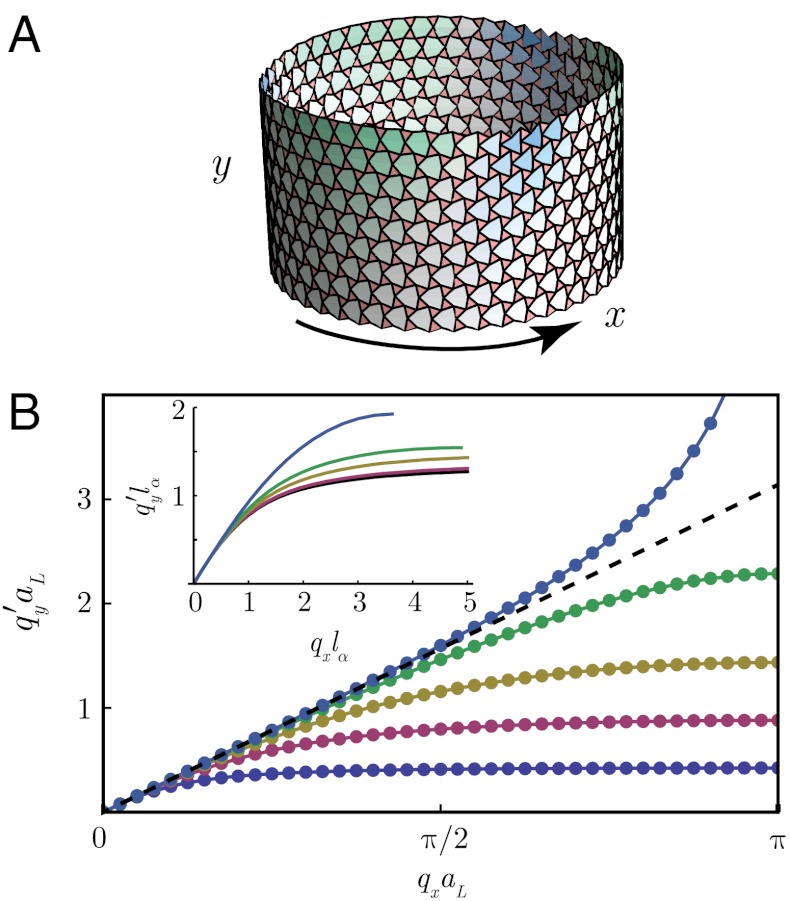
Fig. 5A shows an example of a surface wave. At the bottom of this figure, u_y(x) is an almost perfect sinusoid. As y decreases toward the surface, the amplitude grows, and in this picture reaches the nonlinear regime by the time the surface at y = 0 is reached. Fig. 5B plots 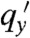as a function of q_x obtained both by direct numerical evaluation and by an analytic transfer matrix procedure (42) for different values of α (SI Text). The Rayleigh limit 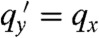is reached for all α as q_x → 0. Interestingly, the Rayleigh limit remains a good approximation up to values of q_x that increase with increasing α. The inset to Fig. 5 plots 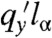as a function of η = q_xl_α and shows that in the limit α → 0 (l_α/a → ∞), 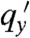obeys an α-independent scaling law of the form 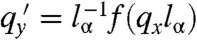. The full complex q_y obeys a similar equation. This type of behavior is familiar in critical phenomena where scaling occurs when correlation lengths become much larger than microscopic lengths. The function f(η) approaches η as η → 0 and asymptotes to 4/3 for η → ∞. Thus for q_xl_α ≪ 1, 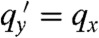and for q_xl_α≫1, 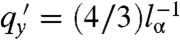. As α increases, l_α/a is no longer much larger than one, and deviations from the scaling law result. The situation for surfaces along different directions (e.g., along x = 0 rather than y = 0) is more complicated and is beyond the scope of this paper.

Fig. 5.

(A) Lattice distortions for a surface wave on a cylinder, showing exponential decay of the surface displacements into the bulk. This figure was constructed by specifying a small sinusoidal modulation on the bottom boundary and propagating lattice-site positions upward to the free boundary at the top under the constraint of constant lengths and periodic boundary conditions around the cylinder. Distortions near and at the top boundary, which have become nonlinear, are not described by our linearized treatment. (B) 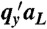as a function of q_xa_L for lattice Rayleigh surface waves for α = π/20, π/10, 3π/20, π/5, π/4, in order from bottom to top. Smooth curves are the analytic results from a transfer matrix calculation, and dots are from direct numerical calculations. The dashed line is the continuum Rayleigh limit 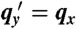. Curves at smaller α break away from this curve at smaller values of q_y than do those at large α. At α = π/4, 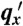diverges at q_ya_L = π. The inset plots 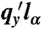as a function of q_xl_α for different α. The lower curve in the inset (black) is the α-independent scaling function of q_yl_α reached in the α → 0 limit. The other curves from top to bottom are for α = π/25, π/12, π/9, and π/6 (chosen to best present results rather than to match the curves in the main figure). Curves for α < π/15 are essentially indistinguishable from the scaling limit. The curve at α = π/6 stops because q_y < π/a_L.

Other Lattices and Relation to Jamming

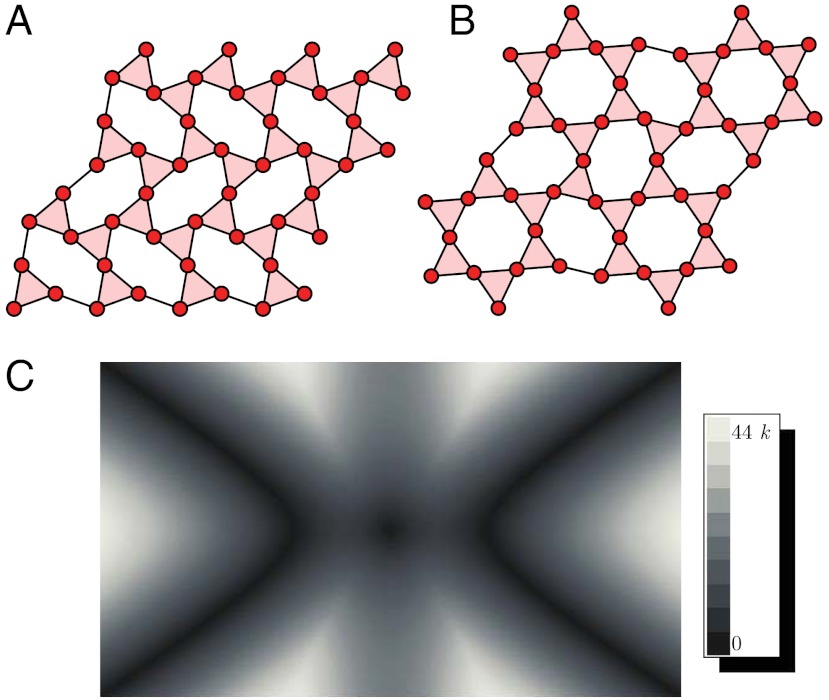
The C_3v twisted kagome lattice is the simplest of many lattices that can be formed from the kagome and other periodic isostatic lattices. Fig. 6 A and B shows two other examples of isostatic lattices constructed from the kagome lattice. Most intriguing is the lattice with pgg symmetry. Its geometry has uniaxial symmetry, yet its long-wavelength elastic energy is identical to that of the C_3v twisted kagome lattice (i.e., it is isotropic with a vanishing bulk modulus), and its mode structure near q = 0 is isotropic as shown in Fig. 6C. Thus, this system loses long-wavelength zero-frequency bulk modes of the undistorted kagome lattice to surface modes. However, at large wavenumber, lattice anisotropy becomes apparent, and (infinitesimal) floppy bulk modes appear. Thus in this and related systems, a fraction of the zero modes under FBCs are bulk modes that are visible under PBCs, and a fraction are surface modes that are not.

Fig. 6.

(A) Kagome-based lattice with pgg space group symmetry and uniaxial C_2v point group symmetry. (B) Lattice with p6 space symmetry but global C₆ point-group symmetry. (C) Density plot of the spectrum of the lowest frequency branch of the pgg uniaxial kagome lattice. The spectrum is absolutely isotropic near the origin point Γ, but it has a zero modes on two symmetry related continuous curves at large values of wavenumber.

Randomly packed spheres above the jamming transition with average coordination number z = 2d + Δz exhibit a characteristic frequency ω^∗ ∼ Δz and length l^∗ ∼ (Δz)^-1 and a transition from a Debye-like (∼ ω^d-1) to a flat density of states at ω ≈ ω^∗ (43, 44). The square and kagome lattices with randomly added NNN springs have the same properties (45, 46). A general “cutting” argument (9, 31) provides a procedure for perturbing away from the isostatic limit and an explanation for these properties. However, it only applies provided a finite fraction of the of order L^d-1 floppy modes of a sample with sides of length L cut from an isostatic lattice with PBCs are extended—i.e., have wave functions that extend across the sample rather than remaining localized either in the interior or at the surface the sample. Clearly the twisted kagome lattice, whose floppy modes are all surface modes, violates this criterion; and indeed, the density of states of the lattice with Δz = 0 shows Debye behavior crossing over to a flat plateau at ω ≈ ω_α. Adding NNN bonds gives rise to a length l_c, which is approximately the parallel combination, 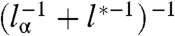, of the lengths l_α and l^∗ arising, respectively, from twisting the lattice and adding NNN springs, and cross-over to the plateau at 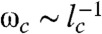. The pgg lattice in Fig. 6A, however, has both extended and surface floppy modes, so its cross-over to a flat plateau occurs at ω ≈ ω^∗ rather than at ω_α or ω_c.

Connections to Other Systems

Our study highlights the rich and remarkable variety of physical properties that isostatic systems can exhibit. Under FBCs, floppy modes can adopt a variety of forms, from all being extended to all being localized near surfaces to a mixture of the two. Under PBCs, the presence of floppy modes depends on whether the lattice can or cannot support states of self-stress. When a lattice exhibits a large number of zero-energy edge modes, its mechanical/dynamical properties become extremely sensitive to boundary conditions, much as do the electronic properties of the topological states of matter studied in quantum systems (47–50). The zero-energy edge modes observed in our isostatic lattices are collective modes whose amplitudes decay exponentially from the edge with a finite decay length, in direct contrast to the very localized and trivial floppy modes arising from dangling bonds. We focused primarily on high-symmetry lattices derived from the kagome lattice, but the properties they exhibit (namely, a deficit of floppy modes in the bulk and the existence of floppy surface modes) are shared by any two-dimensional system with a vanishing bulk modulus (or the equivalent in anisotropic systems). Three-dimensional analogs of the twisted kagome lattice can be constructed by rotating tetrahedra in pyrochlore and zeolite lattices (19, 20) and in cristobalites (18). These lattices are anisotropic. With NN forces only, they exhibit a vanishing modulus for compression applied in particular planes rather than isotropically, but we expect them to exhibit many of the properties the two-dimensional lattices exhibit. Finally, we note that Maxwell’s ideas can be applied to spin systems such as the Heisenberg antiferromagnet on the kagome lattice (51, 52), and the possibility of unusual edge states in them is intriguing.