Topological soft matter: Kagome lattices with a twist

The elastic response of many natural and man-made solid structures, ranging from atomic lattices to bridges, can be understood by viewing them as a network of balls (nodes) connected by springs (compressible struts). The rigidity of the resulting solids depends crucially on the average coordination number of the elastic network, z (i.e., the average number of nodes each node is connected to). This number specifies the average topology of the network. It is a global feature that cannot be changed by smoothly deforming the positions of the nodes; instead, you need to cut the struts.

Reducing the network coordination number, z, makes the structure less rigid until a critical point is reached when the solid can be infinitesimally deformed without incurring any energy cost, thereby losing rigidity (1). In PNAS, Sun et al. (2) study a class of lattices (Fig. 1A) right at the threshold of mechanical rigidity. Their analysis reveals that these systems are extremely sensitive to boundary conditions and display unusual mechanical properties; the vibrational modes can be zero-energy surface phonons that share some similarities with electronic edge states in topological quantum matter (3). However, the character of these unusual phonons is not purely dictated by network topology; rather, any smooth deformation (i.e., a gentle twist) matters.

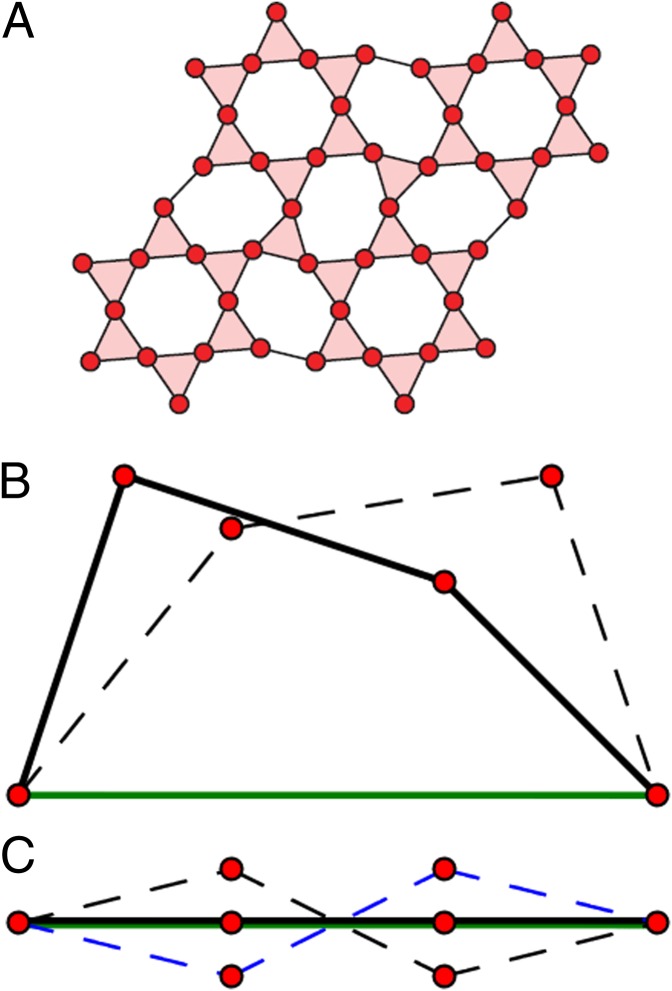
Fig. 1.

(A) Isostatic lattice created from a Kagome lattice. (B) Weakly connected network of struts and balls exhibits a finite amplitude mode of deformation that costs zero energy, represented by the dashed line. (C) Topologically equivalent network obtained by smoothly deforming the system shown in B violates the Maxwell criterion and displays five zero-energy modes [Adapted from Sun et al. (2)].

The role of topology in the study of soft materials has a long history; however, to date, it has been mostly confined to describing intriguing topological structures that exist in real space, such as knotted proteins and DNA (4, 5), topological defects in liquid crystals (6, 7), or higher genus membranes (8). Sun et al. (2) ask a subtler question: What is the consequence of the topology (or average connectivity) of an elastic network on the nature of its elementary classical excitations?

It was Maxwell (9), concerned with the stability of architectural structures, who first calculated the minimum connectivity, z_c, below which a mechanical structure displays floppy modes, deformations that cost zero energy. He concluded that for a large 2D network composed of N nodes, interacting with central forces, the critical connectivity, z_c = 4, is obtained by exactly balancing the number of translational degrees of freedom, 2N, with the number of constraints or bonds, which is equal to Nz/2.

According to Maxwell’s rule, if the network connectivity, z, is less than z_c, there are modes of deformation of the whole network that cost zero energy and the system is said to be below the isostatic point. The floppy-to-rigid transition that these simple models undergo shares similarities with analogous phenomena in randomly packed spherical grains near the jamming transition (10–13), biopolymer networks (14–16), and network glasses (1, 17, 18).

Maxwell’s counting implies that the number of zero-energy modes is simply equal to the number of degrees of freedom minus the number of mechanical constraints. For example, in Fig. 1B, there are eight (translational) degrees of freedom (corresponding to 4 nodes) and four struts; this leaves four zero-energy modes. Three of these modes are trivial rigid translations and rotation, but there is also a global finite amplitude deformation, which is shown as a dashed line in Fig. 1B.

Maxwell’s rule is a global criterion that considers purely the topology or connectivity of the network (embedded in its average coordination number), but it neglects its detailed architecture. Sun et al. (2) demonstrate that although network topology is key to understanding the existence of floppy modes, their nature depends sensitively on how the nodes and forces between them are distributed spatially throughout.

To gain qualitative insight into how Maxwell’s rule breaks down, consider the configuration of balls and struts shown in Fig. 1C, which is topologically equivalent to Fig. 1B. No struts are cut; the only difference is that their lengths are adjusted so that all the masses become nearly collinear. This seemingly innocuous architectural change causes Maxwell’s naive counting criterion to break down. The floppy mode in Fig. 1B no longer exists, but it is replaced by the two zero-energy modes shown as dashed blue and black lines in Fig. 1C. Once added to the three finite translations and rotation, we count five floppy modes and not merely four, as predicted by Maxwell.

Sun et al. (2) calculate the elastic properties and vibrational modes of a model system constructed by twisting the Kagome lattice, as shown in Fig. 1A. They find that network topology is not everything. The character of the floppy modes depends sensitively on boundary conditions and network architecture (e.g., on the relative angle between bonds and not merely on the average coordination number). This conclusion can help to elucidate more complex questions concerning the heat capacity and thermal conductivity of covalent network glasses at low temperature and sound propagation in granular media (19).

In addition, the twisted Kagome lattices have a peculiar elastic response compared with most materials: If you stretch them, they expand, rather than contract, in the direction perpendicular to stretching. The root cause of this unusual behavior is the vanishingly small bulk modulus that causes the speed of acoustic surface waves to vanish. As a result, even the tiniest surface strains may propagate supersonically through this fragile material. Although focused primarily on linear phonons, the work of Sun et al. (2) also opens up the possibility of studying supersonic strain propagation by means of solitons and shocks within the framework of a nearly isostatic model amenable to analytical treatment (20).

The elastic theory of these lattices already exhibits a very intriguing mathematical structure. Sun et al. (2) set out to answer the following question: What is the mathematical structure of an elastic system characterized by vanishing bulk moduli and extreme sensitivity to boundary conditions? Their study reveals that at large scales, these nearly isostatic lattices are described by a bulk elastic energy that is unchanged under local stretching of the underlying metric of space (conformal invariance) and encoded in the boundary of the sample (holography).

The blend of conformal invariance and holography is one of the leitmotifs of string theory, and, more recently, it has been used to understand the properties of exotic quantum matter (21). It is intriguing

Sun et al. calculate the elastic properties and vibrational modes of a model system constructed by twisting the Kagome lattice.

that these two ingredients naturally show up when you try to describe mathematically the floppy modes that arise from Maxwell’s intuitive reasoning.

It is tempting to remark on the mathematical similarities that exist between the floppy vibrational modes that live at the surface of the twisted Kagome lattices (with free boundary conditions) and edge electronic states in topological quantum matter. Although the mathematical similarities are suggestive, a crucial element seems to be missing in this correspondence: Edge electronic states are protected by topological rules that arise from symmetry considerations (3). It is this distinctive feature of topological quantum matter that is so attractive for sophisticated applications, such as quantum computing.

Going beyond the twisted Kagome lattices, we raise a more speculative question: Can one design useful soft topological materials with classical excitations that are truly topologically protected?