Abstract
This paper reviews several critical issues facing signal processing for brain–computer interfaces (BCIs) and suggests several recent approaches that should be further examined. The topics were selected based on discussions held during the 4th International BCI Meeting at a workshop organized to review and evaluate the current state of, and issues relevant to, feature extraction and translation of field potentials for BCIs. The topics presented in this paper include the relationship between electroencephalography and electrocorticography, novel features for performance prediction, time-embedded signal representations, phase information, signal non-stationarity, and unsupervised adaptation.
1. Introduction
The signal processing (i.e. feature extraction and translation) scheme is the most vital component in the design of a successful brain–computer interface (BCI), which translates signals produced by the brain into useful device commands. A workshop at the 4th International BCI Meeting was organized to review and evaluate the current state of signal processing of field potentials for BCIs. Field potentials represent the summed activity of multiple neurons recorded from implanted electrodes, electrodes placed on the surface of the cortex, or electrodes placed on the scalp. This paper discusses the crucial questions and strategies for BCI signal processing proposed by workshop participants.
2. Critical questions
-
Should future BCI research emphasis shift from scalp-recorded electroencephalography (EEG) to electrocorticography (ECoG), and how are the signals from the two modalities related?
A step toward answering this question is to better understand the relationship between EEG and ECoG. Section 3.1 examines this by comparing and contrasting the contribution of population synchronized (rhythmic) and asynchronous changes in the EEG and ECoG potential measurements.
-
What promising feature extraction and translation techniques deserve more attention?
There are a number of promising approaches which have been presented in recent years that are currently underutilized. Sections 3.2 and 3.3 provide a review of two of these promising approaches: time-embedded EEG prediction and the utilization of phase information.
-
Why are some individuals unable to use BCIs, and what are the predictors of BCI performance?
Despite intensive research, a substantial percentage of users still appear incapable of learning how to operate a BCI. Recently, particular features that are predictors of BCI performance for sensorimotor rhythm (SMR) paradigms have been identified. Section 3.4 addresses this issue by investigating the causal influences of other oscillations on SMRs.
-
How can feature and classifier adaptation be used to cope with signal non-stationarities and aid user training, and what are effective approaches to encourage neuroplasticity in rehabilitation applications?
Section 3.4 discusses novel features that can aid user training, while section 3.5 reviews and compares a number of state-of-the-art unsupervised adaptation approaches and presents new results.
3. Proposed strategies
3.1. A ‘back of the envelope’ comparison between EEG and ECoG
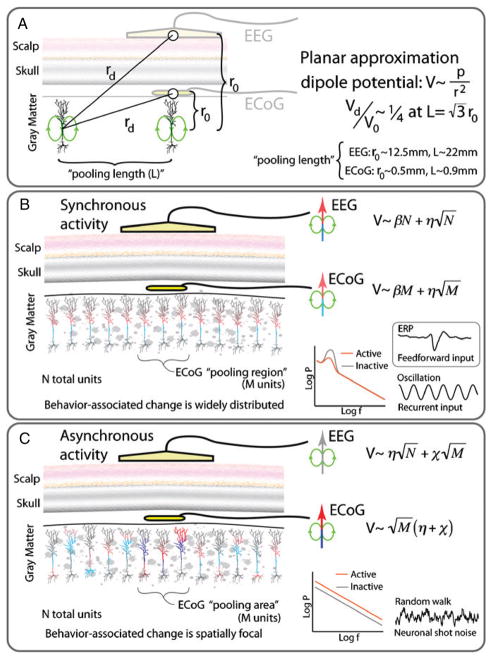
In order to understand the relationship between neuronal population processing and the measured potential in both EEG and ECoG, we make the following simplifications (following Nunez and colleagues [48–50]) to compare the contribution of population synchronized (rhythmic) and asynchronous (broadband, 1/f) changes in the EEG and ECoG potential measurements [39] (figure 1(A)).
Figure 1.
Illustration of basic comparison between EEG and ECoG (see the text for details): (A) simple heuristic for comparison, (B) synchronized cortical activity and (C) asynchronous cortical activity.
Planar approximation—we will initially ignore curvature of gyri, brain surface, skull, and scalp, and treat them all as having a stacked planar conformation.
Point measurement approximation—consider the potential only at the centers of an ECoG electrode and an EEG electrode.
Neglect effect of neuropil, tissue, skull, etc—solely consider the implications of the distance from the source of current density and the electrode.
A point dipole approximation is used for the contribution to the electric potential of the current source density of an individual pyramidal neuron. At the EEG distance, this is appropriate, but at the ECoG distance, the quadripole moment will also likely contribute.
The depth of the current dipole is approximated as 0.5 mm from the gyral surface (i.e. the depth of neurons in the upper cortical layers). The scalp surface is approximated as 12.5 mm from the most superficial gyral surface.
Ignore angular dependence of dipole field.
The lateral extent is considered to the limit where the contribution of a unit is 1/4 as large as the contribution directly below the electrode.
These assumptions lead us to the following approximations.
The contribution to the potential due to a single unit with dipole moment p at a distance r from the unit is .
The perpendicular distance, L, from the electrode to the furthest unit we consider (‘Pooling length’—the radial distance to a unit with contribution to the potential which is 1/4 that of the closest unit) is then , where r0 is the perpendicular distance from the electrode to a dipole source directly beneath. For EEG, this corresponds to a distance of ~22 mm, and for ECoG, it corresponds to a distance of ~0.9 mm. This corresponds to the area of pooling in EEG that is of the order of 500 times larger than that of ECoG.
To assess the contribution to the signal from cortical surface distributions of different sizes, we approximate the spatial extent of a coherent activity of the synchronized phenomenon as being of the same order as that of the pooling region of an EEG electrode (N total units) with coefficient β (figure 1(B)), and the spatial extent of an asynchronous, broadband change [40], to be of the same order as that of the pooling region of an ECoG electrode (M total units, figure 1(C)). Note that ‘units’ might refer to the dipole moment produced by an input to a single synapse rather than the net dipole moment of a neuron, since macroscale field potentials are understood to reflect a synaptic input [45]. To first order, these can be treated as independent, although they will actually be correlated because of the nonlinear potential dependence of active channels in the dendrite [60]. We will approximate the sources that lie within our ‘pooling region’ as being of equal magnitude for a first-order approximation. (Our cutoff was derived from the fact that contributions further away were of less magnitude.)
In comparing synchronous and asynchronous cortical sources, we keep in mind that they will be accompanied by a constant magnitude, task-independent 1/f noise throughout the whole pooling range, with coefficient η.
Synchronized units add in linearly V ~ βN, and asynchronous changes add in quadrature . Therefore, for an activity that is synchronized across the whole EEG pooling region (figure 1(B)),
.
For an activity that is asynchronous, and task-modulated at the scale of the ECoG pooling region (figure 1(C)),
.
These approximations suggest that synchronized cortical oscillations may be differently reflected at the EEG scale than the ECoG scale. Because of the influence of rhythms on the local cortical activity clusters by gyral anatomy [42], a rhythm may be more pronounced in ECoG (at the brain surface) than EEG, which averages over a spatial area (diameter 2L = ~4–5 cm) that is larger than the width of a gyrus (diameter ~2 cm). At the EEG scale, a rhythm might be more pronounced, due to averaging, than that of a single ECoG measurement because the synchronized portion of the cortical activity adds linearly, while the background noise adds in quadrature. Likewise, a feed-forward, weak-but-synchronized [8], event-related potential (ERP) may be more dramatic when observed at the larger scale of EEG, where unrelated 1/f noise has been averaged away.
Broadband, 1/f, spectral changes have been demonstrated to be extremely robust correlates of the local cortical activity in the ECoG signal [39, 40, 42], and are the most robust correlates of the mean population firing rate at the LFP scale [35, 42]. These are spatially very focal, with very different behavioral specificity in adjacent electrodes that are 1 cm from one another [40]. Because these broadband shifts scale like , even very large increases in χ will be lost at the larger EEG scale. It is very likely that many of the reports of ‘high gamma’ oscillations in ECoG are, in fact, shifts in 1/f phenomena [40, 42].
Real neuronal populations that are measured by either ECoG or EEG will, of course, not be matched to one scale or another, but will exist in one of the three regimes. They will be less than N, greater than N but less than M, or greater than M.
Cortical columns (or ‘modules’) represent the minimum cluster of neurons involved in a particular aspect of task-related processing, and are typically of the order of ~0.5–0.7 mm in diameter, although they vary in size by the cortical region [27]. Therefore, the standard clinical ECoG electrode, which has 2.3 mm diameter exposed to the cortical surface, for a total ~4 mm pooling when one considers the above estimate, will pool over <20 such columns. A broadband 1/f spectral change will then have to satisfy χ * C ≈ 20η to be perceptible in the ECoG measurement (where C is the number of columns that are activated at strength χ during task engagement).
Can these broadband changes be captured at the EEG scale? To have the same contribution to EEG that a single cortical column would need to have to be measured in ECoG, the spatial extent of cortical activity would have to span nearly the full width of a gyrus, and nearly a centimeter longitudinally. Based upon ECoG measurements of the 1/f change in the visual cortex, it might be possible to extract during the visual input directly over the occipital pole [41]. In the precentral motor cortex, the movement of several digits in concert might also produce a widespread change dramatic enough to be measured in the EEG [40].
3.2. Time-embedded EEG and neural networks
Current feature generation methods used in non-invasive BCI systems typically involve the use of power-spectral densities (PSDs) or time embedding. Although each of these methods has been applied with a level of success [1, 44], they both have a limited ability to capture the temporal information present within a signal. PSDs represent only the estimated power across a range of frequencies. Consequently, any correlations or differences in the phase across multiple channels or sensors are not readily expressed using a standard PSD. Time embedding, on the other hand, attempts to account for temporal information by embedding a number of time steps into a single sample. Although time embedding may be capable of reflecting more specific temporal information, it is limited by the size of the embedding dimension and may require larger training sets in order to sufficiently sample the higher dimensional output space.
The use of recurrent artificial neural networks (RNNs), artificial neural networks that contain feedback connections, may provide solutions to these problems. These feedback connections give RNNs an intrinsic state that allows them to incorporate information from previous inputs. Certain classes of RNNs, such as Elman’s simple recurrent network (SRN) [30], are capable of representing complex, nonlinear, spatiotemporal patterns. Such a model can also be allowed to become an autonomous and dynamical system by operating over its own predictions as inputs. When using a sufficient number of units (several hundred), these autonomous models produce very rich and accurate EEG predictions.
To explore the practical ability of RNNs to model neural signals, SRNs were trained using conjugate gradient backpropagation [46, 69] to forecast the EEG for each distinct mental state. In this way, an expert at modeling the signals belonging to each class is created [51]. The feature space can then be viewed as the forecasting error and the classification of previously unseen data can be performed by selecting the class associated with the model that performed best, or by using various alternative approaches. A range of other neural network-based approaches involving EEG predictions and the prediction error have also shown promise in this regard [13–16, 26, 29, 47].
3.3. Sensorimotor representations by phase information
The amplitude and the phase of neural oscillations are spatially and temporally modulated while processing information [9, 20, 36, 43, 52]. Furthermore, amplitude–phase cross-frequency coupling is suggested to play an important role in neural coding [10, 41]. However, while neural representations of movement kinematics and movement imagination by amplitude information in the sensorimotor cortex have been extensively reported using different oscillatory signals (LFP, ECoG, MEG, EEG) [38–40, 53, 67], the role of the phase has been largely unexplored. To date, the published experimental evidence for representations by phase information in the sensorimotor cortex is restricted to studies describing the synchronized activity between M1 and hand speed [28], cortico-muscular coupling (see [2] for a review), movement-related cortico–cortical coupling [11, 17], and the instructed-delay reaching task study by Rubino et al [55] reporting phase tuning to targets to be reached when LFP beta oscillations phase locked to target cue onset. With the exception of the phase-locking value (PLV) [24, 68], most state-of-the-art BCI methods [3, 32] rely on different amplitude/power-related estimators and non-circular statistics, respectively.
In addition to its technological use, BCI control is an experimental paradigm that can provide valuable information about the neural code and neural plasticity in the motor system by assessing neural activity–behavior mapping dynamics. Further research extending the feature extraction and translation methods utilized in BCI systems in order to assess the complementary information encoded by amplitude and phase would contribute to a better understanding of sensorimotor representations, as well as leading to enhanced BCI performance.
3.4. Causal influence of gamma oscillations on the sensorimotor-rhythm
Recently, evidence has been presented that processes generating distributed γ-range oscillations also exert a causal influence on the SMR [17, 23]. For BCIs, these results imply that processes generating γ-range oscillations act as a modulatory variable on a subject’s capability of volitionally controlling the SMR by means of motor imagery, providing an explanation for the trial-to-trial performance variation. More importantly, these results further suggest that subjects might benefit from receiving feedback on their current state of γ-power, as this feedback may help the user to modulate their mental states to enhance performance. Others have shown that the SMR during rest can predict a subject’s capacity to successfully operate a sensorimotor BCI [6].
Exploring feature spaces informative of a subject’s capacity to operate a BCI, rather than feature spaces optimal for intention inference, may have a large impact on performance; however, several fundamental problems need to be addressed. For example, the neuro-physiological causes of good or poor BCI performance remain largely unknown. While recent investigations show promise [6, 23], a multitude of currently unknown brain processes most likely affects BCI performance, and may vary across experimental paradigms. These need to be explored in order to design feedback procedures optimal for teaching subjects how to operate a BCI. Study differences should be taken into account as the causes of BCI performance can be investigated on several different levels: Blankertz et al [6] investigate across-subject performance predictors, while Grosse-Wentrup et al [23] address the within-subject variation in performance. Finally, the importance of transferring insights gained from healthy subjects to patients cannot be overemphasized.
3.5. Unsupervised adaptation in sensorimotor rhythms BCIs
Accurate and robust unsupervised adaptation is considered a key challenge for BCI deployment outside the lab where the intent of the subject and class information is unknown. Issues and approaches to address this include the following.
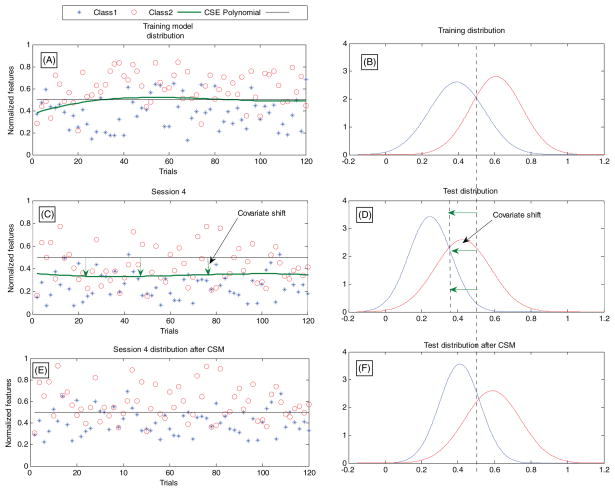
Covariate shift adaptation/minimization. When the distribution of the training features and test features follows different distributions while the conditional distribution of the output values (of the classifier) and the features is unchanged, it is referred to as covariate shift [63] (refer to figure 2). Unsupervised covariate shift minimization (CSM) [56, 57] can be achieved by estimating the shift in distribution using a least-squares fitting polynomial for each feature and removing the shift by adding the common mean of the training feature distributions so that the feature space distribution remains constant over time, as described in [56, 57]. Off-line supervised methods have also been proposed to address the covariate shift problem [5, 33, 63].
Feature adaptation/regression. This involves adapting the parameters of the feature extraction methods to account for subject learning. An approach to adaptively weight features based on μ and β rhythm amplitudes and their interactions using regression [37] resulted in significant performance improvements and may be adapted for unsupervised feature adaptation. CSM [56, 57] can be considered an anti-biasing method because it prevents the classifier biasing, whereas feature adaptation/regression is likely to result in the need to adapt the classifier to suit new feature distributions.
Classifier adaptation. Unsupervised classifier adaptation has received more attention than feature adaptation with a number of methods proposed [7, 18, 22, 25, 31, 34, 37, 58, 62, 64–66]. Classifier adaptation is required when significant learning (or relearning) induced plasticity in the brain significantly alters the brain dynamics resulting in a shift in feature distribution as well as significant changes in the conditional distribution between features and classifier output, as opposed to cases where only the covariate shift has occurred. In [65], a number of unsupervised classifier adaptation methods were proposed.
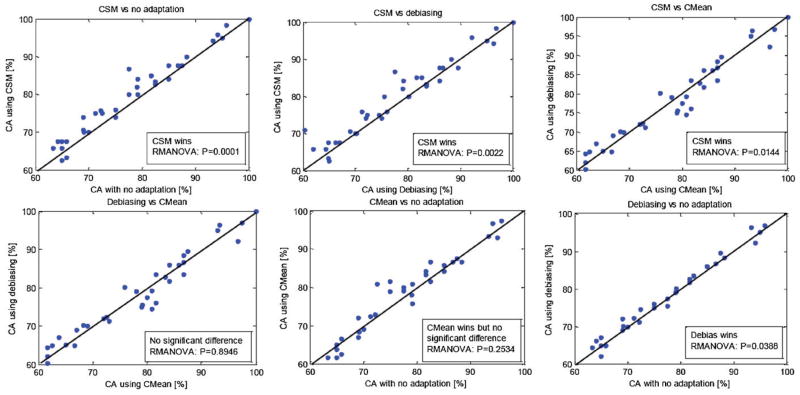
Post-processing. To account for short-term biasness, de-biasing the classifier output, in its simplest form, can be performed in an unsupervised manner by removing the mean calculated from a window of recent classifier outputs from the instantaneous value of the classifier [58], referred to as normalization in [19] where the standard deviation is also used to produce a control signal which is assumed to be stationary. De-biasing is suitable when the covariate shift has not been accounted for and can improve the online feedback response but may only provide a slight performance improvement. It has been shown that unsupervised feature adaptation through CSM can outperform unsupervised classifier adaptation and post-classification processing [54] (refer to the results presented in figure 3). See [37] for an interesting discussion of the interplay between feature regression and classifier adaptation.
Figure 2.
Feature distribution and covariate shift minimization [56, 57]. Reproduced from [56] with permission from IEEE.
Figure 3.
Comparative plots for CSM versus no-adaptation (left), de-biasing versus no-adaptation (center) and CSM versus de-biasing (right). Reproduced with permission from [57].
The success of adaptation depends upon the context in which the BCI is used, be it for alternative communication where the probability of interpreting the user’s intent correctly is maximized, or for inducing neuroplastic changes in specific cortical areas, e.g., in stroke rehabilitation [39, 54, 61]. Additionally, several key questions regarding adaptation rates remain: whether online adaptation is necessary, stability of various signals, and whether ECoG translation algorithms require less adaptation compared to EEG [4, 12, 37, 59].
4. Summary
As BCI signal processing continues to evolve, the next horizon is to better incorporate additional information about neurophysiology, disease traits and progression, signal dynamics, feature relationships, and feature trainability into the current or prospective approaches.
Acknowledgments
The authors would like to thank the other workshop participants for their contributions to the workshop discussions. D Coyle would like to thank A Satti for providing input to section 3.4, based on ongoing research in unsupervised BCI adaptation. D J Krusienski is funded in part by the National Science Foundation (0905468) and the National Institutes of Health (NIBIB/NINDS EB00856). D Coyle is funded in part by the UK Engineering and Physical Sciences Research Council (EP/H012958/1) and the Centre of Excellence in Intelligent Systems project funded by Invest Northern Ireland. K J Miller is funded by the National Aeronautics and Space Administration Graduate Student Research Program. C W Anderson is funded in part by the National Science Foundation (0208958). F Galán was funded by the German Federal Ministry of Education and Research (grant 01GQ0830 to the BFNT-Bernstein Focus Neurotechnology Freiburg*Tuebingen and grant 01GQ0762).
References
- 1.Anderson CW, Bratman JA. Translating thoughts into actions by finding patterns in brainwaves. Proc. of the 14th Yale Workshop on Adaptive and Learning Systems; New Haven, CT, USA. 2008. pp. 1–6. [Google Scholar]
- 2.Baker SN. Oscillatory interactions between sensorimotor cortex and the periphery. Curr Opin Neurobiol. 2007;17:649–55. doi: 10.1016/j.conb.2008.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bashashati A, Fatourechi M, Ward RK, Birch GE. A survey of signal processing algorithms in brain–computer interfaces based on electrical brain signals. J Neural Eng. 2007;4:R32–57. doi: 10.1088/1741-2560/4/2/R03. [DOI] [PubMed] [Google Scholar]
- 4.Blakely T, Miller KJ, Zanos S, Rao RP, NOjemann JG. Robust long term control of an electrocorticographic brain–computer interface with fixed parameters. Neurosurg Focus. 2009;27:E13. doi: 10.3171/2009.4.FOCUS0977. [DOI] [PubMed] [Google Scholar]
- 5.Blankertz B, Kawanabe M, Tomioka R, Hohlefeld F, Nikulin V, Müller KR. Advances in Neural Information Processing Systems. Vol. 20. Cambridge, MA: MIT Press; 2008. Invariant common spatial patterns: alleviating nonstationarities in brain–computer interfacing. [Google Scholar]
- 6.Blankertz B, Sannelli C, Halder S, Hammer EM, Kübler A, Müller KR, Curio G, Dickhaus T. Neurophysiological predictor of SMR-based BCI performance. Neuro Image. 2010;51:1303–9. doi: 10.1016/j.neuroimage.2010.03.022. [DOI] [PubMed] [Google Scholar]
- 7.Blumberg J, Rickert J, Waldert S, Schulze-Bonhage A, Aertsen A, Mehring C. Conf Proc IEEE Engineering in Medicine and Biology Society. Vol. 1. Piscataway, NJ: IEEE; 2007. Adaptive classification for brain–computer interfaces; pp. 2536–9. [DOI] [PubMed] [Google Scholar]
- 8.Bruno RM, Sakmann B. Cortex is driven by weak but synchronously active thalamocortical synapses. Science. 2006;312:1622. doi: 10.1126/science.1124593. [DOI] [PubMed] [Google Scholar]
- 9.Busch NA, Dubois J, VanRullen R. The phase of ongoing EEG oscillations predicts visual perception. J Neurosci. 2009;29:7869–76. doi: 10.1523/JNEUROSCI.0113-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Canolty RT, Edwards E, Dalal SS, Soltani M, Nagarajan SS, Kirsch HE, Berger MS, Barbaro NM, Knight RT. High gamma power is phase-locked to theta oscillations in human neocortex. Science. 2006;313:1626–8. doi: 10.1126/science.1128115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Canolty R, Ganguly K, Kennerley S, Cadieu CF, Koepsell K, Wallis J, Carmena JMC. Oscillatory phase coupling coordinates anatomically dispersed functional cell assemblies. PNAS. 2010;107(40):17356–61. doi: 10.1073/pnas.1008306107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chao ZC, Nagasaka Y, Fujii N. Long-term asynchronous decoding of arm motion using electrocorticographic signals in monkeys. Front Neuroeng. 2010;3:3. doi: 10.3389/fneng.2010.00003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Coyle D. Neural network based auto association and time-series prediction for biosignal processing in brain–computer interfaces. IEEE Comput Intell Mag. 2009;4:47–59. [Google Scholar]
- 14.Coyle D, Prasad G, McGinnity TM. Faster self-organizing fuzzy neural network training and a hyperparameter analysis for a brain–computer interface. IEEE Trans Syst Man Cybern B. 2009;39:1458–71. doi: 10.1109/TSMCB.2009.2018469. [DOI] [PubMed] [Google Scholar]
- 15.Coyle D, Prasad G, McGinnity TM. A time-series prediction approach for feature extraction in a brain–computer interface. IEEE Trans Neural Syst Rehabil Eng. 2005;13:461–7. doi: 10.1109/TNSRE.2005.857690. [DOI] [PubMed] [Google Scholar]
- 16.Coyle D, Satti A, McGinnity TM. Predictive-spectral-spatial preprocessing for a multiclass brain–computer interface. Int. Joint Conf. on Neural Networks; Barcelona, Spain. 2010. pp. 3347–64. [Google Scholar]
- 17.Darvas F, Miller KJ, Rao RP, NOjemann JG. Nonlinear phase–phase coupling mediates communication between distant sites in human neocortex. J Neurosci. 2009;29:426–35. doi: 10.1523/JNEUROSCI.3688-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Eren S, Grosse-Wentrup M, Buss M. Unsupervised classification for non-invasive brain–computer interfaces. Proc. of Automed Workshop; Dusseldorf, Germany: VDI; 2007. pp. 65–6. [Google Scholar]
- 19.Fabiani GE, McFarland DJ, Wolpaw JR, Pfurtscheller G. Conversion of EEG activity into cursor movement by a brain–computer interface (BCI) IEEE Trans Neural Syst Rehabil Eng. 2004;12:331–8. doi: 10.1109/TNSRE.2004.834627. [DOI] [PubMed] [Google Scholar]
- 20.Freeman WJ. Origin, structure, and role of background EEG activity: II. Analytic phase. Clin Neurophysiol. 2004;115:2089–107. doi: 10.1016/j.clinph.2004.02.028. [DOI] [PubMed] [Google Scholar]
- 21.Galán F, Witte M, Waldert S, Aertsen A, Birbaumer N, Braun C, Mehring C. The phase of neuronal oscillations encodes hand movement direction. 4th Int. BCI Meeting; Monterey, CA, USA. 2010. [Google Scholar]
- 22.Gan J. Self-adapting BCI based on unsupervised learning. Proc. of the 3rd Int. Workshop on Brain–Computer Interfaces; Graz, Austria. 2006. pp. 50–1. [Google Scholar]
- 23.Grosse-Wentrup M, Schölkopf B, Hill J. Causal influence of gamma-oscillations on the sensorimotor-rhythm. Neuro Image. 2010 doi: 10.1016/j.neuroimage.2010.04.265. (at press) [DOI] [PubMed] [Google Scholar]
- 24.Gysels E, Celka P. Phase synchronization for the recognition of mental tasks in a brain–computer interface. IEEE Trans Neural Syst Rehabil Eng. 2004;12:406–15. doi: 10.1109/TNSRE.2004.838443. [DOI] [PubMed] [Google Scholar]
- 25.Hasan B, Gan J. Unsupervised adaptive GMM for BCI. Proc. of the 4th Int. IEEE EMBS Conf. on Neural Engineering; Antalya, Turkey. 2009. pp. 295–8. [Google Scholar]
- 26.Haselsteiner E, Pfurtscheller G. Using time-dependent NNs for EEG classification. IEEE Trans Rehabil Eng. 2000;8:457–62. doi: 10.1109/86.895948. [DOI] [PubMed] [Google Scholar]
- 27.Horton JC, Adams DL. The cortical column: a structure without a function. Phil Trans R Soc B. 2005;360:837. doi: 10.1098/rstb.2005.1623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Jerbi K, Lachaux JP, N’Diaye K, Pantazis D, Leahy R, Garnero L, Baillet S. Coherent neural representation of hand speed in humans revealed by MEG imaging. PNAS. 2007;104:7676–81. doi: 10.1073/pnas.0609632104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kohlmorgen J, Müller K-R, Rittweger J, Pawelzik K. Biological Cybernetics. Vol. 83. Berlin: Springer; 2000. Identification of nonstationary dynamics in physiological recordings; pp. 73–84. [DOI] [PubMed] [Google Scholar]
- 30.Kremer SC. On the computational power of Elman–Style recurrent networks. IEEE Trans Neural Netw. 1995;6:1000–4. doi: 10.1109/72.392262. [DOI] [PubMed] [Google Scholar]
- 31.Liu G, Huang G, Meng J, Zhang D, Zhu X. Unsupervised adaptation based on fuzzy c-means for brain–computer interface. 1st Int. Conf. on Information Science and Engineering; Nanjing, China. 2009. pp. 4122–5. [Google Scholar]
- 32.Lotte F, Congedo M, L’ecuyer A, Lamarche F, Arnaldi B. A review of classification algorithms for EEG-based brain–computer interfaces. J Neural Eng. 2006;4:R1–13. doi: 10.1088/1741-2560/4/2/R01. [DOI] [PubMed] [Google Scholar]
- 33.Lotte F, Guan C. Regularizing common spatial patterns to improve BCI designs: unified theory and new algorithms. IEEE Trans Biomed Eng. 2010 doi: 10.1109/TBME.2010.2082539. (at press) [DOI] [PubMed] [Google Scholar]
- 34.Lu S, Guan C, Zhang H. Unsupervised brain–computer interface based on inter-subject information. 30th Annu. Int. IEEE EMBS Conf; Vancouver, British Columbia, Canada. 2008. pp. 638–41. [DOI] [PubMed] [Google Scholar]
- 35.Manning JR, Jacobs J, Fried I, Kahana MJ. Broadband shifts in local field potential power spectra are correlated with single-neuron spiking in humans. J Neurosci. 2009;29:13613. doi: 10.1523/JNEUROSCI.2041-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Mathewson KE, Gratton G, Fabiani M, Beck DM, Ro T. To see or not to see: prestimulus alpha phase predicts visual awareness. J Neurosci. 2009;29:2725–32. doi: 10.1523/JNEUROSCI.3963-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.McFarland DJ, Wolpaw JR. Sensorimotor rhythm-based brain–computer interface (BCI): feature selection by regression improves performance. IEEE Trans Neural Syst Rehabil Eng. 2005;13:372–9. doi: 10.1109/TNSRE.2005.848627. [DOI] [PubMed] [Google Scholar]
- 38.Mehring C, Rickert J, Vaadia E, Cardoso de Oliveira S, Aertsen A, Rotter S. Inference of hand movements from local field potentials in monkey motor cortex. Nat Neurosci. 2003;6:1253–4. doi: 10.1038/nn1158. [DOI] [PubMed] [Google Scholar]
- 39.Miller KJ, Leuthardt EC, Schalk G, Rao RP, Anderson NR, Moran DW, Miller JW, Ojemann JG. Spectral changes in cortical surface potentials during motor movement. J Neurosci. 2007;27:2424–32. doi: 10.1523/JNEUROSCI.3886-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Miller KJ, Zanos S, Fetz EE, den Nijs M, Ojemann JG. Decoupling the cortical power spectrum reveals real-time representation of individual finger movements in humans. J Neurosci. 2009;29:3132. doi: 10.1523/JNEUROSCI.5506-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Miller KJ, et al. Dynamic modulation of local population activity by rhythm phase in human occipital cortex during a visual search task. Front Hum Neurosci. 2010;4:197. doi: 10.3389/fnhum.2010.00197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Miller KJ. Broadband spectral change: evidence for a macroscale correlate of population firing rate? J Neurosci. 2010;30:6477. doi: 10.1523/JNEUROSCI.6401-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Miller KJ, Schalk GS, Fetz EE, den Nijs M, Ojemann JG, Rao RPN. Cortical activity during motor movement, motor imagery, and imagery-based online feedback. PNAS. 2010;107:4430–5. doi: 10.1073/pnas.0913697107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Millán JDR, Ferrez PW, Galán F, Lew E, Chavarriaga R. Non-invasive brain–machine interaction. Int J Pattern Recognit Artif Intell. 2008;22:959–72. [Google Scholar]
- 45.Mitzdorf U. Current source-density method and application in cat cerebral cortex: investigation of evoked potentials and EEG phenomena. Physiol Rev. 1985;65:37. doi: 10.1152/physrev.1985.65.1.37. [DOI] [PubMed] [Google Scholar]
- 46.Møller MF. A scaled conjugate gradient algorithm for fast supervised learning. Neural Netw. 1993;6:525–33. [Google Scholar]
- 47.Müller KR, Kohlmorgen J, Pawelzik K. Analysis of switching dynamics with competing neural networks. IEICE Trans Fundam Electron Commun Comput Sci E. 1995;78-A:1306–15. [Google Scholar]
- 48.Nunez PL, Cutillo BA. Neocortical Dynamics and Human EEG Rhythms. New York: Oxford University Press; 1995. [Google Scholar]
- 49.Nunez PL, Wingeier BM, Silberstein RB. Spatial-temporal structures of human alpha rhythms: theory, microcurrent sources, multiscale measurements, and global binding of local networks. Hum Brain Mapp. 2001;13:125–64. doi: 10.1002/hbm.1030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Nunez PL, Srinivasan R. Electric Fields of the Brain: The Neurophysics of EEG. New York: Oxford University Press; 2006. [Google Scholar]
- 51.Oeda S, Kurimoto I, Ichimura T. Time series data classification using recurrent neural network with ensemble learning. Lecture Notes Comput Sci. 2006;4253:742–8. [Google Scholar]
- 52.Pfurstcheller G, Lopes da Silva FH. Event-related EEG/MEG synchronization and desynchronization: basic principles. Clin Neurophysiol. 1999;110:1842–57. doi: 10.1016/s1388-2457(99)00141-8. [DOI] [PubMed] [Google Scholar]
- 53.Pisthol T, Ball T, Schulze-Bonhage A, Aertsen A, Mehring C. Prediction of arm movement trajectories from ECoG-recordings in humans. J Neurosci Methods. 2008;167:105–15. doi: 10.1016/j.jneumeth.2007.10.001. [DOI] [PubMed] [Google Scholar]
- 54.Prasad G, Herman P, Coyle D, McDonough S, Crosbie J. Using a motor imagery-based brain–computer interface for post-stroke rehabilitation. Proc. 4th IEEE EMB Conf. on Neural Engineering; Antalya, Turkey. 2009. pp. 258–62. [Google Scholar]
- 55.Rubino D, Robbins DR, Hatsopoulos NG. Propagating waves mediate information transfer in the motor cortex. Nat Neurosci. 2006;9:1549–57. doi: 10.1038/nn1802. [DOI] [PubMed] [Google Scholar]
- 56.Satti A, Guan C, Prasad G, Coyle D. A covariate shift minimisation method to alleviate non-stationarity effects for an adaptive brain–computer interface. 20th Int. Conf. Pattern Recognition; Istanbul, Turkey. 2010. pp. 105–8. [Google Scholar]
- 57.Satti A, Coyle D, Guan C, Prasad G. Anti-biasing using feature-space covariate shift minimization versus post-classification de biasing for an unsupervised adaptive BCI. (submitted) [Google Scholar]
- 58.Satti A, Coyle D, Prasad G. Continuous EEG classification for a self-paced BCI. Proc. of the 4th IEEE EMB Conf. on Neural Engineering; Antalya, Turkey. 2009. pp. 315–8. [Google Scholar]
- 59.Schalk G. Can electrocorticography (ECoG) support robust and powerful brain–computer interfaces? Front Neuroeng. 2010;3:9. doi: 10.3389/fneng.2010.00009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Segev I, London M. Untangling dendrites with quantitative models. Science. 2000;290:744. doi: 10.1126/science.290.5492.744. [DOI] [PubMed] [Google Scholar]
- 61.Sharma N, Pomeroy VM, Baron JC. Motor imagery: a backdoor to the motor system after stroke? Stroke. 2006;37:1941–52. doi: 10.1161/01.STR.0000226902.43357.fc. [DOI] [PubMed] [Google Scholar]
- 62.Shenoy P, Krauledat M, Blankertz B, Rao RP, Müller KR. Towards adaptive classification for BCI. J Neural Eng. 2006;3:R13–23. doi: 10.1088/1741-2560/3/1/R02. [DOI] [PubMed] [Google Scholar]
- 63.Sugiyama M, Krauledat M, Müller K. Covariate shift adaptation by importance weighted cross validation. J Mach Learn Res. 2007;8:985–1005. [Google Scholar]
- 64.Tsui C, Gan J. Comparison of three methods for adapting LDA classifiers with BCI application. 4th Int. Workshop on Brain–Computer Interfaces; Graz, Austria. 2008. pp. 116–21. [Google Scholar]
- 65.Vidaurre C, Schlogl A, Blankertz B, Kawanabe M, Müller K. Unsupervised adaptation of the LDA classifier for brain–computer interfaces. Proc. 4th Int. Brain–Computer Interface Workshop and Training Course; Graz, Austria. 2008; 2008. pp. 122–7. [Google Scholar]
- 66.Vidaurre C, Schlogl A, Cabeza R, Scherer R, Pfurtscheller G. Study of on-line adaptive discriminant analysis for EEG-based brain–computer interfaces. IEEE Trans Biomed Eng. 2007;54:550–6. doi: 10.1109/TBME.2006.888836. [DOI] [PubMed] [Google Scholar]
- 67.Waldert S, Preissl H, Demandt E, Braun C, Birbaumer N, Aertsen A, Mehring C. Hand movement direction decoded from MEG and EEG. J Neurosci. 2008;28:1000–8. doi: 10.1523/JNEUROSCI.5171-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Wei Q, Wang Y, Gao X, Gao S. Amplitude and phase coupling measures for feature extraction in an EEG-based brain–computer interface. J Neural Eng. 2007;4:120–9. doi: 10.1088/1741-2560/4/2/012. [DOI] [PubMed] [Google Scholar]
- 69.Williams RJ, Peng J. An efficient gradient-based algorithm for on-line training of recurrent network trajectories. Neural Comput. 1990;2:490–501. [Google Scholar]
- 70.Witte M, Galán F, Waldert S, Aertsen A, Birbaumer N, Braun C, Mehring C. An online-BCI system using hand movement recognition from MEG. 4th Int. BCI Meeting; Monterey, CA, USA. 2010. [Google Scholar]