Single-Pixel Optical Fluctuation Analysis of Calcium Channel Function in Active Zones of Motor Nerve Terminals

Abstract

We used high-resolution fluorescence imaging and single-pixel optical fluctuation analysis to estimate the opening probability of individual voltage-gated calcium (Ca²⁺) channels during an action potential and the number of such Ca²⁺ channels within active zones of frog neuromuscular junctions. Analysis revealed ∼36 Ca²⁺ channels within each active zone, similar to the number of docked synaptic vesicles but far less than the total number of transmembrane particles reported based on freeze-fracture analysis (∼200–250). The probability that each channel opened during an action potential was only ∼0.2. These results suggest why each active zone averages only one quantal release event during every other action potential, despite a substantial number of docked vesicles. With sparse Ca²⁺ channels and low opening probability, triggering of fusion for each vesicle is primarily controlled by Ca²⁺ influx through individual Ca²⁺ channels. In contrast, the entire synapse is highly reliable because it contains hundreds of active zones.

Introduction

Nerve terminal active zones contain highly organized components that underlie synaptic vesicle docking and fusion (Zhai and Bellen, 2004). Such organization is readily apparent in adult frog neuromuscular junctions (NMJs), in which electron microscopy has revealed hundreds of linear active zones, each arrayed with 200–250 intramembraneous particles and 25–40 closely associated synaptic vesicles (Heuser et al., 1979; Pawson et al., 1998; Harlow et al., 2001; Rizzoli and Betz, 2005). Previous investigators have hypothesized that these intramembraneous particles include the presynaptic Ca²⁺ channels that trigger vesicle fusion (Pumplin et al., 1981; Robitaille et al., 1990; Cohen et al., 1991). Because other channels and release machinery proteins are also present in the active zone (Robitaille et al., 1993), only some of the active zone particles observed in freeze-fracture replicas are expected to represent voltage-gated Ca²⁺ channels. Although the NMJ is known as a reliable synapse in which a single presynaptic action potential (AP) can trigger release of several hundred quanta (eliciting an action potential in the muscle) (Wood and Slater, 2001), each individual active zone operates as a low probability release site, averaging only one vesicle released following every other action potential (Katz, 1969; Katz and Miledi, 1979; Poage and Meriney, 2002).

Despite >60 years of study, many important questions persist regarding Ca²⁺-dependent transmitter release. For example, it is not known how many voltage-gated Ca²⁺ channels are positioned in an active zone or what is the in situ probability (p) that they will open during an action potential [which is distinct from the channel open probability (P_o) traditionally measured during long depolarizing steps]. Answers to both of these questions will provide important constraints on models of Ca²⁺-triggered vesicle fusion, including the stoichiometric and spatial relationships between Ca²⁺ channels and docked vesicles. To address these questions, we developed single-pixel optical fluctuation analysis (SPOFA) and applied it to action potential-evoked Ca²⁺ indicator fluorescence measurements in frog motor nerve terminals.

Variance analysis of Ca²⁺ fluorescence signals has been applied previously to small neuronal compartments and used to reveal stochastic openings of Ca²⁺ channels in presynaptic boutons and postsynaptic spines (Frenguelli and Malinow 1996; Sabatini and Svoboda, 2000) (but see Brenowitz and Regehr, 2007). In addition, we have previously described stochastic Ca²⁺ signals arising from frog NMJ active zones (Wachman et al., 2004). We now extend this approach to automated acquisition and analysis of signal variance at the level of single pixels overlying portions of active zones. In doing so, we characterize the spatial resolution of data acquisition, the methods used for selection of active zone pixels, and the possible contribution of single-channel current variability to the measured variability. We demonstrate optical resolution at subactive zone dimensions, show that our results are primarily independent of pixel selection criteria, and also consider the effect of additional sources of variation on our results via Monte Carlo (MCell) simulations. Based on our findings, we conclude that relatively few Ca²⁺ channels line each active zone of frog NMJs and that each action potential normally opens only a small fraction of such channels. These results lead us to hypothesize that action potential-evoked vesicle fusion at this synapse is likely triggered by the Ca²⁺ ion flux through one or very few Ca²⁺ channels.

Materials and Methods

Dye loading and staining of cutaneous pectoris nerve–muscle preparations

Adult frogs (Rana pipiens) were decapitated and pithed after anesthesia in 0.1% tricaine methane sulfonate. Cutaneous pectoris muscles were dissected bilaterally and bathed in normal frog Ringer's solution (NFR) (in mm: 116 NaCl, 2 KCl, 1.8 CaCl₂, 1 MgCl₂, and 5 HEPES, pH 7.4). The nerve was cut near its entrance into the muscle, and the cut end was drawn into a Vaseline well containing 30 mm Calcium Green-1 (3000 molecular weight dextran conjugate; Invitrogen) dissolved in distilled water. After 7–8 h of dye loading at room temperature, the preparation was rinsed in NFR and stored at 4°C for 2–3 h. For stimulation and imaging, preparations were pinned over an elevated Sylgard (Dow Corning) platform in a 35 mm dish mounted on the microscope stage. The nerve was drawn into a suction electrode, and stimulation threshold was determined by observation of muscle twitch. Postsynaptic acetylcholine receptors then were blocked and labeled using 2 μg/ml Alexa Fluor 594-conjugated α-bungarotoxin (α-BTX) for 10 min. α-BTX staining was used to locate and focus the postsynaptic receptor bands, which are directly opposed to the presynaptic active zones, and to evaluate possible z-axis drift over the course of data collection. Superficial nerve terminals were chosen for study, and most lay in a single focal plane as judged by α-BTX staining. Except as noted, all Ca²⁺ imaging was performed in NFR containing 10 μm curare to prevent nerve-evoked muscle contractions not completely blocked by α-BTX.

Calcium imaging and nerve stimulation protocol

Images were collected at 0.5 Hz using a 1 ms laser illumination time. An acousto-optic tunable filter (ChromoDynamics) was used to select wavelengths and gate the laser with submillisecond time resolution (krypton–argon laser; Innova 70 Spectrum; Coherent). The laser was fiber coupled to the epi-illumination port of an upright fluorescence microscope (Olympus BX61WI) equipped with a long-working-distance water-immersion objective (100×, 1.0 NA; Lumplan/FL IR; Olympus). Calcium Green-1 was excited at 488 nm, and emitted light was collected through a 530 ± 20 nm filter. Alexa Fluor 594–α-BTX was excited at 567 nm, and emitted light was collected using a 620 ± 30 nm filter. Images were recorded on one of two cooled, back-thinned CCD cameras (LN1300B by Roper Scientific; or Ixon DV887 by Andor), which provided the high sensitivity and low noise necessary for imaging acquisition during 1 ms illumination times. Pixel size was 200 nm (LN1300B) or 160 nm (Ixon DV887). Analysis of data from either camera gave similar results. In comparing theoretical Rayleigh's and FWHM criteria (based on the optics within our microscope and the excitation wavelength of the fluorescent dye), our axial resolution can be no better than between 864 and 976 nm. The lateral resolution of the microscope was experimentally determined by measuring the point-spread function (PSF) imaged using 20 nm fluorescent beads (after Gaussian fit, width at half-maximum amplitude of 450 nm) (Fig. 1C). Furthermore, a plot of the cross-correlation analysis of action potential-evoked fluorescent signals in the nerve terminal detected by adjacent pixels revealed a width at half-maximum amplitude of 410 nm (Fig. 1D). These data indicate that, as a result of our brief 1 ms acquisition window, signals sampled by a given pixel derive mainly from channels underlying this pixel. This distribution is best fit by a Lorentzian function because there is some optical signal that appears to contribute to the “tails” of this distribution. The signal sampled by one pixel does not derive exclusively from a single point source (a single open Ca²⁺ channel centered below the pixel), but rather there are likely neighboring sources that contribute some elevated signal because we predict that several spatially distributed Ca²⁺ channels likely open within one active zone after each action potential. Given the anatomical organization of active zones and considering our 1 ms illumination timed with action potential invasion (which limits time for diffusion), a pixel that is positioned over one active zone will likely not sample significant signal derived from calcium channel flux originating within neighboring active zones. However, within the sampling region detected by one pixel, we do not have a good method for determining the heterogeneity in contribution that might arise from different Ca²⁺ channels that might be at slightly different distances from the center of one pixel.

Figure 1.

Pixel and optical resolution for calcium imaging in the adult frog neuromuscular junction. A, Diagram of the adult frog neuromuscular junction. B, Magnified active zones (boxed region in A) with highly organized active zone proteins, which include voltage-gated Ca²⁺ channels, and docked synaptic vesicles. The estimated relationship between active zone dimensions, pixel size, and optical resolution are also shown (left). For comparison, a composite image that includes fluorescent staining of postsynaptic acetylcholine receptors (background, grayscale) overlaid with Ca²⁺-evoked fluorescent signals after nerve stimulation (foreground, false color) is shown on the right. Scale bar, 1 μm. C, Experimentally measured point spread function of the optical system from a fluorescent bead with diameter of 0.02 μm. The Gaussian fit (red) has a width at half-amplitude of 0.45 μm. We thus estimated that approximately half the length of a single active zone can be resolved optically. D, Correlation coefficient of neighboring pixels that detected AP-evoked fluorescence signals after repeated low-frequency nerve stimulus tightly depends on the distance between pixels. The Lorentzian fit (red) has a width at half-amplitude of 0.41 μm (points represent mean ± SD; n = 4361 pixels). These data are fit best with a Lorentzian function, rather than a Gaussian, likely because of the presence of some signal contributing from neighboring sites, especially at the tails of the distribution. E, Predicted active zone regions of a representative frog motor nerve terminal identified by labeling the postsynaptic acetylcholine receptor clusters with Alexa Fluor 594–α-bungarotoxin. F, Representative difference images showed a large trial-to-trial variability in the spatial distribution of Ca²⁺ entry evoked by single APs. Scale bar, 2 μm (applies to E, F).

During acquisition, images were collected in sets of 20. Within each set, the first 10 were acquired without nerve stimulation to obtain resting (background) fluorescence, whereas each of the second 10 followed nerve stimulation at 5× threshold to obtain action potential-dependent fluorescence. A delay of 1.5 ms between stimulation and illumination was used to account for nerve conduction delay in this preparation. In most experiments, 10 sets of trials were performed sequentially to obtain a total of 100 background images interleaved with 100 images after stimulation. Between sets, we confirmed or adjusted focus based on α-BTX staining (which allowed a characterization of active zone distribution and focal plane) and discarded image sets from analysis if they showed noticeable z-axis drift or significant changes in average background fluorescence. In some experiments, the preparation subsequently was exposed to the potassium channel blocker 3,4-diaminopyridine (DAP) (5 μm for 30 min), and another 10 sets of images were obtained in the continued presence of DAP. Because there is active propagation of action potentials along the length of motor nerve terminals (Katz and Miledi, 1965, 1968; Braun and Schmidt, 1966; Mallart, 1984), DAP treatment will block presynaptic potassium channels, prolonging the duration of the action potential (Kirsch and Narahashi, 1978; Durant and Marshall, 1980), without altering propagation within the nerve terminal. As such, this treatment will indirectly increases the probability (p) that Ca²⁺ channels open after nerve stimulation but leave the number of channels (n) unchanged. This differential effect allows subsequent analysis of fluorescence fluctuations across repeated trials to determine p and n on a per pixel basis (see below).

Image registration and analysis

Before analysis, all images collected from individual terminals were registered to the first image to correct for slight fluctuations in the x–y (or lateral) position of the preparation during data collection. Registration software was written at the National Resource for Biomedical Supercomputing (www.nrbsc.org) at the Pittsburgh Supercomputing Center. To avoid aligning on background features, we sampled the most prominent aspects of the background (including any artifacts) and subtracted this background from the images. We then used the raw calcium-dependent fluorescence to create a mask that represented the detailed shape of the nerve terminal in each image. With this approach, we used custom-written nonlinear registration software to warp each image in a time series to the first image of that series. Although the software was capable of generalized rotational and nonlinear corrections, virtually all of the adjustments necessary for these experiments were simple interpolated translational movements of one pixel or less. Stimulus-dependent changes in fluorescence intensity were small (typically 3–4% above background; see Results), and so the registration step brought the shape of the nerve terminal into alignment without being confounded by large and variable changes in signal strength within regions of nerve terminals. Analysis of registered images was performed using MATLAB. To create difference images showing stimulus-dependent fluorescence changes (ΔF_s) for each pixel, we calculated the average background fluorescence of each pixel (f̄_b), subtracted it from the fluorescence (f_s) obtained after a stimulation trial, and then normalized the resulting differences to f̄_b, i.e., per pixel $\Delta f_s=\frac{f_s-{\overline{f}}_b}{{\overline{f}}_b}$. Resulting difference images were displayed in pseudocolor. For subsequent calculation of n and p (see below), analysis for each pixel also included calculation of the background variance (σ_b²), the mean fluorescence (f̄_s) and variance (σ_s²) after nerve stimulation, and the mean fluorescence (f̄_Ds) and variance (σ_Ds²) after stimulation combined with DAP treatment. Within image sets from individual terminals, the variance of background fluorescence arises from dark noise and photon shot noise and, under our experimental conditions, was dominated by Gaussian shot noise. Conversely, background photoelectron counts from different visualized nerve terminals varied according to differences in geometry and dye loading and ranged from 1500 to 6000 per pixel. With resting photoelectron counts this high and stimulated fluorescence changes that were <15%, the contribution of differences in shot noise between resting and stimulated measurements to our final results would have been very small (<1%) and were thus ignored.

Determination of n and p

Over the course of repeated stimulation trials, the mean fluorescence intensity f̄_s is expected to exceed the mean background level f̄_b for pixels that overlie a subregion of an active zone and periodically detect Ca²⁺ influx through one or more open Ca²⁺ channels. We limited our subsequent analysis to those pixels within active zone regions that reported significant action potential-evoked fluorescence signals under control conditions. We evaluated a range of criteria for significance to rule out sampling effects on our results as much as possible. For most of our analyses, we settled on using the criterion that the stimulus-dependent mean fluorescence (Δf_s; see below) be greater than the SD of background fluorescence σ_b (SD criterion). We demonstrated that the choice of selection criterion had little or no effect on our estimates of n and p by comparing results using this criterion with a Student's t test using different levels of significance (Table 1) (see Figs. 6 and 7).

Table 1.

The impact of pixel selection on average values of p and n

Pixel selection criteria	p	n
p < 10−2	0.26 ± 0.11	12.1 ± 2.8
p < 10−3	0.26 ± 0.11	14.1 ± 3.0
p < 10−6	0.25 ± 0.10	17.7 ± 4.2
p < 10−9*	0.24 ± 0.10	18.4 ± 1.2
SD criterion	0.24 ± 0.11	18.3 ± 4.8

Pixels were selected for analysis based on a Student's t test (p values) or our SD criterion (see Materials and Methods). Values shown are mean ± SD for four or three (asterisk) nerve terminals, and the values for p correspond to the control (pre-DAP treatment) condition.

Figure 6.

Varying the criterion for pixel selection does not bias our estimate for the probability that Ca²⁺ channels open during an action potential. A, Mask for the pixels selected after using different criteria, i.e., SD criterion, or a Student's t test using different significance levels (p < 10⁻², 10⁻³, 10⁻⁶, or 10⁻⁹). All pixels selected are shown in either red or white; only the pixels shown in white could be used to derive a meaningful p value (i.e., 0 < p < 1). B, Histogram distribution of opening probability calculated from the selected pixels under each criterion. C, In each graph, CV_s is plotted against opening probability to reveal subsets of the data that are selected under each criterion. Comparing B and C demonstrates that the distribution of opening probability of Ca²⁺ channels during an AP is not changed as more restrictive criteria eliminate a subset of the data. D, Predicted active zone regions of the example nerve terminal identified by labeling the postsynaptic acetylcholine receptor clusters with Alexa Fluor 594–α-bungarotoxin. Scale bar, 5 μm (also applies to the images in A). E, Plot of the total number of pixels selected by each criterion (yellow) and the corresponding subset of these pixels that either do (white) or do not (red) resolve a meaningful p value (i.e., 0 < p < 1).

Figure 7.

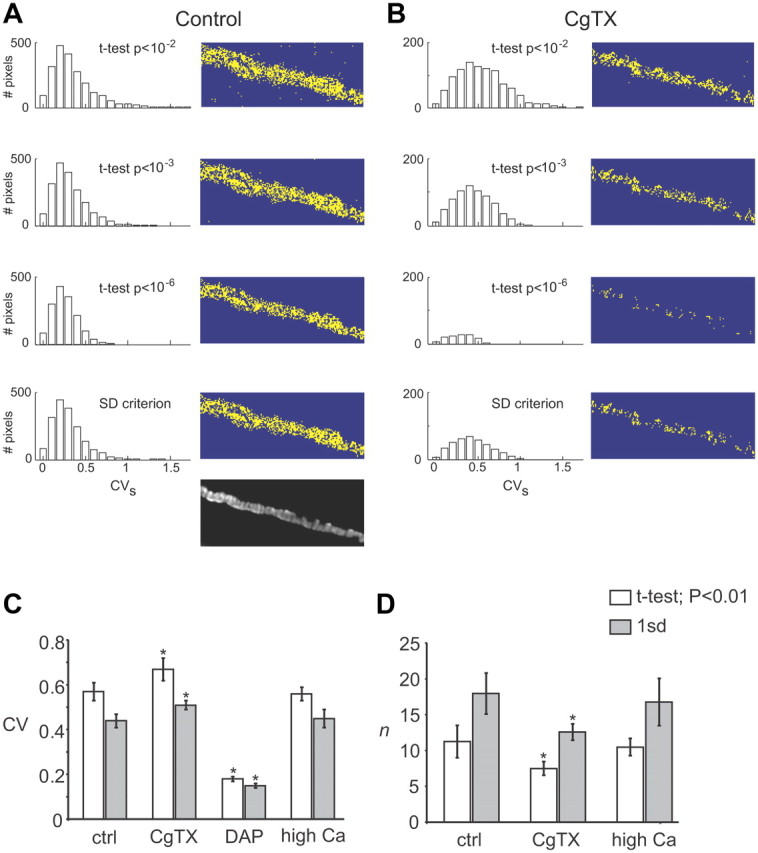
Effects of CgTX on CV_s measured using a variety of pixel selection criteria and the summary data for measured CV_s values and calculated n values under different treatment conditions. A, Distribution of CV_s values (left) and mask for the pixels selected after using different criteria (right), i.e., SD criterion, or a Student's t test using different significance levels (p < 10⁻², 10⁻³, or 10⁻⁶) from a representative nerve terminal under control conditions. The grayscale image at the bottom represents the predicted active zone regions of the nerve terminal identified by labeling the postsynaptic acetylcholine receptor clusters with Alexa Fluor 594–α-bungarotoxin. B, Distribution of CV_s values (left) and mask for the selected pixels from the same nerve terminal as is A after treatment with 100 nm CgTX for 30 min. C, Summary plot of the calculated CV_s values (mean ± SEM) for pixels sampling active zone regions of control nerve terminals (ctrl), those exposed to 100 nm CgTX, 5 μm DAP, or elevated extracellular Ca²⁺ (3.6 mm; high Ca²⁺) when using either the SD criterion (gray bars) or a Student's t test (p < 0.01; white bars). D, Summary plot of the calculated number of Ca²⁺ channels (n) sampled by active zone pixels (mean ± SEM) under control conditions (ctrl), after exposure to 100 nm CgTX, and after increasing extracellular Ca²⁺ to 3.6 mm (high Ca²⁺) when using either the SD criterion (gray bars) or a Student's t test (p < 0.01; white bars). *p < 0.05, significantly different from control, one-way ANOVA with Tukey's post hoc test.

We calculated n and p for selected pixels using two measurable ratios, R_F and R_CV (Sabatini and Svoboda, 2000). The mean of the stimulus-dependent fluorescence signals before and after DAP treatment are as follows:

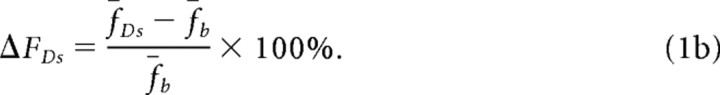We define R_F as the ratio of stimulus-dependent fluorescence signals before and after DAP treatment:

Similarly, the coefficient of variation (CV) in the stimulus-dependent fluorescence signals before and after DAP treatment are as follows:

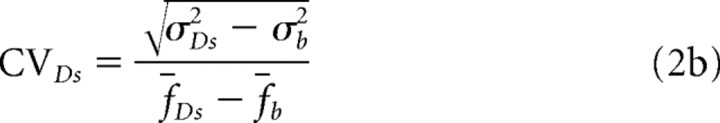R_CV is defined as follows:

To calculate n and p from the experimental R_F (Eq. 1c) and R_CV (Eq. 2c) values, we assume that each Ca²⁺ channel acts independently and opens during an action potential with probability p before DAP treatment and p_D after DAP treatment. The corresponding probabilities of remaining closed are (1 − p) and (1− p_D), respectively. Under each condition, the number of channels that open from trial to trial is expected to follow a binomial distribution. From standard binomial theory, in a sub-active zone region containing n channels, the average number that will open (μ) before DAP treatment is given by:

Assuming a linear detection system (see Results), the mean fluorescence arising from Ca²⁺ entering through open channels (ΔF_s; Eq. 1a) will be proportional to μ, thus

Similarly, after DAP treatment, the mean fluorescence arising from entering Ca²⁺ (ΔFD_s; Eq. 1b) will be proportional to the average number that will open μ_D after DAP treatment:

The mean stimulus-dependent fluorescence signals before and after DAP treatment should be governed by the number of Ca²⁺ channels opened by an action potential.

From Equations 1c, 5, and 6, we now have

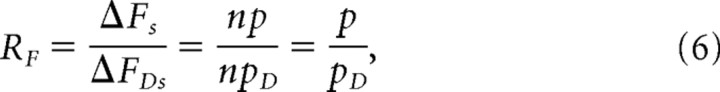where we assume that DAP treatment does not affect the number of functional Ca²⁺ channels n as well as the amount of Ca²⁺ flux through single open channels (see Results).

Again from standard binomial theory, the predicted variance for channel opening before DAP treatment σ² is

The SD (σ) is thus:

Using Equations 3 and 8, the CV in the number of open channels is

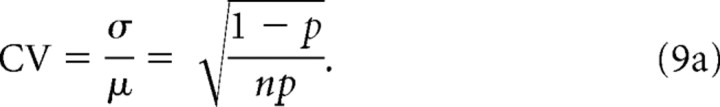If all of the variance in measured stimulus-dependent fluorescence arises from the random openings of channels from trial to trial, then from Equations 2a and 7,

and from Equations 2a and 9b,

Similarly, after DAP treatment,

Therefore, from Equations 2c, 11, and 12, we have

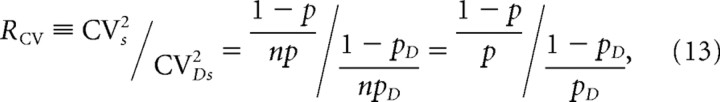where again we assume that DAP treatment does not affect the number of Ca²⁺ channels n as well as the amount of Ca²⁺ flux through single open channels.

In Equations 6 and 13, we have the two measured ratios R_F and R_CV, as well as the two unknown probabilities p and p_D. Rearranging Equation 6 for p_D yields the following:

After using Equation 14 to substitute for p_D in Equation 13, algebraic rearrangement now provides an expression for p that includes only the measured ratios R_F and R_CV:

Equation 15 was therefore used to calculate p, and Equation 14 was used to calculate p_D. Finally, a rearranged form of Equation 11 was used to estimate n:

Computational modeling of action-potential-triggered Ca²⁺ fluorescence

Generation of action potentials.

Action potentials were generated with a standard Hodgkin–Huxley model using the NEURON simulation environment (release 7.1.) (Hines and Carnevale, 1997; Carnevale and Hines, 2006). The parameters for the Hodgkin–Huxley model were chosen based on two criteria for the resulting action potentials. First, because adult motor nerve terminals are not accessible to direct recordings of action potential shape, we based our assumptions for AP shape on experimentally measured synaptic action potential waveforms from embryonic cultured motor nerve terminals, which are very narrow. Second, when used within our computational model of action-potential-triggered Ca²⁺ influx (see below), we aimed for a Ca²⁺ channel open probability p under control conditions of ∼0.2 (AP1, 0.18; AP2, 0.20). In choosing modeled APs for our analysis, we sought to use one AP shape that was very similar to the recorded AP from embryonic cultured motor nerve terminals (AP2). Because we cannot be sure of the exact shape of the AP at adult frog motor nerve terminals and to be more rigorous in our analysis, we also considered a second AP (AP1) with a distinctly different AP shape but still subject to the same constraints on open probability p for Ca²⁺ channels. The two thus generated action potential waveforms AP1 and AP2 are depicted in Figure 3A. Figure 3B shows both action potentials together with an experimentally recorded action potential recorded from cultured embryonic Xenopus nerve–muscle synapses (Pattillo et al., 2001).

Figure 3.

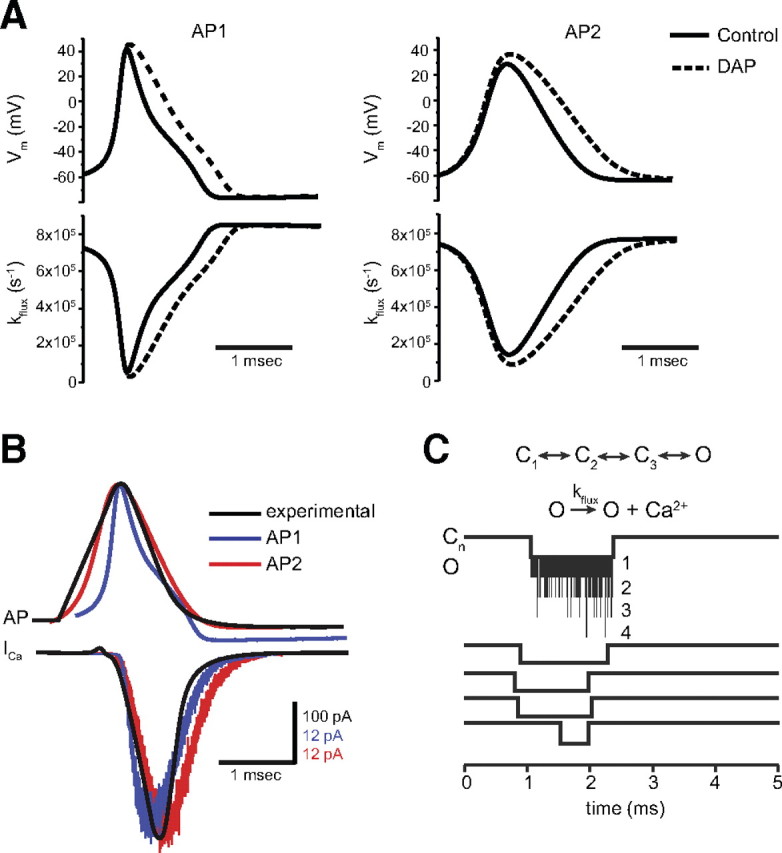
Simulated action potentials and computational model of action-potential-triggered Ca²⁺ influx. A, Simulation program NEURON generated action potentials AP1 and AP2 under control conditions and in the presence of DAP. The bottom panels show the Ca²⁺ flux k_flux through the open Ca²⁺ channels proportional to the driving force V_m − E_Ca. B, Comparison of AP1 (blue) and AP2 (red) with an experimentally recorded action potential from cultured Xenopus nerve–muscle synapses (black) (Pattillo et al., 2001) and the corresponding whole-cell Ca²⁺ currents simulated (blue and red) and recorded from a presynaptic cultured neuromuscular junction varicosity (black) (Pattillo et al., 2001). C, The top depicts a schematic diagram of our kinetic Ca²⁺ channel model with three closed and one open state. The open state conducts Ca²⁺ ions according to the driving force given by k_flux (see also A). Below, we show plots of the channel open duration for five representative simulations. In addition, the first plot gives the number of Ca²⁺ ions conducted per unit time interval.

The effect of DAP on action potential shape was modeled by reducing the g_k,max value of the potassium gating particles in the Hodgkin–Huxley model. The resulting broadening of the action potentials (see Fig. 3A) led to an increase in the Ca²⁺ channel open probability p, and g_k,max was chosen to yield a p value of ∼0.6 (AP1, 0.56; AP2, 0.65). It is important to point out that the values we chose for p were arbitrary (but very close to experimental observations) because our computational validation procedure only seeks to establish the ability of SPOFA to estimate the values of p and n regardless of their actual values.

Monte Carlo simulations of action-potential-triggered Ca²⁺ influx.

To test whether SPOFA is able to estimate p and n from measured fluorescence data, we developed a computation model of action-potential-triggered Ca²⁺ influx through voltage-gated Ca²⁺ channels. All simulations were performed with MCell version 3 (Monte Carlo Cell) (Stiles et al., 1996; Stiles and Bartol, 2001; Kerr et al., 2008) and were typically run on a desktop computer running the Linux operating system. MCell allows one to perform continuous time stochastic simulations of action-potential-triggered Ca²⁺ channel opening and subsequent Ca²⁺ ion flux into the presynaptic nerve terminal through the channel. We created several simulation models each containing a fixed number of Ca²⁺ channels (1, 10, 15, 20, 30, and 40 Ca²⁺ channels, respectively) embedded in a membrane. During each simulation, Ca²⁺ channels opened stochastically driven by the action potential and permeated Ca²⁺ ions according to the kinetic scheme depicted in Figure 3C consisting of three closed states, one open state, and voltage-dependent rates between states. The driving force k_flux for Ca²⁺ through the open channels is shown in the bottom of Figure 3A. Rates were chosen such that the model reproduced the experimentally known single-channel conductance (2.6 pS in 2 mm extracellular Ca²⁺) (Church and Stanley, 1996) and the experimentally measured whole-cell currents (see Fig. 3B) and Pattillo et al. (2001). For each model containing a given number of Ca²⁺ channels and action potential AP1 and AP2, we ran 10,000 simulations under control and DAP conditions. The resulting Ca²⁺ currents were recorded and then used as a proxy for fluorescence in our SPOFA procedure assuming a linear relationship between Ca²⁺ influx and resulting fluorescence (as determined experimentally; see below). In addition, the models containing a single Ca²⁺ channel were used to compute the distribution of channel open latencies and open times as shown in Figure 4.

Figure 4.

Properties of MCell Ca²⁺ channel model. Shown are distributions of channel open latencies (A), channel open times (B), and Ca²⁺ current integrals (C) for AP1 and AP2 under both control and DAP conditions using the late acquisition scenario (see Results). The “dimples” observed in the DAP plots for C are an artifact of our 1 ms acquisition window and the decrease in driving force for DAP-modified APs that depolarize to potentials closer to the modeled calcium channel equilibrium potential, followed by a slightly later return to a strong driving force as the AP repolarizes.

Results

Spatial resolution of data acquisition

Adult frog NMJs are characterized by long linear nerve terminals containing numerous active zones and thus allow simultaneous imaging of multiple clearly defined active zones subsequent to nerve stimulation (Wachman et al., 2004). Each active zone is ∼1 μm long, is oriented perpendicular to the long axis of the terminal, overlies a postsynaptic junctional fold containing densely packed nicotinic acetylcholine receptors, and is separated from adjacent active zones by ∼1 μm (shown schematically in Fig. 1A,B, left). Approximately 200–250 intramembraneous particles (denoted active zone proteins in Fig. 1B, left) include N-type voltage-gated Ca²⁺ channels, are arrayed in parallel double rows running the length of the active zone, and are bordered by 25–40 docked synaptic vesicles. For Ca²⁺ imaging (Fig. 1B, right), terminals were loaded with Calcium Green-1 Dextran (3000 molecular weight, K_D ∼540 nm), and postsynaptic acetylcholine receptors were labeled with Alexa Fluor 594-conjugated α-bungarotoxin. Regions of terminals containing well-focused active zones were identified by receptor fluorescence before initiation of low-frequency nerve stimulation (0.5 Hz) and acquisition of Ca²⁺ fluorescence.

To determine the effective optical resolution of our imaging system, we measured its PSF using sparsely distributed 20 nm fluorescent beads. Figure 1C shows that the results were well fit by a Gaussian function and that the full width at half-maximum amplitude was 450 nm. This distance, as indicated schematically in Figure 1B (left), is approximately two to three times larger than the pixel size of our cameras (see Materials and Methods) and approximately half the length of an active zone. Thus, we concluded that each pixel selected for analysis (see below) actually sampled an area approximately equivalent to one-half of an active zone. To confirm this conclusion with Ca²⁺-dependent fluorescence imaging from a dye-loaded frog nerve terminal, we performed cross-correlation analysis of stimulus-dependent signals detected by adjacent pixels within active zones. As shown in Figure 1D, a Lorentzian fit of our results gave a half-width of 410 nm, very close to the value obtained for the PSF. We therefore reasoned that our high-speed fluorescence acquisition system (1.5 ms delay after stimulation, 1 ms acquisition window; see Materials and Methods) captured signals primarily limited by the optical PSF and not by spatiotemporal spread of the Ca²⁺ fluorescence. Together, our PSF and cross-correlation results provide strong evidence that subsequent findings from variance analysis correspond to a space approximately equivalent to one-half of an active zone.

Selection of active zone pixels

We have shown previously that action potential-evoked Ca²⁺ signals in this preparation are detected in active zones of nerve terminals and arise exclusively from Ca²⁺ entry through N-type Ca²⁺ channels, with no contribution from Ca²⁺-induced Ca²⁺ release (Wachman et al., 2004). During low-frequency stimulation, large trial-to-trial variability in Ca²⁺-dependent fluorescence signals was evident in different active zone regions of the nerve terminal. Figure 1E shows α-bungarotoxin labeling of postjunctional membrane underlying four to five active zones, and Figure 1F shows variability in Ca²⁺-dependent fluorescence images captured for the same field of view after six different stimuli selected at random from a train of ∼100 (see Materials and Methods).

Highly variable fluorescence signals can result from detection of a small number (n) of Ca²⁺ channels that function independently and have a small probability (p) of opening during an action potential. In principle, binomial fluctuation analysis can provide estimates of n and p under such conditions, using two independent experimental measurements from which to calculate the two unknowns. For example, early binomial analysis of quantal neurotransmitter release (Del Castillo and Katz, 1954) was based on determination of the failure rate together with the frequencies of single (quantal) and multiple responses. In the present case, however, failures and quantal responses cannot be determined with certainty because the signal-to-noise ratio is very low, i.e., the difference between stimulus-dependent Ca²⁺ fluorescence and resting background fluorescence is very small. Therefore, a different approach must be taken and we followed previous reports of optical fluctuation analysis (Sabatini and Svoboda, 2000), using two ratios of values (fluorescence intensity and the squared coefficient of variation; see below) measured before and after an experimental manipulation that specifically increases p. In this way, one then can calculate p and n without direct determination of the failure rate or the size of a quantal response (see Materials and Methods).

Over the course of repeated trials, the stimulus-dependent mean fluorescence (f̄_s) (Fig. 2C) and the variability of fluorescence (e.g., σ_s) are expected to exceed the corresponding background levels [f̄_b (Fig. 2B) and σ_b, respectively] for pixels that periodically detect Ca²⁺ influx through one or more open Ca²⁺ channels. To apply fluctuation analysis to data obtained from individual pixels (SPOFA), we first had to identify those pixels that responded to repeated stimulation with both a statistically significant percentage increase in mean fluorescence (ΔF_s = (f̄_s − f̄_b)/f̄_b × 100) (Fig. 2D) and also an increase in the variance of fluorescence intensity (σ_s² − σ_b² > 0). As expected, increasingly restrictive criteria for statistical significance reduced the number of pixels selected for analysis. In addition, and again as one would expect, the remaining pixels were increasingly restricted to regions directly over active zones (Figs. 1B, right, 2A,E). In fact, we could predict how the results of fluctuation analysis would be influenced by the choice of criterion for statistical significance, particularly with respect to the apparent number (n) of functional Ca²⁺ channels “seen” by selected pixels. To test our prediction and confirm interpretation of our results, we repeated our analysis using a wide range of significance levels and characterized the impact on calculated values of n and p (see subsequent discussion of Table 1 and Fig. 6 below).

Figure 2.

Method used to define active zone regions of the nerve terminal within which action potential-evoked Ca²⁺ influx is restricted. A, Acetylcholine receptor distribution determined using Alexa Fluor 594-conjugated α-bungarotoxin. B, Resting fluorescence image of a frog motor nerve terminal averaged over 100 trials. C, Fluorescence image of the nerve terminal after a single AP stimulation averaged over 100 trials. D, Average (100 trials) Ca²⁺ influx within active zone regions of the nerve terminal evoked by a single AP. The pattern of Ca²⁺ influx averaged over 100 stimulus trials decorates nerve terminals with fluorescence signals that can visually identify active zone regions. E, Masking the active zone regions with the criterion that pixels have a mean stimulated fluorescence intensity exceeding 1 SD above resting fluorescence (SD criterion). Scale bar, 5 μm. F, Histogram distribution of CVs over 100 stimulus trials for all pixels selected by the criterion shown in E.

To illustrate one highly selective criterion, Figures 1B (right) and 2 show pixel selection based on a 1 SD method, i.e., for a given pixel to be included in additional analysis, the mean fluorescence after stimulation had to be at least 1 SD above the average background fluorescence (SD criterion, f̄_s > f̄_b + σ_b). As shown, pixels selected by the SD criterion overlie active zone locations identified by postsynaptic acetylcholine receptor staining. As introduced above, SPOFA also requires the use of coefficient of variation values $\left({\text{CV}}_s=\frac{\sqrt{{\sigma }_s^2-{\sigma }_b^2}}{{\overline{f}}_s-{\overline{f}}_b}\right)$, and Figure 2F shows the distribution obtained from a representative nerve terminal using pixels that met the SD criterion. In this example, the median value was 0.45, and similar CVs values were obtained from a total of seven nerve terminals (0.44 ± 0.08, mean ± SD; range, 0.32–0.54).

Numerical validation of SPOFA

We wanted to determine p and n based on observed changes in both mean fluorescence and the variability of fluorescence subsequent to an experimental manipulation that specifically increases p. As detailed in Materials and Methods, we treated the terminal with DAP, which blocks a fraction of voltage-gated potassium channels and thus increases the size and duration of the action potential. Our calculation of n and p from fluorescence measurements is based on the assumption that fluctuations in fluorescence are attributable to a binomial distribution of n channels that open with probability p. However, in reality, other sources of variability contribute to the stimulus-dependent fluorescence signal. For example, the amount of Ca²⁺ flux through an open channel varies because of the distribution of times to channel opening (opening latencies) as well as the distribution of open durations. Through both of these effects, the size and timing of single-channel Ca²⁺ signals (total, or integrated, single-channel currents) may be affected. Furthermore, because the duration of individual Ca²⁺ signals may exceed the image acquisition window and may do so by differing amounts, the fraction of total signal captured before and after DAP treatment may also change. Thus, to estimate p and n accurately and establish error estimates for their values, these additional contributions may need to be taken into account.

To assess the possible impact of all these factors on our ability to calculate p and n via binomial analysis, we used computer simulations to investigate the Ca²⁺ flux through individual channels in response to action potentials (NEURON and MCell simulations; see Materials and Methods). We could then use SPOFA to calculate the values of p and n based on the simulated fluorescence, compare directly with the known values of p and n chosen for the simulation, and then determine error estimates to be used with binomial analysis of our experimental fluorescence measurements.

Figure 3A shows two representative action potentials (AP1 and AP2) under control conditions and in the presence of DAP generated via the NEURON simulation environment (Carnevale and Hines, 2006). As shown in Figure 3B, the generated action potentials agree well with experimental recordings from cultured Xenopus nerve–muscle synapses (Pattillo et al., 2001). We used these action potentials in MCell simulations (Stiles et al., 1996; Stiles and Bartol 2001; Kerr et al., 2008) to drive stochastic voltage-dependent changes in Ca²⁺ channel conformation, as well as stochastic voltage-dependent Ca²⁺ ion flux through the channel while it was in the open state. Figure 3C shows corresponding closed-to-open and open-to-closed transitions obtained over the course of repeated trials (cases in which the channel did not open at all are not shown). In the same figure, instances of Ca²⁺ ion flux through the open state (single, or rarely, multiple ions) during discrete time intervals are also indicated, and it is evident that such permeation events were more likely when the driving force for Ca²⁺ entry was high. In Figure 3B, we compare computed whole-cell Ca²⁺ currents with recordings from cultured Xenopus nerve–muscle synapses (Pattillo et al., 2001). Both simulated action potential waveforms give rise to currents that match the time course of experimental data well, particularly AP2.

To estimate the amount of Ca²⁺ signal that would be detected experimentally as mean fluorescence, we chose a 1 ms time window corresponding to our experimental image acquisition time and then summed all Ca²⁺ ions that passed through channels before and during the acquisition window. Because experimentally we do not know precisely where within the duration of the action potential our 1 ms acquisition window falls, we used two different modeling scenarios to bracket the behavior of the system. In the first, the acquisition window starts shortly after action potential onset after the integrated Ca²⁺ current has reached 5% of its maximum value. We call this early acquisition. In the second, acquisition starts only after the integrated Ca²⁺ current has reached 50% of its maximum value. Here, our 1 ms acquisition window captures most of the total Ca²⁺ signal entering the terminal during the action potential. We call this second scenario late acquisition.

Initially, we simulated models containing a single Ca²⁺ channel. To illustrate the data obtained over repeated trials, Figure 4 shows histograms of channel opening latencies (Fig. 4A), channel open times (Fig. 4B), and total single-channel Ca²⁺ ion passage (current integral, Fig. 4C obtained via late acquisition) obtained during repeated trials for the two action potential waveforms AP1 and AP2. The mean channel open times under control conditions (AP1, 0.56 ± 0.3 ms; AP2, 0.65 ± 0.35 ms) and in the presence of DAP (AP1, 0.77 ± 0.34; AP2, 0.91 ± 0.4) are below 1 ms, indicating that our 1 ms acquisition window is sufficient to capture most of the Ca²⁺ signal particularly in the late acquisition scenario (however, see discussion of current distribution below). Figure 4C depicts the Ca²⁺ current distributions generated with AP1 and AP2 under control and DAP conditions. Overall, the current distributions under both conditions are similar. The fact that, in the presence of DAP, we sample slightly lower maximum current values is attributable to the prolonged action potential duration and correspondingly lower driving force combined with a fixed 1 ms acquisition window.

Our next step in modeling studies was to use multiple Ca²⁺ channels in each simulation and to determine the time course of the summed Ca²⁺ signal for different combinations of action potential waveform, number of channels, and with or without DAP treatment. For each set of conditions, we ran thousands of simulations and obtained the average number of permeant Ca²⁺ ions as a function of time (data not shown). The resulting Ca²⁺ currents were then used to compute values for p and n according to the SPOFA procedure outlined in Materials and Methods. We used the number of Ca²⁺ ions summed over a 1 ms acquisition window as proxy for measured fluorescence. As an example, Table 2 gives values for summed Ca²⁺ ions, CV values, R_F, R_CV, and calculated values of p for a system driven by action potential AP1 under an early acquisition scenario for simulation systems containing 1, 10, 15, 20, 30, or 40 Ca²⁺ channels. The computed value of p across all these systems was fairly consistent with a mean of p of ∼0.16, in good agreement with the actual value of p = 0.18 used in the simulations. The last column in Table 2 gives the corresponding values for n computed via Equation 11 using the computed average p value. Thus, in this particular scenario, SPOFA underestimates the true values of n by ∼25%.

Table 2.

Statistical properties of computational calcium channel model

n	Ca2+ count control	Ca2+ count DAP	RF	CV2	CVDAP2	RCV2	p	n
1	44	144	0.306	6.96	1.25	5.57	0.15	0.74
10	443	1407	0.315	0.72	0.13	5.56	0.17	7.18
15	660	2122	0.311	0.49	0.09	5.69	0.16	10.59
20	889	2821	0.315	0.35	0.06	5.58	0.17	14.56
30	1339	4248	0.315	0.24	0.04	5.47	0.16	21.88
40	1770	5676	0.312	0.18	0.03	5.74	0.17	28.37
Avg.							0.16

Shown are data from a model driven by a NEURON-generated AP (AP1) (Fig. 3) and our stochastically gated channel model shown in Figure 3. The actual open probabilities in the model are p = 0.18 and p_DAP = 0.63 for control and after DAP treatment, respectively. The data were acquired with a 1 ms sampling window, and data collection started after the current integral reached 5% of its maximum value (early acquisition; see Results).

Finally, in Table 3, we summarize the relative errors in the computed values of p and n for models driven by action potential waveforms AP1 and AP2 under both early and late acquisition scenarios. Based on these results, we can infer that the early acquisition scenario provides good estimates of p but tends to underestimate n by up to 30%. Conversely, the late acquisition scenario tends to underestimate the value of p by up to 30% but results in good estimates of n. Because our experimental acquisition window lies somewhere between these two extremes, we can thus argue that SPOFA applied to our experimental data provides reliable estimates of both p and n and will at most underestimate either one by ∼30%. These findings are consistent for both action potential waveforms studied, suggesting that the predictive power of our SPOFA method is independent of the detailed shape of the underlying action potential when it is within these ranges.

Table 3.

Average relative errors for calculated values of p and n with respect to the known values

Simulation type	Average relative error in p	Average relative error in n
AP1 (early acquisition)	−0.091	−0.278
AP1 (late acquisition)	−0.343	−0.019
AP2 (early acquisition)	0.032	−0.326
AP2 (late acquisition)	−0.351	0.068

Each row corresponds to a simulation using one of the two action potential waveforms. Positive and negative values for relative errors signify over and underestimates obtained via optical fluctuation analysis, respectively.

The probability (p) that Ca²⁺ channels open during an action potential

Our use of SPOFA to determine p and n from single-pixel fluorescence measurements was based on the use of two ratios, for which each component value was measured before and after an experimental manipulation that specifically increased p. Preparations were treated with 5 μm DAP for 30 min to block potassium channels selectively and, as a result, broaden the action potential (Bostock et al., 1981; Thomsen and Wilson, 1983; Augustine, 1990) and secondarily increase p (Augustine, 1990).

Figure 5, A and B, shows Ca²⁺ imaging data from a representative nerve terminal before and after DAP exposure. Using our SD criterion to select pixels, we calculated per pixel values of ΔF_s and CV_s under both conditions, and Figure 5, C and D, shows the corresponding frequency distributions. Although DAP exposure strongly increased ΔF_Ds, it simultaneously decreased CV_Ds compared with control, and both of these effects are consistent with an increase in p according to standard binomial theory. In brief, if n Ca²⁺ channels are detected by a pixel and open independently with an average probability p during an action potential, the expected number of open channels per trial will follow a binomial distribution. The mean of a binomial distribution μ is given simply by np, and so an increase in p will clearly increase μ, or, in our case, the mean value of ΔF_s. The binomial variance σ² and coefficient of variation CV are given by (1 − p)np and $\frac{1-p}{np}$, respectively. From the latter, an increase in p will decrease CV, or CV_s in our experiments.

Figure 5.

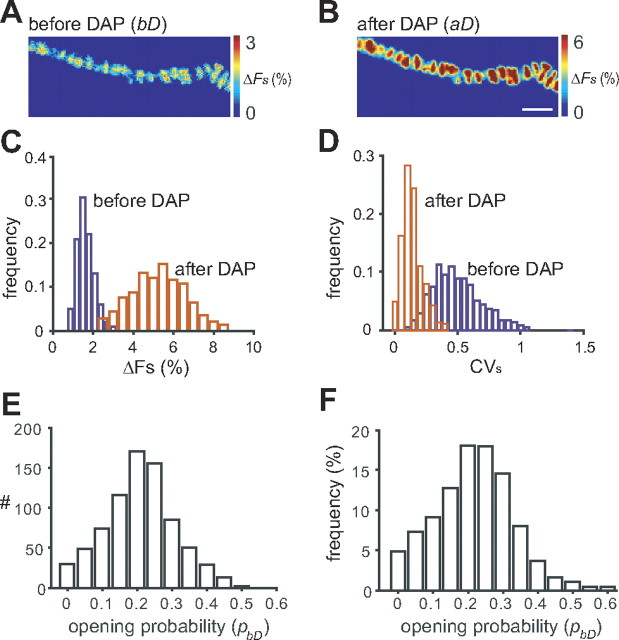
Opening probability of Ca²⁺ channels during an action potential. A, Averaged AP-evoked Ca²⁺ influx under control condition (90 trials). B, Averaged AP-evoked Ca²⁺ influx after 5 μm 3,4-diaminopyridine treatment (90 trials). Scale bar, 5 μm. C, Histogram distribution of the fluorescence intensity reported by individual pixels before (blue) and after (red) exposure to DAP. D, Histogram distribution of the stimulus-dependent coefficient of variation of individual pixels before (blue) and after (red) DAP exposure. E, Histogram distribution plotting opening probability of Ca²⁺ channels during an action potential calculated from individual pixels for the example control terminal shown in A. F, Histogram distribution plotting the average opening probability of Ca²⁺ channels during an action potential calculated from individual pixels pooled from a total of four control nerve terminals.

To estimate p, we used the ratio of ΔF_s and ΔF_Ds, together with the ratio of CV_s² and CV_Ds², measured before and after DAP treatment. These calculations allow us to obtain values for p both before (control) and after the DAP treatment (see Eqs. 14 and 15 in Materials and Methods). Figure 5E shows the distribution of control values obtained from the data shown previously for a representative nerve terminal in Figure 5A–D. Because the distribution was not Gaussian, we used the median value (0.22) as our estimate of the mean opening probability (p) for Ca²⁺ channels in this nerve terminal. After DAP treatment, the estimated mean opening probability increased to 0.72. Similar results were obtained from four nerve terminals for which we pooled all the single-pixel data and generated a frequency histogram for p under control conditions (Fig. 5F). The median value was 0.24 for the pooled data. Taking into account our numerically derived error estimates (see above, Numerical validation of SPOFA), we can derive a lower limit of 0.23 and an upper limit of 0.37 for p with the actual value likely to be somewhere between.

The number (n) of Ca²⁺ channels in active zones

We based our initial estimates of n on pixel data obtained from the four nerve terminals used in the DAP studies outlined above. For each terminal, the median p and CV_s² values were used to calculate a value of n (see Eq. 16 in Materials and Methods; pixel selection was performed using the SD criterion). Using this approach, we found that n ranged from 14 to 24 across the four terminals, with a mean ± SD value of 18.3 ± 4.8. When values of n were calculated individually for each pixel and then averaged together, the results were not significantly different.

In addition, we analyzed the seven nerve terminals not treated with DAP discussed previously (see above, Selection of active zone pixels). Because these terminals were not exposed to DAP, we did not have an independent estimate of p. Instead, we used the median value (p = 0.24) determined from the DAP experiments on the initial four terminals. Using this value for p, together with the median CV_s² value for each untreated terminal, we calculated values of n, which ranged from 11 to 31, with a mean ± SD value of 18.0 ± 7.5. This average was not significantly different from the result obtained with the DAP-treated terminals (unpaired Student's t test, p = 0.9). Thus, we pooled the data from all 11 nerve terminals to obtain a final estimate of n, 18.1 ± 6.4 (mean ± SD). From our previous characterization of the PSF and pixel correlation analysis (Fig. 1), we estimated that single pixels sample spatial regions approximately equivalent to one-half of an active zone. Thus, our data indicate that each active zone has ∼2n, or only ∼36 Ca²⁺ channels that are capable of opening in response to an action potential (functional channels). Taking into account our numerically derived error estimates (see above, Numerical validation of SPOFA), we can compute a lower limit of 34 and an upper limit of 53 for the number of Ca²⁺ channels, with the actual value likely falling somewhere between. Presumably, these functional channels are distributed among the 200–250 intramembraneous particles described in freeze-fracture replicas.

The impact of pixel selection on estimates of p and n

Given that we used up to 100 nerve stimuli during image acquisition and also that individual pixels sampled an area of approximately half an active zone, we had two primary expectations regarding the selection of pixels for analysis. First, notwithstanding the low signal-to-noise ratio, a relatively low level of statistical significance should be able to differentiate between pixels that overlie the nerve terminal as opposed to the surrounding tissue. Second, as the criterion for statistical significance became more restrictive and fewer pixels were selected, those remaining should be completely restricted to the nerve terminal, and, in addition, should be increasingly restricted to positions centered over active zones (and therefore over functional Ca²⁺ channels). We then reasoned that values calculated for n should be smaller with less restrictive selection criteria, because an increasing fraction of pixels would “see” an area on the periphery of an active zone and therefore would detect a fluorescence signal originating from fewer channels. Conversely, values calculated for p should remain fairly constant over a wide range of selection criteria, assuming that functional channels have identical gating characteristics regardless of their location in the active zone, or that any possible heterogeneity of gating function occurs over a spatial scale much smaller than the resolution of our optical system.

Figure 6 and Table 1 summarize the results that verify our predictions for the impact of pixel selection on estimates of p and n. Whereas the data shown in Figure 6 are based on a single terminal treated with DAP, Table 1 includes final average values of p and n calculated from multiple DAP-treated terminals (additional analysis of the data presented previously in Fig. 5). Figure 6A (top) shows that a significance criterion as permissive as p < 10⁻² (Student's t test) selected an appreciable number of pixels that lay beyond the borders of the nerve terminal itself (compare position of red and white dots to fluorescence image of postsynaptic bungarotoxin stain in Fig. 6D). Values of CV_s and p were widely scattered (Fig. 6B,C, top), although clustering was still apparent and indicated a midrange value for p of ∼0.2. When more restrictive criteria were used to determine significance (p < 10⁻³, 10⁻⁶, or 10⁻⁹, or using our SD criterion instead), the number of pixels selected for analysis decreased (Fig. 6E), the pixels were increasingly restricted to the nerve terminal and active zones (Fig. 6A, top to bottom), and clustering of CV_s and p values became evident (Fig. 6C, top to bottom). The number of selected pixels converged toward an apparent minimum obtained with either p < 10⁻⁹ (Student's t test) or our SD criterion (Fig. 6E; recall that the SD criterion was highly restrictive because inclusion of a pixel required that its average fluorescence was greater than the average background value by more than 1 SD). Figure 6, A and E, also shows how pixels were subdivided into those that had increased (white) or decreased (red) variance compared with background variance levels (σ_s² vs σ_b²), despite the prerequisite increase in average fluorescence. Although the presence of pixels with decreased variance at first may seem counterintuitive, in fact it is expected because of the very small absolute size of the stimulus-dependent fluorescence signal (ΔF_s of only several percent) (Figs. 1, 2, 5). Unlike a system at the opposite extreme, in which there is a clearly discernible quantal response, here, because of the low open probability p and correspondingly small increase in fluorescence, one expects only a small excess of pixels with increased variance, whereas the remainder may show decreased variance simply by random chance. An examination of the total number of pixels with increased (white squares) and decreased (red squares) variance shown in Figure 6E reveals that this was the case for our data, and careful inspection also shows a minor trend toward a higher fraction of pixels with increased variance as the criterion for selection became more restrictive. Limiting our analysis to selected pixels with increased variance, we found, as predicted, that average values obtained for p were virtually indistinguishable regardless of the pixel selection criterion (Table 1). Table 1 also shows that, as predicted, average values obtained for n increased as the criterion for pixel selection became more restrictive, until nearly identical results were obtained with the two most selective criteria.

Control measurements

Our SPOFA depends on a linear relationship between ΔF_s and Δ[Ca²⁺]. To confirm the linearity of our measurements, we varied extracellular Ca²⁺ and measured the resulting change in fluorescence. After doubling extracellular Ca²⁺ concentration (from 1.8 to 3.6 mm, enhancing Ca²⁺ influx per open channel), the Ca²⁺ signal detected within active zone regions of the nerve terminal increased by 102 ± 2% (n = 4 terminals). In contrast, the CV_s value obtained with high extracellular Ca²⁺ was not significantly different from that obtained with normal extracellular Ca²⁺ (p > 0.05, one-way ANOVA with Tukey's post hoc test) (Fig. 6A). This doubling in Ca²⁺ signal, coupled with an unchanged CV_s, supports the conclusion that the reduced CV_s obtained after DAP exposure was indeed caused by an increase in p and not by a potential saturation of measured fluorescence. Based on this analysis, we can also conclude that the concentration of extracellular Ca²⁺ (and thus the magnitude of Ca²⁺ influx through open channels) does not alter our quantitative analysis of variability in presynaptic fluorescence signals. Therefore, this experiment serves as a control for the validity of our fluctuation analysis.

A lack of significant dye saturation during low-frequency stimulation might be expected given the ordered geometry of adult frog NMJ active zones (long, linear arrays of presynaptic Ca²⁺ channels distributed spatially at some distance from one another) (Fig. 1), combined with the prediction that there are few Ca²⁺ channel openings within each active zone during a single action potential (Wachman et al., 2004; this study). The absence of significant dye saturation under similar imaging conditions at this synapse was also reported by Shahrezaei et al. (2006). The linearity of fluorescence and Ca²⁺ signal in our experiments is fortuitous, and both fluorescence detection and calcium-sensitive dye interactions with calcium ions are expected to saturate outside our experimental conditions.

Finally, to further validate our fluctuation analysis, we also examined the effects of exposure to a submaximal concentration of ω-conotoxin GVIA (CgTX) (100 nm). This treatment is known to completely and irreversibly block (over the course of our experiments) a subset of N-type Ca²⁺ channels without affecting the probability of opening for channels that remain unblocked (Kerr and Yoshikami, 1984; Stocker et al., 1997). Exposure to 100 nm CgTX blocked total action-potential-evoked Ca²⁺ entry in the nerve terminal by 70 ± 5.9% (mean ± SD, 5 nerve terminals). As a result, the stimulus-dependent fluorescence signals were very weak, and we had to use a less restrictive pixel selection criterion to be able to select a sufficient number of pixels for analysis. Using a Student's t test to select active zone pixels (p < 0.01) (Fig. 7, Table 4), the average CV_s after CgTX treatment increased significantly above control to a value of 0.67 ± 0.11 (one-way ANOVA with Tukey's post hoc test, p < 0.05; mean ± SD, 5 nerve terminals). Using the estimated p (0.24) determined above (CgTX does not affect the gating properties of unblocked channels) and the CV_s from CgTX-treated nerve terminals, the average n (n = 7.5 ± 2.1) was significantly decreased compared with control (one-way ANOVA with Tukey's post hoc test, p < 0.05). The difference in magnitude of CgTX-mediated reduction of total Ca²⁺ indicator fluorescence (∼70%) and the reduction in calculated Ca²⁺ channel number (∼33%) is attributable to the following. When measuring total Ca²⁺ indicator fluorescence, we observe the change in the total stimulus-dependent fluorescence within the entire nerve terminal area. This includes some active zone regions of the nerve terminal in which all Ca²⁺ channels were completely blocked by the CgTX treatment and others in which some Ca²⁺ channels remained unblocked after exposure to CgTX. In contrast, our SPOFA analysis can only consider pixels in which some signal remains after CgTX treatment. Under these conditions, the SPOFA analysis underestimates the reduction in n that occurs because there are some pixels that sample active zone regions of the nerve terminal in which n drops to zero after CgTX treatment, and these are not included in the SPOFA analysis. Regardless of this quantitative difference, a decrease in n is consistent with the expected effects of CgTX. Therefore, our method of variance analysis is sensitive to treatments known to alter either p (DAP) or n (CgTX), because the measured CV_s values vary as expected (Fig. 7).

Table 4.

Pixel selection criteria and their impact on our estimates of CV_s and n in CgTX-treated nerve terminals

Pixel selection criteria	CVs	n
Student's t test, p < 10−2	0.67 ± 0.11	7.5 ± 2.1
Student's t test, p < 10−3	0.58 ± 0.09	10.0 ± 2.8
Student's t test, p < 10−6	0.48 ± 0.11	15.9 ± 8.1
SD criterion	0.51 ± 0.05	12.6 ± 2.6

Figure 7B displays the impact of these selection criteria on the number of pixels selected for analysis in a representative nerve terminal (values represent mean ± SD; n = 5 terminals).

Discussion

In this study, we have combined variance analysis with high-resolution Ca²⁺ imaging techniques and Monte Carlo simulations to estimate the number and probability of opening of Ca²⁺ channels within presynaptic active zones. Our results predict that a single active zone at the frog NMJ contains a relatively small number of Ca²⁺ channels, each with low probability of opening during an action potential.

The opening probability of active zone Ca²⁺ channels during action potential stimulation

The probability that presynaptic Ca²⁺ channels open in response to a single action potential is primarily determined by the activation kinetics of Ca²⁺ channels and the shape of the action potential. This is distinct from the probability that a channel opens in response to a prolonged voltage step (P_o), which typically is calculated as the steady-state fraction of time that the channel is in the open state. Here we are interested in the likelihood that a Ca²⁺ channel will open during a brief action potential depolarization. Indeed, by broadening the action potential with DAP, we have shown that the opening probability of presynaptic Ca²⁺ channels increase significantly. In a limited number of cases, it has been possible to estimate the opening probability of presynaptic Ca²⁺ channels from patch-clamp recordings of Ca²⁺ current. At the squid giant synapse (Augustine, 1990), the chick ciliary ganglion calyx (Bertram et al., 1996), and cultured Xenopus neuromuscular varicosities (Poage and Meriney, 2002), it has been estimated that opening probability is relatively small (0.1–0.3). In contrast, evidence from the rat calyx of Held (Borst and Sakmann, 1998), hippocampal mossy fiber boutons (Bischofberger et al., 2002), and cerebellar granule cell synapses onto Purkinje neurons (Sabatini and Regehr, 1997) indicate that action potentials activate a large fraction of available Ca²⁺ current (0.7–0.9). Thus, it is likely that the proportion of presynaptic Ca²⁺ channels that open with action potential stimulation may be variable between synaptic preparations. Furthermore, Ca²⁺ channels have characteristic gating kinetics that depend on Ca²⁺ channel type, splice variant, and auxiliary subunits (Jones and Marks, 1989; Lin et al., 1997, 1999). In fact, striking differences in the rate of activation (∼15-fold) have been observed when comparing isoforms of the α_1B N-type Ca²⁺ channel derived from rat brain (Stea et al., 1999). Therefore, Ca²⁺ entry during an action potential can vary widely when examined across synapses and model preparations, even within the same family of Ca²⁺ channels. Despite these differences between synaptic preparations, our data are consistent with previous work at the frog neuromuscular junction that support the conclusion that the probability of Ca²⁺ channel opening during an action potential is very low. Using SPOFA, we were able to calculate the opening probability p in our experimental preparation to be 0.24, in agreement with previous estimates (Wachman et al., 2004). Furthermore, based on error estimates taken from extensive computer simulations, we show that the opening probability p in our sample is likely somewhere in the range of 0.23–0.37.

Our analysis approach assumes that all Ca²⁺ channels we sampled have the same probability of opening during an action potential. Thus, our calculation of the probability of opening during an action potential represents an average of the actual values for individual Ca²⁺ channels. It would be interesting to know how much variability in p exists among individual active zone Ca²⁺ channels. Furthermore, it is likely that the probability of Ca²⁺ channel opening during an action potential can be modulated under different conditions (i.e., disease, altered synaptic activity, or pharmacologic treatment). In particular, this characteristic may be one that is modulated under conditions that trigger presynaptic mechanisms for transmitter release homeostasis (Wang et al., 2004; Frank et al., 2009).

The number of Ca²⁺ channels within single active zones of the motor nerve terminal

Despite previous work presenting evidence that the ∼200–250 active zone intramembraneous particles observed in freeze-fracture active zone replicas include the voltage-gated Ca²⁺ channels that trigger vesicle release (Pumplin et al., 1981; Robitaille et al., 1990; Cohen et al., 1991) as well as Ca²⁺-activated potassium channels (Robitaille et al., 1993), it remains unknown how many of these active zone intramembraneous particles actually represent presynaptic Ca²⁺ channels. Furthermore, the stoichiometric relationship between presynaptic Ca²⁺ channels and the docked synaptic vesicles that line both sides of the active zone is unknown. In our experiments, an average of ∼18 Ca²⁺ channels was reported by individual imaging pixels positioned over active zone regions of the nerve terminal. When we extended this single-pixel estimate to the number that would be expected to be present in an entire active zone (based on the optical resolution of the system) (Fig. 1), we estimate that each active zone has only ∼36 voltage-gated Ca²⁺ channels along its entire length. Because we used the measured variance of fluorescence signal to calculate the number of Ca²⁺ channels in the active zone, other sources of variance (i.e., fluctuating Ca²⁺ flux through single channels) can influence this estimate. Based on error estimates for our SPOFA procedure obtained by extensive Monte Carlo simulations (see Results and Table 3), we predict that the number of voltage-gated Ca²⁺ channels per active zone is somewhere in the range of 34–53.

Therefore, our results suggest that the number of active Ca²⁺ channels in an entire active zone constitutes only a small proportion (∼20%) of total intramembraneous particles (200–250) observed in freeze-fracture replicas. Because there are ∼25–40 docked synaptic vesicles per active zone, our data raise the interesting possibility that each docked synaptic vesicle is tightly associated with only one voltage-gated Ca²⁺ channel (Fig. 8). Although this idea is consistent with the highly ordered Ca²⁺-regulated release machinery at the active zone (Harlow et al., 2001), we are unable to exclude the possibility of a heterogeneous distribution of Ca²⁺ channels along the active zone.

Figure 8.

Conceptual model of a single active zone showing graphically the stoichiometric and functional relationship between Ca²⁺ channels and docked synaptic vesicles. Replica from a freeze-fractured frog neuromuscular junction (adapted from Heuser and Reese, 1981) showing a linear array of intramembraneous active zone particles. Superimposed on this image is a graphic representation of the hypothesized number and position of associated synaptic vesicles (white circles), voltage-gated Ca²⁺ channels (black circles), and the number of these voltage-gated Ca²⁺ channels that are predicted to open after stimulation by a single action potential (filled black circles).

Of course, our analysis only estimates the number of functional presynaptic Ca²⁺ channels present in the active zone. There may be additional Ca²⁺ channels present that are “silent” as a result of some form of modulation such that they do not open during our experiments. A “silencing” of ion channels has been observed for potassium channels as a result of sumoylation (Rajan et al., 2005; Wilson and Rosas-Acosta, 2005), and something similar could occur with synaptic Ca²⁺ channels using any of a variety of potential mechanisms (Pun et al., 1986; Lipscombe et al., 1989; Faber et al., 1991; Voronin and Cherubini, 2004; Toselli et al., 2005). Variability in the number of active Ca²⁺ channels in an active zone then could be explained by some mechanism that underlies a “silent” to “functional” interconversion. Under this scenario, it is possible that some of the particles identified in freeze-fracture replicas of the frog neuromuscular junction may be silent Ca²⁺ channels.

The Ca²⁺ channel–vesicle release relationship

The question of how many Ca²⁺ channels must open to trigger a single release event is particularly intriguing and contributes to our understanding of how Ca²⁺ regulates synaptic vesicle fusion in the nerve terminal. Historically, at some synapses, it has been proposed that many Ca²⁺ channels normally open to provide the Ca²⁺ trigger for vesicle fusion (Wheeler et al., 1994; Mintz et al., 1995; Borst and Sakmann, 1996; Wu et al., 1999), whereas at others it appears that one or only a few Ca²⁺ channels open to trigger each vesicle fusion event (Yoshikami et al., 1989; Augustine et al., 1991; Stanley, 1993; Brandt et al., 2005; Gentile and Stanley, 2005; Shahrezaei et al., 2006; Bucurenciu et al., 2010). Within individual active zones of the frog motor nerve terminal, our experimental data lead us to predict that an average of approximately nine Ca²⁺ channels open after an action potential (in which the range might be 8–18 based on Monte Carlo simulations of predicted error), whereas vesicles are released with a probability of only ∼0.5. Therefore, there appears to be a relatively low probability that these Ca²⁺ channel openings trigger vesicle fusion. One possible explanation is that each vesicle release event requires the summed Ca²⁺ flux through many open Ca²⁺ channels. However, previous studies at this synapse have suggested that Ca²⁺ flux through only one to two Ca²⁺ channels normally trigger transmitter release (Yoshikami et al., 1989; Shahrezaei et al., 2006). If only a few Ca²⁺ channel openings are required to trigger vesicle fusion, it is possible that these openings need to occur in close proximity to one another in the active zone to be effective at evoking transmitter release. The probability that two channel openings would occur in close proximity is low, which could therefore limit the occurrence of vesicle fusion from each active zone. Alternatively, each vesicle fusion event might be controlled predominately by one tightly associated Ca²⁺ channel positioned nearby but that Ca²⁺ flux through these single open channels might only trigger vesicle fusion with a low probability (5–10%). In this case, the release probability within individual active zones would be determined by both the number of open Ca²⁺ channels and the probability that a single open Ca²⁺ channel triggers vesicle fusion.