Coagulation of human prostate volumes with MRI-controlled transurethral ultrasound therapy: Results in gel phantoms

Abstract

Purpose: The feasibility and safety of magnetic resonance imaging (MRI)-controlled transurethral ultrasound therapy were demonstrated recently in a preliminary human study in which a small subvolume of prostate tissue was treated prior to radical prostatectomy. Translation of this technology to full clinical use, however, requires the capability to generate thermal coagulation in a volume up to that of the prostate gland itself. The aim of this study was to investigate the parameters required to treat a full 3D human prostate accurately with a multi-element transurethral applicator and multiplanar MR temperature control.

Methods: The approach was a combination of simulations (to select appropriate parameters) followed by experimental confirmation in tissue-mimicking phantoms. A ten-channel, MRI-compatible transurethral ultrasound therapy system was evaluated using six human prostate models (average volume: 36 cm³) obtained from the preliminary human feasibility study. Real-time multiplanar MR thermometry at 3 T was used to control the spatial heating pattern in up to nine planes simultaneously. Treatment strategies incorporated both single (4.6 or 8.1 MHz) and dual (4.6 and 14.4 MHz) frequencies, as well as maximum acoustic surface powers of 10 or 20 W cm⁻².

Results: Treatments at 4.6 MHz were capable of coagulating a volume equivalent to 97% of the prostate. Increasing power from 10 to 20 W cm⁻² reduced treatment times by approximately 50% with full treatments taking 26 ± 3 min at a coagulation rate of 1.8 ± 0.4 cm³ min⁻¹. A dual-frequency 4.6/14.4 MHz treatment strategy was shown to be the most effective configuration for achieving full human prostate treatment while maintaining good treatment accuracy for small treatment radii. The dual-frequency approach reduced overtreatment close to the prostate base and apex, confirming the simulations.

Conclusions: This study reinforces the capability of MRI-controlled transurethral ultrasound therapy to treat full prostate volumes in a short treatment time with good spatial targeting accuracy and provides key parameters necessary for the next clinical trial.

INTRODUCTION

The incidence of localized prostate cancer has increased considerably over the past 20 years, due in part to the introduction of widespread screening with PSA¹ and transrectal biopsy.^{2, 3} A consequence of this widespread screening is that approximately 85% of newly diagnosed prostate cancers represent low- to intermediate-risk localized disease.⁴ For these men, a major issue is the overtreatment of clinically insignificant disease with significant risk of long-term impairment to quality of life caused by existing radical treatments.⁵ In this context, the choice of treatment strategy becomes a significant consideration for the majority of patients with newly diagnosed prostate cancer.

Transrectal high-intensity focused ultrasound (HIFU) therapy has been developed as a minimally invasive image-guided treatment for localized prostate cancer, involving the coagulation of prostate tissue using high-intensity ultrasound energy delivered from the rectum. Compared to conventional surgery, HIFU treatments can be performed in a single outpatient setting with shorter recovery times which may offer significant benefits for both patients and the cost of managing the disease.^{6, 7, 8, 9} Long-term clinical followup of ultrasound-guided transrectal HIFU confirms the feasibility and efficacy of this technique for localized prostate cancer therapy, reporting acceptable local control of disease and some potential for a reduced impact on quality of life.^{10, 11, 12, 13, 14} Recent investigations have demonstrated the capability of high-intensity ultrasound energy for treating prostate tissues using transrectal, interstitial or transurethral devices.^{15, 16, 17, 18, 19} All of these approaches would benefit from real-time monitoring of the temperature distribution during the formation of the thermal coagulation volume.

Magnetic resonance imaging (MRI) is emerging as a robust modality for prostate cancer assessment and is showing encouraging results in enabling accurate knowledge of the extent and location of the cancer within the prostate gland.^{20, 21} Integrating high-intensity ultrasound treatment into the MRI environment could present many advantages for the management of localized prostate cancer. In particular, the capability of MRI to perform noninvasive thermometry during treatment can provide accurate monitoring of the volumetric heating pattern produced by ultrasound therapy.^{15, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32}

Our group has been developing a MRI-controlled transurethral ultrasound therapy system for treatment of localized prostate cancer.^{15, 32, 33, 34, 35, 36, 37, 38} Compared with transrectal HIFU, transurethral delivery enables the use of simple planar unfocused transducers within the prostate, avoiding the need to propagate sound through sensitive structures such as the rectal wall. The continuous delivery of ultrasound energy from multiple planar transducers enables a higher volumetric rate of coagulation compared with a focused approach. This approach, however, requires very accurate image guidance during treatment to control the spatial pattern of heating accurately. Previous preclinical studies performed by our group and others have demonstrated the feasibility of using a rotating planar ultrasound transducer for the treatment of targeted 3D volumes in tissue-mimicking gel phantoms, canines, and human subjects.^{32, 39, 40} In all of these studies, conservative treatments (i.e., treatment volumes < prostate volume) were demonstrated under active MR temperature control. Recent simulations and experiments from our group suggest that a dual-frequency multi-element approach can achieve full treatment volumes in canine prostates with an accuracy of approximately 2 mm.³⁸ The aim of this comparative study was to determine appropriate combinations of acoustic power and frequency for full human prostate thermal therapy (using a multi-element, dual-frequency transducer configuration) and to evaluate statistically these parameters in phantoms with various prostate geometries. Unique to this study was the use of human prostate geometries segmented from an initial pilot clinical study conducted by our group,⁴⁰ thereby providing for the first time an accurate representation of the target volumes and 3D geometries after the insertion of a rigid transurethral device. The best treatment strategies were compared experimentally with tissue-mimicking phantoms in a 3 T MRI system using closed-loop temperature feedback for monitoring the entire prostate gland. This comparative study was set to confirm experimentally, and in realistic clinical geometries, all the possibilities offered by the transurethral approach in preparation for a subsequent clinical trial.

MATERIAL AND METHODS

Patient-specific prostate geometries

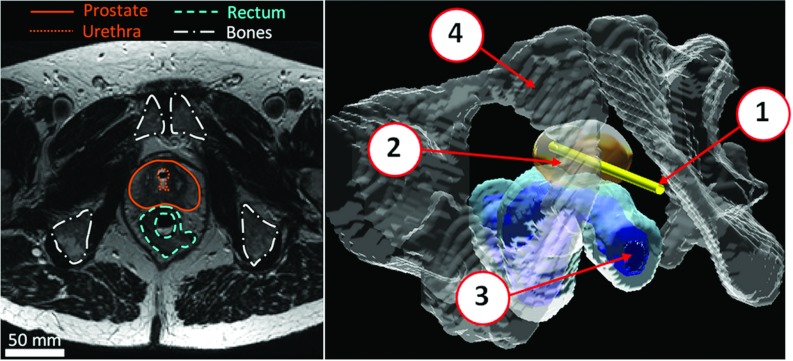
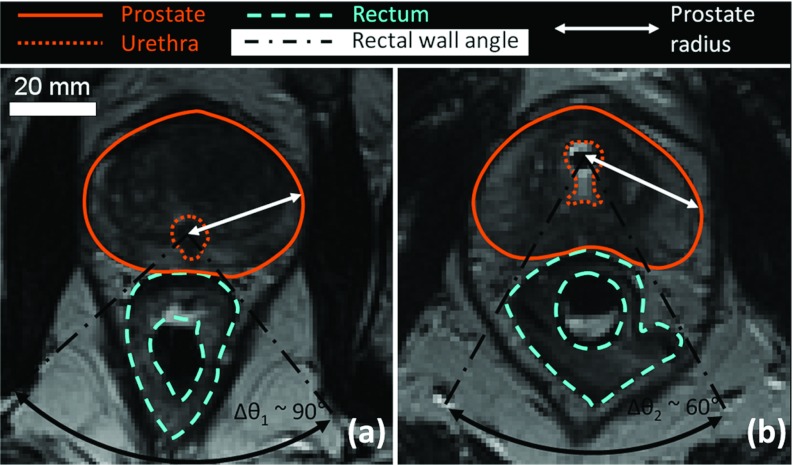
3D pelvic anatomical models of human prostate cancer patients were constructed from MR images obtained during a recent pilot human study (Fig. 1).^{37, 40} The relevant structures within the human pelvis (prostate, urethra, rectum, and pelvic bones) were segmented manually by an experienced body MRI radiologist from high-resolution T2-weighted axial images. These 3D models represent the actual geometry during treatment, including slight deformations of the prostate gland caused by the rigid transurethral ultrasound applicator. These models exhibited a significant shift of the urethra anteriorly relative to the prostate boundary, creating the largest treatment radii towards the posterior gland (Fig. 2). This was opposite to the geometries previously encountered from diagnostic MR images,³⁵ where the presence of an endorectal imaging coil created the shortest treatment radii posteriorly. Six representative pelvic models were created from the initial human feasibility study. Prostate radius values, defined as the radial distance from the urethra center to the outer prostate boundary, ranged from 6 to 40 mm. Prostate lengths were on average 30 ± 3 mm (range 25–35 mm) from base to apex, and total prostate volumes were 36 ± 6 cm³ (range 31–47 cm³). Average characteristics are shown in Table 1. This 3D anatomical database was used in both numerical simulations and gel phantom experiments to investigate appropriate parameters for whole-prostate treatment using MRI-controlled transurethral ultrasound therapy.

Figure 1.

Segmentation of pelvic structures under clinical conditions from axial MR images acquired after the insertion of a transurethral ultrasound device for prostate cancer treatment. (1) Transurethral device; (2) Prostate; (3) Rectum; (4) Bones.

Figure 2.

Clinical MR images from previous studies on two different patients. (a) Zoomed axial view and critical angle for rectal safety without transurethral device insertion; (b) Change in the conformation of the prostate due to the insertion of the ultrasound device in the urethra of a patient. The urethra was shifted toward the anterior region of the prostate, affecting the prostate radius distribution and the critical rectal angle.

Table 1.

Dimensions of prostate profiles studied during in vitro ultrasound treatment.

Patient #	1	2	3	4	5	6	Mean ± Standard deviation
Total prostate volume (cm3)	30.5	31.6	31.1	35.3	39.0	46.6	35.7 ± 6.2
Min radius (mm)	6	8	8	9	7	8	8 ± 1
Max radius (mm)	32	33	31	29	40	31	33 ± 4
Base to apex distance (mm)	29	31	25	31	29	35	30 ± 3
Number of activated elements on the applicator	5	6	5	6	6	7	6 ± 1
Total length of the applicator (mm)	25	30	25	30	30	35	29 ± 4
Treatable prostate volume (cm3)	28.5	31.6	31.1	34.2	39.5	46.0	35.2 ± 6.5
Ratio treatable to total prostate volume (%)	93	100	100	97	101	99	98 ± 3

Multiplanar MR thermometry control algorithm for transurethral ultrasound therapy

In the pilot human study, the initial treatments were very conservative, involving less than 30% of the gland due to the emphasis on safety imposed by the study protocol.⁴⁰ The work in this paper was conducted to determine appropriate ultrasound configurations for treatment of a volume equivalent to the entire prostate gland, using temperature feedback as described in Burtnyk et al.³⁵ A planar multi-element transducer rotates inside the urethra to generate a region of irreversible coagulation radially in the prostate gland. The heating pattern in the prostate gland is repeatedly measured using multiplanar MR thermometry, with each imaging slice centered on an individual ultrasound element. The MR temperature measurements in each slice are used to control the power (range: 0–20 W cm⁻²) and frequency from each transducer element. These values are chosen based on the temperature measured along the beam direction to the prostate boundary, and at the radius of the prostate boundary along the beam.³⁵ This method reduces the complex problem of controlling the 3D temperature distribution to a collection of single-point control equations described in Algorithm 1. For each element i, the temperature at two spatial locations along the direction of ultrasound beam is considered—the current maximum temperature (Tmax_i) and the current target boundary temperature (Tb_i). The goal of the control algorithm is to raise Tb_i from the initial tissue temperature (T₀ = 37 °C) to a temperature Tc = 55 °C (ΔTc = Tc − T₀ = 18 °C) during a single complete rotation of the transurethral device. To avoid excessive tissue heating close to the device which could degrade sound penetration, power to a transducer element is turned off if the maximum temperature along the beam direction exceeds a temperature threshold Th = 90 °C (ΔTh = Th − T₀ = 53 °C). During treatment, acoustic power (p_i), frequency (f_i), and rotation rate (ω_i) vary, as described in Algorithm 1, based on the current prostate radius (r_i) and the current temperature differences ΔTb_i and ΔTh_i, where ΔTb_i = Tc − Tb_i and ΔTmax_i = Th − Tmax_i. The rotation rate (ω), acoustic power (P_i), and frequency (f_i) also depend on functions tuned in preliminary simulations: k_ω(r_i, f_i, P_max) is the rotation gain function, k_p(r_i, f_i, P_max) is the power gain function, and R_co(f_low, f_high, P_max) the crossover radius for switching between the fundamental (f_low) and third harmonic (f_high) in dual-frequency configurations. The method of tuning to determine those parameters has been described previously.^{35, 38}

Table .

Control algorithm: calculating rotation rate, acoustic power and frequency.

$$\begin{array}{c}\forall i\in [1,n],\hfill \\ \omega =\underset{i=1..n}{min}\left\{\left.{\omega }_i\right\},\right.{\omega }_i=\left\{\begin{array}{cc}\hfill {\omega }_{\min }\le k_{\omega }(r_i,f_i,P_{\max })/\Delta T{b}_i\le {\omega }_{\max },& \hfill \Delta T{b}_i>0\mathrm{and}\Delta T{\max }_i>0\\ \hfill {\omega }_{\min }& \hfill \Delta T{b}_i>0\mathrm{and}\Delta T{\max }_i\le 0\\ \hfill {\omega }_{\max }& \hfill \Delta T{b}_i\le 0\end{array}\right.\hfill \\ \\ P_i=\left\{\begin{array}{cc}\hfill P_{\min }\le k_p(r_i,f_i,P_{\max })·\Delta T{b}_i\le P_{\max },& \hfill \Delta T{b}_i>0\mathrm{and}\Delta T{\max }_i>0\\ \hfill P_{\min },& \hfill \Delta T{b}_i>0\mathrm{and}\Delta T{\max }_i\le 0\\ \hfill P_{\min },& \hfill \Delta T{b}_i\le 0\end{array}\right.\hfill \\ \\ f_i=\left\{\begin{array}{cc}\hfill f_{\mathrm{low}},& \hfill r_i<R_{\mathrm{co}}(f_{\mathrm{low}},f_{\mathrm{high}},P_{\max })\\ \hfill f_{\mathrm{high}}\approx 3·f_{\mathrm{low}},& \hfill r_i<R_{\mathrm{co}}(f_{\mathrm{low}},f_{\mathrm{high}},P_{\max })\end{array}\right.\hfill \\ \\ \mathrm{with}\left\{\begin{array}{cc}\hfill {\omega }_{\min }=8^{\circ }{\min }^{-1},& \hfill {\omega }_{\max }={120}^{\circ }{\min }^{-1}\\ \hfill P_{\min }=0\mathrm{W}{\mathrm{cm}}^{-2},& \hfill P_{\max }=10\mathrm{or}20\mathrm{W}{\mathrm{cm}}^{-2}.\end{array}\right.\hfill \end{array}$$

MRI-compatible transurethral ultrasound therapy system

Based on the prostate measurements in Table 1, extensive modifications were made to our transurethral therapy system. New multi-element applicators were constructed capable of transmitting ultrasound at two discrete frequencies, 4.6 and 14.4 MHz (fundamental and third harmonic). The transducer was constructed using PZT piezoceramic (DL-47, DelPiezo) with nine elements, each 4 mm wide × 5 mm long. This active length up to 45 mm enabled covering the entire prostate length from base to apex (L_B2A) for all prostate profiles in this study (maximal L_B2A: 35 mm) with some additional capacity if longer prostates are encountered in future clinical studies. Over the nine elements of the device, average electroacoustic efficiencies for the fundamental and third harmonic frequencies were 58 ± 4% (range 51%–59%) and 29 ± 3% (range 27%–33%), respectively. The elements were capable of delivering at least 20 W cm⁻² reliably for the duration of a typical treatment (30 min). For comparison, the transducer used in the initial human study had four elements (approximately the same dimensions) operating at 8.1 MHz. A ten-channel RF amplifier (NP2942, NP Technologies) and custom-built ten-channel RF signal generator were used to drive the transducers during treatment. The software used to control the hardware, process MR temperature maps, and the rotational positioning system were similar to those used in previous studies.³²

Tissue-mimicking phantom experiments

Heating experiments were performed in a homogeneous polyacrylamide-based phantom (Zerdine^®, CIRS Inc., Norfolk, VA) with tissue-mimicking ultrasound and thermal properties: density: 1030 kg m⁻³ (CIRS data sheet), speed of sound: 1540 m s⁻¹ (CIRS data sheet), thermal conductivity and heat capacity: 0.56 W m⁻¹ °C⁻¹ and 3.8 J g⁻¹ °C⁻¹, respectively.⁴¹ The attenuation coefficient at 1 MHz was measured to be 0.56 dB cm⁻¹.³⁶ These properties are similar to data reported by Duck⁴² for biological tissues. Transurethral ultrasound applicators were inserted into the center of a cylindrical container (diameter: 11 cm) which was placed in the standard quadrature head coil of a 3.0 T MR imager (Discovery MR750, GE HealthCare) parallel to the main magnetic field B₀. Axial gradient-echo images (transverse to the transurethral device) were obtained for MR thermometry using the following parameters: n = 9 slices, TE = 3.0 ms, TR = 50.0 ms, NEX = 1, FOV = 20 cm, slice thickness = 5 mm, image size = 128 × 128 pixels, bandwidth = ± 31.25 kHz, frequency-encoding direction: A/P, flip = 30°, and acquisition time = 7 s. Slice locations were carefully prescribed from high-resolution T2-weighted FSE images acquired along the length of the device as described previously.^{36, 38} MR thermometry was performed using the proton resonance frequency (PRF) shift method.^{22, 23} A phase drift correction was applied in real-time by monitoring the temperature in unheated cylindrical phantoms filled with oil and positioned around the heated gel phantom, ∼6 cm away from the urethra. This corresponds to the location of muscles in transverse pelvic images, which we have confirmed can be used to perform baseline drift correction in human prostate studies. Treatment delivery was implemented such that each element i of the n-element transducer was controlled independently according to Algorithm 1. The number of active ultrasound elements for each prostate model was determined based on the prostate length from base to apex. All temperatures are described in terms of in vivo conditions, but the gel experiments were conducted 15 °C lower (starting from room temperature of 22 °C) for experimental convenience. This is possible because all controller decisions are based on relative temperatures differences (ΔTc, ΔTh, ΔTb_i, ΔTmax_i) (Algorithm 1).

Whole-prostate treatments in tissue-mimicking phantoms

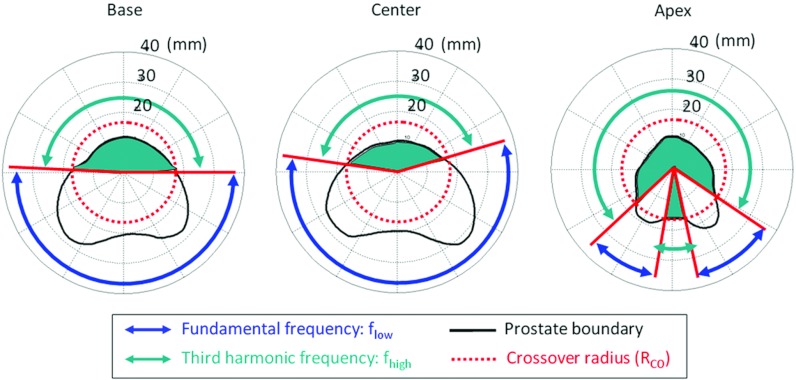
The primary challenge of this study was to determine ultrasound parameters which achieved excellent treatment accuracy over the entire range of prostate radii encountered in our clinical database (r_i = 6–40 mm). Based on simulations described in Sec. 2F, dual-frequency ultrasound exposures were implemented to achieve efficient heat deposition in regions of the prostate with both large and short radii. The method for generating multiple frequencies is based on the ability to drive an ultrasound transducer using the fundamental frequency (f_low) for large prostate radii or the third harmonic component (f_high) for small radii (Fig. 3). The crossover radius (R_co) for switching between frequencies was chosen based on tuning results³⁸ to achieve short treatment time while maintaining good treatment accuracy. The value of R_co is power and frequency specific (Table 2). A series of heating experiments was performed in a tissue-mimicking phantom to evaluate the performance of five different treatment strategies in each of the six anatomical models of the prostate gland (30 experiments in total). Group A (control) maintained parameters used during our previous preclinical and clinical studies to validate conservative treatments: P_max = 10 W cm⁻² and single fundamental frequency f = 8.1 MHz. Four additional groups (B–E) investigated the effects of higher maximum power, lower frequency, and two dual-frequency strategies, as summarized in Table 2.

Figure 3.

Dual-frequency principle. A crossover radius (R_CO) is defined to switch between fundamental frequency (f_low) and third harmonic (f_high) for optimization of targeting accuracy and treatment speed. Three slices of the same prostate are shown.

Table 2.

Description of the groups involved in the in vitro gel phantom comparison study.

Groups	A (Control)	B	C	D	E
Frequency configuration	Single	Single	Single	Dual	Dual
Acoustic frequency (MHz)	8.1	8.1	4.6	4.6/14.4	4.6/14.4
Maximum surface acoustic power (W cm−2)	10	20	20	20/20	20/10
Crossover radius, Rco (mm)	…	…	…	18	9

Numerical simulations of whole-gland treatment using MRI-controlled transurethral ultrasound therapy

3D simulations of MRI-controlled transurethral ultrasound therapy were carried out using a numerical model described previously in detail by Burtnyk et al.^{35, 43} and N’Djin et al.³⁸ with the human prostate boundaries from Table 1. One objective was to evaluate the impact of these new prostate conformations on treatment accuracy compared with previous studies in canine geometries³⁸ or in human geometries segmented from diagnostic human prostate images.³⁵ Single frequency treatments were studied over the range 1–15 MHz, with maximum acoustic powers of 10 and 20 W cm⁻². Based on these results, dual-frequency configurations were investigated in simulation and, based on targeting accuracy and treatment time, parameters of Table 2 were chosen for testing in the gel phantom experiments. Finally, simulations were performed to model more realistic in vivo conditions. In particular, a wide range of tissue perfusion was studied to determine how it could impact the choice of frequency for full prostate treatment, the treatment time, and the targeting accuracy. Conditions of very low perfusion (∼0 ml/min 100 g) as might be encountered during retreatment (following radiotherapy or therapeutic ultrasound) and high tissue perfusion (∼30–50 ml/min 100 g) were studied in addition to normal prostate perfusion of 16 ml/min 100 g.⁴⁴ The effect of rectal cooling on treatment safety was also investigated in simulations. All numerical simulations were performed modeling the following MR thermometry parameters: temperature noise = ±1 °C, pixel size = 1.56 × 1.56 mm², slice thickness = 5 mm, and image acquisition time = 7 s. Prostate tissue physiological parameters are summarized in Table 3.

Table 3.

Prostate tissue and bone parameters used during numerical modeling of transurethral ultrasound prostate treatment.

	Soft tissue	Bone (Refs. 43, 47)
Soft tissue density	1030 (Ref. 42)	1700
(kg m−3)
Acoustic attenuation	0.6 (Ref. 36)	12.7
(dB cm−1 MHz−1)
Specific heat capacity	3700 (Ref. 41)	1600
(J kg−1 °C−1)
Thermal conductivity	0.5 (Ref. 41)	0.6
(W m−1 °C−1)
Speed of sound	1540 (Ref. 42)	2333
(m s−1)
Blood perfusion	16 (Ref. 44)	0
(ml min−1 100 g−1)

Safety considerations in surrounding tissues

Simulations were carried out to evaluate the amount of heating in the rectal wall during whole-gland treatments for the 3D prostate geometries in Table 1. In particular, thermal dose [in cumulative equivalent minutes at 43 °C (CEM43)] in the rectal wall was calculated to determine if those tissues were safe (0 EM < CEM43 < 42 EM), reversibly damaged (42 EM < CEM43 < 85 EM), or irreversibly damaged (CEM43 ≥ 85) (Refs. ^{43, 45}, and ⁴⁶) in the absence or presence of rectal cooling. Rectal cooling was implemented as a constant temperature reservoir at 22 °C within the lumen of the rectum. The treatment safety was also modeled with regards to pelvic bone heating and thermal dose in bones was calculated to determine if they were safe (0 EM < CEM43 < 60 EM), reversibly damaged (60 EM < CEM43 < 2185 EM), or irreversibly damaged (CEM43 ≥ 2185).^{43, 47} Bones physiological parameters used in these simulations are summarized in Table 3. The interest of using dual-frequency exposures to minimize uncontrolled heating in pelvic bones and surrounding soft tissues was studied in realistic conditions, by accounting for human pelvis clinical conformation after the insertion of the transurethral device. Special attention was also paid to temperature increases outside the prostate close to the base and apex in the direction perpendicular to the MR slices which might impact the bladder (prostate base) or the urethral sphincter (prostate apex).

Assessment of results

The same parameters were used to assess treatments for both simulations and gel experiments. Full treatment was defined when at least 95% of the total prostate volume exceeded 55 °C. Treatment time, targeting accuracy, and treatment safety were analyzed with the following parameters: treatment time (s), treatment rate (cm³ min⁻¹), coagulation volume (cm³), radial volumetric overtreatment and undertreatment (cm³ and %), radial targeting accuracy (mm), adjacent slice volumetric overtreatment and undertreatment (cm³ and %). Radial differences (distance and volume) were calculated along the direction of ultrasound propagation, while adjacent slice over- and undertreatment were measured in the immediately adjacent slices where transducer elements were inactive. The assumption of normality and standard deviation were inspected for all variables by histograms and found to be justified. Results from simulations and gel phantom experiments were averaged over all six prostate models and were formatted in the text as mean value ± standard deviation (range min value–max value). Statistical significance for the group comparisons in the gel phantom results were assessed using a two-sided paired Student t test. The significance level for all tests was fixed at p = 0.05. The statistical analyses were performed using R^® software (The R Foundation for Statistical Computing, Vienna, Austria).

RESULTS

Parameters for whole-prostate treatments from simulations

The frequencies that achieved whole prostate treatment with the least amount of under- or overtreatment lay between 2 and 5 MHz, similar to the trends reported previously for canine prostate geometries.³⁸ At 4 MHz, maximum acoustic power of 20 W cm⁻² decreased the undertreatment by 56% and treatment time by 35% compared to 10 W cm⁻². Higher frequencies limited maximum treatment radius inappropriately to 22 mm for 8 MHz and to 18 mm for 14 MHz. Frequencies lower than 2 MHz suffered from insufficient energy absorption in prostate tissue, and risked increased heating at tissue interfaces outside the prostate gland such as bone. For an average prostate perfusion of 16 ml/min 100 g,⁴⁴ the simulations suggested a reduction in frequency by approximately a factor of 2 from the initial 8 MHz human study in order to achieve whole-gland prostate treatments.

The range of frequencies suitable for full prostate heating was only slightly dependent on the perfusion. When tripling the perfusion from 16 to 50 ml/min 100 g in prostate tissue model, the treatment time remained close to 25 min on average (f = 4 MHz, surface P_max = 20 W cm⁻²). To maintain acceptable treatment outcomes, ultrasound exposures were consequently delivered at P_max more often and the average acoustic energy generated by the device increased by 20% (Table 4). The targeting error, however, doubled from −0.7 ± 1.1 mm to −1.4 ± 1.2 mm leading to a 40% increase in undertreatment. Ultrasound treatments were also simulated for poorly perfused prostates, as seen in some patients not yet treated⁴⁴ or in HIFU retreatment when the blood flow is already reduced by previous ultrasound exposures.^{48, 49, 50} For these conditions, the optimal frequency range was very similar to that for simulations at average perfusion. In the case of no prostate perfusion, the radial targeting error could be reduced to −0.2 ± 1.0 mm.

Table 4.

Effect of prostate tissue perfusion on transurethral ultrasound full prostate heating.

Perfusion (ml/min 100g)	0	16	50
Time spent at Pmax (% of treatment time)	27 ± 6	31 ± 5	36 ± 5
		(p0/16 = 0.26)	(p16/50 = 0.10)
			(p0/50 = 0.01)
Total acoustic energy delivered (W h)	29 ± 3	31 ± 4	35 ± 5
		(p0/16 = 0.22)	(p16/50 = 0.17)
			(p0/50 = 0.02)
Treatment time (min)	22 ± 3	24 ± 3	25 ± 3
		(p0/16 = 0.48)	(p16/50 = 0.45)
			(p0/50 = 0.17)
Targeting error (mm)	−0.2 ± 1.0	−0.7 ± 1.1	−1.4 ± 1.2
		(p0/16 = 0.37)	(p16/50 = 0.31)
			(p0/50 = 0.07)

Dual-frequency configurations using the frequency pairs of 3/9, 4/12, and 5/15 MHz were then simulated. Results showed that dual-frequency strategies improved the treatment accuracy and homogeneity for regions of short prostate radii by using the third harmonic frequency rather than the fundamental low frequency. Otherwise, the use of the fundamental frequency for treating large prostate radii maintained treatment accuracy in extended prostate regions, such as in posterior peripheral zones. These results reinforced interest in comparing previous transducers working at 8.1 MHz with dual-frequency 4.6/14.4 MHz transducers during gel phantom experiments leading to the treatment parameters chosen in Table 2.

Whole-gland treatments in tissue-mimicking gel phantoms

Experimental MR thermometry feedback control of the whole prostate gland

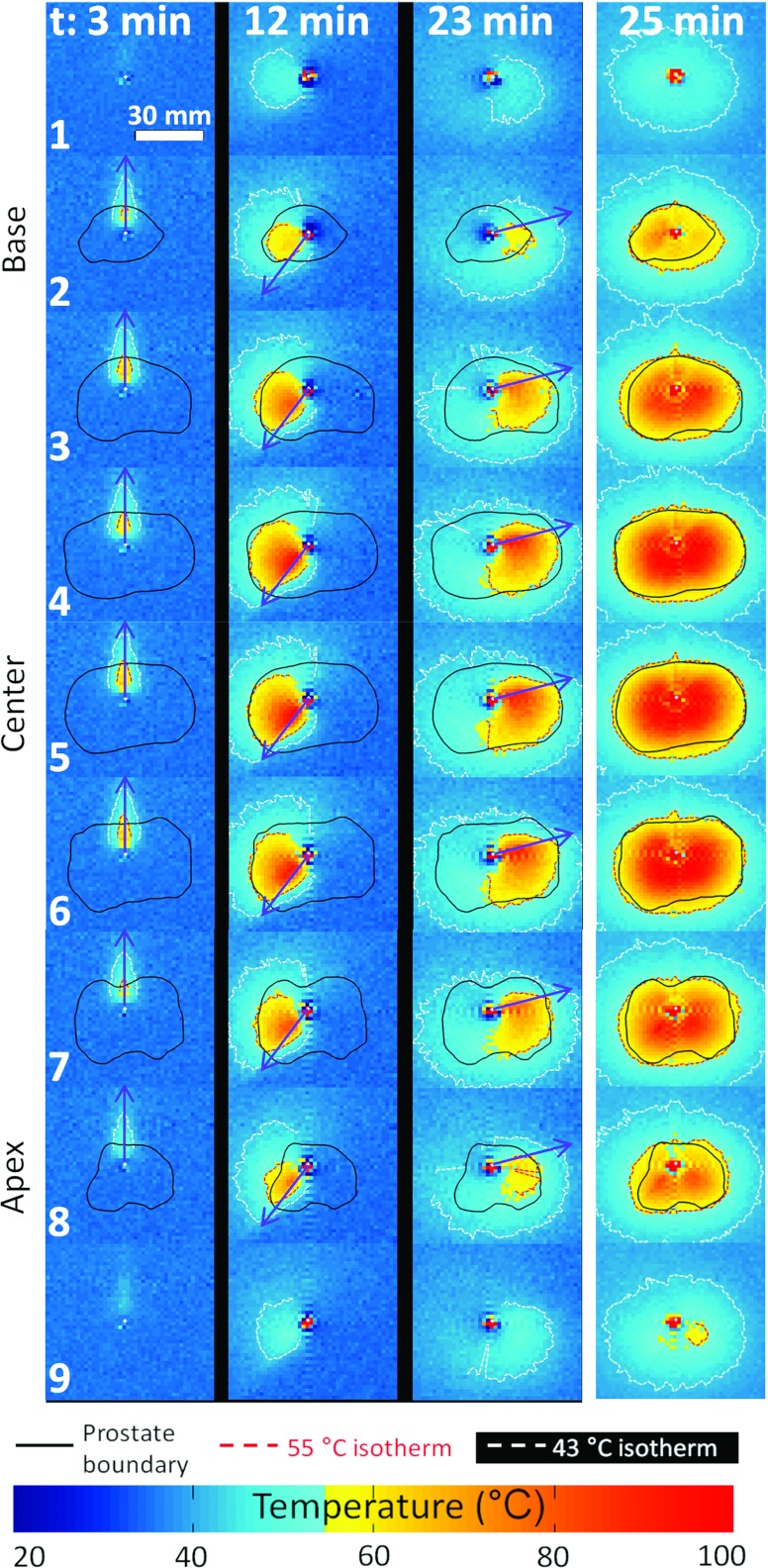
The shift of our transurethral system from 1.5 to 3.0 T provided improvements in terms of volumetric coverage and treatment control within the prostate gland. Higher SNR provided greater flexibility in imaging parameters such that more simultaneous thermometry planes could be acquired. The number of imaging planes acquired in the prostate volume was increased from five used in previous studies^{36, 38} to nine, while keeping an acceptable MR acquisition time of 7 s compared to the previous 5 s. The spatial resolution was also enhanced by increasing the size of the acquired matrix from 64 × 128 pixels to 128 × 128 pixels while maintaining good SNR and temperature uncertainty. The measured temperature uncertainty was ±1 °C. Significant background phase drift was observed during experiments (corresponding to a temperature drift from −0.2 to −0.7 °C min⁻¹), requiring correction in order to avoid significant errors in the PRF calculation. After correction, the observed temperature drift ranged from 0.0 to 0.1 °C min⁻¹. A ripple artifact was observed which started when the rotation of the device was initiated. This artifact was observed along the phase and frequency axis and followed a sinc function centered on the device but did not affect the treatment controller decision significantly since: (i) it concerned four particular angles only, (ii) the controller decisions were updated every 7 s, while the rotation rate was continuous with a non-null minimum rate (8°/min), and (iii) the artifact decreased rapidly with the distance from the device (urethra). For distances greater than 20 mm, the artifact amplitude was less than 10% of its maximum amplitude. The temperature distribution measured in the gel phantom at three times during treatment at a single frequency and the cumulative maximal temperature distribution at the end of the treatment are shown in Fig. 4. Such results agreed closely with the corresponding simulations, and no significant difference has been noticed on the controller decisions between simulations and gel experiments.

Figure 4.

Full prostate gland treatment with nine-slice simultaneous MR control. Experimental results in gel phantom on the biggest prostate (Patient 6). The three first columns show the temperature distribution at different time points. The right column shows the maximum cumulative temperature after the treatment has completed.

Single frequency ultrasound exposures

Increasing the surface acoustic power at 8.1 MHz from P_max = 10 W cm⁻² to 20 W cm⁻² resulted in a reduction in average treatment time by approximately 26%, from 37 ± 5 min (range 30–45 min) in Group A to 27 ± 4 min (range 22–35 min) in Group B (p_A/B < 0.01). There was no increase in overtreatment volume because the higher acoustic power was balanced by a faster rotation of the device. At 8.1 MHz, however, the undertreated volume observed at P_max = 20 W cm⁻² was greater than that measured at 10 W cm⁻² (Table 5). These results agreed with the simulations where acoustic power increase was expected to be the most effective for frequencies around 4 MHz. The simulations suggested that decreasing the frequency from 8 to 4 MHz while increasing the surface acoustic power from 10 to 20 W cm⁻² would enable deeper tissue penetration simultaneously with faster treatment time.

Table 5.

Results of the in vitro gel phantom comparison study in five groups. Report of parameters related to full gland treatment feasibility, treatment speed, treatment accuracy, and treatment safety.

Group	Control (A)	B	C	D	E
Parameters related to the feasibility of full prostate gland treatment
Maximum treated prostate radius (mm)	25 ± 1	25 ± 1	31 ± 1	30 ± 1	30 ± 2
		(pA/B = 0.92)	(pB/C < 0.01)1	(pC/D = 0.75)1	(pD/E = 0.32)1
Radial volumetric undertreatment (cm3)	3.8 ± 2.9	5.2 ± 3.4	0.9 ± 1.0	1.3 ± 2.4	1.4 ± 1.8
		(pA/B = 0.65)	(pB/C = 0.03)1	(pC/D = 0.76)1	(pD/E = 0.90)
					(pC/E = 0.56)1
Treated to treatable volume ratio (%)	84 ± 10	82 ± 10	97 ± 3	97 ± 6	96 ± 6
		(pA/B = 0.65)	(pB/C = 0.01)1	(pC/D = 0.81)1	(pD/E = 0.78)
					(pC/E = 0.53)1
Type of treatment	Partial gland	Partial gland	Full gland1	Full gland1	Full gland1
Parameters related to treatment speed
Treatment time (min)	37 ± 5	27 ± 4	25 ± 3	34 ± 7	24 ± 2
		(pA/B < 0.01)1	(pB/C = 0.39)1	(pC/D = 0.03)	(pC/E = 0.45)
					(pB/E = 0.18)1
Normalized treatment rate (cm3 min−1 elt−1)	0.16 ± 0.02	0.22 ± 0.04	0.33 ± 0.04	0.27 ± 0.03	0.30 ± 0.05
		(pA/B = 0.02)	(pB/C < 0.01)1	(pC/D = 0.02)	(pC/E = 0.37)1
Parameters related to treatment accuracy during full prostate gland treatment
Radial targeting accuracy (mm)	…	…	2.5 ± 1.5	1.8 ± 1.1	1.5 ± 2.0
				(pC/D = 0.36)2	(pD/E = 0.77)2
Radial targeting accuracy for prostate radii < 18 mm (mm)	…	…	2.8 ± 2.3	1.9 ± 0.8	1.8 ± 2.5
				(pC/D = 0.38)2	(pD/E = 0.95)2
Parameters related to safety in prostate surrounding tissues during full prostate gland treatment
Radial volumetric overtreatment (cm3)	…	…	8.4 ± 4.8	5.6 ± 2.3	5.8 ± 3.6
				(pC/D = 0.24)2	(pD/E = 0.93)2
Radial volumetric overtreatment for prostate radii < 18 mm (cm3)	…	…	4.0 ± 3.3	2.1 ± 1.2	2.9 ± 2.1
				(pC/D = 0.21)2	(pD/E = 0.41)2
Adjacent slice volumetric overtreatment (cm3)	…	…	2.9 ± 1.8	4.3 ± 1.7	2.2 ± 1.5
				(pC/D = 0.19)	(pD/E = 0.04)1

¹Statistically significant enhancement.

²Not statistically significant enhancement.

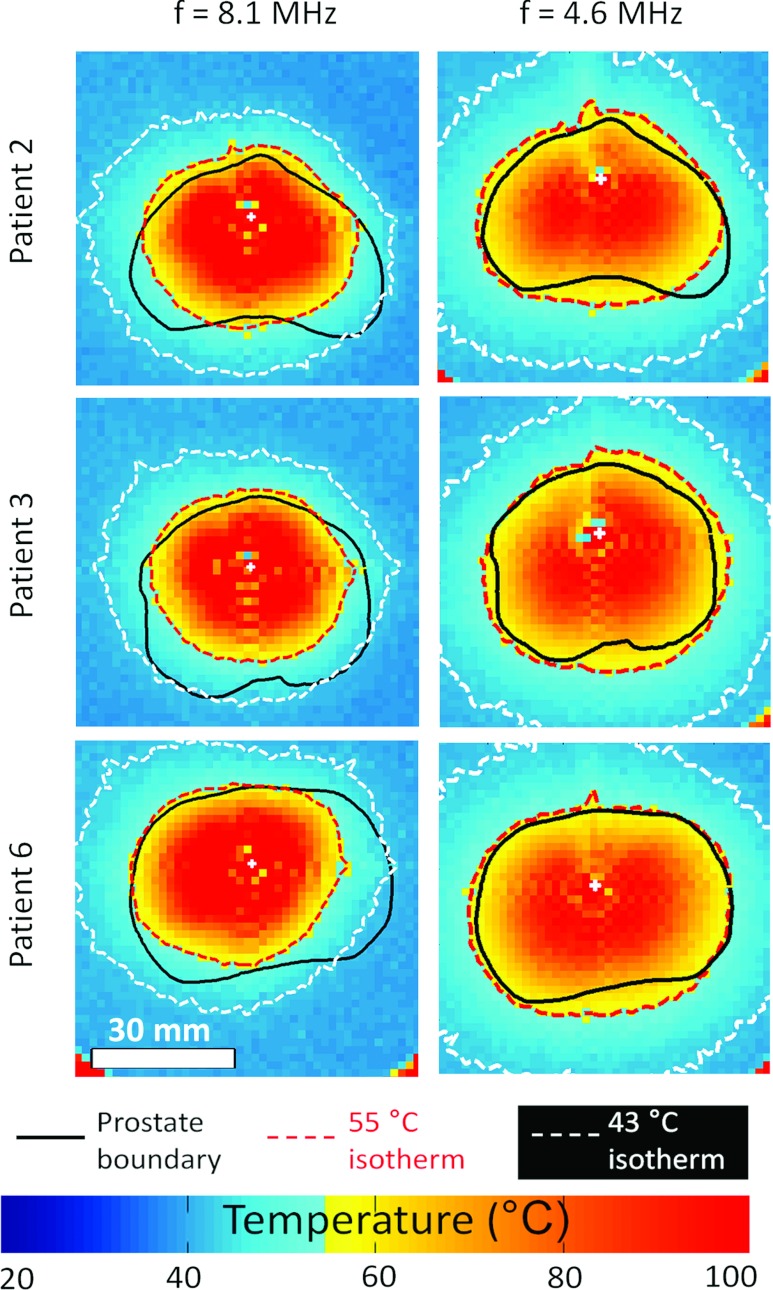
Lowering the operating frequency from 8.1 to 4.6 MHz enabled the maximum treated prostate radius to increase from 25 ± 1 mm (range 23–27 mm) to 31 ± 1 mm (range 30–33 mm) (p_B/C < 0.01), improving the ability to deliver whole-prostate treatments. The results in gel phantoms correlated closely with the simulations. At P_max = 20 W cm⁻², undertreatment of 5.2 ± 3.4 cm³ in Group B at 8.1 MHz was significantly reduced in Group C (0.9 ± 1.0 cm³) when using 4.6 MHz (p_B/C = 0.03). Decreasing the frequency from 8.1 to 4.6 MHz in experiments produced shorter treatment times by ∼10% compared to the predication from simulations of ∼26%. The average volume treated, however, increased significantly from 82% of the prostate at 8.1 MHz to 97% of the gland at 4.6 MHz (p_B/C = 0.01). The normalized treatment rate per ultrasound element increased significantly when frequency was reduced from 8.1 to 4.6 MHz, from 0.22 ± 0.04 cm³ min⁻¹ elt⁻¹ to 0.33 ± 0.04 cm³ min⁻¹ elt⁻¹, respectively (p_B/C < 0.01) (Table 5).

Single-frequency, high surface power ultrasound exposures at P_max = 20 W cm⁻² and f = 4.6 MHz were capable of whole-gland treatments; however, there were some negative consequences of these aggressive acoustic parameters. First, a lack of treatment homogeneity was observed in regions of short prostate radii, as previously predicted for radii ≤ ∼16 mm.³⁸ For the six prostate geometries used in this study, these radii are encountered at the prostate base and apex, as well as at the anterior region of the prostate gland. Second, whole-gland treatment was achieved with a reduction in targeting accuracy and safety. As shown in Table 5, both radial and adjacent slice volumetric overtreatment were not satisfactory. Thus, although the simple configuration of Group C showed good results (Fig. 5), more sophisticated dual-frequency configurations were tested to improve treatment outcomes such as accuracy and safety.

Figure 5.

Influence of frequency in achieving full prostate heating for three prostate models. Experimental results in gel phantom at P_max = 20 W cm⁻². View of the middle prostate slice. Decreasing frequency from 8.1 MHz to 4.6 MHz enabled sufficient heat deposition for a wider range of prostate radii (7–30 mm).

Effects of dual-frequency exposures on treatment accuracy and safety

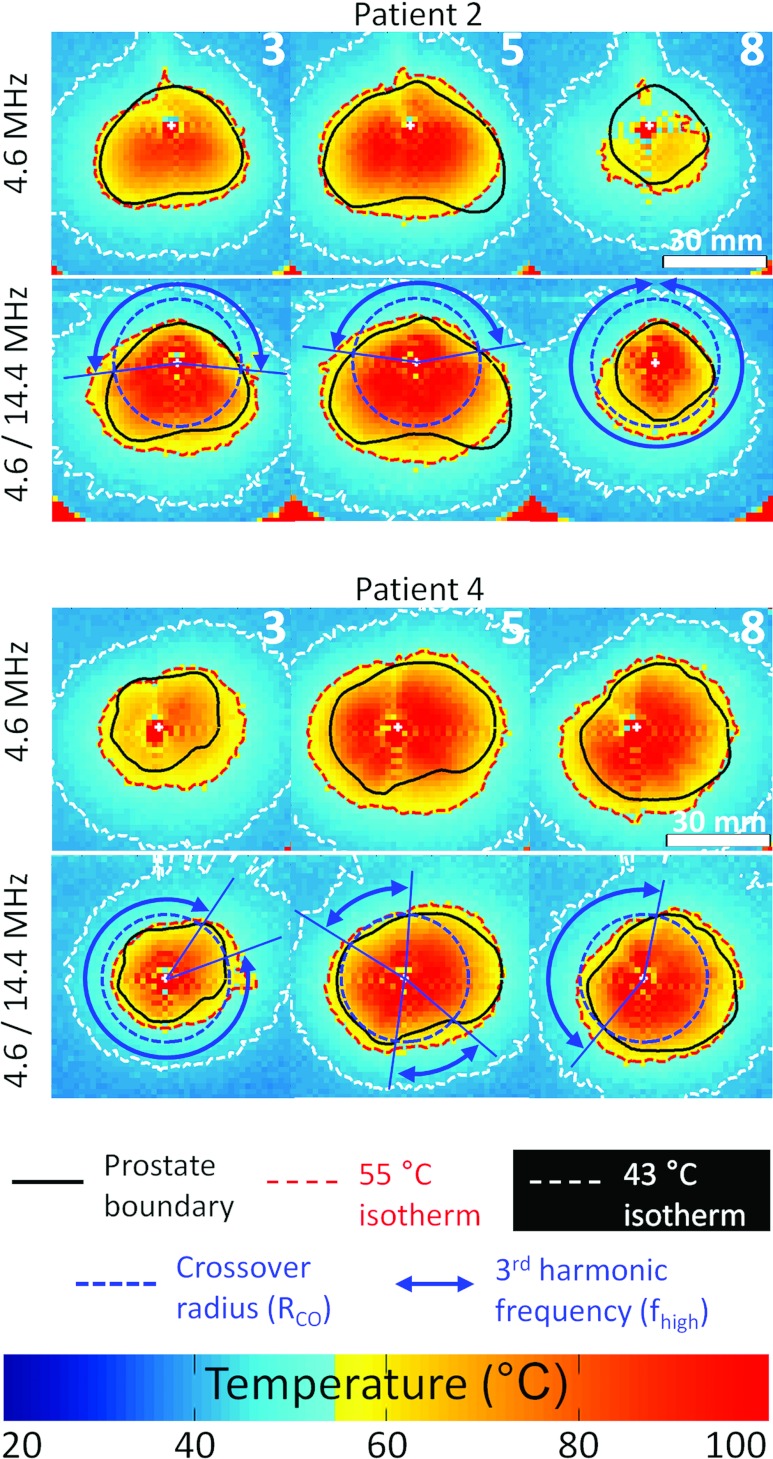
The dual-frequency combination 4.6/14.4 MHz was tested in Groups D and E with gel phantoms using high powers 20/20 W cm⁻² and mixed powers 20/10 W cm⁻² for the first and third harmonics, respectively. In particular, the third harmonic ultrasound exposures improved treatment accuracy for short treatment radii such as at the prostate base and apex (Fig. 6).

Figure 6.

Illustration of the benefits provided by dual-frequency transurethral ultrasound exposures for full human prostate boundaries heating. Experimental results in gel phantom at P_max = 20 W cm⁻². Patient 2: Enhancement of the treatment homogeneity at the apex (slice 8) and reduction of the heating outside the prostate in the posterior-anterior direction. Patient 4: Improved targeting accuracy in all prostate slices.

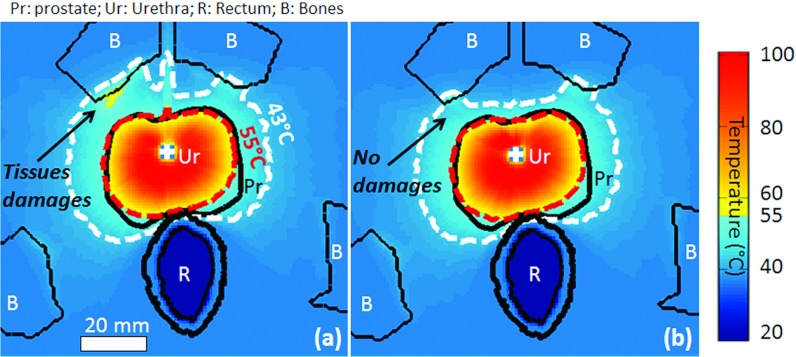
The parameters of Group D enhanced overall radial targeting accuracy by 30% (1.8 ± 1.1 mm) when compared to Group C (Figs. 67) and the average overtreatment volume was reduced by 35% (5.6 ± 2.3 cm³). Dual-frequency strategies improved treatment safety when the third harmonic frequency was used. In prostate regions with radii less than 18 mm, the overtreatment volume was reduced by 50% compared to the single frequency strategy. As shown in Table 5, however, the third harmonic frequency at high power also led to increased adjacent slice overtreatment at the prostate base and apex. Those increases reached 50% in Group D (4.3 ± 1.7 cm³) compared to Group C. In Group E, the third harmonic was used at a reduced maximum power of 10 W cm⁻² while keeping the fundamental frequency at 20 W cm⁻². This strategy reduced adjacent slice overtreatment significantly by 50% (2.2 ± 1.5 cm³) (p_D/E = 0.4) while conserving comparable treatment outcomes (Fig. 7). These results obtained outside the prostate near the base and apex showed experimentally that treatment safety could potentially be enhanced in bladder (prostate base) and urethral sphincter (prostate apex). Detailed values are summarized in Table 5.

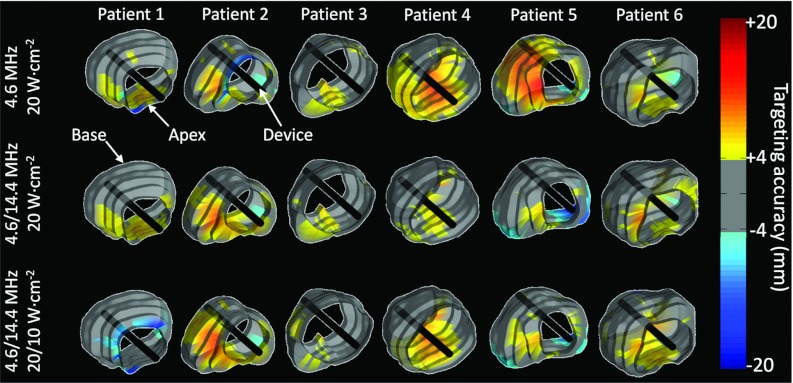
Figure 7.

Effect of acoustic power, fundamental ultrasound frequency, and dual-frequency ultrasound exposures on targeting accuracy after full prostate transurethral ultrasound treatment. Experimental results in gel phantom. 3D surface visualization of the radial targeting accuracy measured in axial planes in six human prostate geometries. The gray regions show excellent targeting accuracy corresponding to ±2 pixels in the thermal map. Hot colors and cool colors correspond, respectively, to over- and undertreatments. The benefit of some parameter combinations depends on the individual prostate shape.

Simulations of rectal wall and pelvic bone heating: protection of surrounding tissue structures during whole-gland treatments

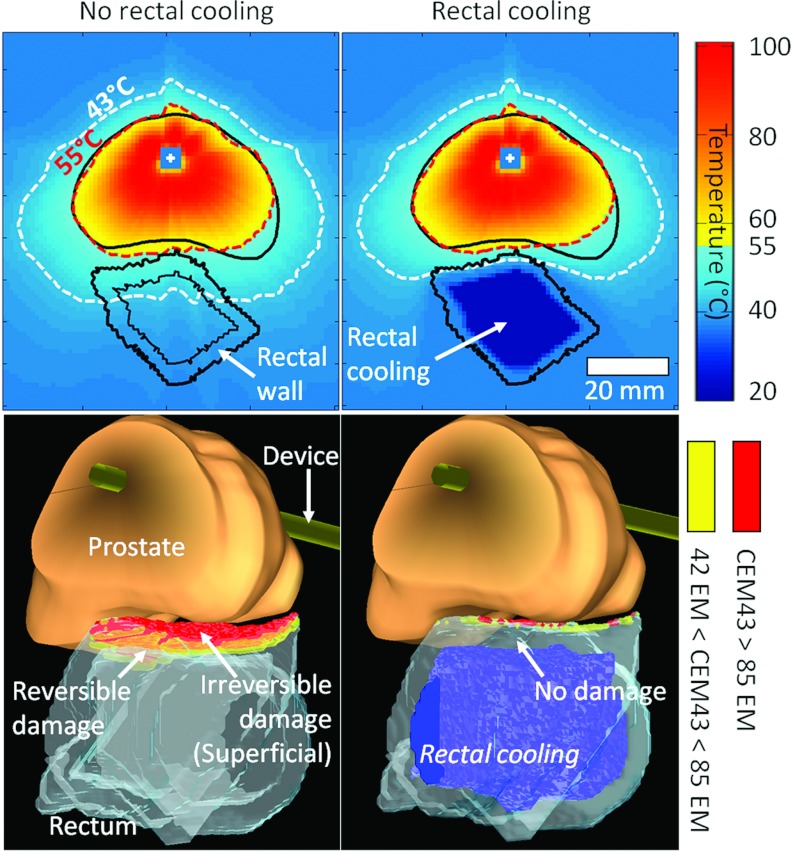
Whole-prostate treatments using Group E were simulated to assess safety in the rectal wall with and without endorectal cooling. The simulations were performed on each of the six prostate geometries from the clinical study. Modeling of the thermal dose (CEM43) in the rectum showed that in the absence of rectal cooling, ∼7% of the rectal wall at risk was irreversibly damaged (CEM43 ≥ 85 EM) and ∼3% was reversibly damaged (42 EM < CEM43 < 85 EM) (Table 6 and Fig. 8). Simple rectal cooling at 22 °C was sufficient to decrease significantly irreversible and reversible damage to 1% and 0.5%, respectively, enhancing the treatment safety with regard to rectum protection. Modeling of the thermal dose in pelvic bones showed that for single frequency exposures at 4 MHz and high surface power (20 W cm⁻²), very few bone regions were irreversibly damaged (less than 0.1% of the total pelvic bone volume). However, undesired irreversible damages were observed outside the prostate in soft tissues located in close vicinity to pelvic bones (CEM43 ≥ 240 EM), as a result of large heat diffusion from bone due to high ultrasound absorption and large temperature increase in this structure. The use of dual-frequency exposures resulted in a 50% decrease in surrounding tissue damage due to short prostate to bone distances (Fig. 9 and Table 7). Short prostate to bone distances were mainly located at the prostate base and apex, in regions where the third harmonic frequency was frequently used to treat short prostate radii. The short ultrasound tissue penetration at the third harmonic frequency enabled dual-frequency exposures to minimize heat deposition in surrounding pelvic bones, when compared to single-frequency exposures.

Table 6.

Treatment safety in rectal wall on Group E.

Rectal cooling at 22 °C	No	Yes
Rectal wall volume (cm3)	14.5 ± 4.4	14.5 ± 4.4
Irreversible damage. Volume of tissues	1.0 ± 0.3	0.1 ± 0.1
with t43 °C ≥ 85 EM (cm3)		(p < 0.01)
Reversible damage. Volume of tissues	0.4 ± 0.1	< 0.1
with 42 EM < t43 °C < 85 EM (cm3)		(p < 0.01)
Volume of tissues with 0 EM	13.1 ± 4.3	14.3 ± 4.4
< t43 °C < 42 EM (cm3)		(p = 0.65)

Figure 8.

Modeling of rectal wall safety during transurethral ultrasound treatment of whole human prostate gland (Patient 2). Efficacy of the rectal cooling in preventing superficial irreversible damages in the rectum (<0.3% of the rectal wall at risk). Treatment at 20/10 W cm⁻², and dual-frequency exposure at 4.6/14.4 MHz. 2D temperature distribution in the axial middle slice of the prostate (top), 3D view of the prostate/rectum and rectal wall damage (bottom).

Figure 9.

Modeling of pelvic bones during full prostate transurethral ultrasound treatment and consequences on treatment safety in surrounding soft tissues. Maximum temperature distribution at prostate apex after: (a) a single frequency treatment; (b) a dual-frequency treatment.

Table 7.

Treatment safety in pelvic bones and damages in surrounding soft tissues due to bone heating.

Ultrasound exposure strategy	Single-frequency		Dual-frequency
Structure observed	Pelvic bone	Soft tissues	Pelvic bone	Soft tissues
Structure volume (cm3)	187.1 ± 45.0		187.1 ± 45.0
Irreversible damage. Volume of tissues with:
t43°C ≥ 2185 EM (bones)	0.1 ± 0.1	0.4 ± 0.2	0.0 ± 0.0	0.2 ± 0.1
t43°C ≥ 240 EM (soft tissues) (cm3)			(p = 0.04)	(p = 0.05)
Reversible damage. Volume of tissues with:
60 EM < t43 °C < 2185 EM (bones)	0.2 ± 0.2	0.5 ± 0.2	0.0 ± 0.0	0.2 ± 0.1
60 EM < t43 °C < 240 EM (soft tissues) (cm3)			(p = 0.04)	(p = 0.03)
Volume of tissues with:
0 EM < t43 °C < 60 EM (bones)	186.7 ± 44.9	2.5 ± 1.3	187.1 ± 45.0	0.7 ± 0.3
0 EM < t43 °C < 60 EM (soft tissues) (cm3)			(p = 0.99)	(p = 0.02)

DISCUSSION

The overall aim of this study was to determine suitable parameters for whole-prostate human treatments using MRI-controlled transurethral ultrasound therapy. Using a combination of numerical simulations and experiments in tissue-mimicking phantoms, the relationships between ultrasound power and frequency and treatment time, accuracy and safety were investigated. The final configuration of dual-frequency exposures (Group E), using P_max = 20 W cm⁻² for the lower frequency, and 10 W cm⁻² for the higher frequency, treated the whole prostate accurately in the six cases studied while maintaining a safe profile with respect to heating in surrounding tissues. The configuration used in our initial human study (8 MHz, 10 W cm⁻²) appears to be unsuitable for whole prostate treatments due mainly to an inability to treat the larger radii encountered in human prostates.

This study also demonstrated for the first time, simultaneous control of heating in up to nine imaging planes using MR thermometry feedback. Although the use of a 3 T head coil for the gel phantom experiments provided SNR superior to that which would be expected for human pelvic imaging, this investigation was primarily focused on the ultrasound parameters and their consequences for treatment accuracy and safety. The MR thermometry sequence utilized was selected mainly to provide up to nine planes with an acquisition time of 7 s. There was some evidence during preliminary measurements that susceptibility artifacts were greater at 3 T than at 1.5 T with comparable TE (10 ms) and slice number (5), as expected. Use of low TE (3 ms) impacted the accuracy of the PRF thermometry measurements but enabled us to acquire the desired number of slices covering the full prostate volume in 7 s using a conventional gradient echo sequence. The number of slices was kept at nine to get information about overtreatment across slices for all prostate sizes studied (longest prostate in the database: seven slices), while keeping the comparative analysis of the various ultrasound exposure strategies independent from the monitoring parameters. To achieve higher SNR or faster update time, however, MR slice number could be optimized based on the prostate base to apex distance. Further investigations at 3 T are required to evaluate the spatial, temporal, and temperature resolution that can be achieved in the prostate gland in humans. Recent studies have demonstrated for different resolutions and FOVs that increased TE (18–34 ms) can be achieved with multislice coverage (4–6 slices) and short acquisition times (∼0.5–3 s) using segmented echo-planar imaging (EPI) approaches.^{51, 52, 53} Nonetheless, the MR thermometry sequence implemented for this study enabled us to implement multiplanar temperature control for transurethral ultrasound therapy and achieve successful treatments of whole-prostate volumes with geometries that are representative of what would be encountered clinically.

This study highlighted the important roles of frequency and power for transurethral ultrasound therapy. The interdependency between power and frequency in affecting treatment outcomes and the need to consider them in parallel were apparent. In particular, increasing acoustic power only offered major advantages for the frequency range from 2 to 5 MHz. Previous studies have already identified that small prostate radii lower than ∼18 mm could benefit from frequencies higher than 2–5 MHz to enhance treatment accuracy.^{15, 35, 38} This study showed the advantages of dual-frequency strategies, particularly to ensure efficient treatment of small prostate radii and to enhance safety of surrounding structures such as rectal wall and bladder. Further studies on dual-frequency configurations will include more complicated models to evaluate the safety of other critical structures such as neurovascular bundles, muscular sphincter, or pelvic bones. Although the dual-frequency concept was recently described in an investigation of the canine model,³⁸ utilization of realistic human prostate models in this study showed much greater benefit in larger prostate volumes which also include significant regions of short treatment radii. Although the canine model is standard for preclinical evaluations, this observation appears to question the overall utility of the canine model for assessment of ultrasound prostate therapies.

The simulations showed that perfusion does not appear to play a large role in transurethral ultrasound therapy. Although associated with an increase in undertreatment, large increases in prostate perfusion (three times as much as the standard value) did not affect the treatment time (∼half an hour) and the targeting accuracy remained within 2 mm for our transurethral technique. The simulations also suggested that simple rectal cooling can eliminate the risk of superficial thermal injury to the rectal wall. Last simulation studies did not observe any significant thermal damage in pelvic bones for all pelvis anatomies studied. But the risk of creating undesired thermal damage in soft tissues adjacent to bone was confirmed when performing full prostate gland heating with single-frequency exposures.⁴⁷ A dual-frequency strategy was showed to provide a better treatment solution by eliminating bone-related tissue damages. While neither of these situations could be confirmed with the simple gel phantoms used in these experiments, the excellent agreement between simulations with no perfusion and gel phantom experiments over a wide range of frequency and power conditions^{36, 38} provides confidence in the results of the simulations.

Particularly important from the viewpoint of treatment safety were the results from Group E. Overtreatment in the direction perpendicular to the MR slices can occur due to thermal diffusion and the fact that the ultrasound beam width is significantly larger than the ultrasound element when using the third harmonic frequency. Reducing the acoustic power when using the third harmonic frequency showed a significant decrease in heating in these regions, which may contribute to treatment safety near the base and apex of the prostate (respectively, the bladder and the urethral sphincter).

Our dual-frequency technique was limited however to two discrete frequencies to treat a continuous spectrum of prostate radii. A continuous modulation of the frequency as a function of radius may represent the ideal multifrequency configuration. Another field of investigation for optimizing dual-frequency configurations could also be the use of a mixture of two frequencies for some range of prostate radii. In this study, however, we explored two discrete frequencies as the simplest approach, which was also implementable for validation in our system. In the future, many developments are possible on the basis of these first validations. Although the results of this study are very promising for a first generation of temperature feedback controller, future developments could propose more complex control of the power and rate of rotation in real time, based, for example, on the prostate boundary curvature to anticipate a risk of overtreatment. These developments are ongoing areas of research in our group.

Overall, the ability to treat various human prostate volumes and shapes with accuracy on the order of a few millimeters and a treatment time under 30 min has been shown. These results compare very favorably with the treatment accuracy and long treatment times published for transrectal HIFU. Both full prostate volume treatment or regional (“focal”) treatment are possible with the transurethral approach and will be explored in future clinical trials.