Accelerated barrier optimization compressed sensing (ABOCS) reconstruction for cone-beam CT: Phantom studies

Abstract

Purpose: Recent advances in compressed sensing (CS) enable accurate CT image reconstruction from highly undersampled and noisy projection measurements, due to the sparsifiable feature of most CT images using total variation (TV). These novel reconstruction methods have demonstrated advantages in clinical applications where radiation dose reduction is critical, such as onboard cone-beam CT (CBCT) imaging in radiation therapy. The image reconstruction using CS is formulated as either a constrained problem to minimize the TV objective within a small and fixed data fidelity error, or an unconstrained problem to minimize the data fidelity error with TV regularization. However, the conventional solutions to the above two formulations are either computationally inefficient or involved with inconsistent regularization parameter tuning, which significantly limit the clinical use of CS-based iterative reconstruction. In this paper, we propose an optimization algorithm for CS reconstruction which overcomes the above two drawbacks.

Methods: The data fidelity tolerance of CS reconstruction can be well estimated based on the measured data, as most of the projection errors are from Poisson noise after effective data correction for scatter and beam-hardening effects. We therefore adopt the TV optimization framework with a data fidelity constraint. To accelerate the convergence, we first convert such a constrained optimization using a logarithmic barrier method into a form similar to that of the conventional TV regularization based reconstruction but with an automatically adjusted penalty weight. The problem is then solved efficiently by gradient projection with an adaptive Barzilai–Borwein step-size selection scheme. The proposed algorithm is referred to as accelerated barrier optimization for CS (ABOCS), and evaluated using both digital and physical phantom studies.

Results: ABOCS directly estimates the data fidelity tolerance from the raw projection data. Therefore, as demonstrated in both digital Shepp–Logan and physical head phantom studies, consistent reconstruction performances are achieved using the same algorithm parameters on scans with different noise levels and/or on different objects. On the contrary, the penalty weight in a TV regularization based method needs to be fine-tuned in a large range (up to seven times) to maintain the reconstructed image quality. The improvement of ABOCS on computational efficiency is demonstrated in the comparisons with adaptive-steepest-descent-projection-onto-convex-sets (ASD-POCS), an existing CS reconstruction algorithm also using constrained optimization. ASD-POCS alternatively minimizes the TV objective using adaptive steepest descent (ASD) and the data fidelity error using projection onto convex sets (POCS). For similar image qualities of the Shepp–Logan phantom, ABOCS requires less computation time than ASD-POCS in MATLAB by more than one order of magnitude.

Conclusions: We propose ABOCS for CBCT reconstruction. As compared to other published CS-based algorithms, our method has attractive features of fast convergence and consistent parameter settings for different datasets. These advantages have been demonstrated on phantom studies.

INTRODUCTION

Recent advances in the compressed sensing (CS) technique enable high-quality CT reconstruction from noisy and highly undersampled projections.^{1, 2, 3, 4} If the original image is known to be sparse or can be sparsified by a given transformation, it can be accurately recovered by minimizing its L1 norm or the L1 norm of its sparsified transformation under the measurement constraints. The CS-based reconstruction has been demonstrated to reduce the data acquisition by more than 90% while keeping the same image quality.^{3, 5, 6, 7} As such, the CS-based iterative reconstruction is promising for advanced clinical applications where radiation dose is a critical concern. For example, low-dose imaging techniques can substantially facilitate the use of onboard cone-beam CT (CBCT) imaging in image guided radiation therapy (IGRT) for treatment guidance,^{8, 9} as the accumulative imaging dose in a radiation treatment course of 4–6 weeks may reach an unacceptable level of 100–300 cGy using a conventional reconstruction method.^{9, 10} Nevertheless, the existing CS reconstruction algorithms are either computationally inefficient or involved with inconsistent regularization parameter tuning. In this paper, we propose a practical CS reconstruction which overcomes the above two drawbacks.

CT images can be sparsified by the derivative operation, since they usually exhibit piecewise constant (or close to) properties.^{3, 4} Total variation (TV, i.e., the L1 norm of the first-order derivative) is often selected as the minimization objective in the CS reconstruction.^{3, 4} The image reconstruction is then formulated as an optimization problem that minimizes the TV term constrained by the data fidelity and image non-negativity^{3, 4}

$$\begin{array}{c}\hfill \overrightarrow{f^{*}}=\arg \min ||\vec{f}|{|}_{\mathrm{TV}},\mathrm{s}.\mathrm{t}.,\frac{1}{2}{\left||M\vec{f}-\vec{b}|\right|}_2^2\le \varepsilon ,\vec{f}\ge 0,\end{array}$$ (1)

where the vector $\vec{b}$ with a length of N_d (i.e., number of detector pixels) represents the line integral measurements, M is the system matrix modeling the forward projection, $\vec{f}$ is the vectorized patient image to be reconstructed with a length of N_i (i.e., number of image voxels), ||•||₂ calculates the L2 norm in the projection space, and ||•||_TV is the TV term defined as the L1 norm of the spatial gradient image. Note that, the user-defined parameter ɛ is interpreted as the variance of the difference between the predicted and the raw projections. After effective data correction for scatter and beam-hardening effects,^{11, 12, 13, 14, 15, 16, 17, 18} most of the projection errors in CT scans are from Poisson statistics of the incident photons, except for very low-dose imaging cases.^{19, 20, 21}ɛ can therefore be readily estimated from the measured projections.

To solve Eq. 1, two alternative solutions have been proposed in the literature. The first method avoids the computational burden of the data fidelity constraint by reformulating Eq. 1 into Eq. 2 shown below^{22, 23}

$$\overrightarrow{f^{*}}=\arg \min \left[\frac{1}{2}||M\vec{f}-\vec{b}|{|}_2^2+\lambda ·{\left||\vec{f}|\right|}_{\mathrm{TV}}\right],\vec{f}\ge 0,$$ (2)

where the objective function includes the data fidelity and a TV regularization term with a penalty weighting factor (λ). This convex optimization problem bounded by a non-negativity constraint of the image ($\vec{f}\ge 0$) can be solved efficiently using many existing algorithms, such as a Bregman iterative regularization algorithm²⁴ and a gradient projection (GP) method.²⁵ In exchange of the computational efficiency, however, the optimal value of the algorithm parameter λ becomes more complicated to calculate. A proper λ value should well balance the data fidelity objective and the TV regularization, such that both terms reach optimal values. The data fidelity errors are mainly determined by the noise levels of the scan, while the optimal TV value depends on the spatial variation of the true object image. As a result, λ needs to be carefully adjusted on scans with different settings and/or on different patients. Though considerable interests are shown in the automatic selection of λ using inverse technique,^{26, 27} a standard solution is still not clear. The clinical performance of TV regularization depends on iterative and subjective tweaking of the λ parameter.

The second type of CS reconstruction directly solves Eq. 1 using data fidelity as a constraint.^{3, 4} Under the condition that Poisson noise is dominant in projection errors, the error tolerance ɛ can be estimated as the total noise variance of the projections. Although the ɛ estimation can be accurately obtained on the measured projections based on Poisson statistics,^{19, 20, 21} the optimization problem becomes more difficult to solve due to the quadratic data fidelity constraint. One possible way is to find the feasible solution set and minimize the TV term along its boundary, which is demonstrated in the adaptive-steepest-descent-projection-onto-convex-sets (ASD-POCS) algorithm.³ ASD-POCS alternatively minimizes the TV norm using adaptive steepest descent (ASD) and data fidelity using projection onto convex sets (POCS). Nevertheless, its computational efficiency substantially drops as compared to that of the TV regularization algorithm because of the time-consuming sequential POCS operations on the projection data, as well as the slow convergence from the alternative minimization strategy on data fidelity and TV term.

We attempt to combine the advantages of the above two categories of algorithms and propose a practical CS reconstruction method for clinical use. Equation 1 is used as the main framework such that the setting of algorithm parameter is consistent on different scans and patients. To accelerate the convergence, we convert the optimization using a logarithmic barrier method²⁸ into a form of TV regularization as shown in Eq. 2 but with a penalty weight on the TV term automatically tuned inside the optimization process. The converted problem is solved using an efficient GP method.²⁵ The proposed algorithm is referred to as accelerated barrier optimization for CS (ABOCS).

In this work, we focus on the implementation of ABOCS on CBCT imaging and demonstrate its main features. On the digital Shepp–Logan phantom, we first investigate the accuracy of the log-barrier approximation. We then compare ABOCS with ASD-POCS on its computational efficiency in MATLAB. More comparison studies are carried out between ABOCS and the TV regularization method to investigate their performance on scans with different noise levels and with different object geometries. Note that the comparison is designed to demonstrate our method's feature of consistent algorithm parameters that is missing in TV regularization approaches. Instead of an incremental improvement, the proposed algorithm avoids the trial-and-error step of parameter tuning in the regularization-based iterative reconstruction by solving a different mathematical problem. The algorithm is implemented on a graphics–processor unit (GPU) workstation and evaluated on a 3D reconstruction of the Shepp–Logan phantom to test its feasibility on a clinical CBCT system. We finally performed a physical phantom study on our tabletop CBCT system to assess the algorithm performance in a realistic application.

METHOD

Formulation of ABOCS framework

We first convert the data fidelity constraint shown in Eq. 1 to part of the objective using a barrier method.²⁸ The optimization problem is rewritten as

$$\begin{array}{c}\hfill \overrightarrow{f^{*}}=\arg \min \left[||\vec{f}|{|}_{\mathrm{TV}}+I_{\_}\left(-\varepsilon +\frac{1}{2}{\left||M\vec{f}-\vec{b}|\right|}_2^2\right)\right],\mathrm{s}.\mathrm{t}.\vec{f}\ge 0,\end{array}$$ (3)

where I_ is the indicator function, defined as

$$I_{\_}\left(u\right)=\left\{\begin{array}{c}0,\\ \infty ,\end{array}\begin{array}{c}\\ \end{array}\begin{array}{c}\begin{array}{cc}\mathrm{if}\hfill & u\le 0\end{array}\\ \mathrm{otherwise}\end{array}\right..$$ (4)

The TV term is calculated as

$$||\vec{f}|{|}_{\mathrm{TV}}=\sum _{k,m,n}u(k,m,n)=\sum _{k,m,n}\sqrt{{\left(f_{k,m,n}-f_{k-1,m,n}\right)}^2+{\left(f_{k,m,n}-f_{k,m-1,n}\right)}^2+{\left(f_{k,m,n}-f_{k,m,n-1}\right)}^2},$$ (5)

where u(k, m, n) represents the voxel value of the gradient image, and (k,m,n) is the voxel index of the 3D volume.

It is difficult to solve Eq. 3 due to the singularity in the derivative calculation of the indicator function. In this paper, we use a logarithmic barrier to approximate the indicator function, and Eq. 3 is rewritten as²⁸

$$\begin{array}{ccc}& & \overrightarrow{f^{*}}=\arg \min \left[||\vec{f}|{|}_{\mathrm{TV}}+\frac{1}{t}\left(-\log \left(\varepsilon -\frac{1}{2}{\left||M\vec{f}-\vec{b}|\right|}_2^2\right)\right)\right],\hfill \\ & & \mathrm{s}.\mathrm{t}.\vec{f}\ge 0,\hfill \end{array}$$ (6)

where the positive parameter t determines the accuracy of the approximation. A small t is more benign for the derivative calculation but makes the approximation less accurate. After optimization as shown later in simulation studies, we set t as 1.0 in all implementations presented in this paper if not specified otherwise.

We then solve the bounded convex optimization problem of Eq. 6 using a GP algorithm. GP searches the optimal decreasing direction by projecting the negative gradient of objective onto the feasible set (non-negative orthant).²⁵ The step size of one GP iteration is given by the Hessian of the objective function, of which the calculation is intensive. We use a Barzilai–Borwein (BB) method²⁹ to approximate the Hessian of objective function. The step size of GP is analytically calculated and adaptively changes during the optimization.³⁰ The high computational efficiency of this GP-BB method has been demonstrated in Refs. ²⁵ and ³⁰ by numerical experiments.

Updating scheme in iterations

The major steps of our algorithm include the calculations of the gradient of the objective function and the step size in each iteration. The gradient of the objective function shown in Eq. 6 is derived as

$$\vec{g}=\nabla {\left||\vec{f}|\right|}_{\mathrm{TV}}+\frac{M^T\left(M\vec{f}-\vec{b}\right)}{\max \left[\beta ,t\left(\varepsilon -\frac{1}{2}|\left|M\vec{f}-\vec{b}\right|{|}_2^2\right)\right]},$$ (7)

where ^T is the transpose operator for the system matrix M. To avoid the zero-dividing errors in the calculation of the derivative of the logarithmic function, max[·,·] in the second term of Eq. 7 selects the maximum value of the two inputs and forces the denominator to be larger than a small positive value β (set as 10⁻⁸ in our algorithm).

The derivative of the TV term is approximated in a similar form as shown in the literature⁵

$$\begin{array}{ccc}\hfill \nabla ||\vec{f}|{|}_{\mathrm{TV}}& =& {\displaystyle \frac{3f_{k,m,n}-f_{k-1,m,n}-f_{k,m-1,n}-f_{k,m,n-1}}{u\left(k,m,n\right)}-\frac{f_{k+1,m,n}-f_{k,m,n}}{u\left(k+1,m,n\right)}-\frac{f_{k,m+1,n}-f_{k,m,n}}{u\left(k,m+1,n\right)}-\frac{f_{k,m,n+1}-f_{k,m,n}}{u\left(k,m,n+1\right)}}\hfill \\ & =& {\displaystyle \frac{3f_{k,m,n}-f_{k-1,m,n}-f_{k,m-1,n}-f_{k,m,n-1}}{\sqrt{\delta +{\left(f_{k-1,m,n}-f_{k,m,n}\right)}^2+{\left(f_{k,m-1,n}-f_{k,m,n}\right)}^2+{\left(f_{k,m,n-1}-f_{k,m,n}\right)}^2}}}\hfill \\ & & {\displaystyle -\frac{f_{k+1,m,n}-f_{k,m,n}}{\sqrt{\delta +{\left(f_{k,m,n}-f_{k+1,m,n}\right)}^2+{\left(f_{k+1,m-1,n}-f_{k+1,m,n}\right)}^2+{\left(f_{k+1,m,n-1}-f_{k+1,m,n}\right)}^2}}}\hfill \\ & & {\displaystyle -\frac{f_{k,m+1,n}-f_{k,m,n}}{\sqrt{\delta +{\left(f_{k-1,m+1,n}-f_{k,m+1,n}\right)}^2+{\left(f_{k,m,n}-f_{k,m+1,n}\right)}^2+{\left(f_{k,m+1,n-1}-f_{k,m+1,n}\right)}^2}}}\hfill \\ & & {\displaystyle -\frac{f_{k,m,n+1}-f_{k,m,n}}{\sqrt{\delta +{\left(f_{k-1,m,n+1}-f_{k,m,n+1}\right)}^2+{\left(f_{k,m-1,n+1}-f_{k,m,n+1}\right)}^2+{\left(f_{k,m,n}-f_{k,m,n+1}\right)}^2}},}\hfill \end{array}$$ (8)

where δ is a small positive number to avoid singularities in the derivative calculation and set as 10⁻⁸ in the algorithm.

The GP algorithm updates f in the (n+1)th iteration as

$$\overrightarrow{f_{n+1}}=\max \left(\begin{array}{cc}\overrightarrow{f_n}-{\alpha }_n\overrightarrow{p_n},& 0\end{array}\right),$$ (9)

where α_n denotes the step size at iteration n, and $\overrightarrow{p_n}$ is the projected gradient, calculated as

$$p_n\left(l\right)=\left\{\begin{array}{cc}{g}_n\left(l\right)\hfill & \mathrm{if}\begin{array}{cc}{g}_n\left(l\right)\le 0,\mathrm{or}\hfill & f_n\left(l\right)>0\end{array}\\ 0\hfill & \mathrm{otherwise}\end{array}\right..$$ (10)

Here, l is the voxel position index. The step size of GP, α_n, can be selected by several approaches. For example, the backtracking method guarantees a monotonic convergence at the cost of increased computational complexity from the additional iterations in the line search.²⁵ In our algorithm, we choose an efficient adaptive BB method to analytically calculate the step size without iterations. Unlike conventional gradient calculation using only the current gradient of objective function, BB method calculates the step size based on both the current and previous gradients, using a scalar approximation to the secant equations.

Though converging faster in the long run, BB often results in an unexpected large step size and deteriorates the local convergence performance. To further improve the convergence speed of the conventional GP-BB method, we employ a dynamic BB step-size selection scheme by adaptively choosing a small or large step size calculated at each iteration.³⁰ The small step size leads to a favorable descent direction for the next iteration, while the large one produces a sufficient reduction of the objective function value. The two step sizes, ${\alpha }_n^{\mathrm{BB}1}$ and ${\alpha }_n^{\mathrm{BB}2}$, are calculated as²⁹

$$\begin{array}{ccc}\hfill {\alpha }_n^{\mathrm{BB}1}& =& \frac{{\left(\overrightarrow{f_n}-\overrightarrow{f_{n-1}}\right)}^T\left(\overrightarrow{f_n}-\overrightarrow{f_{n-1}}\right)}{{\left(\overrightarrow{f_n}-\overrightarrow{f_{n-1}}\right)}^T\left(\overrightarrow{p_n}-\overrightarrow{p_{n-1}}\right)},\hfill \\ \hfill {\alpha }_n^{\mathrm{BB}2}& =& \frac{{\left(\overrightarrow{f_n}-\overrightarrow{f_{n-1}}\right)}^T\left(\overrightarrow{p_n}-\overrightarrow{p_{n-1}}\right)}{{\left(\overrightarrow{p_n}-\overrightarrow{p_{n-1}}\right)}^T\left(\overrightarrow{p_n}-\overrightarrow{p_{n-1}}\right)}.\hfill \end{array}$$ (11)

The step size is chosen as³⁰

$${\alpha }_n=\left\{\begin{array}{cc}{\alpha }_n^{\mathrm{BB}2}\hfill & \begin{array}{cc}\mathrm{if}\hfill & {\alpha }_n^{\mathrm{BB}2}{\alpha }_n^{\mathrm{BB}1}<\kappa \end{array}\\ {\alpha }_n^{\mathrm{BB}1}\hfill & \mathrm{otherwise}\end{array}\right..$$ (12)

where κ is the positive adaptation constant less than 1. We fix the value as 0.3 in all the studies shown in this paper.

Estimation of data fidelity tolerance

The only data-specific parameter of the ABOCS algorithm is the tolerance of data fidelity error, ɛ. To find an appropriate value of ɛ, we first estimate the error variance in the line integral measurements due to Poisson noise on the projection images, ɛ_noise. From Taylor expansion of a logarithmic function, the noise of each line integral measurement, b_i, can be estimated as n_P/P_i, where P_i is the mean detected photon number on pixel i and n_P is its associated noise.¹⁹ In CT imaging, Poisson statistics describes the behavior of the majority of the measurement noise, i.e., var(n_P) = P_i.^{19, 31} Approximate P_i as the noisy measurement, p_i, and one obtains the noise variance of the line integral at pixel i as

$${\varepsilon }_{\mathrm{noise}}\left(i\right)=\frac{1}{P_i}\approx \frac{1}{p_i}=\frac{1}{I_0\left(i\right)\times \exp \left(-b_i\right)},$$ (13)

where I₀(i) is the intensity distribution of the flat field in the unit of photon number. The total noise variance is then estimated as the summation of Eq. 13 over all the detector elements

$${\varepsilon }_{\mathrm{noise}}\approx \sum _{i=1}^{N_d}\frac{1}{I_0\left(i\right)\times \exp \left(-b_i\right)},$$ (14)

where N_d is the total number of elements on the detector.

After the effective data correction algorithms already implemented on a CBCT system, including scatter and beam-hardening corrections,^{11, 12, 13, 14, 15, 16, 17} the residual nonstatistical errors on the projections are expected to be small as compared to the Poisson noise. In this paper, we assume that this condition is true. ɛ_noise calculated using Eq. 14 is used as the data error tolerance in all the optimal reconstructions of different studies.

Note that, to extend our ABOCS algorithm for use in practice where projection data contain large errors other than noise, we can simply estimate the error tolerance ɛ in the ABOCS algorithm by multiplying ɛ_noise with a factor (μ) of slightly larger than 1

$$\varepsilon =\mu ·{\varepsilon }_{\mathrm{noise}}.$$ (15)

Using a data error tolerance of Eq. 14 is equivalent to setting μ = 1 in Eq. 15.

Stopping criterion

We use the image difference between two adjacent iterations as the indicator of the algorithm convergence, which is calculated as

$$res=\frac{1}{N_i}·\sum _{l=1}^{N_i}\left|f\left(l\right)-f(l-1)\right|,$$ (16)

where N_i is the total number of image voxels. res would converge to zero once the iteration number increases. We use a threshold on res as the stopping criterion of the iteration. In the 2D image reconstruction using MATLAB, res threshold is set as 10⁻¹² mm⁻¹. In the GPU implementation, to save the computation time of 3D reconstruction, we use a relatively large res threshold (10⁻² mm⁻¹) to terminate the program after a small number of iterations.

Pseudocode for the ABOCS algorithm

In summary, we present the pseudocode of the ABOCS algorithm as below. The symbol : = means assignment. Both image and data space variables are denoted by a vector sign, e.g., $\vec{f}$ and $\vec{b}$.

Pseudocode for ABOCS (the comments are shown in italic).

The parameters in line 1 control the whole algorithm. Their typical values are shown in the code, which are used to acquire the results in this paper. The initial guess image is generated using the standard Feldkamp–Davis–Kress (FDK) reconstruction³² or the algebraic reconstruction technique (ART), shown in line 2. Zero initial will give the same optimal solution but increases the computation time. The main loop, lines 3–25, solves Eq. 6 using GP method with a consistent μ and adaptively selected step size (lines 10–14). The updated image (line 15) is enforced to be non-negative (line 18). If the image error (res) is less than a preset threshold (lines 22–24), the iteration stops with a returned optimal image $\vec{f}$ (line 26).

Evaluation

The performance of the algorithm has been evaluated on both a digital and a physical head phantom. The head phantom data were acquired on our tabletop CBCT system at Georgia Institute of Technology. The geometry of this system exactly matches that of a Varian On-Board Imager (OBI) CBCT system on the Trilogy radiation therapy machine. The geometry and parameters of the system can be found in Ref. 12. The geometry of the tabletop system was also simulated in the digital phantom study. In each dimension, the detector has 512 pixels with 0.776 mm resolution.

Digital phantom study

We first implement ABOCS in MATLAB on a 3.0 GHz PC with 4 GB memory. The imaging performance is evaluated on the Shepp–Logan phantom and compared with those of ASD-POCS and the TV regularization method. The phantom is mainly water equivalent with several ellipses to mimic different structures. The linear attenuation coefficients are 0.02 mm⁻¹, 0.06 mm⁻¹, and 0.00 mm⁻¹ for soft tissues, bones, and gas pockets, respectively. The projections are simulated using mono-energetic x-ray beams, covering 360° with an equal angular spacing. The reconstructed image has a dimension of 512 × 512 with a pixel size of 0.5 × 0.5 mm².

We compare the computation times required by different algorithms. Investigations are then carried out on the proper settings of the algorithm parameters when the noise level of projection images, the object geometry, and the number of projections change. The root-mean-square error (RMSE) of the images compared to the ground truth is used as image quality metrics.¹¹

After a thorough evaluation of the algorithm parameters, we implement ABOCS on an Amax^® GPU workstation (www.amax.com) using CUDA C (NVIDIA, Santa Clara, CA) to utilize the massive parallel computational capability of the GPU for a 3D CBCT reconstruction. A single TESLA C2075 card is installed on the workstation, which consists of 448 processing cores with 1.15 GHz clock speed and 6 GB memory. The parameters of the 3D Shepp–Logan phantom are taken from Ref. 33. The reconstructed volume has a size of 256 × 256 × 256 with a voxel resolution of 1 × 1 × 1 mm³.

Head phantom study

The ABOCS algorithm is further evaluated on head phantom data acquired on our tabletop CBCT system. The system was operated in the short-scan mode with 199° angular coverage. A bowtie filter was mounted on the outside of the x-ray collimator. To avoid the data errors from the sources other than statistical noise, the phantom data were acquired using a narrowly opened collimator (a width of ∼10 mm on the detector). In this fan beam equivalent geometry, scatter signals were inherently suppressed and the data errors were considered from statistical noise only.

Note that, the data fidelity tolerance calculated using Eqs. 14, 15 requires a flat-field image in the unit of photon number. To convert the measured flat field in detector unit on a clinical system to that in the number of photons, we calculate the I₀ image used in the total noise variance estimation [Eq. 14] as

$$I_0=k·I_{\det },$$ (17)

where I_det is the measured flat field in detector unit. The constant k is determined based on the Poisson statistics on I₀, i.e., mean(I₀) = var(I₀), which leads to

$$k=\frac{\mathrm{mean}\left(I_{\det }\right)}{\mathrm{var}\left(I_{\det }\right)},$$ (18)

where mean(·) is the mathematical expectation of the pixel value and var(·) is the corresponding variance, both of which are calculated using the datasets from the consecutive flat-field scans (no object in the field of view).

RESULTS

Digital phantom study

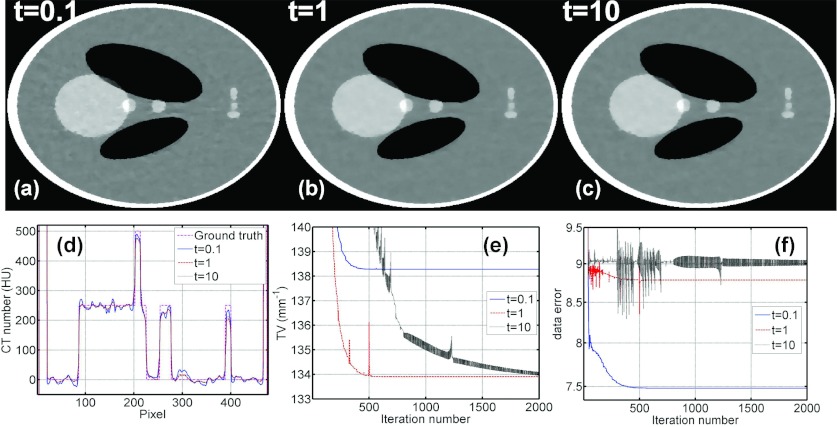
ABOCS converts the optimization formulation from Eq. 1 to Eq. 6 using a logarithmic function to approximate the indicator function shown in Eq. 3. A large t value is needed in the log-barrier function for this approximation to be more accurate. However, if the t value is too large, the algorithm has more oscillations as the iteration goes, which significantly reduces the convergence rate and therefore the reconstruction efficiency. To investigate the effect of t values, Fig. 1 shows the ABOCS reconstruction of the digital Shepp–Logan phantom from 66 projections under a clinical noise level (a flat-field intensity of I₀ = 5 × 10⁴ photons per ray) with different t values. As seen in the comparison, a small t (0.1) results in large errors in the log-barrier approximation and the data fidelity constraint cannot be correctly enforced. Consequently, the resulting image has an erroneous high TV value and more noise artifacts. The ABOCS reconstructions using t = 1 and t = 10 converge to images with a similar quality. A large t (e.g., t = 10), however, causes oscillations of TV values and data fidelity errors during the iteration [see Figs. 1e, 1f]. The iteration number to reach the convergence is much larger than that of t = 1. Based on the above simulation study, we choose t = 1 as the optimal value and fix this value for all other implementations presented in our paper to balance the tradeoff between the approximation accuracy and the computation speed.

Figure 1.

Comparison of CT images, 1D image profiles, image TV values, and data fidelity errors using ABOCS with different t values. (a)–(c): CT images reconstructed using ABOCS with t = 0.1, 1, and 10, respectively. Display window: [−500, 500] HU. (d) Central horizontal 1D profiles of CT images reconstructed using ABOCS with different t values and the ground truth. (e) TV values at different iterations. (f) Data fidelity errors at different iterations. In the simulation, the total number of projections is 66 and the flat-field intensity is I₀ = 5 × 10⁴ photons per ray. In the ABOCS reconstruction, the data error (ɛ) is 9.05 based on Eq. 14 and μ = 1 in Eq. 15.

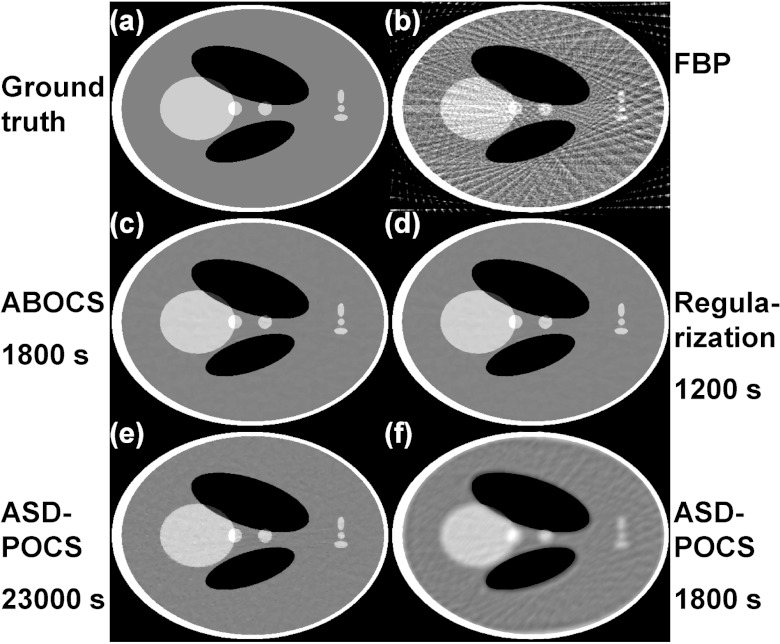
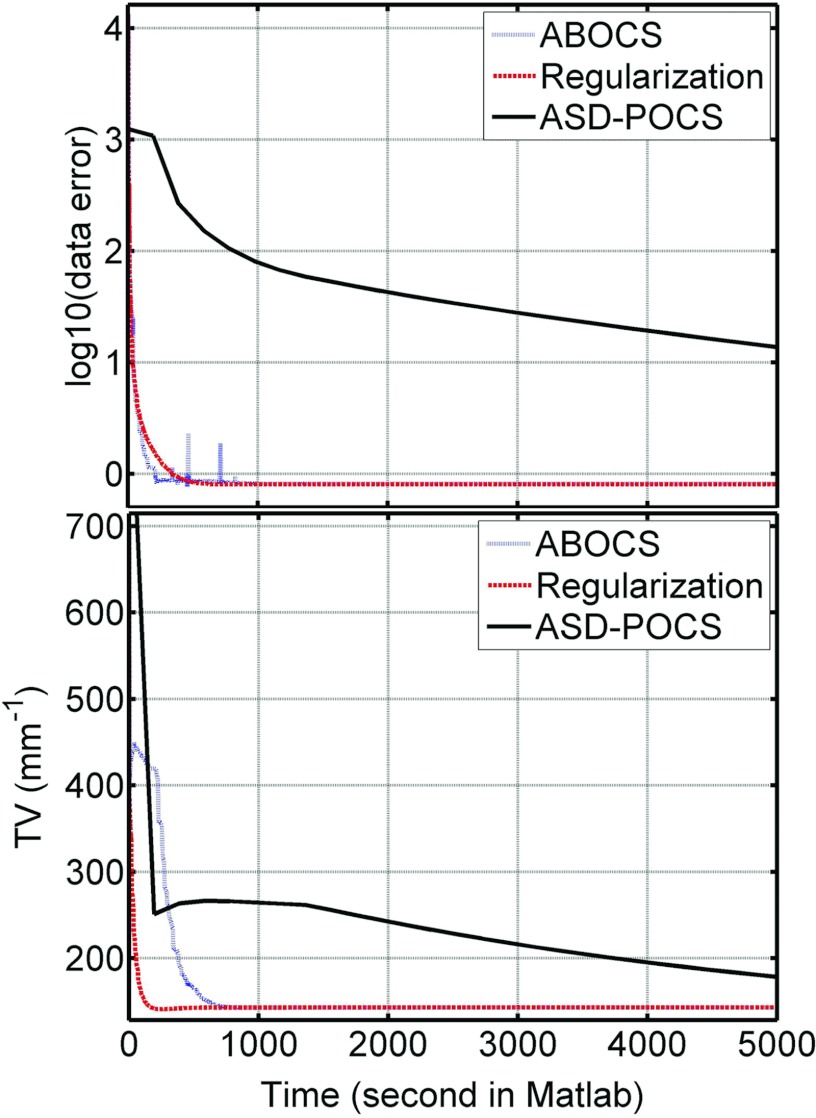
Figure 2 shows the CT images reconstructed from 66 projection views over 360° using different algorithms. Aliasing artifacts are observed in the image from standard FBP reconstruction [Fig. 2b], and are well suppressed in the iterative reconstructions [Figs. 2c, 2d, 2e]. However, the computation speeds of the three CS-based algorithms (ABOCS, TV regularization, and ASD-POCS) vary significantly. For a comparable image quality, ASD-POCS takes 13 times longer than ABOCS and 20 times longer than the TV regularization method. If ASD-POCS iterations terminates at the time required by the ABOCS reconstruction, large residual artifacts still remain in the image as shown in Fig. 2f. To further evaluate the computational efficiency, we plot the data fidelity error and TV term as a function of computation time shown in Fig. 3. ABOCS and the TV regularization method converge much faster than ASD-POCS. Note that, our implementation of ASD-POCS is exactly the version used in Ref. 3 with the same structure and algorithm parameters. Some recent research shows that it is possible to further improve the computation speed of ASD-POCS, especially the POCS step (equivalent to the conventional ART reconstruction), using a parallel computation structure as in simultaneous algebraic reconstruction technique (SART).³⁴

Figure 2.

CT images reconstructed from 66 projections over 360° using (b) standard FBP; (c) ABOCS; (d) conventional regularization using Eq. 2; (e) ASD-POCS; (f) ASD-POCS with ten iterations only for a total computation time comparable to that of (c). (a) Ground truth. The image RMSEs from (b) to (f) are: 211, 24, 24, 24, and 93 HU, respectively. Display window: [−500, 500] HU. The computation time is shown under each iterative algorithm name.

Figure 3.

Data fidelity error and TV term as the functions of computation time, for ABOCS, TV regularization method and ASD-POCS.

As seen in the above results, ABOCS requires a slightly longer reconstruction time than the TV regularization method. A unique feature we gain from the extra computation load, however, is that the algorithm parameter values become more consistent in ABOCS than those in the TV regularization method for different scans on different objects. ABOCS is therefore more convenient for practical use.

To support our argument, we reconstruct the Shepp–Logan phantom with different noise levels (i.e., different I₀ values) and with modified geometries as shown in Fig. 4. ABOCS accurately estimates the data fidelity tolerance used in the algorithm from the raw data using Eq. 14. Equivalently, we use μ = 1 in Eq. 15 for all the ABOCS reconstructions (the first column of Fig. 4). These results well balance the tradeoff between spatial resolution and image noise. A proper value of the penalty weight, λ, in the TV regularization method depends not only on the data fidelity error but also on the TV value of the true image. To obtain images similar to those in the ABOCS reconstruction (shown in the third column of Fig. 4), λ needs to be tuned in a large range when the image noise level or the object geometry changes. For example, λ needs to be increased by a factor of 4.7 when the imaging dose decreases by a factor of 10 [see Figs. 4a, 4b]. Even if the imaging dose is unchanged, the optimal λ value changes for different object geometries. As seen in Fig. 4c, when we remove the low-intensity ellipsoids in the Shepp–Logan phantom, λ needs to be further increased by a factor of 1.5 as compared to that of Fig. 4b.

Figure 4.

CT images reconstructed with different noise levels and object structures using 66 projections. (a) I₀ = 5 × 10⁵; (b) I₀ = 5 × 10⁴; (c) I₀ = 5 × 10⁴ with the geometry modified on the Shepp–Logan phantom. All units are in photon counts. First row of each subfigure shows the reconstructed images (display window: [−100, 100] HU), while second row contains the difference images (display window: [−20, 20] HU). Column (1): Using ABOCS, with a constant μ as 1. Column (3): Using the TV regularization method, with a comparable image quality to that of (1) by a manually tuned λ. Columns (2) and (4): Using the TV regularization method with λ about 1/4 and 4 times of that in (3), respectively.

More importantly, the λ value heavily determines the image quality of the TV regularization reconstruction. The images generated using 1/4 and 4 times the optimal λ value are shown in the second and the fourth column of Fig. 4, respectively. It is seen that the image quality changes dramatically for different λ values. A small λ does not effectively suppress noise, while a large λ oversmoothes the image. Overall, it is difficult to find a small and consistent range of optimal λ values for different imaging cases. Practical implementation of TV regularization entails careful tuning of λ values. Such tuning is tedious and often relies heavily on individual experiences.

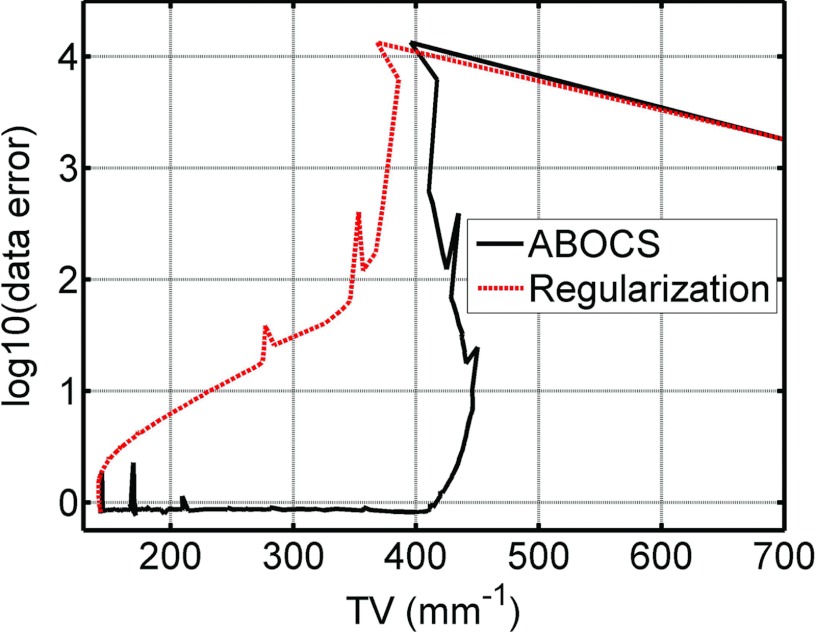
The data fidelity parameter in ABOCS only depends on the Poisson statistics of CT projections, while an optimal λ value in the TV regularization method needs an estimate of the TV value of the true image. It is conceivable that ABOCS requires more computation time than the TV regularization method with an optimized λ for the same image quality, as the latter uses more prior knowledge of the object. This fact can be better seen in the plot of the optimization trajectories in the space of TV values and data fidelity errors shown in Fig. 5. The reconstructed image at each iteration generates one data point on the plot. The λ value in the TV regularization method is manually tuned such that both algorithms achieve the same optimal solution. Both ABOCS and the TV regularization method drive the data point from the same starting position (upper right) of a large TV value and a high data fidelity error toward the origin. The TV regularization method chooses a more direct route since the λ value implies the TV value of the final image. The data fidelity error and the TV value are minimized simultaneously. On the other hand, ABOCS uses a detoured trace as it does not use the information of the optimal TV value. The algorithm first finds a solution that satisfies the data fidelity constraint and then searches for the image with a minimum TV value inside the solution pool of the data fidelity constraint. The iteration number using ABOCS is therefore larger than that of the TV regularization method.

Figure 5.

Plot of data fidelity error and TV value for ABOCS and the TV regularization method as the iteration proceeds. I₀ = 5 × 10⁵ photon counts.

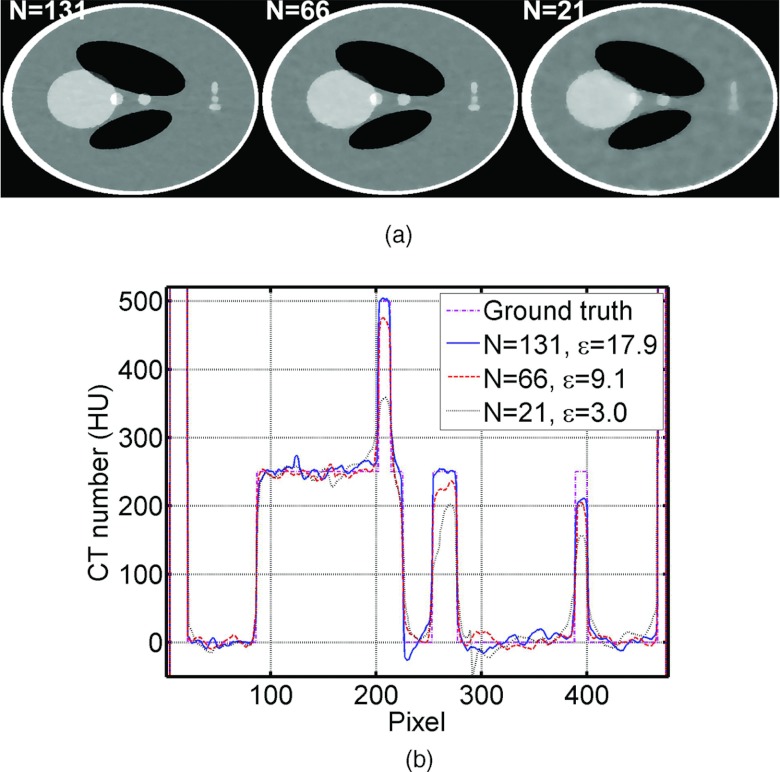
The optimal ɛ also depends on the number of views. This effect has already been included in the calculation of ɛ [Eq. 14], as the formula sums up the estimated noise for all the projection rays. To further demonstrate this point, we include simulation results with different numbers of views shown below in Fig. 6. The same algorithm parameters are used in all the ABOCS reconstructions.

Figure 6.

Reconstructed images of the digital Shepp–Logan phantom using ABOCS with different numbers of projections. (a) CT images, display window: [−500, 500] HU; (b) 1D central horizontal profiles of CT images shown in (a) and the ground truth. The number of projections N and estimated ɛ are listed in the images and the 1D profiles. In the simulation, the flat-field intensity is I₀ = 5 × 10⁴ photons per ray, and μ = 1 in the ABOCS reconstruction.

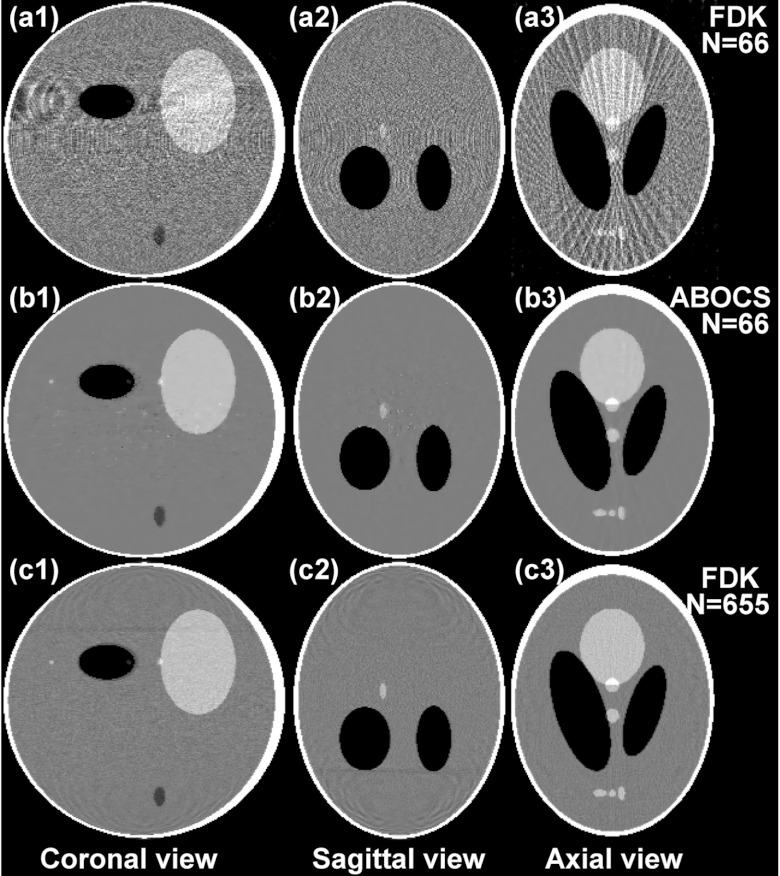
We further evaluate the performance of ABOCS implemented on a GPU workstation by a 3D Shepp–Logan phantom study. Figure 7 shows the coronal, sagittal, and axial views of the reconstructed volumes with the FDK algorithm and ABOCS from 66 projections, and with the FDK algorithm from 655 projections as the reference. To ensure the high quality of the reconstructed image, ABOCS takes about 700 iterations and 18 min on GPU. As compared to the sparse-few FDK reconstruction, ABOCS effectively suppresses the view aliasing artifacts.

Figure 7.

3D reconstructions of the Shepp–Logan phantom. Display window: [−500, 500] HU. Row: (a) FDK reconstruction on 66 projections; (b) ABOCS reconstruction on 66 projections; (c) FDK reconstruction on 655 projections. Column (1): Coronal view; (2) sagittal view; (3) axial view.

Head phantom study

The superior performance of ABOCS is further demonstrated in a head phantom study. Figure 8 shows the axial views of the reconstructed images with the FBP algorithm and ABOCS from 91 and 362 projections on a short scan of 199°. By comparing Figs. 8b, 8c, we find that ABOCS achieves a comparable image equality as the FBP algorithm using the total 362 projections. The advantage of ABOCS appears when the projections are reduced to 25% [see Fig. 8e]. The view aliasing artifacts as in the few-view FBP reconstruction [Fig. 8a] are not present in the ABOCS reconstruction, and the image noise is well suppressed without losing fine structures in the image (see the sinus area).

Figure 8.

Reconstructed head phantom images using FBP and ABOCS from a short-scan data set (over 199°). (a) FBP reconstruction from 91 projections; (b) ABOCS reconstruction with μ = 1 from all 362 projections; (c) FBP reconstruction from all 362 projections; (d)–(f) ABOCS reconstruction from 91 projections with μ = 0.7, 1.0, and 1.3, respectively. Display window: [−430, 430] HU. The number of projections N and μ are listed in the images. The corresponding λ values to achieve similar image equality with a regularization-based method [Eq. 2] are also shown in the figure.

Note that, we use Eq. 14 in the calculation of the data error tolerance in the ABOCS reconstruction of Fig. 8e, which is equivalent to Eq. 15 with μ = 1. To demonstrate the effect of data error estimation (ɛ) accuracy on the image quality, we perform more ABOCS reconstruction with different μ values. Figure 8f shows the reconstruction with μ = 1.3, where the overestimation of ɛ results in image blurs. Some fine structures are lost in the image, which is also obvious in the comparison of 1D profiles passing through the sinus bone region shown in Fig. 9. As seen in Fig. 8d with μ = 0.7, the reconstructed image contains large noise and view aliasing artifacts when ɛ is underestimated. The ABOCS result using μ = 1 achieves an optimized balance between the suppression of view aliasing errors and the preservation of small structures. Since the superior results in both simulation and phantom studies are always obtained with μ = 1, we argue that our algorithm does not require parameter tuning on the data error tolerance for different imaging cases. This claim is valid as long as Poisson noise is dominant in the projection measurement errors.

Figure 9.

Comparison of 1D profiles taken at the vertical dashed line indicated in Fig. 8a. The number of projections N and μ are listed.

Furthermore, the images obtained by ABOCS are similar to those by the conventional regularization method (Eq. 2) since these two algorithms can be equivalent to each other with proper settings of μ and λ values. The equivalent λ values for the images shown in the second row of Fig. 8 are also shown in the figure. Note that, these λ values are quite different from the one used in the Shepp–Logan simulation studies, but we can still use μ = 1 in ABOCS reconstruction to achieve the optimal result.

DISCUSSION

The proposed ABOCS method has the advantages of consistent parameter setting and high computational efficiency since it addresses the issue of the correct selection on data fidelity tolerance [ɛ in Eq. 14] and avoids the tedious parameter tuning process in a regularization-based iterative reconstruction. During the preparation of the paper, we notice a recent publication on the topic of implementing an optimal first-order method for strongly convex total variation regularization proposed by Jensen et al..³⁵ The performances of both the GP-BB and Nesterov-based algorithms have been extensively demonstrated with a CT model. However, a regularization-based structure [Eq. 2] is used in their design, and therefore tuning of λ values is required for an optimal performance of these algorithms.

The main user input parameter of ABOCS, μ in Eq. 15, quantifies the ratio of the estimated data fidelity error. In this work, we propose an estimation method for the data error tolerance with the assumption that the measurement errors are dominated by Poisson noise. Under such an assumption, our algorithm accurately calculates the data error tolerance for an optimal imaging performance. The parameter μ becomes redundant and can always be set to the value of 1. This argument is supported by both Shepp–Logan simulation and head phantom studies. μ = 1 always achieves a well-balanced tradeoff between the reconstruction error and the image noise. Nevertheless, although Poisson statistics is a valid approximation on detector measurement noise in CT imaging, the measurement errors in real imaging applications stem from multiple sources besides statistical fluctuation, including scatter, beam-hardening effects, detector lag, etc. We therefore introduce an extra parameter μ in front of the data error tolerance, with the intention that our ABOCS algorithm can be easily extended to applications where the measurement errors cannot be easily estimated.

Despite the promising results shown in the paper, more investigations are needed on the ABOCS algorithm to further improve its performance for practical use.

In the current ABOCS implementation, the design of stopping criteria is heuristic. There are many mathematically elegant optimality conditions proposed in the literature that may further improve the algorithm. For example, Sidky and Pan derived the optimality condition from the Karush–Kuhn–Tucker (KKT) conditions for the original constrained optimization problem [Eq. 1] based on the angle between the gradient vectors of the TV and the data fidelity, α.³ We will conduct more in-depth investigations on this issue in our future studies using a recent proposed concept of gradient map.³⁵

Although ABOCS achieves a higher computation speed than ASD-POCS, it shows a slightly inferior convergence as compared to the TV regularization method [Eq. 2], attributed to the detour trace in the search for an optimal solution (see Fig. 5). We may further improve the computational efficiency by improving the search trajectory. For example, we may use a large μ in the early-stage iterations such that the algorithm enters the phase of reducing TV value earlier in the optimization, and then gradually reduce the μ value to reach the final optimal solution. Or we can apply the two-level optimization scheme presented in Ref. 36 to further improve the convergence speed. Such an algorithm improvement will be another future research direction on ABOCS.

As a final remark, the proposed algorithm should be considered as an improved implementation of the CS reconstruction. Therefore, ABOCS also inherits the advantages of the conventional CS reconstruction, such as dose reduction⁷ and spatial resolution improvement,^{37, 38} which have already been demonstrated in the literature. Our method may even shed light on the algorithm design in other scenarios of sparse signal recovery where the CS theory is applicable.^{39, 40}

CONCLUSION

In this paper, we propose ABOCS, a new CS-based CBCT reconstruction for few-view and highly noisy data with improved consistency and convergence over existing methods. Using simulation studies, we demonstrate that ABOCS shortens the computation time by one order of magnitude compared to ASD-POCS with the same objective and constraints. We also show that without changing algorithm parameter, our method achieves a consistent reconstruction performance on projections of different noise levels or different object geometries. On the contrary, although with the same high efficiency, the TV regularization method requires careful tuning of the penalty weight for a performance matching that of ABOCS. We further evaluate the practicality of ABOCS in a 3D Shepp–Logan phantom reconstruction and a head phantom study. Our method achieves an image quality comparable to that of a full-view FBP reconstruction but with only 25% projections.