Evaluating the Evidence for the General Factor of Personality across Multiple Inventories

Abstract

A general factor of personality (GFP) has been proposed as the apex of a personality trait hierarchy that explains covariance among the lower-order factors measured by various personality inventories. In this study we evaluated the GFP hypothesis across several personality inventories, unlike most previous research in which the GFP has been derived from individual instruments in isolation. Exploratory analyses did not produce substantial evidence for the existence of a single cross-instrument higher-order factor of factors and efforts to specify a range of GFP-inspired models in a confirmatory framework led to significant estimation difficulties and poor fit to the data. Overall these results fail to support a common GFP that is positioned at the top of a personality trait hierarchy.

Multi-trait models such as the Big Five (Goldberg, 1990; John, Naumann, & Soto, 2008) or Big Three (e.g., Clark & Watson, 2008; Tellegen, 1985) provide organizational frameworks for classifying broad personality dispositions into conceptually meaningful units with empirical utility. An important assumption in these frameworks is the idea that each dimension represents a fundamental unit of personality. For example, the Big Five domains (i.e., neuroticism [N], extraversion [E], openness [O], agreeableness [A], and conscientiousness [C]) are thought to reflect basic tendencies that are linked with reasonably distinct neurobiological systems (McCrae & Costa, 2008). One complicating empirical fact is the repeated demonstration that observed scores on measures of the Big Five and similar models are correlated. The existence of such correlations points to the possibility of higher-order personality factors.

Digman (1997) identified two higher-order “metatraits” that he argued explained the associations among Big Five dimensions such that a superordinate “Alpha” factor explained associations among neuroticism, conscientiousness, and agreeableness whereas a super-ordinate “Beta” factor explained the correlation between extraversion and openness. Alpha can be thought of as a constellation of socially advantageous attributes that reflect the ability to get along well in society. Beta can be thought of a constellation of attributes that facilitate personal growth and exploration. More recently, DeYoung (2006) respectively referred to these meta-traits as Stability and Plasticity because he believed that those terms were more descriptive than Digman’s Alpha and Beta terminology (see e.g., p. 1149). Theoretical precedent exists for conceptualizing two similar higher-order organizing concepts termed Agency (Beta/Plasticity) and Communion (Alpha/Stability) (Bakan, 1966; Wiggins, 1991).

The identification of meta-traits or higher-order dimensions of personality that explain associations among lower order dimensions has led to more recent interest in a General Factor of Personality (GFP; see Rushton & Irwing, 2011). The GFP is posited to exist at the apex of the personality trait hierarchy, thus explaining the correlation that is sometimes found between Alpha and Beta (e.g., Musek, 2007; Rushton, 1985, 1990, Rushton, Bons, & Hur, 2008; Rushton & Irwing, 2008, 2009a, 2009b; van der Linden, te Nijenhuis, & Bakker, 2010). The GFP is thought to capture a broad array of attributes that facilitate or inhibit personality-related success (Rushton, 1985; 1990; Rushton & Irwing 2011), analogous to the ‘g’ factor of cognitive abilities (Spearman, 1904).

A series of studies that have identified a single higher-order “factor of factors” from omnibus personality inventories have been offered as evidentiary support for the GFP. For example, using data from 16 Big Five studies Rushton and Irwing (2009a) reported that a Confirmatory Factor Analytic (CFA) model with orthogonal higher-order Alpha and Beta factors fit worse than a model that specified that Alpha and Beta were explained by a single higher-order factor – the GFP¹. Several similar studies based on factor analytic techniques using a variety of measures have been presented as further evidence in favor of the GFP (e.g., Rushton and Irwing, 2009b; van der Linden et al. 2010). Other studies suggest that the correspondence of the GFP is stronger among monozygotic than dizygotic twins (Veselka et al., 2009), and that the GFP is related to criterion variables such as self-esteem (Erdle, Irwing, Rushton, & Park, 2009) and peer reports of popularity and likeability (van der Linden, Scholte, et al., in press).

Some of these findings are predictable given that it is already well-known that personality dimensions are partly heritable (e.g., Bouchard & Loehlin, 2001) and able to predict consequential life outcomes (Roberts, Kuncel, Shiner, Caspi, & Goldberg, 2007; Ozer & Benet-Martínez, 2006). Moreover, previous analyses of Big Five measures have suggested the existence of two oblique higher order factors (Digman, 1997; DeYoung, Peterson, & Higgins, 2002; DeYoung, 2006). The fact that the Big Two factors are sometimes modestly correlated (DeYoung et al., 2002) means that this association can be re-expressed as a higher-order factor.

However, there are grounds to suspect that some of the correlations found in CFA studies of personality measures are inflated. Although it is possible to create reasonably orthogonal measures of the Big Five (Donnellan, Oswald, Baird, & Lucas, 2006; Saucier, 2002), even in the most discriminant valid instruments modest domain-level inter-correlations often persist in practice. Yet Marsh et al. (2010) suggested that a considerable amount of this covariation emerges in CFA contexts is attributable to unspecified cross-loadings that usually accompany these kinds of analyses. These cross-loadings are often small by exploratory factor analytic standards (e.g. .30 or less) but omitting these parameters from the CFA models will often lead to inflated inter-factor correlations. Indeed, inter-factor correlations are reduced when these seemingly trivial cross-loadings are estimated as occurs when using exploratory-based factor analytic techniques (see Marsh et al., 2010). Given these hints in the psychometric literature, we suspect that some of the evidence for the GFP that is based on CFA methods may be artifactual.

Consistent with this suspicion, the substantive interpretation of GFP offered by Rushton and Irwing has been questioned by researchers who have interpreted the GFP as a psychometric artifact. For instance, Ashton et al. (2009) suggested that the correlations among broad traits reflect the fact that many lower-order factors (and even personality items, see Goldberg & Velicer, 2006) represent blends of different broad traits. When this fact is not accounted for in the analyses, non-substantive higher-order factors seem to emerge. However, in a direct comparison of higher-order and ‘blended variable’ models, the latter fit personality trait data better than the former (Ashton et al., 2009). As another example, Backstrom et al. (2009) showed using non-evaluative, neutral items limits the potential to identify higher-order factors, suggesting that such factors may be a function of social desirability effects in responding rather than substantive effects (see also Anusic et al., 2009).

The potential existence of a GFP is important for personality science, personality assessment, and evolutionary personality psychology. For example, to the extent that personality is related to basic neurological systems, the number of basic dimensions that emerge from personality inventories will influence the number of candidate neural systems sought in studies of the biological underpinnings of personality. Likewise, decisions by evolutionary theorists to regarding how many and which personality dimensions to focus on are currently guided, in part, by psychometric considerations. As a practical matter, if the GFP exists as a substantive dimension, it might be efficient to simply construct reliable and valid measures of that construct for use in studies designed to predict important life outcomes. It might be reasonable to develop a single GFP measure that could provide a “personality quotient”. The implications of such a quotient may be broad, given the widespread influence of IQ on how individuals think about their own and others’ cognitive abilities.

The goal of this study was to evaluate evidence for the GFP across several personality inventories that were administered to the same sample. Proponents of the GFP argue that it is a “robust” dimension that emerges across a diverse range of personality inventories (see e.g., Rushton & Irwing, 2011, p.155 – 156). Thus, the same higher-order dimension should emerge across different omnibus inventories that are designed to capture a wide range of important individual differences in personality. However the majority of prior studies that have explored the GFP have evaluated one inventory at a time. Evidence of strong convergence across a set of comprehensive personality measures would be consistent with the GFP hypothesis, whereas failure to find strong convergence would cast doubt on the hypothesis of a robust and unitary GFP.

Method

This study used data from the Eugene-Springfield (Oregon) Community Sample (ESCS; Goldberg, 2008), in which individuals in the community completed a number of commonly-used personality measures. Data were collected via the mail from 1993-2003. We analyzed data from the 16pf (Conn & Rieke, 1994; N = 680), 6 Factor Personality Questionnaire (6fpq; Jackson, Paunonen, & Tremblay, 2000; N = 714), California Psychological Inventory (CPI; Gough & Bradley, 1996; N = 792), HEXACO Personality Inventory (HEXACO-PI; Lee & Ashton, 2004; N = 734), Hogan Personality Inventory (HPI; Hogan & Hogan, 1995; N = 742), Multidimensional Personality Questionnaire (Tellegen & Waller, 1994; N = 733), NEO Personality Inventory-Revised (NEO-PI-R; Costa & McCrae, 1992; N = 857), and Temperament and Character Inventory-Revised (TCI-R; Cloninger, Przybeck, Svrakic, & Wetzel, 1994; N = 727). The features of these well-known measures are described in primary sources and their psychometric characteristics in the ESCS are described in previous reports (e.g., Hopwood & Donnellan, 2010; Grucza & Goldberg, 2007).

We conducted three sets of analyses. First, we subjected the lower order scales from each of these instruments to a set of separate principal axis exploratory factor analyses (EFA). We estimated and saved factor scores for factors with eigenvalues >1. We then factored the estimates derived in the first analysis for each instrument separately, using the same analytic methods. We continued this process until we achieved a single factor, which we regarded as an estimate of that instrument’s GFP. We then conducted a cross-instrument principal axis EFA on the GFP estimates derived from each instrument. We expected that the different GFPs embedded in each inventory would cohere into a common higher order factor based on the idea that each inventory ultimately assesses the same GFP.

Second, we conducted a joint EFA on the lower-order scales of all the inventories and evaluated the matrix of factor correlations emerging from oblique rotations. This approach is similar to the strategy used by Markon, Kreuger, and Watson (2005) to evaluate the hierarchy of personality constructs. However, our explicit focus was on the magnitude of the factor inter-correlations that emerge from a joint analysis of multiple personality inventories whereas Markon et al. (2005) used orthogonal rotations so that the factor inter-correlations were fixed to zero. We used EFA rather than CFA for these analyses to limit the likelihood that correlations among higher-order factors would be artificially high because of unspecified cross-loadings.

Third, we specified a series of seven CFA models testing the validity of a cross-instrument GFP, as described in detail below. These CFA models were intended to be analogous to those that have been tested in the literature with single instruments. Thus, we only used the scales of measures from the ESCS for which the structure has been tested in previous GFP research, which were the CPI (Rushton & Irwing, 2009a), HPI (Rushton & Irwing, 2008) MPQ (Rushton & Irwing, 2009b), NEO-PI-R (Rushton & Irwing, 2008), and TCI (Rushton & Irwing, 2009a).

Results

Testing Convergence of Single Higher Order Factors Derived from Multiple Inventories

We first conducted a principal axis EFA in PASW 18 on the lower order scales of all eight instruments we evaluated and rotated the resulting factors with Oblimin. We then factored these factor score estimates, factored the resulting estimates, and so on until we were able to achieve a single ‘factor of factors’ for each instrument². The inter-correlations of factor scores in this analysis are reported in Table 1. Notably, there were several modest correlations in this matrix (e.g., 15 of 28 correlations were < ȣ.30ȣ), providing an initial indication that these GFP variables were not tapping the same construct. To evaluate the coherence of general factors across different inventories, we conducted a principal axis EFA on the factor score estimates from each independent inventory. The first three factors had eigenvalues of 3.43, 1.77, and 1.04 which together explained 61.73% of the covariance in factor scores. Although parallel analysis suggested extracting only two factors, doing so rendered the communality for the 6fpq GFP estimate .04, and it did not load strongly onto either factor (pattern coefficients = −.03, .20). This suggested that the GFP estimate from this measure was splitting off as its own, third factor. In the interest of meaningful evaluating GFP estimates from all inventories, we extracted three factors. The pattern coefficients, after Oblimin rotation, are given in Table 2. The factor scores from four measures tended to load more strongly on factor 1 (CPI, HPI, MPQ, TCI) whereas three others loaded more strongly on factor 2 (16pf, HEXACO-PI, NEO-PI-R). As expected, the 6fpq alone loaded most strongly on factor 3. Thus our first effort to identify a unitary cross-instrument GFP failed.

Table 1.

Inter-correlations of General Factors of Personality derived from Eight Personality Inventories.

	16pf	6fpq	CPI	HEXACO-PI	HPI	MPQ	NEO-PI-R
6fpq	.10
CPI	−.28	.06
HEXACO-PI	.27	.03	.49
HPI	−.28	−.15	.66	.31
MPQ	.39	.29	.29	.58	.07
NEO-PI-R	−.38	−.04	.68	.32	.62	.12
TCI	−.21	.00	.56	.35	.61	.27	.74

Note. N = 433. 6fpq = Six Factor Personality Questionnaire; CPI = California Personality Inventory; HPI = Hogan Personality Inventory; MPQ = Multidimensional Personality Questionnaire; TCI = Temperament Character Inventory.

Table 2.

Communalities and Oblimin rotated factor pattern coefficients from an Exploratory Factor Analysis of General Factors of Personality Computed for Eight Personality Measures.

	Communality	Factor 1	Factor 2	Factor 3
16pf	.49	−.42	.60	−.05
6fpq	.31	−.03	.00	.56
CPI	.68	.81	.07	.06
HEXACO-PI	.65	.42	.66	−.08
HPI	.66	.78	.02	−.23
NEO-PI-R	.75	.17	.69	.38
MPQ	.82	.91	−.11	.06
TCI	.59	.76	.07	.05

6fpq = Six Factor Personality Questionnaire; CPI = California Personality Inventory; HPI = Hogan Personality Inventory; MPQ = Multidimensional Personality Questionnaire; TCI = Temperament Character Inventory. Factor 1 correlated .18 with factor 2 and .00 with factor 3; factors 2 and 3 correlated .23.

To further evaluate the interpretive meaning of these cross-instrument factors, we correlated them with the Big 5 dimensions from the NEO-PI-R (Table 3). Factor 1 seems to involve emotional resilience and surgency, as its strongest correlates were extraversion and (low) neuroticism, and it correlated positively with openness and conscientiousness. Factor 2 seems to involve antagonism and sensation-seeking, given its strong negative correlation with agreeableness and positive correlations with extraversion and openness. Factor 3 primarily reflects openness. We also correlated the GFP estimate from each instrument with the NEO-PI-R scales (Table 3), and observed notable variability in these patterns of correlations. For instance, whereas GFP estimates from measures that loaded strongly on factor 1 tended to have sizeable correlations with neuroticism (Mdn ȣrȣ = .51), the 6fpq estimate, which did not load strongly on factor 1, was uncorrelated with this trait.

Table 3.

Correlations of General Factors of Personality estimates derived from each instrument, and higher-order factors from a cross-instrument exploratory factor analysis of these estimates, with NEO-PI-R scale scores.

	Neuroticism	Extraversion	Openness	Agreeableness	Conscientiousness
Cross-Instrument Higher Order Factors
Factor 1	−.73	.69	.46	.05	.46
Factor 2	.30	.24	.28	−.57	−.19
Factor 3	.15	−.01	.56	.04	−.35
Within Instrument GFPs
16pf	.45	−.18	−.09	−.51	−.16
6fpq	.00	−.25	.39	−.08	−.33
CPI	−.52	.57	.47	−.12	.17
HEXACO-PI	−.05	.45	.39	−.47	.02
HPI	−.63	.52	.08	−.05	.38
MPQ	.22	.34	.45	−.37	−.22
NEO	−.72	.67	.50	.23	.58
TCI	−.50	.59	.34	.13	.44

6fpq = Six Factor Personality Questionnaire; CPI = California Personality Inventory; HPI = Hogan Personality Inventory; MPQ = Multidimensional Personality Questionnaire; TCI = Temperament Character Inventory.

Evaluating the Existence of the GFP Using a Joint EFA of Several Personality Inventories

Our second set of analyses was based on the approach used by Markon et al. (2005) to evaluate the hierarchical structure of personality. First, we created a file that had the lower-order scales from the three large omnibus inventories that were also included in the Markon et al. (2005) investigations – the NEO-PI-R, the MPQ, and the TCI. A total of 72 personality scales were used for this analysis (30 from the NEO-PI-R, 11 from the MPQ, and 31 from the TCI; N = 946; this covariance matrix is available at www..edu). We then subjected these scales to a series of EFA analyses using the oblique GEOMIN rotation procedure with maximum likelihood estimation as implemented in Mplus 6 (this estimation procedure also addresses missing data issues). Our focus here was on both the nature of the factors that emerged from the analyses and especially the degree of correlation between the factors, as a considerable degree of factor inter-correlations seems like a natural starting point for inferring the existence of higher-order factors.

Thirteen eigenvalues based on the sample correlation matrix (the procedure used in Mplus) were above 1 but an inspection of the scree plot and various solutions suggested an interpretable Big 5 structure (see also Markon et al., 2005). Of note, the inter-factor correlations for the five factor model were not substantial using most rules of thumb (N and E: −.23; N and A: .03; N and C: −.23; N and O: −.03; E and A: .05; E and C: .06; E and O: .39; A and C: −.02; A and O: −.16; C and O: .02). We then submitted this matrix to a second maximum likelihood EFA and attempted to extract higher-order factors. However, this model would not converge within 1000 iterations and the estimates were not sensible when the number of iterations was increased to 5,000 (e.g., the loading for E was estimated at 33.497 and no standard error could be computed).

To evaluate whether our results were a function of the GEOMIN rotation, we also used an Oblimin rotation to extract five factors from the 72 scales. The matrix of inter-factor correlations was generally similar to the GEOMIN results (N and E: −.21; N and A: .−01; N and C: −.26; N and O: .00; E and A: .10; E and C: .12; E and O: .26; A and C: .01; A and O: −.06; C and O: .07). When this matrix was submitted to a second EFA, it was possible to obtain a solution; however, only the 1 factor solution would converge. Loadings for this dimension were −.27 for N, .79 for E, .10 for A, .18 for C, and .31 for O. Thus, this common factor seems to approximate Extraversion or perhaps Beta/ Plasticity/Agency more so than the GFP.

We also conducted similar analyses using the scales from the 6fpq, the 16pf, the NEO-PI-R, the HEXACO-PI, and the MPQ given that previous research suggests that these inventories have a reasonably well defined higher-order structure ranging from 3 to 6 factors each. A total of 99 personality scales were used for this analysis (18 from the 6fpq, 16 from the 16pf, 24 from the HEXACO-PI, 11 from the MPQ, and 30 from the NEO-PI-R; N = 956; covariance matrix available at www..edu). Seventeen eigenvalues for the sample correlation matrix were above 1. Once again, an inspection of the scree plot and the interpretability of several solutions suggested a Big Five structure. As before, the inter-factor correlations for the five factor model were modest (E and O: .22; E and N: −.14; E and A: .03; E and C: .07; O and N: −.17; O and A: −.20; O and C: −.05; N and A: .07; N and C: −.17; A and C: −.01). We then submitted this matrix to a second maximum likelihood EFA and attempted to extract higher-order factors. We could not estimate a two-factor solution but a 1 factor model would estimate. Loadings for this dimension were .18 for E, 1.24 for O, −.13 for N, −.16 for A, and −.05 for C. This solution was not clearly interpretable as a GFP. In fact, it was mostly related to the Big Five domain with the most modest relation to adaptation, Openness to Experience.

Evaluating the Existence of the GFP Using CFA Techniques

In a final set of analyses, we used a confirmatory factor analytic (CFA) framework to investigate the evidence for the convergence of GFPs across inventories. Following prior published work on the GFP (e.g., Rushton & Irwing, 2008, 2009a, 2009b) we used the TCI, NEO-PI-R, CPI, HPI, and MPQ in these analyses. In order to derive manifest variables across measures that were comparable to each other, we first conducted EFAs on the MPQ and CPI, which each have a large number of lower order scales that have been shown to load on a smaller number of higher-order factors. This was accomplished using principal axis factoring with Oblimin rotation in PASW 18. In an effort to remain consistent with prior GFP work, we followed Rushton and Irwing (2009a, 2009b) by requesting five factors for the MPQ and six for the CPI, whereas we used the scale structure defined by the authors of the measure for the NEO-PI-R, TCI, and HPI. There were a total of 29 scales used as manifest variables in the CFA models (7 for TCI; 5 for NEO-PI-R; 6 for CPI; 6 for HPI, and 5 for MPQ; N = 556; covariance matrix available at www..edu). Given the wide differences in variance across scales from different measures, the variables were rescaled to standard scores in order to avoid problems with CFA estimation associated with differing variances across indicators. All CFA models were estimated in Mplus 6 (Muthén & Muthén, 2010) from the observed data file using maximum likelihood.

Three modeling approaches were adopted in an effort to estimate an overall GFP in a CFA framework. The first general approach (Models 1 and 2) attempted to evaluate the GFP directly by modeling the scales from all instruments in hierarchical models. The second general approach (Models 3-5) conceptualized an intermediary factor structure involving ‘Alpha’, ‘Beta’, and in some cases ‘Gamma’ constructs for each instrument. The final general approach (Models 6 and 7) conceptualized these intermediary factors across instruments.

Models 1 and 2 – Convergence Across Measure Specific GFPs

Model 1 allowed each scale from a given measure to load on to one of five factors (i.e., measure specific general factors) which were allowed to correlate freely. That is, we estimated a TCI GFP, a NEO-PI-R GFP, a CPI GFP, a HPI GFP, and a MPQ GFP. These five GFPs were then freed to correlate with each other. This model had a poor fit across multiple indices (Table 4). In addition, the matrix for the factor correlations had a large number of Heywood cases (i.e., correlations greater than 1.00). In spite of these limitations, we estimated Model 2 with a second-order structure that allowed all of the measure specific GFPs to load freely on one higher-order factor (i.e., the across measure GFP). Overall fit for this model was also poor and demonstrated a decrease in fit (χ² df = 5; χ² = 87.57, p < .001). Moreover, there were indications of serious misspecification with three (NEO-PI-R, MPQ, HPI) of the five first-order factors having negative variances. Thus, this approach failed to provide clear support for a GFP.

Table 4.

Summary of fit statistics for confirmatory factor analysis models.

	df	χ 2	χ2 p	RMSEA	RMSEA 90% CI	CFI	TLI	SRMR	BIC	AIC
Model 1	367	8042.24	0.00	0.194	0.190-0.198	0.34	0.27	0.19	42385.86	41966.74
Model 2	372	8129.81	0.00	0.194	0.190-0.197	0.33	0.27	0.19	42441.83	42044.32
Model 3	318	5066.78	0.00	0.164	0.160-0.168	0.59	0.48	0.14	39720.12	39089.28
Model 4	363	7365.54	0.00	0.186	0.183-0.190	0.40	0.32	0.19	41298.04	41734.44
Model 5	364	6984.86	0.00	0.181	0.177-0.185	0.43	0.36	0.21	41347.44	40915.36
Model 6	356	4583.88	0.00	0.146	0.142-0.150	0.64	0.58	0.15	38997.03	38530.38
Model 7	361	4626.82	0.00	0.146	0.142-0.149	0.63	0.59	0.15	39008.36	38563.32

Note. N = 556 . df = Degrees of Freedom; χ² = Chi-Square; RMSEA = Root Mean Square Error of Approximation; RMSEA 90% CI = 90% Confidence interval for RMSEA; CFI = Comparative Fit Index; TLI = Tucker-Lewis Fit Index; SRMR = Standardized Root Mean Square Residual; BIC = Bayesian Information Criterion; AIC = Akaike Information Criterion.

Models 3, 4, and 5 – Intermediary Alpha, Beta, and Gamma Factors

The majority of prior research has used observed variables at the same level of analysis as we have employed here (e.g., NEO-PI-R Extraversion Domain Scores as opposed to facets scores). However, past research has also overwhelmingly relied on an intermediary factor structure between the observed personality scales and the GFP’s single factor by having the basic input measures serve as indicators for higher-order factors identified in the literature (e.g., Alpha and Beta) which in turn serve as indicators for GFP. This practice is consistent with the idea that the GFP is a factor of factors. Therefore, a series of models were estimated based on prior GFP research specifying two intermediary factors.

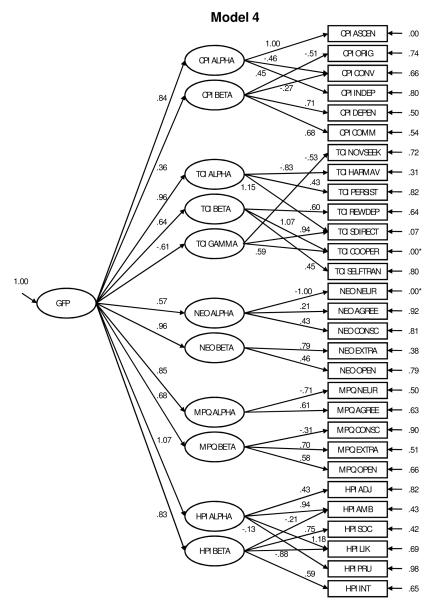
First, Model 3 was estimated in which Alpha and Beta, or Alpha, Beta, and Gamma in the case of the TCI (see Rushton & Irwing, 2009a), were specified for each omnibus inventory. This model had eleven higher order factors (Alphas and Betas for all 5 inventories and 1 Gamma for the TCI) which were freed to correlate. This model seemed to fit the underlying data better than Models 1 and 2 (see Table 4). However, there were a number of inadmissible values (i.e., greater than 1) in the factor correlations. Estimating a second-order general factor in Model 4 resulted in a notably worse fit across all indices (Table 4). Additionally, this model demonstrated clear misspecification in the form of two negative first-order factor variances and two negative error variances (TCI Cooperativeness and NEO-PI-R Neuroticism). The fit of Model 4 presented in Table 4 is from a modified model with these error variances fixed to 0. Figure 1³ provides a conceptual diagram along with the standardized factor loadings and error variances.

Figure. 1.

Note. CPI = California Personality Inventory; TCI = Temperament-Character Inventory; NEO = NEO Personality Inventory Revised; MPQ = Multidimensional Personality Questionnaire; HPI = Hogan Personality Inventory.

*Indicates variance fixed to 0.00.

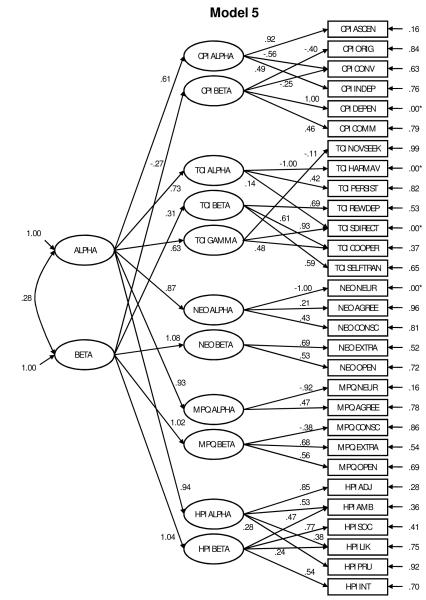
Model 5 also estimated a two-factor higher-order structure. This model, however, specified higher-order Alphas and Betas across inventories. This was accomplished by allowing each first-order “Alpha” factor and the TCI “Gamma” factor to load freely on a higher order “Alpha” factor, and each of the first-order “Beta” factors to load on a higher-order “Beta” factor. Relative to the one-factor higher-order model this model had significantly improved fit (Table 4). The conceptual model and standardized coefficients are presented in Figure 2. Although this model converged, four error variances were negative and subsequently fixed to zero whereas three first-order factor variances were negative. Attempts to specify factors with non-negative variance resulted in models that would not converge. The overall model is probably untrustworthy but we note that the correlation between the alpha and beta factors was .28 (i.e., they share less than 8% of their variance). No single-factor third-order model was estimated as this would merely be a quantitative rearticulation of this correlation.

Figure. 2.

Note. CPI = California Personality Inventory; TCI = Temperament-Character Inventory; NEO = NEO Personality Inventory Revised; MPQ = Multidimensional Personality Questionnaire; HPI = Hogan Personality Inventory.

*Indicates variance fixed to 0.00.

Models 6 and 7 – Modeling the cross-instrument trait hierarchy

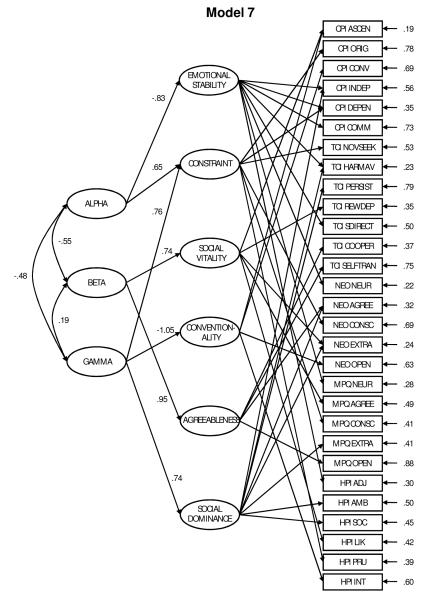
We anticipated that a model with 5 to 7 first-order factors might provide a better fit to the data, given that the indicators from different inventories often measure similar dimensions of personality. To determine the structure most likely to achieve the best fit, an EFA was conducted on the 29 scales, again with Oblimin rotation. Six factors were retained with eigenvalues > 1. Model 6 was estimated as a freely covarying six-factor first-order solution suggested by the results of the EFA (Figure 3). Factor loadings of .30 and above from the EFA were used as the basis for freeing factor loadings in this model. This 6 factor structure appears to have two factors associated with the broader Extraversion domain, which we have tentatively labeled “Social Dominance” and “Social Vitality” following prior empirical work that has emphasized a similar distinction (Roberts, Walton, & Viechtbauer, 2006).

Figure. 3.

Note. CPI = California Personality Inventory; TCI = Temperament-Character Inventory; NEO = NEO Personality Inventory Revised; MPQ = Multidimensional Personality Questionnaire; HPI = Hogan Personality Inventory.

Table 5 summarizes the factor correlations and standardized factor loadings. Model 6 proved to be a considerably better fit to the data than prior models (Table 4). Finally, Model 7 was estimated with a three-factor higher-order structure which resulted in a decrease in fit from Model 6 based on the χ² difference test (Δdf = 5; Δχ² = 42.94, p < .001), but the remaining fit indices did not evidence substantial change. A conceptual diagram and higher-order factor loadings is provided in Figure 3. As with the majority of previous models, this model exhibited some negative first-order factor variance. Nonetheless, as compared with previous models, the models based on a six-factor solutions show much better specification in the form of fewer negative factor and error variances⁴. Again, a third-order model was not estimated⁵.

Table 5.

Model 6 Factor Correlations and Standardized Factor Loadings.

	Emotional		Social			Social
	Stability	Constraint	Vitality	Conventionality	Agreeableness	Dominance
Factor Correlation Matrix
Emotional Stability	1.00
Constraint	−0.24	1.00
Social Vitality	0.33	−0.13	1.00
Conventionality	−0.43	−0.45	−0.21	1.00
Agreeableness	0.43	−0.24	0.70	−0.11	1.00
Social Dominance	0.20	0.43	0.26	−0.76	0.02	1.00
Standardized Factor Loadings
CPI Communion	0.52
CPI Independence	0.24					0.55
CPI Dependability	0.53	−0.51
TCI Harm Avoidance	−0.56					−0.57
TCI Directedness	0.71
NEO Neuroticism	−0.88
MPQ Neuroticism	−0.85
HPI Adjustment	0.84
CPI Originality		0.47
TCI Novelty Seeking		0.69
NEO Conscientiousness		−0.55
MPQ Conscientiousness		−0.77
HPI Prudence		−0.78
TCI Reward Dependence			0.80
CPI Ascendance			0.30	−0.80
NEO Extraversion			0.54			0.58
MPQ Agreeableness			0.72
HPI Likeability			0.76
CPI Conventionality				0.57
NEO Openness				−0.59
HPI Intelectance				−0.62
TCI Cooperativeness					0.82
TCI Self-Transcendence					0.50
NEO Agreeableness					0.72	−0.40
MPQ Openness					0.31
TCI Persistence						0.43
MPQ Extraversion						0.77
HPI Ambition						0.69
HPI Sociability						0.77

Note. N = 556. TCI = Temperament Character Inventory; HPI = Hogan Personality Inventory; NEO = NEO Personality Inventory Revised; MPQ = Multidimensional Personality Questionnaire; CPI = California Personality Inventory.

Discussion

Researchers have become increasingly interested in the existence and interpretation of higher-order dimensions of personality, including the possibility of a General Factor of Personality (GFP). Rushton and Irwing (2011, p. 132) suggest that high scores on the GFP reflect a “good” personality whereas low scores reflect a “difficult” personality. Proponents of the GFP suggest that this dimension is the outcome of evolutionary processes that selected certain attributes like emotional stability, openness, cooperativeness, agency, and conscientiousness to promote survival, growth, and reproduction (Musek, 2007; Rushton, 1985; Rushton & Irwing, 2011). Proponents also regard the GFP as considerably robust based on their identification of this higher-order dimension in personality inventories of varying content (e.g., normal vs. disordered personality) and development approach (e.g., theoretical vs. eclectic, empirical vs. rational). Indeed, they note that: “Its location at the apex of the hierarchy should be almost completely fixed in any large data set” (Rusthon & Irwing, 2011, p. 155).

In general, our findings do not support the existence of a GFP as a single factor of factors at the apex of a personality trait hierarchy that is common across personality inventories. In an EFA context we found that interpretively different GFPs seemed to emerge from different instruments. The discrepancies across measures may be explained by their different content foci (e.g., some measures, such as the HPI, may have been constructed to emphasize adaptation to a work environment more so than others) or development strategies (e.g., the role of factor analysis was greater for some measures, such as the NEO-PI-R, than others, such as the CPI). In general, to the extent that the covariation among personality scales cannot be represented with a single construct, a factor summarizing the covariation of all the scales of any broadband measure should be somewhat arbitrary. It would be questionable in this case to expect a summary score from one measure to relate to a similar summary score on another measure. We suspect the fact that there was any convergence at all likely reflects the validity of some higher-order level of personality below the supposed GFP. For instance, the results from this study suggested that the apex factor of some measures appeared to reflect emotional resilience and social surgency (Table 3, factor 1) whereas the apex factor of others involved agreeableness vs. antagonism (factor 2). It would be interesting for future research to investigate the relative saturation of various measures from personality variance associated with the Big 2 alpha/stability/communion and beta/plasticity/agency conceptualizations.

We experienced a similar failure to find strong evidence for the GFP when we examined the matrices of inter-factor correlations that emerge from a joint analysis of the scales from multiple inventories. This approach was based on the strategy used by Markon and colleagues (2005) to evaluate the hierarchical nature of pathological personality traits. However, here we used oblique rotations so that we could uncover correlated dimensions of personality rather than assuming that factors were uncorrelated as would be the case with orthogonal rotations. Using this approach, we replicated previous evidence for the robustness of Big Five domains but we noted that these five dimensions were reasonably uncorrelated. This finding undermines the case for the GFP, as second-order factors can only be obtained from correlated first-order factors.

Last, we tested a series of CFA models, based on the common use of this method in previous GFP studies. We constructed a series of models that varied from estimating a single-factor solution for each measure, a two-factor solution for each measure, and a shared 6-factor solution. However, we encountered several estimation challenges and a number of modeling approaches based on prior GFP research yielded inadmissible solutions. Despite our attempts to address Heywood cases and negative factor variances, the various CFA models yielded a complicated pattern of results that failed to support the GFP hypothesis.

In summary, our general strategy was to use a variety of factor analytic approaches in the hope of finding a robust GFP “signal” that was strong enough to exceed the noise of different ways of modeling personality data. This strategy was guided by the view that if the GFP is as robust as Rushton and Irwing (2011) suggest, it should emerge across a variety of analytic techniques and instruments. The fact that we failed to find convincing evidence for the GFP that converged across instruments casts doubt on its importance as a substantive personality construct.

We acknowledge that there are many potential strategies for testing the degree to which a single trait can explain the covariation among all other traits, and recognize the possibility that different GFP estimation methods could lead to different conclusions about the consistency of the GFP across measures. Indeed many approaches have been employed to identify the GFP in previous research (Ferguson et al., 2011). Because standards for factor analytic practice are fuzzy (e.g., Hopwood & Donnellan, 2010; Marsh, Hau, & Wen, 2004) there exists a good deal of subjectivity in the interpretation of these kinds of results. In this context proponents of the GFP with considerable factor analytic expertise might find a way to indentify a very specific model or small number of models that would appear to support the GFP proposal. However, we suspect that such models would likely fail to generalize to new samples and may even contradict less controversial features of the personality trait hierarchy (e.g., which traits from the Big Five level load onto the Big Two).

We would also note that the failure of a GFP to explain the covariance among all personality factors in a manner that is consistent across several measures does not necessarily contradict the idea of a broad higher-order factor related to some aspects of personality functioning. For example, some clinical theories posit such a trait (e.g., Menninger, Waymer, & Pruyser, 1963; Kernberg, 1984), and recent research has found that the simple sum of all of the DSM-IV personality disorder symptoms reflects a strong predictor of clinical dysfunction (Hopwood et al., in press; Jahng et al., in press). One could select certain items or scales among the measures examined here that are consistently related to psychological health, scale them on the same metric and in the same direction for each inventory, and derive meaningful “personality severity” scores. These scores may furthermore relate systematically to one another across measures. Such an index could serve the applied purpose of predicting broad dysfunction without necessarily having theoretical coherence or construct validity in the traditional sense. Alternatively, such theories may have identified a factor similar to Alpha/Stability/Communion, which appears to be more strongly related to psychopathology than Beta/Plasticity/Agency. In either case this broad trait from the clinical literature would not be expected to explain the covariation of all normative and pathological personality dimensions, as has been proposed for the GFP.

The present results are situated within an emerging body of substantive and methodological critiques of the GFP (see e.g., Ashton et al., 2009; Ferguson et al., 2011). For instance, Rushton and Irwing’s (2011) analogy between the GFP for personality and ‘g’ in cognitive abilities appears to break down in several respects. Foremost, unlike ‘g’, for which higher scores are unambiguously better, the relation between personality traits and adaptation may be non-linear or moderated to a greater extent by environmental factors. For example, some personality theorists assert that extreme scores on otherwise beneficial personality traits are maladaptive, such as when high agreeableness connotes pathologically dependent behavior (Lowe, Edmundson, & Widiger, 2009). To the extent that extreme traits are generally maladaptive, the suggestion that the GFP evolved via directional selection (such that over time population means shifted in a certain direction because individuals at one end of a trait are more likely to survive) may be called into question (Ferguson et al., 2011).

Evolutionary personality theorists have also argued that unlike cognitive abilities, traits tend to be differentially selective in different environments – which would subject traits to different evolutionary mechanisms than ‘g’ (Denissen & Penke, 2009). For instance, personality researchers drawing on evolutionary theory have argued that even relatively high levels of certain dimensions of personality that seem so problematic in contemporary society (such as neuroticism; see Lahey, 2009) can confer benefits for survival and reproduction in some specific environments (see e.g., Nettle, 2006). Likewise, whereas ‘g’ is a robust correlate of attributes linked to fitness (e.g., longevity, mate preferences, reproductive success, and adaptation to environmental disruption), different personality traits seem to have more specific connections to behaviors linked with fitness (Ferguson et al., 2011). For example, Conscientiousness predicts longevity (Roberts et al., 2007), Neuroticism predicts adaption to stress (Lahey, 2009), and Extraversion predicts exploratory tendencies (see e.g., Nettle, 2011). Finally, whereas in cognitive abilities the higher levels of the hierarchy are more heritable than the lower levels (Friedman et al., 2008), this is not the case in personality, where the heritability of the GFP (Rushton, Bons, & Hur, 2008) is in the range of heritability estimates for lower order traits.

Beyond these substantive concerns, methodological critiques have also been leveled at the substantive interpretation of the GFP, as discussed in the Introduction. These include that the GFP is an artifact of the preponderance of scales that reflect blends of core traits (e.g., Ashton et al., 2009) and that response tendencies such as socially desirable responding and halo effects contribute to general factors that explain covariation among personality scales (e.g., Anusic et al., 2009; Bäckström et al., 2009). It has also been suggested that the overall statistical importance of a GFP is of a much lower magnitude than that of ‘g’ in the cognitive domain (Revelle & Wilt, 2010), implying that less attention should accordingly be paid to the substantive interpretation of GFP than is given to the interpretation of ‘g’.

In conclusion, this study was designed to contribute to ongoing debates in the personality literature about the existence and meaning of the GFP. We noted that previous studies supporting the GFP are generally based on analyses of single, omnibus personality inventories. However, the GFP proposal would appear to predict that a higher-order factor from different broad-band personality inventories should correlate strongly across measures. Our objective was to determine how strongly GFPs from different inventories converged with each other using a variety of analytic techniques. We reasoned that strong convergence of apex dimensions across inventories would provide important evidence for the substantive case for the GFP⁶. Overall, the failure to find convergence across these measures in this study casts significant doubt on the importance of the GFP.

A General Factor of Personality (GFP) has been proposed as the apex of the personality trait hierarchy.

We evaluated the cross-measure consistency of the GFP.

We used various factor analyses of multiple personality inventories in a large sample.

Results fail to support a common GFP that is positioned at the top of a personality trait hierarchy.