Calibrating parametric subject-specific risk estimation

Summary

For modern evidence-based medicine, decisions on disease prevention or management strategies are often guided by a risk index system. For each individual, the system uses his/her baseline information to estimate the risk of experiencing a future disease-related clinical event. Such a risk scoring scheme is usually derived from an overly simplified parametric model. To validate a model-based procedure, one may perform a standard global evaluation via, for instance, a receiver operating characteristic analysis. In this article, we propose a method to calibrate the risk index system at a subject level. Specifically, we developed point and interval estimation procedures for t-year mortality rates conditional on the estimated parametric risk score. The proposals are illustrated with a dataset from a large clinical trial with post-myocardial infarction patients.

1. Introduction

The choice of disease prevention or management strategy for an individual from a population of interest is often made based on his/her risk of experiencing a certain clinical event during a specific follow-up time period. Subjects classified as high risk may be recommended for intensive prevention or therapy. The risk is usually estimated via a parametric or semiparametric regression model using baseline risk factors. For example, Eagle et al. (2004) created a simple bedside risk index system to predict six-month post-discharge mortality for patients hospitalized due to acute coronary syndrome. A proportional hazards model (Cox, 1972) was utilized to fit the data on post-discharge follow-up mortality and all potential predictors taken at admission as well as during hospitalization. The six-month post-discharge mortality rate is then estimated with the fitted model for each future individual patient.

An empirical model is merely an approximation to a true model, and it is crucial to assess its performance for appropriate clinical decision making. In addition to checking the fitted model with routine goodness-of-fit techniques, the model-based scoring system is often evaluated or validated globally based on specific summary measures, such as the receiver operating characteristic curve (Pepe et al., 2004; Wang et al., 2006; Ware, 2006; Cook, 2007), expected Brier score (Gerds & Schumacher, 2006) or the net reclassification index (Pencina et al., 2008). For example, Uno et al. (2007) developed procedures for evaluating the accuracy of empirical parametric models in predicting t-year survival with respect to various global accuracy measures. For the aforementioned post-discharge mortality example, the investigators used an independent cohort to validate their system with an overall c-statistic. However, even if the risk index system is acceptable using a global average measure, for the group of patients with the same model-based risk score, the corresponding parametric risk estimator may not approximate its true mortality rate well. Consequently, clinicians may be misguided in choosing therapies for treating these individuals.

In this paper, we propose a procedure for calibrating the parametric risk estimates. Specifically, under a general survival analysis setting, a consistent estimation procedure is proposed for t-year mortality rates of patients grouped by a parametric risk score. Furthermore, we provide pointwise and simultaneous confidence intervals for such risks over a range of estimated risk scores. These interval estimates quantify the precision of our consistent point estimator. Moreover, the upper or lower bounds of the intervals provide valuable information for complex cost-benefit decision making. Pointwise confidence interval estimates of the true average risk may be of interest to individual patients with a specific risk score. Simultaneous interval estimates can be used to identify subgroups with differential risks and to assist in selecting target populations for appropriate interventions. Our proposal is also useful for calibrating a risk index system when applied to populations different from the study population. For example, the Framingham Risk Score (Anderson et al., 1991) for predicting the risk of coronary heart disease was developed based on a U.S. population. Its applicability to other populations has been extensively investigated in recent years (D’Agostino et al., 2001; Brindle et al., 2003; Zhang et al., 2005). For a new population, our procedure can be used to assess the true risk of coronary heart disease for subjects with any given Framingham Risk Score.

2. A Consistent estimator for the mean risk of subjects with the same model-based risk score

Consider a subject randomly drawn from the study population. Let T̃ be the time to the occurrence of a specific event since baseline and U be the corresponding set of risk factors/markers ascertained at baseline; some marker values may be collected repeatedly over time. In this paper, we assume that markers are measured at a well-defined time zero. Discussions on the setting where time zero is not well defined are given in §5. Now, assume that T̃ has a continuous distribution given U. Also, let 𝒫(u) = pr(T̃ < t₀ | U = u). The event time T̃ may be censored by a random variable C, which is assumed to be independent of T̃ and U. For T̃, one can only observe T = min(T̃, C) and δ = I (T̃ ⩽ C), where I(·) is the indicator function. Our data {(T_i, δ_i, U_i), i = 1, . . ., n} consist of n independent copies of (T, δ, U).

One may estimate 𝒫(u) fully nonparametrically. Li & Doss (1995) and Nielsen (1998) considered local linear estimators of the conditional hazard function by smoothing over the q-dimensional U. However, such nonparametric estimates may not behave well when q > 1 and n is not large. A standard, feasible way to reduce the dimension of u is to approximate 𝒫(u) with a working parametric or semiparametric model such as the proportional hazards model:

$$𝒫(u)=g\{\text{log}\mathrm{\Lambda }\left(t_0\right)+{\beta }^{\text{T}}x\},$$ (1)

where g(s) = 1 − exp(−e^s), Λ(·) is the working baseline cumulative hazard function for T̃; x, a p × 1 vector, is a function of u; and β is an unknown vector of regression parameters.

To obtain an estimate for 𝒫(u) via (1), one may employ the maximum partial likelihood estimator β̂ for β with all mortality information from the data collected up to time t₀. That is, β̂ is the maximizer of the log partial likelihood function,

$$\sum _{i=1}^n{\int }_0^{t_0}\left[{\beta }^{\text{T}}{X}_i-\text{log}\left\{\sum _{j=1}^n{Y}_j(t)\text{exp}({\beta }^{\text{T}}{X}_j)\right\}\right]d{N}_i(t),$$

where N_i (t) = I (T_i ⩽ t)δ_i and Y_i (t) = I (T_i ⩾ t), for i = 1, . . ., n. When the model (1) is correctly specified, β̂ consistently estimates the true value of β. On the other hand, if there is no vector ζ such that pr(T₁ > T₂ | ζ^TX₁ > ζ^TX₂, T₂ ⩽ t₀) = 1, then β̂ converges to a finite constant β₀, as n → ∞, even when the model (1) is misspecified (Hjort, 1992). Alternatively, one may use an estimate of β by fitting a global Cox model without truncating at t₀, denoted by β̃. When the Cox model fits the data well, β̃ may be more efficient than β̂.

Next, we estimate Λ(t) in (1) with Breslow’s estimator (Kalbfleisch & Prentice, 2002),

$$\widehat{\mathrm{\Lambda }}(t)=\sum _{i=1}^n{\int }_0^t\frac{d{N}_i(s)}{{\sum }_{j=1}^n{Y}_j(s)\text{exp}({\widehat{\beta }}^{\text{T}}{X}_j)},$$

which is a step function that only jumps at observed failure times. It follows that a model-based estimate of 𝒫(u) is 𝒫̂(u) = g(γ̂^Tx₊), where γ̂ = [log{Λ̂(t₀)}, β̂^T]^T and x₊ = (1, x^T)^T. Following from the convergence of β̂ and arguments given in Hjort (1992), 𝒫̂(u) converges to a deterministic function 𝒫̄(u) in probability, as n → ∞. When (1) is correctly specified, 𝒫̄(u) = 𝒫(u).

Although most likely (1) is not the true model, the parametric risk scores {𝒫̂(u)} or {γ̂^Tx₊} can be used as a risk index system for future populations similar to the study population. Consider a future subject with (T̃, U, X) = (T̃⁰, U⁰, X⁰) and $\widehat{𝒫}(U^0)=g({\widehat{\gamma }}^{\text{T}}{X}_{+}^0)=v$. When (1) is misspecified, the risk of T̃⁰ < t₀ may be quite different from v. To calibrate the subject-level model-based risk estimate, one needs a consistent estimate for

$$\tau (v;t_0)=\text{pr}\{{\tilde{T}}^0<t_0|\widehat{𝒫}(U^0)=v\},$$

the mortality rate among subjects with risk score 𝒫̂(U⁰) = v. Here, the probability is with respect to T̃⁰, U⁰ and {(T_i, δ_i, U_i), i = 1, . . ., n}.

To estimate τ (v; t₀), let Λ_v (t) = − log{1 − τ (v; t)} be the corresponding cumulative hazard function and we propose a nonparametric kernel Nelson–Aalen estimator for Λ_v (t) based on {T_i, δ_i, 𝒫̂(U_i)}, for i = 1, . . ., n. As for the standard one-sample estimation of the cumulative hazard function, we focus on the class of potential estimators which are step functions over t and only jump at the observed failure times with jump sizes ΔΛ_v (t). First, we consider a local constant estimator by assuming that for v′ in a small neighbourhood of v, ΔΛ_v′(t) ≈ ΔΛ_v (t). Specifically, for any given t and v, we obtain ΔΛ̃_v(t) as the following minimizer:

$$\underset{a}{\text{arg} \text{min}}\sum _{i=1}^n{K}_h({\widehat{D}}_{vi}){\{\mathrm{\Delta }{N}_i(t)-Y_i(t)a\}}^2=\frac{{\sum }_{i=1}^n{K}_h({\widehat{D}}_{vi})\mathrm{\Delta }{N}_i(t)}{{\sum }_{i=1}^n{K}_h({\widehat{D}}_{vi})Y_i(t)},$$ (2)

where $\mathrm{\Delta }{N}_i(t)=N_i(t)-N_i(t-)={\text{lim}}_{w\to 0}{\int }_{t-w}^{t}d{N}_i(s)$; D̂_vi = ψ{𝒫̂(U_i)} − ψ(v); K (·) is a smooth symmetric density function; K_h(x) = K (x h)/h, h = O(n^−v) is a bandwidth with 1/2 > v > 0; and ψ(·) : (0, 1) → (−∞, ∞) is a known increasing smooth function (Wand et al., 1991; Park et al., 1997). Based on (2), we obtain a local constant estimator for Λ_v (t₀) as

$${\tilde{\mathrm{\Lambda }}}_v(t_0)={\int }_0^{t_0}\frac{{\sum }_{i=1}^n{K}_h({\widehat{D}}_{vi})d{N}_i(t)}{{\sum }_{i=1}^n{K}_h({\widehat{D}}_{vi})Y_i(t)}.$$

Here, we adopt the notation ∫ΔN_i (t)W(t)dt ≡ ∫ W(t)d N_i (t) as in Nielsen & Tanggaard (2001). When 𝒫̂(·) is deterministic, the limiting distribution of such a nonparametric estimator with a fixed v has been derived by Nielsen & Linton (1995) and Du & Akritas (2002). Here, we investigate the asymptotic properties of Λ̃_v (t₀) over a set of v at a given time t₀ in the presence of the additional variability in 𝒫̂(·).

The above estimator can potentially be improved by considering a local linear approximation to Λ_v (t) (Fan & Gijbels, 1996; Li & Doss, 1995). That is, for v′ in a small neighbourhood of v, we assume ΔΛ_v′(t) ≈ ΔΛ_v (t) + b_v (t){ψ(v′) − ψ(v)}. Thus, for any given t and v, we replace a in (2) by a local linear function a + bD̂_vi with unknown intercept and slope parameters a and b. The resulting estimator ΔΛ̂_v(t) is the intercept of the vector that minimizes

$$\sum _{i=1}^n{K}_h({\widehat{D}}_{vi}){\{\mathrm{\Delta }{N}_i(t)-Y_i(t)(a+b{\widehat{D}}_{vi})\}}^2$$

with respect to (a, b). The corresponding estimator Λ̂_v(t) for Λ_v(t) is the sum of ΔΛ̂_v(·) over all distinct observed death times by t. The resulting estimator for τ (v; t₀) is τ̂(v; t₀) = 1 −exp{−Λ̂_v(t₀)}. In Appendix A, we show that under mild regularity conditions, if h = O(n^−ν) with 1/5 < ν < 1/2, τ̂(v; t₀) is consistent for τ (v; t₀), uniformly in v ∈ 𝒥 = [ψ⁻¹(ρ_l + h), ψ⁻¹(ρ_r − h)], where (ρ_l, ρ_r) is a subset contained in the support of ψ{𝒫̄(U)}.

3. Pointwise and simultaneous interval estimation procedures for τ (v; t₀) over risk score V

For any fixed v ∈ 𝒥, we show in Appendix A that the distribution of

$${\left(nh\right)}^{1/2}\{{\widehat{\mathrm{\Lambda }}}_v(t_0)-{\mathrm{\Lambda }}_v(t_0)\}$$ (3)

can be approximated well by the conditional distribution of a zero-mean normal distribution

$$n^{-1/2}{h}^{1/2}\sum _{i=1}^n{K}_h({\widehat{D}}_{vi}){\widehat{𝒱}}_i(v;t_0){\xi }_i+{\left(nh\right)}^{1/2}\{{\widehat{\mathrm{\Lambda }}}_v(t_0,{\widehat{\gamma }}^{*})-{\widehat{\mathrm{\Lambda }}}_v(t_0)\},$$ (4)

given the data for large n and h = O(n^−ν) with 1/5 < ν < 1/2, where Ξ = (ξ₁, . . ., ξ_n) are standard normal random variables independent of the data, ${\widehat{𝒱}}_i(v;t_0)={\int }_0^{t_0}\{d{N}_i(s)-Y_i(s)d{\widehat{\mathrm{\Lambda }}}_v(s)\}/\{n^{-1}{\sum }_{j=1}^n{K}_h({\widehat{D}}_{vj})Y_j(s)\}$, Λ̂_v (t₀, γ) is given in (A3) and γ̂^* is given in (A5). A perturbed version of the observed Λ̂_v(t₀) is Λ̂_v(t₀, γ̂^*) with the same perturbation variables Ξ, which accounts for the extra variability of γ̂. Although asymptotically one only needs the first term of (4) since γ̂ = O(n^−1/2), the inclusion of the second term is likely to improve the approximation to the distribution of (3) in finite sample. This perturbation method is similar to the so-called wild bootstrap (Wu, 1986; Härdle, 1990; Mammen, 1992) and has been used successfully for a number of interesting problems in survival analysis (Jin et al., 2001; Park & Wei, 2003; Cai et al., 2005). The distribution of (4) can be easily approximated by generating a large number M of realizations of Ξ.

With the above approximation, for any v ∈ 𝒥, one may obtain a variance estimator of (3), ${\widehat{\sigma }}_v^2(t_0)$, based on the empirical variance of M realizations from (4). For any given α ∈ (0, 1), a 100(1 − α)% confidence interval for Λ_v(t₀) can be obtained as Λ̂_v(t₀) ± (nh)^−1/2cσ̂_v(t₀), where c is the 100(1 − α/2)th percentile of the standard normal. The corresponding pointwise 100(1 − α)% confidence interval for τ(v; t₀), the mortality rate with score v, is

$$1-\text{exp}\{-{\widehat{\mathrm{\Lambda }}}_v\left(t_0\right)\pm {\left(nh\right)}^{-1/2}c{\widehat{\sigma }}_v\left(t_0\right)\}.$$

To make inference about the mortality rate over a range of v, one may construct simultaneous confidence intervals for {τ(v; t₀), v ∈ 𝒥} by considering a suptype statistic

$$W={\text{sup}}_{v\in 𝒥}\left|{\left(nh\right)}^{1/2}\frac{{\widehat{\mathrm{\Lambda }}}_v(t_0)-{\mathrm{\Lambda }}_v(t_0)}{{\widehat{\sigma }}_v(t_0)}\right|.$$ (5)

However, the distribution of (nh)^1/2{Λ̂_v(t₀) − Λ_v(t₀)} does not converge as a process in v, as n → ∞. Therefore, we cannot use the standard large sample theory for stochastic processes to approximate the distribution of W. On the other hand, by the strong approximation arguments and extreme value limit theorem (Bickel & Rosenblatt, 1973), we show in Appendix B that a standardized version of W converges in distribution to a proper random variable. In practice, for large n, one can approximate the distribution of W by W^*, the supremum of the absolute value of (4) divided by σ̂_v (t₀), with (4) perturbed by the same set of Ξ for all v ∈ 𝒥. It follows that the 100(1 − α)% simultaneous confidence interval for τ (v; t₀) is

$$1-\text{exp}\{-{\widehat{\mathrm{\Lambda }}}_v(t_0)\pm {\left(nh\right)}^{-1/2}d{\widehat{\sigma }}_v(t_0)\},$$

where the cut-off point d is chosen such that pr(W^* < d) ⩾ 1 − α.

As for any nonparametric functional estimation problem, the choice of h for τ̂(v; t₀) is crucial for making inferences about τ (v; t₀). To incorporate censoring, we propose obtaining an optimal h by minimizing mean integrated squared martingale residuals over time interval (0, t₀) through K -fold crossvalidation. Such a procedure has been successfully used for bandwidth selection in Tian et al. (2005). Specifically, we randomly split the data into K disjoint subsets of about equal sizes denoted by {ℐ_k, k = 1, . . ., K}. For each k, we use all observations not in ℐ_k to obtain Λ_v (t) with a given h. Let the resulting estimators be denoted by Λ̂_v(k)(t). We then use the observations from 𝒥_k to calculate the sum of integrated squared martingale residuals

$${\int }_0^{t_0}\sum _{j\in {ℐ}_k}{\left\{N_j(t)-{\int }_0^t{Y}_j(s)d{\widehat{\mathrm{\Lambda }}}_{\widehat{𝒫}(u_j)(k)}(s)\right\}}^{2}d\left\{\sum _{j^i\in {ℐ}_k}{N}_{j^i}(t)\right\}.$$ (6)

Lastly, we sum (6) over k = 1, . . ., K, and then choose h_opt as the minimizer of the sum of K martingale residuals. Since the order of h_opt is expected to be n^−1/5 (Fan & Gijbels, 1995), the bandwidth we use for estimation is h = h_opt × n^−d₀ with 0 < d₀ < 3/10 such that h = n^−ν with 1/5 < ν < 1/2. This ensures that the resulting functional estimator Λ̂_v (t₀) with the data-dependent smooth parameter has the above desirable large sample properties.

4. Numerical studies

4.1. Example

We illustrate the new proposal with a dataset from the Valsartan in Acute Myocardial Infarction study (Pfeffer et al., 2003). This large clinical study, often referred to as the VALIANT study, was conducted to evaluate the effect of angiotensin II receptor blocker and angiotensin converting enzyme inhibitors on overall mortality among patients with myocardial infarction complicated by left ventricular systolic dysfunction and/or heart failure. The trial was designed to compare three treatments, angiotensin II receptor blocker valsartan, angiotensin converting enzyme inhibitor captopril and a combination of these two drugs, for treating high-risk patients after myocardial infarction with respect to mortality and morbidity. The study was conducted from 1999 to 2003 with a total of 14 703 patients assigned randomly and equally to the three groups. The median follow-up time was 24.7 months. There are no significant differences among the three groups with respect to the overall mortality and thus we combine all three groups to develop a risk scoring system for mortality.

For simplicity, we used 11 baseline covariates from each study subject considered by Solomon et al. (2005) in our analysis. These 11 predictors are potentially the most significant ones among the risk factors identified by Anavekar et al. (2004) for the overall mortality based on this study. We fitted the survival data with an additive Cox model using these 11 covariates to obtain a parametric risk score for each individual. Specifically, the vector U = X consists of age, X₁; Killip class, X₂; estimated glomerular filtration rate, X₃; history of myocardial infarction, X₄; history of congestive heart failure, X₅; percutaneous coronary intervention after index myocardial infarction, X₆; atrial fibrillation after index myocardial infarction, X₇; history of diabetes, X₈; history of chronic obstructive pulmonary disease, X₉; new left bundle-branch block, X₁₀; and history of angina, X₁₁. Our analysis includes n = 14 088 patients who had complete information on these 11 covariates.

First, suppose that we are interested in predicting the six-month mortality rates of future patients. To this end, we let t₀ = 6 months and fitted the survival observations truncated slightly after six months with a Cox model (1) and x = u. The estimated regression coefficient vector β̂ is given in Table 1. These estimates, coupled with the estimated intercept γ̂ = −6.02, create a risk score 𝒫̂(u) for six-month mortality of future patients. To obtain τ̂(v, 6) for a given 𝒫̂(u) = v, we let K (·) be the Epanechnikov kernel, and ψ(v) = log{− log(1 − v)}, which leads to ψ{𝒫̂(U)} = γ̂^TX₊. The smoothing parameter h = 0.18 was obtained by multiplying h_opt by a factor of n^−0.07 as defined in §3, with ten-fold crossvalidation. We chose the second and 98th percentiles of the empirical distribution of {γ̂^TX_+i}_i=1,...,n as the boundary points ρ_l and ρ_r for interval 𝒥. To approximate the distribution of (3) and W in (5), we used the perturbation-resampling method (4) with M = 500 independent realized standard normal samples Ξ.

Table 1.

Estimates of the regression coefficients, the corresponding standard errors and p-values, multiplied by 100, derived from fitting the Cox model to the VALIANT dataset based on survival time information up to t₀ and based on the entire dataset

		X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	X11
t0 = 6	Est	2.8	28.9	−1.2	20.6	24.2	−43.3	25.2	24.1	16.1	22.0	16.4
	SE	0.3	3.2	0.2	6.6	7.2	10.7	7.2	6.1	8.8	10.8	6.2
	p	0.0	0.0	0.0	0.2	0.1	0.0	0.1	0.0	7.0	4.2	0.8
t0 = 24	Est	3.0	23.7	−1.0	29.5	32.7	−46.3	29.6	26.8	24.3	23.1	23.5
	SE	0.2	2.3	0.1	4.7	5.1	7.7	5.2	4.4	6.2	8.0	4.5
	p	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.4	0.0
Global	Est	2.7	27.3	−1.1	24.1	28.3	−50.6	26.3	26.4	19.6	22.7	18.2
	SE	0.3	3.0	0.2	5.6	6.8	9.3	6.2	5.2	7.6	9.5	5.8
	p	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	1.0	1.7	0.2

Est, estimates; SE, standard error; p, p-value; Global, entire dataset.

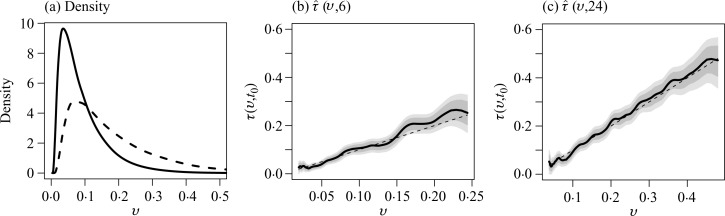
The smoothed density estimate for 𝒫̂(U), shown in Fig. 1(a), provides useful information regarding the relative size of the subgroup of individuals with 𝒫̂(U) = v, where v ∈ 𝒥 = [0.02, 0.24]. In Fig. 1(b), we present the point and interval estimates for τ (v, 6). The estimated risk scores for most patients are less than 0.15. For groups of subjects with low risk scores, their interval estimates tend to be tight. For example, among subjects with 𝒫̂(u) = 0.045, the six-month mortality rate is likely to be between 0.03 and 0.05, based on the 95% point-wise confidence interval. The corresponding simultaneous confidence interval is [0.02, 0.06]. For this subgroup, the Cox model appears to be slightly overestimating the risk with a p-value of 0.08 when testing the difference τ (v, 6) − v = 0. For patients whose risk scores are greater than 0.15, the interval estimates are relatively wide, as expected. For example, the mortality rate among patients with 𝒫̂(u) = 0.17 is estimated as 0.21 with a 95% pointwise confidence interval of [0.18, 0.23] and a simultaneous interval of [0.17, 0.25]. The Cox model underestimates the risk of this subgroup substantially with a pointwise p-value of 0.001 and a familywise adjusted p-value of 0.04 after controlling for the overall Type I error. For comparison, we also obtained the regression coefficient estimates based on the global Cox model without truncation. As shown in Table 1, the estimates are slightly different from the ones obtained based on survival information up to six months only. Under the global model, when the Cox model predicted risk is 0.045, the calibrated risk estimate is 0.034 with 95% pointwise and simultaneous confidence intervals being [0.03,0.04] and [0.02,0.05]. Overall, we find that the global model and the truncated version lead to very similar interval estimates for the present case.

Fig. 1.

Prediction of six-month and 24-month mortality risks based on the 11 risk factors. Panel (a) shows the estimated density function of the model-based risk estimate for t₀ = 6 (solid line) and 24 (dashed line) months. Shown also are the point (thick solid curve) estimate of the true risk function τ (v, t₀) along with their point-wise (dark shaded region) and simultaneous (light shaded region) confidence intervals for (b) t₀ = 6 months; and (c) t₀ = 24 months. The dashed line is the 45° reference line.

Next, suppose that we are interested in predicting long-term survival for future patients similar to the VALIANT study population. Here, we let t₀ = 24 months and fitted the survival observations slightly truncated at 24 months with a Cox model and x = u. The resulting regression coefficient estimates are also given in Table 1. For this case, the bandwidth h = 0.15 and the range of the estimated risk score v is from 0.04 to 0.48. The smoothed density function estimation of the parametric score is also given in Fig. 1(a). Relatively few patients have scores beyond 0.3. Our point and interval estimates for the true mortality rate are given in Fig. 1(c). For example, for subjects with a risk score of 0.1, their 24-month mortality rate is estimated as 0.09 with 95% pointwise and simultaneous confidence intervals being [0.08, 0.11] and [0.07, 0.12], respectively. For patients whose risk scores are high, as expected, their interval estimates can be quite wide. For example, for subjects with a risk score of 0.3, the true mortality rate is likely to be between 0.26 and 0.37 based on the 95% simultaneous confidence interval. Under the global model, the calibrated risk estimates at risk scores of 0.1 and 0.3 are similar to the above results based on the truncated fitting.

4.2. Simulation studies

We conducted simulation studies to examine the validity of the proposed inference procedures; and compared the performance of the calibrated prediction procedures with that of the prediction based on the Cox model. We first simulated data from a normal mixture model under which the Cox model is misspecified. In particular, we generated all discrete covariates, X_D = (X₂, X₄, X₅, X₆, X₇, X₈, X₉, X₁₀, X₁₁)^T, based on their empirical distribution from the observed data. Then, for each given value of X_D, we generated the corresponding value of X_C = (X₁, X₃), from N (μ_XD, Σ), where μ_XD is the empirical mean of X_C given X_D and Σ is the empirical covariance matrix of X_C in the VALIANT dataset. Then, we generated T from

$$\text{log}\tilde{T}={\alpha }_{X_4{X}_8}+{\beta }_{X_4{X}_8}^{\text{T}}{X}_{-\left(48\right)}+{\sigma }_{X_4{X}_8}\epsilon ,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\epsilon ~N\left(0,1\right),$$

where for (X₄, X₈) = (0, 0), (0, 1), (1, 0) and (1, 1), we let α_X4X8 = 11.5, 8.5, 5.5, 8.5 and σ_X4X8 = 0.9, 1.5, 1.3, 1.0; X₋₍₄₈₎ denotes the covariate vector with (X₄, X₈) excluded and β_X4X8 is obtained from fitting a lognormal model to the subset of VALIANT data with a given value of (X₄, X₈). The censoring was generated from a Weibull (5, 30) that was obtained by fitting the Weibull model to the VALIANT data. This results in about 77% censoring and overall event rates of 17% by month 10 and 22% by month 24. We considered a moderate sample size of 5000 and a relatively larger sample size of 10 000. For all the simulation studies, we obtain β̂ based on the truncated partial likelihood function at t₀. For ease of computation, the band-width for constructing the nonparametric estimate was fixed at h = 0.37, 0.38, 0.29 and 0.27 for (i) n = 5000, t₀ = 10; (ii) n = 5000, t₀ = 24; (iii) n = 10 000, t₀ = 10; and (iv) n = 5000, t₀ = 24, respectively. Here, h was chosen as the average of the bandwidths selected based on (6) with d₀ = 0.1 from 10 simulated datasets.

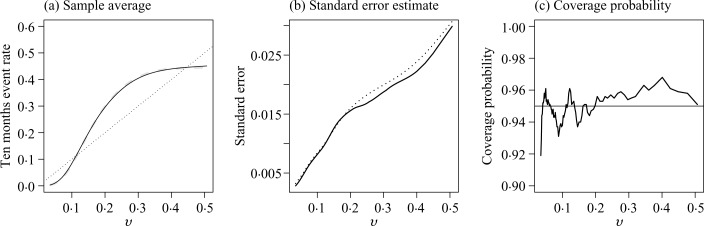
Across all four settings, the nonparametric estimator has negligible bias, the estimated standard errors are close to their empirical counterparts, and the empirical coverage levels of the 95% confidence intervals are close to the nominal level. The coverage levels of the simultaneous confidence band were 93.7%, 94.5%, 93.1% and 94.1%, for settings (i), (ii), (iii) and (iv), respectively. In Fig. 2, we summarize the performance of the point and interval estimates of the proposed nonparametric procedure for n = 5000 and t₀ = 10. Under the correct model specification, we would expect that the true risk against the predicted risk from the Cox model is a 45° diagonal line. For the present case, the predicted risk based on the Cox model is severely biased. For example, the event rate at t₀ = 10 is 0.31 among the subjects whose predicted risk is 0.20 based on the Cox model. It is interesting that the standard test has very low power in detecting the lack of fit for the misspecified model. For example, the test based on the Schoenfeld residuals has about 15% power when n = 5000 and 25% power when n = 10 000.

Fig. 2.

Performance of the new procedure under a misspecified model with sample size 5000 for t₀ = 10: (a) the sample average of τ̂(v, t₀) (solid) compared with truth (dashed); (b) the empirical standard error estimate (solid) and the average of the estimated standard errors (dotted); and (c) the empirical coverage of the 95% confidence intervals based on the proposed resampling procedures. The 45° reference line in (a) corresponds to the Cox-model-based risk estimates.

We also conducted simulation studies to evaluate the performance of the proposed procedure under the correct model specification. To this end, we generated the covariates and the censoring time from the same distribution as described above, but generated T̃ from an exponential model with coefficients obtained by fitting the model to the VALIANT data. The proposed estimators also perform well with little bias for the point estimation and proper coverage level for intervals estimators. For example, when n = 5000 and t₀ = 10, the empirical coverage level ranges from 0.94 to 0.98 for the pointwise confidence intervals and is about 0.96 for the simultaneous confidence interval. Similar patterns were observed for t₀ = 24.

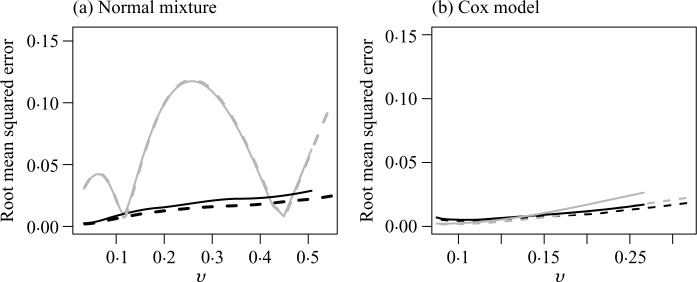
Lastly, we examined the performance of the nonparametric calibrated risk estimates with respect to their true predicted risks conditional on the observed data under correctly, and also incorrectly, specified models. Specifically, for each simulated dataset, we obtained γ̂_obs based on the above Cox models to calculate $\widehat{𝒫}(U^0)=g({\widehat{\gamma }}_{\text{obs}}^{\text{T}}{X}_{+}^0)$ for any given covariate U⁰, and then assign future subjects to a risk group Ω_v = {U⁰ : 𝒫̂(U⁰) = v}. A standard Cox model would estimate the event rate for the subgroup Ω_v as v. On the other hand, the nonparametric procedure would produce a calibrated estimate τ̂(v; t₀) for the event rate among Ω_v, while the true event rate conditional on the observed data is $\tau (v;t_0,{\widehat{\gamma }}_{\text{obs}})=\text{pr}\{T^0⩽t_0|g({\widehat{\gamma }}_{\text{obs}}^{\text{T}}{X}_{+}^0)=v,{\widehat{\gamma }}_{\text{obs}}\}$. In the previous simulation studies, τ (v; t₀) = E{τ (v; t₀, γ̂_obs)} with expectation taken over the observed data. For each dataset, we summarized the performance of the proposed and the parametric risk prediction procedures based on their squared distance from the true event rate. The root mean squared errors of the Cox and calibrated estimates for t₀ = 10, denoted rmse_Cox and rmse_Calib, respectively, are shown in Fig. 3. Under the above misspecified normal mixture model, the parametric procedure is severely biased. For instance, when n = 5000, rmse_Cox can be as high as 0.12 while rmse_Calib is below 0.03. Under model misspecification, over 90% of the root mean squared error is due to bias for most of the risk estimates. On the other hand, under the correct specification of the Cox model, the risk estimators from the nonparametric procedure are only slightly inefficient compared to the Cox procedure. For example, at t₀ = 10 with a sample size of 5000, (rmse_Cox, rmse_Calib) is (0.003, 0.006) when v = 0.05, is (0.005, 0.008) when v = 0.10 and is (0.017, 0.021) when v = 0.20.

Fig. 3.

The root mean squared error of the risk estimates for t₀ = 10 based on the Cox model and the nonparametric calibrated procedure when the data were generated from (a) a normal mixture; and (b) a Cox model, with n = 5000 (solid) and n = 10 000 (dashed) on both panels.

5. Remarks

Due to the complexity of the disease process and heterogeneity among study subjects, it is unlikely, if not impossible, that a fitted parametric or semiparametric model is the true one. On the other hand, a reasonable approximation to the true model can be quite useful in practice. Generally, the standard goodness-of-fit tests only provide qualitative assessment of the model fitting and may have little power when n is not large. An alternative way to evaluate the overall adequacy of the fitted model is to use a reasonable, physically interpretable distance function between the observed and predicted responses averaged over the entire study population (Cook, 2007; Uno et al., 2007). In this paper, we make an extra effort to calibrate the estimation of the mean risk for subgroups indexed by a parametric score. Through extensive numerical studies, we find that our two-stage procedure significantly outperforms purely model-based counterparts.

While one may obtain β̂ by fitting a global Cox model, the parametric risk score 𝒫̂(U⁰) = g{Λ̂(t₀) + β̂^TX⁰} established based on the survival time observations up to t₀ is preferable when the primary interest is in estimating the t₀-year survival rate and the Cox model does not fit the data well. For such settings, the covariate effects on the t₀-year survival rate may vary markedly across t₀. Indeed, we often find that certain covariates are essential for predicting short-term survival, but not so for predicting long-term survival. On the other hand, for overall decision making, it may be interesting to construct a unified risk score system, not specific to a time-point t₀. Such a global score may be obtained by fitting the full dataset with a Cox model and obtaining β̂ as the maximum partial likelihood estimator. Subsequently, one can group future subjects with β̂^TX⁰ = u and consistently estimate τ_u(t) = pr(T̃⁰ ⩽ t | β̂^TX⁰ = u) for various ts. For a finite set of time-points, using similar techniques utilized in this article, it is straightforward to obtain the pointwise and simultaneous confidence intervals for such multiple survival probabilities. For example, for patients with a risk score of β̂^TX⁰ = 1.40 in the aforementioned VALIANT study, the simultaneous confidence region for {τ_1.40(6), τ_1.40(24)} is [0.03, 0.05] × [0.05, 0.09], for t = 6, 24. For patients with a parametric risk score of β̂^TX⁰ = 2.87, the corresponding simultaneous confidence region is [0.19, 0.25] × [0.30, 0.38]. A challenging problem is how to construct a simultaneous confidence band for the subject-specific survival function over an entire time interval of interest. We expect that the technique developed in Li & Doss (1995) may be extended to the present case with extra care for the additional variability in 𝒫̂(U).

For the present paper, we assume that there are so-called baseline covariates available for each study patient. Often the baseline is not clearly defined. That is, it may be difficult to define the time zero for the study patient’s follow-up time. Let S denote the study entry time since time zero and let U(S) denote the corresponding covariate vector. For the VALIANT trial, every study participant had a recent nonfatal myocardial infarction with certain complications when entering the trial. For this case, the time zero for the patient’s survival can be reasonably defined as the study entry date, which is approximately the time of occurrence of myocardial infarction. Therefore, S = 0, T̃ represents the survival time since the myocardial infarction and U = U(0) is the covariate level measured near the time of myocardial infarction. The proposed procedure would be valid for predicting the risk of death within t₀ since experiencing myocardial infarction for a future population whose distribution of (T̃⁰, U⁰) is the same as that of (T̃, U).

In general, S may not be well defined or observable. For example, in AIDS studies with HIV infected patients, the time zero could be the unknown time of infection and S is the time interval between infection and study entry. For such cases, the observable event time T̃ discussed in this paper, can be viewed as the residual life after S. Even when S is unknown, our new proposal is still valid for future subject-specific risk prediction provided that the joint distribution of {T^†, S, U(S)} for the study population is the same as that of {T^†0, S⁰, U⁰(S⁰)} for the future population, where T^† is the event time since time zero, and T̃ = T^† − S is the residual life from the entry time. Specifically, one can make inferences about the risk function

$$\tau (v;t_0)=P[T^{†0}-S^0⩽t_0|T^{†0}>S^0,\widehat{𝒫}\{U^0(S^0)\}=v]=P[{\tilde{T}}^0⩽t_0|\widehat{𝒫}\{U^0(S^0)\}=v].$$

Here, the probability is taken over T^†0, U⁰(S⁰), S⁰ and the observed data. The quantity τ (v; t₀) is the event rate by t₀ among the subgroup of patients who were event-free at study entry with 𝒫̂ {U⁰(S⁰)} = v.

When U(s) is measured repeatedly over time, the prediction of residual life with longitudinal markers is an interesting yet challenging problem. It is generally difficult even to identify a coherent prediction model for such settings. While the article focuses on the relatively simple objective of predicting survival time with baseline biomarker value U(0), it is often of interest, though difficult, to predict the residual life repeatedly based on periodically measured time-dependent biomarker U(s). In such a case, it is desirable to make predictions based on a fitted global model describing the dynamic association between the longitudinal markers and survival time. However, it is generally difficult even to specify a coherent prediction model for such a setting. For example, in general, imposing the commonly used proportional hazards or accelerated failure time model on the relationship between the most updated marker value and residual life over a time span of interest leads to an inconsistent model (Jewell & Nielsen, 1993, Theorem 1). See Jewell & Nielsen (1993) and Mammen & Nielsen (2007) for excellent discussions on the prediction of survival times with time-varying markers.

Appendix

In the Appendix, we use standard notation for the empirical process: 𝕇_n and 𝕇 represent the expectation with respect to the empirical distribution generated {(T_i, δ_i, X_i), i = 1, . . ., n} and the distribution generated by (T, δ, X), respectively. Similarly, 𝔾_n = n^1/2(𝕇_n − 𝕇). We assume that the covariate X is bounded, h = O(n^−ν) with 1/5 < ν < 1/2, K(x) is a symmetric smooth kernel function with a bounded support [−1, 1] and ∫ K̇(x)²dx < ∞, where K̇(x) = dK(x)/dx. For convenience, we use the following notation: K_j (x) = K (x)x^j, K_j,h(x) = K_j (x/h)/h and $m_2={\int }_{-1}^1{K}^2(x)dx$. Unless noted otherwise, suprema are taken over [ψ⁻¹(ρ_l + h), ψ⁻¹(ρ_r − h)] for v and over [0, t₀] for t.

Appendix A

Asymptotic properties of τ̂(v; t₀)

We first derive the asymptotic properties of τ̂(v; t₀), for v ∈ [ψ⁻¹(ρ_l + h), ψ⁻¹(ρ_r − h)]. Without loss of generality, we choose ψ(x) = log{− log(1 − x)}. Thus, $\psi \left\{\overline{𝒫}(U)\right\}={\gamma }_0^{\text{T}}{X}_{+}$, ψ{𝒫̂(U_i)} = γ̂^TX_+i, and ψ {𝒫̂(U_i)} − ψ {𝒫̄(U_i)} = O_p(n^−1/2). Let ṽ = ψ(v), λ_v(t) be the hazard function of T̃ conditional on ${\gamma }_0^{\text{T}}{X}_{+}=\tilde{v}$, ${\mathrm{\Lambda }}_v(t)={\int }_0^t{\lambda }_v(s)ds$; ζ(·) be the density function of ${\gamma }_0^{\text{T}}{X}_{+}$; and $M_i(t)=N_i(t)-{\int }_0^t{Y}_i(s)d{\mathrm{\Lambda }}_{{\gamma }_0^{\text{T}}{X}_{+i}}(s)$. In view of τ̂(v; t₀) = 1 − exp{−Λ̂_v(t)} and the delta method, we next establish the asymptotic properties of Λ̂_v(t). Furthermore, we will repeatedly use the fact that

$$\underset{e_0\in \left[a,b\right]}{\text{sup}}|{\mathbb{P}}_n\left[K_h(E-e_0)F-\mathbb{P}\{K_h(E-e_0)F\}\right]|=O_p[{\{{\left(nh\right)}^{-1}\text{log}\left(n\right)\}}^{1/2}],$$ (A1)

where {(E_i, F_i)}_i=1,...,n are independent and identically distributed realizations of (E, F), satisfying sup_e0 𝕇(|F|^s | E = e₀) < ∞, for all s > 0.

To derive asymptotic properties of Λ̂_v (t₀), we first show that there is no additional variability due to γ̂. To this end, we write Λ̂_v(t₀) = Λ̂_v(t₀, γ̂) and aim to show that if γ̂ = γ₀ + O_p(n^−1/2),

$$\underset{v}{\text{sup}}|{\widehat{\mathrm{\Lambda }}}_v(t_0,\widehat{\gamma })-{\widehat{\mathrm{\Lambda }}}_v(t_0,{\gamma }_0)|=o_p\{{\left(nh\right)}^{-1/2}\},$$ (A2)

where

$${\widehat{\mathrm{\Lambda }}}_v(t_0,\gamma )={\int }_0^{t_0}\{{\widehat{R}}_v^{(2)}\left(t,\gamma \right)d{\widehat{N}}_v^{(0)}\left(t,\gamma \right)-{\widehat{R}}_v^{(1)}\left(t,\gamma \right)d{\widehat{N}}_v^{(1)}\left(t,\gamma \right)\},$$ (A3)

${\widehat{R}}_v^{(j)}={\widehat{\pi }}_v^{(j)}/[{\widehat{\pi }}_v^{(2)}{\widehat{\pi }}_v^{(0)}-{\{{\widehat{\pi }}_v^{(1)}\}}^2]$; ${\widehat{N}}_v^{(j)}\left(t,\gamma \right)={\sum }_i{K}_{j,h}\{D_{vi}(\gamma )\}{N}_i(t)/n$; D_vi (γ) = ψ{g(γ^TX_+i)} − ψ(v); and ${\widehat{\pi }}_v^{(j)}\left(t,\gamma \right)={\sum }_{i=1}^n{K}_{j,h}\{D_{vi}(\gamma )\}{Y}_i(t)/n$. We next show that

$$\underset{t,v}{\text{sup}}\left|{\widehat{\pi }}_v^{(j)}\left(t,\widehat{\gamma }\right)-{\widehat{\pi }}_v^{(j)}(t,{\gamma }_0)\right|=o_p\{{\left(nh\right)}^{-1/2}\}.$$

Since ${\widehat{\pi }}_v^{(j)}\left(t,\gamma \right)=\int K_{j,h}\left(x-\tilde{v}\right)d{\mathbb{P}}_n\{I({\widehat{\gamma }}^{\text{T}}{X}_{+}⩽x)Y(t)\}$,

$$\begin{array}{lll}\left|{\widehat{\pi }}_v^{(j)}(t,\widehat{\gamma })-{\widehat{\pi }}_v^{(j)}\left(t,{\gamma }_0\right)\right|\hfill & ⩽\hfill & \left|n^{-1/2}\int K_{j,h}\left(x-\tilde{v}\right)d{𝔾}_n\{I({\widehat{\gamma }}^{\text{T}}{X}_{+}⩽x)Y(t)-I({\gamma }_0^{\text{T}}{X}_{+}⩽x)Y(t)\}\right|\hfill \\ \hfill & \hfill & +\left|\int K_{j,h}\left(x-\tilde{v}\right)\mathbb{P}\{I({\widehat{\gamma }}^{\text{T}}{X}_{+}⩽x)Y(t)-I({\gamma }_0^{\text{T}}{X}_{+}⩽x)Y(t)\}\right|\hfill \\ \hfill & ⩽\hfill & h^{-1}{n}^{-1/2}{\Vert {𝔾}_n\Vert }_{{\mathscr{H}}_{\delta }}+O_p(n^{-1/2}),\hfill \end{array}$$

where ${\mathscr{H}}_{\delta }=\{I({\gamma }^{\text{T}}{X}_{+}⩽x)Y(t)-I({\gamma }_0^{\text{T}}{X}_{+}⩽x)Y(t):x,t,\left|\gamma -{\gamma }_0\right|⩽\delta \}$ is a class of functions indexed by x, t and δ. Furthermore, ℋ_δ is uniformly bounded by an envelope function of order δ^1/2 with respect to the L₂ norm. By the maximum inequality (Van der Vaart & Wellner, 1996, Theorem 2.14.2) and |γ̂ − γ₀| = O_p(n^−1/2), we have h⁻¹n^−1/2||𝔾_n||_ℋδ ≲ O_p{h⁻¹n^−1/2n^−1/4 log(n)}. It follows that $|{\widehat{\pi }}_v^{(j)}(t,\widehat{\gamma })-{\widehat{\pi }}_v^{(j)}(t,{\gamma }_0)|={\left(nh\right)}^{-1/2}{(n{h}^2)}^{-1/4}\text{log}(n)+O_p(n^{-1/2})=o_p\{{\left(nh\right)}^{-1/2}\}$. Consequently, by (A1),

$$\begin{array}{l}\underset{t,v}{\text{sup}}|{\widehat{R}}_v^{(j)}(t,{\gamma }_0)-{\widehat{R}}_v^{(j)}\left(t,\widehat{\gamma }\right)|=o_p\{{(nh)}^{-1/2}\}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(k=0,1\right),\\ \underset{t,v}{\text{sup}}\{|{\widehat{R}}_v^{(2)}(t,{\gamma }_0)-r_v^{(2)}(t)|+|{\widehat{R}}_v^{(1)}(t,{\gamma }_0)|\}=O_p\{{(nh)}^{-1/2}\text{log}{\left(n\right)}^{1/2}+h^2\},\end{array}$$

where $r_v^{(2)}(t)=1/\left\{\zeta (\tilde{v}){𝒮}_v(t)\right\}$ and ${𝒮}_v(t)=\text{pr}(T⩾t|{\gamma }_0^{\text{T}}{X}_{+}=\tilde{v})$. Next, we note that

$$\left|{\int }_0^{t_0}{\widehat{R}}_v^{(2)}\left(t,\widehat{\gamma }\right)d{\widehat{N}}_v^{(0)}\left(t,\widehat{\gamma }\right)-{\int }_0^{t_0}{\widehat{R}}_v^{(2)}(t,{\gamma }_0)d{\widehat{N}}_v^{(0)}(t,{\gamma }_0)\right|⩽{\widehat{∊}}_1+{\widehat{∊}}_2+{\widehat{∊}}_3,$$

where

$$\begin{array}{l}{\widehat{∊}}_1={\mathbb{P}}_n\left[{\int }_0^{t_0}\left|{\widehat{R}}_v^{(2)}(t,\widehat{\gamma })-{\widehat{R}}_v^{(2)}(t,{\gamma }_0)\right|K_h({\widehat{\gamma }}^{\text{T}}{X}_{+}-\tilde{v})dN(t)\right],\\ {\widehat{∊}}_2={\mathbb{P}}_n\left|\{K_h({\widehat{\gamma }}^{\text{T}}{X}_{+}-\tilde{v})-K_h({\gamma }_0^{\text{T}}{X}_{+}-\tilde{v})\}{\int }_0^{t_0}|{\widehat{R}}_v^{(2)}(t,{\gamma }_0)-r_v^{(2)}(t)|dN(t)\right|,\\ {\widehat{∊}}_3=\left|{\mathbb{P}}_n\left[\{K_h({\widehat{\gamma }}^{\text{T}}{X}_{+}-\tilde{v})-K_h({\gamma }_0^{\text{T}}{X}_{+}-\tilde{v})\}{\int }_0^{t_0}{r}_v^{(2)}(t)dN(t)\right]\right|.\end{array}$$

We next bound these three terms. For the first term, ∊̂₁ ⩽ o_p{(nh)^−1/2}𝕇_n {K_h(γ̂^TX₊ − ṽ)N(t₀)} = o_p{(nh)^−1/2}. For the second term, ${\widehat{∊}}_2⩽h^{-1}{\text{sup}}_t|{\widehat{R}}_v^{(2)}(t,{\gamma }_0)-r_v^{(2)}(t)|{\text{sup}}_x[{\mathbb{P}}_n\{|I({\widehat{\gamma }}^{\text{T}}{X}_{+}⩽x)-I({\gamma }_0^{\text{T}}{X}_{+}⩽x)|N(t_0)\}]$, which is bounded by O_p{h⁻¹(nh)^−1/2 log(n)^1/2 + h} O_p(n^−1/2) = o_p{(nh)^−1/2}. For the last term,

$$\begin{array}{lll}{\widehat{∊}}_3\hfill & ⩽\hfill & n^{-1/2}{h}^{-1}\underset{x}{\text{sup}}\left|{𝔾}_n\left[\{I({\widehat{\gamma }}^{\text{T}}{X}_{+}⩽x)-I({\gamma }_0^{\text{T}}{X}_{+}⩽x)\}{\int }_0^{t_0}{r}_v^{(2)}(t)dN(t)\right]\right|+O_p(n^{-1/2})\hfill \\ \hfill & =\hfill & O_p\{n^{-1/2}{h}^{-1}{n}^{-\frac{1}{4}}\text{log}(n)\}=o_p\{{(nh)}^{-1/2}\}.\hfill \end{array}$$

Therefore, ${\text{sup}}_v|{\int }_0^{t_0}{\widehat{R}}_v^{(2)}(t,\widehat{\gamma })d{\widehat{N}}_v^{(0)}(t,\widehat{\gamma })-{\int }_0^{t_0}{\widehat{R}}_v^{(2)}(t,{\gamma }_0)d{\widehat{N}}_v^{(0)}(t,{\gamma }_0)|=o_p\{{(nh)}^{-1/2}\}$. Similarly, ${\int }_0^{t_0}{\widehat{R}}_v^{(1)}(t,\widehat{\gamma })d{\widehat{N}}_v^{(1)}(t,\widehat{\gamma })-{\int }_0^{t_0}{\widehat{R}}_v^{(1)}(t,{\gamma }_t)d{\widehat{N}}_v^{(1)}(t,\gamma )=o_p\{{(nh)}^{-1/2}\}$, and thus (A2) holds. On the other hand, following Li & Doss (1995), we can show sup_v |Λ̂_v (t₀, γ₀) − Λ_v (t₀)| → 0, in probability. It follows that sup_v (|Λ̂_vt₀) − Λ_v(t₀)| ⩽ sup_v |Λ̂_v(t₀, γ̂) − Λ̂_v (t₀, γ₀)| + sup_v |Λ̂_v(t₀, γ₀) − Λ_v(t₀)| → 0, in probability. This establishes the uniform consistency of Λ̂_v (t₀).

We next derive the asymptotic distribution of 𝒲̂_v(t₀) = (nh)^1/2{Λ̂_v(t₀) − Λ_v(t₀)}. From (A2), we have 𝒲̂_v (t₀) = 𝒲̃_v(t₀) + o_p(1), where 𝒲̃_v(t₀) = (nh)^1/2{Λ̂_v(t₀, γ₀) − Λ_v(t₀)}. Noting that n^1/2h^5/2 = o_p(1) and the decomposition that

$$\begin{array}{lll}{\widetilde{𝒲}}_v(t_0)\hfill & =\hfill & {\left(nh\right)}^{1/2}{\mathbb{P}}_n\left[{\int }_0^{t_0}\{{\widehat{R}}_v^{(2)}(t,{\gamma }_0)K_h({\gamma }_0^{\text{T}}{X}_{+}-\tilde{v})-{\widehat{R}}_v^{(1)}(t,{\gamma }_0)K_{1,h}({\gamma }_0^{\text{T}}{X}_{+}-\tilde{v})\}dM(t)\right]\hfill \\ \hfill & \hfill & +{\left(nh\right)}^{1/2}\left\{\frac{h^2+o_p(h^2)}{2}{\int }_0^{t_0}\frac{{\widehat{\pi }}_v^{(2)}{(t,{\gamma }_0)}^2-{\widehat{\pi }}_v^{(1)}(t,{\gamma }_0){\widehat{\pi }}_v^{(3)}(t,{\gamma }_0)}{{\widehat{\pi }}_v^{(2)}(t,{\gamma }_0){\widehat{\pi }}_v^{(0)}(t,{\gamma }_0)-{\widehat{\pi }}_v^{(1)}{(t,{\gamma }_0)}^2}\frac{{\partial }^2{\lambda }_v(t)}{\partial {\tilde{v}}^2}ds\right\},\hfill \end{array}$$

we have

$${\widetilde{𝒲}}_v(t_0)={\left(nh\right)}^{1/2}{\mathbb{P}}_n\left[{\int }_0^{t_0}\{{\widehat{R}}_v^{(2)}(t,{\gamma }_0)K_h({\gamma }_0^{\text{T}}{X}_{+}-\tilde{v})-{\widehat{R}}_v^{(1)}(t,{\gamma }_0)K_{1,h}({\gamma }_0^{\text{T}}{X}_{+}-\tilde{v})\}dM(t)\right]+o_p(1).$$

By integration by part and maximum inequality for empirical process, we have

$$\begin{array}{r}\hfill {\left(nh\right)}^{1/2}{\mathbb{P}}_n\left\{K_{1,h}({\gamma }_0^{\text{T}}{X}_{+}-\tilde{v}){\int }_0^{t_0}{\widehat{R}}_v^{(1)}(t,{\gamma }_0)Y(t)dM(t)\right\}=o_p(1),\\ \hfill {\left(nh\right)}^{1/2}{\mathbb{P}}_n\left[K_h({\gamma }_0^{\text{T}}{X}_{+}-\tilde{v}){\int }_0^{t_0}\{{\widehat{R}}_v^{(2)}(t,{\gamma }_0)-r_v^{(2)}(t)\}dM(t)\right]=o_p(1),\end{array}$$

uniformly in ṽ. Therefore,

$${\widehat{𝒲}}_v(t)={\left(nh\right)}^{1/2}{\mathbb{P}}_n\left\{K_h({\gamma }_0^{\text{T}}{X}_{+}-\tilde{v}){\int }_0^{t_0}{r}_v^{(2)}(t)dM(t)\right\}+o_p(1).$$ (A4)

For any fixed v or ṽ, by martingale central limit theorem, ${\left(nh\right)}^{1/2}{\mathbb{P}}_n\{K_h({\gamma }_0^{\text{T}}{X}_{+}-\tilde{v}){\int }_0^{t_0}{r}_v^{(2)}(t)dM(t)\}\to N\{0,{\sigma }_v^2(t_0)\}$, in distribution, as n → ∞, where ${\sigma }_v^2\left(t_0\right)=m_2{\int }_0^{t_0}{r}_v^{(2)}(t)d{\mathrm{\Lambda }}_v(t)$. It follows that for any fixed v, 𝒲̂_v(t) converges in distribution to $N\{0,{\sigma }_v^2(t_0)\}$.

To demonstrate the validity of the resampling variance estimator, we define

$${\widehat{\gamma }}^{*}={[\text{log}\{{\widehat{\mathrm{\Lambda }}}_0^{*}(t_0)\},{\widehat{\beta }}^{{*}^{\text{T}}}]}^{\text{T}},$$ (A5)

where

$$\begin{array}{r}\hfill {\widehat{\beta }}^{*}=\widehat{\beta }+{\widehat{𝔸}}^{-1}\sum _{i=1}^n\int \left[{\xi }_i\left\{X_i-\frac{{\widehat{\mathrm{\Pi }}}^{(1)}\left(t,\widehat{\beta }\right)}{{\widehat{\mathrm{\Pi }}}^{(0)}\left(t,\widehat{\beta }\right)}\right\}-\frac{{\sum }_{j=1}^n{\xi }_j{Y}_j(t)\text{exp}({\widehat{\beta }}^{\text{T}}{X}_j)\{{\widehat{\mathrm{\Pi }}}^{(0)}\left(t,\widehat{\beta }\right)X_j-{\widehat{\mathrm{\Pi }}}^{(1)}\left(t,\widehat{\beta }\right)\}}{n{\widehat{\mathrm{\Pi }}}^{(0)}{\left(t,\widehat{\beta }\right)}^2}\right]d{N}_i(t),\\ \hfill \text{log}\{{\widehat{\mathrm{\Lambda }}}_0^{*}\left(t_0\right)\}=\text{log}\left\{{\widehat{\mathrm{\Lambda }}}_0\left(t_0\right)\right\}+\frac{n^{-1}}{{\widehat{\mathrm{\Lambda }}}_0(t)}\sum _{i=1}^n{\int }_0^t\left[\frac{{\xi }_i}{{\widehat{\mathrm{\Pi }}}^{(0)}\left(s,\widehat{\beta }\right)}-\frac{{\sum }_{j=1}^n{\xi }_j{Y}_j(s)\text{exp}({\widehat{\beta }}^{\text{T}}{X}_j)+{\widehat{\mathrm{\Pi }}}^{(1)}{\left(t,\widehat{\beta }\right)}^{\text{T}}({\widehat{\beta }}^{*}-\widehat{\beta })}{n{\widehat{\mathrm{\Pi }}}^{(0)}{\left(s,\widehat{\beta }\right)}^2}\right]d{N}_i(s),\end{array}$$

${\widehat{\mathrm{\Pi }}}^{(j)}\left(t,\beta \right)=n^{-1}{\sum }_{j=1}^n{Y}_j(t)\text{exp}({\beta }^{\text{T}}{X}_j)X_j^{\otimes k}$ and for any vector x, x^⊗0= 1, x^⊗1 = x and x^⊗2= xx^T. It is straightforward to show that n^1/2(γ̂^* − γ̂) conditional on the data and n^1/2(γ̂ − γ₀) converge to the same limiting distribution. From γ̂^* = γ₀ + O_p(n^−1/2) and (A2), (4) = n^−1/2h^1/2 ${\sum }_{i=1}^n{K}_h({\widehat{D}}_{vi}){\widehat{𝒱}}_i(v;t_0){\xi }_i+o_p(1)$. Thus the variance estimator for (nh)^1/2{Λ̂_v(t₀) − Λ_v(t₀)} is

$$\begin{array}{lll}{\widehat{\sigma }}_v^2(t_0)\hfill & =\hfill & \text{var}\left\{n^{-1/2}{h}^{1/2}\sum _{i=1}^n{K}_h({\widehat{D}}_{vi}){\widehat{𝒱}}_i(v;t_0){\xi }_i|(T_i,{\delta }_i,U_i)\left(i=1,\dots ,n\right)\right\}+o_p(1)\hfill \\ \hfill & =\hfill & \mathbb{P}\left\{h{K}_h^2({\gamma }_0^{\text{T}}{X}_{+}-\tilde{v}){\int }_0^{t_0}{r}_v^{(2)}{\left(t\right)}^{2}Y(t)d{\mathrm{\Lambda }}_v(t)\right\}+o_p(1)={\sigma }_v^2(t_0)+o_p(1),\hfill \end{array}$$

which converges to ${\sigma }_v^2(t_0)$ in probability.

Appendix B

Justification for the validity of the confidence band for τ̂(v; t₀)

We first justify that with proper standardization, W = sup_v |(nh)^1/2Λ̂_v (t₀) − Λ_v(t₀)/σ̂_v (t₀)| converges weakly. It follows from (A4) and the consistency of σ̂_v (t₀) for σ_v (t₀) that

$$W=\underset{v}{\text{sup}}\left|{\left(nh\right)}^{1/2}{\mathbb{P}}_n\left\{K_h({\gamma }_0^{\text{T}}{X}_{+}-\tilde{v}){\int }_0^{t_0}\frac{r_v^{(2)}(t)}{{\sigma }_v(t_0)}d{M}_i(t)\right\}\right|+o_p(1).$$

This, together with the continuity of $r_v^{(2)}(t)/{\sigma }_v(t_0)$, implies that

$$W=\underset{v}{\text{sup}}\left|{\left(nh\right)}^{1/2}{\mathbb{P}}_n\{K_h({\gamma }_0^{\text{T}}{X}_{+}-\tilde{v})\eta \}\right|+o_p(1),$$

where $\eta ={\int }_0^{t_0}{r}_{{\psi }^{-1}({\gamma }_0^{\text{T}}{X}_{+})}^{(2)}(t)dM(t)/{\sigma }_{{\psi }^{-1}({\gamma }_0^{\text{T}}{X}_{+})}(t_0)$. It follows from a similar argument in Bickel & Rosenblatt (1973) that pr { a_n(W − d_n) < x} → e^−2e−x, where

$$a_n={\left[2\text{log}\left\{\frac{\psi ({\rho }_r)-\psi ({\rho }_l)}{h}\right\}\right]}^{1/2}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{d}_n=a_n+a_n^{-1}\text{log}\left\{\frac{1}{4m_2\pi }\int \dot{K}{\left(t\right)}^{2}dt\right\}.$$

To justify the validity of the resampling procedure for constructing the confidence band, we consider

$$W^{*}=\underset{v}{\text{sup}}\left|\frac{{\left(nh\right)}^{1/2}}{{\widehat{\sigma }}_v(t_0)}\sum _{i=1}^n{\xi }_i{\int }_0^{t_0}\frac{K_h({\widehat{\gamma }}^{\text{T}}{X}_{+i}-\tilde{v})\{d{N}_i(t)-Y_i(t)d{\widehat{\mathrm{\Lambda }}}_v(t)\}}{{\widehat{\pi }}_v^{(0)}\left(t,\widehat{\gamma }\right)}+{\left(nh\right)}^{1/2}\{{\widehat{\mathrm{\Lambda }}}_v(t_0,{\widehat{\gamma }}^{*})-{\widehat{\mathrm{\Lambda }}}_v(t_0,\widehat{\gamma })\}\right|.$$

Again, since |γ̂^* − γ̂| = O_p(n^−1/2), from (A2), we have

$$W^{*}=\underset{v}{\text{sup}}\left|\frac{{\left(nh\right)}^{1/2}}{{\widehat{\sigma }}_v(t_0)}\sum _{i=1}^n{\xi }_i{\int }_0^{t_0}\frac{K_h({\widehat{\gamma }}^{\text{T}}{X}_{+i}-\tilde{v})\{d{N}_i(t)-Y_i(t)d{\widehat{\mathrm{\Lambda }}}_v(t)\}}{{\widehat{\pi }}_v^{(0)}\left(t,\widehat{\gamma }\right)}\right|+o_p(1).$$

It follows from the same argument as given in Tian et al. (2005) that

$$\underset{x}{\text{sup}}|\text{pr}\{a_n(W^{*}-d_n)<x|(T_i,{\delta }_i,U_i),i=1,\dots ,n\}-e^{-2e^{-x}}|\to 0$$

in probability as n → ∞. Therefore, the conditional distribution of a_n(W^* − d_n) can be used to approximate the distribution of a_n(W − d_n) for large n.