The distribution-based p-value for the outlier sum in differential gene expression analysis

Abstract

Outlier sums were proposed by Tibshirani & Hastie (2007) and Wu (2007) for detecting outlier genes where only a small subset of disease samples shows unusually high gene expression, but they did not develop their distributional properties and formal statistical inference. In this study, a new outlier sum for detection of outlier genes is proposed, its asymptotic distribution theory is developed, and the p-value based on this outlier sum is formulated. Its analytic form is derived on the basis of the large-sample theory. We compare the proposed method with existing outlier sum methods by power comparisons. Our method is applied to DNA microarray data from samples of primary breast tumors examined by Huang et al. (2003). The results show that the proposed method is more efficient in detecting outlier genes.

1. Introduction

DNA microarray technology, which simultaneously probes thousands of gene expression profiles, has been successfully used in medical research for disease classification (Agrawal et al., 2002; Ohki et al., 2005). For example, in breast cancer research, Sorlie et al. (2003) used gene expression to classify malignant breast tumors into five distinct molecular subtypes. In lymphoma research, Alizadeh et al. (2000) reported that patients with one type of molecular pattern, germinal center B-like diffuse large B-cell lymphoma, had a significantly better chance of overall survival than those with another molecular pattern, activated B-like diffuse large B-cell lymphoma. Recently, investigators have extended the disease classification capability of microarray analysis to identifying outlier genes that are overexpressed only in a small number of disease samples. Tomlins et al. (2005) introduced an approach called cancer outlier profile analysis to identify outlier genes. This approach standardizes gene expression by centring at the median and scaling by the median absolute deviation. A kth percentile of the standardized expression value is then used as a cut-off point to determine an outlier gene. Later, two outlier sum approaches, the outlier sum statistic (Tibshirani & Hastie, 2007) and the outlier robust t-statistic (Wu, 2007), were developed to improve detection of outlier genes. Both approaches use the summation of extreme high expression values, instead of the kth percentile of the standardized gene expression, to identify outlier genes. Empirical studies have shown that both outlier sum approaches are more powerful in detecting outlier genes than standard approaches, such as the t-test. However, the development of distribution theory for these statistics is still primitive. In this paper, we derive an explicit form for the p-value of an outlier sum test statistic. The approach is empirically proven to be generally more powerful than the other methods.

2. The new outlier sum and its p-value

In a study that consists of n₁ subjects in the normal control group and n₂ subjects in the disease group, suppose that there are m genes to be investigated. Their gene expression can be represented as X_ij (i = 1, . . . , n₁, j = 1, . . . , m) for the normal control group and Y_ij (i = 1, . . . , n₂, j = 1, . . . , m) for the disease group. For a fixed gene j, let μ_j represent the parameter for central tendency that is used for measuring distance for observations in the disease group, let η_j represent the cut-off point that is used for identifying an observation in the disease group as an outlier, and let σ_j represent the scale parameter that is used for standardizing the sum of outliers. Let μ̂_j, η̂_j and σ̂_j denote their corresponding estimators.

A standardized version of the outlier sum statistic for gene j defined by Tibshirani & Hastie (2007) and Wu (2007) may be represented as ${\sum }_{i=1}^{n_2}{\widehat{\sigma }}_j^{-1}\left(Y_{ij}-{\widehat{\mu }}_j\right)I\left(Y_{ij}>{\widehat{\eta }}_j\right)$. The former uses combined observations of X_ij s and Y_ij s for estimation of μ_j, η_j and σ_j and the latter uses only X_ij s for estimation of the same set of parameters. In this paper, we present a nonstandardized outlier sum formulated in (1) and use its mean statistic to derive the p-value based on the large-sample theory of this statistic. In the following, we drop the gene index j from all mathematical expressions unless otherwise noted. The outlier sum and its mean statistic for a gene are, respectively, formulated as

$$L=\sum _{i=1}^{n_2}{Y}_{i}I(Y_i>\widehat{\eta }),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\overline{L}=\frac{1}{{\sum }_{i=1}^{n_2}I(Y_i>\widehat{\eta })}\sum _{i=1}^{n_2}{Y}_{i}I(Y_i>\widehat{\eta }).$$ (1)

Let F_X and F_Y denote the distribution functions, respectively, for variables X and Y. For testing H₀ : F_Y = F_X, we will further assume that there are the unknown location and scale parameters for this outlier mean, denoted by μ_ℓ and σ_ℓ, respectively, and they satisfy

$${\text{pr}}_{H_0}\left\{\frac{n_2^{1/2}\left(\overline{L}-{\mu }_{\ell }\right)}{{\sigma }_{\ell }}⩽z\right\}\to \mathrm{\Phi }(z),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{n}_2\to \infty ,$$ (2)

for any real number z, where Φ represents the cumulative distribution function of a standard normal variate. We also set two constraints on the cut-off point η̂ and the sample sizes n₁ and n₂, stated in Assumptions 1 and 2 in the Appendix.

From the relationship between the outlier mean and the outlier sum in (1) and from Assumption 1 for the proportion of the outlier samples, we can infer from Slutsky’s theorem and equation (2) that ${(n_2^{1/2}\beta {\sigma }_{\ell })}^{-1}$ (L − n₂βμ_ℓ) has an approximate N (0, 1) distribution. This provides a natural candidate for the test statistic based on the outlier sum statistic:

$$Z_{\text{test}}=\frac{L-n_2\widehat{\beta }{\widehat{\mu }}_{\ell }}{n_2^{1/2}\widehat{\beta }{\widehat{\sigma }}_{\ell }},$$ (3)

where β^{^}, μ̂_ℓ and σ̂_ℓ are estimators for β, μ_ℓ and σ_ℓ, respectively.

The p-value for the outlier sum can be expressed as

$$p=1-\mathrm{\Phi }(z_{\text{test}}),$$ (4)

where z_test is the sample realization of Z_test and estimates β̂, μ̂_ℓ and σ̂_ℓ are computed based on the observations x_i s from the normal group.

3. Asymptotic properties of the outlier mean

In a study of the outlier mean or sum, the cut-off point is usually chosen to be a certain multiple of the interquartile range away from the median. For example, in the outlier robust t-statistic approach, one interquartile range away from the median is adopted as the cut-off point. In the proposed method, we allow a flexible selection of the cut-off point and express it as $\eta =F_X^{-1}(0.5)+1.5k\{F_X^{-1}(0.75)-F_X^{-1}(0.25)\}$ for mathematical convenience, where k > 0 is a constant. To develop the p-value based on large sample theory, we suggest use of $\widehat{\eta }={\widehat{F}}_X^{-1}(0.5)+1.5k\times {\text{IQR}}_X$ as the cut-off point for estimating η, where ${\text{IQR}}_X={\widehat{F}}_X^{-1}(0.75)-{\widehat{F}}_X^{-1}(0.25)$ is the sample interquartile range for the distribution of variables {X_i}. Consider that the underlying distribution F_X is normal, for k = 1, the population cut-off point becomes $\eta ={\mu }_X+1.5\{F_X^{-1}(0.75)-F_X^{-1}(0.25)\}=F_X^{-1}(0.75)+\{F_X^{-1}(0.75)-F_X^{-1}(0.25)\}$. In this case, the cut-off point η̂ for the outlier sum is equal to the outlier robust t-statistic approach. Hence, $L={\sum }_{i=1}^{n_2}{Y}_{i}I[Y_i>\{{\widehat{F}}_X^{-1}(0.5)+1.5{\text{IQR}}_X\}]$ for k > 0 may serve as a generalization of the classical outlier sum. However, one interesting study is to see if k = 1 provides the desired results for gene expression analysis.

Let us now study the asymptotic distribution of the outlier mean L̄ in this specification of η̂. A Bahadur representation for the outlier mean can be stated in the following theorem.

Theorem 1. If Assumptions 1, 2, 3 and 4 in the Appendix are true, a Bahadur representation of the outlier mean is

$$\begin{array}{lll}{n}_2^{1/2}(\overline{L}-{\mu }_{\ell })\hfill & =\hfill & \frac{1}{4}(2b_1+b_2-3b_3)\times n_1^{-1/2}\sum _{i=1}^{n_1}I\{X_i⩽F_X^{-1}(0.25)\}\hfill \\ \hfill & \hfill & +\frac{1}{4}(2b_1+b_2+b_3)\times n_1^{-1/2}\sum _{i=1}^{n_1}I\{F_X^{-1}(0.25)⩽X_i⩽F_X^{-1}(0.5)\}\hfill \\ \hfill & \hfill & +\frac{1}{4}(-2b_1+b_2+b_3)\times n_1^{-1/2}\sum _{i=1}^{n_1}I\{F_X^{-1}(0.5)⩽X_i⩽F_X^{-1}(0.75)\}\hfill \\ \hfill & \hfill & +\frac{1}{4}(-2b_1-3b_2+b_3)\times n_1^{-1/2}\sum _{i=1}^{n_1}I\{X_i⩾F_X^{-1}(0.75)\}\hfill \\ \hfill & \hfill & +\frac{1}{\beta }{n}_2^{-1/2}\sum _{i=1}^{n_2}\{(Y_i-{\mu }_Y)I(Y_i>\eta )-{\mu }_{\eta }\}+o_p(1),\hfill \end{array}$$

where ${\mu }_{\eta }={\beta }^{-1}{\int }_{\eta }^{\infty }(y-{\mu }_Y)f_Y(y)dy$, ${\mu }_{\ell }={\beta }^{-1}{\int }_{\eta }^{\infty }y{f}_Y(y)dy$, $b_1=(\eta -{\mu }_Y){\beta }^{-1}{f}_Y(\eta ){\gamma }^{1/2}{f}_X^{-1}\{F_X^{-1}(0.5)\}$, $b_2=(1.5k)(\eta -{\mu }_Y){\beta }^{-1}{f}_Y(\eta ){\gamma }^{1/2}{f}_X^{-1}\{F_X^{-1}(0.75)\}$ and $b_3=(1.5k)(\eta -{\mu }_Y){\beta }^{-1}{f}_Y(\eta ){\gamma }^{1/2}{f}_X^{-1}\{F_X^{-1}(0.25)\}$. In this case, β = pr(Y ⩾ η).

The asymptotic distribution of the outlier mean can be obtained from the central limit theorem.

Theorem 2. If Assumptions 2, 3 and 4 in the Appendix are true, then $n_2^{1/2}(\overline{L}-{\mu }_{\ell })$ converges in distribution to N (0, ${\sigma }_{\ell }^2$), where

$$\begin{array}{lll}{\sigma }_{\ell }^2\hfill & =\hfill & {\sigma }_{\ell }^2(b_1,b_2,b_3,\upsilon )\hfill \\ \hfill & =\hfill & \frac{3}{256}\{{(2b_1+b_2-3b_3)}^2+{(2b_1+b_2+b_3)}^2+{(-2b_1+b_2+b_3)}^2+{(-2b_1-3b_2+b_3)}^2\}+\upsilon ,\hfill \\ \upsilon \hfill & =\hfill & \frac{1}{{\beta }^2}\text{var}\{(Y-\eta )I(Y>\eta )\}.\hfill \end{array}$$

After replacing the population parameters by their corresponding estimators in the formulas of Theorem 2 and in (3), the p-value in (4) can be computed.

There are two scenarios that require different approaches to find estimators of β, μ_ℓ and σ_ℓ. When distributions F_X and F_Y are known but involve some unknown parameters, maximum likelihood estimation can be used. When the distributions F_X and F_Y are unknown, a nonparametric technique can be used for estimating β, μ_ℓ and σ_ℓ by first estimating the mean μ_Y, percentile $F_X^{-1}(\alpha )$, truncated mean μ_ℓ, truncated variance ${\sigma }_{\ell }^2$ and densities f_X and f_Y. Theorem 2, along with equation (4), provides a new method for computing the p-value that can be useful in different scenarios. Although the nonparametric approach can broaden the application areas, this paper focuses on the parametric model.

In the rest of this section, we develop an explicit form for the p-value under an added assumption that variables X and Y have normal distributions N (μ_X, ${\sigma }_X^2$) and N (μ_Y, ${\sigma }_Y^2$). Under these assumptions, we have $F_X^{-1}(\alpha )={\mu }_X+z_{\alpha }{\sigma }_X$, which implies $F_X^{-1}(0.5)+1.5k\{F_X^{-1}(0.75)-F_X^{-1}(0.25)\}={\mu }_X+3k{z}_{0.75}{\sigma }_X$, where z_α is the 100αth percentile of the standard normal distribution. This gives the outlier sum

$$L=\sum _{i=1}^{n_2}{Y}_{i}I(Y_i>{\widehat{\mu }}_X+3k{z}_{0.75}{\widehat{\sigma }}_X)$$ (5)

after replacing μ_X and σ_X by their estimators. Using equation (5) and the aforementioned properties and substituting the population parameters by their estimates, i.e. γ̂ = n₂/n₁, ${\widehat{\mu }}_X=\overline{x}=n_1^{-1}{\sum }_{i=1}^n{x}_i$, ${\widehat{\sigma }}_X^2=s_x^2={(n_1-1)}^{-1}{\sum }_{i=1}^{n_1}{(x_i-\overline{x})}^2$, we obtain

$$\begin{array}{ll}\ell =\sum _{i=1}^{n_2}{y}_{i}I(y_i>\overline{x}+3k{z}_{0.75}{s}_x),\hfill & \beta =1-\mathrm{\Phi }(3k{z}_{0.75}),\hfill \\ {\widehat{\mu }}_{\ell }=\overline{x}+\frac{s_x}{\beta }{\int }_{(3k{z}_{0.75})}^{\infty }z\varphi (z)dz,\hfill & {\widehat{b}}_1=\frac{{(2\pi )}^{1/2}}{\beta }3k{z}_{0.75}{s}_x\varphi (3k{z}_{0.75}){\widehat{\gamma }}^{1/2},\hfill \\ {\widehat{b}}_2={\widehat{b}}_3=\frac{1.5k{\widehat{b}}_1{\varphi }^{-1}(z_{0.75})}{{(2\pi )}^{1/2}},\hfill & \widehat{\upsilon }=\frac{s_x^2}{{\beta }^2}\left[{\int }_{(3k{z}_{0.75})}^{\infty }{z}^2\varphi (z)dz-{\left\{{\int }_{(3k{z}_{0.75})}^{\infty }z\varphi (z)dz\right\}}^2\right],\hfill \end{array}$$

where β is a known constant in this parametric setting.

With the above formulas, Theorem 2 permits the computation of ${\widehat{\sigma }}_{\ell }^2={\sigma }_{\ell }^2({\widehat{b}}_1,{\widehat{b}}_2,{\widehat{b}}_3,\widehat{\upsilon })$. By plotting stimates of μ_x and σ_x, the p-value of (4) can be obtained. This technique can be extended to other known population distributions of X and Y.

4. Simulation study

4.1. Type I error

This simulation study examines whether the location of the cut-off point affects Type I error. From (5), we will make comparisons based on the value of k. We assume that gene expression in both control and disease groups follows a standard normal distribution, and each has a sample size n = 20. The p-value is computed based on (4). Type I error is calculated as the proportion of the p-values less than 0.05 among simulation runs. The results show that as k increases, or equivalently, the cut-off point shifts more away from the median, Type I error gets smaller and the chance of rejecting the null hypothesis decreases. Type I errors are 0.058, 0.0075, 0.00043, 0.00002 and 0.000002 for k = 1, 1.5, 2, 2.5 and 3, respectively, at α = 0.05. Clearly, when k = 1, Type I error is closest to the targeted significance level. When the adjusted p-value cut-off is 0.038, Type I error reaches 0.05 for k = 1. Thus, we opt for k = 1 for the distribution-based p-value approach to compare with other outlier statistics and choose 0.038 as the significance level to control for Type I error at 0.05 in the power study.

4.2. Power analysis

In the power study, we compare the distribution-based p-value approach with four other approaches: two-sample t-test, the cancer outlier profile analysis approach, the outlier sum approach, and the outlier robust t-statistic approach. Three scenarios are examined: (a) the genes in the control and disease groups follow the N (0, 1) distribution, except for the first gene in the n₀ outlier samples from the disease group that follows the N (d, 1) distribution, where d is the effect size; (b) the genes in the control and disease groups follow the t-distribution with four degrees of freedom, except for the first gene in the n₀ outlier samples from the disease group, which follows the noncentral t-distribution with four degrees of freedom and noncentrality d; (c) the genes in the control and disease groups follow the N (0, σ²) distribution, except for each gene in the n₀ outlier samples from the disease group that follows the N (2σ, σ²) distribution. For scenarios (a) and (b), we evaluate how the effect size, noncentrality, and number of outlier samples affect the power. Specifically, we simulate 1000 genes for each of the 20 control and 20 disease samples and choose d from 1, 1.5, 2, 3, to 4. In addition, we let n₀ vary from 1 to 20. For scenario (c), each gene has a different variance, but the effect size, the ratio of mean and standard deviation, is each fixed at 2. To replicate our data sample presented in § 5, we simulate 12 625 genes for each of the 19 control and 18 disease samples and allow each gene to have a separate σ, estimated from the data sample and ranging from 0.1 to 2.4. In this scenario, we let n₀ vary from 1 to 18.

Power is calculated as the proportion of 1000 simulation runs that have a significant difference based on Type I error 0.05. For scenarios (a) and (b), power calculation is based on the first gene. For scenario (c), the average power of all genes is used. Significance is determined by the p-value when methods have a p-value formula available. Otherwise, significance is determined by whether the test statistic is greater than the 95th percentile of the outlier statistic, based on the parametric bootstrapping method.

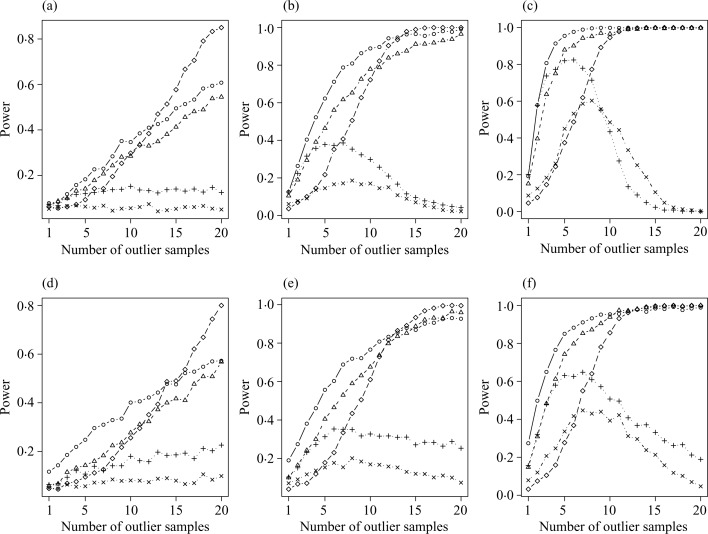
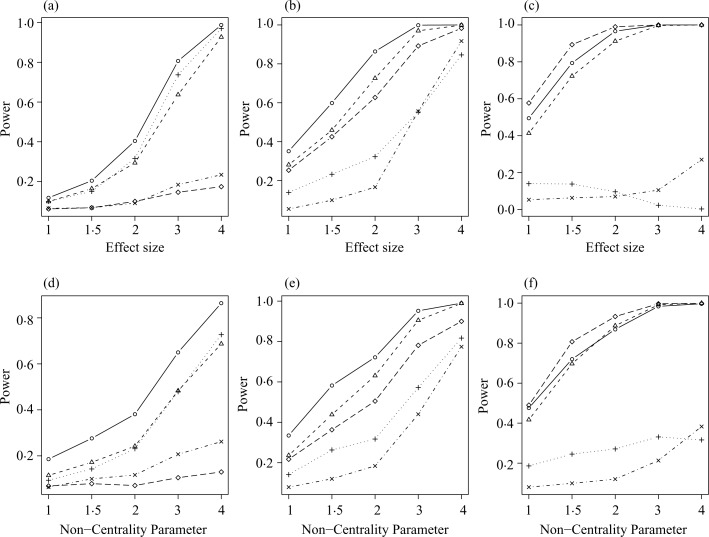
From Fig. 1, the distribution-based p-value approach has the highest power when the number of outlier samples is smaller than 10. In contrast, when the number of outlier samples becomes large, such as greater than 15, the t-test yields the highest power. Interestingly, the distribution-based p-value approach and the outlier robust t-statistic approach also perform well. On the other hand, the cancer outlier profile analysis and the outlier sum have low power overall. From Fig. 2, with three outlier samples or less, power increases as effect size increases in the distribution-based p-value, the outlier robust t-statistic, and the outlier sum approaches, but not in the other two approaches for both normal and t-distributions. The distribution-based p-value approach performs best in most cases. As the number of outlier samples increases to 15 or more, the t-test performs best, but the distribution-based p-value approach and the outlier robust t-statistic approach yield a comparable power. In contrast, the other two approaches have a power less than 0.4. The results demonstrate that the distribution-based p-value approach has better power to identify outliers. When the number of outlier samples is large, the strength of identifiability diminishes. For example, when all disease samples are outliers in the extreme case, the statistical issue becomes a standard two-group comparison and hence the identifiability of the outlier approaches disappears. For scenario (c) of differing variances, the results, not presented, are similar to those of Fig. 1 at the effect size equal to 2. Moreover, all five approaches show a very weak correlation between power and standard deviation. This phenomenon indicates that the power to detect outliers is independent of the variance as long as the effect size is fixed.

Fig. 1.

Power comparison of various effect sizes with equal variance for (a)–(c) normal distribution with an effect size of 1, 2 and 3, respectively, and for (d)–(f) t-distribution with 4 degrees of freedom and noncentrality of 1, 2 and 3, respectively. The following approaches are illustrated: distribution-based p-value for the outlier sum (○); outlier robust t-statistic (▵); outlier sum (+); cancer outlier profile analysis (×); and two-sample t-test (♦).

Fig. 2.

Power comparison for various numbers of outlier tissues for (a)–(c) normal distribution with an effect size of 1, 2 and 3, respectively, and for (d)–(f) t-distribution with 4 degrees of freedom and noncentrality of 1, 2 and 3, respectively. The following approaches are illustrated: distribution-based p-value for the outlier sum (○); outlier robust t-statistic (▵); outlier sum (+); cancer outlier profile analysis (×); and two-sample t-test (♦).

5. Data example

We apply all five approaches discussed in § 4 to the breast cancer microarray data reported by Huang et al. (2003). This dataset contains the expression levels of 12 625 genes from 37 breast tumor samples: 19 of them have no positive nodes discovered and are treated as the control group and the other 18 samples have identifiably positive nodes and are treated as the disease group. Since we test 12 625 genes simultaneously, errors in inference are more likely to occur without p-value adjustment. To account for multiple testing, the false discovery rate method (Benjamini & Hochberg, 1995) is used to correct for the p-value at the 0.05 level for the distribution-based p-value approach and the t-test. For the other three approaches, the 99th percentile of each outlier statistic is used as the cut-off point to identify significant outlier genes based on the parametric bootstrapping method.

Results show that the t-test does not identify any significant outlier genes. In contrast, the other four approaches identify 584, 535, 740 and 695 outlier genes, respectively, for the distribution-based p-value approach, the outlier robust t-statistic approach, the outlier sum approach and the cancer outlier profile analysis approach. We further find that four disease samples are consistently ranked in the top four in number of outlier genes by the distribution-based p-value approach, the outlier robust t-statistic approach and the outlier sum approach. Each of these four disease samples has at least 20% of the outlier genes with a higher expression, suggesting abnormal up-regulation in gene expression. In addition, there are eight outlier genes consistently showing high expression in all four samples.

This application highlights the strength of the four outlier approaches, which identify many significant outlier genes and point out several disease samples with an abnormally large number of outlier genes. On the other hand, the t-test fails to detect any outlier gene. In addition, computation of the p-value is easier with the distribution-based p-value approach than the other three outlier approaches. These three approaches lack a distribution theory and hence need special procedures, such as the parametric bootstrapping method, to define a cut-off point for each outlier gene as the variance changes.

Appendix

Four assumptions for the outlier sum test statistic are as follows.

• Assumption 1. The proportion of outlier samples, $n_2^{-1}{\sum }_{i=1}^{n_2}I(Y_i>\widehat{\eta })$, converges in probability to β with 0 < β < 1.

• Assumption 2. The limit γ = lim_n2,n1→∞ n₂/n₁ exists.

• Assumption 3. The probability density function f_X is bounded away from zero in a neighbourhood of $F_X^{-1}(\alpha )$ for α ∈ (0, 1).

• Assumption 4. The probability density function f_Y is bounded away from zero in a neighbourhood of the population cut-off point η.

Proof of Theorem 1. With Assumption 3, a representation of ${\hat{F}}_X^{-1}(\alpha )$ such as

$$n_1^{1/2}\{{\widehat{F}}_X^{-1}(\alpha )-F_X^{-1}(\alpha )\}=f_X^{-1}\{F_X^{-1}(\alpha )\}{n}_1^{-1/2}\sum _{i=1}^{n_1}[\alpha -I\{X_i⩽F_X^{-1}(\alpha )\}]+o_p(1),$$ (A1)

implies that $\widehat{\eta }={\widehat{F}}_X^{-1}(0.5)+1.5k\times {\text{IOR}}_X$ satisfies $T=n_1^{1/2}(\widehat{\eta }-\eta )=O_p(1)$ (Ruppert & Carroll, 1980). From the expression of the outlier mean in (1), we have

$$\begin{array}{lll}\overline{L}\hfill & =\hfill & {\left\{\sum _{i=1}^{n_2}I(Y_i>\widehat{\eta })\right\}}^{-1}\sum _{i=1}^{n_2}{Y}_{i}I(Y_i>\widehat{\eta })\hfill \\ \hfill & =\hfill & {\left\{\sum _{i=1}^{n_2}I(Y_i>\widehat{\eta })\right\}}^{-1}\sum _{i=1}^{n_2}{Y}_{i}I(Y_i>\eta +n_1^{-1/2}T)\hfill \\ \hfill & =\hfill & {\mu }_Y+{\left\{\sum _{i=1}^{n_2}I(Y_i>\widehat{\eta })\right\}}^{-1}\sum _{i=1}^{n_2}(Y_i-{\mu }_Y)I(Y_i>\eta +n_1^{-1/2}T).\hfill \end{array}$$

The above expression can be rewritten as

$$n_2^{1/2}(\overline{L}-{\mu }_Y)={\left\{\sum _{i=1}^{n_2}I(Y_i>\widehat{\eta })\right\}}^{-1}{n}_2^{1/2}\sum _{i=1}^{n_2}(Y_i-{\mu }_Y)I(Y_i>\eta +n_1^{-1/2}T).$$ (A2)

With (A1), Assumptions 2 and 4, and techniques from Ruppert & Carroll (1980) and Chen & Chiang (1996), a modified second term on the right-hand side of (A2), can be expressed as

$$\begin{array}{l}{n}_2^{-1/2}\sum _{i=1}^{n_2}(Y_i-{\mu }_Y)\{I(Y_i>\eta +n_1^{-1/2}T)-I(Y_i>\eta )\}+n_2^{-1/2}\sum _{i=1}^{n_2}(Y_i-{\mu }_Y)I(Y_i>\eta )\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=-n_2^{-1/2}\sum _{i=1}^{n_2}(Y_i-{\mu }_Y)\left\{I(Y_i⩽\eta +n_1^{-1/2}T)-I(Y_i⩽\eta )\right\}+n_2^{-1/2}\sum _{i=1}^{n_2}(Y_i-{\mu }_Y)I(Y_i>\eta )\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=-(\eta -{\mu }_Y)f_Y(\eta ){\gamma }^{1/2}T+n_2^{-1/2}\sum _{i=1}^{n_2}(Y_i-{\mu }_Y)I(Y_i>\eta )+o_p(1).\end{array}$$ (A3)

By the same rationale and the weak law of large numbers, we can derive

$$n_2^{-1}\sum _{i=1}^{n_2}I[Y_i>{\widehat{F}}_X^{-1}(0.5)+1.5k\{{\widehat{F}}_X^{-1}(0.75)-{\widehat{F}}_X^{-1}(0.75)\}]=n_2^{-1}\sum _{i=1}^{n_2}I(Y_i>\eta )+o_p(1)$$ (A4)

which converges to pr(Y ⩾ η).

Combining (A2), (A3) and (A4), a Bahadur representation of the outlier mean is

$$\begin{array}{l}{n}_2^{1/2}(\overline{L}-[{\mu }_Y+{\beta }^{-1}E\{(Y-\eta )I(Y⩾\eta )\}])=-{\beta }^{-1}(\eta -{\mu }_Y)f_Y(\eta ){\gamma }^{1/2}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times n_1^{1/2}(\widehat{\eta }-\eta )+{\beta }^{-1}{n}_2^{-1/2}\sum _{i=1}^{n_2}\{(Y_i-{\mu }_Y)I(Y_i>\eta )-E\{(Y-\eta )I(Y⩾\eta )\}+o_p(1).\end{array}$$