Stochastic approximation with virtual observations for dose-finding on discrete levels

Summary

Phase I clinical studies are experiments in which a new drug is administered to humans to determine the maximum dose that causes toxicity with a target probability. Phase I dose-finding is often formulated as a quantile estimation problem. For studies with a biological endpoint, it is common to define toxicity by dichotomizing the continuous biomarker expression. In this article, we propose a novel variant of the Robbins–Monro stochastic approximation that utilizes the continuous measurements for quantile estimation. The Robbins–Monro method has seldom seen clinical applications, because it does not perform well for quantile estimation with binary data and it works with a continuum of doses that are generally not available in practice. To address these issues, we formulate the dose-finding problem as root-finding for the mean of a continuous variable, for which the stochastic approximation procedure is efficient. To accommodate the use of discrete doses, we introduce the idea of virtual observation that is defined on a continuous dosage range. Our proposed method inherits the convergence properties of the stochastic approximation algorithm and its computational simplicity. Simulations based on real trial data show that our proposed method improves accuracy compared with the continual re-assessment method and produces results robust to model misspecification.

1. Introduction

The early phase clinical development of a new drug typically involves testing several doses of the new drug, with safety as the primary concern. A specific objective is to identify the maximum tolerated dose, defined as the largest dose that causes toxicity with a prespecified probability. Traditionally, the maximum tolerated dose is approached from a low dose according to a 3 + 3 algorithm whereby escalation occurs after cohorts of three nontoxic observations. As this traditional algorithm is criticized for its arbitrary statistical properties, several authors propose novel designs, such as the continual re-assessment method (O’Quigley et al., 1990) and rigorous extension of the 3 + 3 algorithm (Lin & Shih, 2001; Cheung, 2007) to address dose-finding as a quantile estimation problem. These designs, utilizing binary toxicity data for estimation, provide clinicians with viable options for testing drugs in general.

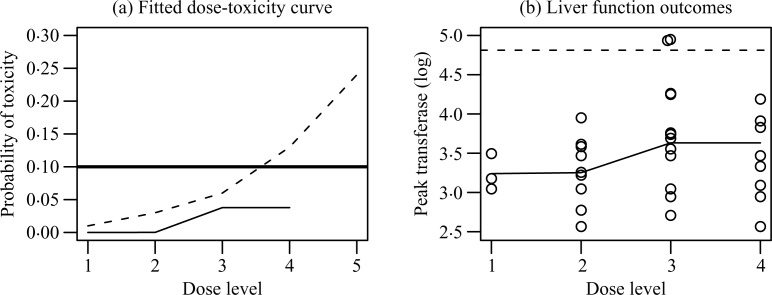
In clinical studies with a biological safety endpoint, the toxicity outcome is often defined by dichotomizing a quantitative biomarker expression. Take for example the Neuroprotection with Statin Therapy for Acute Recovery Trial, NeuSTART, a recent phase I trial of lovastatin in acute ischemic stroke patients conducted at Columbia University (Elkind et al., 2008). In this trial, high dose lovastatin was administered to patients for three days followed by a standard dose for 30 days. A primary safety concern for administering high dose lovastatin is toxicity measured by the elevation in liver enzyme alanine aminotransferase. In NeuSTART, each patient was evaluated up to day 30 after the start of treatment, and toxicity was said to occur if the patient’s post-treatment peak transferase exceeded three times the upper normal limit of 123 U/L. The objective of the trial was to estimate the dose with toxicity probability closest to 10%. A two-stage continual re-assessment method (Cheung, 2005) was used for dose escalation in 33 subjects at five high-dose levels. Table 1 summarizes the liver function outcomes by dose group in the study: two patients at dose level 3 exhibited elevated liver function, and the trial did not reach the highest dose. According to the continual re-assessment method, dose level 4 was estimated to be the maximum tolerated dose with a 13% toxicity rate. However, an isotonic fit to the continuous transferase measurements suggested a much smaller rate of 4% for dose level 4. Details of the continual re-assessment method and the isotonic fit are described in § 5.

Table 1.

Summary of the liver function data in NeuSTART

Dose	Cohort size	Patients with toxicity	log(alt)		Isotonic		Toxicity rate
k			Mean	sd	Estimate	sd	crm	Isotonic
1	3	0	3.24	0.23	3.24	0.23	0.01	0.00
2	10	0	3.25	0.42	3.25	0.42	0.03	0.00
3	12	2	3.78	0.72	3.63	0.66	0.06	0.04
4	8	0	3.42	0.54	3.63	0.66	0.13	0.04
5	0	–	–	–	–	–	0.24	–

alt, peak alanine aminotransferase; crm, continual re-assessment method; sd, standard deviation.

In retrospect, we realized that statistical efficiency might have been lost by using only the dichotomized data, and that the original measurements might be utilized to retain information. In this article, we propose a variant of the Robbins–Monro (1951) stochastic approximation that uses the quantitative measurements for dose-finding in phase I trials. The Robbins–Monro procedure is a stochastic root-finding method, and is a natural method of choice for the quantile estimation objective in dose-finding (Anbar, 1977, 1984). While their paper has generated a voluminous statistical and engineering literature, the stochastic approximation has seldom been considered for use in clinical trials; exceptions are Anbar (1984) and O’Quigley & Chevret (1991). Two considerations render application of the Robbins–Monro procedure unsuited to many phase I trial settings. First, from a statistical viewpoint, the method has been demonstrated to be inferior to parametric procedures such as the maximum likelihood recursion for binary data (Wu, 1985). In our current application where the binary outcome is defined by a continuous measurement, this difficulty can be resolved if we make appropriate use of the original continuous data. Second, the method entails the availability of a continuum of doses. This is neither feasible in practice nor preferred for reporting purposes in publications. In addition, in trials involving combination of treatments, each subsequently higher regimen may involve incrementing doses of different treatments and hence there is no natural scale of dosage. This important point has been noted in O’Quigley & Chevret (1991) and Shen & O’Quigley (2000), both of whom address the problem by rounding the stochastic approximation output to its closest dose at each step. We shall return to this when we introduce a novel concept called virtual observation.

2. Stochastic approximation with virtual observations

2.1. Problem formulation

Consider a trial in which patients are enrolled in small cohorts of size m. Let $X_i^{*}$ and X_i respectively denote the dose assigned to the ith cohort and the actual dose given to patients. The assigned dose $X_i^{*}$ can take on any real number from a conceptual scale that represents an ordering of doses or regimens. Suppose for the moment that X_i can take on any real number and that X_i = $X_i^{*}$ for all i. Let Y_ij be the safety measurement of the j th patient in the i th cohort; the patient is said to experience toxicity if Y_ij exceeds some threshold t₀. The objective of a dose-finding study is the identification of θ such that π (θ) = p, where π (x) = P(Y_ij > t₀ | X_i = x) is the probability of toxicity at dose x.

Assume that Y_ij = M(X_i) + σ(X_i)∊_ij, where the ∊ s are independently distributed according to a common distribution G with E(∊) = 0 and var(∊) = 1, so that M(x) and σ (x), respectively, denote the mean and the standard deviation of the safety outcome at dose x. Both M(x) and σ (x) are unspecified. Under this regression model, the toxicity probability at dose x,

$$\pi (x)=1-G\left\{\frac{t_0-M(x)}{\sigma (x)}\right\},$$ (1)

and the target dose θ can be re-expressed as the solution to the equation f (x) ≡ M(x) + z_pσ (x) = t₀, where z_p is the upper pth percentile of G. For brevity, suppose that π (x) and f (x) are strictly increasing on the relevant dose range so that the root θ exists uniquely. This monotone dose-toxicity assumption is reasonable in phase I trials, although the main results in this article hold under the much weaker assumptions stated in the Appendix. In practice, the actual dose given is confined to a discrete set of K levels, denoted by {1, . . . , K}, with π (1) < ⋯ < π (K) and f (1) < ⋯ < f (K). As such, it is possible that π (k) ≠ p and f (k) ≠ t₀ for all k. One may then define the maximum tolerated dose by ν₁ = arg min_k |π (k) − p| as in O’Quigley et al. (1990). Alternatively, under the current formulation, it is natural to define the maximum tolerated dose by ν₂ = arg min_k | f (k) − t₀|. The objectives ν₁ and ν₂ represent the closest doses to θ on two different scales, and are not necessarily identical.

Lemma 1. Define c_k such that G(c_k) = 1 − π (k) for k = 1, . . . , K. (a) Assume π (ν₁) ⩾ p. If π(k) < 1 − G{z_p + σ (ν₁)(z_p − c_ν1)/σ(k)} for all k < ν₁, then ν₂ = ν₁; else, ν₂ = ν₁ − 1.

(b) Assume π (ν₁) ⩽ p. If π (k) > 1 − G{z_p + σ (ν₁)(z_p − c_ν1)/σ (k)} for all k > ν₁, then ν₂ = ν₁;else, ν₂ = ν₁ + 1.

Therefore, ν₂ = ν₁ if π (ν₁) = p. Lemma 1 also implies that ν₂ = ν₁ when the dose-toxicity curve is steep around ν₁. In other words, when ν₂ ≠ ν₁, π (ν₁) and π (ν₂) will be quite close to each other, thus rendering both objectives similar. For clarity in presentation, we will focus on the estimation of ν₁ in accordance with the conventional phase I objective.

2.2. The procedure

Let U_i = Ȳ_i + [E{S_i /σ(X_i)}]⁻¹z_p S_i, where Ȳ_i and S_i are the respective sample mean and standard deviation of the measurements in the m subjects of cohort i, so that E(U_i | X_i) = f (X_i). Since S_i /σ (X_i) is a pivotal quantity that depends on the ∊ s but not M and σ, we can derive E{S_i /σ (X_i)} for any given distribution G either by analytical calculation or by simulation. Define, for the ith cohort, a virtual observation V_i = U_i + β ( $X_i^{*}$ − X_i) made at the assigned dose $X_i^{*}$ for some β > 0. Then the next assigned dose $X_{i+1}^{*}$ is calculated via a stochastic approximation recursion based on the virtual observation:

$$X_{i+1}^{*}=X_i^{*}-\frac{1}{i\beta }(V_i-t_0)$$ (2)

and the next actual dose X_i+1 = C( $X_{i+1}^{*}$), where C (x) =k if l_k ⩽ x < l_k+1 with l₁ = −∞, l_{K +1} = ∞, and l_k = k − 0.5 for k = 2, . . . , K. That is, C(x) is the rounded value of x if 0.5 ⩽ x < K + 0.5.

There are various ways to initiate the recursion. One could start the first cohort at the lowest dose, i.e. $X_i^{*}$ = X_i = 1, or at the prior maximum tolerated dose as in O’Quigley et al. (1990). One may also institute a predetermined escalation sequence until the first sign of toxicity appears. Specifically, let $X_i^{*}$ = X_i = x_0,i for the i th cohort, where x_0,i is a nondecreasing sequence of dose levels with x_0,i ⩽ x_0,i+1, and switch to recursion (2) once a toxicity is observed. While a two-stage strategy is not necessary for the method’s implementation, it may be practical to dictate the pace of escalation in accordance with the clinician’s preference when there is no toxicity (Cheung, 2005).

Another way to avoid aggressive escalation is by restricting the trial from skipping an untested dose. That is, the next assigned dose would be min( $X_{i+1}^{*}$, max_{1 ⩽n ⩽i} X_n + 2) instead of $X_{i+1}^{*}$. If this restriction is to be applied, then it should be only to the first few cohorts because the increment diminishes as i increases.

2.3. Discrete barrier: an illustration

As an alternative to the virtual observation recursion (2), we may generate a discretized stochastic approximation of the given dose X_i based on the actual observations U_i by taking the closest dose to the value obtained from a recursion output; that is,

$$X_{i+1}=C\left\{X_i-\frac{1}{i\beta }(U_i-t_0)\right\}.$$ (3)

O’Quigley & Chevret (1991) and Shen & O’Quigley (2000) take a similar discretization approach to accommodate the use of discrete doses in the context of different dose-finding designs. The discretized stochastic approximation (3) is straightforward and at first looks reasonable, but may indefinitely confine the design sequence to a wrong dose. Consider a two-stage design for five dose levels with t₀ = 4.81. In the event of no toxicity, i.e. Y_ij ⩽ 4.81, escalation will proceed according to an initial sequence: x_0,1 = 1, x_0,2 = 2, x_0,3 = x_0,4 = 3, x_0,5 = x_0,6 = x_0,7 = 4 and x_0,i = 5 for i ⩾ 8. Once the first toxicity is seen, recursion (3) with β = 0.05 will be used to assign doses. Take a simple instance with negligible variability so that U_i = f (X_i) with f (1) = 4.20, f (2) = 4.67, f (3) = 4.80, f (4) = 4.93 and f (5) = 5.30; hence, the correct dose is level 3. The outcome sequence will follow the initial design and yield (X₁, U₁) = (1, 4.20), (X₂, U₂) = (2, 4.67), (X₃, U₃) = (X₄, U₄) = (3, 4.80) and (X₅, U₅) = (4, 4.93), after which recursion (3) will come into effect and give X₆ = C{4 − (5 × 0.05)⁻¹(4.93 − 4.81)} = 4, and U₆ = 4.93. It is easy to see that the remaining patients will receive dose 4. If, instead, we use the virtual observation recursion (2) after the initial design, then $X_6^{*}$ = 3.52 which gives X₆ = 4, U₆ = 4.93 and V₆ = 4.906, followed by $X_7^{*}$ = 3.14 and X₇ = 3. The remaining process will continue at the correct dose 3.

To see how the virtual observation recursion corrects the problem, consider another instance with f (x) = t₀ + β (x − θ), where θ is an integer, and U_i is observed with noise Z_i, i.e. U_i = f (X_i) + Z_i. If the i th dose X_i is an overdose dose, namely, X_i = θ + Δ_i for some Δ_i > 0, then the update according to (3) is X_i+1 = X_i + [C{(1 − i⁻¹)Δ_i − (iβ)⁻¹Z_i} − Δ_i]. As i grows, the second term is likely to equal zero and does not contribute to future updates. A discrete barrier is thus built by rounding. The virtual observation recursion (2) updates a dose with $X_{i+1}^{*}=X_i^{*}-i^{-1}({\mathrm{\Delta }}_i^{*}+Z_i/\beta )$, where ${\mathrm{\Delta }}_i^{*}=X_i^{*}-\theta$. The second term, which is of the order O(i⁻¹), can be carried over to future updates and provides continuation to overcome the discrete barrier.

3. Design properties

The idea of virtual observation is to create an objective function h(x) = E(V_i | $X_i^{*}$ = x) with a local slope at the available doses {1, . . . , K}. To be precise, h(x) = f {C(x)} + β{x − C(x)} is piecewise continuous with jumps at {0.5, 1.5, . . . , K − 0.5} and is linearly increasing with slope β except at the jumps. Following from the standard results of stochastic approximation (Sacks, 1958; Lai & Robbins, 1979), under the condition that h(x) = t₀ has a unique root at θ_β, the virtual dose $X_n^{*}$ generated by (2) is consistent for θ_β, and X_n for C (θ_β). Furthermore, since the objective h(x) is equal to the target f (x) on the actual doses, i.e. h(k) = f (k), we hope that the root θ_β will be close to θ, and C(θ_β) to ν₁.

Proposition 1. (a) Assume ν₁ = ν₂. If B_ν1 < β < min_{k ≠ ν1} B_k, then X_n = ν₁ eventually with probability one, where B_k = 2σ (k)|c_k − z_p|.

(b) Assume ν₁ ≠ ν₂. If β < min_{k ≠ ν1} B_k, then pr(X_n = ν₁ or ν₂ eventually) = 1 and

$$|\pi (X_n)-p|\le \left|G\left\{z_p+\frac{\sigma ({\nu }_1)}{\sigma ({\nu }_2)}(z_p-c_{{\nu }_1})\right\}-G(c_{{\nu }_1})\right|-|\pi ({\nu }_1)-p|$$

eventually with probability one.

Supposing c_ν1 ≈ z_p, i.e. B_ν1 ≈ 0, and the parameter β is adequately small, Proposition 1 implies that X_n will eventually recommend a neighbouring dose of ν₁, if not ν₁ itself. The specific choice of β can be aided by the knowledge about π and σ. While these quantities are often unknown prior to the trial, we illustrate in § 4 how β may be determined with only mild prior inputs under a semiparametric mean-variance assumption.

Proposition 1(b) prescribes how far X_n may deviate from θ on the probability scale if β is adequately small. For example, if p = 0.1 and π (ν₁) = 0.08, applying Proposition 1(b) gives |π (X_n) − 0.1| ⩽ 0.024 eventually by assuming σ (ν₁) = σ (ν₂). The maximum deviation is only slightly larger than |π (ν₁) − p| = 0.02. The deviation will be bounded above by 0.037 if we conservatively assume σ (ν₁) = 1.5σ (ν₂), while we would expect σ (ν₁)/σ (ν₂) ≈ 1 as ν₁ and ν₂ are neighbours.

4. Design calibration

4.1. Consistency

The virtual observation recursion is specified by a tuning parameter β. Assuming that the condition for consistency in Proposition 1 holds, we can further show that $X_n^{*}$ is asymptotically normal with mean θ_β and variance β⁻²var(V_i | $X_i^{*}$ = θ_β). To minimize the asymptotic variance, therefore, we should set β at its largest possible value that guarantees consistency. However, since the upper bound of β depends on the unknown π (k) and σ (k), to simplify the calibration process, we restrict our attention to scenarios in which

$$\pi ({\nu }_1)=\pi ({\nu }_2)=p,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\pi (k)\le p_L<p<p_U\le \pi (k^{\prime }),$$ (4)

for k < ν₁ < k′ and some prespecified limits p_L, p_U. This class of scenarios consists of toxicity configurations in which there is an unambiguous target with θ = ν₁ = ν₂ = θ_β, and the toxicity probabilities at the other doses lie outside the interval (p_L, p_U). By not considering scenarios with π (k) ∈ (p_L, p_U), we are in a sense indifferent to whether such a dose should be selected as the maximum tolerated dose. Thus, the interval (p_L, p_U) is called the indifference interval (Cheung & Chappell, 2002).

Proposition 2. Assume that σ (k) depends on dose k only via M(k) as follows: s{σ (k)} = s{σ (θ)} + ϕ{M(k) − M(θ)} for some ϕ ⩾ 0 and some smooth function s(σ) with s(σ) ⩾ 0 and s′(σ) > 0. Under (4), X_n is consistent for θ if 0 < β/{2σ (θ)} < w ≡ min(z_p − $z_p^2$/z_L, z_p − z_U), where z_L = G⁻¹(1 − p_L) and z_U = G⁻¹(1 − p_U).

The consistency upper bound for β depends on the unknown σ (θ). On the other hand, we can often obtain clinical data to estimate the standard deviation σ₀ of the safety measurements in a comparable population that is untreated or treated at lower doses. Since σ₀ ⩽ σ (θ) by the assumption that variance increases with doses, we may use 2wσ₀ as a conservative consistency upper bound for β.

4.2. Robustness

Our proposed method works under a fairly general dose-toxicity relationship as described in Proposition 2, but requires us to specify a distribution G. To provide some assurance in an application, it is important to evaluate the method’s robustness against misspecification. Suppose we assume ∊_ij follows G̃ instead of the true G, and generate recursion (2) based on Ṽ_i = Ỹ_i + [E_G̃ {S_i /σ (X_i)}]⁻¹z̃_p S_i + β { $X_i^{*}$ − C( $X_i^{*}$)} where E_G̃ (·) denotes expectation computed under G̃ and G̃ (z̃_p) = 1 − p. Furthermore, let

$${\tilde{z}}_p^{*}=\frac{E_G\{S_i/\sigma (X_i)\}}{E_{\tilde{G}}\{S_i/\sigma (X_i)\}}{\tilde{z}}_p$$

and h̃(x) ≡ E_G (Ṽ_i | $X_i^{*}$ = x) = M{C(x)} + ${\tilde{z}}_p^{*}$σ{C(x)} + β{x − C(x)}. If β is chosen such that h̃(x) = t₀ has a unique solution at θ̃_β, then it can be shown that the virtual dose $X_n^{*}$ generated based on Ṽ_i s will converge to θ̃_β and X_n to C (θ̃_β).

Proposition 3. Define ν̃ = arg min_k B̃_k, where B̃_k = 2σ (k)| c_k − ${\tilde{z}}_p^{*}$|. (a) Under (4), ν̃ = θ if p_L < 1 − G{ ${\tilde{z}}_p^{*}$ + σ(θ)|z_p − ${\tilde{z}}_p^{*}$|/σ(1)} ≡ p̃_L and p_U > 1 − G{ ${\tilde{z}}_p^{*}$ − |z_p − ${\tilde{z}}_p^{*}$|} ≡ p̃_U.

(b) Assume that the mean-variance relationship in Proposition 2 holds, and that p_L < p̃_L and p_U > p̃_U under (4). Then, X_n is consistent for C (θ̃_β) = ν̃ = θ if |z_p − ${\tilde{z}}_p^{*}$| < β /{2σ (θ)} < w̃ ≡ min(z_p − z_p ${\tilde{z}}_p^{*}$/z_L, ${\tilde{z}}_p^{*}$ − z_U).

Proposition 2 is a special case of Proposition 3 when G̃ = G. Generally, Proposition 3 states that the false objective θ̃_β will coincide with the true θ under a steep dose-toxicity curve, where steepness is quantified by p̃_L and p̃_U. For example, Table 2 displays the key robustness quantities for recursion (2) with standard normal G̃, m = 3 and p = 0.1 evaluated under the logistic, t₅, and Gumbel distributions standardized so that they have mean zero and variance one; the logistic distribution has location 0 and scale 0.55; the noise under t₅ is generated as a t-variate with 5 degrees of freedom multiplied by 0.77; the distribution function for the Gumbel distribution is G(z) = exp[− exp{(−0.45 − z)/0.78}]. To evaluate p̃_L we set σ (1) = 0.25σ (θ). Table 2 shows that p̃_L and p̃_U are within 0.05 of the target p, suggesting mild conditions on the dose-toxicity curve for robust estimation of θ. In addition, |z_p − ${\tilde{z}}_p^{*}$| is generally small, and is much smaller than w̃, when computed with p_L = 0.05, p_U = 0.15. We thus anticipate that a wide range of β will satisfy the consistency conditions under misspecification of the model.

Table 2.

Robustness analysis of the virtual observation recursion with standard normal G̃, m = 3 and p = 0.1

G	zp	EG {Si /σ (Xi)}	${\tilde{z}}_p^{*}$	p̃L	p̃U	|zp − ${\tilde{z}}_p^{*}$|	w̃
N (0, 1)	1.282	0.8862	1.282	0.100	0.100	0.000	0.245
Logistic	1.211	0.8663	1.253	0.071	0.100	0.041	0.277
t5	1.143	0.8438	1.220	0.053	0.100	0.077	0.250
Gumbel	1.305	0.8514	1.231	0.076	0.119	0.073	0.265

5. Application to NeuSTART

5.1. Trial design and data

In NeuSTART, we adopted a two-stage continual re-assessment method for dose escalation in 33 subjects at five dose levels using the initial sequence given in § 2.3. Once the first toxicity was seen, the dose-toxicity curve would be updated after an observation was made from the most recent patient, and the next patient would be given the dose with toxicity probability estimated to be closest to p = 0.10. The toxicity probability for dose k was modelled as $d_k^{\psi }$ with d₁ = 0.02, d₂ = 0.06, d₃ = 0.10, d₄ = 0.18 and d₅ = 0.30, where ψ was a priori lognormal with location 0 and scale 1.34 (O’Quigley & Shen, 1996). Enrolment into the trial began in October 2005 and was completed in August 2007. The first sign of elevated liver function test was seen in the eighth subject who was given dose level 3. The subsequent dose assignments were then model-based.

Table 1 reports the sample mean and the standard deviation of peak transferase levels (on log scale) for each dose. Assuming monotone dose-toxicity, we estimate M(k) and σ (k) by pooling data in dose levels 3 and 4, because the sample mean of dose 3 is larger than that of dose 4. Substituting these estimates for the corresponding parameter values in (1) gives an isotonic fit of π (k), which is shown in the last column of Table 1 and plotted in Fig. 1(a). The estimate of π (4) based on the isotonic fit is much lower than the target 10%. In contrast, the continual re-assessment method estimates that π (4) exceeds the target, even though no toxicity was observed at dose level 4. This is indeed a feature of the continual re-assessment method that allows strong influence of observations at lower doses on estimation at the higher doses via parametric extrapolation.

Fig. 1.

Model fits for the NeuSTART data. (a) Fitted dose-toxicity curve by the continual reassessment method (dashed) and the isotonic fit (solid); the target probability is also indicated (thicker solid line). (b) Liver function outcomes. Each observation is indicated (o), as well as the isotonic fit (solid) and the toxicity threshold (dashed).

Figure 1(b) displays the liver function data by dose, and reveals that the two toxic outcomes were results of peak transferase levels exceeding the threshold t₀ = log(123) by a slight margin. Were these measurements to drop a few units, the trial outcomes would have been quite different. Such sensitivity in dichotomized analysis speaks favourably for using the original continuous measurements as the basis of estimation, especially when the data are subject to measurement errors.

The liver function data demonstrate heteroscedasticity in Table 1 and Fig. 1(b). Specifically, the variance increases with dose as the mean increases. Such a monotone mean-variance relationship is typical for biological laboratory values, although the exact form of the relationship is usually hard to estimate. Finally, to identify the noise distribution, we calculate the standardized residual for each observation via centring the transferase measurement by the isotonic estimate of its mean and standardization by its standard deviation estimate. A normal Q–Q-plot of these standardized residuals shows that the noise ∊_ij fits well to the standard normal distribution.

5.2. Redesign of NeuSTART

Having checked all the model components, we may consider the virtual observation recursion assuming standard normal noise, so that E{S_i /σ (X_i)} = 0.886 and z_p = 1.28 for a trial with m = 3 and p = 0.1. To determine β, we approximate σ₀ by σ̂_0,low = 0.59, which is the 80% confidence lower limit based on the 20 observations in the combined dose levels 3 and 4. Then the upper bound for β is 0.29 according to Proposition 2 if we set p_L = 0.05 and p_U = 0.15, and it is less than 2w̃σ̂_0,low under various noise distributions, see Table 2. This estimate is conservative as far as consistency and robustness are concerned, because σ̂_0,low tends to underestimate σ₀ and hence σ (θ). Also, 0.29/{2σ (θ)} > |z_p − ${\tilde{z}}_p^{*}$| under the distributions in Table 2, unless the true σ (θ) ⩾ 3.77, which is very unlikely. Therefore, recursion (2) will be generated based on V_i = Ȳ_i + 1.446 S_i + 0.29( $X_i^{*}$ − X_i).

5.3. Simulation study

Simulations were run to compare the performance of the virtual observation recursion and the continual re-assessment method. In the simulation, we used the same two-stage strategies for both methods: start at the lowest dose, follow the initial sequence as in § 2.3 and switch to the continual re-assessment method or recursion (2) upon the first toxic outcome. Furthermore, we applied the restriction that no untested level would be skipped in escalation. For the purposes of theoretical comparisons, we also ran simulations using the nonparametric optimal design described in O’Quigley et al. (2002). The design assumed that the binary toxicity outcomes at every test dose were observable for each given patient and used the complete toxicity profile to evaluate the sample toxicity proportion at each dose. It can be readily shown that this design is optimal in that the sample proportion for π (k) achieves the Cramer–Rao lower bound with ′ variance proportional to G(c_k){1 − G(c_k)}. While the nonparametric optimal design cannot be implemented in practice where each patient is treated at a single dose, the design’s performance can be evaluated in simulations and can be used as a benchmark for efficiency.

In each simulated trial, a true dose-toxicity curve π (k) was first generated from the posterior distribution under the assumed model in the continual re-assessment method, i.e. π (k) = $d_k^{\psi }$ with ψ drawn from the posterior given the NeuSTART data. Continuous outcomes were generated from a normal distribution with mean and standard deviation determined so that, for a given π(k), σ⁴(k) = log{α + 0.52M(k)} for some α ∈ [−1, 1]. With p = 0.1 and t₀ = log(123), the values of σ (θ) represent a wide range of variability from 0.57 to 1. For each generated π (k), we recorded the true ν₁; ran the continual re-assessment method, the nonparametric optimal design and the virtual observation recursion with β = 0.15, 0.29 or 0.45 under various values of α; and recorded their recommended doses.

Figure 2(a) plots the proportions of selecting ν₁ against σ (θ) in 10 000 generated dose-toxicity curves. Since π (ν₁) ≠ 0.1 in general in the simulated configurations, it may be acceptable to select a dose with π (k) ∈ (0.05, 0.15). Figure 2(b) displays the proportions of selecting such an acceptable dose; these proportions were calculated after discarding dose-toxicity curves with π (ν₁) ∉ / (0.05, 0.15). The virtual observation recursion with β = 0.29 is uniformly better than the continual re-assessment method and exceeds the nonparametric optimal design. Using β = 0.15 leads to inferior performance especially as σ (θ) increases; this is in accordance with the fact that a small β is associated with a large asymptotic variance of $X_n^{*}$. Using β = 0.45 exhibits a reverse trend where performance improves as σ (θ) increases and is generally better than the continual re-assessment method. This suggests not only that we can use data to form a good choice of β, but also that improvement over the continual re-assessment method can be achieved on a wide range of β.

Fig. 2.

(a) and (c) The proportion of selecting ν₁ vs. σ (θ) by the virtual observation recursion assuming normal noise. (b) and (d) The proportion of selecting an acceptable dose by our method. Our method was run with β = 0.15 (dot-dashed), 0.29 (solid), 0.45 (dotted) under normal noise in (a) and (b), and with β = 0.29 and noise generated from the logistic (solid), t₅ (dotted) and Gumbel (dot-dashed) distributions in (c) and (d). The selection probabilities of the continual re-assessment method (heavier solid) and the nonparametric optimal design (heavier dashed) are indicated.

The efficiency gain is achieved through the use of the continuous data with an additional normality assumption. Figures 2(c) and 2(d) display the operating characteristics of the virtual observation recursion with β = 0.29 under G other than normal. The accuracies of the method are quite comparable and remain superior to the continual re-assessment method under model misspecification, thus offering assurance of robustness in our application.

6. Discussion

In many dose-finding studies, the experimental drug is available only at a discrete set of doses. This is an important feature that distinguishes the phase I dose-finding literature from the large literature of stochastic approximation and its well-studied descendants, although both deal with quantile estimation. Shen & O’Quigley (1996, 2000) point out the difficulty in the theoretical investigation of dose-finding methods due to the discrete barrier. In this article, we introduce the idea of virtual observations to bridge the gap between stochastic approximation for continuous dosage ranges and practical situations in phase I trials. On a technical note, if we apply (2) by replacing β with some other value 0 < b < 2β, then, assuming consistency, the sequence $X_n^{*}$ will be asymptotically normal with mean θ_β and variance {b(2β − b)}⁻¹var(V_i | $X_i^{*}$ = θ_β). This leads to the well-established fact that b = β is the optimal choice that achieves the minimum asymptotic variance. Thus, by creating an objective function h(x) using virtual observation, we set up a root-finding problem with a known slope β around the root. This is a nice design feature that makes the application of stochastic approximation stable and reliable in small-sample settings.

A specific contribution of this article is the use of continuous data in phase I trials, in which the safety outcomes are typically dichotomized. We demonstrate via simulation based on the NeuSTART data that our procedure does better than the continual re-assessment method and the nonparametric optimal design. At first glance, it appears inconceivable that any method can improve on the Cramer–Rao lower bound. A closer look reveals that this is to be expected, as we set out to retrieve information through the use of the original continuous data. Precisely, an efficient estimator for π (k) based on Y_ij s observed at dose k has asymptotic variance proportional to $a_k^{\text{T}}$Σa_k, where a_k = {G′(c_k), c_kG′(c_k)}^T and Σ is the inverse of the information matrix for {M(k), σ (k)} with diagonals I₁₁ = ∫ {G″(z)/G′(z)}² dG(z), I₂₂ = ∫ {zG″(z)/G′(z) + 1}² dG(z), and off-diagonals I₁₂ = I₂₁ = ∫ z{G″(z)/G′(z)}² dG(z); see Lehmann (1983). For standard normal G, for instance, the ratio of $a_k^{\text{T}}$Σa_k to the Cramér–Rao lower bound for π (k) is {G′(c_k)}²(1 + $c_k^2$/2)[G(c_k){1 − G(c_k)}]⁻¹, and attains a maximum 0.663 when π (k) = 0.21 or 0.79, and converges to 0 as π (k) approaches 0 or 1. With a target p = 0.10, this variance ratio at θ is 0.623. In other words, 33 continuous measurements observed at θ contain about the same amount of information as 42 dichotomized outcomes. To verify this intuition, we ran the nonparametric optimal design with a sample size of 42 under the simulation set-up in § 5.3 and it was uniformly superior to the virtual observation recursion with 33 subjects: the proportion of selecting ν₁ was 0.58 and that of selecting an acceptable dose was 0.75. This might be because the optimal design had observations from all patients at the true ν₁ but the recursion did not. The efficiency advantage should be considered in light of the computational ease and operational transparency of the stochastic approximation. First, dose assignment for the next cohort can be obtained by a hand calculator using (2). Second, the update rule (2) is intuitive and easy to explain: de-escalation occurs if V_i is large because of either a large sample mean Ȳ_i or a large variance $S_i^2$ observed in the current cohort. As shown in Fig. 1(b), an increase in drug level raises not only the mean level of the liver function test but also its variability. For biological measurements, the drug impact on the variance is usually larger than that on the mean. Therefore, it is sensible for a dose-finding method to curb its escalation pace in the presence of increased variability.

Appendix

Technical details

In this appendix, we first state and discuss the conditions on π (x), f (x) and h(x) required by the lemma and the propositions. Recall that ν₁ = arg min_k |π (k) − p|.

Condition 1. The functions π (x) and f (x) are assumed to be weakly monotone in x such that (a) π (k′) < π (ν₁ − 1) < π (ν₁) < π (ν₁ + 1) < π (k), (b) f (k′) < f (ν₁ − 1) < f (ν₁) < f (ν₁ + 1) < f (k), (c) π (k′) < π (ν₁ − 1) < p < π (ν₁ + 1) < π (k) and (d) f (k′) < f (ν₁ − 1) < t₀ < f (ν₁ + 1) < f (k) for all k′ < ν₁ − 1 and k > ν₁ + 1.

To account for scenarios with ν₁ = 1 or = K, define π (0) = 0, π (K + 1) = 1, f (0) = −∞ and f (K + 1) = ∞. Condition 1 does not require π and f to be monotone for doses below ν₁ − 1 and above ν₁ + 1 as long as doses below (above) ν₁ are less (more) toxic than the target level. It is easy to see that strict monotonicity satisfies Condition 1. Condition 1(c) is an easy consequence of Condition 1(a) and the definition of ν₁, and Condition 1(d) follows Condition 1(b): because f (k) = M(k) + c_k σ (k) + σ (k)(z_p − c_k) = t₀ + σ (k)(z_p − c_k), we have π (ν₁ − 1) < p implies f (ν₁ − 1) < t₀, and π (ν₁ + 1) > p implies f (ν₁ + 1) > t₀.

Condition 2. One and only one of the following statements is true:

1. The equation h(x) = t₀ has a unique root, denoted by θ_β, not among the jump points {l₂, . . . , l_K}.

2. The root of h(x) = t₀ does not exist.

3. The equation h(x) = t₀ has multiple roots, with the smallest root denoted by θ′ and the largest root by θ″. Both θ′ and θ″ are not among the jump points.

We require that the roots (θ_β, θ′ and θ″) are not among the jump points so as to satisfy the Lipschitz condition around the roots. For example, Condition 2(c) guarantees that there exist K′ > 0 and K″ > 0 such that |h(x) − h(θ′)| ⩽ K′|x − θ′| and |h(x) − h(θ″)| ⩽ K″|x − θ″| for all x.

Proof of Lemma 1. For Lemma 1(a), suppose that π (ν₁) ⩾ p. Because f (k) = t₀ + σ (k)(z_p − c_k), π(ν₁) ⩾ p implies f (ν₁) ⩾ t₀. Thus, by Condition 1(d) and definition of ν₂, we know that ν₂ = ν₁ or ν₁ − 1. More precisely, ν₁ = ν₂ if and only if f (ν₁) − t₀ < t₀ − f (k) if and only if σ (ν₁)(z_p − c_ν1) < σ(k)(c_k − z_p) if and only if c_k > z_p + σ (ν₁)(z_p − c_ν1)/σ(k) for all k < ν₁, giving the desired result. The proof of Lemma 1(b) is analogous.

Proof of Proposition 1(a). First, the assumption β > 2σ (ν₁)|c_ν1 − z_p| implies that h(θ_β) = t₀ for some θ_β with C(θ_β) = ν₁. When π (ν₁) = p, h(ν₁) = f (ν₁) = t₀ and hence θ_β = ν₁. When π (ν₁) > p, we have h(ν₁) = f (ν₁) > t₀ and h(ν₁ − 0.5) = h(ν₁) − 0.5β = t₀ + σ (ν₁)(z_p − c_ν1) − 0.5β < t₀; the last inequality holds by the assumption. By continuity, there exists θ_β ∈ (ν₁ − 0.5,ν₁) so that h(θ_β) = t₀ and C(θ_β) = ν₁. Similar arguments can be made for the case π (ν₁) < p.

Second, the assumption β < min_{k ≠ ν1} 2σ(k)|c_k − z_p| precludes the scenarios where h(x) = t₀ has multiple roots, because the assumption implies h(k′ + 0.5) = t₀ + σ (k′)(z_p − c_k′) + 0.5β < t₀ for all k′ < ν₁ and h(k − 0.5) = t₀ + σ (k)(z_p − c_k) − 0.5β > t₀ for all k > ν₁.

Consequently, h(x) = t₀ has a unique root at θ_β. Using standard convergence results of the stochastic approximation gives $X_n^{*}$ → θ_β with probability one, and X_n = C( $X_n^{*}$) C(θ_β) = ν₁ by the Lipschitz assumption; cf. Condition 2.

Proof of Proposition 1(b). When π (ν₁) > p, ν₂ = ν₁ − 1 by Lemma 1(a) and the assumption ν₁ ≠ ν₂. Furthermore, we have h(ν₁) − t₀ > t₀ − h(ν₂) > 0.5β; the first inequality holds by definition of ν₂, the second by the assumption β < min_{k ≠ ν1} 2σ (k)|c_k − z_p|. As a result, the root of h(x) = t₀ does not exist with h(ν₂ + 0.5) < t₀ and h(ν₁ − 0.5) > t₀. More precisely, we have (x − l_ν1) { h(x) − t₀} > 0 for all x ≠ l_ν1 and h(l_ν1) > t₀ and h(l_ν1 −) < t₀, where l_ν1 − indicates a number that is arbitrarily close to l_ν1 from the left. Define Z_i = V_i − h( $X_i^{*}$) and let ℐ_i denote the σ-field generated by { $X_1^{*}$, Z₁, . . . , Z_i} so that V_i is ℐ_i-measurable and $X_i^{*}$ is ℐ_i−1-measurable. Following the algebraic steps similar to those of Robbins & Monro (1951), we obtain

$${(X_{i+1}^{*}-l_{{\nu }_2})}^2={(X_i^{*}-l_{{\nu }_1})}^2-\frac{2(X_i^{*}-l_{{\nu }_1})\{h(X_i^{*})-t_0\}}{i\beta }-\frac{2(X_i^{*}-l_{{\nu }_1})Z_i}{i\beta }+O(i^{-2}).$$

Taking conditional expectation on both sides with respect to ℐ_i−1, we have

$$E\left\{{(X_{i+1}^{*}-l_{{\nu }_1})}^2\right|{ℱ}_{i-1}\}⩽{(X_i^{*}-l_{{\nu }_1})}^2-\frac{2(X_i^{*}-l_{{\nu }_1})\{h(X_i^{*})-t_0\}}{i\beta }+\frac{K^m}{i^2}$$

for some K″′ > 0. Applying Theorem 1 of Robbins & Siegmund (1971) for nonnegative almost supermartingale, we can show that lim_i→∞( $X_i^{*}$ − l_ν1)² exists and ${\sum }_{i=1}^{\infty }(X_1^{*}-l_{{\nu }_1})\{h(X_1^{*})-t_0\}<\infty$ almost surely. Also, since ( $X_i^{*}$ − l_ν2){h( $X_i^{*}$) − t₀} > 0, we can conclude that $X_i^{*}$ → l_ν1 and pr(X_n = ν₁ or ν₂ eventually) = 1. By definition of ν₁, |π (ν₁) − p| < |π (ν₂) − p|. Thus, for sufficiently large n,

$$\begin{array}{lll}|\pi (X_n)-p|⩽|\pi ({\nu }_2)-p|\hfill & =\hfill & \{\pi ({\nu }_1)-\pi ({\nu }_2)\}-\{\pi ({\nu }_1)-p\}\hfill \\ \hfill & ⩽\hfill & \left|G\left\{z_p+\frac{\sigma ({\nu }_1)}{\sigma ({\nu }_2)}(z_p-c_{{\nu }_1})\right\}-G(c_{{\nu }_1})\right|-|\pi ({\nu }_1)-p|.\hfill \end{array}$$ (A1)

The inequality (A1) is due to Lemma 1(a) under the assumptions ν₁ ≠ ν₂ and π (ν₁) > p. The proof is completed by analogous arguments for the case π (ν₁) < p.

Proof of Proposition 3(a). First, it is easy to see that σ (k) < σ (θ) < σ (k′) for k < θ < k′ under the assumed mean-variance relationship and Condition 1. Since s{σ (k)} − s{σ (θ)} = ϕ{M(k) − M(θ)} = ϕ{f (k) − f (θ)} − ϕ{σ(k) − σ (θ)}, we have f (k) < f (θ) if and only if σ (k) < σ (θ) because s(σ) is increasing. Now, the assumption p_L < p̃_L implies

$$c_k>{\tilde{z}}_p^{*}+\frac{\sigma (\theta )}{\sigma (1)}|z_p-{\tilde{z}}_p^{*}|⩾{\tilde{z}}_p^{*}+\frac{\sigma (\theta )}{\sigma (k)}|z_p-{\tilde{z}}_p^{*}|$$

because σ (k) < σ (θ). Hence B̃_k = 2σ (k)(c_k − ${\tilde{z}}_p^{*}$) > 2σ (θ)|z_p − ${\tilde{z}}_p^{*}$| = B̃_θ for all k < θ. Using similar arguments, we can show p_U > p̃_U implies B̃_k′ > B̃_θ for k′ >θ. Thus, ν̃ = θ by definition.

Proof of Proposition 3(b). First, following similar arguments in the proof of Proposition 1(a), we can prove that h̃(x) = t₀ has a unique root at θ̃_β with C(θ̃_β) = ν̃ if B̃_ν̃ < β < min_{k ≠ ν̃} B̃_k. Applying standard convergence results of stochastic approximation gives the consistency of X_n for ν̃, which is equal to θ by Proposition 3(a).

Next, because c_k ⩽ z_U < ${\tilde{z}}_p^{*}$ by the assumption p_U < p̃_U and σ(θ) ⩽ σ (k) for k >θ, we have 2σ (θ)( ${\tilde{z}}_p^{*}$ − z_U) ⩽ 2σ (k)( ${\tilde{z}}_p^{*}$ − c_k) = B_k for k >θ. Hence,

$$2\sigma (\theta )({\tilde{z}}_p^{*}-z_U)\le \underset{k>\theta }{\text{min}}{B}_k.$$ (A2)

For the case k < θ, we have c_k ⩾ z_L > max(z_p, ${\tilde{z}}_p^{*}$) and σ (k) ⩽ σ (θ). Substituting M(k) = M(θ) + [s{σ (k)} − s{σ (θ)}]/ϕ into c_k = {t₀ − M(k)}/σ (k) gives

$$c_k\sigma (k)=t_0-M(\theta )-\frac{s\{\sigma (k)\}-s\{\sigma (\theta )\}}{\phi }$$ (A3)

for ϕ > 0. Fix M(θ) and σ (θ). For any given c_k, we differentiate both sides of (A3) with respect to ϕ and get

$$\left[\frac{s^{\prime }\{\sigma (k)\}}{\varphi }+c_k\right]\frac{\partial \sigma (k)}{\partial \varphi }=\frac{s\{\sigma (k)\}-s\{\sigma (\theta )\}}{{\varphi }^2}$$

for ϕ > 0. Therefore, ∂σ (k)/ ∂ϕ < 0 as long as c_k ⩾ 0 which holds for most practical purposes; i.e. it suffices to have z_p ⩾ 0, and σ(k) is minimized as ϕ grows large upon which M(k) → M(θ). Specifically, its infimum is achieved by taking the limit ϕ → ∞ in (A3):

$$\underset{\varphi >0}{\text{inf}}\sigma (k)=\frac{t_0-M(\theta )}{c_k}<\frac{t_0-M(\theta )}{z_p}=\sigma (\theta ).$$

Also, since σ (k) = σ (θ) when ϕ = 0, the above expression provides the minimum value of σ (k) over all possible ϕ ⩾ 0 for a given c_k. Thus,

$$\underset{k<\theta }{\text{min}}{B}_k⩾\underset{k<\theta }{\text{min}}\underset{\varphi ⩾0}{\text{inf}}2\sigma (k)(c_k-{\tilde{z}}_p^{*})=2\{t_0-M(\theta )\}\underset{k<\theta }{\text{min}}(1-{\tilde{z}}_p^{*}/c_k)=2\sigma (\theta )z_p(1-{\tilde{z}}_p^{*}/z_L).$$

This, together with (A2), implies that |z_p − ${\tilde{z}}_p^{*}$| < β/{2σ (θ)} < w̃ suffices the consistency condition, B̃_θ < β < min_{k ≠ θ} B̃k.