Joint estimation of multiple graphical models

Summary

Gaussian graphical models explore dependence relationships between random variables, through the estimation of the corresponding inverse covariance matrices. In this paper we develop an estimator for such models appropriate for data from several graphical models that share the same variables and some of the dependence structure. In this setting, estimating a single graphical model would mask the underlying heterogeneity, while estimating separate models for each category does not take advantage of the common structure. We propose a method that jointly estimates the graphical models corresponding to the different categories present in the data, aiming to preserve the common structure, while allowing for differences between the categories. This is achieved through a hierarchical penalty that targets the removal of common zeros in the inverse covariance matrices across categories. We establish the asymptotic consistency and sparsity of the proposed estimator in the high-dimensional case, and illustrate its performance on a number of simulated networks. An application to learning semantic connections between terms from webpages collected from computer science departments is included.

1. Introduction

Graphical models represent the relationships between a set of random variables through their joint distribution. Generally, the variables correspond to the nodes of the graph, while edges represent their marginal or conditional dependencies. The study of graphical models has attracted much attention both in the statistical and computer science literature; see, for example, the books by Lauritzen (1996) and Pearl (2009). These models have proved useful in a variety of contexts, including causal inference and estimation of networks. Special members of this family of models include Bayesian networks, which correspond to a directed acyclic graph, and Gaussian models, which assume the joint distribution to be Gaussian. In the latter case, because the distribution is characterized by its first two moments, the entire dependence structure can be determined from the covariance matrix, where off-diagonal elements are proportional to marginal correlations, or, more commonly, from the inverse covariance matrix, where the off-diagonal elements are proportional to partial correlations. Specifically, variables j and j^′ are conditionally independent given all other variables, if and only if the (j, j^′)th element in the inverse covariance matrix is zero; thus the problem of estimating a Gaussian graphical model is equivalent to estimating an inverse covariance matrix.

The literature on estimating an inverse covariance matrix goes back to Dempster (1972), who advocated the estimation of a sparse dependence structure, i.e., setting some elements of the inverse covariance matrix to zero. Edwards (2000) gave an extensive review of early work in this area. A standard approach is the backward stepwise selection method, which starts by removing the least significant edges from a fully connected graph, and continues removing edges until all remaining edges are significant according to an individual partial correlation test. This procedure does not account for multiple testing; a conservative simultaneous testing procedure was proposed by Drton & Perlman (2004).

More recently, the focus has shifted to using regularization for sparse estimation of the inverse covariance matrix and the corresponding graphical model. For example, Meinshausen & Bühlmann (2006) proposed to select edges for each node in the graph by regressing the variable on all other variables using ℓ₁-penalized regression. This method reduces to solving p separate regression problems, and does not provide an estimate of the matrix itself. A penalized maximum likelihood approach using the ℓ₁ penalty has been considered by Yuan & Lin (2007), Banerjee et al. (2008), d’Aspremont et al. (2008), Friedman et al. (2008) and Rothman et al. (2008), who have all proposed different algorithms for computing this estimator. This approach produces a sparse estimate of the inverse covariance matrix, which can then be used to infer a graph, and has been referred to as the graphical lasso (Friedman et al., 2008) or sparse permutation invariant covariance estimator (Rothman et al., 2008). Theoretical properties of the ℓ₁-penalized maximum likelihood estimator in the large p scenario were derived by Rothman et al. (2008), who showed that the rate of convergence in the Frobenius norm is O_p[{q(log p)/n}^1/2], where q is the total number of nonzero elements in the precision matrix. Fan et al. (2009) and Lam & Fan (2009) extended this penalized maximum likelihood approach to general nonconvex penalties, such as the smoothly clipped absolute deviation penalty (Fan & Li, 2001), while Lam & Fan (2009) also established a so-called sparsistency property of the penalized likelihood estimator, implying that it estimates true zeros correctly with probability tending to 1. Alternative penalized estimators based on the pseudolikelihood instead of the likelihood have been recently proposed by G. V. Rocha, P. Zhao, and B. Yu, in a 2008 unpublished preprint, arXiv:0811.1239, and Peng et al. (2009); the latter paper also established consistency in terms of both estimation and model selection.

The focus so far in the literature has been on estimating a single Gaussian graphical model. However, in many applications it is more realistic to fit a collection of such models, due to the heterogeneity of the data involved. By heterogeneous data we mean data from several categories that share the same variables but differ in their dependence structure, with some edges common across all categories and other edges unique to each category. For example, consider gene networks describing different subtypes of the same cancer: there are some shared pathways across different subtypes, and there are also links that are unique to a particular subtype. Another example from text mining, which is discussed in detail in §5, is word relationships inferred from webpages. In our example, the webpages are collected from university computer science departments, and the different categories correspond to faculty, student, course, etc. In such cases, borrowing strength across different categories by jointly estimating these models could reveal a common structure and reduce the variance of the estimates, especially when the number of samples is relatively small. To accomplish this joint estimation, we propose a method that links the estimation of separate graphical models through a hierarchical penalty. Its main advantage is the ability to discover a common structure and jointly estimate common links across graphs, which leads to improvements compared to fitting separate models, since it borrows information from other related graphs. While in this paper we focus on continuous data, this methodology can be extended to graphical models with categorical variables; fitting such models to a single graph has been considered by M. Kolar and E. P. Xing in a 2008 unpublished preprint, arXiv:0811.1239, Hoefling & Tibshirani (2009) and Ravikumar et al. (2009).

2. Methodology

2.1. Problem set-up

Suppose we have a heterogeneous dataset with p variables and K categories. The kth category contains n_k observations ${\left(x_1^k,\dots ,x_{n_k}^{(k)}\right)}^{\text{T}}$, where each $x_i^{(k)}=\left(x_{i,1}^{(k)},\dots ,x_{i,p}^{(k)}\right)$ is a p-dimensional row vector. Without loss of generality, we assume that the observations in the same category are centred along each variable, i.e., ${\sum }_{i=1}^{n_k}{x}_{i,j}^{(k)}=0$ for all j = 1, . . . , p and k = 1, . . . , K. We further assume that $x_1^{(k)},\dots ,x_{n_k}^{(k)}$ are an independent and identically distributed sample from a p-variate Gaussian distribution with mean zero, without loss of generality since the data are centred, and covariance matrix Σ^(k). Let ${\mathrm{\Omega }}^{(k)}={\left({\mathrm{\Sigma }}^{(k)}\right)}^{-1}={\left({\omega }_{j,j^{\prime }}^{(k)}\right)}_{p\times p}$. The loglikelihood of the observations in the kth category is

$$l\left({\mathrm{\Omega }}^{(k)}\right)=-\frac{n_k}{2}\text{log}(2\pi )+\frac{n_k}{2}\left[\text{log}\left\{\text{det}\left({\mathrm{\Omega }}^{(k)}\right)\right\}-\text{tr}\left({\widehat{\mathrm{\Sigma }}}^{(k)}{\mathrm{\Omega }}^{(k)}\right)\right],$$

where Σ̂^(k) is the sample covariance matrix for the kth category, and det(·) and tr(·) are the determinant and the trace of a matrix, respectively.

The most direct way to deal with such data is to estimate K individual graphical models. We can compute a separate ℓ₁-regularized estimator for each category k (k = 1, . . . , K) by solving

$$\underset{{\mathrm{\Omega }}^{(k)}}{\text{min}}\text{tr}\left({\widehat{\mathrm{\Sigma }}}^{(k)}{\mathrm{\Omega }}^{(k)}\right)-\text{log}\left\{\text{det}\left({\mathrm{\Omega }}^{(k)}\right)\right\}+{\lambda }_k\sum _{j\ne j^{\prime }}\left|{\omega }_{j,j^{\prime }}^{(k)}\right|,$$ (1)

where the minimum is taken over symmetric positive definite matrices. The ℓ₁ penalty shrinks some of the off-diagonal elements in Ω^(k) to zero and the tuning parameter λ_k controls the degree of the sparsity in the estimated inverse covariance matrix. Problem (1) can be efficiently solved by existing algorithms such as the graphical lasso (Friedman et al., 2008). We will refer to this approach as the separate estimation method and use it as a benchmark to compare with the joint estimation method we propose next.

2.2. The joint estimation method

To improve estimation when graphical models for different categories may share some common structure, we propose a joint estimation method. First, we reparameterize each off-diagonal element ${\omega }_{j,j^{\prime }}^{(k)}$ as ${\omega }_{j,j^{\prime }}^{(k)}={\theta }_{j,j^{\prime }}{\gamma }_{j,j^{\prime }}^{(k)}$ (1 ⩽ j ≠ j^′ ⩽ p; k = 1, . . . , K). An analogous parameterization in a dimension reduction setting was used in Michailidis & de Leeuw (2001). To avoid sign ambiguity between θ and γ, we restrict θ_{j, j′} ⩾ 0, 1 ⩽ j ≠ j^′ ⩽ p. To preserve symmetry, we require that θ_{j, j′} = θ_{j′, j} and ${\gamma }_{j,j^{\prime }}^{(k)}={\gamma }_{j^{\prime },j}^{(k)}$ (1 ⩽ j ≠ j^′ ⩽ p; k = 1, . . . , K). For all diagonal elements, we also require θ_{j, j} = 1 and ${\gamma }_{j,j^{\prime }}^{(k)}={\omega }_{j,j}^{(k)}$ (j = 1, . . . , p; k = 1, . . . , K). This decomposition treats ( ${\omega }_{j,j^{\prime }}^{(1)},\dots ,{\omega }_{j,j^{\prime }}^{(K)}$) as a group, with the common factor θ_{j, j′} controlling the presence of the link between nodes j and j^′ in any of the categories, and ${\gamma }_{j,j^{\prime }}^{(k)}$ reflects the differences between categories. Let Θ = (θ_{j, j′})_p×p and ${\mathrm{\Gamma }}^{(k)}={\left({\gamma }_{j,j^{\prime }}^{(k)}\right)}_{p\times p}$. To estimate this model, we propose the following penalized criterion subject to all constraints mentioned above:

$$\underset{\mathrm{\Theta },{\left({\mathrm{\Gamma }}^{(k)}\right)}_{k=1}^K}{\text{min}}\sum _{k=1}^K\left[\text{tr}\left({\widehat{\mathrm{\Sigma }}}^{(k)}{\mathrm{\Omega }}^{(k)}\right)-\text{log}\left\{\text{det}\left({\mathrm{\Omega }}^{(k)}\right)\right\}\right]+{\eta }_1\sum _{j\ne j^{\prime }}{\theta }_{j,j^{\prime }}+{\eta }_2\sum _{j\ne j^{\prime }}\sum _{k=1}^K\left|{\gamma }_{j,j^{\prime }}^{(k)}\right|,$$ (2)

where η₁ and η₂ are two tuning parameters. The first, η₁, controls the sparsity of the common factors θ_j,j′ and can effectively identify the common zero elements across Ω⁽¹⁾, . . . , Ω^(K); i.e. if θ_j,j′ is shrunk to zero, there will be no link between nodes j and j^′ in any of the K graphs. If θ_j,j′ is not zero, some of the ${\gamma }_{j,j^{\prime }}^{(k)}$, and hence some of the ${\omega }_{j,j^{\prime }}^{(k)}$, can still be set to zero by the second penalty. This allows graphs belonging to different categories to have different structures. This decomposition has also been used by N. Zhou and J. Zhu in a 2007 unpublished preprint, arXiv:1006.2871, for group variable selection in regression problems.

Criterion (2) involves two tuning parameters η₁ and η₂; it turns out that this could be reduced to an equivalent problem with a single tuning parameter. Specifically, consider

$$\underset{\mathrm{\Theta },{\left({\mathrm{\Gamma }}^{(k)}\right)}_{k=1}^K}{\text{min}}\sum _{k=1}^K\left[\text{tr}\left({\widehat{\mathrm{\Sigma }}}^{(k)}{\mathrm{\Omega }}^{(k)}\right)-\text{log}\left\{\text{det}\left({\mathrm{\Omega }}^{(k)}\right)\right\}\right]+\sum _{j\ne j^{\prime }}{\theta }_{j,j^{\prime }}+\eta \sum _{j\ne j^{\prime }}\sum _{k=1}^K\left|{\gamma }_{j,j^{\prime }}^{(k)}\right|,$$ (3)

where η = η₁η₂. For two matrices A and B of the same size, we denote their Schur–Hadamard product by A · B. Criteria (2) and (3) are equivalent in the following sense.

Lemma 1. Let {Θ̂*, ${\left({\widehat{\mathrm{\Gamma }}}^{(k)*}\right)}_{k=1}^K$} be a local minimizer of criterion (3). Then, there exists a local minimizer of criterion (2), denoted as {Θ̂**, ${\left({\widehat{\mathrm{\Gamma }}}^{(k)**}\right)}_{k=1}^K$}, such that Θ̂** · Γ̂^(k)**·= Θ̂* · Γ̂^(k) for all k = 1, . . . , K. Similarly, if {Θ̂**, ${\left({\widehat{\mathrm{\Gamma }}}^{(k)**}\right)}_{k=1}^K$} is a local minimizer of criterion (2), then there exists a local minimizer of criterion (3), denoted as {Θ̂*, ${\left({\widehat{\mathrm{\Gamma }}}^{(k)*}\right)}_{k=1}^K$}, such that Θ̂** · Γ̂^(k)** = Θ̂* · Γ̂^(k)* for all k = 1, . . . , K.

The proof follows closely the proof of the lemma in Zhou and Zhu’s unpublished 2007 preprint, and is omitted. This result implies that in practice, instead of tuning two parameters η₁ and η₂, we only need to tune one parameter η, which reduces the overall computational cost.

2.3. The algorithm

First we reformulate the problem (3) in a more convenient form for computational purposes.

Lemma 2. Let ${\left({\widehat{\mathrm{\Omega }}}^{(k)}\right)}_{k=1}^K$ be a local minimizer of

$$\underset{{\left({\mathrm{\Omega }}^{(k)}\right)}_{k=1}^K}{\text{min}}\sum _{k=1}^K\left[\text{tr}\left({\widehat{\mathrm{\Sigma }}}^{(k)}{\mathrm{\Omega }}^{(k)}\right)-\text{log}\left\{\text{det}\left({\mathrm{\Omega }}^{(k)}\right)\right\}\right]+\lambda \sum _{j\ne j^{\prime }}{\left(\sum _{k=1}^K\left|{\omega }_{j,j^{\prime }}^{(k)}\right|\right)}^{1/2},$$ (4)

where λ = 2η^1/2. Then, there exists a local minimizer of (3), {Θ̂, ${\left({\widehat{\mathrm{\Gamma }}}^{(k)}\right)}_{k=1}^K$}, such that Ω̂^(k) = Θ̂ · Γ̂^(k), for all k = 1, . . . , K. On the other hand, if {Θ̂, ${\left({\widehat{\mathrm{\Gamma }}}^{(k)}\right)}_{k=1}^K$} is a local minimizer of (3), then there also exists a local minimizer of (4), ${\left({\widehat{\mathrm{\Omega }}}^{(k)}\right)}_{k=1}^K$, such that Ω̂^(k) = Θ̂ · Γ̂^(k), for all k = 1, . . . , K.

The proof follows closely the proof of the lemma in Zhou and Zhu’s unpublished 2007 preprint, and is omitted. To optimize (4) we use an iterative approach based on local linear approximation (Zou & Li, 2008). Specifically, letting ${\left({\omega }_{j,j^{\prime }}^{(k)}\right)}^{(t)}$ denote the estimates from the previous iteration t, we approximate ${\left({\sum }_{k=1}^K\left|{\omega }_{j,j^{\prime }}^{(k)}\right|\right)}^{1/2}\sim {\sum }_{k=1}^K\left|{\omega }_{j,j^{\prime }}^{(k)}\right|/{\left\{{\sum }_{k=1}^K\left|{\left({\omega }_{j,j^{\prime }}^{(k)}\right)}^{(t)}\right|\right\}}^{1/2}$. Thus, at the (t + 1)th iteration, problem (4) is decomposed into K individual optimization problems:

$${\left({\mathrm{\Omega }}^{(k)}\right)}^{(t+1)}=\underset{{\mathrm{\Omega }}^{(k)}}{\text{argmin}}\left[\text{tr}\left({\widehat{\mathrm{\Sigma }}}^{(k)}{\mathrm{\Omega }}^{(k)}\right)-\text{log}\left\{\text{det}\left({\mathrm{\Omega }}^{(k)}\right)\right\}\right]+\lambda \sum _{j\ne j^{\prime }}{\tau }_{j,j^{\prime }}^{(k)}\left|{\omega }_{j,j^{\prime }}^{(k)}\right|,$$ (5)

where ${\tau }_{j,j^{\prime }}^{(k)}={\left\{{\sum }_{k=1}^K\left|{\left({\omega }_{j,j^{\prime }}^{(k)}\right)}^{(t)}\right|\right\}}^{-1/2}$. Criterion (5) is exactly the sparse inverse covariance matrix estimation problem with weighted ℓ₁ penalty; the solution can be efficiently computed using the graphical lasso algorithm of Friedman et al. (2008). For numerical stability, we threshold ${\left\{{\sum }_{k=1}^K\left|{\left({\omega }_{j,j^{\prime }}^{(k)}\right)}^{(t)}\right|\right\}}^{1/2}$ at 10⁻¹⁰. In summary, the proposed algorithm for solving (4) is:

• Step 0. Initialize Ω̂^(k) = (Σ̂^(k) + νI_p)⁻¹ for all k = 1, . . . , K, where I_p is the identity matrix and the constant ν is chosen to guarantee Σ̂^(k)+ νI_p is positive definite.

• Step 1. Update Ω̂^(k) by (5) for all k = 1, . . . , K using graphical lasso.

• Step 2. Repeat Step 1 until convergence is achieved.

2.4. Model selection

The tuning parameter λ in (4) controls the sparsity of the resulting estimator. It can be selected either by some type of Bayesian information criterion or through crossvalidation. The former balances the goodness of fit of the model and its complexity, while the latter seeks to optimize its predictive power. Specifically, for the proposed joint estimation method we define

$$\text{BIC}(\lambda )=\sum _{k=1}^K\left[\text{tr}\left({\widehat{\mathrm{\Sigma }}}^{(k)}{\widehat{\mathrm{\Omega }}}_{\lambda }^{(k)}\right)-\text{log}\left\{\text{det}\left({\widehat{\mathrm{\Omega }}}_{\lambda }^{(k)}\right)\right\}+{\text{df}}_k\text{log}\left(n_k\right)\right],$$

where ${\widehat{\mathrm{\Omega }}}_{\lambda }^{(1)},\dots ,{\widehat{\mathrm{\Omega }}}_{\lambda }^{(K)}$ are the estimates from (4) with tuning parameter λ and the degrees of freedom are defined as ${\text{df}}_k=\#\left\{\left(j,j^{\prime }\right):j<j^{\prime },{\widehat{\omega }}_{j,j^{\prime }}^{(k)}\ne 0\right\}$. An analogous definition of the degrees of freedom for the lasso has been proposed by Zou et al. (2007).

The crossvalidation method randomly splits the dataset into D segments of equal size. For the kth category, we denote the sample covariance matrix using the data in the dth segment (d = 1, . . . , D) by Σ̂^(k,d) and the inverse covariance matrix estimated using all the data excluding those in the dth segment and the tuning parameter λ by ${\widehat{\mathrm{\Omega }}}_{\lambda }^{\left(k,-d\right)}$. Then we choose λ that minimizes the average predictive negative loglikelihood as follows:

$$\text{CV}(\lambda )=\sum _{d=1}^D\sum _{k=1}^K\left[\text{tr}\left({\widehat{\mathrm{\Sigma }}}^{\left(k,d\right)}{\widehat{\mathrm{\Omega }}}_{\lambda }^{\left(k,-d\right)}\right)-\text{log}\left\{\text{det}\left({\widehat{\mathrm{\Omega }}}_{\lambda }^{\left(k,-d\right)}\right)\right\}\right].$$

Crossvalidation can in general be expected to be more accurate than the heuristic bic; it is much more computationally intensive however, which is why we consider both options. We provide some comparisons between the tuning parameter selection methods in §4.

3. Asymptotic properties

Next, we derive the asymptotic properties of the joint estimation method, including consistency, as well as sparsistency, when both p and n go to infinity and the tuning parameter goes to zero at a certain rate. First, we introduce the necessary notation and state certain regularity conditions on the true precision matrices ( ${\mathrm{\Omega }}_0^{(1)},\dots ,{\mathrm{\Omega }}_0^{(K)}$), where ${\mathrm{\Omega }}_0^{(k)}={\left({\omega }_{0,j,j^{\prime }}^{(k)}\right)}_{p\times p}$ (k = 1, . . . , K).

Let T_k = {(j, j^′) : j ≠ j^′, ${\omega }_{j,j^{\prime }}^{(k)}\ne 0$} be the set of indices of all nonzero off-diagonal elements in Ω^(k), and let T = T₁ ∪ ⋯ ∪ T_K. Let q_k = |T_k| and q = |T| be the cardinalities of T_k and T, respectively. In general, T_k and q_k depend on p. In addition, let ‖ · ‖_F and ‖ · ‖ be the Frobenius norm and the 2-norm of matrices, respectively. We assume that the following regularity conditions hold.

Condition 1. There exist constants τ₁, τ₂ such that for all p ⩾ 1 and k = 1, . . . , K, 0 < τ₁ < ${\varphi }_{\text{min}}\left({\mathrm{\Omega }}_0^{(k)}\right)⩽{\varphi }_{\text{max}}\left({\mathrm{\Omega }}_0^{(k)}\right)$ < τ₂ < ∞, where ϕ_min and ϕ_max indicate the minimal and maximal eigenvalues.

Condition 2. There exists a constant τ₃ > 0 such that min_k=1,...,K ${\text{min}}_{\left(j,j^{\prime }\right)\in T_k}\left|{\omega }_{0,j,j^{\prime }}^{(k)}\right|⩾{\tau }_3$.

Condition 1 is standard, and is also used in Bickel & Levina (2008) and Rothman et al. (2008), which guarantees that the inverse exists and is well conditioned. Condition 2 ensures that nonzero elements are bounded away from zero.

Theorem 1 (Consistency). Suppose Conditions 1 and 2 hold, (p + q)(log p)/n = o(1) and Λ₁{(log p)/n}^1/2 ⩽ λ ⩽ Λ₂{(1 + p/q)(log p)/n}^1/2 for some positive constants Λ₁ and Λ₂. Then there exists a local minimizer ${\left({\widehat{\mathrm{\Omega }}}^{(k)}\right)}_{k=1}^K$ of (4), such that

$$\sum _{k=1}^K{\Vert {\widehat{\mathrm{\Omega }}}^{(k)}-{\mathrm{\Omega }}_0^{(k)}\Vert }_F=O_{\text{p}}\left[{\left\{\frac{\left(p+q\right)\text{log}p}{n}\right\}}^{1/2}\right].$$

Theorem 2 (Sparsistency). Suppose all conditions in Theorem 1 hold. We further assume ${\sum }_{k=1}^K{\Vert {\widehat{\mathrm{\Omega }}}^{(k)}-{\mathrm{\Omega }}_0^{(k)}\Vert }^2=O_{\text{p}}\left({\eta }_n\right)$, where η_n → 0 and ${\left\{\left(\text{log}p\right)/n\right\}}^{1/2}+{\eta }_n^{1/2}=O(\lambda )$. Then with probability tending to 1, the local minimizer ${\left({\widehat{\mathrm{\Omega }}}^{(k)}\right)}_{k=1}^K$ in Theorem 1 satisfies ${\widehat{\omega }}_{j,j^{\prime }}^{(k)}=0$ for all $\left(j,j^{\prime }\right)\in T_k^c$, k = 1, . . . , K.

This theorem is analogous to Theorem 2 of Lam & Fan (2009). The consistency requires both an upper and a lower bound on λ, whereas sparsistency requires consistency and an additional lower bound on λ. To make the bounds compatible, we require ${\left\{\left(\text{log}p\right)n\right\}}^{1/2}+{\eta }_n^{1/2}=O\left[{\left\{\left(1+p/q\right)\left(\text{log}p\right)/n\right\}}^{1/2}\right]$. Since η_n is the rate of convergence in the operator norm, we can bound it using the fact that ${\Vert M\Vert }_F^2/p⩽{\Vert M\Vert }^2⩽{\Vert M\Vert }_F^2$. This leads to two extreme cases. In the worst-case scenario, ${\sum }_k\Vert {\widehat{\mathrm{\Omega }}}^{(k)}-{\mathrm{\Omega }}_0^{(k)}\Vert$ has the same rate as ${\sum }_k{\Vert {\widehat{\mathrm{\Omega }}}^{(k)}-{\mathrm{\Omega }}_0^{(k)}\Vert }_F$ and thus η_n = O{(p + q)(log p)/n}. The two bounds are compatible only when q = O(1). In the best-case scenario, ${\sum }_k\Vert {\widehat{\mathrm{\Omega }}}^{(k)}-{\mathrm{\Omega }}_0^{(k)}\Vert$ has the same rate as ${\sum }_k{\Vert {\widehat{\mathrm{\Omega }}}^{(k)}-{\mathrm{\Omega }}_0^{(k)}\Vert }_F/p^{1/2}$. Then, η_n = O{(1 + q/p)(log p)/n} and we have both consistency and sparsistency as long as q = O(p).

4. Numerical evaluation

4.1. Simulation settings

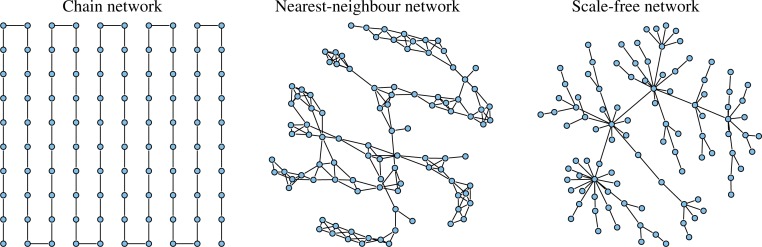
In this section, we assess the performance of the joint estimation method on three types of simulated networks: a chain, a nearest-neighbour and a scale-free network. In all cases, we set p = 100 and K = 3. For each k = 1, . . . , K, we generate n_k = 100 independently and identically distributed observations from a multivariate normal distribution N{0, (Ω^(k))⁻¹}, where Ω^(k) is the inverse covariance matrix of the kth category. The details of the three simulated examples are as follows.

In the first example, we follow the simulation set-up in Fan et al. (2009) to generate a chain network, which corresponds to a tridiagonal inverse covariance matrix. The covariance matrices Σ^(k) are constructed as follows: let the (j, j′)th element ${\sigma }_{j,j^{\prime }}^{(k)}=\text{exp}\left(-\left|s_j-s_{j^{\prime }}\right|/2\right)$, where s₁ < s₂ < ⋯ < s_p and s_j − s_j−1 ∼ Un(0.5, 1) (j = 2, . . . , p).

Further, let Ω^(k) = (Σ^(k))⁻¹. The K precision matrices generated by this procedure share the same pattern of zeros, i.e. the common structure, but the values of their nonzero off-diagonal elements may be different. The left panel of Fig. 1 shows the common link structure across the K categories. Further, we add heterogeneity to the common structure by creating additional individual links as follows: for each Ω^(k) (k = 1, . . . , K), we randomly pick a pair of symmetric zero elements and replace them with a value uniformly generated from the [−1, −0.5] ∪ [0.5, 1] interval. This procedure is repeated ρM times, where M is the number of off-diagonal nonzero elements in the lower triangular part of Ω^(k) and ρ is the ratio of the number of individual links to the number of common links. In the simulations, we considered values of ρ = 0, 1/4, 1 and 4, thus gradually increasing the proportion of individual links.

Fig. 1.

The common links present in all categories in the three simulated networks.

In the second example, the nearest-neighbour networks are generated by modifying the data generating mechanism described in Li & Gui (2006). Specifically, we generate p points randomly on a unit square, calculate all p(p − 1)/2 pairwise distances, and find m nearest neighbours of each point in terms of this distance. The nearest neighbour network is obtained by linking any two points that are m-nearest neighbours of each other. The integer m controls the degree of sparsity of the network and the value m = 5 was chosen in our study. The middle panel of Fig. 1 illustrates a realization of the common structure of a nearest-neighbour network. Subsequently, K individual graphs were generated, by adding some individual links to the common graph with ρ = 0, 1/4, 1, 4 by the same method as described in Example 1, with values for the individual links ${\omega }_{j,j^{\prime }}^{(k)}$ generated from a uniform distribution on [−1, 0.5] ∪ [0.5, 1].

In the last example, we generate the common structure of a scale-free network using the Barabasi–Albert algorithm (Barabasi & Albert, 1999); a realization is depicted in the right panel of Fig. 1. The individual links in the kth network (k = 1, . . . , K), are randomly added as before, with ρ = 0, 1/4, 1, 4 and the associated elements in Ω^(k) are generated uniformly on [−1, −0.5] ∪ [0.5, 1].

We compare the joint estimation method to the method that estimates each category separately via (1). A number of metrics are used to assess performance, including receiver operating characteristic curves, average entropy loss, average Frobenius loss, average false positive and average false negative rates, and the average rate of misidentified common zeros among the categories. For the receiver operating characteristic curve, we plot sensitivity, the average proportion of correctly detected links, against the average false positive rate over a range of values of the tuning parameter λ. The average entropy loss and average Frobenius loss are defined as

$$\begin{array}{lll}\text{EL}\hfill & =\hfill & \frac{1}{K}\sum _{k=1}^K\text{tr}\left\{{\left({\mathrm{\Omega }}^{(k)}\right)}^{-1}{\widehat{\mathrm{\Omega }}}^{(k)}\right\}-\text{log}\left[\text{det}\left\{{\left({\mathrm{\Omega }}^{(k)}\right)}^{-1}{\widehat{\mathrm{\Omega }}}^{(k)}\right\}\right]-p,\hfill \\ \text{FL}\hfill & =\hfill & \frac{1}{K}\sum _{k=1}^K{\Vert {\mathrm{\Omega }}^{(k)}-{\widehat{\mathrm{\Omega }}}^{(k)}\Vert }_F^2/{\Vert {\mathrm{\Omega }}^{(k)}\Vert }_F^2.\hfill \end{array}$$ (6)

The average false positive rate gives the proportion of false discoveries, that is, true zeros estimated as nonzero; the average false negative rate gives the proportion of off-diagonal nonzero elements estimated as zero; and the common zeros error rate gives the proportion of common zeros across Ω⁽¹⁾, . . . , Ω^(K) estimated as nonzero. The respective formal definitions are

$$\begin{array}{l}\text{FP}=\frac{1}{K}\sum _{k=1}^K\frac{{\sum }_{1⩽j<j^{\prime }⩽p}\text{I}\left({\omega }_{j,j^{\prime }}^{(k)}=0,{\widehat{\omega }}_{j,j^{\prime }}^{(k)}\ne 0\right)}{{\sum }_{1⩽j<j^{\prime }⩽p}\text{I}\left({\omega }_{j,j^{\prime }}^{(k)}=0\right)},\\ \text{FN}=\frac{1}{K}\sum _{k=1}^K\frac{{\sum }_{1⩽j⩽j^{\prime }⩽p}\text{I}\left({\omega }_{j,j^{\prime }}^{(k)}\ne 0,{\widehat{\omega }}_{j,j^{\prime }}^{(k)}=0\right)}{{\sum }_{1⩽j<j^{\prime }⩽p}\text{I}\left({\omega }_{j,j^{\prime }}^{(k)}\ne 0\right)},\\ \text{CZ}=\frac{{\sum }_{1⩽j<j^{\prime }⩽p}\text{I}\left({\sum }_{k=1}^K\left|{\omega }_{j,j^{\prime }}^{(k)}\right|=0,{\sum }_{k=1}^K\left|{\widehat{\omega }}_{j,j^{\prime }}^{(k)}\right|\ne 0\right)}{{\sum }_{1⩽j<j^{\prime }⩽p}\text{I}\left({\sum }_{k=1}^K\left|{\omega }_{j,j^{\prime }}^{(k)}\right|=0\right)}.\end{array}$$ (7)

4.2. Simulation results

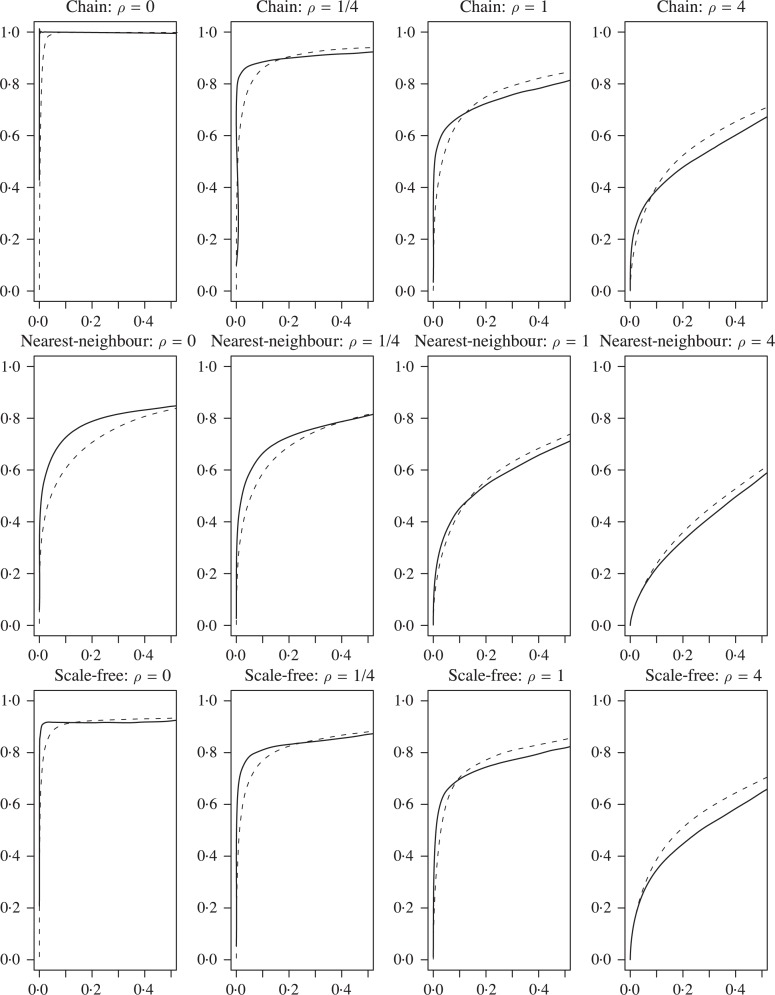
Figure 2 shows the estimated roc, receiver operating characteristic, curves averaged over 50 replications for all three simulated examples, obtained by varying the tuning parameter. It can be seen that the curves estimated by the joint estimation method dominate those of the separate estimation method when the proportion of individual links is low. As ρ increases, the structures become more and more different, and the joint and separate methods move closer together, with the separate method eventually slightly outperforming the joint method at ρ = 4, although the results are still fairly similar. This is precisely as it should be, since the joint estimation method has the biggest advantage with the most overlap in structure. In order to assess the variability of the two methods, we drew the boxplots of the sensitivity of the two models with the false positive rate controlled at 5%; the results indicate that as long as there is a substantial common structure, the joint method is superior to the separate method and the difference is statistically significant.

Fig. 2.

Receiver operating characteristic curves. The horizontal and vertical axes in each panel are false positive rate and sensitivity, respectively. The solid line corresponds to the joint estimation method, and the dashed line corresponds to the separate estimation method. ρ is the ratio of the number of individual links to the number of common links.

Table 1 summarizes the results based on 50 replications with the tuning parameter selected by bic(λ) and crossvalidation as described in §2.4. In general, the joint estimation method produces lower entropy and Frobenius norm losses for both model selection criteria, with the difference most pronounced at low values of ρ. For the joint method, the two model selection criteria exhibit closer agreement in false positive and false negative rates and the proportion of misidentified common zeros. For the separate method, however, crossvalidation tends to select more false positive links, which result in more misidentified common zeros.

Table 1.

Results from the three simulated examples. In each cell, the numbers before and after the slash correspond to the results from selected by bic and crossvalidation, respectively

Example	ρ	Method	el	fl	fn (%)	fp (%)	cz (%)
Chain	0	S	20.7 / 21.9	0.5 / 0.5	0.8 / 0.1	5.7 / 21.8	14.5 / 51.0
		J	12.8 / 6.6	0.3 / 0.3	0.0 / 0.0	4.3 / 0.5	7.0 / 1.2
	1/4	S	21.3 / 16.6	0.5 / 0.5	41.3 / 9.0	1.3 / 18.7	3.8 / 46.0
		J	9.5 / 8.7	0.3 / 0.3	15.6 / 17.6	1.7 / 0.7	3.2 / 1.4
	1	S	23.0 / 17.1	0.5 / 0.5	73.7 / 24.4	0.7 / 18.8	1.9 / 46.4
		J	12.5 / 12.4	0.4 / 0.4	44.2 / 45.8	1.6 / 1.1	3.0 / 2.0
	4	S	29.8 / 20.2	0.6 / 0.5	97.3 / 47.5	0.1 / 19.5	0.3 / 47.8
		J	20.0 / 20.7	0.5 / 0.5	75.5 / 76.2	1.9 / 1.8	3.2 / 3.0
Nearest-neighbour	0	S	11.9 / 15.9	0.4 / 0.5	40.1 / 33.5	2.2 / 16.1	6.1 / 40.5
		J	6.1 / 11.3	0.3 / 0.4	18.5 / 52.7	1.6 / 0.6	3.2 / 1.3
	1/4	S	13.9 / 17.1	0.4 / 0.5	44.0 / 32.5	2.4 / 17.6	6.9 / 43.9
		J	8.1 / 14.5	0.3 / 0.4	27.4 / 57.5	1.7 / 1.0	2.9 / 1.7
	1	S	18.5 / 18.0	0.5 / 0.5	48.5 / 45.3	4.0 / 17.8	11.2 / 44.3
		J	13.0 / 19.0	0.4 / 0.5	40.0 / 77.3	2.8 / 1.2	3.8 / 2.0
	4	S	24.8 / 20.1	0.5 / 0.5	98.7 / 65.5	0.1 / 18.1	0.3 / 44.9
		J	19.3 / 23.8	0.7 / 0.5	80.8 / 95.0	3.2 / 1.0	4.8 / 1.6
Scale-free	0	S	16.9 / 15.5	0.5 / 0.5	20.7 / 6.4	1.9 / 17.1	5.3 / 42.1
		J	8.1 / 7.0	0.3 / 0.3	9.4 / 11.2	1.5 / 0.5	2.8 / 1.0
	1/4	S	17.1 / 14.5	0.5 / 0.4	49.6 / 17.5	1.2 / 16.6	3.7 / 41.8
		J	9.4 / 9.1	0.3 / 0.3	29.3 / 32.2	1.3 / 0.8	2.4 / 1.4
	1	S	22.3 / 18.1	0.5 / 0.5	51.8 / 22.5	2.8 / 19.3	8.2 / 47.4
		J	15.2 / 15.3	0.4 / 0.4	42.5 / 43.1	2.2 / 2.0	3.2 / 2.9
	4	S	27.9 / 20.0	0.6 / 0.5	99.6 / 49.6	0.0 / 19.1	0.0 / 47.0
		J	23.0 / 23.8	0.5 / 0.5	82.5 / 84.1	2.1 / 1.8	3.2 / 2.7

S, the separate method; J, the joint method; el, fl, fn, fp and cz are defined in equations (6) and (7); ρ the ratio of the number of individual links to the number of common links.

5. University webpages example

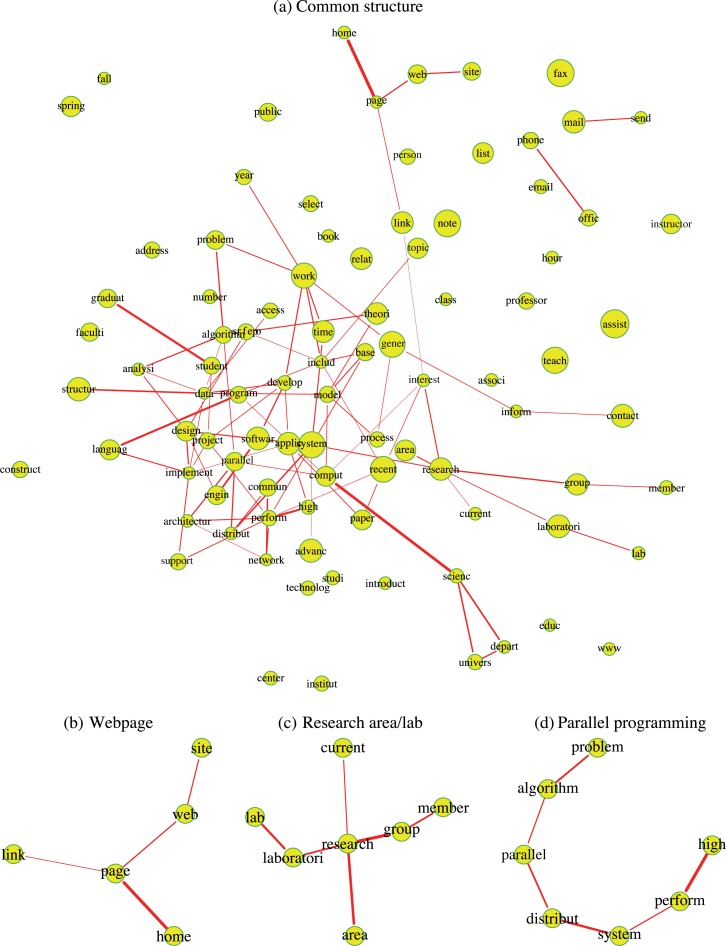
The dataset was collected in 1997 and includes webpages from computer science departments at Cornell, the University of Texas, University of Washington and University of Wis-consin. The original data have been pre-processed using standard text processing procedures, such as removing stopwords and stemming the words. The pre-processed dataset can be downloaded from http://web.ist.utl.pt/~acardoso/datasets/. The webpages were manually classified into seven categories, from which we selected the four largest for our analysis: student, faculty, course and project, with 544, 374, 310 and 168 webpages, respectively. The log-entropy weighting method (Dumais, 1991) was used to calculate the term-document matrix X = (x_{i, j})_n×p, with n and p denoting the number of webpages and distinct terms, respectively. Let f_i,j (i = 1, . . . , n; j = 1, . . . , p) be the number of times the jth term appears in the ith webpage and let $p_{i,j}=f_{i,j}/{\sum }_{i=1}^n{f}_{i,j}$. Then, the log-entropy weight of the j th term is defined as $e_j=1+{\sum }_{i=1}^n{p}_{i,j}\left(\text{log}{p}_{i,j}\right)/\text{log}n$. Finally, the term-document matrix X is defined as x_{i, j} = e_j log(1 + f_i,j) (i = 1, . . . , n; j = 1, . . . , p) and it is normalized along each column. We applied the proposed joint estimation method to n = 1396 documents in the four largest categories and p = 100 terms with the highest log-entropy weights out of a total of 4800 terms. The resulting common network structure is shown in Fig. 3(a). The area of the circle representing a node is proportional to its log-entropy weight, while the thickness of an edge is proportional to the magnitude of the associated partial correlation. The plot reveals the existence of some high degree nodes, such as research, data, system, perform, that are part of the computer science vocabulary. Further, some standard phrases in computer science, such as home-page, comput-scienc, program-languag, data-structur, distribut-system and high-perform, have high partial correlations among their constituent words in all four categories. A few subgraphs extracted from the common network are shown in Fig. 3(b)–(d); each graph clearly has its own semantic meaning, which we loosely label as webpage generic, research area/lab and parallel programming.

Fig. 3.

Common structure in the webpages data. Panel (a) shows the estimated common structure for the four categories. The nodes represent 100 terms with the highest log-entropy weights. The area of the circle representing a node is proportional to its log-entropy weight. The width of an edge is proportional to the magnitude of the associated partial correlation. Panels (b)–(d) show subgraphs extracted from the graph in panel (a).

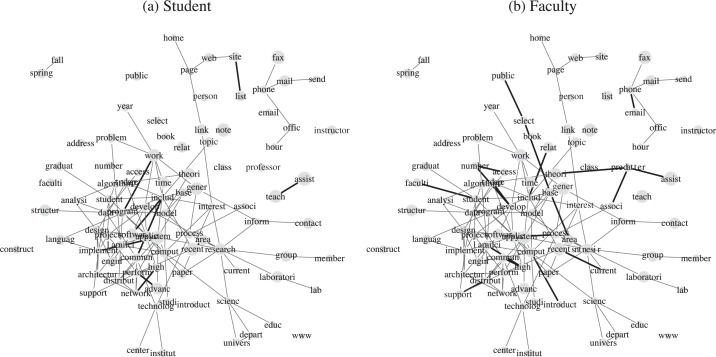
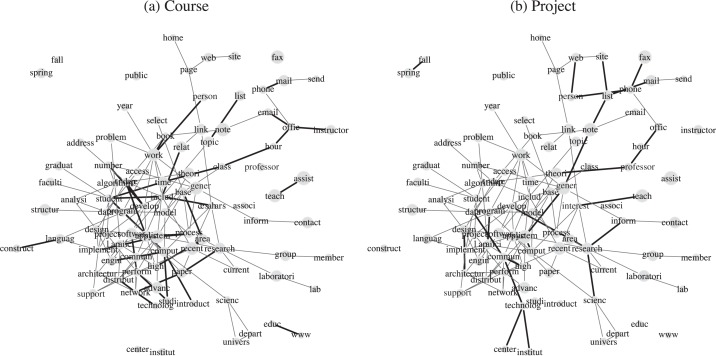
The model also allows us to explore the heterogeneity between different categories. As an example, we show the graphs for the student and faculty categories in Fig. 4. It can be seen that terms teach and assist are only linked in the student category, since many graduate students are employed as teaching assistants. On the other hand, some term pairs only have links in the faculty category, such as select-public, faculti-student, assist-professor and associ-professor. Similarly, we illustrate the differences between the course and project categories in Fig. 5. Some teaching-related terms are linked only in the course category, such as office-hour, office-instructor and teach-assist, while pairs in the project category are connected to research, such as technolog-center, technolog-institut, research-scienc and research-inform. Overall, the model captures the basic common semantic structure of the websites, but also identifies meaningful differences across the various categories. When each category is estimated separately, individual links dominate, and the results are not as easy to interpret. The graphical models obtained by separate estimation are not shown for lack of space.

Fig. 4.

‘Student’ and ‘Faculty’ graphs. The thin light lines are the links appearing in both categories, and the thick dark lines are the links only appearing in one category.

Fig. 5.

‘Course’ and ‘Project’ graphs. The thin light lines are the links appearing in both categories, and the thick dark lines are the links only appearing in one category.

Appendix

In the beginning, we state some results used in the proof of Theorem 1 that were established in Rothman et al. (2008, Theorem 1). We use the following notation: for a matrix M = (m _j,j′)_p×p, |M|₁ = ∑_j,j′ |m_j,j′|, M⁺ is a diagonal matrix with the same diagonal as M, M⁻ = M − M⁺ and M_S is M with all elements outside an index set S replaced by zeros. We also write M^˜ for the vectorized p² × 1 form of M, and ⊗ for the Kronecker product of two matrices. In addition, we denote ${\mathrm{\Sigma }}_0^{(k)}={\left({\mathrm{\Omega }}_0^{(k)}\right)}^{-1}$ as the true covariance matrix of the kth category (k = 1, . . . , K).

Lemma A1. Let l(Ω^(k)) = tr(Σ̂^(k)Ω^(k)) − log {det(Ω^(k))}. Then for any k = 1, . . . , K, the following decomposition holds:

$$\begin{array}{r}\hfill l\left({\mathrm{\Omega }}_0^{(k)}+{\mathrm{\Delta }}^{(k)}\right)-l\left({\mathrm{\Omega }}_0^{(k)}\right)=\text{tr}\left\{\left({\widehat{\mathrm{\Sigma }}}^{(k)}-{\mathrm{\Sigma }}_0^{(k)}\right){\mathrm{\Delta }}^{(k)}\right\}+{\left({\tilde{\mathrm{\Delta }}}^{(k)}\right)}^{\text{T}}\{{\int }_0^1\left(1-\upsilon \right){\left({\mathrm{\Omega }}_0^{(k)}+\upsilon {\mathrm{\Delta }}^{(k)}\right)}^{-1}\\ \hfill \otimes {\left({\mathrm{\Omega }}_0^{(k)}+\upsilon {\mathrm{\Delta }}^{(k)}\right)}^{-1}d\upsilon \}{\tilde{\mathrm{\Delta }}}^{(k)}.\end{array}$$ (A1)

Further, there exist positive constants C₁ and C₂ such that with probability tending to 1

$$\left|\text{tr}\left\{\left({\widehat{\mathrm{\Sigma }}}^{(k)}-{\mathrm{\Sigma }}_0^{(k)}\right){\mathrm{\Delta }}^{(k)}\right\}\right|⩽C_1{\left(\frac{\text{log}p}{n}\right)}^{1/2}{\left|{\mathrm{\Delta }}^{(k)-}\right|}_1+C_2{\left(\frac{p\text{log}p}{n}\right)}^{1/2}{\Vert {\mathrm{\Delta }}^{(k)+}\Vert }_F,$$ (A2)

$${\left({\tilde{\mathrm{\Delta }}}^{(k)}\right)}^{\text{T}}\left\{{\int }_0^1\left(1-\upsilon \right){\left({\mathrm{\Omega }}_0^{(k)}+\upsilon {\mathrm{\Delta }}^{(k)}\right)}^{-1}\otimes {\left({\mathrm{\Omega }}_0^{(k)}+\upsilon {\mathrm{\Delta }}^{(k)}\right)}^{-1}d\upsilon \right\}{\tilde{\mathrm{\Delta }}}^{(k)}⩾\frac{1}{4{\tau }_2^2}{\Vert {\mathrm{\Delta }}^{(k)}\Vert }_F^2.$$ (A3)

Proof of Theorem 1. In a slight abuse of notation, we will write $\mathrm{\Omega }={\left({\mathrm{\Omega }}^{(k)}\right)}_{k=1}^K$, ${\mathrm{\Omega }}_0={\left({\mathrm{\Omega }}_0^{(k)}\right)}_{k=1}^K$, and $\mathrm{\Delta }={\left({\mathrm{\Delta }}^{(k)}\right)}_{k=1}^K$, where ${\mathrm{\Delta }}^{(k)}={\left({\delta }_{j,j^{\prime }}^{(k)}\right)}_{p\times p}$ is defined as Δ^(k) = Ω^(k) − ${\mathrm{\Omega }}_0^{(k)}$ (k = 1, . . . , K). Let Q(Ω) be the objective function of (4), and let G(Δ) = Q(Ω₀ + Δ) − Q(Ω₀). If we take a closed bounded convex set 𝒜 which contains 0, and show that G is strictly positive everywhere on the boundary ∂𝒜, then it implies that G has a local minimum inside 𝒜, since G is continuous and G(0) = 0. Specifically, we define 𝒜 = $\left\{\mathrm{\Delta }:\left({\sum }_{k=1}^K{\Vert {\mathrm{\Delta }}^{(k)}\Vert }_F\right)⩽M{r}_n\right\}$, with boundary $\partial 𝒜=\left\{\mathrm{\Delta }:\left({\sum }_{k=1}^K{\Vert {\mathrm{\Delta }}^{(k)}\Vert }_F\right)=M{r}_n\right\}$, where M is a positive constant and r_n = {(p + q)(log p)/n}^1/2.

By the decomposition (A1) in Lemma A1, we can write G(Δ) = I₁ + I₂ + I₃ + I₄, where

$$\begin{array}{l}{I}_1=\sum _{k=1}^K\text{tr}\left\{\left({\widehat{\mathrm{\Sigma }}}^{(k)}-{\mathrm{\Sigma }}_0^{(k)}\right){\mathrm{\Delta }}^{(k)}\right\},\\ I_2=\sum _{k=1}^K{\left({\tilde{\mathrm{\Delta }}}^{(k)}\right)}^{\text{T}}\left\{{\int }_0^1\left(1-\upsilon \right){\left({\mathrm{\Omega }}_0^{(k)}+\upsilon {\mathrm{\Delta }}^{(k)}\right)}^{-1}\otimes {\left({\mathrm{\Omega }}_0^{(k)}+\upsilon {\mathrm{\Delta }}^{(k)}\right)}^{-1}d\upsilon \right\}{\tilde{\mathrm{\Delta }}}^{(k)},\\ I_3=\lambda \sum _{\left(j,j^{\prime }\right)\in T^c}{\left(\sum _{k=1}^K\left|{\delta }_{j,j^{\prime }}^{(k)}\right|\right)}^{1/2},\\ I_4=\lambda \sum _{j\ne j^{\prime }:\left(j,j^{\prime }\right)\in T}\left\{{\left(\sum _{k=1}^K\left|{\omega }_{j,j^{\prime }}^{(k)}\right|\right)}^{1/2}-{\left(\sum _{k=1}^K\left|{\omega }_{0,j,j^{\prime }}^{(k)}\right|\right)}^{1/2}\right\}.\end{array}$$

We first consider I₁. By applying inequality (A2) in Lemma A1, we have |I₁| ⩽ I_1,1 + I_1,2, where $I_{1,1}=C_1{\left\{\left(\text{log}p\right)/n\right\}}^{1/2}{\sum }_{k=1}^K{\left|{\mathrm{\Delta }}_T^{\left(k\right)-}\right|}_1+C_2{\left\{\left(p\text{log}p\right)/n\right\}}^{1/2}{\sum }_{k=1}^K{||{\mathrm{\Delta }}^{\left(k\right)+}||}_F$ and $I_{1,2}=C_1{\left\{\left(\text{log}p\right)/n\right\}}^{1/2}{\sum }_{k=1}^K{\left|{\mathrm{\Delta }}_{T^c}^{\left(k\right)-}\right|}_1$. By applying the bound ${\left|{\mathrm{\Delta }}_T^{\left(k\right)-}\right|}_1⩽q_k^{1/2}{\Vert {\mathrm{\Delta }}_T^{\left(k\right)-}\Vert }_F$, we have

$$\begin{array}{lll}{I}_{1,1}\hfill & ⩽\hfill & C_1{\left(\frac{q\text{log}p}{n}\right)}^{1/2}\sum _{k=1}^K{\Vert {\mathrm{\Delta }}_T^{\left(k\right)-}\Vert }_F+C_2{\left(\frac{p\text{log}p}{n}\right)}^{1/2}\sum _{k=1}^K{\Vert {\mathrm{\Delta }}^{\left(k\right)+}\Vert }_F\hfill \\ \hfill & ⩽\hfill & \left(C_1+C_2\right){\left\{\frac{\left(p+q\right)\text{log}p}{n}\right\}}^{1/2}\sum _{k=1}^K{\Vert {\mathrm{\Delta }}^{(k)}\Vert }_F⩽M\left(C_1+C_2\right)\frac{\left(p+q\right)\text{log}p}{n}\hfill \end{array}$$

on the boundary ∂𝒜.

Next, since for r_n small enough we have $I_3⩾\lambda {\sum }_{k=1}^K{\left|{\mathrm{\Delta }}_{T^c}^{\left(k\right)-}\right|}_1$, the term I_1,2 is dominated by the positive term I₃:

$$\begin{array}{lll}{I}_3-I_{1,2}\hfill & ⩾\hfill & \lambda \sum _{k=1}^K{\left|{\mathrm{\Delta }}_{T^c}^{\left(k\right)-}\right|}_1-C_1{\left(\frac{\text{log}p}{n}\right)}^{1/2}\sum _{k=1}^K{\left|{\mathrm{\Delta }}_{T^c}^{\left(k\right)-}\right|}_1\hfill \\ \hfill & ⩾\hfill & \left({\mathrm{\Lambda }}_1-C_1\right){\left(\frac{\text{log}p}{n}\right)}^{1/2}\sum _{k=1}^K{\left|{\mathrm{\Delta }}_{T^c}^{\left(k\right)-}\right|}_1.\hfill \end{array}$$

The last inequality uses the condition λ ⩾ Λ₁{(log p)/n}^1/2. Therefore, I₃ − I_1,2 ⩾ 0 when Λ₁ is large enough. Next we consider I₂. By applying inequality (A3) in Lemma A1, we have $I_2⩾\left(1/4{\tau }_2^2\right){\sum }_{k=1}^K{\Vert {\mathrm{\Delta }}^{(k)}\Vert }_F^2⩾\left\{M^2/\left(8{\tau }_2^2\right)\right\}\left\{\left(p+q\right)\left(\text{log}p\right)/n\right\}$. Finally consider the remaining term I₄. Using Condition 2, we have

$$\begin{array}{l}\left|I_4\right|⩽\lambda \sum _{j\ne j^{\prime }:\left(j,j^{\prime }\right)\in T}\frac{{\sum }_{k=1}^K\Vert {\omega }_{j,j^{\prime }}^{(k)}|-|{\omega }_{0,j,j^{\prime }}^{(k)}\Vert }{{\left({\sum }_{k=1}^K\left|{\omega }_{j,j^{\prime }}^{(k)}\right|\right)}^{1/2}+{\left({\sum }_{k=1}^K\left|{\omega }_{0,j,j^{\prime }}^{(k)}\right|\right)}^{1/2}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}⩽\frac{\lambda }{{\tau }_3^{1/2}}\sum _{k=1}^K\sum _{j\ne j^{\prime }:\left(j,j^{\prime }\right)\in T}\left|{\omega }_{j,j^{\prime }}^{(k)}-{\omega }_{0,j,j^{\prime }}^{(k)}\right|⩽\frac{\lambda }{{\tau }_3^{1/2}}{q}^{1/2}\sum _{k=1}^K{\Vert {\mathrm{\Delta }}^{(k)}\Vert }_F⩽\frac{M{\mathrm{\Lambda }}_2}{{\tau }_3^{1/2}}\frac{(p+q)\left(\text{log}p\right)}{n}.\end{array}$$

The last inequality uses the condition λ ⩽ Λ₂ {(1 + p/q)(log p)/n}^1/2. Putting everything together and using I₂ > 0 and I₃ − I_1,2 > 0, we have

$$G(\mathrm{\Delta })⩾I_2-I_{1,1}-\left|I_4\right|⩾M^2\frac{\left(p+q\right)\text{log}p}{n}\left(\frac{1}{8{\tau }_2^2}-\frac{C_1+C_2+{\mathrm{\Lambda }}_2/{\tau }_3^{1/2}}{M}\right).$$

Thus for M sufficiently large, we have G(Δ) > 0 for any Δ ∈ ∂𝒜.

Proof of Theorem 2. It suffices to show that for all $\left(j,j^{\prime }\right)\in T_k^c$ (k = 1, . . . , K), the derivative $\partial Q/\partial {\omega }_{j,j^{\prime }}^{(k)}$ at ${\widehat{\omega }}_{j,j^{\prime }}^{(k)}$ has the same sign as ${\widehat{\omega }}_{j,j^{\prime }}^{(k)}$ with probability tending to 1. To see that, suppose that for some $\left(j,j^{\prime }\right)\in T_k^c$, the estimate ${\widehat{\omega }}_{j,j^{\prime }}^{(k)}\ne 0$. Without loss of generality, suppose ${\widehat{\omega }}_{j,j^{\prime }}^{(k)}>0$. Then there exists ξ > 0 such that ${\widehat{\omega }}_{j,j^{\prime }}^{(k)}-\xi >0$. Since Ω̂ is a local minimizer of Q(Ω), we have $\partial Q/\partial {\omega }_{j,j^{\prime }}^{(k)}<0$ at ${\widehat{\omega }}_{j,j^{\prime }}^{(k)}-\xi$ for ξ small, contradicting the claim that $\partial Q/\partial {\omega }_{j,j^{\prime }}^{(k)}$, at ${\widehat{\omega }}_{j,j^{\prime }}^{(k)}$, has the same sign as ${\widehat{\omega }}_{j,j^{\prime }}^{(k)}$.

The derivative of the objective function can be written as

$$\frac{\partial Q}{\partial {\omega }_{j,j^{\prime }}^{(k)}}=2\left\{{\alpha }_{j,j^{\prime }}^{(k)}+{\beta }_{j,j^{\prime }}\text{sgn}\left({\omega }_{j,j^{\prime }}^{(k)}\right)\right\},$$ (A4)

where ${\alpha }_{j,j^{\prime }}^{(k)}={\widehat{\sigma }}_{j,j^{\prime }}^{(k)}-{\sigma }_{j,j^{\prime }}^{(k)}$, and ${\beta }_{j,j^{\prime }}=\lambda /{\left({\sum }_{k=1}^K\left|{\omega }_{j,j^{\prime }}^{(k)}\right|\right)}^{1/2}$. Arguing as in Lam & Fan (2009, Theorem 2), one can show that max_k=1,...,K ${\text{max}}_{j,j^{\prime }}\left|{\alpha }_{j,j^{\prime }}^{(k)}\right|=O_{\text{p}}\left[{\left\{\left(\text{log}p\right)/n\right\}}^{1/2}+{\eta }_n^{1/2}\right]$. On the other hand, by Theorem 1, we have ${\sum }_{k=1}^K\left|{\omega }_{j,j^{\prime }}^{(k)}-{\omega }_{0,j,j^{\prime }}^{(k)}\right|⩽{\sum }_{k=1}^K{\Vert {\mathrm{\Omega }}^{(k)}-{\mathrm{\Omega }}_0^{(k)}\Vert }_F=O_{\text{p}}\left({\eta }_n\right)=o(1)$. Then for any ∊ > 0 and large enough n we have ${\sum }_{k=1}^K\left|{\omega }_{j,j^{\prime }}^{(k)}\right|⩽{\sum }_{k=1}^K\left|{\omega }_{0,j,j^{\prime }}^{(k)}\right|+∊$. Then we have $\left|{\beta }_{j,j^{\prime }}\right|⩾\lambda /{\left(1+{\sum }_{k=1}^K\left|{\omega }_{0,j,j^{\prime }}^{(k)}\right|\right)}^{-1/2}$. By assumption, ${\left\{\left(\text{log}p\right)/n\right\}}^{1/2}+{\eta }_n^{1/2}=O(\lambda )$, and thus the term β _j,j′ dominates ${\alpha }_{j,j^{\prime }}^{(k)}$ in (A4) for any $\left(j,j^{\prime }\right)\in T_k^c$ (k = 1, . . . , K). Therefore, $\text{sgn}\left\{{\partial Q/\partial {\omega }_{j,j^{\prime }}^{(k)}|}_{{\omega }_{j,j^{\prime }}^{(k)}={\widehat{\omega }}_{j,j^{\prime }}^{(k)}}\right\}=\text{sgn}\left({\widehat{\omega }}_{j,j^{\prime }}^{(k)}\right)$.