Estimating treatment effects with treatment switching via semicompeting risks models: an application to a colorectal cancer study

Summary

Treatment switching is a frequent occurrence in clinical trials, where, during the course of the trial, patients who fail on the control treatment may change to the experimental treatment. Analysing the data without accounting for switching yields highly biased and inefficient estimates of the treatment effect. In this paper, we propose a novel class of semiparametric semicompeting risks transition survival models to accommodate treatment switches. Theoretical properties of the proposed model are examined and an efficient expectation-maximization algorithm is derived for obtaining the maximum likelihood estimates. Simulation studies are conducted to demonstrate the superiority of the model compared with the intent-to-treat analysis and other methods proposed in the literature. The proposed method is applied to data from a colorectal cancer clinical trial.

1. Introduction

Treatment switching commonly occurs in clinical trials such as in cancer or in other diseases, where patients who fail on the control treatment may begin taking the experimental treatment. This often happens in cancer clinical trials when the control arm consists of a placebo or no treatment. In such trials, patients in the control arm who experience an intermediate event, such as disease progression, may begin taking the experimental treatment to receive a rescue medication. As discussed in Marcus & Gibbons (2001), an intent-to-treat analysis will lead to attenuated treatment effect estimates, and thus one must properly model the data accommodating this switching effect and then appropriately estimate the treatment effect.

In clinical trials, there are many types of switching possibilities. Drop-in refers to situations where control subjects start taking an active treatment. There is also switching due to drop-out, where subjects stop taking the active treatment. Here we focus on the drop-in problem of control subjects switching to the experimental treatment after experiencing an intermediate event.

Methods have been advocated to compensate for the effects of drop-in, assuming an intent-to-treat analysis. This could be a viable approach if the drug effect is believed to be sufficiently large to yield a clinically meaningful intent-to-treat effect. Various methods for sample size adjustment are described by Lachin & Foulkes (1986), Lakatos (1988), Lu & Pajak (2000), Porcher et al. (2002), Jiang et al. (2004) and Barthel et al. (2006). Although these approaches manage the risk of a false-negative error, they may result in a larger than needed sample size and yield an effect estimate of marginal clinical significance that fails to address the drop-in bias, especially when appreciable drop-in occurs nonrandomly. In the presence of drop-in, analysis methods to estimate the treatment’s causal effect that do not respect randomization are potentially confounded. Common examples include an analysis treating the drop-in time as a censoring time, or the exclusion of patients with drop-in. Law & Kaldor (1996) proposed a multiplicative Cox model in which patients are divided into subgroups based on their randomized and observed subsequent therapy. As noted by White (1997), their model is flawed since subgroup membership at a particular time depends on the future, and estimates will tend to be biased under the null. Other approaches that respect the randomization include the use of causal models with counterfactuals (Lunceford et al., 2002; White et al., 2003; London et al., 2010). Related approaches are marginal structural models (Robins et al., 2000). For valid causal inference, these models must account for all confounders that predict drop-in and there must be no censoring bias. Even when these conditions apply, model estimates can become unstable when drop-in is certain among all patients with a specific value of a time-dependent covariate. Examples of applying marginal structural models are provided by Hernán et al. (2000) and Yamaguchi & Ohashi (2004).

When marginal structural models are not applicable, a structural nested model may be used (Yamaguchi & Ohashi, 2004; Greenland et al., 2008) In particular, based on the methods of Robins & Tsiatis (1991), Branson & Whitehead (2002) developed an estimation method for an accelerated failure-time model similar to a structural nested model to estimate the true effect. Their model assumes that the effect of the experimental treatment is the same at randomization in the test arm as at drop-in in the control arm. In addition, their model assumes that patients who receive drop-in therapy are comparable to those who do not, although the authors noted that baseline covariates could be incorporated, and thus their model could include factors that predict drop-in. Shao et al. (2005) extended the Branson & Whitehead (2002) methodology to allow the effect of drop-in to vary with time receiving the drop-in therapy, and also defined a latent hazard rate model with the same features. White (2006) noted that the recensoring procedure of Branson & Whitehead (2002) needs to be modified when the control arm survival time without drop-in depends on the drop-in time, otherwise a bias towards the null results if drop-in patients have a poor prognosis, and away from the null if they have a good prognosis. White (2006) also pointed out that the estimation procedure proposed in Shao et al. (2005) is biased when the drop-in time is prognostic. For the structural nested modelling approaches, such as those of Branson & Whitehead (2002) and Shao et al. (2005), one major concern is that the assumed model for the true survival time does not account for the disparity that some subjects experience the intermediate event while others do not. Furthermore, assuming a constant experimental treatment effect between treatment arms may be questionable since the disease course is more advanced among drop-in patients that receive delayed therapy.

In this paper, we tackle this practical problem from a completely different modelling perspective than the aforementioned methods. Instead of modelling the true survival time using either the accelerated failure time model or the proportional hazards model, we model the observed event times using a semiparametric hazards model. To account for the fact that some subjects do not experience the intermediate event, we introduce a mixture model to characterize the progression and nonprogression subpopulation. Furthermore, for the progression population, we separately model the time to the intermediate event and the time from the intermediate event to death. We also include baseline covariates and prognostic covariates in both time-to-event regression models. In this way, we not only account for the heterogeneity at baseline, but also capture the heterogeneity at treatment switching. Finally, our model assumes a parametric switching effect at the time of the intermediate event, which may be different from the baseline treatment effect. The advantages of our model are clear: we model only observed event times which makes it possible to assess model assumptions and check model fit using the observed data; we allow the treatment effect at switching to be completely different from the baseline treatment effect; and the model can handle both baseline covariates and prognostic covariates at switching.

2. Panitumumab study

Our proposed methodology was motivated by the panitumumab colorectal cancer clinical trial conducted by Amgen Inc. (Amado et al., 2008). This clinical trial was an open label, randomized, phase III multicentre study designed to compare the efficacy and safety of panitumumab plus best supportive care versus best supportive care alone in colorectal cancer patients. One objective was to compare the treatment effect on the overall survival time in this subject population.

Subjects were randomly assigned to receive treatment or control. Panitumumab was administered until disease progression, inability to tolerate the investigational product, or other reasons for discontinuation. During the study, subjects in the control group who had disease progression at any time were eligible to receive panitumumab at 6 mg/kg administered once every 2 weeks as part of a separate protocol. Figure 1 shows the counts for each group in the follow-up period. Among the 223 patients on the control arm, 201 patients had disease progression, of which 167 switched over to the treatment arm. Due to this substantial switching percentage, this study provides strong motivation for developing new statistical models as well as new methods for estimating the true causal effect of the treatment in the presence of a semicompeting risk.

Fig. 1.

Graphical representation of the panitumumab data: total n = 454.

3. Proposed method

3.1. Models and assumptions

In cancer clinical trials, some subjects experience the intermediate event of disease progression and others do not and these subjects are censored for the event. To address this issue, we propose a mixed semicompeting risks transition model. We assume that the population consists of two subpopulations, where one population will eventually develop disease progression before death, but the other population will never experience disease progression. For the no-progression population, the only event time of interest is time-to-death, but for the progression population, both the time to disease progression and the event of death need to be considered.

To introduce our statistical models, we use the following notation: a dichotomous variable U is used to denote the lifetime disease progression status of the subjects, U = 1 if the subject has disease progression before death and 0 otherwise; we let T_D denote the time to death for the no-progression subjects with U = 0; for the other subjects with U = 1, we use T_U to denote their time to disease progression and let G denote the time from disease progression to death.

The proposed statistical model has three components. The first component models the distribution of the progression status given the baseline covariates X and randomized treatment R:

$$\text{logit}\left\{\text{pr}\left(U=1|R,X\right)\right\}={\alpha }_0+{\alpha }_{1}R+{\alpha }_{2}X,$$ (1)

where R = 1 if the patient is on the experimental treatment arm and 0 otherwise, and the αs are unknown regression coefficients. The second component models the survival distribution for the no-progression population given X and R:

$$h_{\text{D}}\left(t|R,X,U=0\right)=h_0(t)\text{exp}\left({\beta }_{0}R+{\gamma }_{0}X\right),$$ (2)

where h_D(t | R, X, U = 0) is the conditional hazard function of T_D given the covariates, h₀(t) is an unknown baseline hazard function and (β₀, ${\gamma }_0^{\text{T}}$)^T are unknown regression coefficients. In the third component, we model the distributions of time to disease progression, T_U, and time from disease progression to death, G, in the progression population, given treatment switching or not, by assuming a transition model structure:

$$\begin{array}{lll}{h}_U\left(t|R,X,U=1\right)\hfill & =\hfill & h_1(t)\text{exp}\left({\beta }_{1}R+{\gamma }_{1}X\right),\hfill \\ h_G\left(t|R,Z,V,U=1,T_U\right)\hfill & =\hfill & h_2(t)\text{exp}\left\{{\beta }_{21}R+{\beta }_{22}V\left(1-R\right)+{\gamma }_2^{\text{T}}{\left(Z^{\text{T}},T_U\right)}^{\text{T}}\right\},\hfill \end{array}$$ (3)

where h_U(t | R, X, U = 1) is the conditional hazard function for T_U, h_G(t | R, Z, U = 1, T_U) is the conditional hazard function of G, both h₁(t) and h₂(t) are unknown baseline hazard functions, and βs and γs are regression coefficients. Here, V indicates the treatment switching and Z, which contains X, reflects covariates collected at baseline and at disease progression, which could be prognostic factors for the switching decision.

Our models naturally account for the situation that some subjects may or may not experience disease progression for reasons other than ignorable censoring and also include the gap time between disease progression and death, thereby automatically implying that disease progression occurs before death. Because we condition on the disease progression status, our model can be considered as a type of pattern-mixture model. As one reviewer points out, our method can also be viewed as an illness-death model with four states: alive with/without progression, and dead with/without progression (Fix & Neyman, 1951; Sverdrup, 1965), but with a pattern-mixture parameterization (Larson & Dinse, 1985). However, our current hazard models have different interpretations in the survival context. For example, all the models are the hazard models for some specific survival events so that all the β parameters give the treatment effects on the risk of these events. Specifically, β₂₁ represents the logarithm of the hazard ratio of treatment post-disease progression while the coefficient of T_U gives the effect of the disease progression time on future death. In the second model of (3), since the switching only happens to some subjects on the control arm; V (1 – R) is used in the regression. Furthermore, our model (3) assumes that, for the same subjects, the hazard function after the switching at disease progression would change by exp(β₂₂), when compared with the case when they had no switching. Obviously, the latter is a structural assumption, which is acceptable in practice.

Our goal is to compare the survival function of death time in the setting when no subjects have switching. To see how to use the proposed models for achieving this goal, we adopt a counterfactual outcome framework by defining $T_{\text{D}}^{*}(a)$ as a potential survival time when a subject receives treatment a and never changes treatment status and letting $S_a(t)=\text{pr}\left\{T_{\text{D}}^{*}(a)>t\right\}$. Thus, we are interested in comparing S₁(t) and S₀(t). As in the usual causal framework, we assume the following consistency assumption and no unobserved confounder assumption:

Assumption 1. Treatment R is completely randomized and $T_{\text{D}}^{*}(a)=T_{\text{D}}(a)$ if a subject never changes treatment.

Assumption 2. Given (R = 0, Z, T_U = s), that is, a subject in the control arm has disease progression at time s and covariates Z, or (R = 1, Z, T_U = s), V is independent of the potential outcomes { $T_{\text{D}}^{*}(0)$, $T_{\text{D}}^{*}(1)$}.

Let f_X (x) and f_Z (z) denote the density functions for X and Z, respectively. Then by the randomization of R, we obtain the potential survival function of treatment a, $\text{pr}\left\{T_{\text{D}}^{*}(a)>t\right\}$, as

$$\begin{array}{l}\text{pr}\left\{T_{\text{D}}^{*}(a)>t|R=a\right\}\\ \begin{array}{ll}=\hfill & {\int }_x\text{pr}\left\{T_{\text{D}}^{*}(a)>t|X,U=0,R=a\right\}\text{pr}\left(U=\mathrm{ 0 }| X,\hspace{0.17em}R=a\right)f_X\left(x|R=a\right)dx\hfill \\ \hfill & +{\int }_{x,z,s}\text{pr}\left\{T_{\text{D}}^{*}(a)>t|T_U=s,Z,U=1,R=a\right\}d\text{pr}\left(T_U\le s | Z,U=1,\hspace{0.17em}R=a\right)\hfill \\ \hfill & \times f_Z\left(z|X,U=1,R=a\right)pr\left(U=1|X,R=a\right)f_X\left(x|R=a\right)dzdx.\hfill \end{array}\end{array}$$

From Assumption 2, $\text{pr}\left\{T_D^{*}(a)>t|T_U=s,X,Z,U=1,\hspace{0.17em}R=a\right\}=\text{pr}\left\{T_D^{*}(a)>t|V=0,\hspace{0.17em}{T}_U=s,X,Z,U=1,\hspace{0.17em}R=a\right\}$. On the other hand, (R = a, U = 0) or (R = a, U = 1, V = 0) implies that the treatment status is never switched so $T_{\text{D}}^{*}(a)$ can be replaced by the observed T_D in the above expression by Assumption 1. Since T_D = G + T_U for subjects with U = 1, we obtain the survival functions S_a(t) as follows:

$$\begin{array}{l}{\int }_x\text{pr}\left(T_{\text{D}}>t|X,U=0,R=a\right)\text{pr}\left(U=0,|X,R=a\right)f_X\left(x|R=a\right)dx\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\int }_{x,z,s}\text{pr}\left(G>t-s|T_U=s,V=0,Z,U=1,R=a\right)d\text{pr}\left(T_U\le s|Z,U=1,R=a\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times f_Z\left(z|X,U=1,R=a\right)\text{pr}\left(U=1|X,R=a\right)f_X\left(x|R=a\right)dzdx\\ ={\int }_x\text{pr}\left(T_D>t|X,U=0,R=a\right)\text{pr}\left(U=0|X,R=a\right)f_X\left(x|R=a\right)dx\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\int }_{x,z}\{\text{pr}\left(T_U>t|Z,U=1,R=1\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\int }_0^t\text{pr}\left(G>t-s|T_U=s,V=0,Z,U=1,R=a\right)d\text{pr}\left(T_U\le s|Z,U=1,R=a\right)\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times f_Z\left(z|X,U=1,R=a\right)\text{pr}\left(U=1|X,R=a\right)f_X\left(x|R=a\right)dzdx.\end{array}$$

In other words, S_a(t) can be expressed in terms of the parameters in our models (1)–(3) and the distributions of X and Z given (X, U = 1, R). Hence, by inserting the estimates of these parameters into the above expression, we will be able to estimate S_a(t), and thus the causal effect of treatment.

In real applications, there is often some potential bias due to censoring and obtaining the differential prognostic covariates at disease progression. To eliminate such bias, we need the following assumptions:

Assumption 3. The censoring time is independent of T_D, G and T_U given the observed covariates.

Assumption 4. For progression subjects, T_U is independent of Z given R and X.

Assumptions 3 and 4 discard the contribution of the censoring distribution. Assumption 4 is plausible if the part of Z excluding X is collected after disease progression.

3.2. Inference procedure

Let Y denote the observed event if no disease progression occurs; otherwise, we use Y to denote the second event time and W to denote the disease progression time. Let Δ be the censoring indicator. The observed data can be divided into four groups of observations:

Group 1. Subjects are observed to die at time Y and no disease progression has been observed. Clearly, these subjects belong to the first subpopulation with U = 0 and T_D = Y. The observed data are (Y, Δ = 1, U = 0, X, R). Thus, the contribution to the likelihood function is h₀(t) exp(β₀ R + γ₀ X) exp{−H₀(t)e^{β₀R+γ₀X}}pr(U = 0 | R, X) f_X(x | R)pr(R).

Group 2. Subjects are observed to have disease progression at W and die at Y. These subjects belong to the second subpopulation (U = 1) and T_U = W, T_D = Y so G = Y – W. The observed data are (T_U, G, Δ = 1, U = 1, V, Z, X, R). Thus, the contribution to the likelihood function is

$$\begin{array}{l}{h}_1(W)\text{exp}\left({\beta }_{1}R+{\gamma }_{1}X\right)\text{exp}\left\{-H_1(W)\text{exp}\left({\beta }_{1}R+{\gamma }_{1}X\right)\right\}{h}_2(G)\text{exp}\{{\beta }_{21}R+{\beta }_{22}V(1-R)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\gamma }_2\left(Z,W\right)\}\text{exp}\left[-H_2(G)\text{exp}\left\{{\beta }_{21}R+{\beta }_{22}V\left(1-R\right)+{\gamma }_2\left(Z,W\right)\right\}\right]f_Z\left(z|X,R,U=1\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times \text{pr}\left(U=1|R,X\right)f_X\left(x|R\right)\text{pr}\left(R\right),\end{array}$$

where pr(Z | X, R, U = 1) = pr(Z without X | X, R, U = 1). We will use this notation for all conditional distributions of Z given X thereafter.

Group 3. Subjects are observed to have disease progression at W and censored at C. The subjects belong to the second subpopulation with U = 1 and T_U = W, T_D > C = Y so G > Y – W. The observed data are (T_U, G > Y, Δ = 0, U = 1, V, Z, X, R). Thus, the contribution to the likelihood function is

$$\begin{array}{l}{h}_1(W)\text{exp}\left({\beta }_{1}R+{\gamma }_{1}X\right)\text{exp}\left\{-H_1(W)\text{exp}\left({\beta }_{1}R+{\gamma }_{1}X\right)\right\}\text{exp}[-H_2\left(Y-W\right)\text{exp}\{{\beta }_{21}R\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\beta }_{22}V\left(1-R\right)+{\gamma }_2\left(Z,W\right)\}]f_Z\left(z|X,R,U=1\right)\text{pr}\left(U=1|R,X\right)f_X\left(x|R\right)\text{pr}(R).\end{array}$$

Group 4. Subjects are only observed to be censored at Y and no disease progression occurs before Y . These subjects may belong to the first subpopulation, U = 0, with T_D > Y; or, they may belong to the second subpopulation, U = 1, with T_U > Y. The observed data are {UT_U + (1 – U)T_D > Y, X, R}. Thus, the contribution to the likelihood function is [exp{−H₀(Y)e^{β₀R+γ₀X}}pr(U = 0 | R, X) + exp{−H₁(Y) e^{β₁R+γ₁X}}pr(U = 1 | R, X)] f_X (x | R)pr(R).

For inference, we estimate all the model parameters, including the βs, γs and Hs, via the nonparametric maximum likelihood approach. In this approach, the baseline hazard functions, H₀, H₁ and H₂, are assumed to be step functions with jumps at the observed event times. To compute the nonparametric maximum likelihood estimates, we will use the expectation-maximization algorithm to facilitate the computation of the nonparametric maximum likelihood estimates. Specifically, we treat U_i for subject i as potential missing data. Then it is clear that only for subjects in Group 4, U_i is not observed. To estimate the asymptotic covariance matrix of the parameter estimates, we treat all the αs, βs, γs and the jump sizes of the Hs as parameters and use their observed information matrix. In particular, the observed information matrix can be calculated using the Louis formula (Louis, 1982) and its inverse is used as the estimator for the asymptotic covariance matrix.

3.3. Prediction of the survival function with partial treatment crossover

To estimate S_a(t), we can estimate each term on the right-hand side of S_a(t), given in § 3.1, using the parameter estimates. Specifically, the estimators are

$$\begin{array}{l}\widehat{\text{pr}}\left(T_{\text{D}}>t|R=a,X,U=0\right)=\text{exp}\left\{-{\widehat{H}}_0(t)\text{exp}\left({\widehat{\beta }}_{0}R+{\widehat{\gamma }}_{0}X\right)\right\},\\ \widehat{\text{pr}}\left(U=0|R=a,X\right)={\left\{1+\text{exp}\left({\widehat{\alpha }}_0+{\widehat{\alpha }}_{1}R+{\widehat{\alpha }}_{2}X\right)\right\}}^{-1},\\ {\widehat{f}}_X\left(x|R=a\right)=\sum _{j=1}^{n}I\left(X_j=x,R_j=a\right)/\sum _{j=1}^n\left(R_j=a\right),\\ \widehat{\text{pr}}\left(T_U>t|Z,U=1,R=1\right)=\text{exp}\left\{-{\widehat{H}}_1(t)\text{exp}\left({\widehat{\beta }}_{1}a+{\widehat{\gamma }}_{1}X\right)\right\},\\ \widehat{\text{pr}}\left(G>s^{\prime }|T_U=s,V=0,Z,U=1,R=a\right)=\text{exp}\left[-{\widehat{H}}_2(s^{\prime })\text{exp}\left\{{\widehat{\beta }}_{21}a+{\widehat{\gamma }}_2\left(Z,s\right)\right\}\right],\\ {\widehat{f}}_Z\left(z|X,R=a,U=1\right)=\frac{{\sum }_{j\in \left(\text{groups\hspace{0.17em}}2,3\right)}\delta \left(Z_j=z\right)K_{a_n}\left(\Vert X_j-X\Vert \right)I\left(R_j=a\right)}{{\sum }_{j\in \left(\text{groups\hspace{0.17em}}2,3\right)}{K}_{a_n}\left(\Vert X_j-X\Vert \right)I\left(R_j=a\right)},\end{array}$$

where in the final expression, δ is the Dirac delta function and K_an is a kernel weight with bandwidth a_n. Either the delta method or resampling techniques like the bootstrap will be used to derive the confidence band of Ŝ_a(t). As demonstrated in the simulation studies in § 5, we find, in practice, that the bootstrap is easy to implement and performs well for moderate sample sizes. In addition, our experience also shows that even though kernel estimation of pr(Z | X, R, U = 1) may be biased if the dimension of the Xs is not small, the final estimate of S_a(t) is not that sensitive to the dimension of X due to the averaging operations used in calculating Ŝ_a(t).

To compare the experimental arm survival function with the control arm survival function without switching, we examine the weighted difference $n{\sum }_{K=1}^K\widehat{\omega }\left(t_k\right){\left\{{\widehat{S}}_1(t_k)-{\widehat{S}}_0(t_k)\right\}}^2$, where t₁,…, t_K are prespecified time-points in [0, τ] and ω̂(t_k) is a weight specified at time t_k. Useful weight functions ω̂(t) can be based on the class of Ŝ₀(t)^ρ₁ {1 – Ŝ₀(t)}^ρ₂, where ρ₁ and ρ₂ are constants in [0, 1] and Ŝ₀(t) can be also replaced by Ŝ₁(t) or a pooled estimator of survival functions. Thus, by choosing different ρ₁ and ρ₂, we can emphasize comparisons at either early stages or late stages of follow-up. In the subsequent analysis, we consider (ρ₁,ρ₂) = (0, 1) or (1/2, 1/2). Under the null hypothesis for which S₀(t) = S₁(t), according to the asymptotic results to be given later, √n{Ŝ₁(t₁) – Ŝ₀(t₁), …, Ŝ₁(t_K) – Ŝ₀(t_K)}^T → N(0, Σ) in distribution for some covariance matrix Σ. Thus, it is easy to see that $n{\sum }_{k=1}^K\widehat{\omega }(t_k){\left\{{\widehat{S}}_1(t_k)-{\widehat{S}}_0(t_k)\right\}}^2$ converges in distribution to 𝒵^TΣ^1/2diag{ω(t₁),…, ω(t_K)}Σ^1/2 𝒵, where 𝒵 denotes a multivariate standard normal variate and ω(t) is the limit of ω̂(t). We reject the null hypothesis if the test statistic is larger than the (1 – α)-percentile of 𝒵^TΣ̂^1/2diag{ω(t₁), …, ω̂(t_K)} Σ̂^1/2𝒵, where Σ̂ is a consistent estimator for Σ.

Remark 1. Because of the randomization, pr(X | R = a) = pr(X), and therefore, we can replace $\widehat{pr}\left(X|R=a\right)$ with the empirical distribution of X. However, we observe very little efficiency gain in numerical studies.

4. Asymptotic properties

We establish the asymptotic properties for the parameter estimators and Ŝ_a(t) using the general nonparametric maximum likelihood theory framed in Zeng & Lin (2010). In addition to Assumptions (1)–(4), we need the following assumptions:

Assumption 5. The true parameters values of the βs, γs and αs, still denoted as θ ≡ (β₀, β₁, β₂₁, β₂₂, γ₀, ${\gamma }_1^{\text{T}}$, ${\gamma }_2^{\text{T}}$, α₀, α₁, ${\alpha }_2^{\text{T}}$)^T belong to a bounded set in real Euclidean space. Moreover, the true baseline functions, still denoted as (h₀, h₁, h₂), are continuous and are bounded away from zero in [0, τ], where τ is the study duration.

Assumption 6. If there is some constant ν such that ν^T(1, R, Z) = 0 with probability one, then ν = 0. Additionally, we assume (R, Z) to have bounded support and there exits a continuous component of X such that its coefficient in model (1) is nonzero.

Assumption 7. With probability one, pr(C ⩾ τ | R, Z) > 0 and pr(V = 1 | R = 0, Z, T_U) ∈ (μ₀, μ₁) for some constant 0 < μ₀ < μ₁ < 1.

Under these conditions, the following theorems give the consistency and asymptotic distribution of the estimators.

Theorem 1. Under Assumptions (1)–(7), $\Vert \widehat{\theta }-\theta \Vert +{\sum }_{k=1}^3{\text{sup}}_{t\in [0,\tau ]}|{\widehat{H}}_k(t)-H_k(t)|\to 0$, almost surely, where θ̂ ≡ (β̂₀, β̂₁, β̂₂₁, β̂₂₂, γ̂₀, ${\widehat{\gamma }}_1^{\text{T}}$, ${\widehat{\gamma }}_2^{\text{T}}$, α̂₀, α̂₁, ${\widehat{\alpha }}_2^{\text{T}}$)^T and Ĥ_k(t) is the estimator of H_k(t).

Theorem 2. Under Assumptions (1)–(7), √n(θ̂ – θ, Ĥ₁ – Ĥ₁, Ĥ₂ – Ĥ₂, Ĥ₃ – H₃) converges in distribution to a mean zero Gaussian process in the metric space R^d × l^∞[0, τ] × l^∞[0, τ] × l^∞[0, τ], where d is the dimension of θ.

Using the results from Theorem 1 and Theorem 2, we can further obtain the asymptotic distribution of Ŝ_a(t) as given in the previous section.

Theorem 3. In addition to Assumptions (1)–(7), we assume that $K_{an}\left(x\right)=a_n^{-d_x}K\left(\Vert x\Vert /a_n\right)$, where d_x is the dimension of X, K (·) is a symmetric kernel density function with ∫ y^s K (y)dy = 0, s = 1, …, (m – 1) with m > d/2, and a_n satisfies $n{a}_n^d\to \infty$, $n{a}_n^{2m}\to 0$. Then with probability one, sup_{t∈[0, τ]} | Ŝ_a(t) – S_a(t) | → 0 and for each fixed t, and √n{Ŝ_a(t) – S_a(t)} converges in distribution to a mean zero normal variate.

5. Simulation studies

5.1. Simulation study I

To examine the small sample performance of the proposed method, we conducted a simulation study by generating data from models (1)–(3). Specifically, the baseline treatment R = 1 for the first half of the subjects and 0 for the other half; two baseline covariates X₁ and X₂ are independently generated from the uniform distribution on [−1, 1], and a Bernoulli with success probability 0.6, respectively. We then use models (2) and (3) to further generate time to events of interest. The susceptibility status is Bernoulli with success probability 1/{1+exp(−1.6+1.8R – X₁–0.1X₂)}. For the no-progression subjects with U = 0, we simulate their death time T_D using model (2) with H₀(t) = t, β₀ = −1 and (γ₀₁, γ₀₂) =(1, 0.2). For the progression subjects, the time to disease progression, T_U, is generated from the first hazard model in (3) with H₁(t) = t/2, β₁ = −0.5 and (γ₁₁, γ₁₂) = (1, 0). Finally, to generate the time from disease progression to death for the progression subjects with U = 1, we first generate the prognostic factors Z at disease progression from the uniform distribution on [0, 1]. The assignment to treatment switching, V, in the untreated subjects is assumed to have a Bernoulli with success probability 1/{1+exp(0.5–0.3T_U – 0.2X₁ – 0.5Z}, yielding a switching rate of 38.7% in the control arm. Then, the time from disease progression to death, G, follows the second hazard model in (3) with H₂(t) = exp(t) – 1, β₂₁ = −0.3, β₂₂ = −0.5, and γ₂₁ = 0.6, γ₂₂ = −0.5, γ₂₃ = 0.5, γ₂₄ = −0.4. Thus, the subjects who change treatment status from untreated to treated will have their hazard risk reduced by exp(0.5) and the longer the time disease progression is, the longer the survival time will be. Finally, the censoring time is generated from a uniform distribution on (1, 7) and the study duration is τ = 3. The latter yields average proportions for groups 1 to 4 as 23, 41, 21 and 13%.

In the simulation study, we consider sample sizes of n = 400 and n = 1000. Bootstrap samples of size 50 are used to construct pointwise 95% confidence intervals for the estimated survival probability. The results from 1000 replicates are given in Table 1. Additionally, we calculate the square root of the mean square error and maximum absolute difference of the estimated survival curve using 200 equally spaced time-points between 0 and the maximum censoring time. In particular, for the methods of intent-to-treat, Branson & Whitehead (2002), Shao et al. (2005), and the proposed model, the square roots of the mean square errors of Ŝ₀(t) are 0.062, 0.050, 0.054 and 0.035, respectively; the square root of the mean square errors of Ŝ₁(t) are 0.032, 0.028, 0.030 and 0.030, respectively; the maximum absolute differences of Ŝ₀(t) are 0.101, 0.067, 0.083 and 0.051, respectively and those of Ŝ₁(t) are 0.061, 0.036, 0.051 and 0.049, respectively.

Table 1.

Simulation study I

		n = 400				n = 1000
Parameter	True	EST	SD	ESE	CP%	EST	SD	ESE	CP%
	Survival model of no-progression population
β0	−1.0	−1.08	0.26	0.26	94	−1.04	0.16	0.16	93
γ01	1.0	0.96	0.23	0.22	94	0.97	0.13	0.13	94
γ02	0.2	0.22	0.23	0.24	94	0.20	0.14	0.14	95
	Disease progression model of progression population
β1	−0.5	−0.54	0.16	0.16	94	−0.52	0.10	0.10	94
γ11	1.0	1.08	0.14	0.14	91	1.04	0.09	0.08	94
γ12	0.0	−0.01	0.14	0.15	94	0.00	0.09	0.09	95
	Gap time model of progression population
β21	−0.3	−0.31	0.19	0.19	95	−0.30	0.12	0.12	95
β22	−0.5	−0.50	0.20	0.20	95	−0.51	0.12	0.12	96
γ21	0.6	0.61	0.18	0.18	95	0.60	0.11	0.11	95
γ22	−0.5	−0.51	0.16	0.16	94	−0.50	0.10	0.10	95
γ23	0.5	0.51	0.17	0.17	94	0.50	0.10	0.10	95
γ24	−0.4	−0.41	0.27	0.28	95	−0.41	0.17	0.17	95
	Susceptibility model
α0	1.6	1.66	0.26	0.26	95	1.63	0.16	0.16	96
α1	−1.8	−1.80	0.27	0.28	94	−1.79	0.17	0.16	96
α21	1.0	0.90	0.24	0.24	93	0.94	0.15	0.15	95
α22	0.1	0.11	0.26	0.27	94	0.11	0.16	0.15	95
	Predicted survival functions in control arm
S0(τ/2)	0.51	0.49	0.04	0.04	91	0.49	0.02	0.02	92
S0(τ)	0.17	0.18	0.03	0.03	91	0.18	0.02	0.02	91
	Predicted survival functions in experimental arm
S1(τ/2)	0.63	0.61	0.03	0.03	94	0.61	0.02	0.02	92
S1(τ)	0.32	0.33	0.03	0.03	93	0.33	0.02	0.02	94

EST, average of the parameter estimates; SD, sample standard deviation of the estimates; ESE, average of the standard error estimates; CP%, coverage probability of the 95% confidence interval based on a normal approximation.

In addition, we study the power of the test statistics proposed in § 3.3 under the simulation setup discussed above, and obtain the Type I error rate by letting β₀ = β₁ = β₂₁ = β₂₂ = α₁ = 0. In particular, we consider two test statistics, test I with (ρ₁,ρ₂) = (0, 1) and test II with (ρ₁,ρ₂) = (0.5,0.5), for sample sizes of n = 400 and n = 1000. When n = 400, the powers are 87.1% for test I, and 85.6% for test II. The power increases to 99.8% for both tests when the sample size increases to 1000. For tests I and II, the Type I error rates are 4.5% and 4.8% when n = 400, respectively; and 5.4% and 4.8% when n = 1000, respectively.

5.2. Simulation study II

In the second simulation study, we use the modified simulation setup as in Shao et al. (2005) to compare the proposed model with existing methods for switching, and to also demonstrate the robustness of the proposed model. In particular, the survival time is generated according to the exponential distribution with hazard rate 0.0693 for the control arm and 0.0462 for the experimental treatment arm. The total sample size of n = 600, with 300 subjects in each arm. For both treatment arms, the random censoring time is generated according to the uniform distribution on the interval of 15–20 months, resulting in an overall censoring percentage of 35.4%. The time-to-event, which is the switching time in Shao et al. (2005), is generated from the exponential distribution with a mean of 7.22 months for the control group and 10.82 months for the experimental treatment group. In this paper, we focus on switching only from the control to treatment arm and let the patients switch at the event time with probability 0.6, yielding a switching rate of 39.0%. After switching, the observed survival time for the switching patients is updated using equation (4) and (11) in Shao et al. (2005) with β = −0.4055, η₀₀ = 0.1, η₀₁ = 0.009 and η₁₀ = η₁₁ = 0.

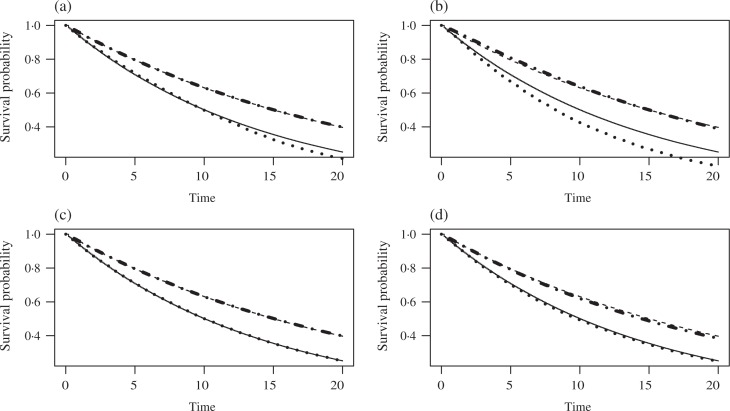
Figure 2 presents the averaged predicted survival curves on [0, 20] for the intent-to-treat Kaplan–Meier, Branson & Whitehead (2002), Shao et al. (2005) and proposed methods using 1000 simulations. The discrepancy in the four different approaches focuses on the estimation of the control group survival curve. In particular, the survival curves generated by Shao et al. (2005) and the proposed model yield survival curves with smaller bias. The square roots of the mean square errors and maximum absolute differences are 0.029 and 0.049, respectively, for Shao et al. (2005), and 0.031 and 0.043, respectively, for the proposed approach. On the other hand, bigger biases are observed for the Branson & Whitehead (2002) and the intent-to-treat approaches. The square roots of the mean square errors and maximum absolute differences are, respectively, 0.073 and 0.088 for the Branson & Whitehead (2002) method, and 0.034 and 0.069 for the intent-to-treat approach.

Fig. 2.

Average predicted survival curves from simulation study II. S(t | R = a) is the potential survival function for subjects with treatment status a if they have no treatment switching. In each panel, the solid curve is the true survival function in the control arm, the dashed curve is the true survival function in the experimental treatment arm, while the dotted and the dash-dotted curves are, respectively, the estimated survival functions in these two arms. The estimates in the plots are based on (a) intent-to-treat analysis, (b) Branson & Whitehead (2002), (c) Shao et al. (2005) and (d) our method.

6. Analysis of the panitumumab data

We carry out here a detailed analysis of the panitumumab study. It is purely an abstract construct of the semicompeting risk nature of the proposed model to assume the existence of a subpopulation that is subject to disease progression, and thus this condition is not assumed to apply literally to this study. The baseline covariates we consider are initial treatment, age in years at screening, baseline electrocorticography performance status with 0 or 1 versus ⩾ 2, primary tumour diagnosis type with rectal versus colon, gender, and region with three levels consisting of western Europe, eastern and central Europe, and rest of the world. In the panitumumab study, the median age was 62.5 years and the interquartile range of age was (55, 69) years. There were 388 patients with electrocorticography score 0 or 1, 287 were male, 151 had rectal cancer, 352 were from Western Europe, 39 were from Eastern and Central Europe, and 63 were from the rest of the world. The median follow-up time was 189.5 days and the interquartile range of the follow-up time was (93, 334) days. Among those 387 patients who developed disease progression, the median disease progression time is 53 days and the interquartile range is (45, 84) days.

The model for the time of disease progression includes all the baseline covariates. Among the 387 patients who developed disease progression, the median age at the time of disease progression was 62.1 years with interquartile range (55.0, 69.1), the numbers of patients who had partial response, stable disease and progressive disease were 19, 86 and 282, respectively. There were 348 patients with baseline electrocorticography score 0 or 1, 286 patients had a last electrocorticography score 0 or 1, and 180 patients had grade 2 or above adverse events.

The covariates at the time from disease progression to death include additional progonostic factors for the switching decision. They are progression time, partial response age, best tumour response with partial response or stable disease versus progressive disease according to investigator assessment, last electrocorticography performance status and grade 2 or above adverse events. We include those prognostic factors based on our best knowledge with assistance from trial clinicians so that Assumption 2 could be valid. Because of the dependency on the unobserved outcome, Assumption 2 is not testable, and the results could be biased if it is violated.

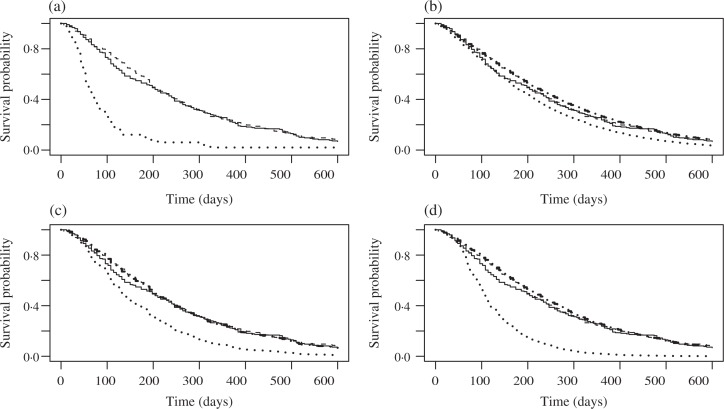
The results from the proposed model are given in Table 2. The survival probability estimates using the intent-to-treat Kaplan–Meier, no switching subgroup analysis using Kaplan–Meier, Branson & Whitehead (2002), Shao et al. (2005), and the proposed methods at the 25, 50, 75 and 100% quartiles of time to death are given in Table 3. The no-switching approach excludes the patients who switched from best supportive care alone to panitumumab plus supportive care. The p-values to test the treatment effect using the above five approaches are 0.577, <0.001, 0.520, 0.002 and <0.001, respectively. For the Branson & Whitehead (2002) method, 1000 bootstrap samples are used to construct the standard error and p-value because the standard errors calculated from the covariance matrix at convergence are too small to construct valid confidence limits (Branson & Whitehead, 2002). Figure 3 provides the predicted survival curves for the two treatment groups of panitumumab plus best supportive care and best supportive care alone using the five approaches. We notice that the intent-to-treat Kaplan–Meier and Branson & Whitehead (2002) approaches yield small survival differences between the panitumumab plus best supportive care and best supportive care alone groups before 200 days and there is little difference after 200 days since enrolment. On the other hand, the subgroup analysis based on no patients switching shows big differences between the two arms for the whole follow-up period. We then investigated the reason for the survival curve discrepancy for best supportive care alone group and found two key contributing factors: a high switching rate for the best supportive care alone group, 167/223=75%; and selection bias, that is, the patients with longer time-to-event were more likely to be switched from best supportive care alone to panitumumab plus best supportive care with a median time-to-event of 40.5 days for the no switching patients and 49 days for the switching patients. The Shao et al. (2005) and the proposed approach both yield big differences in the estimated survival curves compared with the control arm with the bigger treatment difference being obtained by the proposed approach.

Table 2.

Model estimates for the panitumumab data

Parameter	EST	SE	P	Parameter	EST	SE	P
	TD Model				TU Model
Treatment	−0.464	3.47	0.182	Treatment	−1.144	1.18	<0.001
Age	0.023	0.15	0.124	Age	−0.015	0.05	0.004
bECOG	−0.589	2.99	0.048	bECOG	−0.805	1.74	<0.001
Rectal	−0.028	3.20	0.929	Rectal	−0.018	1.10	0.871
Male	−0.288	3.05	0.345	Male	−0.054	1.09	0.622
CenEastEU	−0.188	6.27	0.764	CenEastEU	0.194	2.50	0.439
WesternEU	0.181	3.99	0.650	WesternEU	−0.068	1.60	0.672
	TG Model				U Model
Treatment	−0.784	2.14	<0.001	Intercept	1.366	9.72	0.160
V*(1-Treatment)	−1.383	2.09	<0.001	Treatment	−1.070	3.19	<0.001
Prog Time	−0.003	0.01	0.039	Age	−0.008	0.14	0.546
PR Age	−0.004	0.05	0.450	bECOG	1.905	3.34	<0.001
BTR PR	−0.226	3.45	0.512	Rectal	0.314	3.31	0.342
BTR SD	−0.180	1.74	0.302	Male	−0.303	3.21	0.346
bECOG	−0.268	1.96	0.173	CenEastEU	0.078	6.23	0.901
LECOG	−1.035	1.48	<0.001	WesternEU	0.346	4.12	0.400
AE	0.295	1.16	0.011

EST, parameter estimates; SD(×10), standard error of the estimates; P, p-values; bECOG, baseline electrocorticography; CenEastEU, central Europe; WesternEU, western Europe; Prog Time, progression time; PR, partial response; BTR, best tumour response; SD, stable disease; LECOG, last electrocorticography; AE, adverse event.

Table 3.

Predicted survival functions for the panitumumab data

Time (Days)	ITT		No Crossover		IPE		Shao Cox		TM
	BSC	P+BSC	BSC	P+BSC	BSC	P+BSC	BSC	P+BSC	BSC	P+BSC
93	0.750	0.793	0.303	0.793	0.722	0.783	0.678	0.798	0.548	0.801
190	0.511	0.533	0.081	0.533	0.454	0.551	0.341	0.536	0.171	0.555
334	0.266	0.260	0.020	0.260	0.201	0.298	0.097	0.258	0.025	0.282
1024	0.013	0.038	0.020	0.038	0.001	0.007	0.001	0.023	0.001	0.026
p-value	0.577		<0.001		0.520		0.002		<0.001

ITT, intent-to-treat; IPE, Branson & Whitehead (2002); Shao Cox, Shao et al. (2005); TM, proposed method; BSC, best supportive care alone; P+BSC, panitumumab plus best supportive care.

Fig. 3.

Predicted survival curves for the panitumumab data. In each panel, the solid curve is the intent-to-treat survival function in the control arm, the dashed curve is the intent-to-treat survival function in the experimental treatment arm, while the dotted and the dash-dotted curves are, respectively, the estimated survival functions in these two arms. The estimates in the survival curves are based on (a) no switching subgroup analysis using the Kaplan–Meier estimates, (b) the Branson & Whitehead (2002) method, (c) the Shao et al. (2005) method and (d) our method.

7. Extensions

We have conducted simulation studies when data are generated from the proposed model or from the models in Shao et al. (2005). Additional simulation studies may be carried out to further examine the robustness of the proposed method to misspecification of models (1)–(3) or to perform sensitivity analysis on the ignorability assumption of switching selection.

Although the proposed model is developed under partial treatment switching, i.e., not all patients switch treatment, it can be easily extended to the case with complete treatment switching in which all patients on the control arm switch to the experimental arm. Specifically, under complete treatment switching, the components of the proposed model for U, T_D and T_U remain the same and only the model in (3) for G needs to be modified as follows

$$h_G\left(t|R,Z,V,U=1,T_U\right)=h_2(t)\text{exp}\left\{{\beta }_{21}R+{\gamma }_2\left(Z,T_U\right)\right\},$$

as in this case β₂₂ is no longer identifiable. However, under complete treatment switching, the estimator of the predictive survival function needs to be rederived, which is much more challenging than under partial treatment switching. In addition, in the proposed model, we build dependence between T_U and G via the transition model. An alternative to the transition model is the frailty model. Under the latter, we have h_U(t | R, X, U = 1) = h₁(t) exp(β₁ R + γ₁ X)ω, and h_G(t | R, Z, V, U = 1, T_U) = h₂(t) exp{β₂₁ R + β₂₂V (1 – R) + γ₂ Z}ω, where ω is a latent gamma-frailty with mean one and variance θ. Compared with the frailty model, the transition model is much more numerically stable in the implementation of the expectation-maximization algorithm. Finally, the proposed method can also be extended to the case where patients may switch from either treatment arm as discussed in Shao et al. (2005). These extensions, along with comparison between the transition model and the frailty model, are currently under investigation.

Appendix

Proof of Theorem 1. Let l_n(θ, H₁, H₂, H₃) denote the observed loglikelihood function for (θ, H), and H{t} = {H(t) – H(t−)}. First, it is easy to see if Ĥ_k{t} = ∞, then l_n(θ̂, Ĥ₁, Ĥ₂, Ĥ₃) = −∞. Moreover, this also holds if the jump size of Ĥ_k at the corresponding events is zero. Thus, the jump sizes of Ĥ_k at the corresponding events are positive and finite so the derivatives of l_n(θ, H₁, H₂, H₃) with respect to each jump size of Ĥ_k should be zero at (θ̂, Ĥ₁, Ĥ₂, Ĥ₃). This gives

$${\widehat{H}}_0\left\{Y_i\right\}=I_i(G_1)/\left\{\sum _{j\in G_1}{e}^{{\widehat{\beta }}_0{R}_j+{\widehat{\gamma }}_0^{\text{T}}{X}_j}+\sum _{j\in G_4}\frac{\left(1-{\widehat{p}}_{uj}\right){\widehat{S}}_{\text{D}}(Y_i)}{\left(1-{\widehat{p}}_{uj}\right){\widehat{S}}_{\text{D}}(Y_i)+{\widehat{p}}_{uj}{\widehat{S}}_U(Y_i)}\right\},$$ (A1)

$${\widehat{H}}_1\left\{W_i\right\}=I_i(G_2,G_3)/\left\{\sum _{j\in G_2,G_3}{e}^{{\widehat{\beta }}_1{R}_j+{\widehat{\gamma }}_1^{\text{T}}{X}_j}+\sum _{j\in G_4}\frac{{\widehat{p}}_{uj}{\widehat{S}}_U(Y_i)}{\left(1-{\widehat{p}}_{uj}\right){\widehat{S}}_{\text{D}}(Y_i)+{\widehat{p}}_{uj}{\widehat{S}}_U(Y_i)}\right\},$$ (A2)

$${\widehat{H}}_2\left\{W_i\right\}=I_i(G_2)/\left\{\sum _{j\in G_2,G_3}{e}^{{\widehat{\eta }}_{Gj}}\right\},$$ (A3)

where G_i denotes group i, I_i(A) = I (i ∈ A), ${\widehat{\eta }}_{\text{D}}={\widehat{\beta }}_{0}R+{\widehat{\gamma }}_0^{\text{T}}X$, ${\widehat{\eta }}_U={\widehat{\beta }}_{1}R+{\widehat{\gamma }}_1^{\text{T}}X$, ${\widehat{\eta }}_G={\widehat{\beta }}_{21}R+{\widehat{\beta }}_{22}V\left(1-R\right)+{\widehat{\gamma }}_2^{\text{T}}\left(Z,W\right)$, and the additional subindex j denotes the expression for the j th subject. In addition, we let Ŝ_D(t) = exp{− Ĥ₀(t)e^η̂_Dj}, Ŝ_U(t) = exp{−Ĥ₁(Y_i)e^η̂_Uj} and ${\widehat{p}}_{uj}=\widehat{\text{pr}}(U=1|R_j,X_j)$. Equation (A3) implies Ĥ₀{Y_i} ⩽ I_i(G₁)/Σ_j∈G1 c₀, where c₀ is a positive lower bound of e^η̂_Dj. Since n⁻¹ Σ_j∈G11 → pr(U = 0, Y ⩽ C) > 0, we obtain $\text{lim}\hspace{0.17em}{\text{sup}}_n{\widehat{H}}_0(\tau )\le \text{lim}\hspace{0.17em}{\text{sup}}_n{n}^{-1}{\sum }_{i=1}^{n}I\left(Y_i\le \tau ,i\in G_1\right)/c_0{n}^{-1}{\sum }_{j\in G_1}1<\infty$. Similarly, equations (A2) and (A3) yield that lim sup_n Ĥ₁(τ) and lim sup_n Ĥ₂(τ) are both finite.

By Helly’s selection theorem, for any subsequence, we can choose a further subsequence such that Ĥ_k weakly converges to an increasing function $H_k^{*}$ for k = 1, 2, 3. Moreover, we can assume θ̂ → θ^*. We then show $H_k^{*}=H_k$and θ^* = θ. To this end, we construct H̃_k such that H̃_k has jumps at the same events as Ĥ_k; moreover, the jumps of H̃_k are given by the right-hand side of (A1) to (A3) except that the parameters on the right-hand side are set to be the true values. It is straightforward to verify that H̃_k converges uniformly to the true function H_k . Furthermore, we can show that d Ĥ_k/d H̃_k converges uniformly to $d\hspace{0.17em}{H}_k^{*}/d\hspace{0.17em}{H}_k$.

Therefore, since l_n(θ̂ Ĥ₁, Ĥ₂, Ĥ₃) – l_n(θ, Ĥ₁, Ĥ₂, Ĥ₃) ⩾ 0, we take limits on both sides and conclude that the Kullback–Leilber information between (θ^*, $H_1^{*}$, $H_2^{*}$, $H_3^{*}$) and (θ, H₁, H₂, H₃) is nonpositive. This immediately implies that the loglikelihood function at (θ^*, $H_1^{*}$, $H_2^{*}$, $H_3^{*}$) is equal to the loglikelihood function at (θ, H₁, H₂, H₃) with probability one. Thus, this equality holds for all subjects in Groups 1 to 4 as defined in § 3. Comparing the differences of the loglikelihood functions from subjects in Group 2 and Group 3, we have

$${\left(H_2^{*}\right)}^{\prime }\left(G\right)e^{{\beta }_{21}^{*}R+{\beta }_{22}^{*}V\left(1-R\right){\gamma }_2^{*}{\text{l}}^{\text{T}}\left(Z,W\right)}={H^{\prime }}_2(G)e^{{\beta }_{2}R+{\beta }_{22}V\left(1-R\right){\gamma }_2{\text{l}}^{\text{T}}\left(Z,W\right)},$$

so by Assumption 6, $H_2^{*}=H_2$, ${\beta }_{21}^{*}={\beta }_{21}$, ${\beta }_{22}^{*}={\beta }_{22}$and ${\gamma }_2^{*}={\gamma }_2$. Let W = 0, we have

$$\left\{h_1^{*}(0)e^{{\alpha }_0^{*}+{\alpha }_1^{*}R+{\alpha }_2^{*}{\text{l}}^{\text{T}}X}\right\}/\left(1+e^{{\alpha }_0^{*}+{\alpha }_1^{*}R+{\alpha }_2^{*}{\text{l}}^{\text{T}}X}\right)=\left\{h_1(0)e^{{\alpha }_0+{\alpha }_{1}R+{\alpha }_2{\text{l}}^{\text{T}}X}\right\}/\left(1+e^{{\alpha }_0+{\alpha }_{1}R+{\alpha }_2{\text{l}}^{\text{T}}X}\right).$$

Now in the loglikelihood for subjects in Group 1, we let Y = 0 and obtain

$$h_0^{*}(0)/\left(1+e^{{\alpha }_0^{*}+{\alpha }_1^{*}R+{\alpha }_2^{*}{\text{l}}^{\text{T}}X}\right)=h_0(0)/\left(1+e^{{\alpha }_0+{\alpha }_{1}R+{\alpha }_2{\text{l}}^{\text{T}}X}\right).$$

Compare the above equations, so ${\alpha }_1^{*}={\alpha }_1,{\alpha }_2^{*}={\alpha }_2$. Since one component of X is continuous and has a nonzero coefficient in α₂, the above equation gives $h_0^{*}(0)=h_0(0)$ and ${\alpha }_0^{*}={\alpha }_0$. Finally, after integrating the likelihood equality function for Group 2 for W from 0 to Y, we have

$$\frac{\left[1-\text{exp}\left\{-H_1^{*}(Y)e^{{\beta }_1^{*}R+{\gamma }_1^{*}{\text{l}}^{\text{T}}X}\right\}\right]e^{{\alpha }_0^{*}+{\alpha }_1^{*}R+{\alpha }_2^{*}{\text{l}}^{\text{T}}X}}{1+e^{{\alpha }_0^{*}+{\alpha }_1^{*}R+{\alpha }_2^{*}{\text{l}}^{\text{T}}X}}=\frac{\left[1-\text{exp}\left\{-H_1(Y)e^{{\beta }_{0}R+{\gamma }_1{\text{l}}^{\text{T}}X}\right\}\right]e^{{\alpha }_0^{*}+{\alpha }_1^{*}R+{\alpha }_2^{*}{\text{l}}^{\text{T}}X}}{1+e^{{\alpha }_0+{\alpha }_1+{\alpha }_2{\text{l}}^{\text{T}}X}}$$

Thus, $H_1^{*}=H_1$ and ${\beta }_1^{*}={\beta }_1$, ${\gamma }_1^{*}={\gamma }_1$. On the other hand, integrating the likehood equality function for subjects in Group 1 for Y from 0 to Y gives

$$\frac{1-\text{exp}\left\{-H_0^{*}(Y)e^{{\beta }_0^{*}R+{\gamma }_0^{*}{\text{l}}^{\text{T}}X}\right\}}{1+e^{{\alpha }_0^{*}+{\alpha }_1^{*}R+{\alpha }_2^{*}{\text{l}}^{\text{T}}X}}=\frac{1-\text{exp}\left\{-H_0(Y)e^{{\beta }_{0}R+{\gamma }_0{\text{l}}^{\text{T}}X}\right\}}{1+e^{{\alpha }_0+{\alpha }_{1}R+{\alpha }_2{\text{l}}^{\text{T}}X}},$$

so ${\beta }_0^{*}={\beta }_0$, ${\gamma }_0^{*}={\gamma }_0$ and $H_0^{*}=H_0$.

We have proved that θ̂ → θ and Ĥ_k converges weakly to H_k . The latter can be further strengthened to uniform convergence in [0, τ ] since H_k is continuous. Therefore, Theorem 1 holds.

Proof of Theorem 2. The proof of Theorem 2 follows from the same argument in proving Theorem 2 in Zeng & Lin (2010). In particular, their conditions (C.1)–(C.4) and (C.6) hold for our specific models. Their first identifiability condition (C.5) has been verified in the proof of Theorem 1. To complete the proof, it remains to verify the second identifiability of their condition (C.7). Consider the score function along a sub model H_k + ∊∫ f_kd H_k and θ+ ∊ν where ν = (β₀,γ₀, β₁,γ₁, β₂₁, β₂₂,γ₂, α₀, α₁, α₂). If this score function is zero with probability one, then we need to show that f_k = 0 and ν = 0. For subjects in Group 2, the score equation is

$$\begin{array}{ll}0=\hfill & f_1(W)+{\eta }_U-{\int }_0^W{f}_1(t)d\hspace{0.17em}{H}_1(t)e^{{\eta }_U}-H_1(Y)e^{{\eta }_U}{\eta }_U+f_2(G)+{\eta }_G\hfill \\ \hfill & -{\int }_0^G{f}_2(t)d\hspace{0.17em}{H}_2(t)e^{{\eta }_G}-H_2(Y)e^{{\eta }_G}{\eta }_G+e^{{\alpha }_0+{\alpha }_{1}R+{\alpha }_2^{\text{T}}X}{\left(1+e^{{\alpha }_0+{\alpha }_{1}R+{\alpha }_2^{\text{T}}X}\right)}^{-2}\hfill \\ \hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times \left({\xi }_0+{\xi }_{1}R+{\xi }_2^{\text{T}}X\right).\hfill \end{array}$$ (A4)

For subjects in Group 3, we obtain the score equation to be

$$\begin{array}{ll}0=\hfill & f_1(W)+{\eta }_U-{\int }_0^W{f}_1(t)d\hspace{0.17em}{H}_1(t)e^{{\eta }_U}-H_1(Y)e^{{\eta }_U}{\eta }_U-{\int }_0^G{f}_2(t)d\hspace{0.17em}{H}_2(t)e^{{\eta }_G}\hfill \\ \hfill & -H_2(Y)e^{{\eta }_G}{\eta }_G+e^{{\alpha }_0+{\alpha }_{1}R+{\alpha }_2^{\text{T}}X}{\left(1+e^{{\alpha }_0+{\alpha }_{1}R+{\alpha }_2^{\text{T}}X}\right)}^{-2}\left({\alpha }_0+{\alpha }_{1}R+{\alpha }_2^{\text{T}}X\right).\hfill \end{array}$$ (A5)

The difference between (A4) and (A5) gives f₂(G) + η_G = 0, so by Assumption 6, f₂ = 0, β₂₁ = 0, β₂₂ = 0 and γ₂ = 0.

Using this result and equation (A5), the score equation for subjects in Group 4 becomes

$$0=-{\int }_0^Y{f}_0(t)d\hspace{0.17em}{H}_0(t)e^{{\eta }_{\text{D}}}-H_0(Y)e^{{\eta }_{\text{D}}}{\eta }_{\text{D}}-\frac{e^{{\alpha }_0+{\alpha }_{1}R+{\alpha }_2^{\text{T}}X}\left({\alpha }_0+{\alpha }_{1}R+{\alpha }_2^{\text{T}}X\right)}{{\left(1+e^{{\alpha }_0+{\alpha }_{1}R+{\alpha }_2^{\text{T}}X}\right)}^2}.$$ (A6)

On the other hand, for subjects in Group 1,

$$0=f_0(Y)+{\eta }_{\text{D}}-{\int }_0^Y{f}_0(t)d\hspace{0.17em}{H}_0(t)e^{{\eta }_{\text{D}}}-H_0(Y)e^{{\eta }_{\text{D}}}{\eta }_{\text{D}}-\frac{e^{{\alpha }_0+{\alpha }_{1}R+{\alpha }_2^{\text{T}}X}\left({\alpha }_0+{\alpha }_{1}R+{\alpha }_2^{\text{T}}X\right)}{{\left(1+e^{{\alpha }_0+{\alpha }_{1}R+{\alpha }_2^{\text{T}}X}\right)}^2}.$$ (A7)

Then the difference between (A6) and (A7) gives f₀(Y) + η_D = 0 which further gives f₀ = 0, β₀ = 0 and γ₀ = 0. As a result, (A7) becomes ${\alpha }_0+{\alpha }_{1}R+{\alpha }_2^{\text{T}}X=0$ so α₀ = 0, α₁ = 0 andα₂ = 0. This further combined with equation (A5) gives f₁ = 0, β₁ = 0 and γ₁ = 0. We have verified condition (C.7) in Zeng & Lin (2010). According to their results, our Theorem 2 holds.

Moreover, from Theorem 3 in Zeng & Lin (2010), we also conclude that the inverse of the observed information is a consistent estimator for the asymptotic covariance.

Proof of Theorem 3. The consistency of Ŝ_a(t) follows from the consistency of the following terms, $\widehat{\text{pr}}\left(T_{\text{D}}>t|R=a,X,U=0\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\widehat{\text{pr}}\left(U=0|R=a,X\right)$, $\widehat{\text{pr}}\left(G+T_U>t|R=a,X,Z,U=1\right)$, from Theorem 1. Moreover, we have the fact that, by the kernel approximation,

$$\begin{array}{c}\frac{{\sum }_{j\in G_2,G_3}\widehat{\text{pr}}\left(G+T_U>t|R=a,X_j,Z_j,U=1\right)K_{a_n}\left(X_j-x\right)I\left(R_j=a\right)}{{\sum }_{j\in G_2,G_3}{K}_{a_n}\left(X_j-x\right)I\left(R_j=a\right)}\\ \to E\left\{\text{pr}\left(G+T_U>t|R=a,X,Z,U=1\right)|X=x,\hspace{0.17em}R=a,\hspace{0.17em}U=1,\hspace{0.17em}{T}_U\le C\right\}\end{array}$$

uniformly in x in the support of X and with probability one. Since Z and (T_U, C) are independent given (R, X), the limit on the right-hand side is also equal to pr(G + T_U > t | X = x, R = a, U = 1). Thus, Ŝ_a(t) → Ŝ_a(t). Note Ŝ_a(t) – Ŝ_a(t) can be written as

$$\begin{array}{ll}\frac{1}{n_a}\hfill & \sum _{i=1}^n\widehat{\text{pr}}\left(T_{\text{D}}>t|R=a,\hspace{0.17em}X=X_i,\hspace{0.17em}U=0\right)\widehat{\text{pr}}\left(U=0|R=a,\hspace{0.17em}{X}_i\right)I\left(R_i=a\right)\hfill \\ \hfill & +\frac{1}{n_a}\sum _{i=1}^{n}E\left\{\widehat{\text{pr}}\left(G+T_U>t|R=a,X,Z,U=1\right)|X=X_i,\hspace{0.17em}R=a,\hspace{0.17em}U=1,\hspace{0.17em}{T}_U<C\right\}\hfill \\ \hfill & \times \widehat{\text{pr}}\left(U=1|X_i,\hspace{0.17em}R=a\right)I\left(R_i=a\right)-S_a(t)\hfill \\ \hfill & +\frac{1}{n_a}\sum _{i=1}^n\left[\frac{{\sum }_{j\in G_2,G_3}\widehat{\text{pr}}\left(G+T_U>t|R=a,X_j,Z_j,U=1\right)K_{a_n}\left(X_j-X_i\right)I\left(R_j=a\right)}{{\sum }_{j\in G_2,G_3}{K}_{a_n}\left(X_j-X_i\right)I\left(R_j=a\right)}\right]\hfill \\ \hfill & -E\left\{\widehat{\text{pr}}\left(G+T_U>t|R=a,X,Z,U=1\right)|X=X_i,R=a,\hspace{0.17em}U=1,\hspace{0.17em}{T}_U<C\right\}]\hfill \\ \hfill & \times \widehat{\text{pr}}\left(U=1|X_i,R=a\right)I\left(R_i=a\right).\hfill \end{array}$$ (A8)

The first two terms are Hadamard differentiable with respect to θ̂, Ĥ_k and the empirical distribution of X given R. Therefore, by the functional delta method, these terms can be approximated as $\mathrm{\Sigma }\left(\widehat{\theta }-\theta \right)+{\sum }_{k=1}^3\int f_k(t)d\left\{{\widehat{H}}_k(t)-H_k(t)\right\}+\int g(x)d\left\{\widehat{F}\left(x|R\right)-F\left(X|R\right)\right\}+o_p\left(n^{-1/2}\right)$ for some bounded functions f_k (t) and g(x), where F̂ (X | R) is the empirical distribution function of X given R. To complete the proof of Theorem 3, we only need to show that the last term in equation (A8) is asymptotically normal.

Denote Q as subjects in Group 2 and Group 3 and use P_n to denote the empirical measure. The last term of (A8) can be reorganized as

$$\begin{array}{l}(P_n-P)[\widehat{\text{pr}}(G+T_U>t|R=a,X,Z,U=1)I(R=a)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times Q{n}_a^{-1}\left\{\sum _{i=1}^n\frac{K_{a_n}(X-X_i)}{n^{-1}{\sum }_{k=1}^n{Q}_k{K}_{a_n}(X_k-X_i)I(R_k=a)}\right\}]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-(P_n-P)[n_a^{-1}\sum _{i=1}^n\frac{E\{\widehat{\text{pr}}(G+T_U>t|R=a,X,Z,U=1)I(R=a)QK(X-X_i)\}}{E{\{Q{K}_{a_n}(X-X_i)I(R=a)\}}^2}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times \hspace{0.17em}\widehat{\text{pr}}(U=1|X_i,R=a)I(R_i=a)]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+n_a^{-1}\sum _{i=1}^n[\frac{E\{\widehat{\text{pr}}(G+T_U>t|R=a,X,Z,U=1)I(R=a)QK(X-X_i)\}}{E\{Q{K}_{a_n}(X-X_i)I(R=a)\}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-U\{\widehat{\text{pr}}(G+T_U>t|R=a,X,Z,U=1)|X=X_i,R=a,U=1,T_U<C\}]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times \widehat{\text{pr}}(U=1|X_i,R=a)I(R_i=a).\end{array}$$ (A9)

In (A9), we can apply the functional central limit result in Theorem 2.11.23 of van der Vaart & Wellner (1996) to show that the first two terms of (A9) converge in distribution to a Gaussian process with a factor n^1/2. From the kernel approximation, the last term is $O\left(a_n^m\right)$, and therefore, is o_p(n^−1/2). Combining the above results, we conclude that Theorem 3 holds.