[Fe^IV=O(TBC)(CH₃CN)]²⁺: Comparative Reactivity of Iron(IV)-Oxo Species with Constrained Equatorial Cyclam Ligation

Abstract

[Fe^IV=O(TBC)(CH₃CN)]²⁺ (TBC = 1,4,8,11-tetrabenzyl-1,4,8,11-tetraazacyclotetradecane) is characterized and its reactivity differences relative to [Fe^IV=O(TMC)(CH₃CN)]²⁺ (TMC = 1,4,8,11-tetramethyl-1,4,8,11-tetraazacyclotetradecane) are evaluated in hydrogen atom (H-atom) abstraction and oxo-transfer reactions. Structural differences are defined using X-ray absorption spectroscopy (XAS) and correlated to reactivities using density functional theory (DFT). The S = 1 ground states are highly similar and result in large activation barriers (~25 kcal/mol) due to steric interactions between the cyclam chelate and the substrate (e.g., ethylbenzene) associated with the equatorial π-attack required by this spin state. Conversely, H-atom abstraction reactivity on an S = 2 surface allows for a σ-attack with an axial substrate approach. This results in decreased steric interactions with the cyclam and a lower barrier (~9 kcal/mol). For [Fe^IV=O(TBC)(CH₃CN)]²⁺, the S = 2 excited state in the reactant is lower in energy and therefore more accessible at the transition state due to a weaker ligand field associated with the steric interactions of the benzyl substituents with the trans-axial ligand. This study is further extended to the oxo-transfer reaction, which is a two-electron process requiring both σ and π electron transfer and thus a non-linear transition state. In oxo-transfer, the S = 2 has a lower barrier due to sequential vs. concerted (S = 1) two electron transfer which gives a high-spin ferric intermediate at the transition state. The [Fe^IV=O(TBC)(CH₃CN)]²⁺ complex is more distorted at the transition state, with the iron farther out of the equatorial plane due to the steric interaction of the benzyl groups with the trans-axial ligand. This allows for better orbital overlap with the substrate, a lower barrier, and an increased rate of oxo-transfer.

1. Introduction

High-valent iron-oxo groups have long been invoked as the active intermediates for many mononuclear non-heme iron enzymes,^1–3 catalyzing a wide variety of key biological reactions ranging from hydroxylation⁴ to oxo-electrophilic aromatic attack.^5,6 Due to their important physiological functions, studies of these enzymes and their reactive intermediates have been an intense area of research focus. In recent years, Krebs, Bollinger, Hausinger, and their co-workers have successfully trapped and characterized Fe^IV-oxo intermediates in the active sites of alpha-ketogluterate dependent and pterin dependent enzymes including taurine: α-KG dioxygenase (TauD),^7–10 prolyl-4-hydroxylase (P4H),¹¹ the halogenase CytC3,^5,6 tyrosine hydroxylase,¹² and recently phenylalanine hydroxylase.¹³ However, due to the reactive nature associated with these intermediates, their detailed spectroscopic characterization has been challenging. Thus, biomimetic model studies of the non-heme Fe^IV=O unit are an essential component for understanding geometric and electronic structure contributions to function.

To date, Fe^IV=O model complexes have been structurally defined for both the low-spin (LS) S = 1^14–31 and high-spin (HS) S = 2^32–36 states. The majority of the models have an S = 1 ground state, while those defined for non-heme enzymes exhibit S = 2 ground states. It has been generally thought that the high-spin S = 2 is more reactive than the low-spin S = 1 state. It has been proposed that this increased reactivity is due to an exchange stabilization of the high-spin d⁴ configuration.³⁷ Alternatively, the role of the exchange stabilization can be to simply lower the energy of the α d_z² σ* orbital so that it is competitive with the β d_xz/yz π* frontier molecular orbitals (FMOs).^4,38 This would allow both σ- and π-type attack on the substrate, whereas for the S = 1, only the β π* FMO is low in energy and therefore only the π attack is possible. It has been shown^39,40 that this π attack requires a side on-approach of the substrate to achieve good orbital overlap with the oxo p_x/y orbital. This can result in a large steric interaction between the substrate and an equatorial chelating ligand, raising the reaction barrier of the π-attack pathway. However, hydrogen atom (H-atom) abstraction reactivity studies³⁴ on the S = 2 [Fe^IV=O(TMG₃tren)]²⁺ (TMG₃tren = 1,1,1-tris{2-[N2-(1,1,3,3-tetramethyl-guanidino)]ethyl}amine) complex find rates similar to those of S = 1 [Fe^IV=O(N4Py)]²⁺ (N4Py = N,N-bis(2-pyridylmethyl)-N-bis(2-pyridyl)methyl-amine). This has been shown to be due to the significant steric bulk of the TMG₃tren ligand which limits substrate access even to the axial position of the enclosed Fe=O group.^34,37,40

In the case of [Fe^IV=O(TMC)(CH₃CN)]²⁺ (TMC = 1,4,8,11-tetramethyl-1,4,8,11-tetraazacyclotetradecane), which utilizes a 14-membered cyclam ring and has an S = 1 ground state,¹⁸ the steric constraints of the cyclam equatorial ligand have been shown to greatly limit the approach and overlap of the substrate with the Fe=O unit required for π attack.³⁹ As a result, [Fe^IV=O(TMC)(CH₃CN)]²⁺ exhibits very low reactivity towards H-atom abstraction reactions and oxo-electrophilic attack (oxo-transfer). In the present study, [Fe^IV=O(TBC)(CH₃CN)]²⁺ (TBC = 1,4,8,11-tetrabenzyl-1,4,8,11-tetraazacyclotetradecane), having an ever more bulky benzyl substituent on the cyclam framework, is observed to exhibit a substantial rate enhancement of more than two orders of magnitude over [Fe^IV=O(TMC)(CH₃CN)]²⁺ for both H-atom and oxo-transfer reactions. X-ray absorption spectroscopy (XAS) measurements combined with density functional theory (DFT) calculations show that the bulky substituents on the TBC ligand weaken both the axial and equatorial ligand fields making the S = 2 state more accessible. This allows participation of the σ FMO for an axial substrate attack along the Fe=O bond and a lower steric contribution to the barrier at the transition state for the TBC complex. This model is then extended to oxo-electrophilic attack, formally a two-electron process, that requires both Fe=O π and σ orbital overlap with the substrate to facilitate reactivity. Again large differences are found for the S = 1 vs. the S = 2 transition state barriers and for the TBC chelate relative to TMC. For oxo-transfer, these differences in barrier height are related to a concerted vs. sequential electron transfer associated with the different spin states and the different structural distortions at the transition state.

2. Materials and Methods

Solvents were dried according to published procedures and distilled under argon prior to use.⁴¹ All chemicals were obtained from Sigma-Aldrich Co. as the highest purity available and were therefore used without further purification unless otherwise indicated.

Synthesis of Materials

Non-heme ferrous complexes, [Fe^II(TBC)(CH₃CN)](OTf)₂ (1) (OTf = CF₃SO₃⁻), [Fe^II(TMC)(CH₃CN)](OTf)₂, and [Fe^II(N4Py)(CH₃CN)](OTf)₂, and their respective oxo-iron complexes, [Fe^IV=O(TBC)(CH₃CN)]²⁺ (2), [Fe^IV=O(TMC)(CH₃CN)]²⁺, and [Fe^IV=O(N4Py)]²⁺, were prepared according to literature methods.^16,18,42,43 Preparation and handling of all air-sensitive materials, such as [Fe^II(TBC)(CH₃CN)](CF₃SO₃)₂ and [Fe^II(TMC)(CH₃CN)](CF₃SO₃)₂, were done under an inert nitrogen atmosphere using a glove box. The TBC ligand was synthesized by the reaction of cyclam (1.0 g, 5.0 mmol) and benzyl bromide (3.76 g, 22.0 mmol) in the presence of potassium carbonate (3.0 g, 22.0 mmol) in anhydrous N,N-dimethylformamide (DMF; 200 mL). The mixture was refluxed overnight under an argon atmosphere and then cooled to obtain a white precipitate at 60% of theoretical yield. The precipitate was then filtered and recrystallized from dichloromethane (CH₂Cl₂). 1 was prepared by the reaction between Fe^II(OTf)₂ (0.095g, 0.268 mmol) and the TBC ligand (0.100g, 0.178 mmol) in 2 mL acetonitrile (CH₃CN) in a glove box at 25 °C. Single crystals of 1 were block shaped and colorless, and were obtained by slow diffusion of diethyl ether (Et₂O) into concentrated CH₃CN solution of 1 under argon atmosphere at −30 °C. Intermediate 2 was generated by the addition of two equivalents of solid iodosylbenzene (PhIO)⁴⁴ into a solution of 1 in CH₃CN and was stirred for 10–20 minutes at 0 °C. PhIO was prepared according to literature method.⁴⁴

Instrumentation

UV-Vis spectra were recorded on a Hewlett Packard 8453 diode array spectrophotometer equipped with a circulating water bath or UNISOKU cryostat system (USP-203; UNISOKU, Japan). Electrospray ionization mass (ESI-MS) spectra were collected on a Thermo Finnigan (San Jose, CA, USA) LCQ™ Advantage MAX quadrupole ion trap instrument, by manually infusing samples directly into the source. The spray voltage was set at 3.7 kV and the capillary temperature at 180 °C. Continuous wave electron paramagnetic resonance (CW-EPR) spectra were recorded at 5 K using an X-band Bruker EMX-plus spectrometer equipped with a dual mode cavity (ER 4116DM). Low temperatures were achieved and controlled with an Oxford Instruments ESR900 liquid He quartz cryostat with an Oxford Instruments ITC503 temperature and gas flow controller. The experimental parameters for the EPR spectra were as follows: Microwave frequency = 9.646 GHz, microwave power = 1 mW, modulation frequency = 100 kHz, and modulation amplitude = 10 G. Resonance Raman (rR) spectra were obtained using a liquid nitrogen cooled CCD detector (CCD-1024×256-OPEN-1LS, HORIBA Jobin Yvon) attached to a 1-m single polychromator (MC-100DG, Ritsu Oyo Kogaku) with a 1200 grooves/mm holographic grating. An excitation wavelength of 442 nm was provided by a Kr⁺ laser (Spectra Physics, BeamLok 2060-RM), with 20 mW power at the sample point. All measurements were carried out with a spinning cell (1000 rpm) at −20 °C. Raman shifts were calibrated with indene, and the accuracy of the peak positions of the Raman bands was ±1 cm⁻¹. Mössbauer spectra were measured either on a low-field Mössbauer spectrometer equipped with a Janis SVT-400 cryostat or an Oxford Instruments Spectromag 4000 cryostat containing an 8T split-pair superconducting magnet. Both spectrometers were operated in constant acceleration mode in transmission geometry. The isomer shifts are referenced against a room-temperature metallic iron foil. Analysis of the data was performed using the program WMOSS (WEB Research).

Spin State Measurements

¹H NMR spectra were measured using a Bruker AVANCE III 400 MHz spectrometer. The effective magnetic moments (μ_eff, BM) of complexes 1 and 2 were determined using the modified method of Evans at room temperature and 15 °C, respectively.^45–47 A WILMAD coaxial insert (sealed capillary) tube containing the blank acetonitrile-d₃ solvent (with 1.0 % tetramethylsilane (TMS)) only was inserted into the normal NMR tubes containing the complexes (4 mM) dissolved in acetonitrile-d₃ (with 0.05 % TMS). The chemical shift of the TMS peak (and/or solvent peak) in the presence of the paramagnetic metal complexes was compared to that of the TMS peak (and/or solvent peak) in the inner coaxial insert tube.

X-ray Structural Analysis

Single crystals of 1 suitable for X-ray analysis were obtained by slow diffusion of Et₂O into an CH₃CN solution of 1. A single crystal was then mounted on a glass fiber tip with epoxy cement. Diffraction data were collected at 100 K on a Bruker SMART AXS diffractometer equipped with a monochromator in the Mo Kα (λ = 0.71073 Å) incident beam. The CCD data were integrated and scaled using the Bruker-SAINT software package, and the structure was solved and refined using SHEXTL V 6.12.⁴⁸ Hydrogen atoms were located in the calculated positions. Crystal data for 1•(CH₃CN)₂: C₄₆H₅₇F₆FeN₇O₆S₂, Triclinic, P₋₁, Z = 2, a = 12.1461(18), b = 13.876(2), c = 17.131(3) Å, α = 67.041(8), β = 72.676(9), γ = 67.039(8)°, V = 2411.7(6) ų, μ = 0.478 mm⁻¹, d_calc = 1.429 g/cm³, R₁ = 0.0733, wR₂ = 0.1734 for 6152 unique reflections, 616 variables. The CCDC (875224) contains the supplementary crystallographic data for 1. These data can be obtained free of charge via www.ccdc.cam.ac.uk/data_request/cif or from the Cambridge Crystallographic Data Centre, 12, Union Road, Cambridge CB2 1EZ, UK; fax: (+44) 1223-336-033; deposit@ccdc.cam.ac.uk.

Reactivity Studies

All reactions were followed using a Hewlett Packard 8453 spectrophotometer to monitor UV-Vis spectral changes of the reaction solutions. [Fe^IV=O(L)]²⁺ (L = TBC, TMC, and N4Py) species were generated in the reaction of [Fe^II(L)(CH₃CN)](OTf)₂ with 2 equiv of solid PhIO in CH₃CN at 0 or 15 °C. The solutions were then filtered for further utilization. Kinetic measurements for C-H activation of ethylbenzene and sulfoxidation of thioanisole by [Fe^IV=O(L)]²⁺ were carried out in CH₃CN at 15 °C under pseudo-first-order conditions, where the concentrations of substrates were maintained in greater than 10-fold excess relative to the [Fe^IV=O(L)]²⁺ (5.0 × 10⁻⁴ M or 1.0 × 10⁻³ M respectively). Rates were monitored by the decay of absorption bands at 885 nm due to [Fe^IV=O(TBC)]²⁺, 820 nm due to [Fe^IV=O(TMC)]²⁺, and 695 nm due to [Fe^IV=O(N4Py)]²⁺, respectively. All reactions were run at least in triplicate and the data reported here represent the average of these reactions.

XAS Measurements

Samples were prepared and frozen under liquid nitrogen in several 2×10 mm pinhole type Delrin cells wrapped with Kapton tape. Samples were oriented at 45° to the incident X-ray beam and maintained at 10 K using an Oxford Instruments CF1208 continuous flow liquid helium cryostat. XAS data were collected at beamline 9-3⁴⁹ at the Stanford Synchrotron Radiation Lightsource (SSRL) under ring operating conditions of 150–200 mA over an energy range of 6785 to 8000 eV (k =15 Å⁻¹) for all complexes. Fluorescence data were collected at 90° to the incident beam using a solid-state 30-element Ge detector array with Soller slits and a six wavelength Mn filter aligned between the detector and sample to improve the Fe Kα fluorescence signal intensity relative to that of the scattered beam.⁵⁰ For all data sets an internal calibration was utilized with the first inflection point of an Fe foil set to 7111.20 eV.⁵¹

During measurements, the data in the Fe K-edge, K pre-edge and EXAFS regions were continuously monitored in order to insure sample integrity by comparing each individual scan to ones taken previously. No sample degradation was observed for the ferrous starting complex [Fe^II(TBC)(CH₃CN)]²⁺ (1) and all scans were included in the final average (15 scans). For [Fe^IV=O(TBC)(CH₃CN)]²⁺ (2) significant photoreduction was observed and data collection was limited to two scans per spot with 4 separate 1×4 mm spots per each 2×10 mm XAS cell (12 scans total). While no photoreduction, or change in the EXAFS signal was evident for 2, a negative shift of ~0.4 eV per-scan was observed in the K-edge energy. As a result, the K-edge data presented in this study are the average of only the first scan on each spot. Iron K-edge, pre-edge, and EXAFS data were also measured for [Fe^IV=O(TMC)(CH₃CN)]²⁺ to allow for a direct comparison to this closely related Fe^IV=O system.

XAS Data Processing

Data reduction, background subtraction and normalization were performed according to established methods^52–54 using the program PySpline,⁵⁵ with the data normalized to a value of 1.0 at 7130.0 eV. The spline function through the EXAFS region was chosen to minimize any residual low-frequency background but not reduce the EXAFS amplitude, as monitored by the Fourier transform intensity. For pre-edge and edge analysis all data sets were truncated to k = 9.5 Å⁻¹ and renormalized using a third-order post-edge polynomial background and a two-segment (three knot) spline for comparison between data sets and to past reference compounds.⁵⁶ Normalization of the EXAFS data was accomplished using a second-order post edge polynomial background fit over the full data range (k = 15 Å⁻¹) and a three-segment (four knot) spline. Normalization was also tested using a four-segment (five knot) spline, however, this resulted in no appreciable change in either the EXAFS or its associated Fourier transform and therefore the three-segment spline was used in the final analysis.

Iron K pre-edge features were modeled with a pseudo-Voigt line shape in a 50:50 ratio of Lorentzian:Gaussian functions using the fitting program EDG_FIT⁵⁷ as part of the program suite EXAFSPAK.⁵⁸ The energy position, full width at half-maximum (FWHM), and peak intensity were all allowed to float throughout the fitting process. A function modeling the background was empirically chosen to give the best fit, floated with all variables, and then varied with different FWHM (± 0.5 fixed from float) to establish confidence limits on pre-edge intensity. In all cases, an acceptable fit reasonably matched both the pre-edge data as well as those of its second derivative. A minimum of three fits with different FWHM (± 0.5 fixed from float) backgrounds were acquired over the energy ranges of 7108–7116, 7108–7117, and 7108–7118 eV for 1, and 7108–7117, 7108–7118, and 7108–7119 eV for 2 to provide at least nine pre-edge fits per data set. These were then averaged to give the final pre-edge energy and intensity values.

EXAFS signals were calculated using FEFF (version 7.0) and the data were fit using the program OPT as part of EXAFSPAK.⁵⁸ In all fits the bond lengths (R) and bond variances (σ²) were allowed to vary, with the initial value for bond variance set to 0.005 Ų, even for fits where single scattering and multiple scattering paths were related to one another. The threshold energy (k = 0, E₀) was also allowed to vary, but was constrained as a common variable (ΔE₀) for all fit paths in a given data set. The amplitude reduction factors (S₀²) were fixed to a value of 1.0 and the coordination numbers (CN) were varied systematically based on a structural model to achieve the best fit to the EXAFS data. The best choice of all available FEFF paths and the goodness of the overall fit were optimized based on a combination of weighted F-factor (F) as well as visual fit to the EXAFS data and their Fourier transform. On the basis of studies of complexes of known structures, the uncertainties in final distances are within 0.02 Å.

The EXAFS data for 1 were fit using both the crystallographic structure as well as a density functional theory (DFT) geometry optimized structure (vide infra) as initial models for [Fe^II(TBC)(CH₃CN)]²⁺. In either case, the similarity between the optimized geometry and crystal structure gave the same values for the final EXAFS fit. In the case of intermediate 2, where a crystal structure is not currently available, the EXAFS data were fit to the computational model (vide infra).

DFT Calculations

All complexes used in EXAFS modeling and reactivity studies were fully optimized using Gaussian 03⁵⁹ and the unrestricted hybrid density functional UB3LYP⁶⁰ (three-parameter Becke GGA exchange modified to include Hartree-Fock mixing with Lee, Yang, and Parr correlation^61,62) with the 6-311G(d) basis set. Singlepoint energies on final geometries were calculated using an expanded basis set of 6-311+G(2df,2pd) with solvent corrections (PCM = acetonitrile) and frequencies calculated with 6-311G(d). In some cases, calculations were also done using UBP86/6-311G(d) (Becke GGA exchange⁶³ with Perdew 1986 non-local correlation⁶⁴) as a comparison between functionals. However, BP86 tended to over-stabilize the low-spin ground state resulting in a large energy splitting between spin states, and in some cases this lead to an incorrect ground state. In addition, B3LYP gave optimized geometries that were more consistent with the EXAFS data, and thus, B3LYP was utilized for the reaction coordinate and transition state calculations. It should be noted that the energetic trend between the S = 1 and S = 2 states for both [Fe^IV=O(TBC)(CH₃CN)]²⁺ and [Fe^IV=O(TMC)(CH₃CN)]²⁺ was consistent regardless of functional.

Transition state geometries were calculated by positioning a pre-optimized substrate molecule above the [Fe^IV=O(L)]²⁺ intermediate at an appropriate distance with the benzylic hydrogen of ethylbenzene or the sulfur of thioanisole oriented towards the Fe=O group along the desired reaction coordinate. In the case of ethylbenzene, the Fe=O bond and the C-H bond were lengthened and frozen in place while allowing the rest of the system to optimize. Once this starting structure converged, frequencies were checked, and if reasonable, a search for the transition state was performed without constraints using the B3LYP/6-311G(d) level of theory. All transition state structures had only one imaginary frequency (along the desired reaction coordinate). Reactant and product complexes were then calculated by following the intrinsic reaction coordinate (IRC) in the forward and reverse direction and then optimizing to the final complexes that contained all real frequencies. Again, final energies were obtained using a larger basis set, 6-311+G(2df,2pd), with corrections for zero point energy, entropy, and solvent (PCM = acetonitrile) performed using the 6-311G(d) basis set. Calculations were analyzed using QMForge⁶⁵ and plotted using a combination of gOpenMol^66,67 and MacPyMol.⁶⁸

3. Results and Analyses

3.1 Characterization of [Fe^II(TBC)(CH₃CN)]²⁺

[Fe^II(TBC)(CH₃CN)](OTf)₂, (1), was synthesized by reacting equimolar amounts of Fe^II(OTf)₂ and the TBC ligand in CH₃CN at 25 °C, and was characterized by EPR, NMR, ESI-MS, Mössbauer, Xray absorption spectroscopy (XAS) and X-ray crystallography.

The electrospray ionization mass (ESI-MS) spectrum of 1 exhibits three prominent ion peaks at m/z 308.2, 328.6, and 765.3, Supporting Information (SI) Figure 1, whose mass and isotope distribution patterns correspond to [Fe^II(TBC)]²⁺ (calcd. m/z 308.2), [Fe^II(TBC)(CH₃CN)]²⁺ (calcd. m/z 328.7), and [Fe^II(TBC)(OTf)]⁺ (calcd. m/z 765.3). The X-band EPR spectrum of 1 exhibited no signals, SI Figure 2, which is consistent with 1 being an integer spin ferrous system. The spin state of 1 (in CH₃CN) was determined using the ¹H NMR Evans method,^45–47 and gave a room-temperature magnetic moment of 5.4 µ_B which indicates a high-spin (S = 2) ferrous species.

The high-spin state of 1 was additionally confirmed by Mössbauer spectroscopy (SI Figure 3). The 4.2 K spectrum shows several quadrupole doublets that were fit with two asymmetric quadrupole doublets whose large isomer shifts and quadrupole splittings (SI Table 1) can only be assigned to high-spin ferrous centers. The presence of two different doublets may be attributed to the existence of different configurational isomers in solution, 1a and 1b. The spectrum of 1b shows an unusually large quadrupole splitting, which could result from a constrained geometry, resulting in a very anisotropic EFG. An additional proof of the S = 2 ground state of 1 was obtained by measuring Mössbauer spectra in strong applied magnetic fields (SI Figure 4). These data were incompatible with anything other than a spin quintet.

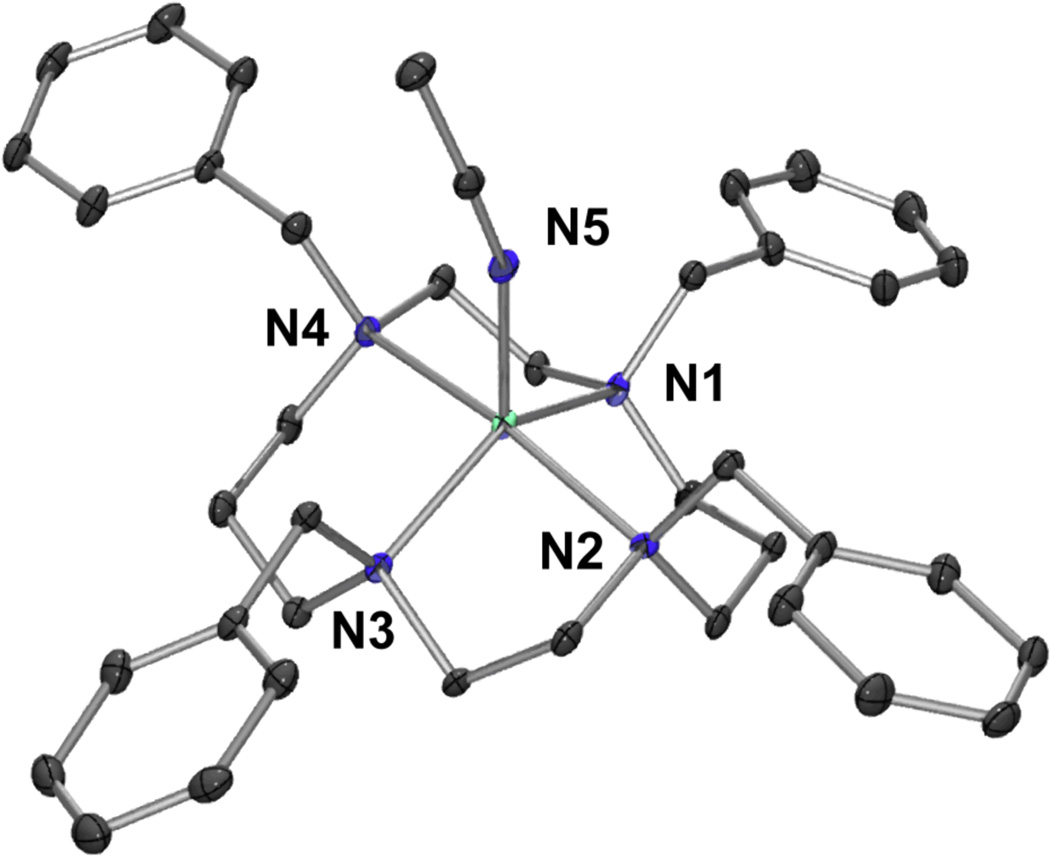
Single crystals of 1 suitable for crystallographic analysis were obtained by the diffusion of Et₂O into an CH₃CN solution of 1. The X-ray crystal structure shows a ferrous center penta-coordinated by the four nitrogen atoms of the TBC ligand and one axial acetonitrile from the solvent orientated syn relative to the benzyl groups of the cyclam. The coordination geometry around the iron is best described as being between a trigonal-bipyramidal and a square-based pyramidal structure, with a τ value of 0.52 ([Figure 1]).

Figure 1.

ORTEP-3 diagram of 1, [Fe^II(TBC)(CH₃CN)]²⁺ with 30% probability displacement ellipsoids. H-atoms have been omitted for clarity. Selected bond distances (Å): Fe-N1 2.143(4), Fe-N2 2.258(3), Fe-N3 2.141(4), Fe-N4 2.290 (3), Fe-N5 2.063(4).

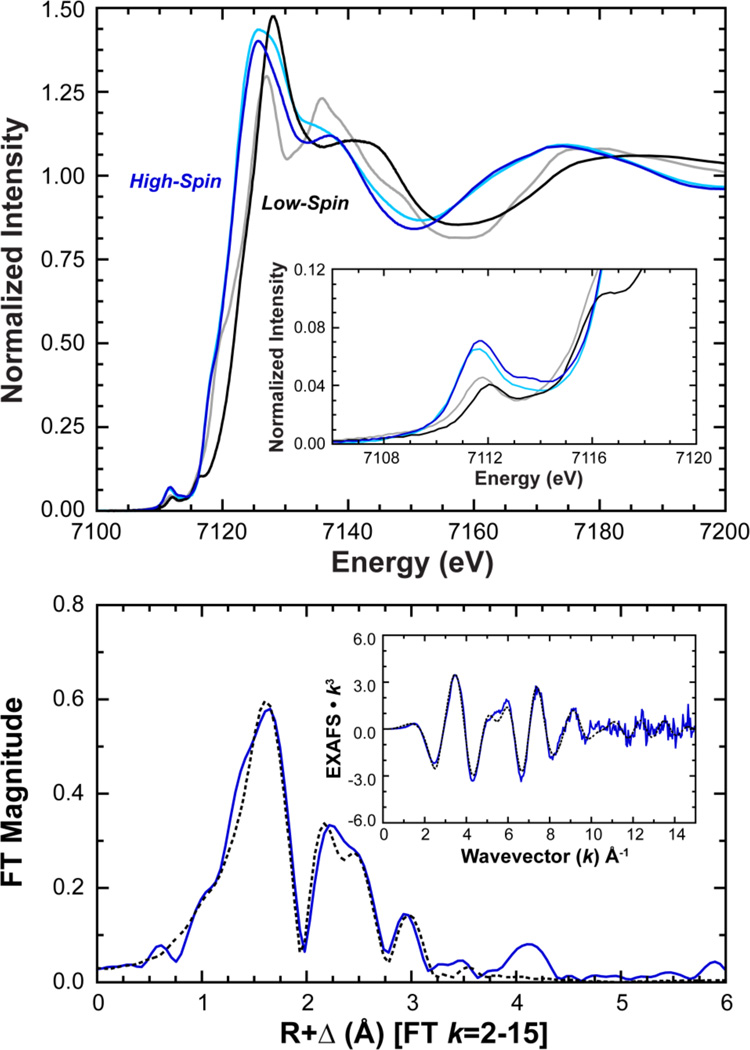
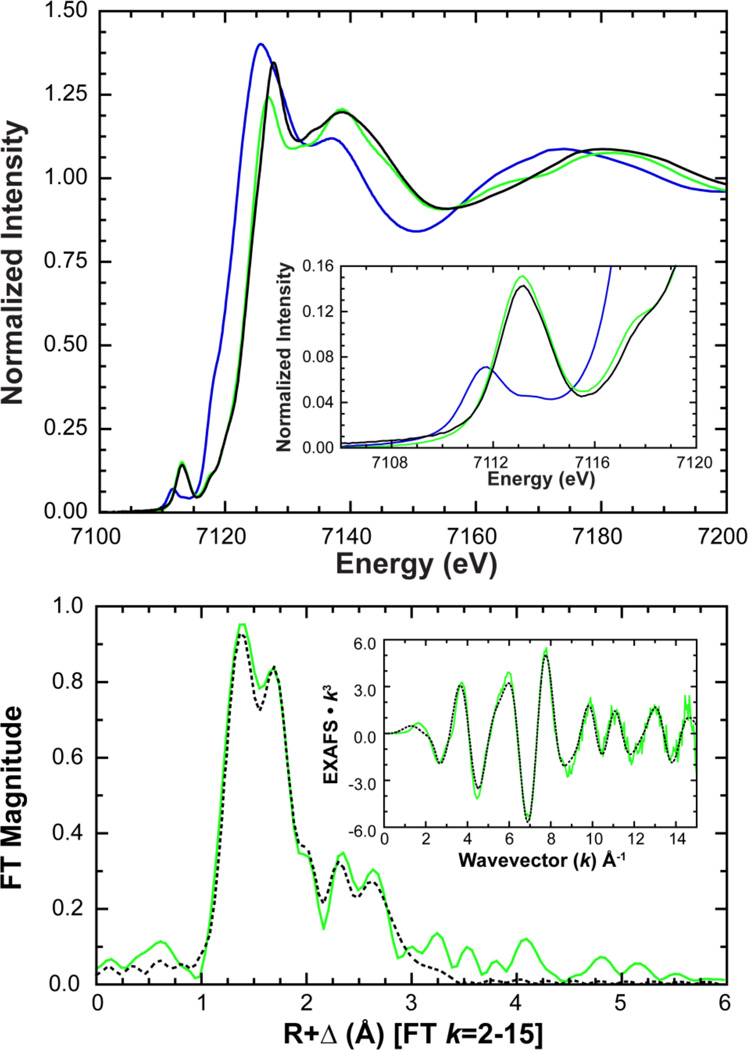
Comparison of the XAS data for 1 to high-spin [Fe^II(TMC)(CH₃CN)]²⁺ shows that the K pre-edge and edge spectra nearly superimpose,⁵⁶ with slightly more intensity for 1 ([Figure 2]). By comparison, [Fe^II(tacn)₂]²⁺ (tacn = 1,4,7-triazacyclononane) and [Fe^II(BQEN)(CH₃CN)₂]²⁺ (BQEN = N,N’-dimethyl-N,N’-bis(8-quinolyl)ethane-1,2-diamine), two low-spin ferrous compounds,^14,56 exhibit K-edge features which are shifted to higher energy relative to 1 and with diminished pre-edge intensities reflecting the fact that these low-spin ferrous complexes are six coordinate and are therefore more centrosymmetric. The pre-edge of 1 exhibits two features centered at 7111.7 and 7113.8 eV with intensities of 12.0 and 4.5 units, respectively, for a total intensity of 16.5 (1.8) normalized units ([Table 1], SI Figure 5). This is greater than the total intensity of 12.7 (0.5) units for [Fe^II(TMC)(CH₃CN)]²⁺, indicating that relative to [Fe^II(TMC)(CH₃CN)]²⁺, 1 has a larger amount of 3d/4p mixing and thus a higher degree of structural distortion.⁵⁶

Figure 2.

Top: Fe K-edge (top) and pre-edge (inset) XAS spectra of 1 (blue) compared with high-spin [Fe^II(TMC)(CH₃CN)]²⁺ (light-blue) and low-spin [Fe^II(BQEN)(CH₃CN)₂]²⁺ (black) and [Fe^II(tacn)₂]²⁺ (grey) reference compounds. Bottom: Fourier transform and EXAFS (inset) data (—) and fit (----) of 1.

Table 1.

XAS Pre-edge Energy and Intensity

	Peak 1 (eV)	Area	Peak 2 (eV)	Area	Total Intensity
1	7111.7	12.0	7113.8	4.5	16.5 ± 1.8
2	7113.0	25.1	7114.0	8.6	33.7 ± 2.5

Fe K pre-edge fits for 1 and 2. Peak energies are listed at maximum, areas are multiplied by 100 for convenience and comparison to previously published data. Total intensity is the sum of both areas. Error values are calculated from total intensity standard deviations across all nine fits. Pre-edge fits are shown in SI Figure 5.

EXAFS data for 1 were collected to k = 15 Å⁻¹ and exhibit a well-defined beat pattern out to ~k = 10 Å⁻¹ giving rise to two main features in the Fourier transform (FT) (Figure 2). The first shell EXAFS data were best fit using a five coordinate (5C) 1:4 split shell at an average distance of 2.20 Å (CN = 4) with a single shorter path at 2.07 Å. These EXAFS distances are in excellent agreement with the crystallographic data (vide supra) that show four Fe-N TBC distances at an average of 2.22 Å and a short Fe-CH₃CN at 2.06 Å. These distances are also consistent with those of other high-spin ferrous systems, including other TMC complexes.^24,69 The second shell EXAFS features were fit by the addition of eight single scattering (SS) carbon based pathways from TBC at a distance of 3.01 Å, followed by a complementary set of 24 multiple scattering (MS) paths at 3.33 Å with a corresponding bond variance of 375 (Fit 1-1 [Table 2], Figure 2). Alternatively, the outer sphere MS contribution could be fit using only two high intensity forward focused MS paths from the axial CH₃CN at a distance of 3.41 Å with a bond variance of 393 (Fit 1-2 Table 2). However, the fits could not simultaneously support both types of MS paths given the similar distance and limited k-range of the data. Yet from the low bond variances that result when only one path is chosen, it is likely that the outer sphere EXAFS signals are in fact combinations of both TBC and CH₃CN MS contributions. Taken together, these XAS data independently define 1 as a distorted five coordinate high-spin ferrous complex; a structural description for 1 in solution (acetonitrile) that is consistent with its solid phase X-ray structure (Figure 1).

Table 2.

Final EXAFS Fits for 1 and 2

[FeII(TBC)(CH3CN)]2+ (1)
Fit 1-1	CN	R(Å)	(Å2)	Fit 1-2	CN	R(Å)	(Å2)
Fe-N	1	2.07	317	Fe-N	1	2.06	302
Fe-N	4	2.20	642	Fe-N	4	2.19	628
Fe-TBC	8	3.01	803	Fe-TBC	8	3.00	1242
TBC MS	24	3.33	375	CH3CN MS	2	3.41	393
E0 = −6.0		Error = 0.264		E0 = −6.0		Error = 0.301
[FeIV=O(TBC)(CH3CN)]2+ (2)
Fit 2-1	CN	R(Å)	(Å2)	Fit 2-2	CN	R(Å)	(Å2)
Fe=O	1	1.64	339	Fe=O	1	1.64	339
Fe-N	5	2.10	556	Fe-N	5	2.11	559
Fe-TBC	8	2.94	1147	Fe-TBC	8	2.99	1030
TBC MS	24	3.16	373	CH3CN MS	2	3.20	483
Fe-TBC	6	3.56	1370	Fe-TBC	6	3.48	1752
E0 = −5.3		Error = 0.252		E0 = −4.9		Error = 0.265
[FeIV=O(TMC)(CH3CN)]2+
Fit 3-1	CN	R(Å)	(Å2)	Fit 3-2	CN	R(Å)	(Å2)
Fe=O	1	1.63	445	Fe=O	1	1.63	441
Fe-N	5	2.09	522	Fe-N	5	2.09	524
Fe-TMC	8	2.95	935	Fe-TMC	8	3.00	1111
TMC MS	24	3.18	362	CH3CN MS	2	3.22	304
Fe-TMC	6	3.55	1360	Fe-TMC	6	3.48	1021
E0 = −4.2		Error = 0.249		E0 = −3.8		Error = 0.254

All distances are in Å. σ² values are multiplied by 10⁵ for convenience. All paths are considered single scattering paths (SS) unless otherwise indicated as multiple scattering (MS). CN = coordination number. Error (F) is defined as F = [Σk⁶(χ_exp−χ_obs)²/Σk⁶(χ_exp)]^1/2

3.2 Characterization of [Fe^IV=O(TBC)(CH₃CN)]²⁺

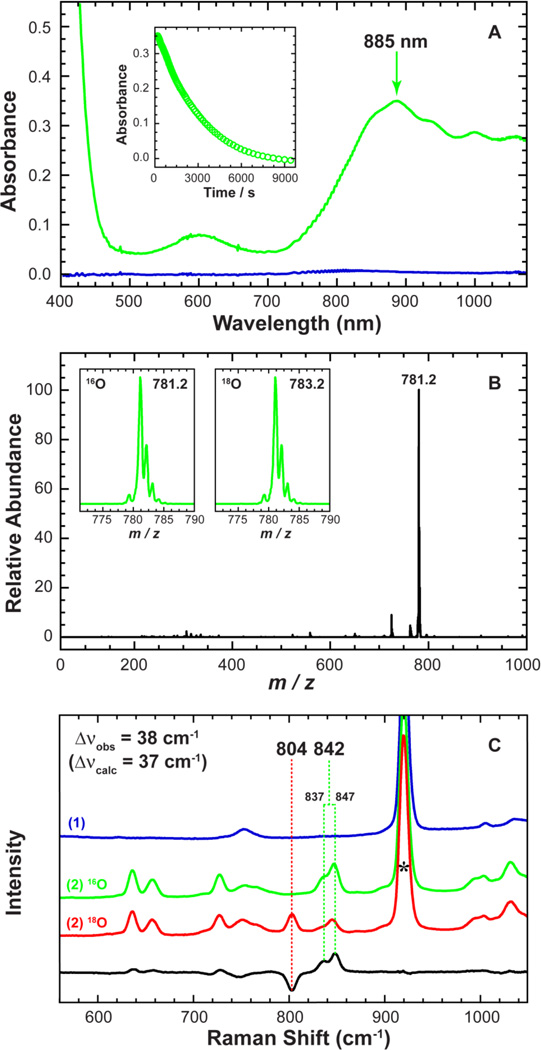
Intermediate 2 was generated by an oxo-transfer reaction between 1 and PhIO and was characterized using a variety of spectroscopic techniques. The reaction of 1 with two equivalents of PhIO in CH₃CN at 15 °C produced a green intermediate, 2, with λ_max at 885 nm (ε = 360 M⁻¹ cm⁻¹; [Figure 3A]) and a relatively stable half-life of t_1/2 ≈ 40 min at 15 °C.

Figure 3.

Top (A): UV-Vis spectra of 1 (blue) vs. intermediate 2 (green). 2 was generated in the reaction of 1 (1.0 mM) and two equivalents of PhIO in CH₃CN at 15 °C. The inset shows the natural decay of 2 monitored at 885 nm (t_1/2 ≈ 40 min). Middle (B): EIS-MS spectrum of intermediate 2. Inset shows observed isotope distribution patterns of 2 in ¹⁶O (left) and ¹⁸O (right). 2-¹⁸O was generated in the reaction of 1 (0.50 mM) and two equivalents PhIO in the presence of H₂ ¹⁸O in CH₃CN at 15°C. Bottom (C): Resonance Raman spectra of 1 (blue), and 2 prepared in the presence of H₂ ¹⁶O (green) and H₂ ¹⁸O (red) showing the isotope sensitivity of the 842 cm⁻¹ band. The black line shows the intensity difference between 2-¹⁶O and 2-¹⁸O. The peak marked with * is from solvent.

Intermediate 2 showed a radically different UV-Vis spectrum from 1 (Figure 3A), with an intense feature at 885 nm that decayed over time. The ESI-MS spectrum of 2 exhibits one prominent isotope sensitive ion peak centered at m/z 781.2, whose mass and distribution patterns correspond to [Fe^IV=O(TBC)(OTf)]⁺ (calculated m/z 781.3) ([Figure 3B]). Upon introduction of ¹⁸O into 2, the ion peak shifts up to m/z 783.2, indicating that 2 contains an iron oxo group. The resonance Raman (rR) spectrum of 2, measured in CH₃CN at −20 °C with 442 nm laser excitation, exhibits a doublet of peaks at 837 and 847 cm⁻¹ arising from a Fermi resonance with an average peak position at 842 cm⁻¹ that shifts to a single peak at 804 cm⁻¹ upon introduction of ¹⁸O ([Figure 3C]). The observed isotopic shift of −38 cm⁻¹ with ¹⁸O substitution is in good agreement with the calculated value (Δν_calculated = −37 cm⁻¹) for the Fe=O diatomic harmonic oscillator.

The X-band EPR spectrum of 2 is silent (SI Figure 2), consistent with 2 being an integer spin system. The spin state of 2 (in CH₃CN) was determined using the ¹H NMR Evans method,^45–47 and gave a magnetic moment of 3.3 µ_B at 15 °C which indicates that 2 is a low-spin (S = 1) Fe^IV=O species.

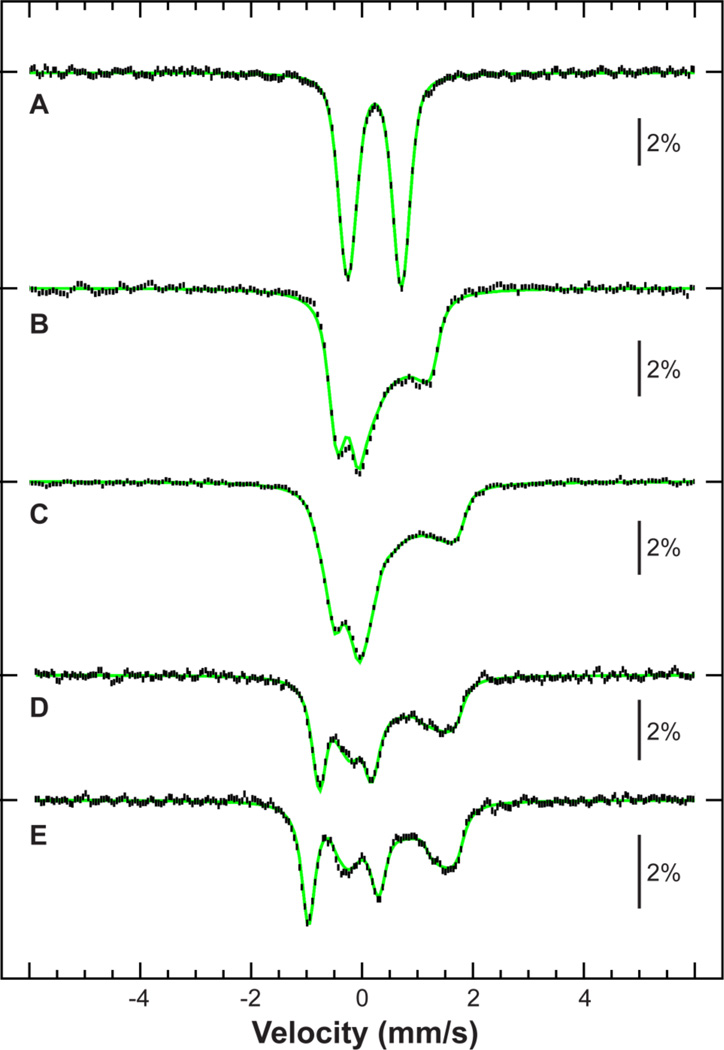
The Mössbauer spectrum of 2 (SI Figure 3) is dominated by a quadrupole doublet that can be assigned to an Fe^IV=O based on its Mössbauer parameters ([Table 3] and SI Table 1). Additionally, a smaller feature at high energy can be discerned, representing a minor contribution of a high-spin ferrous species, with parameters corresponding to those of 1 (SI Figure 3 and 6). To further characterize 2, field-dependent experiments were performed at 4.2 K in magnetic fields of 60 mT, 4 T, and 7 T applied parallel to the γ-rays ([Figure 4 A–C]). The experiment that yielded the highest proportion of oxoferryl intermediate (78 %) also yields a 1:1 ratio of 1a:1b, similar to that found in the starting material. It should be noted that no ferrous contaminant was observed in the XAS data (vide infra). Therefore, a synthetic spectrum of 2 was constructed by subtracting a 22% contribution of 1 measured under identical conditions. The procedure is validated by the resultant flat baseline. The synthetic spectrum was fit with one unique set of spin-Hamiltonian parameters corresponding to an axially distorted S = 1 ground state (Figure 4).⁷⁰ Temperature-dependent spectra (Figure 4 D and E) were also measured to assess the zero-field splitting, and could be framed between 28 cm⁻¹ and 31 cm⁻¹. The spectra were therefore fit assuming D = 29.5 cm⁻¹, E/D = 0, g_x = g_y = 2.3 and g_z = 2.0,⁷¹ and afforded hyperfine parameters of A_x,y,z/g_Nβ_N = (−18, −18, −2) T and η = 0.36. These results are also consistent with the NMR data, and therefore 2 can be described as an S=1 Fe^IV=O species.

Table 3.

Mössbauer and Spin-Hamiltonian Parameters for TMC and TBC Fe^IV=O (S = 1) Complexes

	[FeIV=O(TBC)]2+ (2)	[FeIV=O(TMC)]2+
D (cm−1)	29.5 ± 1.5	28
E/D	0a	0a
gx, gy, gz	2.3, 2.3, 2.0b	2.3, 2.3, 2.0b
Ax,y,z/gNβN, (T)	−18 ± 1, −18c, −2 ± 5	−25, −20, −5
δ (mm/s)	0.22 ± 0.01	0.17
ΔEQ (mm/s)	0.97 ± 0.01	1.24
η	0.36 ± 0.3	0.50

Mössbauer and spin-Hamiltonian parameters for 2 vs. [Fe^IV=O(TMC)(CH₃CN)]²⁺ (from literature).^17,18 Data collected on frozen CH₃CN solution at 4.2 K.

^aFixed.

^bCalculated from ligand-field treatment.⁷¹

^cA_x=A_y fixed. Data and fit are shown in SI Figure 3 and Figure 4 in text.

Figure 4.

Mössbauer spectra of 2 (vertical bars), obtained by subtraction of a 22% contribution of 1 measured under identical conditions. Spectra measured at 4.2 K (A, B and C), 41 K (D) or 78 K (E) in a magnetic field of 60 mT (A), 4 T (B) or 7 T (C, D and E) applied parallel to the γ-rays. Spin-Hamiltonian simulation (green) was fit with a unique set of parameters for all spectra (Table 3), with A fit to an asymmetric quadrupole doublet.

To confirm the identity of 2, Fe K pre-edge and edge XAS data were measured ([Figure 5]). Compared to 1, the XAS data are shifted to higher energy, indicative of an increase in Z_eff for the iron, a change that is also consistent with the Mössbauer assignment of an Fe^IV oxidation state. Additionally, the pre-edge of 2 exhibits a large increase in intensity and was fit with two features having 25.1 and 8.6 intensity units, centered at 7113.0 and 7114.0 eV for a total intensity of 33.7 (2.5) units (Table 1, SI Figure 5). This is more than double the pre-edge intensity of 1 (16.5 units) and is indicative of the formation of an Fe^IV=O species as the presence of a short and highly covalent Fe=O bond increases the pre-edge intensity through additional 4p mixing into the 3d manifold.⁵⁶ A pre-edge intensity of 33.7 units is comparable to, but larger than, values observed for other six coordinate (6C) non-heme Fe^IV=O complexes;^17,18,72 in particular [Fe^IV=O(TMC)(CH₃CN)]²⁺ (included as a reference in Figure 5), which has an established value of 30.0 units (SI Table 2),¹⁷ indicating 2 contains a more distorted metal site and/or a more covalent Fe=O bond.

Figure 5.

Top: Fe K-edge and enlarged pre-edge (inset) showing the increased pre-edge intensity of 2 (green) relative to 1 (blue) upon reaction with PhIO in acetonitrile. XAS data of [Fe^IV=O(TMC)(CH₃CN)]²⁺ (black) are included for reference. Bottom: Fourier transform and EXAFS, data (—) and fit (----), of 2 showing the strong first shell intensity contribution resulting from a short (1.64 Å) Fe=O bond.

EXAFS data for 2 were measured up to k = 15 Å⁻¹ and are shown along with the final EXAFS fit in Figure 5 with fit parameters given in Table 2 and a comparison to 1 in SI Figure 7. Unlike the EXAFS of 1, which greatly diminished around k = 10 Å⁻¹, the EXAFS of 2 have a strong and distinctive beat pattern all the way to k = 15 Å⁻¹ that gives rise to two main features in the Fourier transform. The first feature around ~1.5 Å (R+Δ) has two prominent peaks which are a result of two closely spaced overlapping waves that are only individually resolved due to the high k-range of the data and large distance between two groups of absorber-scatter atom pairs. The second feature around ~2.7 Å (R+Δ) is also resolvable into two features, both of which, similar to 1, are likely to be from a combination of outer shell single and multiple scattering contributions from the TBC cyclam ring.

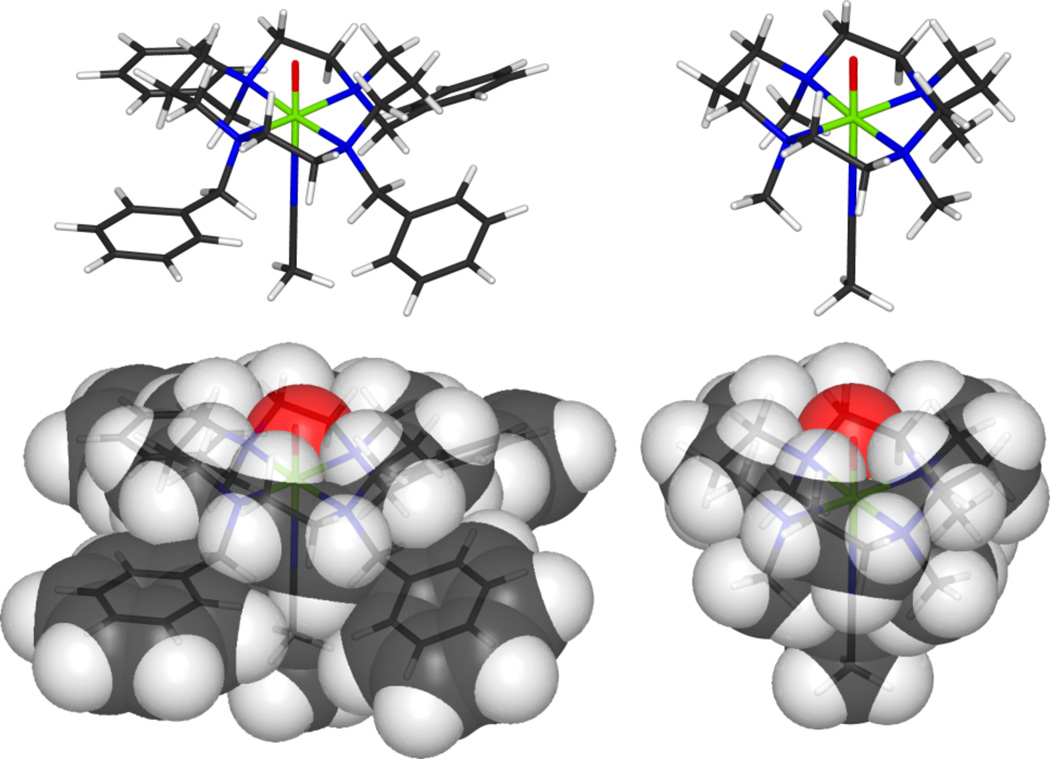
Based on the above spectroscopic characterization of 1 and 2, the EXAFS data were fit to a computational model (vide infra) of [Fe^IV=O(TBC)(CH₃CN)]²⁺. EXAFS fits determined a 1:5 split first shell with a single short path at 1.64 Å, and 5 Fe-N SS atoms at an average distance of 2.11 Å. In order to test this coordination number, a 1:4 fit was also tried. However, this coordination resulted in an unreasonably low bond variance for the four remaining nitrogen atoms, a worse error, and an EXAFS fit with inadequate beat pattern intensity. Considered along with the pre-edge intensity (33.7 units), which is considerably lower than that of a 5C Fe^IV=O complex,²⁸ these data exclude a 5C structure. The second shell EXAFS feature was fit in an analogous fashion to 1 using either an 8:24 SS:MS path ratio for TBC (Fit 2-1 in Table 2), or only two MS paths from the axial CH₃CN (Fit 2-2 in Table 2,). Analogous to the final fit of 1, using only two MS contributions from CH₃CN gave similar bond variances as 24 MS paths from TBC. However, the overall fit quality was worse suggesting that while there are multiple scattering contributions from the axial CH₃CN ligand, the majority of the contribution originates from the cyclam ring. To arrive at a final structure, six more SS paths were added at a distance of 3.56 Å to account for both the benzyl carbons and distal carbon atoms of the TBC ring. Similar to the pre-edge and edge energy and intensity, these EXAFS distances are consistent with those distances found for other 6C S = 1 Fe^IV=O complexes^17,18,22,72 including [Fe^IV=O(TMC)(CH₃CN)]²⁺ for which a crystal structure is available. Combined, these data confirm that a new Fe^IV=O model complex has been successfully synthesized using the more sterically strained TBC ligand, and identify intermediate 2 as [Fe^IV=O(TBC)(CH₃CN)]²⁺ ([Figure 6]).

Figure 6.

Final geometry optimized model for 2 used in conjunction with fitting the EXAFS data. Space filling models of 2 (left) compared with [Fe^IV=O(TMC)(CH₃CN)]²⁺ (right) show increased steric interactions between the benzyl groups and with the cyclam ring. These interactions result in a greater distortion at the iron and a smaller oxo cage.

For a direct comparison between 2 and [Fe^IV=O(TMC)(CH₃CN)]²⁺, analogous EXAFS data were also measured for [Fe^IV=O(TMC)(CH₃CN)]²⁺ (SI Figure 8) and fit in an identical way as for 2 but using a geometry optimized model based on the known crystal structure.¹⁸ EXAFS distances for [Fe^IV=O(TMC)(CH₃CN)]²⁺ gave first shell bond lengths of 1.63 Å and 2.09 Å for the Fe=O bond and the Fe-N coordination of the TMC ligand and axial acetonitrile (Table 2). As was found for the EXAFS data on 1 and 2, the outer shell of [Fe^IV=O(TMC)(CH₃CN)]²⁺ could also be fit well using either multiple scattering paths from TMC or the intense forward focused multiple scattering from the axial CH₃CN, but not both simultaneously, as the two paths are not individually resolvable given the overlap of the EXAFS waves and k range of the data. The EXAFS of 2 and [Fe^IV=O(TMC)(CH₃CN)]²⁺ are very similar, with the most notable difference being the consistently larger bond variance values across most paths of 2, implying a more disordered metal site. The exception to this is the bond variance of the Fe=O path which is roughly ~100 Ų less for 2 relative to [Fe^IV=O(TMC)(CH₃CN)]²⁺. This indicates that 2 has more constrained Fe=O unit, suggesting a smaller oxo-cage, or a stronger Fe=O bond relative [Fe^IV=O(TMC)(CH₃CN)]²⁺. These differences are also consistent with the more intense pre-edge discussed above.

3.3 Reactivity of [Fe^IV=O(TBC)(CH₃CN)]²⁺

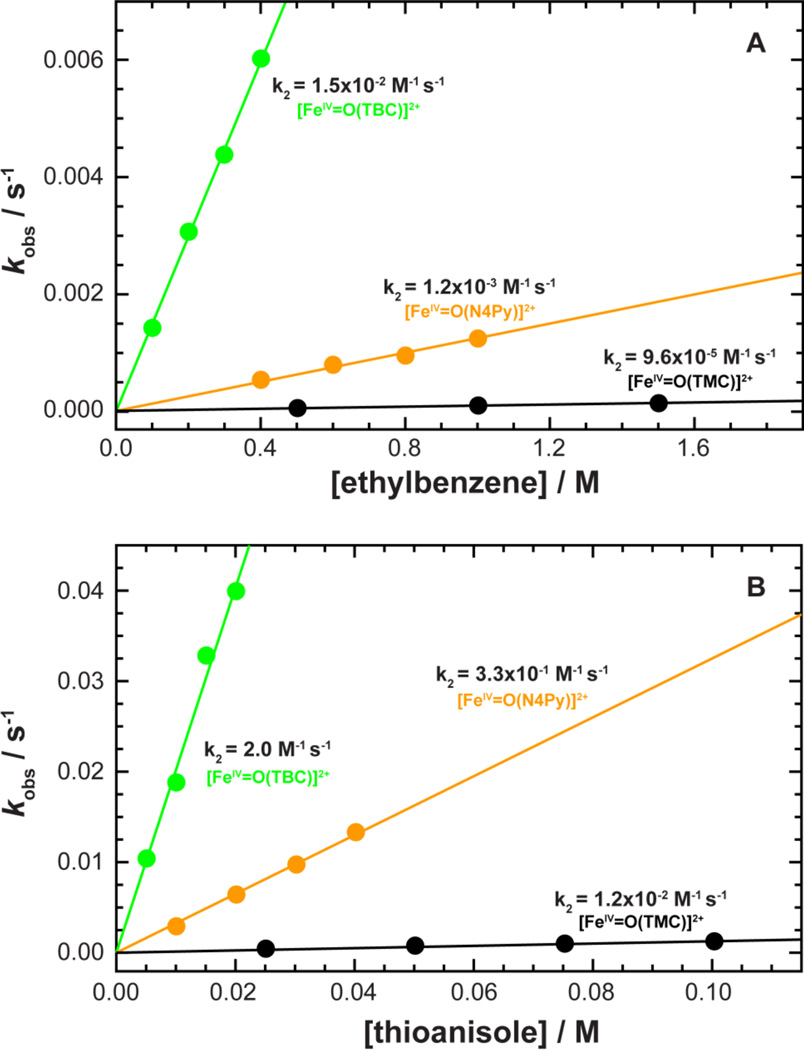
The reactivity of 2 was first investigated for its activation of an H-atom from ethylbenzene, where an H-atom is abstracted from the benzylic position,¹⁶ and gave a second-order rate constant of 1.5(2) × 10⁻² M⁻¹ s⁻¹. Using deuterated ethylbenzene-d₁₀, a large kinetic isotope effect (KIE) with a value of 17 was also determined (SI Figure 9); a value similar to those observed in the oxidation of ethylbenzene by other non-heme iron(IV)-oxo complexes.^14,70 This indicates that the C-H bond activation of ethylbenzene is involved in the rate-determining step in the oxidation reaction of ethylbenzene by 2. For comparison, the reactivities of [Fe^IV=O(N4Py)]²⁺ and [Fe^IV=O(TMC)(CH₃CN)]²⁺ were also investigated and yielded a second-order rate constant of 1.3(2) × 10⁻³ M⁻¹ s⁻¹ for [Fe^IV=O(N4Py)]²⁺, while in the case of [Fe^IV=O(TMC)(CH₃CN)]²⁺, very little reactivity was observed, with the upper limit determined as < 9.6 × 10⁻⁵ M⁻¹ s⁻¹ ([Figure 7A]). These results indicate that 2 is ten time more reactive than [Fe^IV=O(N4Py)]²⁺ and two orders of magnitude larger than [Fe^IV=O(TMC)(CH₃CN]²⁺ in the oxidation of ethylbenzene.

Figure 7.

Observed reaction rates and second-order rate constants for 2 compared to other known non-heme Fe^IV=O models. Top (A): k_obs vs. the concentration of ethylbenzene in H-atom abstraction reactions. Bottom (B): k_obs vs. the concentration of thioanisole in oxo-transfer reactions. [Fe^IV=O(TBC)(CH₃CN)]²⁺ (2) (green), [Fe^IV=O(N₄Py)]²⁺ (orange), and [Fe^IV=O(TMC)(CH₃CN)]²⁺ (black).

Second, the oxo-transfer reactivity of 2 was investigated using thioanisole derivatives, where upon addition of thioanisole (10 mM) to a solution of 2 (0.50 mM), the oxo group was successfully transferred from the Fe^IV=O to the substrate, and the intermediate quantitatively converted back to the starting ferrous complex, yielding methyl phenyl sulfoxide (SI Figure 10). Pseudo-first-order rate constants determined by fitting the kinetic data for the decay of 2 increased linearly with substrate concentration and yielded a second-order rate constant of 2.0(2) M⁻¹ s⁻¹ (SI Figure 11A). Pseudo-first-order rate constants were also determined using various para-substituted thioanisoles and plotted against σ_p, enabling the determination of a Hammett value ρ = −2.3 (SI Figure 11B). The negative ρ value indicates both the electrophilic character of the oxo group in the non-heme Fe^IV=O complexes and a positive charge buildup on sulfur in sulfoxidation reactions.⁷³ The reactivities of [Fe^IV=O(N4Py)]²⁺ and [Fe^IV=O(TMC)(CH₃CN)]²⁺were also investigated with thioanisole and afforded second-order rate constants with a reactivity order of [Fe^IV=O(TBC)]²⁺ > [Fe^IV=O(N4Py)]²⁺ > [Fe^IV=O(TMC)(CH₃CN)]²⁺ (Figure 7B); again a more than two order of magnitude increase from 1.2 × 10⁻² M⁻¹ s⁻¹ to 2.0 M⁻¹ s⁻¹ for [Fe^IV=O(TMC)(CH₃CN)]²⁺ and 2, respectively.

4. Density Functional Theory Calculations (DFT)

In order to understand the observed reactivity differences between [Fe^IV=O(TBC)(CH₃CN)]²⁺ (2) and [Fe^IV=O(TMC)(CH₃CN)]²⁺, a series of density functional theory (DFT) calculations were conducted for both H-atom abstraction and oxo-transfer reactions. A table comparing the effects of functional, basis set, and solvent on the final energy splitting between the ground and excited states for Fe^II and Fe^IV=O TBC and TMC is provided in SI Table 3.

As a calibration, DFT calculations were first performed on the known system [Fe^IV=O(TMC)(CH₃CN)]²⁺, with an S = 1 ground state, as both a single point on the crystal structure (CSD 192768)¹⁸ and as a fully optimized geometry. Geometry optimization did not appreciably change the structure from that of the crystallography, calculating the Fe=O bond at ~1.61 Å, the equatorial iron-nitrogen TMC distances at an average of ~2.13 Å, and the axial acetonitrile at 2.12 Å ([Table 4] and SI Table 4 with SI Figure 12 as reference). In all cases, values for orbital energies and covalencies agreed well with previous calculations on this system.³⁹

Table 4.

Key Bond Distances and Angles for S = 1 and S = 2 for Fe^IV=O Complexes

	[FeIV=O(TBC)]2+ (2)			[FeIV=O(TMC)]2+
Bond Dist./Angle	S = 1	S = 2	Δ	S = 1	S = 2	Δ
Fe=O	1.61	1.61	0.00	1.62	1.61	0.00
Fe-N CH3CN	2.12	2.09	−0.04	2.12	2.08	−0.04
Ave. Fe-N TXC	2.15	2.24	0.09	2.14	2.22	0.08
Fe-N Plane	−0.06	−0.08	−0.02	−0.05	−0.08	−0.03
O-H Plane	−0.38	−0.40	−0.02	−0.37	−0.39	−0.03
Ave. O-H Crown	2.37	2.39	0.02	2.41	2.43	0.02
Nitrogen SD	0.03	0.07	0.05	0.01	0.06	0.06
∠ O-Fe-TXC	88.32	87.93	−0.39	88.70	88.16	−0.54
∠ TXC-Fe-CH3CN	91.69	92.10	0.41	91.32	91.88	0.56
∠ Equatorial SD	6.38	7.79	1.41	6.05	6.45	0.40

Geometric parameters for the S = 1 ground state and the S = 2 excited state for [Fe^IV=O(TBC)(CH₃CN)]²⁺ (2) and [Fe^IV=O(TMC)(CH₃CN)]²⁺. Structures calculated using B3LYP/6-311G(d). All distances are given in Å, all angles (∠) are in degrees, SD = Standard Deviation. A more extensive table is reproduced in SI Table 4.

As crystallographic data are not currently available for [Fe^IV=O(TBC)(CH₃CN)]²⁺, a low-spin S = 1 geometry was calculated based on the above spectroscopic characterizations. An initial starting geometric structure was constructed based on a similar nickel-containing TBC complex [Ni^II(TBC)(Cl)]⁺ by changing the Ni^II to an Fe^IV, adding an oxo and acetonitrile group in the trans-axial position and optimizing the geometry. To ensure the correct conformation of [Fe^IV=O(TBC)(CH₃CN)]²⁺, the structure was evaluated by interchanging the oxo and axial acetonitrile groups from oxo-anti to oxo-syn relative to the benzyl groups. Comparison of the final energies of the reoptimized conformations indicated that the conformation with oxo anti to the benzyl groups was energetically favorable by ~3.2 kcal/mol (SI Table 5). As a calibration, these results were compared with the crystallographic data on [Fe^IV=O(TMC)(CH₃CN)]²⁺ where the oxo is defined to be orientated anti to the methyl groups. The calculations for [Fe^IV=O(TMC)(CH₃CN)]²⁺ also show that the syn confirmation is energetically unfavorable by ~4.0 kcal/mol.

4.1 Comparison of Fe^IV=O TBC to TMC

A direct comparison of the geometry optimized models of [Fe^IV=O(TBC)(CH₃CN)]²⁺ and [Fe^IV=O(TMC)(CH₃CN)]²⁺ in the S = 1 ground state reveals several small but significant differences. In [Fe^IV=O(TBC)(CH₃CN)]²⁺, the substitution of benzyl groups on the cyclam ligand adds an appreciable amount of steric bulk next to the axial acetonitrile over the methyl groups in [Fe^IV=O(TMC)(CH₃CN)]²⁺. This leads to twists and tilts of the benzyl rings and a slight folding of the cyclam ring, decreasing the cavity for the oxo group, as the bottom portion of the complex is splayed out to accommodate the increased steric bulk (Figure 6). From the optimized geometries, this substitution also results in slightly longer equatorial Fe-N bond lengths, a tighter hydrogen-oxo cage (Ave. O-H Crown), an iron that is farther below the nitrogen equatorial plane (Table 4, Fe N-Plane, more acute ∠ O-Fe-TBC, and more obtuse ∠ TBC-Fe-CH₃CN angles), and an overall more distorted complex, evident by the three fold larger standard deviation (SD) in the equatorial bond lengths as well as by the increased SD in the ∠ N-Fe-N equatorial angles (Table 4, Fe^IV=O TBC and TMC S = 1).

These calculations reproduce the differences between [Fe^IV=O(TBC)(CH₃CN)]²⁺ and [Fe^IV=O(TMC)(CH₃CN)]²⁺ that were observed in the EXAFS data, where the fits of [Fe^IV=O(TBC)(CH₃CN)]²⁺ show both slightly longer Fe-N bonds and a larger degree of bond variance, indicating a more distorted metal environment (Fit 2-1 vs. 3-1, Table 2). These calculations also reproduced the intensity difference observed in the pre-edge data between [Fe^IV=O(TBC)(CH₃CN)]²⁺ and [Fe^IV=O(TMC)(CH₃CN)]²⁺ (33.7 and 30.0 normalized units, respectively), as these gave a total metal 4p mixing of 29.8 % for [Fe^IV=O(TBC)(CH₃CN)]²⁺ and 24.5 % for [Fe^IV=O(TMC)(CH₃CN)]²⁺. Based on previously determined values⁵⁶ where 1 % metal 4p character corresponds to ~1.22 (0.5) units of pre-edge intensity, the calculations (including the quadrupole contribution from the d character) predict pre-edge intensities of 36 and 29 units for [Fe^IV=O(TBC)(CH₃CN)]²⁺ and [Fe^IV=O(TMC)(CH₃CN)]²⁺, respectively; a result consistent with the greater structural distortion reflected in the larger EXAFS bond variances and the larger calculated displacement of the iron from the equatorial nitrogen plane, further calibrating the DFT calculations to the experiment.

Based on the spectroscopic differences observed experimentally and the insight gained through the geometry optimized structures showing that the Fe=O unit is more constrained in the cyclam for [Fe^IV=O(TBC)(CH₃CN)]²⁺ relative to [Fe^IV=O(TMC)(CH₃CN)]²⁺, an even lower rate of reaction would be expected. However, this is in contrast to the reactivity studies (vide supra) where [Fe^IV=O(TBC)(CH₃CN)]²⁺ exhibited rate constants that are two orders of magnitude larger than those measured for [Fe^IV=O(TMC)(CH₃CN)]²⁺.

The structures of [Fe^IV=O(TBC)(CH₃CN)]²⁺ and [Fe^IV=O(TMC)(CH₃CN)]²⁺ were therefore also optimized for the S = 2 excited states. These calculations revealed that the energetic gap between the S = 1 and the S = 2 is smaller by ~3.2 kcal/mol for [Fe^IV=O(TBC)(CH₃CN)]²⁺ relative to [Fe^IV=O(TMC)(CH₃CN)]²⁺ ([Table 5], ΔG (solv), B3LYP), as the more distorted ligand environment caused by the steric interaction of the benzyl rings (Figure 6) weakens the equatorial and axial ligand field, stabilizing the d_x²−y² and d_z² orbitals. This is consistent with the measurably larger D value defined for [Fe^IV=O(TBC)(CH₃CN)]²⁺ (29.5 cm⁻¹) relative to [Fe^IV=O(TBC)(CH₃CN)]²⁺ (28 cm⁻¹), Table 3.^17,18,28 The lower energy of the S = 2 excited state for [Fe^IV=O(TBC)(CH₃CN)]²⁺ provides a pathway for its increased reactivity (vide infra).

Table 5.

Calculated Energy Differences; Fe^IV=O S = 2 Excited State Relative to S = 1 Ground State

	[FeIV=O(TBC)(CH3CN)]2+ (2)		[FeIV=O(TMC)(CH3CN)]2+
	B3LYP	BP86	B3LYP	BP86
Δε (gas)	3.2	13.5	4.9	15.0
Δε (solv)	2.7	13.0	5.8	16.1
ΔE (solv)	1.0	11.2	3.9	14.1
ΔH (solv)	1.4	11.7	4.5	14.8
ΔG (solv)	−0.3	9.7	2.9	12.7

All values in kcal/mol, calculated for just Fe^IV=O TBC and TMC; Δε (gas) G03/6-311+G(2df,2pd) without zero-point energy (ZPE); ΔE (solv) with ZPE correction and solvent (acetonitrile). Geometry optimization done using G03/B3LYP or BP86/6-311G(d).

4.2 Hydrogen Atom Abstraction

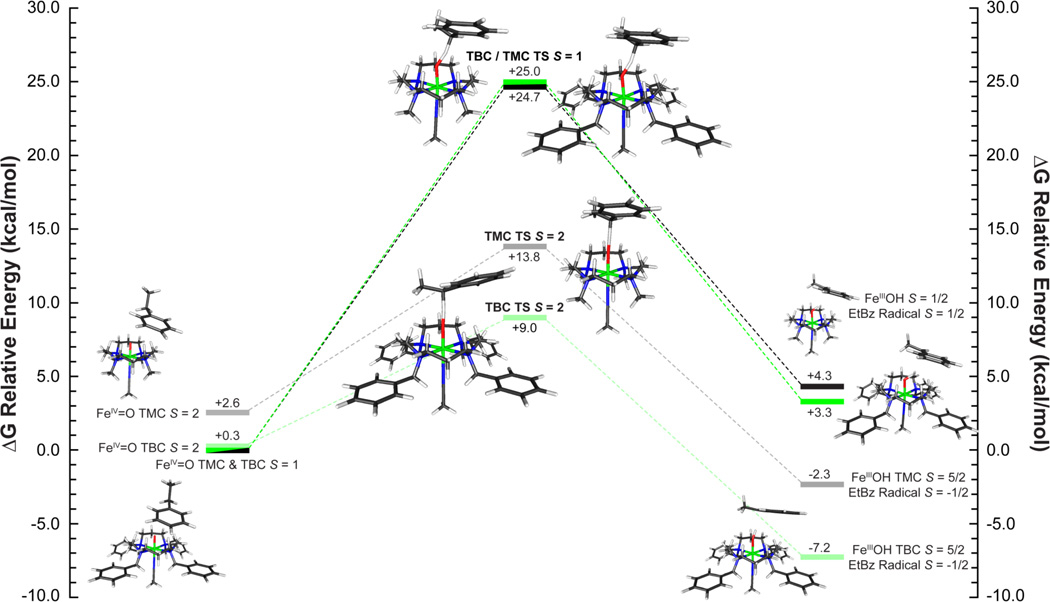
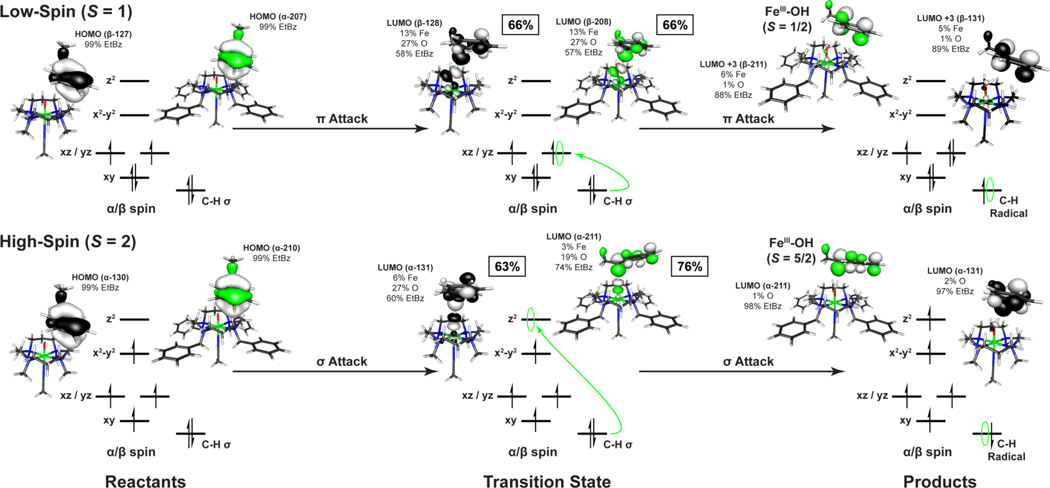
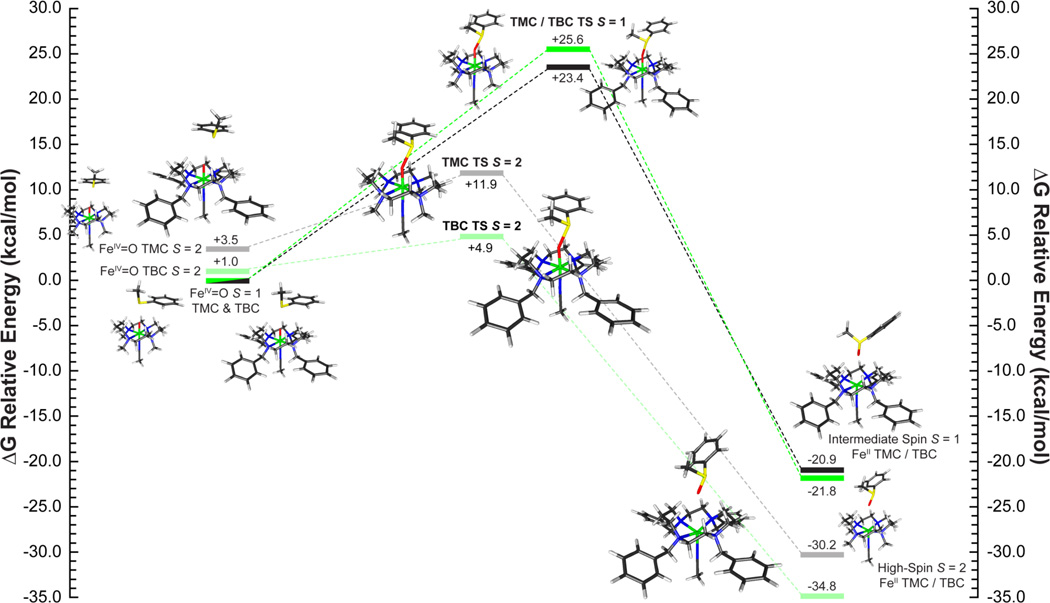
A set of two reaction coordinates were calculated for both [Fe^IV=O(TBC)(CH₃CN)]²⁺ and [Fe^IV=O(TMC)(CH₃CN)]²⁺ starting from the experimentally determined S = 1 ground state utilizing ethylbenzene. (Reaction coordinate diagram for ΔG(solv) in [Figure 8]. ΔE(solv) in SI Figure 13. Select geometric parameters are available in [Table 6] with additional values in SI Table 6.) As observed in previous studies,^4,39,40 an electrophilic attack by a low-spin Fe^IV=O species is enabled through a π-attack of the oxo p_x/y frontier molecular orbital (FMO). This leads to the transfer of a hydrogen atom along with a single β-spin electron from the HOMO of the substrate into the d_xz/yz π* orbital of the iron to generate a low-spin ferric product and a radical on the substrate ([Figure 9], top). Since the electron is transferred into the π set of iron d-orbitals, this requires a side-on approach of the C-H bond of the substrate relative to the Fe=O to ensure good orbital overlap. In the case of a sterically hindered cyclam ligand, this results in a very large transition state barrier. For both [Fe^IV=O(TBC)(CH₃CN)]²⁺ and [Fe^IV=O(TMC)(CH₃CN)]²⁺, the transition state has an Fe-O-substrate angle of ~144° and calculated barrier heights of ΔG^‡ = 24.7 kcal/mol and 25.0 kcal/mol, with that for [Fe^IV=O(TBC)(CH₃CN)]²⁺ slightly higher due to its more constrained oxo-cage (Figure 8, S = 1 TS). Barrier heights of this magnitude are too large to correlate with the observed H-atom reactivity of [Fe^IV=O(TBC)(CH₃CN)]²⁺. In addition, the low-spin ferric products of this reaction are calculated to be endergonic by around ~4 kcal/mol. Therefore, reactivity on the S = 1 surface is not feasible for an Fe^IV=O unit with the sterically hindered cyclam ligand, and reaction coordinates were evaluated for each complex on the S = 2 surface.

Figure 8.

Hydrogen atom abstraction reaction coordinate of [Fe^IV=O(TBC)(CH₃CN)]²⁺ (S = 1 green, S = 2 light green) and [Fe^IV=O(TMC)(CH₃CN)]²⁺ (S = 1 black, S = 2 grey) with ethylbenzene. Energies given for ΔG (solv = acetonitrile) in units of kcal/mol, with the S = 1 ground state of each series defined as 0.0 kcal/mol.

Table 6.

Geometric Parameters for 2 and [Fe^IV=O(TMC)(CH₃CN]²⁺ for H-atom Transfer and Oxo-Transfer Transition State Complexes

	[FeIV=O(TBC)(CH3CN)]2+ (2)						[FeIV=O(TMC)(CH3CN)]2+
	GS / ES		H-Atom Transfer		Oxo-Transfer		GS / ES		H-Atom Transfer		Oxo-Transfer
Measurement	S = 1	S = 2	S = 1	S = 2	S = 1	S = 2	S = 1	S = 2	S = 1	S = 2	S = 1	S = 2
Oxo-H/S (H-C)	- - -	- - -	1.27(1.34)	1.25(1.34)	2.03	2.07	- - -	- - -	1.28(1.33)	1.42(1.23)	1.92	2.07
Fe=Oxo	1.61	1.61	1.75	1.76	1.87	1.78	1.62	1.61	1.75	1.73	1.86	1.80
Fe-N CH3CN	2.12	2.09	2.10	2.36	2.30	4.08	2.12	2.08	2.09	2.32	2.28	2.51
Ave. Fe-N Equatorial	2.15	2.24	2.16	2.25	2.17	2.21	2.14	2.22	2.13	2.23	2.16	2.23
Fe Out of Plane	−0.06	−0.08	−0.03	0.05	0.01	0.34	−0.05	−0.07	−0.02	0.05	0.04	0.13
O-H Plane Distance	−0.38	−0.40	−0.21	−0.11	−0.04	0.23	−0.37	−0.39	−0.20	−0.14	−0.01	0.03
Ave. O-H Distance	2.37	2.39	2.39	2.41	2.42	2.55	2.41	2.43	2.43	2.45	2.51	2.51
Nitrogen Shell SD	0.03	0.07	0.04	0.06	0.07	0.84	0.01	0.06	0.03	0.04	0.06	0.13
∠ Fe-O-Substrate	- - -	- - -	144.04	176.45	153.07	154.84	- - -	- - -	143.64	176.12	148.98	153.46
∠ θ (Horiz. to O Px/y)	- - -	- - -	61.24	86.28	44.79	34.57	- - -	- - -	60.75	86.57	52.23	40.79
Δ (Horiz. Offset O Pz)	- - -	- - -	1.24	0.17	0.92	0.88	- - -	- - -	1.26	0.16	0.99	0.93
H-Plane-Sub. Dist.	- - -	- - -	2.14	2.47	1.85	2.15	- - -	- - -	2.15	2.51	1.75	1.95

Geometric parameters for the S = 1 ground state (GS) and the S = 2 excited state (ES) reproduced from Table 4 along with those of the corresponding H-atom abstraction and oxo-transfer transition state complexes of [Fe^IV=O(TBC)(CH₃CN)]²⁺ (2) and [Fe^IV=O(TMC)(CH₃CN)]²⁺. Structures calculated using B3LYP/6-311G(d). All distances are given in Å, all angles (∠) are in degrees, SD = Standard Deviation. Reference SI Figure 12 for descriptions and SI Table 4, 6 and 7 for additional parameters.

Figure 9.

Comparison of low- and high-spin frontier molecular orbitals involved in the H-atom transfer reaction for [Fe^IV=O(TBC)(CH₃CN)]²⁺ (green) and [Fe^IV=O(TMC)(CH₃CN)]²⁺ (black) with ethylbenzene.

In contrast to the π-attack required by the side-on approach for the low-spin complex, H-atom abstraction by an S = 2 Fe^IV=O complex to form a high-spin ferric product involves a σ-attack and the transfer of an α-spin electron from the HOMO of the substrate into the unoccupied d_z² σ* orbital on the iron (Figure 9, bottom). As the d_z² is σ anti-bonding with the oxo p_z orbital, good orbital overlap will result from an end-on approach of the substrate, as is observed in the transition state, with the Fe-O-H-C (substrate) bond angle now close to linear (~176°) for both complexes (Figure 8 S = 2 TS, Table 6). The end-on approach of the substrate substantially lowers the barrier to reactivity by decreasing the substrate-cyclam steric interaction, yielding reduced barrier heights of ΔG^‡ = 13.8 and 9.0 kcal/mol (ΔG (solv=acetonitrile), B3LYP) for [Fe^IV=O(TMC)(CH₃CN)]²⁺ and [Fe^IV=O(TBC)(CH₃CN)]²⁺, respectively. This difference in the calculated transition state barrier height for the two complexes is now 4.8 kcal/mol, with [Fe^IV=O(TBC)(CH₃CN)]²⁺ lower; a result that is comparable to the observed >10² rate increase of H-atom reactivity by [Fe^IV=O(TBC)(CH₃CN)]²⁺.

It is important to note that the energetic gap between the S = 1 and the S = 2 states in the complete reactant complex (substrate included) is smaller by 2.3 kcal/mol for [Fe^IV=O(TBC)(CH₃CN)]²⁺ relative to [Fe^IV=O(TMC)(CH₃CN)]²⁺ (Figure 8). This difference, which was due to the weaker ligand field [Fe^IV=O(TBC)(CH₃CN)]²⁺, becomes even larger at the transition state (ΔΔG^‡ = 4.8 kcal/mol), as the transfer of an electron into the d_z² orbital combined with the steric bulk of the benzyl substituents elongates the trans-axial CH₃CN bond allowing greater out-of-plane movement of the iron, a longer Fe=O bond, and a more exposed oxo which is now just below the cyclam hydrogen crown (SI Figure 12). These changes further lower the steric contribution to the barrier for [Fe^IV=O(TBC)(CH₃CN)]²⁺ and yield the faster rate of H-atom abstraction.

4.3 Oxo-Transfer Reactivity

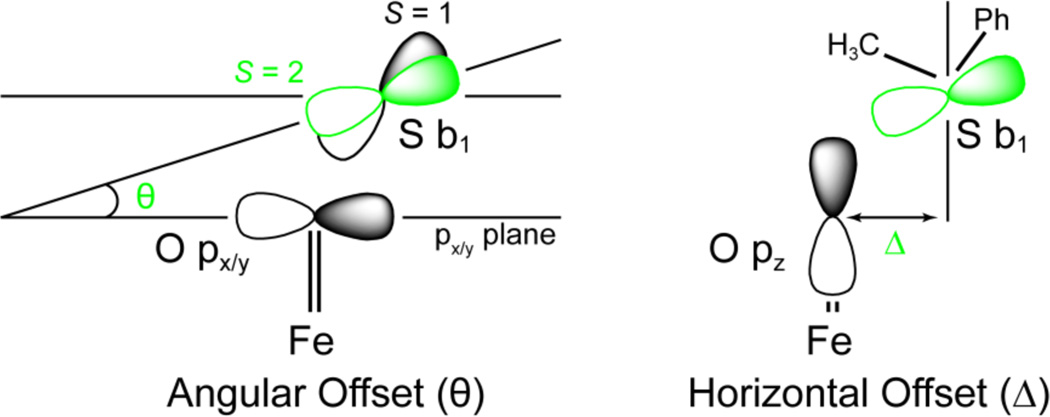
To correlate with the reactivity data and elucidate the differences between H-atom abstraction and oxo-transfer reactions, S = 1 and S = 2 transition states and IRCs were calculated for the reaction coordinate of thioanisole with Fe^IV=O TBC and TMC ([Figure 10] and SI Figure 14). Energetically, oxo-transfer parallels H-atom abstraction with the S = 1 surface having unreasonably large transition state barriers (ΔG^‡ = 25.0 and 24.7 kcal/mol), and the S = 2 surface having a lower barrier for [Fe^IV=O(TBC)(CH₃CN)]²⁺ relative to [Fe^IV=O(TMC)(CH₃CN)]²⁺ (9.0 vs. 13.8 kcal/mol). While the energy differences for H-atom abstraction could be accounted for by the relative orientations of substrate approach required by the FMOs (~150° vs. 176° relative to the Fe=O bond), in the oxo-transfer transition state, the substrate approaches with an angle of ~150° for both complexes in both spin states (Table 6, SI Table 7). This is due to the fact that in contrast to an H-atom abstraction reaction, which is a one-electron process, the sulfoxidation reaction is a two-electron process, which results in the formation of a ferrous product complex. As such, regardless of spin state, the two-electron transfer requires that the donor orbital of the substrate achieves both π and σ overlap with the sterically shielded oxo group. Therefore, the critical angle is not the Fe-O-substrate angle as in H-atom abstraction, but the orientation of the donor orbital of the substrate relative to the oxo p_z and p_x/y FMOs. For thioanisole, the DFT calculations define the substrate FMO as the sulfur b₁, which is oriented perpendicular to the CH₃-S-Ph plane, and transfers two electrons, one α and one β, into the iron d_z² σ* and d_xz/yz π* orbitals, respectively. As such, the tilt (θ) and horizontal offset (Δ) of the b₁ orbital relative to the oxygen p_X/Y and p_z orbitals will affect its ability to overlap with these FMOs of the Fe^IV=O group ([Figure 11]).

Figure 10.

Oxo-transfer reaction coordinate of [Fe^IV=O(TBC)(CH₃CN)]²⁺ (S = 1 green, S = 2 light green) and [Fe^IV=O(TMC)(CH₃CN)]²⁺ (S = 1 black, S = 2 grey) with thioanisole. Energies given for ΔG (solv = acetonitrile) in units of kcal/mol, with the S = 1 ground state of each series defined as 0.0 kcal/mol. Transition states have been shifted right/left of center, based on the lengths of the Fe=O bond, to indicate reaction progress (Table 6).

Figure 11.

Orbital diagram illustrating how the angular offset θ (left, oxo p_x/y plane set to 0.0°) and the horizontal offset Δ (right, oxo p_z axis set to 0.0) effect ability of the sulfur b₁ to maintain orbital overlap with the oxygen p_x/y and p_z to transfer both the β (π) and α (σ) electrons to the iron d_xz/yz and d_z² orbital, respectively; S = 1 (black), S = 2 (green).

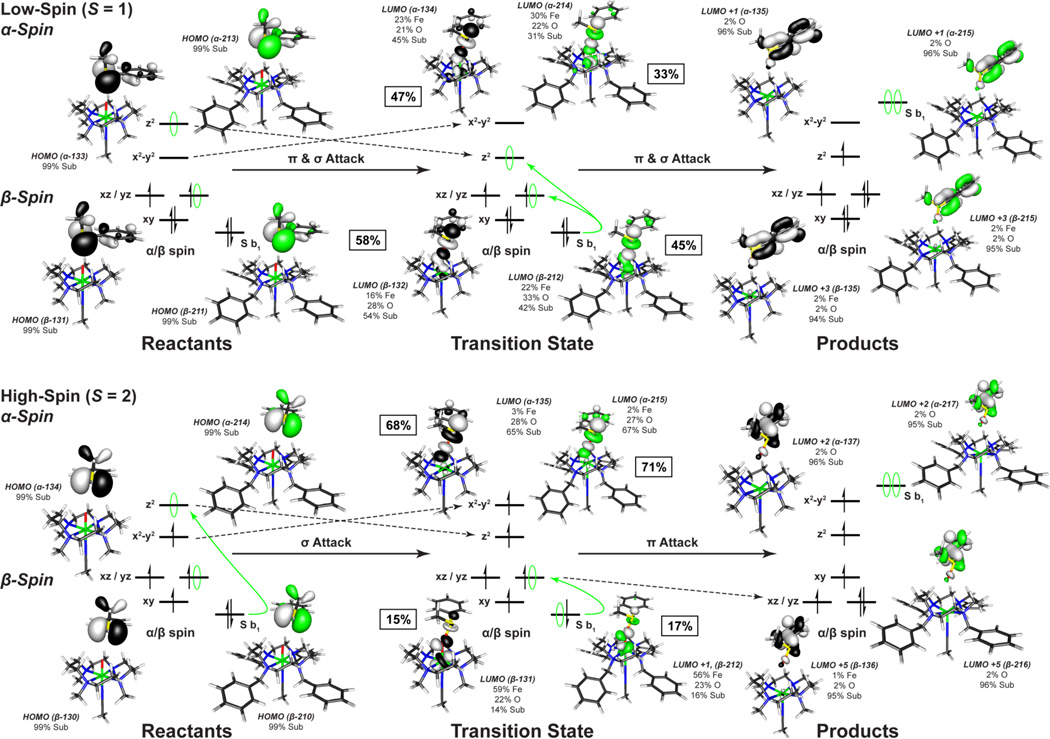
On the S = 1 surface, the unoccupied d_z² orbital on the iron is high in energy due to the strong Fe=O bond and thus only d_xz/yz orbital is available for π-attack. From the DFT calculations, π-attack of the sulfur b₁ FMO on the sterically hindered d_xz/yz orbitals results in a significant elongation of the Fe=O bond (1.61 to 1.87 Å, for both complexes, Table 6), a smaller cyclam-substrate distance (H-plane-substrate distance ~1.8 Å), and a large steric contribution to the S = 1 transition state barrier (~25 kcal/mol) (Figure 10). This cyclam-substrate steric interaction produces a b₁ angle θ of ~48.5° relative to the oxo p_x/y orbital plane and limited overlap between the S b₁ and oxo p_x/y FMOs. However, as the β electron transfers, the Fe=O bond elongates and stabilizes the d_z² orbital making it accessible for the transfer of the second (α) electron. This yields an almost concerted electron transfer for the S = 1 surface, with ~52% β vs. ~40% α electron transferred at the TS ([Figure 12] (top), SI Table 8).

Figure 12.

Comparison of low- and high-spin frontier molecular orbitals involved in the oxo-transfer reaction for [Fe^IV=O(TBC)(CH₃CN)]²⁺ (green) and [Fe^IV=O(TMC)(CH₃CN)]²⁺ (black) with thioanisole. From the S = 1 ground state, both electrons are transferred in a concerted process at similar rates. On the S = 2 surface, the electrons are transferred sequentially through a high-spin ferric transition state. The percent of electron transfer is given next to each transition state complex and in SI Table 8.

On the S = 2 surface, the α d_z² orbital is low in energy and the exposed oxo p_z orbital allows for direct σ-attack and results in the transfer of a single α electron from the sulfur b₁ to the iron d_z² σ* orbital early in the reaction coordinate (~70% α-spin relative to ~16% β transferred at the TS) (Figure 12 (bottom), SI Table 8). This sequential electron transfer leads to a high-spin ferric transition state where the addition of the α electron into the iron d_z² orbital weakens both the Fe=O and the trans-axial iron-acetonitrile bond. As a result of their high-spin ferric character, the S = 2 transition states also have longer Fe-N equatorial bonds, which in combination with the weaker trans-axial acetonitrile, allow for greater out-of-plane displacement of the iron and more flexibility for the cyclam ring to distort and expose the oxo group, which is now above the plane of the cyclam hydrogen crown (O-H Plane Distance, Table 6).

An overlay of the S = 1 vs. S = 2 transition states for the two complexes reveals that the high-spin transition states have a less sterically hindered oxo-cage and a greater cyclam-substrate distance ([Figure 13]), as reflected in the average O-H distance and the H-plane-substrate distance (Table 5). These structural changes for the S = 2 states allow the sulfur b₁ FMO to adopt a smaller angle θ of 34.6° relative to the oxo p_x/y plane (Figure 11) at the transition state that results in better overlap. These geometric changes facilitate the transfer of the second (β) electron without an additional contribution to the barrier.

Figure 13.

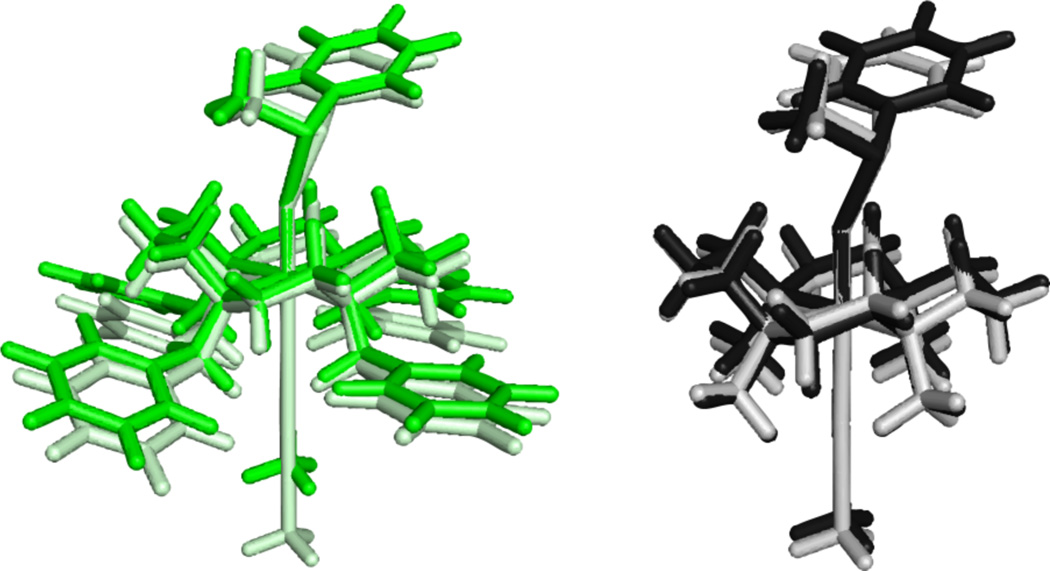
Overlay of the oxo-transfer transition state geometries for [Fe^IV=O(TBC)(CH₃CN)]²⁺ S = 1 (green) and S = 2 (light green) and [Fe^IV=O(TMC)(CH₃CN)]²⁺ S = 1 (black) and S = 2 (grey).

As with H-atom abstraction, the ~7 kcal/mol difference at the transition state between [Fe^IV=O(TBC)(CH₃CN)]²⁺ and [Fe^IV=O(TMC)(CH₃CN)]²⁺ on the S = 2 surface reflects the additional effects of the TBC ligand; the largest of which is that the axial acetonitrile bond is now 4.08 Å (vs. 2.51 Å in TMC, Table 6). With the axial ligand displaced by the bulk of the benzyl groups, the iron center is 5-coordinate which results in a larger out-of-plane displacement (0.34 vs. 0.13 Å), and a greater flexibility for the cyclam ring to expose the oxo group (0.23 vs. 0.03 Å for Fe^IV=O TBC and TMC, respectively, Table 6 and SI Figure 13). These changes allow for better accessibility of the substrate and greater orbital overlap at a long cyclam-substrate distance (2.15 Å for TBC vs. 1.95 Å for TMC, Table 6) and therefore result in the lowest barrier for oxo-transfer.

Discussion

The TBC ligand is a simple derivative of TMC where four benzyl groups have replaced the methyl groups, resulting in greater cyclam strain and steric interactions between these groups. Fe^IV=O intermediates, which have been synthesized using the TMC ligand, are generally unreactive as the steric interaction between the substrate and the cyclam ring blocks the π-attack required for overlap with the frontier molecular orbitals in the S = 1 ground state. However, despite the increased steric bulk trans-axial to the oxo, [Fe^IV=O(TBC)(CH₃CN)]²⁺ exhibits >10² accelerated rates for both H-atom abstraction and oxo-transfer reactions. From the spectroscopic and computational results presented here, the increased steric interactions of the benzyl groups distort the cyclam ring and weaken the axial and equatorial ligand fields. This stabilizes the d_x²−y² and d_z² orbitals and decreases the energetic difference between the S = 1 and S = 2 spin states, and thereby allows [Fe^IV=O(TBC)(CH₃CN)]²⁺ greater accessibility to the S = 2 surface for reactivity.

For the single electron transfer in a H-atom abstraction reaction, the S = 2 surface yields a linear transition state (~176°) involving a σ-attack of the substrate FMO with the oxygen p_z orbital and limited steric interactions between the substrate and the cyclam ring. This yields a lower steric contribution to the barrier at the transition state for the S = 2 surface. Conversely, reactivity on the S = 1 surface requires π-attack of the substrate FMO with the oxygen p_x/y orbital and therefore a side-on approach of the substrate (~144°). In both cyclam complexes, this results in large steric interactions between the substrate and the cyclam ring, and produces a large barrier at the transition state (~25 kcal/mol), inconsistent with the observed reaction rates. Thus for an H-atom abstraction reaction by a sterically hindered S = 1 Fe^IV=O intermediate, such as the cyclam complexes considered in this study, the rate of reactivity will be determined by the ability to access the S = 2 surface for axial attack.⁷⁴

In contrast to the H-atom abstraction reaction, where the difference in the transition state barrier between the S = 1 and the S = 2 surface reflects the angle of substrate approach, oxo-transfer is a two electron process requiring both π- and σ-attack of the substrate and good overlap with both the oxo p_x/y and p_z orbitals, respectively. On the S = 1 surface, this results in a large elongation of the Fe=O bond and a greater cyclam-substrate steric interactions as only the β d_xz/yz FMO is energetically available for π-attack. This produces a large transition state barrier. Conversely, on the S = 2 surface the α d_z² orbital is low in energy due to the spin polarization (i.e. electron exchange) and allows the direct σ-attack and the early transfer of a single α electron leading to a high-spin ferric species in the transition state. The addition of this electron into the d_z² orbital weakens both the Fe=O and the trans-axial iron-acetonitrile bonds and allows the Fe=O to move out of the Fe-N equatorial and cyclam hydrogen plane. This results in a smaller angle of the substrate donor orbital and better β π overlap for the transfer of the second electron without a large steric barrier.

Conclusion

Various factors including the structure and topology of supporting ligands,^16,70,75 the identity of axial ligands,^76,77 the spin states of iron(IV) ion,³⁷ and the binding of metal ions and proton on the iron-oxo moiety^78–81 have been considered in the reactivities of mononuclear non-heme iron(IV)-oxo complexes. The present study emphasizes the importance of the steric interactions between the substrates and the iron chelate as directed by the frontier molecular orbitals associated with the different spin states in non-heme Fe^IV=O reactivity.^49,58,65