Constrained De Novo Sequencing of Conotoxins

Abstract

De novo peptide sequencing by mass spectrometry (MS) can determine the amino acid sequence of an unknown peptide without reference to a protein database. MS-based de novo sequencing assumes special importance in focused studies of families of biologically active peptides and proteins, such as hormones, toxins, and antibodies, for which amino acid sequences may be difficult to obtain through genomic methods. These protein families often exhibit sequence homology or characteristic amino acid content, yet current de novo sequencing approaches do not take advantage of this prior knowledge and hence search an unnecessarily large space of possible sequences. Here, we describe an algorithm for de novo sequencing that incorporates sequence constraints into the core graph algorithm, and thereby reduces the search space by many orders of magnitude. We demonstrate our algorithm in a study of cysteine-rich toxins from two cone snail species (Conus textile and Conus stercusmuscarum), and report 13 de novo and about 60 total toxins.

1. Introduction

There are two basic approaches to peptide sequencing by tandem mass spectrometry (MS/MS): database search, which looks for the peptide that produced the mass spectrum in a protein database, and de novo sequencing, which attempts to infer the peptide from the spectrum alone. Database search, embodied in programs such as SEQUEST¹ and Mascot,² is the dominant method, because comprehensive protein databases are now available for the most commonly studied organisms, and because successful de novo sequencing requires unusually high quality spectra with low noise and nearly complete fragmentation. De novo sequencing, as embodied in programs such as PEAKS,³, rarely computes an exactly correct sequence for peptides larger than about 13 residues or 1500 Daltons,⁴ and hence it is most often used in contexts in which a short exact sequence or a longer approximate sequence suffices. A correct three-residue sequence tag^5-7 can pinpoint a small number of candidate peptides in a protein database in order to speed up database search allowing unknown modifications. A longer approximate sequence, say at least 8 residues long, may be characteristic enough to infer protein family or function from the results of a sequence search using a generic tool such as BLAST, or a more specialized sequence search tool designed for mass spectrometry.^{8, 9}

There are, however, contexts in which only a long exact sequence is useful. Researchers would like to observe bioactive peptides such as hormones, neurotransmitters, and toxins in their mature forms, meaning after posttranslational processing, because the activity of these peptides can vary widely with proteolytic truncations or posttranslational modifications (PTMs). Toxins from the Conus genus of marine snails are especially interesting de novo sequencing targets, because these molecules have great potential both as pharmaceuticals^{10, 11} and as natural probes for the study of ion channels.¹² These toxins are also challenging de novo sequencing targets, because their masses range from about 1000 – 4000 Da and they contain numerous posttranslational modifications such as hydroxyproline, amidated C-terminus, and bromotryptophan.¹³

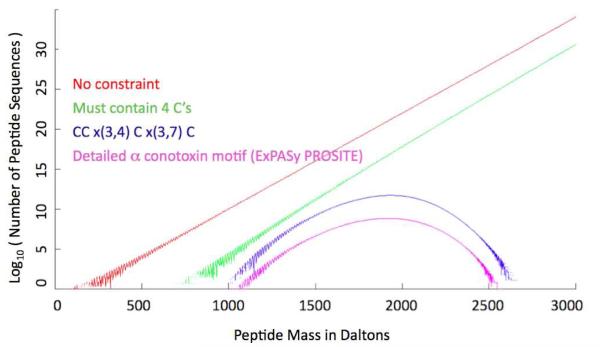
Here we present a novel and flexible method for improving de novo sequencing. The method incorporates prior sequence knowledge into the dynamic programming algorithm that generates candidate peptide sequences from observed MS/MS spectra. The algorithm employs a path algorithm on a cross-product of two graphs, a “spectrum graph” encoding the peaks of the MS/MS spectrum and a “constraint graph” encoding the prior sequence knowledge. The same algorithm can accommodate various forms of constraints, such as “the sequence must contain four cysteines”, “the sequence must end in ASTK”, or “the sequence must fit the motif CC×(3,4)C×(3,7)C”, where ×(3, 7) means at least three and at most seven amino acid residues of any kind. These three examples are not arbitrary: the number of cysteines in an unknown peptide can be determined by the mass shift after cysteine derivatization;¹⁴ peptides with constant C-terminal ASTK flank the junction and hypervariable complementarity determining region 3 (CDR3) in human antibodies and were recently used to identify antibodies reactive to HIV;¹⁵ and CC×(3,4)C×(3,7)C is a known motif for α-conotoxins (PS60014 from prosite.expasy.org). Other sources of constraints include characteristic neutral losses, such as −98 Da from phosphoserine or phosphothreonine and −64 Da from oxidized methionine; “split” isotope peaks from certain modifications, such as bromotryptophan; immonium ions indicative of particular amino acid residues; composition constraints computed from accurate precursor masses;^{16, 17} and partial sequence from other MS/MS spectra or previous rounds of chemical, computational, or genomic sequencing on the same or related peptides. As shown in Figure 1, constraints can greatly reduce the number of possible peptide sequences. For example, there are on the order of 10²² possible peptides of mass 2000 ± 0.5 Da, but only 10¹⁶ containing four cysteines (assuming alkylated cysteine with mass 160 Da), and only 10¹¹ fitting the CC×(3,4)C×(3,7)C motif. It is important to incorporate constraints into the candidate generation algorithm rather than apply constraints as a filter after unconstrained candidate generation, because there may be very few or no candidates satisfying the constraints among those computed by an unconstrained candidate generator.

Figure 1. Search space size.

The four curves show peptides with: no constraint, a 4C constraint (must contain 4 cysteines), a simple motif constraint, and a more detailed motif constraint from ProSite, C - C - [S H Y N] - × (0, 1) - [P R G] - [R P A T V] - C - [A R M F T N H G] - × (0, 4) - [Q W H D G E N F Y V P] - [R I V Y L G S D W] - C. Here ×(0,4) means a sequence of 0 to 4 residues of any type, and [P R G] means one residue chosen from the set { P, R, G }.

We apply our novel algorithm to analyzing MS/MS data of venom components from Conus textile, a relatively well-studied species with large (milligram) amounts of venom per snail and approximately 40 toxin sequences in GenBank¹⁸ and Conoserver,¹⁹ and Conus stercusmuscarum, an essentially unstudied species with no previously observed toxins. The MS/MS data were acquired on a Thermo LTQ Orbitrap XL instrument, using both ion-trap collision-induced dissociation (CID) and beam type CID (called HCD), and Orbitrap mass analysis for both single- and tandem-MS, as described previously.²⁰ We report about 60 toxin sequences, including 13 de novo sequences with no database entries within one mutation. We report 43 mature toxins from C. textile, improving upon the numbers reported by Ueberheide et al.¹⁴ and Tayo et al.²⁰ in previous work on the same species.

2. Methods

We implemented and tested constrained de novo sequencing in a new program called Conovo, which generates candidate peptide sequences in FASTA format that can then be scored with any database search program. We gave a preliminary “theoretical” report on Conovo in a bioinformatics conference²¹ and we describe the program more fully below. For scoring, we used our own in-house program Byonic,²² which is now available as a commercial product (Protein Metrics, San Carlos, CA) by June, 2012.

2.1. Sample Preparation

Sample preparation and data acquisition are described in detail by Tayo et al.²⁰ Briefly, venom duct contents were extracted with sonication using 40% acetonitrile, and separated by centrifugation. Extracted venom was denatured with urea, reduced with TCEP, and alkylated with iodoacetamide. Some aliquots were digested with trypsin and some were not. The venom, whether digested or undigested, was separated by 180-min acetonitrile-gradient HPLC from 0 – 100% buffer B, in which buffer A was 5% ACN / 0.1% formic acid and buffer B was 80% ACN / 0.1% formic acid. The sample was electrosprayed directly into an LTQ-Orbitrap XL mass spectrometer (Thermo Fisher Scientific), using a cycle of one full scan (m/z range 400 – 2000, resolution 60,000) followed by three data-dependent MS/MS scans (resolution 30,000), using either CID or HCD fragmentation. Altogether the data sets used in this study include 95 LC runs with a total of ~277,000 MS/MS scans: 79 LC runs (13 digested and 66 undigested) from C. textile, and 16 LC runs (4 digested and 12 undigested) from C. stercusmuscarum.

2.2. Data Analysis Pipeline

Most de novo sequencing programs^{3, 4, 23-26} generate candidate sequences from one or two spectra at a time, which are then scored against the candidates to produce a single best answer that can be sequence-searched against a protein database. In this work, however, we directly scored batches of spectra against both de novo candidates and database sequences. More specifically, we used Conovo to construct a “database” for each “interesting” spectrum, meaning a spectrum that could not be identified by database search and/or appeared to contain a peptide with two or more cysteines. After scoring the candidates with Byonic, the de novo sequences with sufficiently high scores for an individual interesting spectrum were then added to a master protein database containing all the sequences from ConoServer, a specialized database of cone snail toxins, all the sequences from GenBank that match the keyword “conus”, along with common contaminants such as trypsin and keratin. All the spectra were then searched against the master database, allowing for digestion and a greater variety of modifications than were considered by the candidate generation stage. This workflow integrates de novo sequencing and database search, so that known components, such as previously discovered conotoxins and likely contaminants, which are quite prevalent in digested samples, can be identified by database search rather than the more difficult approach of de novo sequencing. Similarly, if a single spectrum is good enough to generate a correct toxin sequence, then the peptides in other spectra, possibly digested or modified, may be identified by database search from the generated sequence.

In the candidate generation stage, we used constraints requiring specific numbers of cysteines (2, 3, …, 6), but we did not use more detailed motif constraints. We allowed for the following variable modifications, which are known to be common in conotoxins: P[+16] (hydroxyproline), C-terminus[−1] (amidation), W[+78] (bromotryptophan), and M[+16] (methionine sulfoxide).

In the database search stage, we allowed for more modifications: the in vivo PTMs, W[+78], V[+16] (hydroxyvaline), Y[+80] (sulfated tyrosine), P[+16], E[+44] (gamma carboxyglutamate), and C-terminus[−1]; the (in vivo or in vitro) oxidations, M[+16], M[+32], W[+16], W[+32], and C[+48]; the (in vivo or in vitro) pyro-glu transformations, N-terminal Q[−17], E[−18], and C[+57][−17]; and the in vitro over-alkylation artifacts, N-terminus[+57], K[+57], and H[+57]. We used the following parameter settings for Byonic: 20 ppm m/z tolerances for both precursors and fragments, and precursor isotope errors (that is, nominal precursor mass is heavier than the true monoisotopic mass) up to 1 Da for precursors from 1000 – 2500 Da, up to 2 for precursors from 2500 to 3500 Da, and up to 3 for precursors over 3500 Da. For modifications, we set cysteine to the fixed modification of carbamidomethylated cysteine C[+57]. We allowed a maximum of two instances per peptide for the more common variable modifications, M[+16], P[+16], and W[+78]; a maximum of at most one instance per peptide for all the other variable modifications; and an overall maximum of four modifications per peptide. All searches, even those on tryptic digests, allowed nonspecific digestion at both termini.

We also ran a blind modification search using Byonic’s wild-card modification,²⁷ which allows one modification of any integer mass on any one residue, with the fractional part of the mass (the mass defect) determined from the precursor mass. Such a search finds unanticipated modifications and amino acid substitutions. Along with the wild card, we allowed the following known modifications: M[+16]; P[+16]; N-terminal Q[−17], E[−18], and C[+57][−17]; N-terminus[+57], K[+57], and H[+57]; and C-terminus[−1].

We reran the entire search each time the master protein database changed significantly. We used manual curation of the Byonic-annotated spectra to decide which novel conotoxin sequences to add or drop from the protein database, primarily to decide between close sequences that were each top-scoring peptides for spectra of the same precursor mass. The amount of manual curation was small, taking a fraction of the time of the machine computation, which took about two weeks on a single computer, due to the large number of candidates generated per spectrum, the large number of modifications allowed in the database searches, and the frequent rescoring of all spectra.

2.3. Conovo Algorithm

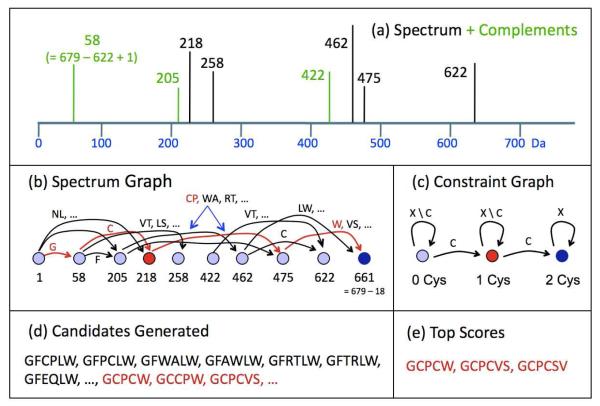
Incorporating sequence constraints into a candidate generation algorithm is convenient and natural, because the best developed approaches to de novo candidate generation and homology modeling both use the same algorithmic paradigm, which represents sequences as paths in a graph. Figure 2 illustrates the steps of our constrained de novo sequencing algorithm for a hypothetical spectrum. For exposition, Figure 2 assumes that spectrum peaks and amino acid residues have integer masses.

Figure 2. Algorithm for constrained de novo sequencing.

Panel (a) shows in black a hypothetical MS/MS spectrum of a peptide with singly charged precursor mass 679 Da. A standard step in de novo sequencing complements each observed peak and adds the artificial green peaks. If the original peak represents a y-ion, the complement peak represents a b-ion. Panel (b) shows a directed graph in which nodes represent peaks from the MS/MS spectrum, and arcs represent either one or two amino acid residues. A path of arcs from the leftmost to the rightmost node defines one or more candidate peptides. The constrained graph in panel (c) builds in the requirement that the candidate contain at least two cysteines: an acceptable path in graph (b) must also complete a left-to-right path in the constraint graph, where X denotes any amino acid residue and X \ C denotes any residue except cysteine. For example, the partial path GC corresponds to node 218 in (b) and 1Cys in (c), and can be completed (red) to give candidate GCPCW. Panel (d) shows that candidates satisfying the constraints (red) constitute only a small fraction of all the best candidates (red and black), so it is advantageous to generate and score only the constraint-satisfying peptides. The final step in de novo sequencing (e) scores the generated candidates using detailed spectrum features that cannot be easily incorporated into the graph algorithm. In this hypothetical example, the candidate GCCPW did not score well, because the position of proline is not consistent with the lack of a peak at 302 for the y-ion CPW⁺ and the strong peaks at 218, 258, and 462 for GC⁺, PC⁺ (an internal fragment), and PCW⁺.

Panel (a) shows a simple spectrum (black) that is augmented with the complements (green) of observed peaks. A peak at mass m from a peptide with singly charged precursor mass M + H has its complement at mass M + H + 1.007 – m; complementation converts a y-ion peak into the b-ion peak from the same peptide bond cleavage. Panel (b) then shows the standard formulation of candidate peptide generation as the problem of finding the k best paths in a graph,²⁸ where k is the number of peptides that the program can afford to score and “best” refers to some optimization criterion that measures the level of agreement between the sequence and the MS/MS spectrum, such as the total number of graph nodes covered by the path. In the formulation, each node corresponds to either a peak in the spectrum or the complement of a peak, and a path that passes through a peak node (respectively peak-complement node) explains the originating peak as a b-ion (respectively, y-ion) of the candidate sequence encoded by the path. This basic formulation allows a path to explain a peak as both a b- and a y-ion and receive credit in the optimization criterion for both explanations, but more sophisticated path algorithms,²⁹ one of which forms the basis of the PEAKS de novo sequencer,³ correct for such double counting. Although the simplified version in Figure 2 uses only integer masses, our actual software²¹ incorporates peak intensities and precise masses, so that an edge between intense peaks at 58.029 Da and 218.060 Da, with close agreement to the mass of carbamidomethylated cysteine (160.0306 Da), gives a better score than an edge between weak peaks at 58.029 and 218.132.

Panel (c) shows our innovation: a second graph that encodes the sequence constraints. In this example, the constraint graph is a finite state machine (FSM), with start state on the left and accepting state on the right, that accepts any sequence with at least two C’s (cysteine residues). In general, the constraint graph can be any deterministic FSM, and the acceptable sequences may be any regular language of peptide sequences. The algorithm generates the k best candidate sequences accepted by the FSM, where best is measured by the same optimization criterion as before. This is equivalent to a k-best-path computation on a newly constructed graph, which is the cross-product of the spectrum graph and the constraint graph. A node in the cross-product graph is a pair of nodes (u, v), where u is a node in the spectrum graph and v is a node in the constraint graph. There is an arc from (u, v) and (u’, v’) in the cross-product graph if and only if there is an arc a_uu’ in the spectrum graph, there is an arc a_vv’ in the constraint graph, and the labels on a_uu’ and a_vv’ agree. In the example shown in Figure 2, (58, 0 Cys) connects to (218, 1 Cys) in the cross-product graph, because there is an arc from 58 to 218 in the spectrum graph, an arc from 0 Cys to 1 Cys in the constraint graph, and these arcs are both labeled by C. The cross-product node (58, 0 Cys) connects to (205, 0 Cys), but not to (205, 1 Cys) because the arc from 58 to 205 in the spectrum graph is labeled with F and the arc from 0 Cys to 1 Cys in the constraint graph is labeled with C. The source node for the k best paths is (1, 0 Cys) and the sink node is (661, 2 Cys).

Panel (d) demonstrates the advantage of constrained de novo sequencing. Without the constraints, all the sequences shown in the panel, along with many more not shown, correspond to 5-node paths in the spectrum graph, and hence are equally good under the basic optimization criterion that simply counts the number of explained peaks. Only the sequences shown in red, however, satisfy the constraint of containing at least two cysteines. In this toy example the constraints reduce the search space by a factor on the order of 10, but as shown in Figure 1, the reduction offered by a realistic conotoxin motifs are much larger.

2.4. Implementation

Here we describe the details of Conovo’s implementation. Steps 1, 2, and 5 below are common to most de novo sequencing programs; steps 3 and 4 are unique to Conovo.

1. Spectrum Preprocessing

Let S be a centroided, de-charged, and de-isotoped tandem mass spectrum of a precursor ion of measured mass M+H. S is a peak list containing pairs of the form (m_i, a_i), where m_i is a mass, derived by de-charging a measured peak series (that is, converting it to an equivalent singly charged peak), and a_i is a measured intensity. Centroiding, de-charging, and de-isotoping are standard steps, included for example, in Mascot Distiller. De-charging and de-isotoping, however, are error-prone steps, especially on low-resolution MS/MS spectra, so Conovo handles ambiguous cases by retaining all possibilities, for example, by retaining a possibly doubly charged peak at m/z 550.3 and also adding a new peak at 1099.6 Da. M+H mass is a conventional way to express peptide ion masses; a mass over charge measurement of m for the monoisotopic peak in a peak series with charge z gives M+H mass of z^.m – (z – 1)^.1.007. Determination of monoisotopic precursor mass is also error-prone, so we allowed for “off-by-one” errors by running spectra with several choices of M+H.

The final step of spectrum preprocessing complements each peak (m_i, a_i) by adding another peak to S at mass m_i’ = M+H + 1.007 – m_i with intensity a_i. Figure 1(a) gives a cartoon version of a spectrum S with complements; for illustrative purposes masses are given as integers.

2. Spectrum Graph

We build a directed graph G in which nodes represent mass ranges, and arcs, which bear both labels and weights, represent amino acid and modified amino acid residues. A peak at mass m_i maps to a node u at the closest integer to 0.9995^.m_i, so that node 1000 corresponds to all the peaks from about 1000 to 1001 Da. If S contains peaks (possibly de-charged, complemented, or both) at masses 1000.45 and 1113.54, then nodes 1000 and 1113 in G would be connected by an arc labeled I/L (isoleucine or leucine), corresponding to an exact mass of 113.08406. The label on the arc gives the amino acid residue(s) corresponding to the arc, in this case I and L. The weight on the arc scores the quality of the connection between the nodes; this is a function of the intensities of the peaks at 1000.45 and 1113.54 and the mass error, that is, the difference between 1113.54 – 1000.45 = 113.09 and the theoretical mass 113.08406. If hydroxyproline is allowed as a modified amino acid residue, then nodes 1000 and 1113 would also be connected by another arc of a slightly different weight, because hydroxyproline has theoretical mass 113.04767.

The weight on an arc from node u at integer mass m(u) to node v at integer mass m(v), is a sum of two terms that depend upon the peaks assigned to u and v. For simplicity assume u and v correspond to a single peaks (m_u, a_u) and (m_v, a_v). Let rank(m_u, a_u) denote the rank of the peak (m_u, a_u), that is, 1 for the tallest peak in S, 2 for the second tallest, and so forth. Let

$$\text{error}({\text{m}}_{\text{u}},{\text{m}}_{\text{v}})=\text{min}\left\{\mid {\text{m}}_{\text{v}}-{\text{m}}_{\text{u}}-{\text{m}}_{\text{aa}}\mid \right\},$$

where the minimum is taken over all (possibly modified) amino acid residue masses m_aa. Then the weight W(u,v) = max { 0, W₁(u, v) + W₂(u, v) }, where

$${\text{W}}_1(\text{u},\text{v})=\text{m}\left(\text{v}\right)-\text{m}\left(\text{u}\right)-3^{.}{2}^{\text{s}},\text{where}\text{s}=1-\text{rank}({\text{m}}_{\text{u}},{\text{a}}_{\text{u}})∕100,\text{and}$$

$${\text{W}}_2(\text{u},\text{v})=-{100}^{.}(1-\text{error}({\text{m}}_{\text{u}},{\text{m}}_{\text{v}}))\text{if}\text{error}({\text{m}}_{\text{u}},{\text{m}}_{\text{v}})<\text{tolerance},\text{and}$$

$${\text{W}}_2(\text{u},\text{v})=150\text{otherwise}.$$

We defined our weights as “costs”, that is, weights are nonnegative and lower-weight arcs are preferred over higher-weight arcs, in order to make use of freely available k-best path code.

If u and/or v correspond to more than one peak in S, then the arc cost is set to be the minimum cost W(u,v) over all the peak pairs, one from u and one from v.

The spectrum graph also includes a source node at mass 1 (for a lone proton) and a destination node at mass M+H.

3. Constraint Graph

Conovo accepts three different types of constraints: multiset, mass, and regular expression (regex) constraints. A multiset constraint specifies the number, but not the order, of a subset of amino acids that must be present in any candidate. A multiset constraint is specified by an expression such as [4C 1W], which specifies that any candidate must contain at least four cysteines and at least one tryptophan in any order. The syntax allows any integer and any single-letter residue abbreviation. Multiset constraints can be concatenated to impose an ordering constraint, so that [4 C] [1W] requires at least four cysteines in some prefix of the candidate sequence and at least one tryptophan in the remaining suffix.

A mass constraint may be added to a multiset constraint. A mass constraint is specified by an expression of the form [4 C][1200]. The mass constraint specifies that the multiset constraint must be satisfied within a mass of 1200 Da, so that a prefix of the candidate of total mass at most 1200 Da must contain four cysteines.

A regex constraint specifies the number and order of every amino acid symbol in a candidate. Such a constraint is specified by a sequence of one-letter amino acid abbreviations along with the special symbol x, denoting any amino acid residue. A regular expression constraint specifies a set of sequences, for example, CxxxCxxxxCC specifies a set of 20⁷ sequences of length 11, one for each distinct setting of the x’s with unmodified amino acid residues. (For conotoxin sequencing, we allowed three modified residues, M[+16], P[+16], and W[+78], interior to the sequence, and considered I and L identical, so that in this case CxxxCxxxxCC specifies 22⁷ sequences. We also allowed amidated C-terminus, thereby doubling the total number of sequences.)

Conovo translates input constraints into a deterministic finite state machine (FSM) in which each node or state represents partial satisfaction of the constraints and one distinguished node represents complete satisfaction of the constraints. For example, the multiset constraint above produces a FSM with ten nodes, corresponding to all 5 × 2 combinations of 0, 1, 2, 3, or 4 cysteines and 0 or 1 bromotryptophans already included in the candidate sequence. The (0, 0) node is the start node, and the (4, 1) node (4 cysteines and 1 bromotryptophan) is the accepting node, representing complete constraint satisfaction. As usual in FSMs, nodes are connected by labeled arcs, giving the conditions for state transitions. For example, adding another cysteine when in the (2, 1) state (2 cysteines and 1 bromotryptophan) advances the sequence to the (3, 1) state.

The regex constraint CxxxCxxxxCC defines a FSM with 12 nodes, corresponding to positions 0, 1, …, 11 in the sequence. A sequence advances from the start node 0 to node 1 only if it begins with cysteine, but any amino acid residue advances the sequence from node 1 to node 2.

Regex constraints can also encode more complicated patterns such as the one from Figure 1,

$$\text{C}-\text{C}-\left[\text{SHYN}\right]-\times (0,1)-\left[\text{PRG}\right]-\left[\text{RPATV}\right]-\text{C}-\left[\text{ARMFTNHG}\right]-\times (0,4)-\left[\text{QWHDGENFYVP}\right]-\left[RIVYLGSDW\right]-\text{C},$$

which is a profile motif for α-conotoxins from prosite.expasy.org. Conovo realizes such a pattern with 10 FSMs, one for each of the combinations of x-string lengths implied by ×(0, 1) and ×(0, 4). Each FSM has at most 15 states, so the overall number of states is not excessive, even though it grows exponentially with the number of variable length x-strings.

4. Cross-Product Graph

We denote the spectrum graph by G and the digraph underlying the constraint FSM by G’. Nodes in the cross-product graph G × G’ are all possible nodes of the form (u, u’) where u is a node from G and u’ is a node from G’. The cross-product graph contains an arc from (u, u’) to (v, v’) if and only if there is an arc in G from u to v, there is an arc in G’ from u’ to v’, and the two arcs have compatible labels. Labels are compatible if and only if there is a residue, or more generally a predefined sequence component (amino acid residue or modification), that appears in both labels, for example, I/L and × are compatible. The cost of the arc from (u, u’) to (v, v’) is the weight w(u, v) from the spectrum graph. The source node in G × G’ is the combination of the source node in G and the start state in G’, and the destination node in G × G’ is the combination of the destination node in G and the accepting state in G’.

5. K-Best Path Algorithm

We used a standard k-best-path algorithm²⁸ to compute the lowest-cost paths in the cross-product graph G × G’. We generally used k = 100,000. For each MS/MS spectrum, we allowed several choices of M+H mass, five different constraints (2C, 3C, 4C, 5C, and 6C), and two different destination masses (for amidated and unmodified C-terminus), so that each spectrum gave on the order of 10⁶ paths. Each path corresponds to a (possibly modified) amino acid sequence. Amino acid modifications and duplicated sequences were discarded from the list of candidates before submission to Byonic for scoring. Like most database search programs, Byonic accepts unmodified protein sequences, and then adds fixed and variable modifications according to user-specified rules.

3. Results

Figures 3 and 4, Tables 1 and 2, and Figures SI.1 – SI.25 in the Supplemental Information show identified conotoxins. Many of the C. textile toxins in Table 1 are well known; for example, CIEQFDPCDMIRHTCCVGVCFLMACI is a known sequence variant of King-Kong 1 conotoxin. CCRTCFGCTPCC[−1] is Conotoxin tx3c, a “scratcher” peptide. Some of the C. stercusmuscarum toxins in Table 2 are also known; for example, GCCSNPVCHLEHSNMC appears in GenBank and ConoServer annotated as Sm1.3, Sequence 102 from patent EP1852440, Sequence 103 from patent US6797808, and gi|207099875 from C. stercusmuscarum. It is one mutation (L→M) away from gi|207100428 from C. achatinus.

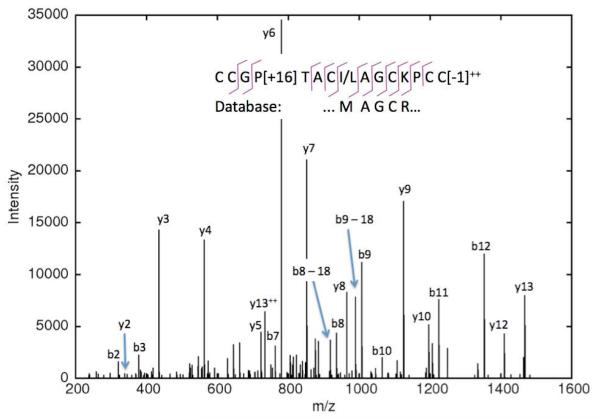
Figure 3. CID spectrum of a C. textile toxin sequenced de novo.

This toxin belongs to the M superfamily and is two mutations away from the closest database sequence.

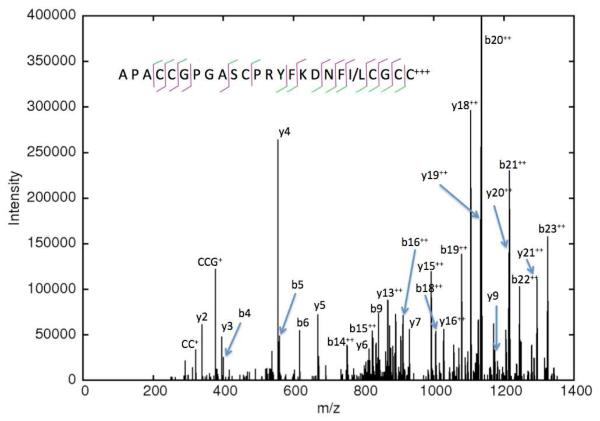
Figure 4. CID spectrum of a C. stercusmuscarum toxin sequenced de novo.

This toxin belongs to the M superfamily and was sequenced by a combination of spectra, including ones shown in the Supplemental Information. The order of the three initial residues is uncertain, but Byonic’s scorer prefers APA over AAP and PAA in order to explain the lack of cleavage at b2 / y22. In the cleavage diagram, a green stroke indicates b- and y-ions observed primarily doubly charged.

Table 1. Characterized conotoxins from C. textile.

This chart lists the mature toxins and natural truncations found in the C. textile data. We used (I/L) for isoleucine/leucine in de novo sequences, but list only a single possibility for database sequences. We include posttranslational modifications W[+78] (bromotryptophan), P[+16] (hydroxyproline), E[+44] (gamma carboxyglutamate), and C-terminus[−1] (amidation), but with a few exceptions we do not include modifications such as pyro-glu N-terminus, over-alkylation, and oxidations, as these may be in vitro artifacts. Masses are calculated masses assuming C[+57] (carbamidomethylated cysteine). The column labeled Prev? indicates with T and U whether the toxins were previously observed by Tayo et al.²⁰ or Ueberheide et al¹⁴. The last six toxins were observed only in digested pieces rather than intact, and small letters as in KEHLQLCDLIFQNCR.gwycllrpc indicate unobserved residues that are probably included in the intact toxin.

Conus textile toxin sequence	Mass	Superfamily	Accession #	Prev?
GCPWQPYC[−1]	1066.423	Contryphan	gi|8979454
CFIRNCPP[+16]	1079.476	Conopressin	gi|229553909	U
CCPPV(I/L)WCC[−1] (Fig. SI.1)	1250.494	T	De Novo
QTCCGSKVFCC[−1] (Fig. SI.11)	1405.548	T	De Novo
CCRPMQDCCS[−1]	1471.537	T	gi|73808830	U
VNCCPIDESCCS NCCPIDE[+44]ESCCS	1500.522 1445.444	T	gi|73808832	U
DPCCGYRMCVP[+16]C[−1]	1589.579	A	gi|229485331	U
QTCCGYRMCVP[+16]C[−1] TCCGYRMCVP[+16]C[−1] CCGYRMCVP[+16]C[−1]	1606.605 1478.547 1377.499	A	gi|229485332	T, U
CCQTFYWCCVQ[−1]	1610.601	T	gi|6103607	T
ICCYPNVW[+78]CCD	1624.469	T	gi|73808810	T, U
CCRTCFGCTPCC[−1] CCRTCFGCTP[+16]CC[−1] TCFGCTPCC[−1] TCFGCTP[+16]C[−1]	1637.557 1653.552 1161.394 1177.389	M	gi|110282951	T, U
NCCRRQICCGRT	1640.698	T	gi|73808820
KPCCSIHDSSCCGI[−1] KPCCSIHDSSCCGI	1679.676 1680.660	T	gi|229485329	T, U
TSDCCFYHNCCC	1683.511	T, Dimer	gi|12619445	U
KPCCSIHDNSCCGI[−1] KPCCSIHDNSCCGI PCCSIHDNSCCGI[−1] CCSIHDNSCCGI	1706.687 1707.671 1551.581 1455.512	T	gi|229485330	T, U
CCGP[+16]TAC(I/L)AGCKPCC[−1] (Figs. 2, SI.12) CCGP[+16]TAC(I/L)AGCKP[+16]CC[−1]	1786.662 1802.657	M	De Novo
CCGP[+16]TACVAGCK[P[+16]C]C[−1] (Fig. SI.6)	1788.641		De Novo
DKQTCCGYRMCVP[+16]C[−1]	1849.727	A	US patent 6767896	T
CCPPVACNMGCKPCC[−1] CCPPVACNM[+16]GCKPCC[−1]	1869.681 1885.676	M	gi|110278932	T
GCCGVPSCMAGCR[PC]C[−1] (Fig. SI.13) GCCGVPSCM[+16]AGCR[PC]C[−1]	1887.667 1903.662	M	De Novo
N(I/L)Q(I/L)(I/L)CCKHTPACCT[−1] (Fig. SI.19)	1874.849	T	gi|229891708	U
GCCSRPPCIANNPDIC[−1]	1889.787	A	gi|229553921	T, U
QCCWYFDISCCITV	1911.753	T	gi|12619455	T
N(I/L)Q(I/L)(I/L)CCKHTPKCCT[−1] (Fig. SI.18)	1931.907	T	gi|229891708 A→K mutation
GCCGAFACRFGCTPCC	1940.679	M	gi|229485326	U
IKIGPPCCSGWCFFACA IKIGPPCCSGW[+78]CFFACA YDCEPPGNFCGMIKIGPPCCSGW[+78]CFFACA YDCEPPGNFCGMIKIGPP[+16]CCSGW[+78]CFFACA	2030.874 2108.785 3536.279 3552.274	O	gi|6409416	T
CCSWDVCDHPSCTCC[−1] CCSW[+16]DVCDHPSCTCCG (Fig. SI.3) CCSW[+32]DVCDHPSCTCCG EIILHALGTRCCSWDVCDHPSCTCC[−1] EIILHALGTRCCSWDVCDHPSCTCCG	2002.643 2076.643 2092.638 3106.288 3164.293	M	gi|12619439	T, U
VCCPFGGCHELCQCCE[−1]	2071.737	M	gi|12619421	T, U
CCKFPCPDSCRYLCC[−1] RCCKFPCPDSCRYLCC[−1]	2081.794 2237.895	M	gi|110278928	T, U
CCNAGFCRFGCTP[+16]CCY SCCNAGFCRFGCTPCCY SCCNAGFCRFGCTP[+16]CCY	2105.721 2176.758 2192.753	M	gi|229485327	T, U
GCCH(I/L)(I/L)ACRMGCSPC[CW] (Figs. SI.14, SI.16) GCCH(I/L)(I/L)ACRM[+16]GCSPC[CW]	2184.814 2200.809	M	De Novo
[GC]CH(I/L)(I/L)ACRMGCTPCCW (Figs. SI.14, SI.15)	2198.827	M	De Novo
CCDDSECSTSCWP[+16]CCY	2224.648	M	gi|12619387
RP[+16]QCCSHP[+16]ACNVDHPEIC	2268.900	A	gi|207099845
FCCDSNWCHISDCECCY[−1] FCCDSNWCHISDCECCY KFCCDSNWCHISDCECCY[−1] KFCCDSNW[+78]CHISDCECCY	2371.775 2372.759 2499.870 2578.765	M	gi|110278923	T, U
NCPYCVVYCCPPAYCEASGCRPP NCPYCVVYCCPPAYCQASGCRPP (Fig. SI.20) NCPYCVVYCCPP[+16]AYCQASGCRPP	2837.107 2836.123 2852.118	O	gi|21362450 with E[−1] or E→Q mutation	T
CYDSGTSCNTGNQCCSGWCIFVCL	2906.077	O	gi|4885004	T
HDSDCCGHLCCAGITCQFTYIPCK	2960.171	I	US Patent 6767895	T
CLDAGEVCDIFFPTCCGYCILLFCA	3061.273	O	gi|4885002	T
CAPFLHPCTFFFPNCCNSYCVQFIC[−1] CAPFLHPCTFFFPNCCNSYCVQFICL	3245.338 3359.406	O	gi|10892	T
CIEQFDPCDMIRHTCCVGVCFLMACI CIEQFDPCDM[+16]IRHTCCVGVCFLMACI	3292.367 3308.362	O	gi|6409410	T
WCKQSGEMCNLLDQNCCDGYCIVLVCT WCKQSGEMCNLLDQNCCDGYC	3383.375 2697.992	O	gi|10888 gi|241606	T, U
wckqsgemcnlld.QNCCDGYCIVLFCT (Fig. SI.22)	1809.708		gi|241606 V→F mutation
DCRGYDAPCSSGAPCCDWW[+78]TCSARTNRCF DCRGYDAP[+16]CSSGAPCCDWW[+78]TCSARTNRCF DCRGYDAP[+16]CSSGAPCCDW[+78]W[+78]TCSARTNRCF	3651.281 3667.275 3745.186	O	gi|12619589	T, U
DCQEKWDYCPVPFLGSRYCCDGFICPSFFCA[−1] DCQEKWDYCPVPFLGSRYCCDGFICPSFFCA	3940.614 3941.598	O	US patent 6762165	T
NYCQEKWDYCPVPFLGSRYCCDGLFCTLFFCA	4133.725	O	gi|4885012	T
DCQEK.WDFCPAPFGSR.yccfglfctlffca		O	gi|6409420	T
KEHLQLCDLIFQNCR.gwycllrpc		O	US patent 6762165	T
ctpagdacdattnccilfcnlatk.KCEVPTFP ctpagdacdattnccilfcnlatk.KCEVPTFP[+16] ctpagdacdattnccilfcnlatk.KCEVP[+16]TFP[+16]			gi|109156732
GCCSRPPCAL.snpdycg		A	gi|12619704
GGCM[+16]AW[+78]FGLCSK.dseccsnscdvtrce. LMP[+16]FP[+16]P[+16]DW			gi|12619736

Table 2. Characterized conotoxins from C. stercusmuscarum.

This chart lists the mature toxins and natural truncations found in the C. stercusmuscarum data. Brackets as in [APA] indicate that the order of the residues is uncertain.

Conus stercusmuscarum toxin sequence	Mass	Superfamily	Accession #
CPWQPWC[−1]	1032.418	Contryphan	gi|20177852
CP[+16]WQPWC[−1]	1048.413
GCPWQPWC[−1]	1089.439
GCP[+16]WQPWC[−1]	1105.434
[KT]PCMCCSFR   (Fig. SI.7)	1346.547	Partial	De Novo
CCHPACGPNYSC[−1]   (Fig. SI.5)	1481.518	A	gi|224487860
CCHPACGP[+16]NYSC[−1]	1497.513		US patent
GRCCHPACGPNYSC[−1]	1694.640		6855805
GRCCHPACGP[+16]NYSC[−1]	1710.635
CCH[PA]CG[EN]YSC[−1]   (Fig. SI.4)	1513.508	A	De Novo
YDCCSGSCSGYTGRC[−1]   (Fig. SI.10)	1788.619	O	De Novo
(I/L)MYDCCSGSCSGYTGRC[−1]   (Fig. SI.9)	2032.744
(I/L)M[+16]YDCCSGSCSGYTGRC[−1]	2048.739
GCCSNPVCHLEHSNMC[−1]	1960.734	A	gi|207099875
GCCSNPVCHLEHSNMC	1961.718
CC(I/L)ARQ(I/L)CEGC(I/L)CC(I/L)   (Fig. SI.21)	1972.799	M	De Novo
Q[−17]ACS(I/L)GPHHCNSMGEC[CSR]   (Fig. SI.8)	2230.830	Partial?	De Novo
[APA]CCGPGASCPRYFKDNF(I/L)CGCC   (Figs. 3, SI.2, SI.17)	2825.118	M	De Novo
[APA]CCGPGASCP[+16]RYFKDNF(I/L)CGCC	2841.113
cr.TW[+78]NAP[+16]CSFTSQCCFGR.cahhr.CIAW[+78]		O	gi|206557914 K→R mutation
STSCMEAGSYCGSTTRCCGYCAYFGK.k.CIDYPSN		O	gi|57898665 gi|18203616

In Tables 1 and 2, we include the modified and truncated forms that seemed most likely to be in vivo forms, based on prevalence and modification type. For example, hydroxyproline, bromotryptophan, and C-terminal amidation are almost surely in vivo, whereas methionine and tryptophan oxidation could be either in vivo or in vitro, so we included only the oxidations observed at levels obviously above the background rate. One de novo sequence, Q[−17]ACS(I/L)GPHHCNSMGEC[CSR], was observed only with pyro-glu N-terminus and only in a digested sample, so we have classified this sequence as a partial toxin. (The brackets in [CSR] denotes uncertain order.) Amidation was observed on one toxin, NCPYCVVYCCPPAYCE[−1]ASGCRPP (Figure SI.20), in an unexpected location. This toxin was also observed without the amidation, and some tandem spectra clearly contain both forms. The amidation could be either an E→Q mutation or an in vitro artifact. It is observed in a large number of spectra in a sample that overall has very few chance amidations, so a mutation seems most likely. Byonic’s wild-card modification, which allows one modification of any mass on any one residue, proved extremely helpful for identifying and localizing modifications and mutations. Wild-card searches also turn up identifiable spectra with mysterious mass shifts and gaps; see Figures SI.23 – SI.25.

By using a combination of de novo sequencing, mutation search, and database search, we identified 43 distinct toxin sequences in C. textile venom, which improves over the numbers identified in previous studies of C. textile venom by Ueberheide et al.¹⁴ and Tayo et al.²⁰ Ueberheide et al.¹⁴ used both CID and ETD on a Thermo LTQ ion trap instrument, along with a chemical derivatization strategy to increase the charge of cysteine-containing peptides and render them more amenable to ETD. Ueberheide et al. found 31 distinct toxins, with 24 distinct amino acid sequences before PTMs. Our list includes 29 of the 31 toxins identified by Ueberheide et al., missing only GCCHPST… at 2016 Da and GCNNSCQ… at 2866 Da. Tayo et al²⁰ used the same data we used and reported 31 distinct amino acid sequences. We found 30 of the 31 toxins identified by Tayo et al., but we found only pieces rather than full toxins for two of those 30. We found no evidence supporting their identification of hydroxyvaline in the toxin CCSWDVCDHPSCTCC, and we believe that this identification may be due to a misplaced modification, as we found a number of spectra of this toxin with oxidized tryptophan (both +16 and +32), one of which is shown in Figure SI.3.

Tables 1 and 2 show many more identified toxins in C. textile than in C. stercusmuscarum. This disparity is probably real and not an artifact of the proteomics experiments or data analysis. C. stercusmuscarum hunts small fish; it is a smaller species than C. textile with a much smaller venom duct, which probably contains fewer types of secretory cells responsible for conotoxin synthesis. C. textile hunts mollusks, which may necessitate a greater diversity of individual toxins or toxin cabals.

4. Discussion

De novo sequencing by mass spectrometry has become much easier in the past few years with high-accuracy instruments such as the Thermo LTQ Orbitrap, and other advances such as ETD fragmentation³⁰ and charge-enhanced ETD.¹⁴ Nevertheless, end-to-end sequencing of long modified peptides remains challenging. Here we have described an algorithmic idea that can extend the sequenceable range by several hundred Daltons. The advantage offered by constrained de novo sequencing naturally depends upon the restrictiveness of the constraints, with a four-cysteine constraint reducing the difficulty of a 2000-Da peptide to roughly that of a 1600-Da peptide, a six-cysteine constraint giving in effect a reduction to about 1400 Daltons, and knowledge of the positions of the cysteines giving still greater reductions.

If the constraints are incorrect, then constrained sequencing gives worse results than unconstrained sequencing, meaning a lower scoring solution that explains fewer spectrum peaks. This bifurcated performance, however, can be advantageous, as constrained de novo sequencing provides a means to find the spectra most likely to satisfy the constraints, and hence most worthy of increased attention, much as SALSA³¹ can find spectra containing specific contiguous sequences. Finding the interesting spectra is a nontrivial and growing issue in the analysis of large data sets.

Constrained de novo sequencing presents the user with a new choice: what are the optimal constraints? For example, a motif constraint such as CC×(3,4)C×(3,7)C might find more α-conotoxins from lower quality spectra than a simple 4C constraint, yet miss a conotoxin, even one from a perfect spectrum, that deviated from the motif. We chose mild constraints (2C, 3C, …) for the analysis of high-accuracy MS/MS spectra, but with low-accuracy spectra, which are generally much harder to sequence, we would have chosen more restrictive constraints.

In the work presented here, we employed constrained sequencing once per spectrum, but the idea also lends itself to iterative approaches. In these approaches, an initial unconstrained or lightly constrained search returns a partially correct sequence, which is then used to produce more restrictive constraints. A human expert could supply the new constraints, or the partially correct sequence could be used to search a protein database for homologous sequences that can be automatically compiled into a regular-expression motif using existing bioinformatics tools.^{32, 33}