Conformational Heterogeneity and Quasi-Static Self-Quenching in DNA Containing a Fluorescent Guanine Analogue, 3MI or 6MI

Abstract

Two different microenvironments in the DNA sequence 5′-act aGa gat ccc tca gac cct ttt agt cag tGt gga-3′ (in both single- and double-stranded forms) are explored using two similar fluorescent nucleoside analogues, 3MI and 6MI. Each probe was evaluated in two environments, one strand with the probe flanked by thymines (PTRT) and the other by adenines (PTRA) with positions indicated by G's in the sequence. Both time-resolved anisotropies and lifetimes of the probes depend upon local interactions, and these are altered by duplex formation. Integrals of lifetime curves compared with quantum yields reveal that each probe displays a “dark” component (below detection limits, with a lifetime of <70 ps). For 6MI in PTRA, this QSSQ “quasi-static self-quenching” or “dark” component represents approximately half the molecules, whether in single-or double-stranded form. In PTRT, 6MI displays an unusual increase in the quantum yield upon formation of the double strand (from 0.107 to 0.189) apparently the result of escape from QSSQ which simultaneously declines from 66 to 33%. This is also accompanied by doubling of steady-state anisotropy. Only 6MI in the PTRT duplex displays a rotational correlation time of >7 ns. In other words, the DS 6MI PTRA environment fails to constrain local motion and QSSQ remains the same as in the single strand; in contrast, the flanking T duplex environment restricts local motion and halves QSSQ. We collected both steady-state and time-resolved fluorescence quenching titrations of 3MI and 6MI in solution with the mononucleotides AMP, CMP, GMP, and TMP. The dynamic quenching rank of the free probes (quenching constant, k_q: T>A>G>C) is totally different from that of incorporated probes. We hypothesize the production of weak 3MI·C or 6MI·C complexes that are somehow rendered less subject to dynamic quenching by collision with subsequent C molecules.

Fluorescent nucleoside analogues can provide a great deal of information about their environment. Variations between two very similar probes placed in chemically identical environments can identify probe-specific capabilities for reporting the structure of the DNA. Thus, we have compared the fluorescence properties of the two fluorescent pteridine guanine analogues, 3MI¹ and 6MI, in a highly quenched (flanked by adenines, PTRA) and a less quenched (flanked by thymines, PTRT) environment in both single and double strands.

Since DNA itself is only weakly fluorescent, fluorophores have been employed to study DNA structure and dynamics for decades. Both intercalators (subject to desorption) and fluorophores linked to nucleotides by flexible arms are subject to questions about how well their dynamics reflect those of natural bases, so fluorescent base analogues have long been sought, with mixed results (1). The most popular analogue, 2-AP, has a moderate quantum yield and has been well studied (2–7).

More recently, pteridine molecules have been modified to serve as guanine (3MI and 6MI) and adenine (6MAP) analogues. These probes have high quantum yields and desirable hydrogen bonding capabilities (8) and have been vetted with respect to structural disruption (via melting temperature changes), whether the analogue rotates independently or is locked to the DNA, and whether useful fluorescence signals represent hydrogen bonding, base flipping, or local melting in the DNA.

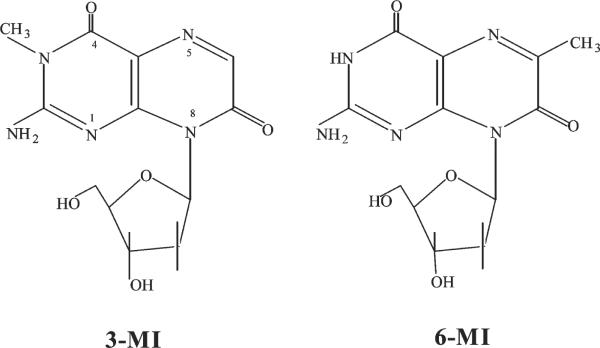
In this work, we compare 3MI and 6MI (Figure 1) that differ only in the location of a methyl group. We find that 6MI surrounded by thymidines (PTRT) base pairs with its complement (cytidine) and rigidly couples to the overall motion. We also examine the strong quenching of the probes by flanking bases, quantifying both dynamic and static quenching terms.

Figure 1.

Structures of the two guanine analogues used in this study. The only structural difference is the position of the methyl group in either the 3- or 6-position.

MATERIALS AND METHODS

Sample Preparation

Probe-containing oligonucleotides (Table 1) were obtained from Fidelity Systems, Inc. (Gaithersburg, MD). For details of the handling of the probes during the synthesis, deprotection, and purification, see ref 9.

Table 1.

Model Sequences Used in This Study^a

PTRT	5′-act aga gat ccc tca gac cct ttt agt cag tFt gga-3′
PTRA	5′-act aFa gat ccc tca gac cct ttt agt cag tgt gga-3′
control	5′-act aga gat ccc tca gac cct ttt agt cag tgt gga-3′
complement	5′-tcc aca ctg act aaa agg gtc tga ggg atc tct agt-3′

^aF denotes the location of the probe.

In either case, the probe is in the fifth position from an end (5′ or 3′). In the duplex state, the probes are paired with cytidine. Sequences were synthesized with either 3MI or 6MI at the position denoted by F.

All sequences were purified through polyacrylamide gel electrophoresis (PAGE) and ethanol precipitation. Samples were stored in a −80 C freezer prior to use.

Duplex Formation

Equimolar complementary sequences were heated to boiling for 2 min and allowed to cool slowly to room temperature for at least 5 h. All samples were prepared in 10 mM Tris (pH 7.5) with 200 mM NaCl.

Melting Temperatures

Melting temperatures of double-stranded oligonucleotides were measured by monitoring the absorbance hyperchromicity at 260 nm in a Hewlett-Packard model 8452a spectrophotometer equipped with a Hewlett-Packard 89090A Peltier temperature controller. Samples were measured in 10 mM Tris (pH 7.5) with 200 mM NaCl. The temperature was increased at a rate of 1 °C/min with a 1 min equilibration time between increments.

Steady-State Fluorescence Measurements

Quantum yields were calculated from steady-state fluorescence emission scans measured on a modular PTI Quantumaster (New Brunswick, NJ) fluorometer equipped with a double-excitation monochromator, polarizers, and a cooled photomultiplier. Excitation slits were set to 16 nm, and the emission slit was set to 8 nm. The sample chamber was equipped with a Peltier temperature controller. Scans were conducted under “magic angle” conditions [emission polarizers oriented 54.7° relative to vertical excitation polarization (10)]. Samples were measured at an absorbance of approximately 0.10 at 360 nm in 10 mM Tris buffer (pH 7.4) in 3 mm × 3 mm quartz cuvettes; thus, inner filter effects are negligible. Corrected emission spectra were integrated and referenced to that of quinine sulfate (QY = 0.51) at an absorbance of 0.04 at 360 nm in 0.1 N H₂SO₄. Absorbance was measured on a Hewlett-Packard (Palo Alto, CA) 8452A spectrophotometer, at 360 nm for the probe and at 260 nm for the DNA. The quantum yield was determined from an average of at least two experiments with each sample prepared and measured in triplicate. Double-stranded probe-containing sequences were analyzed after annealing in the presence of 200 mM NaCl.

Steady-state anisotropies (r) were calculated at 440 nm using eq 1:

$$r=\frac{I_{\parallel }-I_{\perp }}{I_{\parallel }+2I_{\perp }}$$ (1)

where I_∥ is the fluorescence intensity measured with polarizers set parallel to the direction of vertically polarized excitation and I_⊥ is intensity measured with polarizers set orthogonal to I_∥.

Pre- and post-laser exposure scans to check for probe photo-degradation were conducted on a Fluorolog-3 instrument (Spex and Jobin-Yvon Horiba, Edison, NJ). Excitation was at 335 nm, and corrected emission was measured between 390 and 500 nm under magic angle conditions.

Time-Resolved Fluorescence Decay Measurements

Time-resolved fluorescence measurements were performed by the time-correlated single-photon counting (TCSPC) technique (11) with the few modifications outlined below. The pump laser, Vanguard 2000-HM532 from Newport/Spectra-Physics (Mountain View, CA), is a solid-state diode-pumped passively mode-locked Nd:YVO₄ oscillator operating at 80 MHz. It is frequency doubled inside the laser head to produce 2 W of power at 532 nm. Spectra-Physics cavity dumper (model 454) synchronization was achieved by means of a Spectra-Physics model 3932-LX fast amplified photodiode. Samples were excited at 335 nm using the second harmonic of a synchronously pumped, cavity-dumped model 3520 DCM dye laser (repetition rate of 4 MHz, pulse width of <2 ps, average UV power of <200 μW). The time-to-amplitude converter resolution was set to 38 ps/channel, and data were collected in 512 channels to a minimum of 10000 counts in the peak channel. Fluorescence intensity decays were collected under magic angle (54.7°) polarization conditions (9) with the emission monochromator (bandpass at 8 nm) set at 430 or 440 nm (a Newport GG400 long-pass glass filter further blocked Raman and Rayleigh scatter). Assuming that fluorescence decay follows a multiexponential law, the total intensity may be modeled as

$$I\left(t\right)={\alpha }_S\delta \left(t\right)+\sum _i^n{\alpha }_i{e}^{-t∕{\tau }_i}$$ (2)

where, for each sample, the relative amplitudes (α_i) and decay constants (τ_i) were the recovered parameters. An independent parameter α_S represents the sum of residual Rayleigh and Raman scattering, and δ(t) is the Dirac delta function. In all time-resolved fluorescence experiments, the instrument response function (IRF) and the color shift used for convolution analysis were tested with a monoexponential standard (9-anthracenecarbonitrile in methanol) with a fluorescence lifetime τ of 11.7 ns.

We fit these data to a multiexponential model (see above) using an iterative reconvolution method with intensity-weighted residuals (12). The goodness of fit was assessed with the χ_R² function (13). The excitation pulse “lamp” profile (IRF) was obtained using a silica gel light-scattering suspension (Silica Colloid or Ludox) from Sigma-Aldrich (St. Louis, MO) and a typically measured fwhm of ≈80 ps. A convolved multiexponential model, I'(t), describing the time course of fluorescence intensity was fit to the measured fluorescence decay data

$$I^{\prime }\left(t\right)=\int L\left(t^{\prime }\right)I(t^{\prime }-t)d{t}^{\prime }$$ (3)

where L(t) is the IRF function and I(t) was defined earlier. The best fit between the theoretical curve and the data was evaluated from the plot of weighted residuals, their autocorrelation function, and the reduced χ² value. All fitting and data analysis were performed with DecayFit, a software package which is currently available from our laboratory (National Heart, Lung, and Blood Institute) upon request.

Dynamic fluorescence quenching experiments were performed by adding small aliquots (5–15 μL) of concentrated solutions (0.56–0.82 M) of each of the four DNA mononucleotides from Sigma-Aldrich dissolved in standard buffer to 100 μL of a 0.015 M solution of either 6MI or 3MI monomer. The quenching data were evaluated using the Stern–Volmer equation

$$\frac{I_0}{I}=\frac{{\tau }_0}{\tau }=1+K_{\text{SV}}\left[\mathrm{Q}\right]$$ (4)

where I₀ and I are the steady-state intensities and τ₀ and τ are the amplitude-weighted fluorescence lifetimes in the absence and presence of quencher Q, respectively. The dynamic Stern–Volmer constant, K_SV, is equal to k_q τ₀, where k_q is the bimolecular quenching rate constant and τ₀ is the lifetime of the fluorophore in the absence of quencher. When the I₀/I slopes differ from τ₀/τ, one may infer static quenching from that difference. (The equation then becomes either quadratic or a product with an exponential, but the first-order static quenching constant, K_s, is the slope difference.) The excitation and emission wavelengths were 335 and 430 nm, respectively, for these quenching experiments.

Time-Resolved Anisotropy Decay Measurements

For time-resolved fluorescence anisotropy studies, the same setup as intensity decay was employed for 10 accumulations with the emission polarizer alternatively set parallel (I_∥) and perpendicular (I_⊥) to the vertically polarized excitation pulse at 335 nm. We use a depolarizer (DPU-25, OFR) in the emission light path, so no polarization bias is incurred (G = 1). Intensity counts were approximately 25000 for the vertical component and 10000–13000 for the horizontal one (in the peak channel). Emission spectra were recorded before and after exposure to rule out degradation during anisotropy measurements. Anisotropy decay profiles were calculated using the “sum-and-difference” method based on eq 5.

$$r\left(t\right)=\frac{I_{\parallel }\left(t\right)-I_{\perp }\left(t\right)}{I_{\parallel }\left(t\right)+2I_{\perp }\left(t\right)}$$ (5)

Associative testing is built into our sum-and-difference software package in a way that makes it easier to test for associative behavior, and therefore, we used it in place of global analysis of I_∥(t) and I_⊥(t). The decay in the fluorescence anisotropy was fit to eq 6

$$r\left(t\right)=\sum _{j=1}^m{\beta }_j{e}^{-t∕{\varphi }_j}$$ (6)

where ϕ_j are the rotational correlation times and β_j are the pre-exponential factors used to describe the orientation of the absorption and emission transition dipoles along the principal diffusion axis at time zero (14). We usually fit using nonassociative behavior; i.e., all fluorescence intensity decay populations are characterized by the same set of anisotropy decay components (15). As in the case of lifetime decay data, goodness of fit was assessed with the χ_R² function (13).

Total fluorescence intensity was calculated using eq 7

$$\mathrm{Int}=\sum _{i=1}^n{\alpha }_i{\tau }_i$$ (7)

and the percentage intensity from each component of the multi-exponential model is

$$\%I=({\alpha }_i{\tau }_i∕\mathrm{Int})\times 100$$ (8)

Mean lifetimes (intensity-weighted lifetime τ_m) and the species concentration-weighted lifetime 〈τ_mol〉 are defined in eqs 9 and 10.

$${\tau }_{\mathrm{m}}=\frac{\sum _{i=1}^n{\alpha }_i{{\tau }_i}^2}{\sum _{i=1}^n{\alpha }_i{\tau }_i}$$ (9)

and

$$\langle {\tau }_{\text{mol}}\rangle =\frac{\sum _{i=1}^n{\alpha }_i{\tau }_i}{\sum _{i=1}^n{\alpha }_i}$$ (10)

The amount of variation from monoexponential decay can be determined by comparing the relative magnitudes of the pre-exponentials (α_i), the percentage contribution to the intensity (I_i) of each component, and the difference between τ_m and 〈τ_mol〉.

To further understand the mechanisms of quenching when the pteridines are inserted into an oligonucleotide, we evaluated the relationships between quantum yields and lifetimes. In pure dynamic quenching (quenching events occurring during the excited state), quenching competes with fluorescence, so

$$\text{QY}=\frac{\tau }{{\tau }_{\text{rad}}}$$ (11)

where QY is the quantum yield, τ is the measured lifetime, and τ_rad is the natural or radiative lifetime (i.e., one that would be observed when QY=1). A case in which τ/QY>τ_rad signifies static (or quasi-static) quenching (ref 16 and references cited therein). When applied to a heterogeneous solution, it may be modified to use a mean lifetime 〈τ_mol〉 (16).

“Absolute alpha”, A_i, was calculated using eq 12 to normalize experiments conducted with different impulse response functions.

$$A_i={\alpha }_i{\left(\frac{\mathrm{Int}}{\text{QY}}\right)}^{-1}$$ (12)

If we presume that the small spectral shifts that occur when the probe is incorporated lead to only negligible changes in the true radiative lifetime τ_rad, we can calculate a dark population amplitude:

$$A_{\text{dark}}=({\tau }_{\text{ref}}∕{\tau }_{rad}-1)\sum A_i$$ (13)

where A_Pi values are again the normalized “absolute” amplitudes α_i[QY/(σα_iτ_i)].

The radiative lifetimes of the reference compound and the measured system are defined as the measured lifetime divided by the QY as shown in eq 11. In a heterogeneous environment like that of DNA, that lifetime will no longer be monoexponential like the reference (e.g., monomer). In that case, the proper lifetime to use is shown in eq 10.

RESULTS

In Prior Studies, 3MI Exhibited Lower Quantum Yields When Flanked by Purines

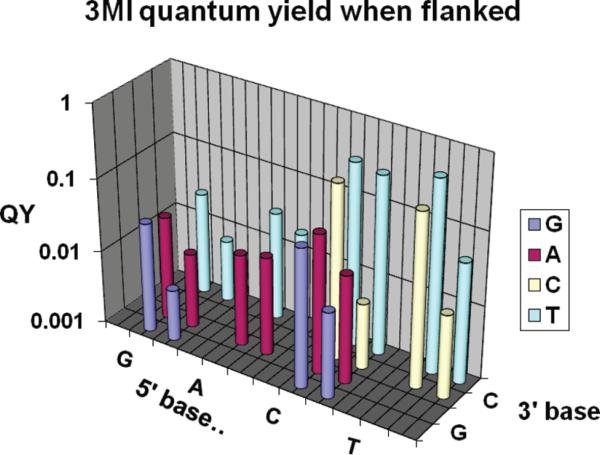
The quantum yields of 3MI flanked by a variety of bases in the study of Driscoll and Laws (17) are replotted in Figure 2, comparing both single-stranded and double-stranded oligonucleotides.

Figure 2.

Effects of flanking bases on quantum yields, replotted from ref 17. In this semilog plot, the QY value of the probe in the single strand is shown to the left of that in the double strand. The base located on the 5′-side of the probe is named on the x-axis, and the base located on the 3′-side of the probe is listed on the z-axis (on the right side of the figure). Clearly, a flanking G and/or A (purines) is predictive of a low QY as compared to a flanking C and/or T (pyrimidines).

Table 2 lists the parameters for 3MI and 6MI in the two very different environments, one flanked by purines and one flanked by pyrimidines (see Table 1). In prior studies, both probes exhibited lower fluorescence yields when flanked by purines (PTRA), with additional quenching seen upon formation of a double strand.

Table 2.

Steady-State Anisotropies, Quantum Yields, and Melting Temperatures of 3MI and 6MI^a

	r		QY		Tm (°C)
	PTRT	PTRA	PTRT	PTRA	PTRT	PTRA
SS 3MI	0.088	0.093	0.084	0.015
SS 6MI	0.103	0.154	0.107	0.044
DS 3MI	0.072	0.054	0.032	0.026	61.9	62.8
DS 6MI	0.243	0.206	0.189	0.037	65.8	66C

^aThe T_m of an identical native sequence is 68.4 °C under the same conditions.

To date, the quantum yield of 6MI has not been measured in as many sequences as 3MI, but observations from our own work and from our 6MI collaborators (data not shown) support a similar picture; for either probe, the QY values are in the following rank order: surrounded by T~C≫G ~ A (18). Purine neighborhoods have generally been seen to be more quenched than pyrimidine neighborhoods in a single-stranded environment.

In the Driscoll study, there were, perhaps, also secondary patterns seen that perhaps can be ascribed to the second flanking base (especially A), but the sequences known to date do not represent the full range of possibilities necessary to reach such conclusions. The primary (purine quenched) pattern is still dominant. We questioned what the origins of such a pattern might be and found the work of Seidel and co-workers intriguing (19). They systematically varied the electronic potential of their fluorophore by synthesizing a series of coumarin derivatives meant to act as base analogues (without base pairing). These were, in turn, used to test whether Rehm–Weller theory for electron transfer could predict the quenching of the probe series by nucleobases. Considerable accordance with the activated electron transfer complex theory was, in fact, seen; the reconciliation of the bimolecular quenching constant (k_q) with the redox potential of the coumarin with respect to the quenching bases was quite persuasive.

Thus, we collected both steady-state and time-resolved fluorescence quenching titrations of 3MI and 6MI in solution with the mononucleotides AMP, CMP, GMP, and TMP. The results are summarized in Table 3 and in Figures 3 and 4. In Table 3, the K_SV values derived from fluorescence intensity (I₀/I) report on the response due to all forms of quenching while K_SVτ values derived from the lifetimes (τ₀/τ) report on only changes due to dynamic quenching. Their difference (ΔK_SV = K_SV – K_SVτ) provides a first-order estimate of the contribution to quenching from static species. In the same table, k_q reports on the bimolecular rate of quenching collisions. Relatively lower values suggest less efficiency or suggest that the fluorophore is somehow shielded from the quencher. In agreement with Seidel, we find the Stern–Volmer plots of steady-state quenching are nearly linear, even though both static and dynamic terms are present. Our attempts to use Rehm–Weller theory to understand the electronic mechanisms between the probes and the mononucleotides were thwarted by the complexities of hydrogen bonding between 6MI and cytidine, both in solution and in double-stranded structures.

Table 3.

Stern–Volmer Constants^a

		A	G	T	C
K SV	6MI	37	25	66	4.3
	3MI	34	62	66	12
K SVτ	6MI	13	17	31	3.3
	3MI	15	17	26	7.2
Δ K SV	6MI	24	8.0	35	1.0
	3MI	19	45	40	4.8
k q	6MI	2.1	2.7	5.0	0.53
	3MI	2.3	2.6	4.0	1.1

^aK_SV, K_SVτ which is K_SV derived from the τ₀/τ data, ΔK_SV which is equal to K_SV − K_SVτ, and k_q which is the bimolecular quenching constant which is equal to K_SVτ/τ₀.

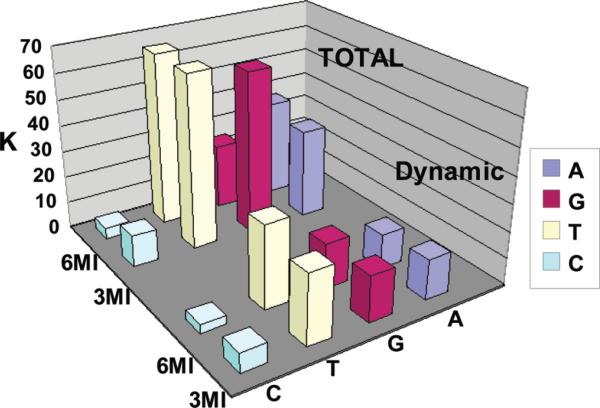
Figure 3.

Stern–Volmer constants showing the effects of each of the four quenchers on the 3MI or 6MI monomers. K_SV is shown in the back corner of the graph (total), and K_SVτ is shown in the foreground (dynamic).

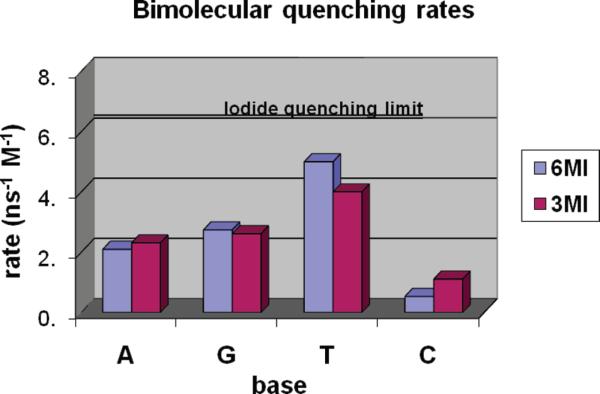
Figure 4.

Bimolecular quenching rates (k_q=K_SVτ/τ₀). A line representing the I⁻ quenching limit has been inserted to provide one estimate for an ideal quenching case.

The Solution Quenching Pattern Is Reversed

Surprisingly, the dynamic quenching of the free isoxanthopterins is totally different from the pattern seen with the incorporated probes (for k_q, T>A>G>C). Inspection of Figure 3 of ref 19 makes it clear that redox potential alone would not predict such a pattern.

Most intriguing is the fact that redox potentials of C and T are nearly identical yet C exhibits a very low quenching constant relative to that of T. The discrepancy could be a result of either T having some exceptional quenching ability or C having reduced efficiency. We questioned whether 3MI and 6MI may form a complex with cytosine, making their titrations with the complementary C behave differently from simple quenching.

We note that the Stern–Volmer plots for C alone display downward curvature signatory of heterogeneous quenching. When we further examined the first ~40 mM of C quenching, we found we could dissect the decay process into a mixture: a nearly constant component of ~2 ns becomes apparent after ~10 mM C along with a term that begins near 6 ns and decreases as expected for efficient quenching (data not shown). We reasoned that both 3MI and 6MI are capable of hydrogen bonding with C, although 6MI would form nativelike triple-bond architecture while 3MI's binding capabilities would be impaired because of the 3-position methyl group blocking the center position of the three potential bonds. Thus, we hypothesize the production of weak 3MI·C or 6MI·C complexes that are somehow rendered less subject to dynamic quenching by collision with subsequent C molecules. The affinity, stoichiometry, and nature of such complexes are beyond the scope of this work and will necessitate a separate study.

Setting C aside, we still must ponder why the highly efficient quenching by T in solution (relative to A and G) is not seen when T is the flanking base in an oligonucleotide. Of course, the stacked bases in an oligonucleotide encounter each other in a conformationally restricted fashion (unlike the randomized collisions expected in solution), so one can imagine the loss of a particular range of encounter geometries. If the geometry of encounter was unimportant, one might expect the bases to act as nearly ideal (diffusion-limited) quenchers. There is also the possibility that the organized charge structure of the single- or double-stranded molecule provides a repulsive charge protecting the fluorophore from the approach by the quenching nucleotides. The Stern–Volmer constants summarized above (Table 3) are all considerably smaller than the (presumably diffusion controlled) value found by Seibert et al. for 6,8DMI quenched by the efficient spin–orbit coupling quencher KI (or I⁻), so quenching inefficiency is certainly possible (20). A line in Figure 4 is placed at the quenching level of I⁻ to provide one estimate for an ideal quenching case, although even I⁻ might quench in a nonideal fashion because of its charge. True diffusion-limited quenching of such small molecules approaches 1 × 10¹⁰ s⁻¹ M⁻¹, and both steric factors and ionic repulsion lead to lower values.

The Base Environment inside Oligonucleotides Is Extremely Heterogeneous

We resolved the fluorescence decay of 3MI and 6MI in prior studies within oligonucleotides, finding a lifetime term similar to that of the probe monomer accompanied by other, shorter-lived components (21). This “unquenched population” phenomenon has also been seen in 2-AP; there, the assumption is that long lifetimes reflect a “flipped out” population which does not suffer the quenching anticipated within the stacked environment (6, 7, 22). In this study, we place either 3MI or 6MI within similar purine (A)-flanked or pyrimidine (T)-flanked sites in oligonucleotides, pairing each with C in the complementary strand. It has been reported that free 3MI might also form a complex with T (23); however, the free 3MI3·T complex (involving the 1- and 8-positions of the pterin ring) reported in such work should not be sterically possible for probes containing a deoxyriboside moiety at the 8-position. Table 4 and Figure 5 summarize our time-resolved decay analysis.

Table 4.

Time-Resolved Decay Analysis^a

	A1	τ 1	A2	τ 2	A3	τ 3	Adark	Krad = (1/τrad)	τ mol	$\mathcal{Q}$	τrad = (τmol/Q)
SS A·6MI	0.010	1.00	0.005	4.7	0.039	0.21	0.056	0.054	0.809	0.044	18.4
DS A·6MI	0.009	0.93	0.003	5.59	0.041	0.34	0.057	0.053	0.703	0.037	19.0
SS T·6MI	0.014	1.52	0.020	4.2	0.009	0.21	0.067	0.043	2.478	0.107	23.2
DS T·6MI	0.041	2.37	0.021	4.12	0.005	0.39	0.042	0.068	2.772	0.189	14.7
SS A·3MI	0.002	1.03	0.003	4.28	0.005	0.15	0.125	0.010	1.491	0.015	99.4
DS A·3MI	0.003	1.25	0.004	5.72	0.019	0.14	0.110	0.025	1.041	0.026	40.0
SS T·3MI	0.023	1.77	0.008	4.55	0.014	0.52	0.090	0.045	1.869	0.084	22.2
DS T·3MI	0.009	1.67	0.003	4.91	0.006	0.37	0.118	0.017	1.837	0.032	57.4
6MI	96.8%	6.3	3.2%	2.8			(0)	0.110	6.2	0.70	8.9
3MI	100%	6.5					(0)	0.135	6.5	0.88	7.4

^aSee Materials and Methods for the definition of terms. A_n (n = 1–3) values are absolute alphas. τ_n values are the lifetimes of corresponding components. K_rad is the radiative rate. τ_rad is the radiative lifetime. τ_mol is the molecular lifetime. $\mathcal{Q}$ is the quantum yield.

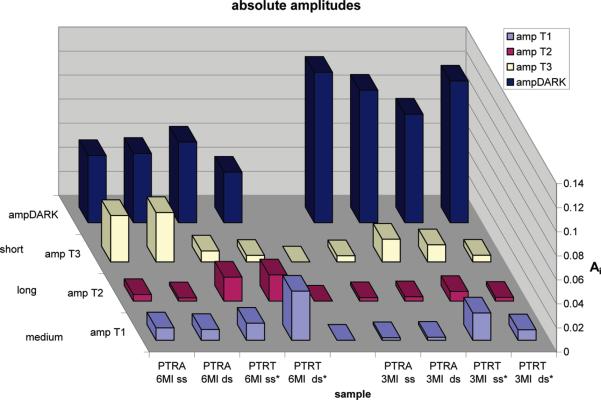
Figure 5.

Display of the absolute amplitudes of the double- and single-stranded forms of the sequences containing either 3MI or 6MI in a quenched or relatively less quenched environment.

Note that the radiative lifetimes for 3MI range from 7 to 99 ns. These are “apparent” radiative lifetimes. The true radiative lifetimes are taken from the standard (monomer) form of the probe. It is, in fact, because of the discrepancy between apparent and true radiative lifetimes that we infer the presence of the dark alpha. Two or three decay rates are necessary to adequately fit these decay transients, and the amplitudes (surrogates for population fractions) change upon formation of the double strand. In addition to the measured amplitudes, we also calculate an amplitude for the population that is quasi-statically self-quenched (QSSQ). The dark population amplitude is calculated with eq 13. Equations 11 and 14 are employed also (24). The dark population thus derived is plotted, along with the other normalized decay amplitudes, in Figure 5. The assumption is made that large variations in τ_rad can be reconciled by the presence of QSSQ. We have unpublished data for tryptophan in dipeptides where large variations in τ_rad could be reconciled by an observed picosecond τ. We suspect that may be the case here as well but have not yet measured ultrafast decay for 3MI and 6MI (J. Xu and J. R. Knutson, manuscript in press in The Journal of Physical Chemistry B).

Considerable Portions of the Probe Populations Are Fully Quenched

Figure 5 reveals that the vast majority of 3MI molecules incorporated into these oligonucleotides are nonfluorescent, due to either true static quenching (in a ground-state complex with a quenching moiety) or QSSQ. Since the A_dark component is large in both single- and double-strand environments, intrastrand quenching to the dark state is dominant and interstrand quenching is a secondary influence. 6MI, on the other hand, exhibits a relatively smaller dark-state population, and the formation of duplexes has more influence on the yield.

The Flanking T Environment Exhibits a Large A_dark Reduction upon Formation of Double Strands for 6MI

In most environments, the formation of a duplex further quenches either 3MI or 6MI through either increases in the dark fraction or shortening of the mean lifetime. This was seen both in Driscoll's data and our prior pteridine-containing sequences (17, 18, 21). The flanking T environment for 6MI presents a novel response to annealing, however. The QY nearly doubles for this sequence. In the flanking A environment (also for 6MI), annealing has no discernible effect on the dark fraction. Figure 5 reveals that this could be in part due to escape from a fully quenched state for a significant subpopulation of strands that instead acquire a lifetime near 2 ns (“medium”). Alternatively, a redistribution of population from the shortest-lived component to the medium (2 ns) component would also increase the overall QY. Using these strands alone, we cannot identify the mode of redistribution. We speculate that quenching by flanking bases is a conformationally constrained process, and the formation of a DNA duplex can either increase or decrease the rates of formation of the encounter complex between the base and its intrastrand neighbors.

Strong base pairing forces might be expected to constrain the central base analogue, inhibiting propellor twist and base tilt in the duplex that might otherwise enable contact with flanking quenchers. The efficacy of base pairing as a dequencher would, of course, also depend on whether the flanking bases are highly mobile and hence able to collide with and quench even a rigidly held central base. If the former speculation is correct, the constrained environment would exhibit both higher yield and limited probe flexibility. We have not studied the weaker inter-strand quenching process, of course, since in these studies we always paired the probe with C as a cognate complement to a G analogue.

Time-Resolved Emission Anisotropy Reveals Local Flexibility for 3MI in All Environments

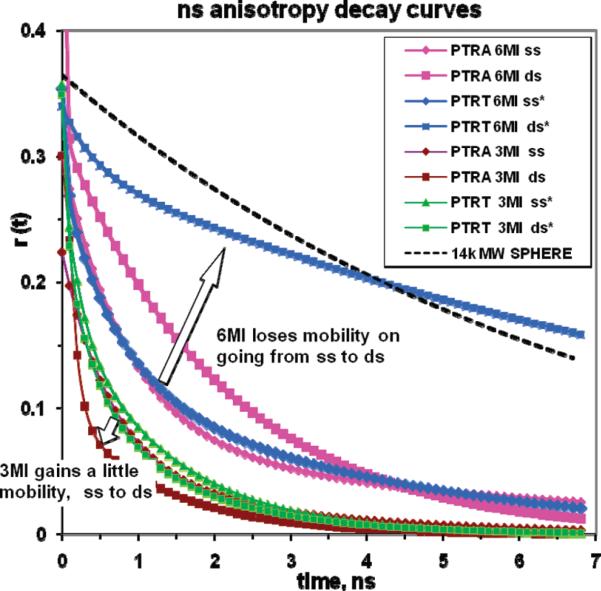
Figure 6 shows the anisotropy decay functions (see Materials and Methods) for the two different analogues in each sequence, both single- and double-stranded. Evidently, none of these environments confine 3MI motion. If the probe were a rigid reporter, it would necessarily show a rotational correlation time in excess of the Stokes–Einstein volume for that much mass (monoexponential guide curve seen in Figure 6). If the duplex was rotating as a hydrated rigid cylinder (i.e., ignoring torsional and other local modes), a longer correlation time, greater than 10 ns, would be predicted from classical hydrodynamic theory (T. Rosales, personal communication).

Figure 6.

Anisotropy decay curves for 3MI- and 6MI-containing sequences. The top line in this graph represents the expected decay for a 14K molecular weight sphere for the sake of comparison.

Time-Resolved Emission Anisotropy Reveals 6MI Is Subject to Local Flexibility When Flanked by A but Is Rigid between T's in a Duplex

Figure 6 also shows that 6MI is unique in this study: it appears to track nearly rigid rotation of the entire duplex [except for small local motions (<10%β)] when symmetrically flanked by T. The flanking adenine environment, in contrast, does not prevent the electronic oscillator within 6MI from rotating with times of <3 ns. We note that the transition moment of the closely related analogue 6,8MI is aligned along the (6MI equivalent) C6–N2 axis (20), implying that large rotations of this vector could not occur without disruption of at least some base pairing.

In the engineering of a base analogue, the ability to faithfully report the existence of a rigid local structure is valuable, so the flanking T environment of 6MI presents unique opportunities. We have not yet investigated whether secondary neighbors interfere or whether the flanking T environment is sufficient. We will not be able to discern whether the flanking A structure generates neighborhood flexibility (or whether it just permits probe rotation) without further study beyond the current scope (e.g., studies of several oligo's possessing TFT sites with secondary flanking A's). Since quenching in these systems has both static and dynamic components, the link between quantum yield and anisotropy can be anomalous. Fortunately, the T-flanked 6MI site emerged as a reporter with high yield and good coupling to the global DNA motion.

DISCUSSION

The engineering of fluorescent reporters for the interior of macromolecules is a daunting task. First and foremost, they need to perturb the native environment as little as possible, mimicking the molecule that would be naturally found in that locus. In this context, that means the probe should be capable of at least two and optimally three base pairing hydrogen bonds and it should have roughly the same size as a nucleoside. 6MI (and, to a lesser extent, 3MI) fulfills these needs.

Second, the probe should provide quality fluorescence emission and excitation characteristics separate from those of the native bands. While no probe simultaneously provides perfect spectra, long lifetime, stability, and yield, the two probes, 3MI and 6MI, provide high blue yield, a lifetime near 6 ns, and good stability in this purpose-constrained shape.

These studies show that the intrastrand quenching process is dominant for both probes (at least in these sequences). Further, the degree of proximity and/or collision between the analogue and its stacking neighbors, which can change upon formation of a duplex, is critical. It is the conformational constraint of collisions in the strands that reverses the quenching order from solution. This is not surprising, given the extremely short (less than ~1 Å) distance for refolding of electron transfer processes (19, 25)which is compatible with either the fixed Marcus or mobile Rehm–Weller viewpoint.

Finally, for this probe empirically, it seems 6MI flanked by T's offers a rigid coupling to the duplex that may be useful in size and flexibility studies.