Abstract
The authors examined whether math fluency was independent from untimed math and from reading using 314 pairs of school-aged twins drawn from the Western Reserve Reading and Math Projects. Twins were assessed through a 90-min home visit at approximately age 10 and were reassessed in their homes approximately 1 year later. Results suggested that the shared environment and genetics influenced the covariance among math fluency, untimed math measures, and reading measures. However, roughly two thirds of the variance in math fluency was independent from untimed math measures and reading, including reading fluency. The majority of this independent variance was the result of genetic factors that were longitudinally stable across two measurement occasions. These results suggest that math fluency, although related to other math measures, may also be a genetically distinct dimension of mathematics performance.
Keywords: mathematics, genetics, reading
Typically, math fluency is assessed by measuring how quickly students are able to calculate simple math problems. This measure has begun to receive significant attention. First, progress monitoring in schools has led to the emergence of timed measures to quickly and repeatedly provide teachers with academic information on large groups of students (Fletcher & Vaughn, 2009). More generally, the importance of mathematical literacy in modern society has led to more systematic and sustained efforts to understand mathematics ability and disability (Butterworth, 1999; Fuchs et al., 2008; Geary, 2010; Geary & Burlingham-Dubree, 1989; Geary & Widaman, 1992; Landerl, Bevan, & Butterworth, 2004; National Mathematics Advisory Panel, 2008; Raghubar, Barnes, & Hecht, 2010; Siegler, 1988). As part of this effort, several recent studies have suggested that math fluency, although related to untimed math measures, may reflect additional variance in math ability above and beyond untimed math performance (Fuchs et al., 2008; Hart, Petrill, & Thompson, 2010; Mazzocco, Devlin, & McKenney, 2008).
After reviewing the literature, the National Mathematics Advisory Panel (2008) suggested that math fluency was an important aspect to many subject areas of mathematics performance, such as number sense and whole number arithmetic. In general, research has examined the relationship between timed fluency and untimed math performance using samples selected for math difficulties. Poor math fluency has been suggested as a possible indicator of mathematical learning disability (MLD; Mazzocco et al., 2008). Indeed, studies have suggested that poor math fluency may be a unique quality of mathematical difficulty and not a predictor of other learning problems such as reading difficulty (Jordan & Hanich, 2003). In examining the difference in math fluency outcomes between children with MLD versus children who were low achievers in math without diagnosed disability, both groups suggested greater total errors on a math fluency measure than their typically developing peers (Mazzocco et al., 2008). This study also examined girls with Fragile X or Turner’s syndrome, both of which have known math performance difficulties. Girls with Turner’s syndrome had difficulties for timed fluency outcomes, whereas girls with Fragile X did not.
In contrast, studies involving unselected samples have eschewed measures of math fluency, instead employing measures of general processing speed. These studies suggest that general processing speed (e.g., speed of visual matching) is a unique indicator of computational skills (e.g., Bull, Johnston, & Roy, 1999; Fuchs et al., 2008; Hecht, Torgesen, Wagner, & Rashotte, 2001). Fuchs et al. (2008) proposed that processing speed may indicate how quickly numbers can be counted in a computational sequence, with slower counting resulting in lower success in problem solving. However, because studies have not included both math- and non-math-based measures of fluency, it is unclear whether this effect is specific to math fluency, a reflection of more general processing speed, or a combination of both general and math-specific fluency.
Behavioral genetic studies have also offered initial evidence concerning the overlapping but unique etiology of math fluency with untimed math outcomes. Identical (monozygotic; MZ) twins share 100% of their additive genetic variance, whereas fraternal (dizygotic; DZ) twins, on average, share 50%. Genetic influences are implied if MZ twins show greater similarity than DZ twins. Shared environmental influences are implied if familial resemblance on a trait is equal for MZ twins and DZ twins. Nonshared environment (including error) is implied if MZ twins are not perfectly correlated. As described more fully in the results section, the twin design can also be used to examine the relationships among a set of variables (also see Plomin, DeFries, McClearn, & McGuffin, 2008).
To date, there have been two behavioral genetic studies involving measures of math fluency. Hart, Petrill, Thompson, and Plomin (2009) examined the relationship among general cognitive ability, reading, and math outcomes, including math fluency. Untimed measures of math performance (e.g., problem solving) were influenced primarily by shared environmental effects. In contrast, timed measure of math fluency indicated significant moderate to high genetic influences. This study further suggested that there was significant genetic overlap between math fluency and rapid automatized naming (RAN), but there was no significant relationship between math fluency and untimed measures of reading. These results suggest that a significant portion of the variance in math fluency is heritable and that these genetic influences are associated with measures of naming fluency. These overlapping genetic effects are consistent with earlier work suggesting that math fluency may involve basic mechanisms of learning that affect multiple domains, such as speed of long-term memory retrieval (Geary & Widaman, 1987, 1992). However, there were also significant independent genetic influences on math fluency above and beyond RAN, suggesting that there may be unique genetic effects on math fluency.
To further explore this result, using the same sample, Hart et al. (2010) examined the relationship among latent factors of untimed reading, decoding fluency, reading comprehension, and math, including math fluency. Confirmatory factor analyses indicated that math fluency was best associated with other untimed math measures instead of decoding fluency measures. This would suggest that despite the general genetic association between measures of fluency described in Hart et al. (2009), when subjected to a measurement model, math fluency was more highly associated with untimed math outcomes than timed reading outcomes. Moreover, the genetic covariance between the math factor (including untimed math and math fluency) and the decoding fluency factor was statistically significant. However, both decoding fluency and math factors also demonstrated significant independent genetic effects, again suggesting a distinct genetic etiology for fluency.
In sum, behavioral genetic studies are consistent with the notion established in the cognitive and educational psychology literatures that math fluency, although correlated with untimed math measures, may also constitute an additional dimension of math performance (e.g., Fuchs et al., 2008; Mazzocco et al., 2008; Tolar, Lederberg, & Fletcher, 2009). These studies also suggest that genetic effects for timed measures may be both general to reading and math as well as specific to math.
Given these findings, three important questions need to be addressed. First, are independent genetic influences on math fluency present above and beyond their association with untimed math measures? Hart et al. (2010) found that math fluency loaded on a general math factor, but 64% of the variance in math fluency was not accounted for by that general math factor. It is unknown as to whether the remaining residual variance is attributable to random error or whether it indicates unique variance related specifically to math fluency. Furthermore, previous work suggests that it is important to understand the possible genetic etiology of this residual variance. This analysis has not been conducted.
A second important question is how math fluency relates to timed and untimed measures of reading ability. Previous work suggests significant common genetic influences between math fluency and naming fluency, but not between math fluency and untimed measures of reading (Hart et al., 2009). We hypothesize that fluency in reading and math may be tapping similar constructs; however, the amount of overlap between reading and math fluency is unclear. Therefore, it is also important to ascertain whether math fluency and reading fluency are influenced by a common set of genetic factors or if math fluency is genetically independent from reading fluency.
Finally, it is well established that mathematical performance is highly stable across measurement occasions (Aunola, Leskinen, Lerkkanen, & Nurmi, 2004; DiPerna, Lei, & Reid, 2007; Jordan & Hanich, 2003), but the role of math fluency in the stability of math performance is poorly understood. At present, the only study of untimed math development found that genetic factors were important for the stability of math across measurement occasions (Kovas, Haworth, Dale, & Plomin, 2007). Importantly, Kovas et al. (2007) also found substantial evidence for unique genetic effects on math separate from general intelligence and reading skills. Thus, we expect that the longitudinal stability of math fluency will be influenced by common genetic factors. However, it is unclear whether this stability will be specific to math fluency, shared with untimed math, and/or shared with timed measures of reading.
Thus, we hypothesize that math fluency will be associated with untimed math performance. Unknown is whether math fluency will show independent genetic effects above and beyond untimed math measures. Furthermore, if independent genetic effects on math fluency are significant, we will examine whether they are correlated with and/or independent from reading fluency. Finally, we examine whether the stability in math fluency across measurement occasions is independent from or correlated with untimed math measures and reading fluency.
Method
Participants
Participants of the present study are enrolled in the ongoing Western Reserve Reading and Math Projects, a longitudinal twin study in Ohio. Recruiting was conducted through Ohio state birth records, school nomination, and media announcements. We have the participation of 293 schools throughout the state, which were asked to send information to parents with twins. We also hired a social worker with longstanding ties to the community to assist in the recruitment of underrepresented groups via face-to-face meetings at places of worship, community centers, and other service organizations.
The project is ongoing (see Petrill, Deater-Deckard, Thompson, DeThorne, & Schatschneider, 2006). Home visits began when children entered school. Waves 1, 2, and 3 focused on early reading skills. Wave 4 examined math skills. The present study is based on home visit Waves 5 and 6, which are the first to focus on both reading and mathematics skills simultaneously. At Wave 5, children were approximately 10 years old (age M = 9.83 years, SD = 0.97 years, range = 7.42–12.75 years). At Wave 6, children were approximately 11 years old (age M = 10.99, SD = 0.89, range = 8.42–13.42 years).
The final sample size of same-sex twin pairs with known zygosity and analyzable data was 260 pairs of MZ (n = 108) and DZ (n = 152) twins. Zygosity was determined using DNA analysis via a cheek swab. For the cases where parents did not consent to genotyping (n = 76), zygosity was determined using a parent questionnaire about the twins similarity (Goldsmith, 1991). Although somewhat positively skewed (skew = .04), parent education levels varied widely and were similar for fathers and mothers: 12% had a high school education or less, 18% had attended some college, 30% had a bachelor’s degree, 24% had some postgraduate training or a degree, and 5% did not specify. Most families were two-parent households (92%), and nearly all were White (92% of mothers, 94% of fathers).
Procedure and Measures
Reading and math from Wave 5 were examined. We also included math data from Wave 6 so that we could test whether the overlapping and independent effects for math fluency identified at Wave 5 were longitudinally stable. All test sessions were conducted in the twins’ homes in separate rooms by separate examiners, and the total time to complete all testing was approximately 60 to 90 min per child.
Reading
Three untimed measures of reading skill were examined in the present study. The outcome of interest in each of these measures is the number of items correctly selected prior to reaching a ceiling. First, the Peabody Individual Achievement Test (PIAT; Markwardt, 1997) requires participants to read a sentence and then select a picture from four choices that best represents the meaning of the sentence. Published test–retest reliability for 10-year-old children is .93. A second measure of reading comprehension was also used, the Woodcock Reading Mastery Test (WRMT; Woodcock, 1987). This test requires children to read a short passage and identify a missing keyword to complete a sentence at the end of the passage. The published median reliability for the test is .83. The final untimed measure was the Word Identification subtest of the WRMT. This test requires students to recognize and read real words aloud. Published split-half reliability for this subtest is .95 (Woodcock, 1987).
Finally, the Test of Word Reading Efficiency (TOWRE; Wagner, Torgesen, & Rashotte, 1999) represents the timed, fluency aspect of reading. In the present study, a composite score of two subtests was used. First, Sight Word Efficiency tests the number of real words read correctly in 45 s. Second, Phonemic Decoding Efficiency tests the number of non-words read correctly in 45 s. Test–retest reliability for both subtests of the TOWRE for children aged 10–18 years is .88.
Math
Four untimed measures of math skill were used in the present study. For each of these measures, the score represents the number of correct responses given prior to reaching a ceiling. First, the Calculation subtest of the Woodcock–Johnson III (WJ-III; Woodcock, McGraw, & Mather, 2001, 2007) measures a child’s ability to perform addition, subtraction, multiplication, and division of positive and negative whole numbers, fractions, percentages, and decimals. The published median reliability of the test is .85. Second, the Applied Problems subtest of the WJ-III requires children to read word problems containing critical and extraneous information, determine which mathematical operation to use to solve the problem, and complete simple calculations. Published median reliability of this subtest is .92.
The third measure used to assess untimed math skill was the Quantitative Concepts portion of the WJ-III. Quantitative Concepts consists of two subtests: Concepts and Number Series. Concepts measures ability to count, identify numbers, shapes, and number sequences, and knowledge of mathematical terms, but no calculation is required. Number Series measures the ability to provide a missing number that will continue a presented series. The median reliability for the Quantitative concepts portion of the WJ-III is .90. Finally, the Math portion of the Wide Range Achievement Test (WRAT; Wilkinson, 1993) requires students to name presented number symbols, solve orally presented problems, and do some computations. The published reliability of the WRAT is .89.
The timed measure of math skill was the Fluency subtest of the WJ-III. This test measures a child’s ability to answer addition, subtraction, multiplication, and division problems in a limited amount of time (3 min). Twins were told to solve a series of calculation problems as quickly as they could. Published median reliability of the Fluency subtest is .89 for children.
Results
Descriptive Statistics
Table 1 presents descriptive information for outcomes at Waves 5 and 6. Mean reading and math scores were slightly above average and variance was somewhat restricted relative to norming populations. There was a range of scores at or near 2 standard deviations above and below the mean for all variables. To maintain consistency with our prior publications, for all subsequent analyses we employed raw reading and math variables residualized for age, age squared, and gender. Also in keeping with our prior publications, math variables were further residualized for school months and school months squared (see Hart et al., 2009). Intraclass correlations are also presented to provide a descriptive picture of genetic and environmental influences related to reading and math measures. Briefly, if additive genetic effects (h2) are significant, MZ correlations should be exactly 2 × DZ correlations, by virtue of the fact that MZ twins share 2 times as much additive genetic variance than fraternal twins. Shared environmental effects are indicated to the extent that MZ-DZ twin resemblance is similar in magnitude. Nonshared environment is suggested to the extent that MZ twin correlations are not equal to 1.0 (which also includes error). MZ intraclass correlations were higher than DZ intraclass correlations for all variables, suggesting genetic influences. Shared environmental effects were also indicated, particularly for untimed math outcomes, as evidenced by DZ intraclass correlations that were greater than expected by genetics alone. Some evidence for dominance genetic effects in reading was suggested because MZ twins are more than 2 × DZ correlations. However, genetic dominance was nonsignificant for all reading measures when estimated in a structural equation modeling framework (available from the first author on request).
Table 1.
Descriptive Statistics
| Variable | M | SD | Min | Max | rMZ | rDZ |
|---|---|---|---|---|---|---|
| Wave 5 | ||||||
| Reading | ||||||
| PIAT Comp | 106.02 | 11.41 | 77.00 | 144.00 | .61 | .21 |
| WRMT Comp | 103.49 | 11.09 | 65.00 | 134.00 | .68 | .26 |
| WRMT Word ID | 106.87 | 10.40 | 68.00 | 140.00 | .83 | .38 |
| TOWRE | 103.61 | 11.99 | 70.00 | 130.50 | .80 | .37 |
| Math | ||||||
| WJ Calc | 106.38 | 13.19 | 71.00 | 152.00 | .73 | .57 |
| WJ Fluency | 101.37 | 14.63 | 62.00 | 154.00 | .83 | .54 |
| WJ Applied Prob | 107.85 | 11.48 | 61.00 | 144.00 | .74 | .56 |
| WJ Quant Concept | 105.55 | 12.92 | 73.00 | 145.00 | .81 | .49 |
| WRAT Math | 103.72 | 13.66 | 68.00 | 153.00 | .77 | .50 |
| Wave 6 | ||||||
| Math | ||||||
| WJ Calc | 106.70 | 13.41 | 69.00 | 151.00 | .73 | .62 |
| WJ Fluency | 101.15 | 14.38 | 65.00 | 153.00 | .83 | .54 |
| WJ Applied Prob | 107.05 | 10.93 | 69.00 | 143.00 | .69 | .51 |
| WJ Quant Concept | 105.56 | 12.55 | 65.00 | 139.00 | .64 | .43 |
| WRAT Math | 104.93 | 14.64 | 68.00 | 150.00 | .66 | .59 |
Note: rMZ = monozygotic; rDZ = dizygotic; PIAT = Peabody Individual Achievement Test; WRMT = Woodcock Reading Mastery Test; TOWRE = Test of Word Reading Efficiency; WJ = Woodcock–Johnson; WRAT = Wide Range Achievement Test.
Next we examined the phenotypic correlations among reading and math outcomes (see Table 2). Statistically significant correlations were found for all bivariate comparisons, ranging from r = .16 between Wave 5 PIAT Reading Comprehension and Wave 6 TOWRE to r = .84 between Wave 5 and Wave 6 WJ Fluency. Most of the remaining comparisons ranged between r = .40 and r = .60.
Table 2.
Phenotypic Correlations Among Wave 5 Reading, Wave 5 Math, and Wave 6 Math Measures
| Wave 5 PIAT Comp |
Wave 5 WRMT Comp |
Wave 5 WRMT Word ID |
Wave 5 TOWRE |
Wave 5 WJ Calc |
Wave 5 WJ Fluency |
Wave 5 WJ Applied Prob |
Wave 5 WJ Quant Concept |
Wave 5 WRAT Math |
|
|---|---|---|---|---|---|---|---|---|---|
| Wave 5 | |||||||||
| WJ Calc | .33* | .40* | .44* | .36* | 1.00 | ||||
| WJ Fluency | .21* | .27* | .32* | .41* | .51* | 1.00 | |||
| WJ Applied Prob | .48* | .59* | .50* | .42* | .65* | .46* | 1.00 | ||
| WJ Quant Concept | .37* | .50* | .44* | .36* | .61* | .48* | .71* | 1.00 | |
| WRAT Math | .30* | .44* | .48* | .42* | .73* | .59* | .61* | .60* | 1.00 |
| Wave 6 | |||||||||
| WJ Calc | .31* | .42* | .43* | .35* | .70* | .54* | .66* | .54* | .65* |
| WJ Fluency | .16* | .26* | .30* | .40* | .54* | .84* | .49* | .41* | .56* |
| WJ Applied Prob | .42* | .55* | .47* | .39* | .61* | .45* | .80* | .67* | .61* |
| WJ Quant Concept | .41* | .52* | .47* | .38* | .62* | .52* | .71* | .72* | .61* |
| WRAT Math | .26* | .40* | .41* | .41* | .59* | .57* | .59* | .50* | .63* |
Note: PIAT = Peabody Individual Achievement Test; WRMT = Woodcock Reading Mastery Test; TOWRE = Test of Word Reading Efficiency; WJ = Woodcock–Johnson; WRAT = Wide Range Achievement Test.
p < .05.
Quantitative Genetic Modeling
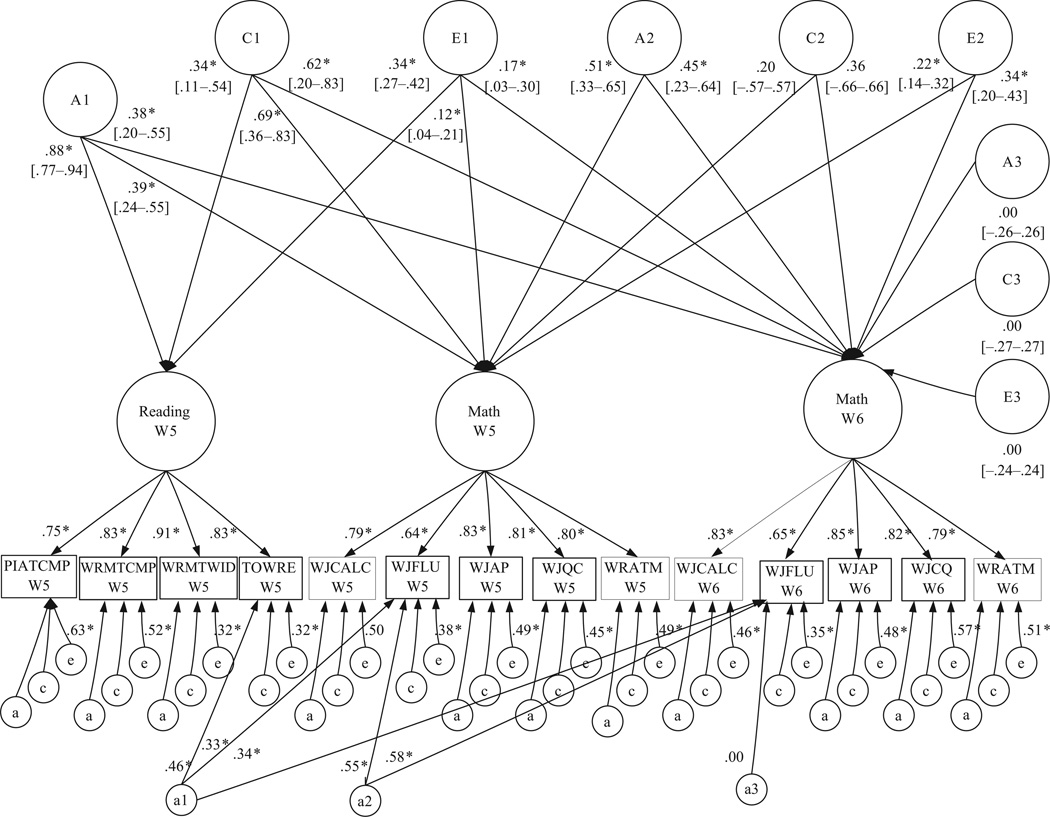
The primary goal of this study was to examine whether math fluency was etiologically distinct for untimed math measures and untimed reading measures and, if so, whether math fluency was correlated with, or independent from, reading fluency. A related question was whether math fluency was longitudinally stable beyond untimed math skills and reading fluency. Figure 1 presents a model that parameterized three latent factors: Reading Skills at Wave 5, Math Skills at Wave 5, and Math Skills at Wave 6. This model was fit to the data using Mx (Neale, Boker, Xie, & Maes, 2006). The overall fit of this model was −2log likelihood = 11770.20, df = 5737, Bayesian information criterion (BIC) = −10065.72, where negative values indicate better fit (Schwarz, 1978). Significance of individual parameters was determined using 95% confidence intervals. The variances of the latent Reading and Math factors were constrained to 1.0 to yield standardized estimates. Standardized factor loadings were significant, ranging from .64 between WJ Calculation Fluency and Wave 5 Math factor and .91 between WJ Word Identification and the Wave 5 Reading Factor.
Figure 1.
Latent factor model with 95% confidence intervals for genetic, shared, and nonshared environmental effects on latent reading and math factors
Note: PIAT = Peabody Individual Achievement Test; WRMT = Woodcock Reading Mastery Test; TOWRE = Test of Word Reading Efficiency; WJ = Woodcock–Johnson; WRAT = Wide Range Achievement Test. Confidence intervals for latent reading and math factor loadings and residual loadings are presented in Table 4.
*p < .05.
The variance and covariance among the Reading and Math factors was simultaneously decomposed into genetic (A1, A2, A3), shared environmental (C1, C2, and C3), and nonshared environmental (E1, E2, E3) factors. Standardized path estimates presented in Figure 1 (with 95% confidence intervals) suggested statistically significant genetic (A1), shared environmental (C1), and nonshared environmental (E1) influences common to Reading and Math factors. In addition, results suggested statistically significant genetic (A2) and nonshared environmental (E2) variance for Math factors above and beyond the Reading factor. A2, and E2, estimates also suggest longitudinal stability between Wave 5 and Wave 6 Math factors independent from the Reading factor. There was no evidence for unique shared environmental effects for the Wave 5 Math factor, as evidenced by nonsignificant path estimates for C2. Furthermore, there was no evidence for independent effects for the Wave 6 Math factor, as evidenced by nonsignificant path estimates for A3, C3, and E3.
These path estimates can also be used to estimate overall heritability (h2), shared environment (c2), and nonshared environment (e2) for the Wave 5 Reading factor, Wave 5 Math factor, and Wave 6 Math factor (see Table 3). These estimates are calculated by squaring the A, C, and E matrices presented in Figure 1 (see Neale & Cardon, 1992). Heritability estimates for reading and math factors were statistically significant, with a trend for higher heritability in Wave 5 Reading (h2 = .77) versus the Math factors at Wave 5 (h2 = .41) and Wave 6 (h2 = .34). Importantly, shared environmental estimates were also statistically significant for all three factors. Shared environmental estimates were statistically significantly lower for the Wave 5 Reading factor (c2 = .12) compared to the Wave 5 Math factor (c2 = .52), as evidenced by nonoverlapping confidence intervals. Shared environmental estimates for Wave 5 Reading was also lower than Wave 6 Math factor (c2 = .52), but this comparison was not statistically significant. Child specific nonshared environmental (e2) estimates were statistically significant for all factors. Importantly, because these are based on latent factors, they do not include random error.
Table 3.
Genetic, Shared environmental, and Nonshared Environmental Estimates for Latent Reading and Math Factors
| Variable | h2 | CI | c2 | CI | e2 | CI |
|---|---|---|---|---|---|---|
| Latent factors | ||||||
| Wave 5 Reading | 0.77 | [0.59–0.89] | 0.12 | [0.01–0.29] | 0.11 | [0.07–0.17] |
| Wave 5 Math | 0.41 | [0.23–0.64] | 0.52 | [0.30–0.69] | 0.07 | [0.03–0.12] |
| Wave 6 Math | 0.34 | [0.14–0.59] | 0.52 | [0.28–0.69] | 0.14 | [0.08–0.22] |
Note: CI = 95% confidence intervals estimated in Mx.
Decomposition of Residuals
The central question of this study is whether unique genetic and/or environmental influences are significant for Math Fluency above and beyond latent Reading and Math factors. The model presented in Figure 1 tests for this explicitly by decomposing the residual variance for each measure into genetic (a), shared environmental (c), and nonshared environmental (e) sources of variance. For presentational purposes, only statistically significant residual estimates are presented in Figure 1, but confidence intervals for residual estimates and factor loadings are presented in Table 4. Nonshared environmental estimates were statistically significant for all residuals. Unlike the latent factors, nonshared environmental influences on the residuals include measurement error. Genetic sources of variance were statistically significant for Wave 5 TOWRE, Wave 5 WJ Calculation Fluency, and Wave 6 WJ Calculation Fluency, suggesting independent genetic influences for fluency residuals after accounting for the latent factors. Shared environmental influences (c) on residuals were not significant.
Table 4.
Residual Genetic, Shared Environmental, and Nonshared Environmental Loadings and Latent Factor Loadings on Wave 5 Reading, Wave 5 Math, and Wave 6 Math Measures
| Variable Name | a | CI | c | CI | e | CI | Factor Loading | CI |
|---|---|---|---|---|---|---|---|---|
| Wave 5 Reading | ||||||||
| PIAT Comp | 0.18 | [−0.35–0.35] | 0.00 | [−0.28–0.28] | 0.63 | 0.56–0.70 | 0.75 | [0.70–0.79] |
| WRMT Comp | 0.00 | [−0.32–0.32] | 0.19 | [−0.30–0.30] | 0.52 | 0.46–0.59 | 0.83 | [0.79–0.87] |
| WRMT Word ID | 0.24 | [−0.36–0.36] | 0.13 | [−0.31–0.31] | 0.32 | 0.26–0.38 | 0.91 | [0.88–0.93] |
| TOWRE | 0.46 | [0.30–0.53] | 0.00 | [−0.31–0.31] | 0.32 | 0.26–0.39 | 0.83 | [0.79–0.86] |
| Wave 5 Math | ||||||||
| WJ Calc | 0.15 | [−0.45–0.45] | 0.32 | [−0.43–0.43] | 0.50 | 0.42–0.56 | 0.79 | [0.74–0.83] |
| WJ Fluency | ||||||||
| From a1 | 0.33 | [0.23–0.51] | ||||||
| From a2 | 0.55 | [0.38–0.64] | 0.20 | [−0.30–0.30] | 0.38 | 0.33–0.43 | 0.64 | [0.57–0.70] |
| WJ Applied Prob | 0.00 | [−0.35–0.35] | 0.25 | [−0.35–0.35] | 0.49 | 0.43–0.56 | 0.83 | [0.79–0.87] |
| WJ Quantconcept | 0.37 | [−0.48–0.48] | 0.00 | [−0.39–0.39] | 0.45 | 0.37–0.55 | 0.81 | [0.76–0.85] |
| WRAT Math | 0.22 | [−0.46–0.46] | 0.26 | [−0.42–0.42] | 0.49 | 0.40–0.58 | 0.80 | [0.75–0.84] |
| Wave 6 Math | ||||||||
| WJ Calc | 0.00 | [−0.37–0.37] | 0.31 | [−0.40–0.40] | 0.46 | 0.39–0.52 | 0.83 | [0.79–0.87] |
| WJ Fluency | ||||||||
| From a1 | 0.34 | [0.24] | [0.24–0.54] | |||||
| From a2 | 0.58 | [0.40] | [0.40–0.65] | |||||
| From a3 | 0.00 | [−0.27–0.27] | 0.00 | [−0.24–0.24] | 0.35 | 0.29–0.42 | 0.65 | [0.59–0.71] |
| WJ Applied Prob | 0.00 | [−0.38–0.38] | 0.24 | [−0.34–0.34] | 0.48 | 0.39–0.56 | 0.85 | [0.80–0.88] |
| WJ Quantconcept | 0.00 | [−0.28–0.28] | 0.00 | [−0.24–0.24] | 0.57 | 0.49–0.63 | 0.82 | [0.77–0.86] |
| WRAT Math | 0.00 | [−0.41–0.41] | 0.34 | [−0.45–0.45] | 0.51 | 0.43–0.60 | 0.79 | [0.73–0.84] |
Note: PIAT = Peabody Individual Achievement Test; WRMT = Woodcock Reading Mastery Test; TOWRE = Test of Word Reading Efficiency; WJ = Woodcock–Johnson; WRAT = Wide Range Achievement Test. CI = 95% confidence intervals estimated in Mx.
We also examined whether the residual genetic effects for Reading and Math Fluency were correlated and/or independent. Genetic variance for Math Fluency was correlated with Reading Fluency both concurrently and longitudinally (indicated by significant a1 loadings in Figure 1 and Table 4). There was also evidence for independent genetic effects for Math Fluency that was stable across measurement occasions (as evidenced by a2 loadings). There was no evidence for independent genetic effects for Math Fluency at Wave 6 above and beyond Wave 5 measures, as evidenced by a loading of 0.00 on a3. Dropping the genetic overlap among residuals led to a significant decrease in fit (χ2change = 269.448, dfchange = 3, BICchange = 126.38), providing further evidence that genetic overlap among residuals is necessary to model fit.
Summary of Latent and Residual Effects on Reading and Math Fluency
Taken together, the a1 and a2 path estimates described in Figure 1 suggest that there is significant genetic overlap among Reading Fluency and Math Fluency as well as significant independent genetic variance for Math Fluency. Both a1 and a2 appear to be longitudinally stable as evidenced by significant loadings with Wave 6 Math Fluency. To provide a better measure of the magnitude of these independent effects, we present the influences of these various pathways on the total variance for Math Fluency. The total variance for Math Fluency at Waves 5 and 6 is divided into genetic (h2), shared environmental (c2), and nonshared environmental (e2) sources of variance that emanate from the latent factors plus variance from residual factors. For example, using the data from Figure 1, the heritability of Wave 5 Math Fluency was
where
| (A1) |
| (A2) |
| (a1) |
| (a2) |
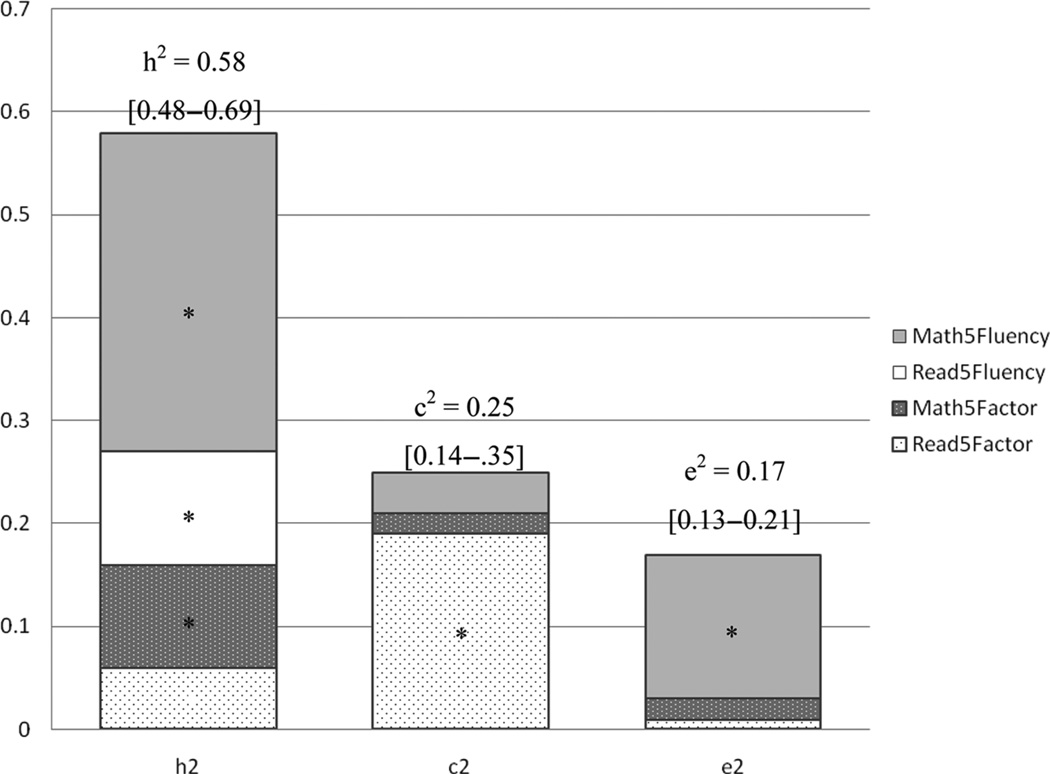
Figure 2 presents the proportion of h2, c2, and e2 of Wave 5 Math Fluency that was explained by these sources of variance along with tests of significance (using confidence intervals, as indicated by an asterisk). Results suggested small but significant genetic effects from the latent factors and reading fluency, with most of the genetic variance specific to math fluency. In contrast, shared environment (c2 = .25) was influenced by the general factor common to all reading and math measures (C1 in Figure 1). Nonshared environment (e2 = .17) was attributable mainly by variance unique to Math Fluency (as well as error). Notably, the estimates of total h2, c2, and e2 for Wave 5 Math Fluency are very similar to what would have been expected from the intraclass correlation results presented in Table 1.
Figure 2.
Proportion of genetic (h2), shared environmental (c2), and nonshared environmental (e2) variance in Wave 5 Math Fluency accounted for by Wave 5 Reading factor (Read5Factor), Math factor (Math5Factor), Reading Fluency (Read5Fluency), and Math Fluency (Math5Fluency), with 95% confidence intervals in braces
*p < .05.
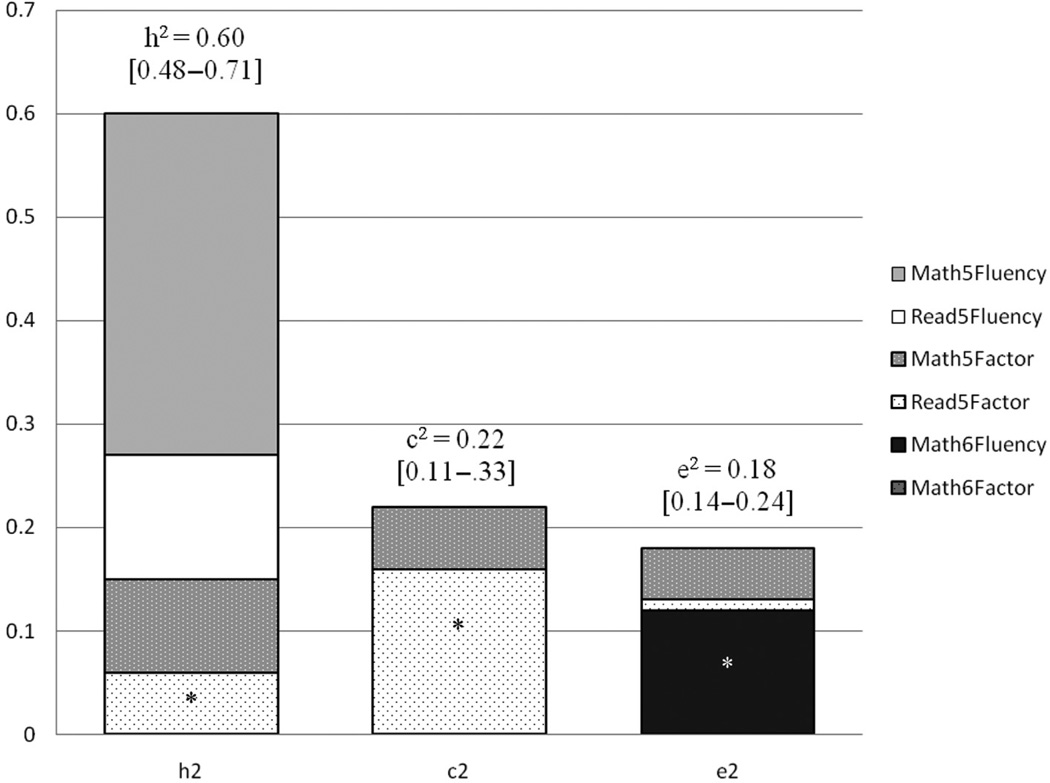
Figure 3 presents estimates for Wave 6 Math Fluency. What is important to note is that the genetic and shared environmental variance at Wave 6 was explained by measures assessed in Wave 5. The majority of the genetic variance in Math Fluency at Wave 6 was explained by genetic variance unique to Math Fluency at Wave 5, whereas most of the shared environmental variance was explained through the latent factors. Nonshared environment (and error) was influenced mostly by variance specific to Wave 6 Math Fluency.
Figure 3.
Proportion of genetic (h2), shared environmental (c2), and nonshared environmental (e2) variance in Wave 6 Math Fluency accounted for by Wave 5 Reading factor (Read5Factor), Math factor (Math5Factor), Reading Fluency (Read5Fluency), and Math Fluency (Math5Fluency), plus Wave 6 Math Fluency (Math6Fluency) residuals, with 95% confidence intervals in braces
Note: No independent variance was attributable to Wave 6 Math factor (Math6Factor).
*p < .05.
Discussion
The purpose of this study was to examine whether math fluency was genetically and/or environmentally distinct from other measures of math and reading performance. Latent factor modeling suggested that two thirds of the variance in math fluency was independent from other math measures. Most of this residual variance was affected by specific genetic influences related to math fluency, with additional genetic variance explained by reading fluency. A secondary purpose of the study was to examine if variance for math fluency was longitudinally stable in late childhood or early adolescence and, if so, if this stability was related to or independent from other math and reading measures. Independent genetic influences for math fluency overlapped completely across two annual measurement occasions, above and beyond reading fluency and untimed math measures. Thus, genetic variance for math fluency was not only etiologically distinct from other math measures but also longitudinally stable over a 1-year period.
In contrast, the majority of the shared environmental influences on math fluency were general, associated via the latent math factor with measures of reading. As was the case for the genetic influences on fluency, complete overlap across measurement occasions suggested strong longitudinal stability. Taken together, genetic effects on math fluency were largely specific, whereas shared environmental effects on math fluency were largely general. Both genetic and shared environmental effects on math fluency were longitudinally stable.
These findings are novel in the following ways. First, this study is the first longitudinal twin study to examine direct assessments of math and the first to examine math fluency. Kovas et al. (2007) employed a longitudinal genetic design in twins who were roughly the same age as our sample (7, 9, and 10 years) but employed teacher ratings. Both studies find evidence for not only significant genetic overlap between math and reading factors but also significant genetic specificity for overall math, separate from reading. Both studies also suggest high longitudinal stability. Unique to our study are significant shared environmental effects for the math factor. Aside from differences in the measurement of math, the Kovas et al. study employed a U.K. sample where there is a national math curriculum. The current study employed a U.S. sample where curricula are locally administered. Because twins attend the same schools, greater variability in the U.S. schools may be reflected in higher estimates of shared environment (see Petrill & Plomin, 2007, for a discussion).
More central to the purpose of the study, results provide strong evidence for the specificity of math fluency as a genetically distinct dimension of math performance. As described in the introduction, unselected studies of math have found that general processing speed (e.g., speed of visual matching) independently predicts computational skills (e.g., Bull & Johnston, 1997; Fuchs et al., 2008; Hecht et al., 2001), whereas studies of math disability have shown that math fluency predicts independent variance in math ability (Jordan & Hanich, 2003; Mazzocco et al., 2008). Our study replicates these findings but further suggests that math fluency, although related to other math measures, may also be influenced by a separate genetically stable component of math performance. As research continues to examine the effects of working memory, general processing speed, number sense, and math problem-solving strategies on math performance, we expect that math fluency will stand apart from these measures. We are currently conducting such a study using a twin sample and expect that independent genetic factors will be primarily responsible for the discriminant validity of math fluency.
Finally, the results of the current study have important implications for progress monitoring, education, and intervention. Timed measures are clearly an efficient means to assess academic performance (Fletcher & Vaughn, 2009), and the literature to date suggests that math fluency does indeed covary with other measures of math. Thus, math fluency does appear to be a viable screening measure. Our data further suggest that the shared environment affects math fluency through variance common to all math measures. However, math fluency also stands apart from other math measures. Our data suggest that two thirds of the variance is unique to math fluency, a large portion of which is affected by independent genetic factors that are longitudinally stable. Intervention studies have shown that math fluency is modifiable but requires different approaches compared to untimed measures (Fuchs et al., 2010). This is not surprising. Genetic influences aside, math fluency, although related to untimed math performance, is not synonymous with untimed math performance. Understanding the multidimensional aspects of math performance is necessary to develop curricula and intervention strategies that target students’ strengths and weaknesses across these domains.
Acknowledgments
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article:
This work is supported by Eunice Kennedy Shriver National Institute of Child Health and Human Development grants HD038075 and HD059215.
Biographies
Stephen Petrill is professor of human development and family science at the Ohio State University. His research interests involve the application of quantitative and molecular genetic designs to the development of math and reading ability/disability
Jessica Logan is a postdoctoral fellow at the Ohio State University. She is a methodologist with expertise in modeling the development of academic achievement.
Sara Hart is a postdoctoral fellow at Florida State University. Her interests include the cognitive underpinnings of mathematics ability and disability.
Pamela Vincent is a graduate fellow at the Ohio State University. Her interests include the development of mathematics and related environmental factors.
Lee Thompson is professor of psychology at Case Western Reserve University. Her research interests involve the genetic and environmental underpinnings of cognitive ability, and their relationship with academic achievement.
Yulia Kovas is a lecturer at the Institute of Psychiatry in London. She has conducted international studies on the genetic and environmental underpinnings of math performance.
Robert Plomin is professor and director of the Social, Genetic, and Developmental Psychiatry Research Centre, at the Institute of Psychiatry. His interests involve the application of quantitative and molecular genetic designs to understand the etiology and development of learning disabilities.
Footnotes
Declaration of Conflicting Interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
References
- Aunola K, Leskinen E, Lerkkanen M-K, Nurmi J-E. Developmental dynamics of math performance from preschool to grade 2. Journal of Educational Psychology. 2004;96:699–713. [Google Scholar]
- Bull R, Johnston RS. Children’s arithmetical difficulties: Contributions from processing speed, item identification, and short term memory. Journal of Experimental Psychology. 1997;65:1–24. doi: 10.1006/jecp.1996.2358. [DOI] [PubMed] [Google Scholar]
- Bull R, Johnston RS, Roy JA. Exploring the roles of the visual-spatial sketch pad and central executive in children’s arithmetical skills: Views from cognition and developmental neuropsychology. Developmental Neuropsychology. 1999;15:421–442. [Google Scholar]
- Butterworth B. The mathematical brain. London, UK: Macmillan; 1999. [Google Scholar]
- DiPerna JC, Lei P-W, Reid EE. Kindergarten predictors of mathematical growth in the primary grades: An investigation using the Early Childhood Longitudinal Study–Kindergarten cohort. Journal of Educational Psychology. 2007;99:369–379. [Google Scholar]
- Fletcher JM, Vaughn S. Response to intervention: Preventing and remediating academic difficulties. Child Development. 2009;3:30–37. doi: 10.1111/j.1750-8606.2008.00072.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs LS, Fuchs D, Stuebing K, Fletcher JM, Hamlett CL, Lambert W. Problem solving and computational skill: Are they shared or distinct aspects of mathematical cognition? Journal of Educational Psychology. 2008;100:30–47. doi: 10.1037/0022-0663.100.1.30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs LS, Powell SR, Seethaler PM, Fuchs D, Hamlett CL, Cirino PT, Fletcher JM. A framework for remediating the number combination deficits of students with mathematics difficulty. Exceptional Children. 2010;76:135–156. doi: 10.1177/001440291007600201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC. Mathematical disabilities: Reflections on cognitive, neuropsychological, and genetic components. Learning and Individual Differences. 2010;20:130–133. doi: 10.1016/j.lindif.2009.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Burlingham-Dubree M. External validation of the strategy choice model for addition. Journal of Experimental Child Psychology. 1989;47:175–192. [Google Scholar]
- Geary DC, Widaman KF. Individual differences in cognitive arithmetic. Journal of Experimental Psychology: General. 1987;116:154–171. doi: 10.1037//0096-3445.116.2.154. [DOI] [PubMed] [Google Scholar]
- Geary DC, Widaman KF. Numerical cognition: On the convergence of componential and psychometric models. Intelligence. 1992;16:47–80. [Google Scholar]
- Goldsmith HH. A zygosity questionnaire for young twins: A research note. Behavior Genetics. 1991;21:257–269. doi: 10.1007/BF01065819. [DOI] [PubMed] [Google Scholar]
- Hart SA, Petrill SA, Thompson LA. A factorial analysis of timed and untimed measures of mathematics and reading abilities in school aged twins. Learning and Individual Differences. 2010;20:63–69. doi: 10.1016/j.lindif.2009.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hart SA, Petrill SA, Thompson LA, Plomin R. The ABCs of math: A genetic analysis of mathematics and its links with reading ability and general cognitive ability. Journal of Educational Psychology. 2009;101:388–402. doi: 10.1037/a0015115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hecht SA, Torgesen JK, Wagner RK, Rashotte CA. The relations between phonological processing abilities and emerging individual differences in mathematical computational skills: A longitudinal study from second to fifth grades. Journal of Experimental Child Psychology. 2001;79:192–227. doi: 10.1006/jecp.2000.2586. [DOI] [PubMed] [Google Scholar]
- Jordan NC, Hanich LB. Characteristics of children with moderate mathematics deficiencies: A longitudinal perspective. Learning Disabilities Research & Practice. 2003;18:213–221. [Google Scholar]
- Kovas Y, Haworth CMA, Dale PS, Plomin R. The genetic and environmental origins of learning abilities and disabilities in the early school years. Monographs of the Society for Research in Child Development. 2007;72:1–144. doi: 10.1111/j.1540-5834.2007.00439.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landerl K, Bevan A, Butterworth B. Developmental dyscalculia and basic numerical capacities: A study of 8–9-year-old students. Cognition. 2004;93:99–125. doi: 10.1016/j.cognition.2003.11.004. [DOI] [PubMed] [Google Scholar]
- Markwardt FC. Peabody Individual Achievement Test–Revised. Bloomington, MN: Pearson Assessments; 1997. [Google Scholar]
- Mazzocco MMM, Devlin KT, McKenney SJ. Is it a fact? Timed arithmetic performance of children with mathematical learning disabilities (MLD) varies as a function of how MLD is defined. Developmental Neuropsychology. 2008;33:318–344. doi: 10.1080/87565640801982403. [DOI] [PubMed] [Google Scholar]
- National Mathematics Advisory Panel. Washington, DC: Author; 2008. Foundations for success: The final report of the National Mathematics Advisory Panel. [Google Scholar]
- Neale MC, Boker SM, Xie G, Maes HH. Mx: Statistical modeling. 7th ed. Richmond: Virginia Common-wealth University, Department of Psychiatry; 2006. [Google Scholar]
- Neale MC, Cardon LR. Methodology for genetic studies of twins and families. Dordrecht, Netherlands: Kluwer; 1992. [Google Scholar]
- Petrill SA, Deater-Deckard K, Thompson LA, DeThorne LS, Schatschneider C. Reading skills in early readers: Genetic and shared environmental influences. Journal of Learning Disabilities. 2006;39:48–55. doi: 10.1177/00222194060390010501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrill SA, Plomin R. Quantitative genetics and mathematical abilities/disabilities. In: Berch DB, Mazzocco MMM, editors. Why is math so hard for some children? The nature and origins of mathematical learning difficulties and disabilities. Baltimore, MD: Brookes; 2007. pp. 307–322. [Google Scholar]
- Plomin R, DeFries JC, McClearn GE, McGuffin P. Behavioral genetics. 5th ed. New York, NY: Worth; 2008. [Google Scholar]
- Raghubar KP, Barnes MA, Hecht SA. Working memory and mathematics: A review of developmental, individual difference, and cognitive approaches. Learning and Individual Differences. 2010;20:110–122. [Google Scholar]
- Schwarz GE. Estimating the dimension of a model. Annals of Statistics. 1978;6:461–464. [Google Scholar]
- Siegler RS. Individual differences in strategy choices: Good students, not-so-good students, and perfectionists. Child Development. 1988;59:833–851. [PubMed] [Google Scholar]
- Tolar TD, Lederberg A, Fletcher J. A structural model of algebra achievement: Computational fluency and spatial visualisation as mediators of the effect of working memory on algebra achievement. Educational Psychology. 2009;29:239–266. [Google Scholar]
- Wagner RK, Torgesen JK, Rashotte CA. Comprehensive Test of Phonological Processing. Austin, TX: Pro-Ed; 1999. [Google Scholar]
- Wilkinson GS. Wide Range Achievement Test–3. Wilmington, DE: Wide Range; 1993. [Google Scholar]
- Woodcock RW. Woodcock Reading Mastery Tests–Revised. Circle Pines, MN: American Guidance Service; 1987. [Google Scholar]
- Woodcock RW, McGraw KS, Mather N. Woodcock–Johnson III Tests of Achievement. Rolling Meadows, IL: Riverside; 2001, 2007. [Google Scholar]