Les liaisons dangereuses: Adhesion molecules do it statistically

In 1970 Jacques Monod—one of the founding fathers of molecular biology—wrote his classic text Le hasard et la nécessité (1), in which he emphasized the fundamentally different role in molecular biology of covalent chemical bonds on the one hand and polar, hydrogen, and van der Waals’ bonding on the other hand. Strong covalent bonds can be broken only by the expenditure of a significant number of ATP fuel molecules and are suitable to hold together the individual atoms of a biological macromolecule, like a protein or DNA. Weaker, noncovalent bonds can be broken by the expenditure of just a single ATP molecule and are more suitable to collectively stabilize the architecture of macromolecules or, since they are easily broken up, to be used by signaling molecules transferring information from one part of the cell to another or from one cell to another.

Can we use this classification also for larger complexes? Adhesion proteins expressed on the surface of a cell play a central role in both providing structural integrity to cells and in transferring information to a cell. For example, the successful establishment of an adhesive link between a cell and a surface by integrins initiates multiple cascades of signaling pathways that can lead to cell motion (2). The nature of the expressed adhesion molecules of a cell also can act as an address of a differentiated cell during the tissue formation of an embryo (3), while endothelial cells lining the gut and blood vessels are stapled together by rivets consisting of clusters of adhesion molecules. Finally, the recognition of “self” from “non-self” during the immune response in part involves “lock-and-key” adhesion between adhesion molecules of the white blood cells of the immune systems with partner adhesion molecules on the target cells (4).

Adhesion molecules rely on noncovalent bonds to establish contact and thus seem to fall naturally in the second group of Monod’s classification. However, it was proposed in 1978 by Bell (5) that the bonding of cellular adhesion molecules really is better considered as belonging to a separate class of bonding characterized by a “classical” adhesion potential energy. This form of bonding was investigated in the late 1930s by the great Dutch physicist H. A. Kramers and has a quite different phenomenolgy. Chemical bonds like the covalent bond are characterized by a well defined binding energy that can be computed by a direct application of the principles of quantum mechanics (or, easier, by looking it up in a table). Bonding of the Kramers type is fuzzier. Depending on the nature and the characteristic time scale of a measurement of the bonding energy, different values may be obtained (see below). It also is best described by combining the language of classical physics with statistical arguments.

Testing Bell’s hypothesis initially proved difficult, but our capability to apply and measure forces at the molecular level has since improved considerably. A range of probes such as the micropipette, the atomic force microscope, the force box, and the optical tweezer have become available. Measurements on adhesion molecules using these or related methods, like those published in the Proceedings by Pierres et al. (6) on the T cell adhesion molecule CD2 with its ligand partner CD48, lead to the conclusions that (i) measured binding energies depend on the time scale of the experiment, and (ii) a statistical distribution of bond energies is encountered rather then a precise single value. In particular, a comprehensive study by Evans and Ritchie (7) comparing the results of different force microscopy probes with the Kramers theory revealed that a specific type of probe only addresses a certain dynamic range of the adhesion bond and that none measures the equilibrium binding energy.

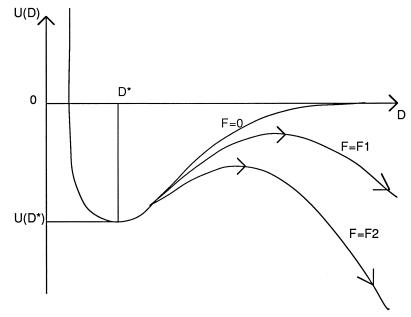
To better appreciate the mysteries of Kramers-type bonding, assume we have two cellular membranes separated by a distance D. Each membrane contains a certain number of adhesion proteins with one end embedded in the membrane. The two free ends of a receptor–ligand pair of adhesion molecules contain complementary molecular groups capable of forming one or more noncovalent bonds (typical binding energies are in the range of 10–30 k_B·T). The active groups normally are only a small part of the protein scaffold presenting the active group to the outside world. Suppose we now plot the potential energy U(D) of a complementary pair of adhesion molecules as a function of the spacing D [a procedure somewhat similar to the Eyring transition state theory of chemical reactions (8)]. The plot has a minimum at some value D*, the optimal spacing between the membranes (Fig. 1). The value −U(D*) represents the equilibrium binding energy of the active groups. As we increase the D spacing, we must increasingly deform the protein to maintain bonding. The reduced energy −U(D) is the binding energy minus the (free) energy cost of the required elastic distortion. Eventually, the deformation cost equals the chemical binding energy. For larger D, we can consider the bond as broken.

Figure 1.

Schematic representation of the potential energy U(D) of an adhesive bond as a function of the spacing D between two cell surfaces for different levels of an external force F. The minimum at D = D* represents the equilibrium spacing. For nonzero values of F, the adhesive bond can rupture by thermal activation over the maximum (arrows). The time required is longer for lower forces (F1) then for higher forces (F2).

Although useful as a visualization tool, the potential energy curve U(D) unfortunately contains the full complexity of the structure of a protein and is in general very difficult to compute ab initio. We could, however, try to probe it, using one of the new force microscopy methods, by applying a force F to the adhesive bond and measuring the value of F required to break the bond (usually in the range of 10–40 pN). But here is the rub: for every nonzero value of F we really have a new and different potential energy curve having a negative slope for large D (Fig. 1). The negative slope arises because we must subtract the work −F·D of the probe from U(D). Each of these new curves has a maximum at some D, resembling a mountain pass. The height of this pass depends on F; the smaller F the higher the pass. Once we are over the pass, though, we can roll down the slope to infinite D (i.e., the bond is broken). Suppose we now are sitting at the minimum of one of these curves, near D*, and ask whether we will be able to cross the pass. This depends on the presence of thermal fluctuations. Thermal fluctuations will allow us to hop over the pass for any F, no matter how small, provided we are prepared to wait long enough. The smaller F, the higher the pass, and the longer you have to wait. It now depends on the dynamic range of the instrument and the force level it applies (and the patience of the experimenter) when the adhesive bond can be said to be broken. Since it relies on thermal fluctuations, the outcome of the measurement also is inherently statistical in nature. There are other sources of statistical uncertainty as well: if two adhesion molecules are not quite properly lined up, the effective binding energy is less because it requires an additional elastic distortion to establish the bond.

Apart from these ambiguities, binding energies estimated using force microscopy methods can considerably exceed the true binding energy −U(D*). The reason is that the energy stored in stretching the molecules during the application of the force, which is dissipated upon fracture of the bond, would appear to be part of the binding energy (an effect well known in materials science). The real importance of force microscopy for adhesion molecules in fact is not as a measuring tool of equilibrium binding energies but rather as a window on the true dynamical and statistical nature of such links under stress or during formation. The difficulties encountered in interpreting the outcome of a force microscopy experiment also will be encountered during experiments on adhesive links between cells. Suppose we consider the force F as the force per adhesion molecule applied by one cell on another cell. To establish or break a bond, we saw that we need a time scale that depends on F. Cells in fact have a menu of adhesion molecules of various binding strength. The collective effect of such a menu could be to present a cascading pathway for adhesion: fast adhesion molecules with low binding energy for initial establishment of the bond and slower adhesion molecules firming up the bond and starting the biochemical signaling. This scenario is in fact believed to be valid for the adhesion of white blood cells to the endothelium (9). The use of microforce probes combined with the Kramers model thus may give important insights in the cooperative nature of various types of adhesion molecules.