SUMMARY
Understanding how complex phenotypes arise from individual molecules and their interactions is a primary challenge in biology that computational approaches are poised to tackle. We report a whole-cell computational model of the life cycle of the human pathogen Mycoplasma genitalium that includes all of its molecular components and their interactions. An integrative approach to modeling that combines diverse mathematics enabled the simultaneous inclusion of fundamentally different cellular processes and experimental measurements. Our whole-cell model accounts for all annotated gene functions and was validated against a broad range of data. The model provides insights into many previously unobserved cellular behaviors, including in vivo rates of protein-DNA association and an inverse relationship between the durations of DNA replication initiation and replication rates. In addition, experimental analysis directed by model predictions identified previously undetected kinetic parameters and biological functions. We conclude that comprehensive whole-cell models can be used to facilitate biological discovery.
INTRODUCTION
Computer models that can account for the integrated function of every gene in a cell have the potential to revolutionize biology and medicine, as they increasingly contribute to how we understand, discover and design biological systems (Di Ventura et al., 2006). Models of biological processes have been increasing in complexity and scope (Covert et al., 2004; Orth et al., 2011; Thiele et al., 2009), but with efforts at increased inclusiveness of genes, parameters, and molecular functions come a number of challenges..
Two critical factors in particular have hindered the construction of comprehensive, “whole-cell” computational models. First, until recently not enough has been known about the individual molecules and their interactions to completely model any one organism. The advent of genomics and other high-throughput measurement techniques have accelerated the characterization of some organisms to the extent that comprehensive modeling is now possible. For example, the mycoplasmas, a genus of bacteria with relatively small genomes that includes several pathogens, have recently been the subject of an exhaustive experimental effort by a European consortium to determine the transcriptome (Güell et al., 2009), proteome (Kuhner et al., 2009), and metabolome (Yus et al., 2009) of these organisms.
The second limiting factor has been that no single computational method is sufficient to explain complex phenotypes in terms of molecular components and their interactions. The first approaches to modeling cellular physiology, based on ordinary differential equations (ODEs) (Atlas et al., 2008; Browning et al., 2004; Castellanos et al., 2004; Castellanos et al., 2007; Domach et al., 1984; Tomita et al., 1999), were limited by the difficulty in obtaining the necessary model parameters. Subsequently, alternative approaches were developed that require fewer parameters, including Boolean network modeling (Davidson et al., 2002) and constraint-based modeling (Orth et al., 2010; Thiele et al., 2009). However, the underlying assumptions of these methods do not apply to all cellular processes and conditions, and building a whole-cell model entirely based on either method is therefore impractical.
Here, we present a “whole-cell” model of the bacterium Mycoplasma genitalium, a human urogenital parasite whose genome contains 525 genes (Fraser et al., 1995). Our model attempts to (1) describe the life cycle of a single cell from the level of individual molecules and their interactions; (2) account for the specific function of every annotated gene product; and (3) accurately predict a wide range of observable cellular behaviors.
EXPERIMENTAL PROCEDURES
Reconstruction
The whole-cell model was based on a detailed reconstruction of M. genitalium developed from over 900 primary sources, reviews, books, and databases. First, we reconstructed the organization of the chromosome including the locations of each gene, transcription unit, promoter, and protein binding site. Second, we functionally annotated each gene beginning with the CMR annotation. Functional annotation was primarily based on homologs identified by bidirectional best BLAST. To fill gaps in the reconstructed organism, and to maximize the scope of the model, we expanded and refined each gene's annotation using primary research articles and reviews (see Data S1 and Table S3). Third, we curated the structure of each gene product, including the post-transcriptional and post-translational processing and modification of each RNA and protein and the subunit composition of each protein and ribonucleoprotein complex. After annotating each gene, we categorized the genes into 28 cellular processes. We curated the chemical reactions of each cellular process. The reconstruction was stored in a MySQL relational database. See Data S1 and Table S3 for further discussion of the reconstruction.
Cellular Process Sub-models
Because biological systems are modular, cells can be modeled by (1) dividing cells into functional processes, (2) independently modeling each process on a short time scale, and (3) integrating process sub-models at longer time scales. We divided M. genitalium into the 28 functional processes illustrated in Figure 1, and modeled each process independently on a 1 s time scale using different mathematics and different experimental data. The sub-models spanned six areas of cell biology: (1) transport and metabolism, (2) DNA replication and maintenance, (3) RNA synthesis and maturation, (4) protein synthesis and maturation, (5) cytokinesis, and (6) host interaction. Sub-models were implemented as separate classes. See Data S1 for further discussion of each sub-model.
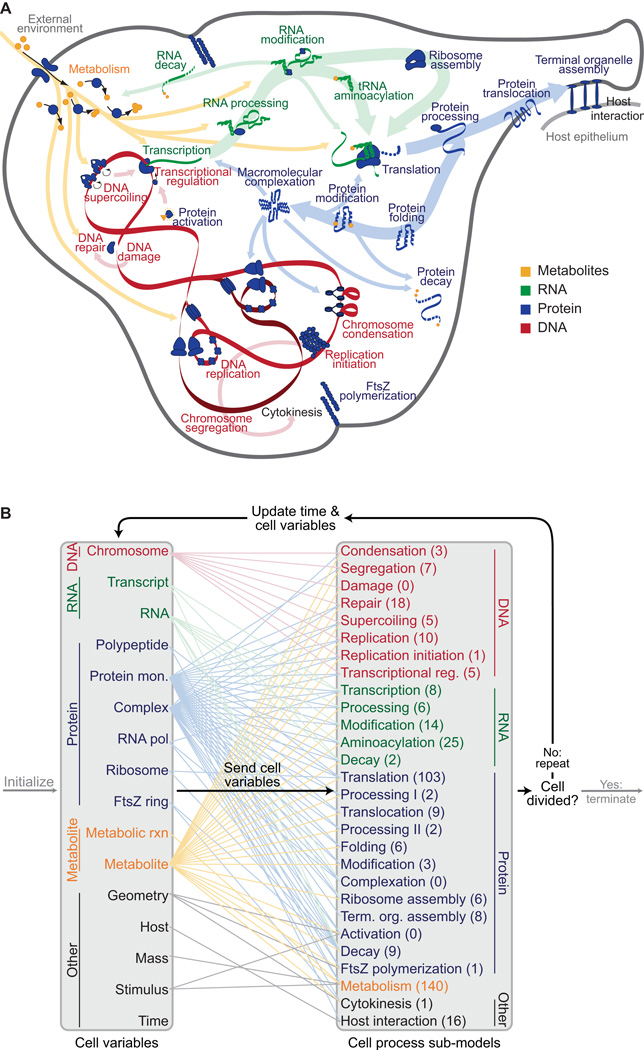
Figure 1. M. genitalium whole-cell model integrates 28 sub-models of diverse cellular processes.
(A) Diagram schematically depicts the 28 sub-models as colored words – grouped by category as metabolic (orange), RNA (green), protein (blue), and DNA (red) – in the context of a single M. genitalium cell with its characteristic flask-like shape. Sub-models are connected through common metabolites, RNA, protein, and the chromosome which are depicted as orange, green, blue, and red colored arrows, respectively.
(B) The model integrates cellular function sub-models through 16 cell state variables. First, simulations are randomly initialized to the beginning of the cell cycle (left grey arrow). Next, for each 1 s time step (dark black arrows) the sub-models retrieve the current values of the cellular variables, calculate their contributions to the temporal evolution of the cell variables, and update the values of the cellular variables. This is repeated thousands of times over the course of each simulation. For clarity, cell functions and variables are grouped into 5 physiologic categories: DNA (red), RNA (green), protein (blue), metabolite (orange), and other (black). Colored lines between the variables and sub-models indicate the cell variables predicted by each sub-model. The number of genes associated with each sub-model is indicated in parentheses. Finally, simulations are terminated upon cell division when the septum diameter equals zero (right grey arrow).
Sub-model Integration
We integrated the sub-models in three steps. First, we structurally integrated the process sub-models by linking their common inputs and outputs through 16 state variables (shown in Figure 1) which together represent the complete configuration of the modeled cell: (1) metabolite, RNA, and protein copy numbers, (2) metabolic reaction fluxes, (3) nascent DNA, RNA, and protein polymers, (4) molecular machines, (5) cell mass, volume, and shape, (6) the external environment including the host urogenital epithelium, and (7) time. Second, the common inputs to the sub-models were computationally allocated at the beginning of each time step. Third, we refined the values of the sub-model parameters to make the sub-models mutually consistent. See Data S1 for further discussion.
Simulation Algorithm
The whole-cell model is simulated using an algorithm comparable to those used to numerically integrate ODEs. First, the cell state variables are initialized. Second, the temporal evolution of the cell state is calculated on a 1 s time scale by repeatedly allocating the cell state variables among the processes, executing each of the cellular process sub-models, and updating the values of the cell state variables. Finally, the simulation terminates when either the cell divides, or the time reaches a predefined maximum value. See Data S1 for further discussion.
Single Gene Disruptions
Single-gene disruptions were modeled by (1) initializing the cell state, (2) deleting the in silico gene, and (3) calculating the temporal evolution of the cell state for the first generation post-disruption. We also calculated the mean growth rate of each single-gene disruption strain at successive generations post-disruption. See Data S1 for further discussion of the implementation of disruption strains and their computational analysis.
Computational Simulation and Analysis
We used the whole-cell model to simulate 192 wild type cells and 3,011 single-gene deletants. All simulations were performed with MATLAB R2010b on a 128 core Linux cluster. The predicted dynamics of each cell was logged at each time point and subsequently analyzed using MATLAB. See Data S1 for further discussion.
Bacterial Culture
M. genitalium wild type and mutant strains with single-gene disruptions by transposon insertion (Glass et al., 2006) were grown in Spiroplasma SP-4 culture media at 37°C and 5% CO2. Growth was detected using the phenol red pH indicator. Cells were harvested for quantitative growth measurement at pH 6.3–6.7. See Data S1 for more information about media and culture conditions.
Colorimetric Assay to Measure Cell Growth
To measure the growth rates of the wild type and mutant strains, cells were collected from 10 cm plate cultures at pH 6.3–6.7, resuspended in 3 ml of FBS, and serial filtered through 1.2, 0.8, 0.45, and 0.2 µm polyethersulfone filters to sterilize and separate individual cells. Cells were then plated at 5-, 25-, and 125-fold serial dilutions in triplicate on a 96-well plate, and incubated at 37°C and 5% CO2. Six wells per plate were filled with blank SP-4 phenol red media as a negative control. Optical density readings were taken twice a day at 550 nm to measure the decrease in phenol red color as pH decreased. Growth rate constants were calculated from the additional time required for consecutive dilutions to reach the same OD550 value, and were averaged over 2–3 independent sets of three replicates. See Data S1 for further description of these calculations. We used a heteroscedastic 2-sample 2-tailed t-test to determine whether the doubling time of each single-gene disruption strain differed significantly from that of the wild type. The growth rates of several slow growing strains were also measured by DNA quantification using a modified version of the procedure described in Glass et al., 2006. See Data S1 for further discussion.
RESULTS
Whole-cell model construction and integration
Our approach to developing an integrative whole cell model was to divide the total functionality of the cell into modules, model each independently of the others, and integrate these sub-models together. We defined 28 modules (Figure 1A) and independently built, parameterized, and tested a sub-model of each. Some biological processes have previously been studied quantitatively and in-depth, while other processes are less well-characterized or are hardly understood. Consequently, each module was modeled using the most appropriate mathematical representation. For example, metabolism was modeled using flux-balance analysis (Suthers et al., 2009) whereas RNA and protein degradation were modeled as Poisson processes.
A key challenge of the project was to integrate the 28 sub-models into a unified model. Although we and others had previously developed methods to integrate ordinary differential equations (ODEs) with Boolean, probabilistic, and/or constraint-based sub-models (Covert et al., 2001; Covert et al., 2004; Covert et al., 2008; Chandrasekaran and Price, 2010), the current effort involved so many different cellular functions and mathematical representations that a more general approach was needed. We began with the assumption that the sub-models are approximately independent on short time scales (less than one second in this work). Simulations are then performed by running through a loop in which the sub-models are run independently at each time step, but depend on the values of variables determined by the other sub-models at the previous time step. Figure 1B summarizes the simulation algorithm and the relationships between the sub-models and the cell state variables. Data S1 provides a detailed description of the complete modeling process, including reconstruction and computational implementation.
Model training and parameter reconciliation
Our model is based on a synthesis of over 900 publications and includes more than 1,900 experimentally observed parameters. Most of these parameters were implemented as originally reported. However, several other parameters were carefully reconciled; for example, the experimentally measured DNA content per cell (Morowitz et al., 1962; Morowitz, 1992) represents less than one third of the calculated mass of the mycoplasma chromosome. Data S1 details how we resolved this and several similar discrepancies among the experimentally observed parameters.
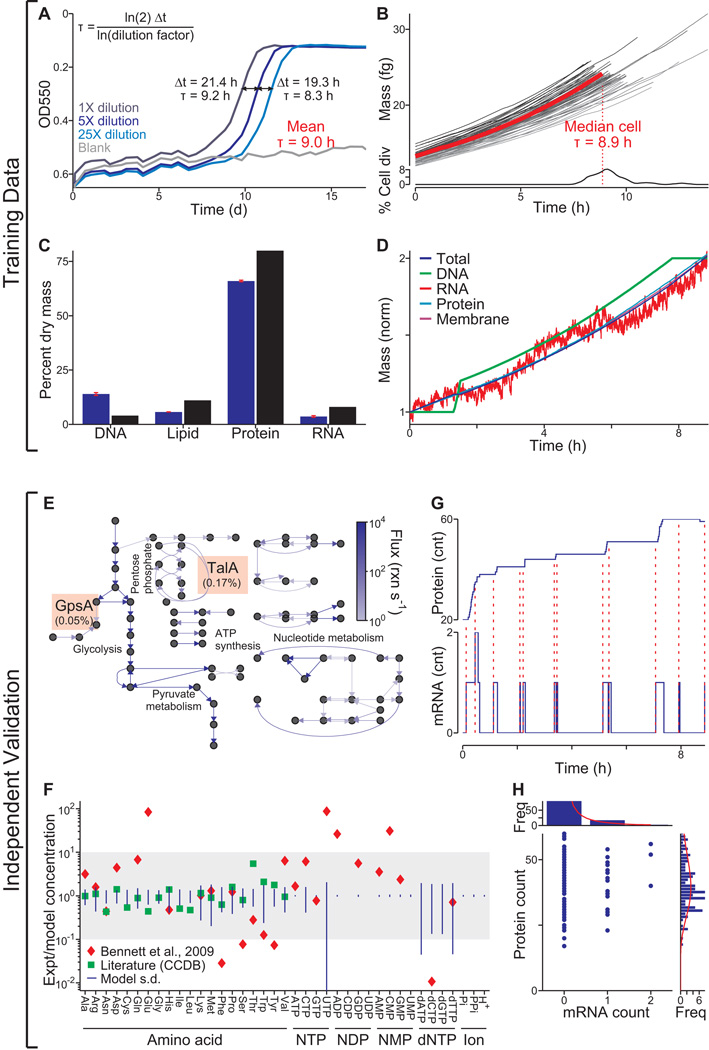
Once the model was implemented and all parameters reconciled, we verified that the model recapitulates key features of our training data. We simulated 128 wild type cells in a typical Mycoplasma culture environment, with each simulation predicting not only cellular properties such as the cell mass and growth rate, but also molecular properties including the count, localization, and activity of each molecule (Movie S1 illustrates the life cycle of one in silico cell). We found that the model calculations were consistent with the observed doubling time (Figure 2A and 2B), cellular chemical composition (Figure 2C), replication of major cell mass fractions (Figure 2D), and gene expression (R2 = 0.68; Figure S1A).
Figure 2. The model was trained with heterogeneous data and reproduces independent experimental data across multiple cellular functions and scales.
(A) Growth of three cultures (dilutions indicated by shade of blue) and a blank control measured by OD550 of the pH indicator phenol red. The doubling time, τ, was calculated using the equation at the top left from the additional time required by more dilute cultures to reach the same OD550 (black lines).
(B) Predicted growth dynamics of one life cycle of a population of 64 in silico cells (randomly chosen from the total simulation set). Median cell is highlighted in red. Distribution of cell cycle lengths is shown at bottom.
(C) Comparison of the predicted and experimentally observed (Morowitz et al., 1962) cellular chemical compositions. Red bars indicate model s.d.; Morowitz et al. did not report s.d.
(D) Temporal dynamics of the total cell mass and four cell mass fractions of a representative in silico cell. Mass fractions are normalized to their initial values.
(E) Average predicted metabolic fluxes (see Figure S1B for metabolite and reaction labels). Arrow brightness indicates flux magnitude. The ratios of the GpsA and TalA fluxes to the Glk flux are indicated in orange boxes and are comparable to experimental data (Yus et al., 2009).
(F) Ratios of observed (Sundararaj et al., 2004; Bennett et al., 2009) and average predicted concentrations of 39 metabolites.
(G) Temporal dynamics of cytadherence high molecular weight protein 2 (HMW2, MG218) mRNA and protein expression of one in silico cell. Red dashed lines indicate the direct link between mRNA synthesis and subsequent bursts in protein synthesis.
(H) HMW2 mRNA and protein copy number distribution of an unsynchronized population of 128 in silico cells. Histograms indicate the marginal distributions of the copy numbers of mRNA (top) and protein (right). Red lines indicate log-normal regressions of these marginal distributions. The absence of correlation between the copy numbers of mRNA and protein and the shapes of the marginal distributions are consistent with recent single-cell measurements by Taniguchi et al., 2010.
Model validation against independent experimental data
Next, we validated the model against a broad range of independent datasets that were not used to construct the model and which encompass multiple biological functions – metabolomics, transcriptomics, and proteomics – and scales, from single cells to populations. In agreement with earlier reports (Yus et al., 2009), the model predicts that the flux through glycolysis is >100-fold more than that through the pentose phosphate and lipid biosynthesis pathways (Figure 2E). Furthermore, the predicted metabolite concentrations are within an order of magnitude of concentrations measured in Escherichia coli for 100% of the metabolites in one compilation of data (Sundararaj et al., 2004) and for 70% in a more recent high-throughput study (Bennett et al., 2009; Figure 2F). Our model also predicts “burst-like” protein synthesis due to the local effect of intermittent mRNA expression and the global effect of stochastic protein degradation on the availability of free amino acids for translation, comparable to recent reports by Yu et al., 2006 and So et al., 2011 (Figure 2G). The mRNA and protein level distributions predicted by our model are also consistent with recently reported single-cell measurements (Figure 2H, compare to Taniguichi et al., 2010). Taking all of these specific tests of the model's predictions together, we concluded that our model recapitulates experimental data across multiple biological functions and scales.
Prediction of DNA binding protein interactions
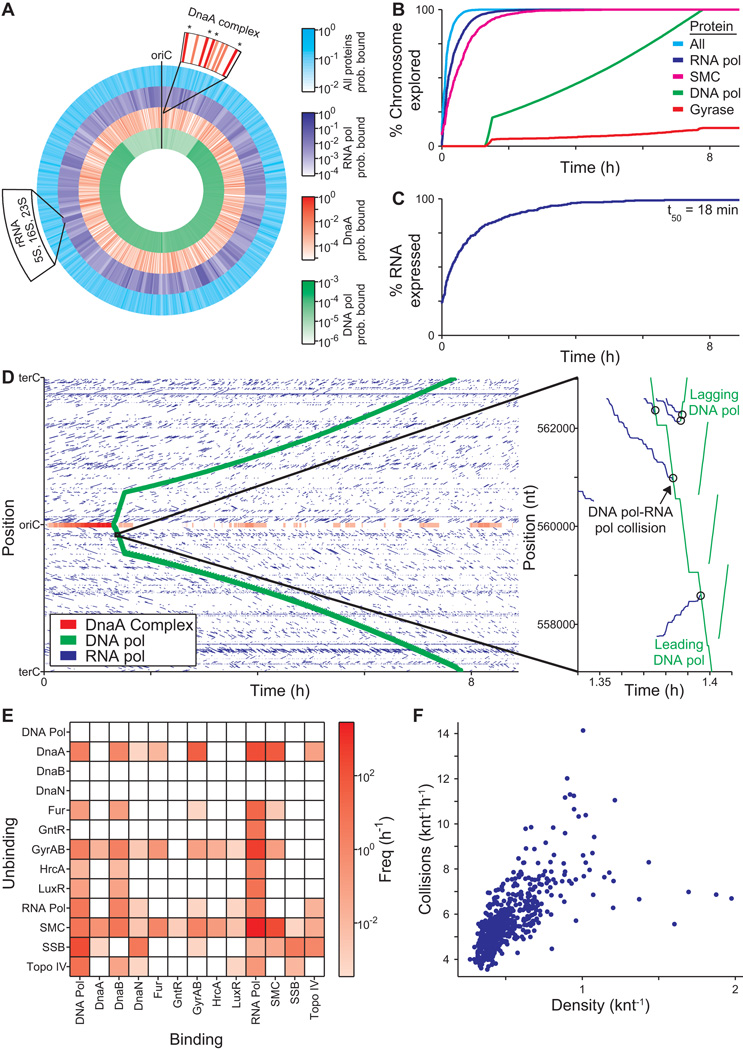
Models are often used to predict molecular interactions that are difficult or prohibitive to investigate experimentally, and our model offers the opportunity to make such predictions in the context of the entire cell. Whereas previous studies have either focused on the genomic distribution of DNA-binding proteins (Vora et al., 2009) or on the detailed diffusion dynamics of specific DNA-binding proteins (Bratton et al., 2011), the whole-cell model can predict both the instantaneous protein chromosomal occupancy as well as the temporal dynamics and interactions of every DNA-binding protein at the genomic scale at single-cell resolution. Figure 3A illustrates the average predicted chromosomal protein occupancy, as well as the predicted chromosomal occupancies for DNA and RNA polymerase and the replication initiator DnaA, three of the 30 DNA binding proteins represented by our model. Consistent with a recent experimental study by Vora et al., 2009, the predicted high-occupancy RNA polymerase regions correspond to highly transcribed rRNAs and tRNAs. In contrast, the predicted DNA polymerase chromosomal occupancy is significantly lower and biased toward the terC (see below for further discussion).
Figure 3. The model highlights the central physiologic role of DNA-protein interactions.
(A) Average density of all DNA-bound proteins and of the replication initiation protein DnaA and DNA and RNA polymerase of a population of 128 in silico cells. Top magnification indicates the average density of DnaA at several sites near the oriC; DnaA forms a large multimeric complex at the sites indicated with asterisks, recruiting DNA polymerase to the oriC to initiate replication. Bottom left label indicates the location of the highly expressed rRNA genes.
(B and C) Percentage of the chromosome that is predicted to have been bound (B), and the number of genes that are predicted to have been expressed (C) as functions of time. SMC is an abbreviated name for the name of the chromosome partition protein (MG298).
(D) DNA-binding and dissociation dynamics of the oriC DnaA complex (red) and of RNA (blue) and DNA (green) polymerases for one in silico cell. The oriC DnaA complex recruits DNA polymerase to the oriC to initiate replication, which in turn dissolves the oriC DnaA complex. RNA polymerase traces (blue line segments) indicate individual transcription events. The height, length, and slope of each trace represent the transcript length, transcription duration, and transcript elongation rate, respectively. Inset highlights several predicted collisions between DNA and RNA polymerases leading to the displacement of RNA polymerases and incomplete transcripts.
The model further predicts that the chromosome is explored very rapidly, with 50% of the chromosome having been bound by at least one protein within the first 6 min of the cell cycle, and 90% within the first 20 min (Figure 3B). RNA polymerase contributes the most to chromosomal exploration, binding 90% of the chromosome within the first 49 min of the cell cycle. On average, this results in expression of 90% of genes within the first 143 min (Figure 3C), with transcription lagging RNA polymerase exploration due to the significant contribution of non-specific RNA polymerase-DNA interactions to RNA polymerase diffusion (Harada et al., 1999).
The model also predicts protein-protein collisions on the chromosome. Previous researchers have studied the collisions of pairs of specific proteins (Pomerantz and O’Donnell, 2010), but experimentally determining the collisions among all pairs of DNA-binding proteins at the genomic scale at single-cell resolution is currently infeasible. Our model predicts that over 30,000 collisions occur on average per cell cycle, leading to the displacement of 0.93 proteins per second. Figure 3D illustrates the binding dynamics of the same proteins depicted in Figure 3A over the course of the cell cycle for one representative simulation, and highlights several protein-protein collisions. Further categorization of the predicted collisions by chromosomal location indicates that the flux of protein-protein collisions correlates strongly with DNA-bound protein density (Figure 3F), and that the majority of collisions are caused by RNA polymerase (84%) and DNA polymerase (8%), most commonly resulting in the displacement of Structural Maintenance of Chromosome (SMC) proteins (70%), or single-stranded binding proteins (6%) (Figure 3E and Table S2F).
Identification of metabolism as an emergent cell cycle regulator
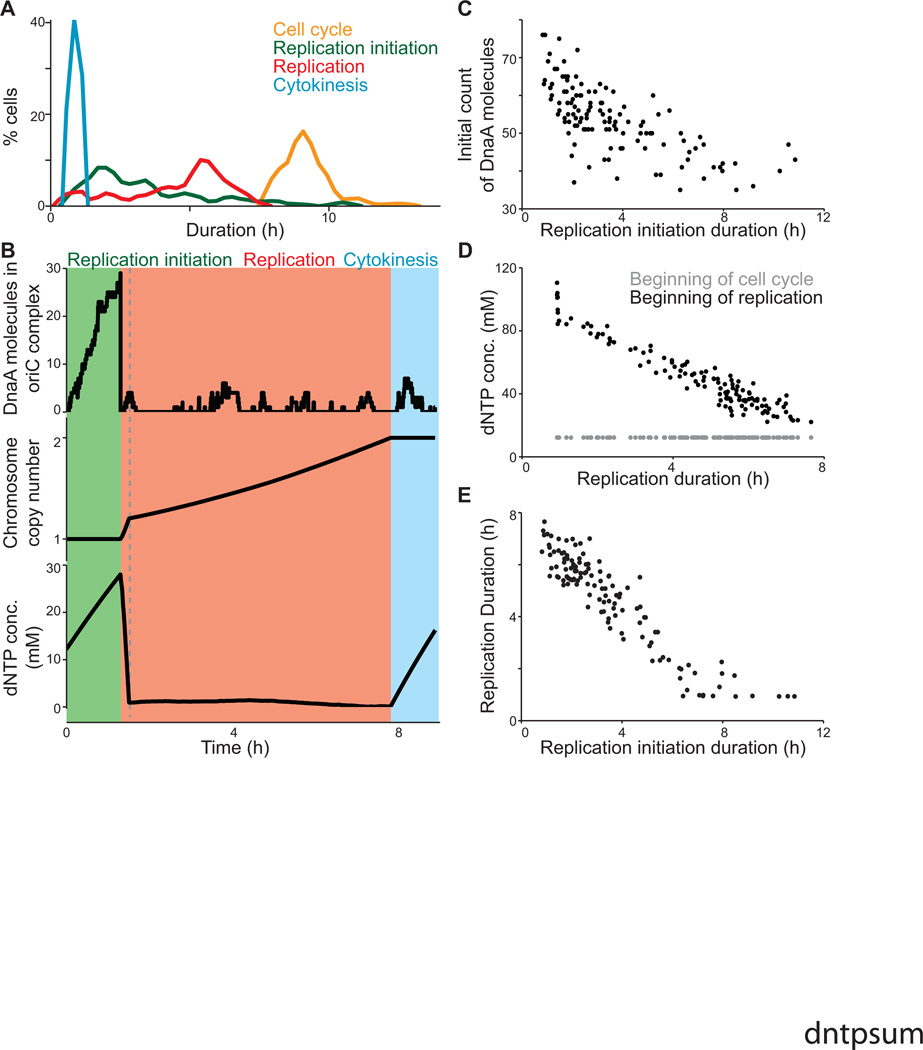
The model can also highlight interesting aspects of cell behavior. In reviewing our model simulations, we noticed variability in the cell cycle duration (Figure 2B), and wanted to determine the source of that variability. The model representation of the M. genitalium cell cycle consists of three stages: replication initiation, replication itself, and cytokinesis. We found that there was relatively more cell-to-cell variation in the durations of the replication initiation (64.3%) and replication (38.5%) stages than in cytokinesis (4.4%) or the overall cell cycle (9.4%; Figure 4A). This data raised two questions: (1) what is the source of duration variability in the initiation and replication phases, and (2) why is the overall cell cycle duration less varied than either of these phases?
Figure 4. The model predictions regarding regulation of the cell cycle duration.
(A) Distributions of the duration of three cell cycle phases, as well as that of the total cell cycle length, across 128 simulations.
(B) Dynamics of macromolecule abundance in a selected cell simulation: top, the size of the DnaA complex assembling at the OriC (in monomers of DnaA); middle, the copy number of the chromosome; and bottom, the cytosolic dNTP concentration. The quantities of these macromolecules correlate strongly with the timing of key cell cycle stages.
(C) Correlation between the initial cellular DnaA content and the duration of the replication initiation cell cycle stage across the same 128 in silico cells depicted in (A).
(D) Correlation between the dNTP concentrations (both at the beginning of the cell cycle and at the beginning of replication) and the duration of replication across the same 128 in silico cells depicted in (A).
(E) Correlation between the duration of replication initiation and replication across the same 128 in silico cells depicted in (A).
With respect to the first question, replication initiation occurs as DnaA protein monomers bind or unbind stochastically and cooperatively to form a multimeric complex at the replication origin (Figure 4B, top) (Browning et al., 2004). When the complex is complete, DNA polymerase gains access to the origin and the complex is displaced. We found a correlation (R2 = 0.49) between the predicted duration of replication initiation and the initial number of free DnaA monomers (Figure 4C); however, the somewhat low correlation indicated that the duration depends on more than the initial conditions. In particular, we observed that the stochastic aspect of the transcription and translation sub-models creates variability in the number of new DnaA monomers produced over time, as well as the DnaA binding and unbinding events themselves. This indicates that the variability in replication initiation duration depends not only on variability in initial conditions, but also in the simulation itself.
As to the second question, because the replication sub-model is substantially more deterministic than the initiation sub-model, we expected to find a straightforward relationship between the progress of replication and the cell cycle. Instead, the model predicts that DNA replication proceeds at two distinct rates during the cell cycle. This is reflected in the motion and DNA-binding density of DNA polymerase (Figure 3A and 3D), and in the dynamics of DNA synthesis as compared to the synthesis of other macromolecules (Figure 4B, middle). Initially replication proceeds quickly, due to the free dNTP content in the cell (Figure 4B, bottom). When DNA polymerase initially binds to the replication origin, dNTPs are abundant and replication can proceed unimpeded. When the dNTP pool is exhausted, however, the rate of replication slows to the rate of dNTP synthesis. Accordingly, the duration of the replication phase in individual cells is more closely related to the free dNTP content at the start of replication than to the dNTP content at the start of the cell cycle (Figure 4D).
This change in the availability of dNTPs imposes a control on the cell cycle duration. Specifically, the duration of the initiation and replication phases are inversely related to each other in single cells (Figure 4E), such that longer initiation times led to shorter replication times. This occurs because cells that require extra time to initiate replication also build up a large dNTP surplus, leading to faster replication. This interplay buffers against the high variability in the duration of replication initiation, giving rise to substantially less variability in the length of the cell cycle. The whole-cell model therefore presents a novel hypothesis of an emergent control of cell-cycle duration that is independent of genetic regulation.
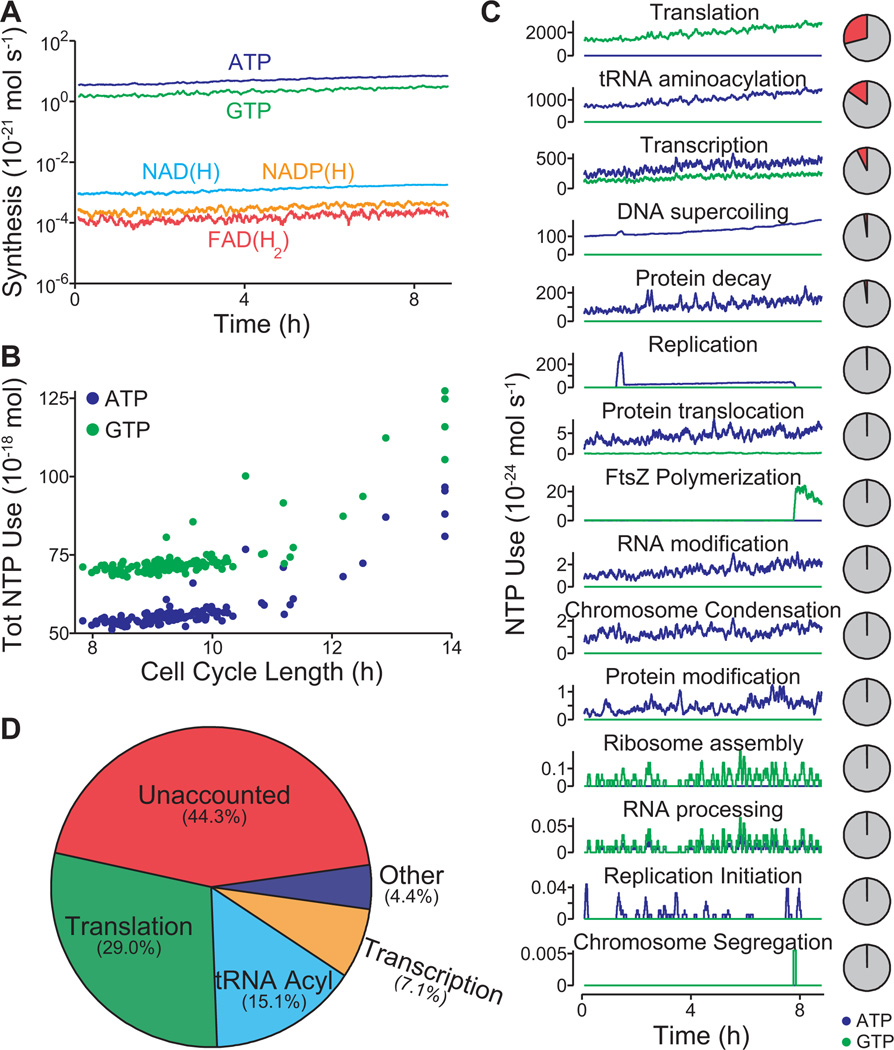
Global distribution of energy
The model also provided an opportunity to develop a quantitative assessment of cellular energetics, which represents one of the most connected aspects of our model. To begin, we investigated the synthesis dynamics of the high energy intermediates ATP, GTP, FAD(H2), NAD(H), and NADP(H), and found that ATP and GTP are synthesized at rates over 1,000-fold higher than the others (Figure 5A). Notably, the overall usage of ATP and GTP did not vary considerably in all but the very slowest of our simulations (Figure 5B), underscoring the role of metabolism in controlling the cell cycle length. We then considered the processes that use ATP and GTP, and found that usage is dominated by production of mRNA and protein (Figure 5C). We also found a large (44%) discrepancy between total energy usage and production (Figure 5D). Others have noted an uncoupling between catabolism and anabolism, attributing the difference to factors such as varying maintenance costs or energy spilling via futile cycles (Russell et al., 1995), and the model’s prediction estimates the total energy cost of such uncoupling.
Figure 5. Model provides a global analysis of the use and allocation of energy.
(A) Intracellular concentrations of the energy carriers ATP, GTP, FAD(H2), NAD(H), and NADP(H) of one in silico cell.
(B) Comparison of the cell cycle length and total ATP and GTP usage of 128 in silico cells.
(C) ATP (blue) and GTP (green) usage of 15 cellular processes throughout the life cycle of one in silico cell. The pie charts at right denote the percentage of ATP and GTP usage (red) as a fraction of total usage. (D) Average distribution of ATP and GTP usage among all modeled cellular processes in a population of 128 in silico cells. In total, the modeled processes account for only 44.3% of the amount of energy that has been experimentally observed to be produced during cellular growth.
Determining the molecular pathologies of single-gene disruption phenotypes
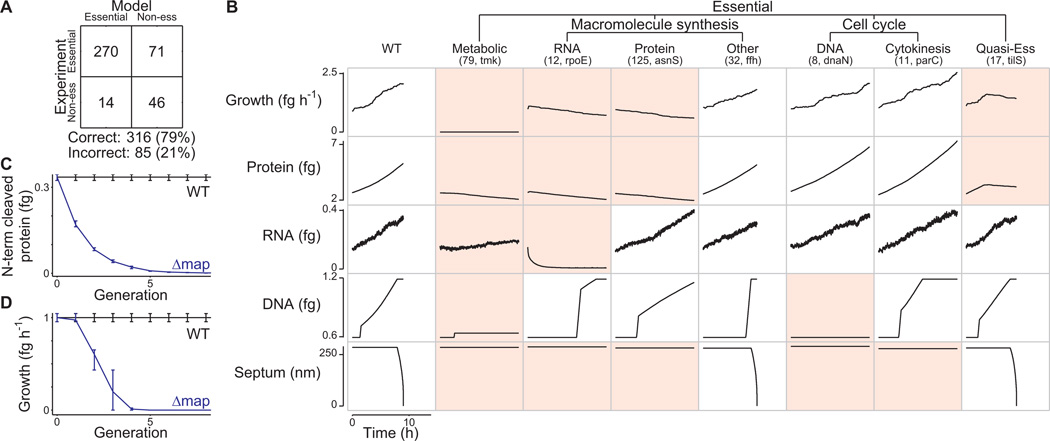
Having considered these above-described model predictions for the wild type M. genitalium strain, we next performed in silico genome perturbations to gain insight into the genetic requirements of cellular life. We performed multiple simulations of each of the 525 possible single-gene disruption strains (over 3,000 total simulations), and found that 284 genes are essential to sustain M. genitalium growth and division, and 117 are non-essential. The model accounts for previously observed gene essentiality with 79% accuracy (P < 10−7; Glass et al., 2006; Figure 6A).
Figure 6. Model identifies common molecular pathologies underlying single-gene disruption phenotypes.
(A) Comparison of predicted and observed (Glass et al., 2006) gene essentiality. Model predictions are based on at least five simulations of each single-gene disruption strain; see Data S1 for details.
(B) Single-gene disruption strains were grouped into phenotypic classes (columns) according to their capacity to grow, synthesize protein, RNA, and DNA, and divide (indicated by septum length). Each column depicts the temporal dynamics of one representative in silico cell of each essential disruption strain class. Disruption strains of non-essential genes are not shown. Dynamics significantly different from wild type are highlighted in red. The identity of the representative cell and the number of disruption strains in each category is indicated in parenthesis.
(C and D) Degradation and dilution of N-terminal protein content (C) of methionine aminopeptidase (map, MG172) disrupted cells causes reduced growth (D). Blue and black lines indicate the map disruption and wild type strains, respectively. Horizontal bars indicate s.d.
See also Figure S2 for the distribution of simulated growth rates.
In cases where the model prediction agrees with the experimental outcome with respect to gene essentiality, we found that a deeper examination of the simulation can generate insight into why the gene product is required by the system. We examined the capacities of the 525 simulated gene disruption strains to produce major biomass components (RNA, DNA, protein, lipid) and to divide. As shown in Figure 6B, the non-viable strains were unable to adequately perform one or more of these major functions. The most debilitating disruptions involved metabolic genes and resulted in the inability to produce any of the major cell mass components. The next most debilitating gene disruptions impacted the synthesis of a specific cell mass component such as RNA or protein. Interestingly, in these cases the model predicted an initial phase of near-normal growth followed by decreasing growth due to diminishing protein content. In some cases (Figure 6B, fifth column), the time required for the levels of specific proteins to fall to lethal levels was greater than one generation (Figure 6C and 6D). A third class of lethal gene disruptions impaired cell cycle processes. For these, the model predicted normal growth rates and metabolism, but incapacity to complete the cell cycle. The remaining lethal gene disruption strains grew so slowly compared to wild type that they were considered non-viable (Figure 6B, Figure S2). We conclude that the model can be used to classify cellular phenotypes by their underlying molecular interactions.
Model-driven biological discovery
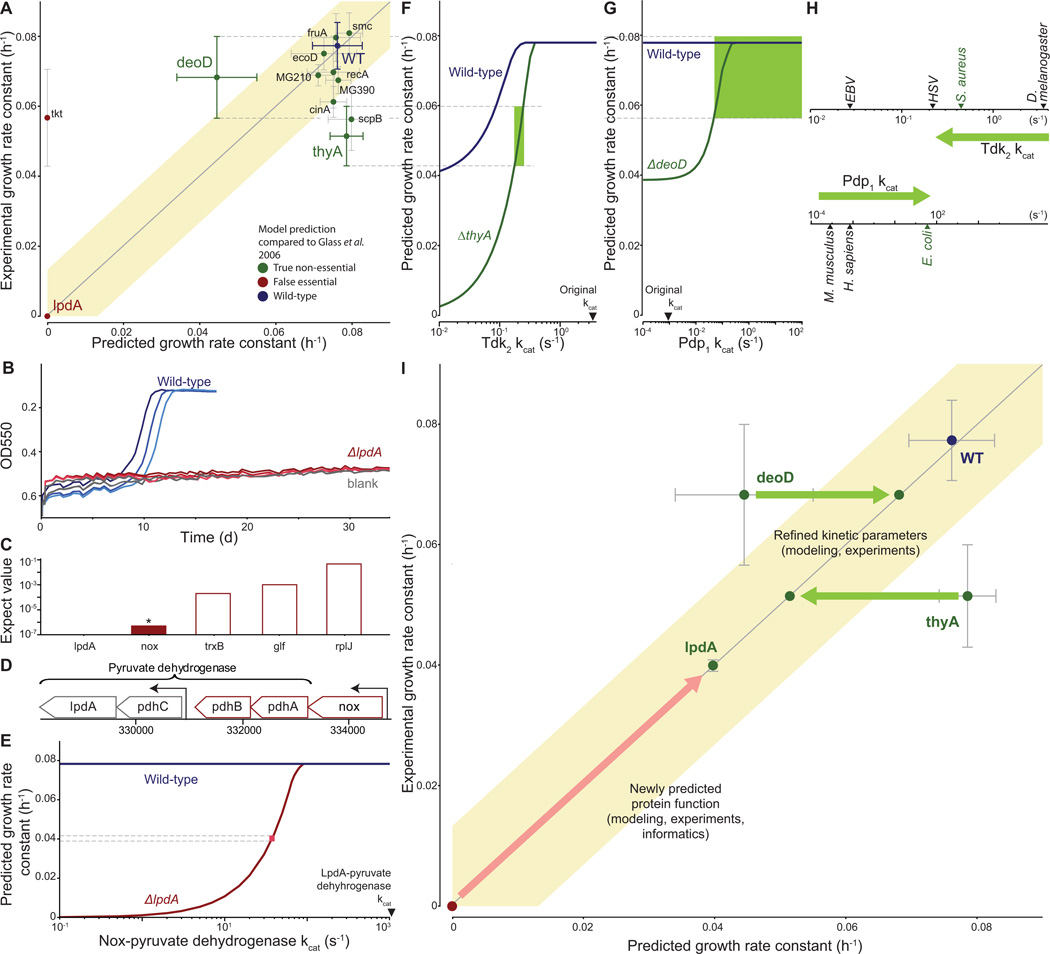
Using computational modeling as a complement to an experimental program has previously been shown to facilitate biological discovery (Di Ventura et al., 2006). This is often accomplished by reconciling model predictions that are initially inconsistent with observations (Covert et al., 2004). To test the utility of the whole-cell model in this context, we experimentally measured the growth rates of twelve single-gene disruption strains – ten of which were correctly predicted to be viable and two of which that were incorrectly predicted to be nonviable – for comparison to our models' predictions (Figure 7A). We found that two-thirds of the predictions were consistent with the measured growth rates.
Figure 7. Quantitative characterization of selected gene disruption strains leads to identification of novel gene functions and kinetic parameters.
(A) Comparison of measured and predicted growth rates for wild type and 12 single-gene disrupted strains. Model predictions that fall within the shaded region were considered consistent with experimental observations; the region has a width of four times the standard deviation of the wild type strain growth measurement. Error bars represent s.d.
(B) Growth curves for the wild type and lpdA gene disruption strains and blank; similar to Figure 2A.
(C) Expectation values determined by performing a pBLAST search of the M. genitalium genome with the LpdA sequence as a query. The asterisk and colored bar indicate a significant match (E < 10−6).
(D) Detail of the M. genitalium genome. The pyruvate dehydrogenase complex genes are indicated by the top bracket, and transcription units identified in M. pneumoniae (Güell et al., 2009) are indicated by arrows. The transcription unit including nox is highlighted in color.
(E) Allowing Nox to partially replace LpdA in pyruvate dehydrogenase reconciles model predictions and experimental observations. The blue and red lines represent the predicted wild type and ΔlpdA strain growth rates as a function of the Nox-pyruvate dehydrogenase kcat. The pink box indicates the kcat at which the model predictions are consistent with both the wild type and ΔlpdA strain experimentally measured growth rates.
(F and G) Diagnosing the discrepancy between predictions and experiment for the thyA (F) and deoD (G) gene disruption strains. Some of the functionalities of ThyA and DeoD can be replaced by the enzymes Tdk and Pdp, respectively. The predicted growth rates of the wild type and gene disruption strains depend on the kcat of these enzymes. The green region highlights the range of kcat values consistent with the measured growth rates of both the wild type and gene disruption strain.
(H) Newly predicted kcat values are similar to values that were measured in closely related organisms. Measured values of kcat for Tdk (top) and Pdp (bottom) are shown; green arrow indicates the initial and revised kcat values. The nearest M. genitalium relative is highlighted in green.
(I) Model-based biological discovery. Comparison of model predictions to experimental measurements identified gene disruption strains of particular interest, including the lpdA, deoD and thyA disruption strains. Further investigation – using a combination of experiments, modeling and/or informatics – led to new and more consistent measurements and predictions. Most importantly, the higher consistency reflected novel insights into M. genitalium biology. The arrows (red for lpdA, green for deoD and thyA) indicate the shift from lower to higher consistency between model and experiment, and each arrow is annotated with the new biological insight and the supporting evidence in parentheses. The overall graph format is the same as Figure 7A.
The most interesting of these comparisons concerned the lpdA disruption strain. The lpdA gene was originally determined to be non-essential (Glass et al., 2006). Consequently, we initially classified the model’s prediction as false (Figure 6A). However, we did not detect growth using our colorimetric assay (Figure 7B), a discrepancy that warranted further investigation. An alternative method to determine the doubling time yielded a value that was 40% lower than the wild type (Table S1). Taken together, the data suggested that disrupting the lpdA gene had a severe, but non-critical impact on cell growth.
In an effort to resolve the discrepancy between our model and the experimental measurements, we determined the molecular pathology of the lpdA disruption strain. The lpdA gene product is part of the pyruvate dehydrogenase complex, which catalyzes the transfer of electrons to NAD as a subset of the overall pyruvate dehydrogenase chemical reaction (de Kok et al., 1998). The viability of the lpdA disruption strain suggests that this reaction could be catalyzed by another enzyme with a lower catalytic efficiency.
Since previous studies have shown that many M. genitalium genes are multi-functional (Pollack et al., 2002; Cordwell et al., 1997), we searched the genome for candidates encoding an alternative NAD electron transfer pathway. We found that the Nox sequence was far more similar to the LpdA sequence than any other gene product in the genome, with 61% coverage, 25% identity, and an expectation value less than 10−6 (Figure 7C). Furthermore, the nox gene product, NADH oxidase, has been shown to oxidize NAD (Schmidt et al., 1986). Moreover, the nox locus falls in a sub-operon that contains two other pyruvate dehydrogenase genes and has been shown to be coexpressed with pdhA (Guell et al., 2009) (Figure 7D), strongly suggesting a functional relationship between the products of these two genes. Our model suggests that to reproduce the observed growth rate in the absence of lpdA, the hypothetical Nox-dependent reaction would require a kcat of approximately 50 s−1 (Figure 7E), which represents only approximately 5% of the maximum throughput of this enzyme. We therefore concluded that substrate promiscuity of Nox is likely to enable the lpdA disruption strain to survive.
Four gene disruption strains exhibited growth rates that were quantitatively different than those predicted by the model (Figure 7A); of these, we used the complete simulations for the thyA and deoD strains to determine the underlying pathology of the respective gene disruptions. The thyA gene product catalyzes dTMP production and can be complemented by the tdk gene product. We therefore hypothesized that by reducing the kcat value for Tdk in the model we would see a reduction in the growth rate of the tdk disruption strain. Reducing the Tdk kcat in the model did indeed reduce the predicted growth rate of the thyA strain, but it also affected the wild type growth rate (Figure 7F). Only a small range of the kcat values both reduced the thyA strain growth rate to the experimentally observed levels and was also consistent with the wild type growth rate.
In a similar case, DeoD catalyzes the conversion of deoxyadenosine to adenine and D-ribose-1-phosphate; these products can also be produced by the pdp gene product from deoxyuridine. We identified a Pdp kcat range for which the wild type and deoD gene disruption strains produce the same growth rate (Figure 7G).
Significantly, these newly predicted kcat values are consistent with previously reported values. In the original model reconstruction, to least constrain the metabolic model, we conservatively set each of these kcats to the least restrictive value found during the reconstruction process. For Tdk and Pdp, these values corresponded to distantly related organisms; however, the newly predicted kcat values are consistent with reports from more closely related species (Figure 7H).
In each of these three cases (lpdA, deoD, thyA), identifying a discrepancy between model predictions and experimental measurements led to further analysis which resolved the discrepancy, and also provided novel insight into M. genitalium biology (Figure 7I). These results support the assertion that large-scale modeling can be used to support biological discovery (Kitano, 2002; Brenner, 2010).
DISCUSSION
We have developed a comprehensive, whole-cell model that accounts for all of the annotated gene functions identified in M. genitalium and explains a variety of emergent behaviors in terms of molecular interactions. Our model accurately recapitulates a broad set of experimental data, provides insight into several biological processes for which experimental assessment is not readily feasible, and enables the rapid identification of novel gene functions as well as specific cellular parameters.
In contemplating these results, we make two observations based on comparing this work in whole-cell modeling with earlier work in whole genome sequencing. First, similar to the first reports of the human genome sequence, the model presented here is a "first draft", and extensive effort is required before the model can be considered complete. Of course, much of this effort will be experimental – for example, further characterization of gene products – but the technical and modeling aspects of this study will also have to be expanded, updated and improved as new knowledge comes to light.
Second, in whole genome sequencing as well as whole-cell modeling, M. genitialium was a focus of initial studies, primarily because of its small genome size. The goal of our modeling efforts, as well as that of early sequencing projects, was to develop the technology in a reduced system before proceeding to more complex organisms. However, M. genitalium presents many challenges with regard to experimental tractability. Resistance to most antibiotics, the lack of a chemically defined medium, and a cell size that requires advanced microscopy techniques for visualization, all greatly limit the range of experimental techniques available to study this organism. As a result, much of the data used to build and validate the model was obtained from other organisms. Therefore, while the results we report suggest several new experiments that could yield important new insight with respect to M. genitalium function, comprehensive validation of our approach will require modeling more experimentally tractable organisms such as E. coli.
We are optimistic that whole-cell models will accelerate biological discovery and bioengineering by facilitating experimental design and interpretation. Moreover, these findings, in combination with the recent de novo synthesis of the M. genitalium chromosome and successful genome transplantation of Mycoplasma genomes to produce a synthetic cell (Gibson et al., 2008; Gibson et al., 2010; Lartigue et al., 2007; Lartigue et al., 2009), raise the exciting possibility of using whole-cell models to enable computer-aided rational design of novel microorganisms. Finally, we anticipate that the construction of whole cell models, and the iterative testing of them against experimental information, will enable the scientific community to assess how well we understand integrated cellular systems.
Supplementary Material
HIGHLIGHTS.
Entire organisms can be modeled in terms of their molecular components
Complex phenotypes can be modeled by integrating cell processes into a single model
Whole-cell models can provide novel insights into unmeasured cellular behaviors
Whole-cell models can be used to facilitate biological discovery
ACKNOWLEDGEMENTS
We thank R. Altman, S. Brenner, Z. Bryant, J. Ferrell, K. Huang, B. Palsson, S. Quake, L. Serrano, J. Swartz, E. Yus and the Covert Lab for numerous enlightening discussions on bacterial physiology and computational modeling; T. Vora for critical reading of the manuscript; M. O'Reilly and J. Maynard for graphical design assistance. This work was supported by an NIH Director’s Pioneer Award (1DP1OD006413) and a Hellman Faculty Scholarship to M.W.C.; NSF and Bio-X Graduate Student Fellowships to J.C.S.; NDSEG, NSF, and Stanford Graduate Student Fellowships to J.R.K.; a Benchmark Stanford Graduate Fellowship to D.N.M.; and a U.S. Department of Energy Cooperative Agreement (No. DE-FC02-02ER63453) to the J. Craig Venter Institute.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
ACCESSION NUMBERS
The model source code, training data, and results are freely available at SimTK (http://www.simtk.org/home/wholecell).
SUPPLEMENTAL INFORMATION
Supplemental Information includes an inventory file, two figures, three tables, one movie, and one data file, and can be found with this article online.
REFERENCES
- Atlas JC, Nikolaev EV, Browning ST, Shuler ML. Incorporating genome-wide DNA sequence information into a dynamic whole-cell model of Escherichia coli: application to DNA replication. IET Syst. Biol. 2008;2:369–382. doi: 10.1049/iet-syb:20070079. [DOI] [PubMed] [Google Scholar]
- Bennett BD, Kimball EH, Gao M, Osterhout R, Van Dien SJ, Rabinowitz JD. Absolute metabolite concentrations and implied enzyme active site occupancy in Escherichia coli. Nat. Chem. Biol. 2009;5:593–599. doi: 10.1038/nchembio.186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bratton BP, Mooney RA, Weisshaar JC. Spatial Distribution and Diffusive Motion of RNA Polymerase in Live Escherichia coli. J. Bacteriol. 2011;193:5138–5146. doi: 10.1128/JB.00198-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenner S. Sequences and consequences. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2010;365:207–212. doi: 10.1098/rstb.2009.0221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browning ST, Castellanos M, Shuler ML. Robust control of initiation of prokaryotic chromosome replication: essential considerations for a minimal cell. Biotechnol. Bioeng. 2004;88:575–584. doi: 10.1002/bit.20223. [DOI] [PubMed] [Google Scholar]
- Chandrasekaran S, Price ND. Probabilistic integrative modeling of genome-scale metabolic and regulatory networks in Escherichia coli and Mycobacterium tuberculosis. Proc. Natl. Acad. Sci. U S A. 2010;107:17845–17850. doi: 10.1073/pnas.1005139107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Covert MW, Schilling CH, Palsson BO. Regulation of gene expression in flux balance models of metabolism. J. Theor. Biol. 2001;213:73–88. doi: 10.1006/jtbi.2001.2405. [DOI] [PubMed] [Google Scholar]
- Covert MW, Knight EM, Reed JL, Herrgard MJ, Palsson BO. Integrating high-throughput and computational data elucidates bacterial networks. Nature. 2004;429:92–96. doi: 10.1038/nature02456. [DOI] [PubMed] [Google Scholar]
- Covert MW, Xiao N, Chen TJ, Karr JR. Integrating metabolic, transcriptional regulatory and signal transduction models in Escherichia coli. Bioinformatics. 2008;24:2044–2050. doi: 10.1093/bioinformatics/btn352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castellanos M, Kushiro K, Lai SK, Shuler ML. A genomically/chemically complete module for synthesis of lipid membrane in a minimal cell. Biotechnol. Bioeng. 2007;97:397–409. doi: 10.1002/bit.21251. [DOI] [PubMed] [Google Scholar]
- Castellanos M, Wilson DB, Shuler ML. A modular minimal cell model: purine and pyrimidine transport and metabolism. Proc. Natl. Acad. Sci. USA. 2004;101:6681–6686. doi: 10.1073/pnas.0400962101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordwell SJ, Basseal DJ, Pollack JD, Humphery-Smith I. Malate/lactate dehydrogenase in mollicutes: evidence for a multienzyme protein. Gene. 1997;195:113–120. doi: 10.1016/s0378-1119(97)00063-2. [DOI] [PubMed] [Google Scholar]
- Davidson EH, Rast JP, Oliveri P, Ransick A, Calestani C, Yuh CH, Minokawa T, Amore G, Hinman V, Arenas-Mena C, et al. A genomic regulatory network for development. Science. 2002;295:1669–1678. doi: 10.1126/science.1069883. [DOI] [PubMed] [Google Scholar]
- de Kok A, Hengeveld AF, Martin A, Westphal AH. The pyruvate dehydrogenase multi-enzyme complex from Gram-negative bacteria. Biochim. Biophys. Acta. 1998;1385:353–366. doi: 10.1016/s0167-4838(98)00079-x. [DOI] [PubMed] [Google Scholar]
- Di Ventura B, Lemerle C, Michalodimitrakis K, Serrano L. From in vivo to in silico biology and back. Nature. 2006;443:527–533. doi: 10.1038/nature05127. [DOI] [PubMed] [Google Scholar]
- Domach MM, Leung SK, Cahn RE, Cocks GG, Shuler ML. Computer model for glucose-limited growth of a single cell of Escherichia coli B/r-A. Biotechnol. Bioeng. 2004;26:1140. doi: 10.1002/bit.260260925. [DOI] [PubMed] [Google Scholar]
- Fraser CM, Gocayne JD, White O, Adams MD, Clayton RA, Fleishmann RD, Bult CJ, Kerlavage AR, Sutton G, Kelley JM, et al. The minimal gene complement of Mycoplasma genitalium. Science. 1995;270:397–403. doi: 10.1126/science.270.5235.397. [DOI] [PubMed] [Google Scholar]
- Gibson DG, Benders GA, Andrews-Pfannkoch C, Denisova EA, Baden-Tillson H, Zaveri J, Stockwell TB, Brownley A, Thomas DW, Algire MA, et al. Complete chemical synthesis, assembly, and cloning of a Mycoplasma genitalium genome. Science. 2008;319:1215–1220. doi: 10.1126/science.1151721. [DOI] [PubMed] [Google Scholar]
- Gibson DG, Glass JI, Lartigue C, Noskov VN, Chuang RY, Algire MA, Benders GA, Montague MG, Ma L, Moodie MM, et al. Creation of a bacterial cell controlled by a chemically synthesized genome. Science. 2010;329:52–56. doi: 10.1126/science.1190719. [DOI] [PubMed] [Google Scholar]
- Glass JI, Assad-Garcia N, Alperovich N, Yooseph S, Lewis MR, Maruf M, Hutchison CA, 3rd, Smith HO, Venter JC. Essential genes of a minimal bacterium. Proc. Natl. Acad. Sci. USA. 2006;103:425–430. doi: 10.1073/pnas.0510013103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Güell M, van Noort V, Yus E, Chen WH, Leigh-Bell J, Michaelodimitrakis K, Yamada T, Arumugam M, Doerks T, Kuhner S, et al. Transcriptome complexity in a genome-reduced bacterium. Science. 2009;326:1268–1271. doi: 10.1126/science.1176951. [DOI] [PubMed] [Google Scholar]
- Hanawalt PC, Donahue BA, Sweder KS. Repair and Transcription: Collision or collusion? Curr. Biol. 2004;4:518–521. doi: 10.1016/s0960-9822(00)00112-3. [DOI] [PubMed] [Google Scholar]
- Harada Y, Funatsu T, Murakami K, Nonoyama Y, Ishihama A, Yanagida T. Single-molecule imaging of RNA polymerase-DNA interactions in real time. Biophys. J. 1999;76:709–715. doi: 10.1016/S0006-3495(99)77237-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lartigue C, Glass JI, Alperovich N, Pieper R, Parmar PP, Hutchison CA, 3rd, Smith HO, Venter JC. Genome transplantation in bacteria: changing one species to another. Science. 2007;317:632–638. doi: 10.1126/science.1144622. [DOI] [PubMed] [Google Scholar]
- Lartigue C, Vashee S, Algire MA, Chuang RY, Benders GA, Ma L, Noskov VN, Denisova EA, Gibson DG, Assad-Garcia N, et al. Creating bacterial strains from genomes that have been cloned and engineered in yeast. Science. 2009;325:1693–1696. doi: 10.1126/science.1173759. [DOI] [PubMed] [Google Scholar]
- Kitano H. Systems biology: a brief overview. Science. 2002;295:1662–1664. doi: 10.1126/science.1069492. [DOI] [PubMed] [Google Scholar]
- Kuhner S, van Noort V, Betts MJ, Leo-Macias A, Batisse C, Rode M, Yamada T, Maier T, Bader S, Beltran-Alvarez P, et al. Proteome organization in a genome-reduced bacterium. Science. 2009;326:1235–1240. doi: 10.1126/science.1176343. [DOI] [PubMed] [Google Scholar]
- Morowitz HJ, Tourtellotte ME, Guild WR, Castro E, Woese C. The chemical composition and submicroscopic morphology of Mycoplasma gallisepticum Avian PPLO 5969. J Mol. Biol. 1962;4:93–103. doi: 10.1016/s0022-2836(62)80041-2. [DOI] [PubMed] [Google Scholar]
- Morowitz HJ. Beginnings of cellular life: metabolism recapitulates biogenesis. New Haven and London: Yale University Press; 1992. [Google Scholar]
- Orth JD, Thiele I, Palsson BO. What is flux balance analysis? Nat. Biotechnol. 2010;28:245–248. doi: 10.1038/nbt.1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orth JD, Conrad TM, Na J, Lerman JA, Nam H, Feist AM, Palsson BO. A comprehensive genome-scale reconstruction of Escherichia coli metabolism--2011. Mol. Syst. Biol. 2011;7:535. doi: 10.1038/msb.2011.65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollack JD, Myers MA, Dandekar T, Herrmann R. Suspected utility of enzymes with multiple activities in the small genome Mycoplasma species: the replacement of the missing “household” nucleoside diphosphate kinase gene and activity by glycolytic kinases. OMICS. 2002;6:247–258. doi: 10.1089/15362310260256909. [DOI] [PubMed] [Google Scholar]
- Pomerantz RT, O'Donnell M. Direct Restart of a Replication Fork Stalled by a Head-On RNA Polymerase. Science. 2010;327:590–592. doi: 10.1126/science.1179595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell JB, Cook GM. Energetics of bacterial growth: balance of anabolic and catabolic reactions. Microbiol. Rev. 1995;59:48–62. doi: 10.1128/mr.59.1.48-62.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saeki H, Svejstrup JQ. Stability, Flexibility, and Dynamic Interactions of Colliding RNA Polymerase II Elongation Complexes. Mol. Cell. 2009;35:191–205. doi: 10.1016/j.molcel.2009.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt HL, Stocklein W, Danzer J, Kirch P, Limbach B. Isolation and properties of an H2O-forming NADH oxidase from Streptococcus faecalis. Eur. J. Biochem. 1986;156:149. doi: 10.1111/j.1432-1033.1986.tb09560.x. [DOI] [PubMed] [Google Scholar]
- So LH, Ghosh A, Zong C, Sepulveda LA, Segev R, Golding I. General properties of transcriptional time series in Escherichia coli. Nat. Genet. 2011;43:554–560. doi: 10.1038/ng.821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sundararaj S, Guo A, Habibi-Nazhad B, Rouani M, Stothard P, Ellison M, Wishart DS. The CyberCell Database (CCDB): a comprehensive, self-updating, relational database to coordinate and facilitate in silico modeling of Escherichia coli. Nucleic Acids Res. 2004;32:D293–D295. doi: 10.1093/nar/gkh108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suthers PF, Dasika MS, Kumar VS, Denisov G, Glass JI, Maranas CD. A genome-scale metabolic model of Mycoplasma genitalium iPS189. PLoS Comput. Bio. 2009;5 doi: 10.1371/journal.pcbi.1000285. e1000285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taniguchi Y, Choi PJ, Li GW, Chen H, Babu M, Hearn J, Emili A, Xie XS. Quantifying E. coli proteome and transcriptome with single-molecule sensitivity in single cells. Science. 2010;329:533–538. doi: 10.1126/science.1188308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thiele I, Jamshidi N, Fleming RM, Palsson BO. Genome-scale reconstruction of Escherichia coli's transcriptional and translational machinery: a knowledge base, its mathematical formulation, and its functional characterization. PLoS Comput. Biol. 2009;5 doi: 10.1371/journal.pcbi.1000312. e1000312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomita M, Hashimoto K, Takahashi K, Shimizu TS, Matsuzaki Y, Miyoshi F, Saito K, Tanida S, Yugi K, Venter JC, et al. E-CELL: software environment for whole-cell simulation. Bioinformatics. 1999;15:72–84. doi: 10.1093/bioinformatics/15.1.72. [DOI] [PubMed] [Google Scholar]
- Vora T, Hottes AK, Tavazoie S. Protein occupancy landscape of a bacterial genome. Mol. Cell. 2009;35:247–253. doi: 10.1016/j.molcel.2009.06.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu J, Xiao J, Ren X, Lao K, Xie XS. Probing gene expression in live cells, one protein molecule at a time. Science. 2006;311:1600–1603. doi: 10.1126/science.1119623. [DOI] [PubMed] [Google Scholar]
- Yus E, Maier T, Michalodimitrakis K, van Noort V, Yamada T, Chen WH, Wodke JA, Guell M, Martinez S, Bourgeouis R, et al. Impact of genome reduction on bacterial metabolism and its regulation. Science. 2009;326:1263–1268. doi: 10.1126/science.1177263. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.