Intravoxel Incoherent Motion (IVIM) MR Imaging for Prostate Cancer: An Evaluation of Perfusion Fraction and Diffusion Coefficient Derived from Different b-Value Combinations

Introduction

Prostate cancer is the second most common cancer in American men; approximately one in six men will be diagnosed with prostate cancer during his lifetime (1). Currently, the definitive diagnosis of prostate cancer depends on histologic confirmation by prostate biopsy or surgery. Compared to conventional blind and random biopsies, Magnetic Resonance (MR) image-guided biopsies of suspicious lesions were shown with increased accuracy and yield (2). Clearly, the key to the success of this targeted biopsy is that MR images should have higher sensitivity and specificity in identifing suspicious lesions. To this end, an advanced multi-parametric (MP) MR imaging paradigm is normally employed to obtain both anatomical and functional images in order to increase the accuarcy of lesions’ detection (3).

Diffusion weighted (DW) imaging is an integral part of MP-MRI acquisition protocol. Normally, the apparent diffusion coefficient (ADC) of water molecules within living tissues is derived analytically from diffusion images with an assumption that the water molecular diffusion is a random process (4), i.e. the chance of a particular molecule diffusing from one location to another in a given time interval is solely determined by a probability distribution function, and this function has a Gaussian line-shape with its width proportional to the diffusion coefficient. This type of diffusion is also known as Gaussian diffusion characterized by a simple mono-exponential decay model.

However, the measured diffusion signals in biological tissues were not always well characterized with this simple function. Le Bihan et al. (5) demonstrated that blood microcirculation in capillary network (perfusion) was capable of altering diffusion signal intensities at very low b-values, and the intravoxel incoherent motion (IVIM) theory was proposed to account for molecular diffusion driven by thermal energy as well as perfusion-based pseudo-diffusion. On the other extreme, the water molecular diffusion in the brain and prostate would also depart from a mono-exponential function at very high b-values (6–10). It was believed that the presence of different barriers in cellular complex structures (e.g. cell membranes and organelle compartments) led to the departure from Gaussian diffusion. To quantify this non-Gaussian diffusion process, diffusion kurtosis MR imaging was developed in which the diffusion signal (in natural logarithm) was represented by a quadratic function, instead of a simple linear function for Gaussian diffusion (11).

In recent years, there has been a renewed interest in IVIM on body parts other than the brain (12–19), thanks to improved MR hardware. In particular, three studies (14–16) reported that diffusion coefficients (D) were decreased in prostate tumors compared to benign tissues, which was consistent with the literature (20); however, perfusion fractions (f) were unexpectedly lower in tumors, which is contrary to what has been known from DCE studies and angiogenesis in tumors (21–22). In these studies, the highest b-values up to 800 s/mm² were used; and diffusion was modeled as a Gaussian diffusion. It was well documented that the deviation from Gaussian diffusion manifested in the form of a bi-exponential (i.e. fast and slow) diffusion model when using an extended range of b-values from 200 to 3000 s/mm² in previous prostate DW studies (6–7). It is clinically relevant to obtain both diffusion and perfusion information simultaneously in an IVIM study; specifically, the perfusion information could be derived without the need for intravenous contrast media, which is especially relevant in patients with compromised renal function or severe allergies who cannot receive intravenous gadolinium-based contrast media (23). However, it is unclear what maximal b-values should be used to obtain unbiased IVIM measurements, in which the contributions from non-Gaussian diffusion are negligible. Thus, we investigated the applicability of IVIM parameters based on different combinations of five b-values (0, 188, 375, 563 and 750 s/mm²) obtained from DW-MR images during MP-MRI prostate studies. The measurements and simulation produced results with significantly increased f and significantly reduced D in tumors compared to benign tissues, provided that the highest b-value (750 s/mm²) was excluded from analysis.

Theory

According to the original IVIM theory (5), the measured diffusion signal S(b), under the influence of a diffusion sensitizing gradient (with a gradient weighting factor of b), is attenuated by two different physical processes, i.e. molecular diffusion and pseudo-diffusion. The pseudo-diffusion coefficient (D*) was reportedly at least one magnitude larger than D; hence, pseudo-diffusion is only significant at very low b-values. Given that a minimum low b-value is above a threshold such that the pseudo-diffusion contribution is negligible, the measured diffusion signal should follow a simple mono-exponential decay if the b-values used in the measurement are increased. But, this is not observed in reality; the departure of diffusion signal from a mono-exponential decay is observed at very high b-values, and can be characterized with diffusion kurtosis MR imaging (11). If this non-Gaussian diffusion is incorporated in the original IVIM theory, S(b) will be rewritten as in Eq. [1].

$$S(b)=S_0\left\{\left(1-f\right)\text{exp}(-\alpha )+f\text{exp}(-\alpha -\beta )\right\}$$ [1]

Where S₀ is the signal intensity without diffusion weighting; f is the fractional signal originating from the pseudo-diffusion; α is equal to bD - b²D²K/6, with diffusion kurtosis of K; and β is equal to bD*. If K set to zero, Eq. [1] will revert to the original IVIM equation. In the current study, the minimal non-zero b-value was 188 s/mm²; so, the contribution from pseudo-diffusion to the total measured signal will be less than 0.1%, if D, K, D* and f are set to the reported values (6, 16) in Table 2. Therefore, the simplified equation Eq. [2] will be acceptable for current data analysis.

$$S(b)\approx S_0\left(1-f\right)\text{exp}(-\alpha )$$ [2]

Table 2.

Diffusion and Perfusion Parameters for IVIM Simulations

	Normal	Tumor
D (10−3 mm2/s)	2.24	1.00
K	0.61	1.47
D* (10−3 mm2/s)	20.0	25.0
f (%)	3.0	6.0

Note. Gaussian diffusion model with K set to zero. Based on Eq. 22 and 23 in the Ref. [11], the values of D and K were converted from three parameters in a two-compartment diffusion model from the Ref. [6]. D* was taken from the Ref. [16].

Based on previous IVIM studies on the brain (5, 24), f was very small so that the higher power series in Taylor expansion of the natural logarithm of (1-f) could drop out. Accordingly, after an equation rearrangement, Eq. [2] becomes a quadratic function in a semi-logarithm plot of S(b) vs. b as shown in Eq. [3].

$$\text{ln}\left(S(b)/S_0\right)\approx -f-bD+b^2{D}^{2}K/6$$ [3]

Furthermore, if the maximum high b-value is chosen below a threshold such that the non-Gaussian diffusion is insignificant, Eq. [3] will become a simple linear function as in Eq. [4], where the straight line’s slope is D and the y-intercept is f (25).

$$\text{ln}\left(S(b)/S_0\right)\approx -f-bD$$ [4]

Material and Methods

Patients

This study was approved by the local institutional review board (IRB) and was compliant with the Health Insurance Portability and Accountability Act (HIPAA); informed consent was obtained from each patient. The study population consisted of 33 patients (mean age of 61.6 years ranging between 53 and 81 years; mean prostate-specific antigen (PSA) of 10 ng/dl ranging between 1.32 and 45 ng/dl) who underwent dual coil MRI of the prostate and subsequently had MR-TRUS fusion biopsies of each lesion. Each lesion was characterized by its Gleason Score (GS), and its malignancy was defined as either high grade (GS > 4+3, N=16) or low grade (GS < 3+4, N=17).

MR Acquisition Protocols

All measurements on patients were performed on a Philips Achieva 3.0-T MRI scanner equipped with a high-performance Quasar Dual gradient system. Following three orthogonal (axial/coronal/sagital) high-resolution T2-weighted turbo spin-echo scans, DW-MRI and DCE-MRI were acquired sequentially on the same axial orientation with a combination of 16-channel SENSE Cardiac Coil and an Endorectal Coil (Medrad, Indianola, PA).

The following parameters were used in DW-MRI, i.e., a single-shot spin-echo echo-planar imaging (EPI) sequence, repetition time and echo time of 4584 and 59 ms, field of view (AP/RL/FH) of 160 / 180 / 60 mm, 20 image slices, a reconstructed voxel size of 0.55*0.55*3.00 mm³ (from acquired 1.25*1.25*3.00 mm³), a maximum gradient strength of 80 mT/m (with gradient overplus on), five different diffusion weighting gradient factors (b-values = 0, 188, 375, 563,750 s/mm²), the number of signal averages (NSA) of 4 or 8 (for b-values of 563,750 s/mm²), a parallel imaging (SENSitivity Encoding [SENSE]) factor of 2 (along the phase encoding [RL] direction) and an over-sampling factor of 2 to avoid fold-over artifacts, a partial Fourier EPI scan factor of 0.73, and spectrally (adiabatic) selective attenuated inversion recovery (SPAIR) for fat suppression. The total scan time for DW-MRI was 5.9 minutes.

Sequentially, a T1-weighted (T1W) DCE-MRI was performed including a pre-contrast scan (with a flip-angle of 5°) and a dynamic scan (with a flip-angle of 15°) after a single-dose injection of gadopentetate dimeglumine (Magnevist; Berlex, Wayne, NJ) at a dose of 0.1 mmol/kg through a peripheral vein at a rate of 3 mL/sec via a mechanical injector (Spectris MR Injection System; Medrad). The temporal resolution of the dynamic scans was either 3 or 5.6 seconds, and final total scan time was kept within 5 minutes. FOV (AP/RL/FH) was 262 / 262 / 60 mm, the voxel size was 1.02*1.02*6 mm³, TR and TE were the shortest possible, and NSA was 10 and 2 for the pre-contrast and the dynamic scans, respectively.

MR Image Analysis

Based on findings in T2W, DW and DCE images, two regions of interest (ROIs) were defined on each patient’s DW images acquired with the highest b-value, i.e., one in tumors in the peripheral zone (PZ) and the other in contra-lateral normal tissues. All data analyses were performed on ROI-based measurements. Four different combinations of b-values (tabulated in Table 1) were used to generate IVIM parameters, where D was obtained using non-zero b-values in Eq. [4], and f was derived from the measured S₀ as well as the extrapolated S₀*(1-f) signal values at b-value of zero. Specifically, D was obtained either by solving two independent linear equations (Group 1–3 in Table 1) or by non-linear least-squares curve fittings (Group 4 in Table 1).

Table 1.

IVIM Measured Parameters in Normal and Tumor Tissues Using Various b-Values

Group	b-values (s/mm2)	f (%)			D (10−3 mm2/s)
		Normal	Tumor	t-Test	Normal	Tumor	t-Test
1	0, 188, 375	3.1 ± 2.3	6.6 ± 3.1	p < 0.05	1.83 ± 0.36	1.04 ± 0.32	p < 0.05
2	0, 375, 563	7.0 ± 4.5	8.2 ± 5.4	p = 0.09	1.73 ± 0.35	0.99 ± 0.28	p < 0.05
3	0, 563, 750	13.4 ± 7.1	13.4 ± 9.5	p = 0.90	1.60 ± 0.39	0.88 ± 0.35	p < 0.05
4	0, 188, 375, 563	3.9 ± 2.4	7.0 ± 2.7	p < 0.05	1.79 ± 0.35	1.02 ± 0.29	p < 0.05

Note. Data are means ± standard deviations. Perfusion fractions (f) are in percentages.

An extended Tofts pharmacokinetic model (26) was used to fit DCE-MRI parameters on the same ROIs used to analyze the DW images. In particular, an efficient matrix-based computation algorithm was implemented for this model (27), from which the contrast volume transfer constant (K^trans), the fractional volume of extravascular-extracellular space (v_e), and the fractional volume of blood plasma (v_p) were derived. Additionally, a special population-averaged arterial input function (AIF) and a pre-contrast T1 map were included in data modeling. In contrast to a previous representative AIF (28), the blood inflow effect and B1 field inhomogeneity were largely suppressed and corrected in the current AIF (29). The intrinsic T1 map of tissues was generated using a conventional dual flip-angle method (30).

All image visualization and analysis was performed on in-house software developed in IDL 6.3 (ITT Visual Information Solutions, Boulder, CO), where the robust non-linear least-squares curve fittings based on the Levenberg-Marquardt algorithm were performed with a publically available IDL routine MPFIT (31).

Statistical Analysis

All measurements are shown as mean ± standard deviation (SD), and D and f with different b-values from 33 patients are tabulated in Table 1. For comparison, DCE and IVIM-derived parameters (Group 4 in Table 1) are listed in Table 4 where the descriptive statistics are based on 31 subjects as two patients did not undergo successful DCE-MRI.

Table 4.

Measured IVIM and DCE Parameters in Normal and Tumor Tissues

Parameters	Normal	Tumor	t-Test
D (10−3 mm2/s)	1.76 ± 0.35	0.99 ± 0.29	p < 0.05
f (%)	3.7% ± 1.9%	7.2% ± 2.6%	p < 0.05
Ktrans (min−1)	0.18 ± 0.10	0.39 ± 0.22	p < 0.05
ve (%)	26% ± 11%	32% ± 14%	p < 0.05
vp (%)	3.4% ± 2.6%	8.4% ± 6.6%	p < 0.05

Note. IVIM parameters were fitted without the b-value of 750 s/mm² (see Group 4 in Table 1). Data are means ± standard deviations (from 31 subjects), and f, v_e, and v_p are in percentages.

A Student’s paired t-test with a two-tail distribution was used to evaluate the difference between normal and tumor tissues for each measure; and the statistical significance was considered at p < 0.05. Scatter plots were used to show a correlation between two parameters; beyond that, an error (or data) ellipse (with 95% confidence level) was also included to highlight data clustering in two dimensions (32). The centroid position, area and orientation of the ellipse were determined by the means, the standard deviations and the correlation coefficient of the two parameters, respectively. Generally, the area of an ellipse could be considered as a figure of merit for data compactness.

IVIM Simulation

The Monte Carlo simulations aimed to fully understand the experimental findings; hence, simulated diffusion signals were generated at the same five b-values used in the study based on Eq. [1] with and without non-Gaussian diffusion. The model parameters obtained from the literature were different for normal and tumor tissues as seen in Table 2. To estimate the measurement errors induced by random noise, Gaussian noise with a mean of zero and a standard deviation of 0.01 was added to the simulated signals resulting in the signal to noise (SNR) ratio of 100, assuming that the simulated signal was one at a b-value of zero. The measurement of unbiased SNR in MR diffusion images was complicated by both the inhomogeneous spatial (due to the parallel imaging) and non-Gaussian statistical noise distributions (33). Nonetheless, we estimated the measured SNR using the noise (σ_mean) determined by the mean of pixel values within an ROI located at the center of the perfluorocarbon-inflated Endorectal coil (see Fig 2a), and the signal (S_mean) determined by the mean of the signals within tissue ROIs. These SNR (S_mean/σ_mean) measurements were performed at b=0 images from 11 subjects, resulting in the values (mean ± SD) of 173±118 and 95±70 in normal and tumor tissues, respectively. Given the large variability in the obtained SNR levels, we chose the value of 100 as the best guess of the unbiased SNR and used it in all simulations. In order to simulate realistic MR data with Rician noise, the sum of the simulated signal and Gaussian noise was forced to the positive value. Each simulation was performed 1000 runs, and the means and the standard deviations of 1000 simulated D and f values were calculated. Finally, the results containing Rician noise were tabulated in Table 3 and plotted in Fig. 4.

Fig. 2.

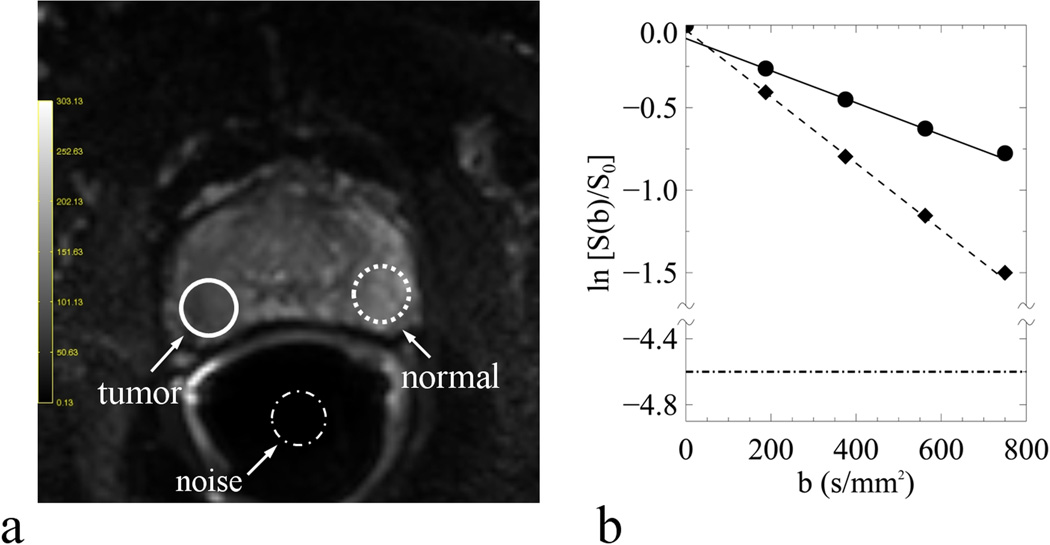
An example of normal (dash line), tumor (solid line) and noise (dash-dot line) ROIs on one DW-MR image (a) and the curve-fittings of normal (diamond) and tumor (circle) diffusion signals within the respective ROIs (b). The DW-MR image was obtained with b-value of zero and the straight lines were fitted with Eq. [4] using b-values of 188, 375, 563 s/mm². Also included in (b) was the noise-floor shown as the horizontal dash-dot line, which was normalized to the normal tissue signal at b-value of zero with SNR of 100.

Table 3.

IVIM Simulated Parameters in Normal and Tumor Tissues Using Various b-Values

Group	b-values (s/mm2)	Model	f (%)		D (10−3 mm2/s)
			Normal	Tumor	Normal	Tumor
1	0, 188, 375	K	6.2 ± 3.6	7.4 ± 2.8	1.96 ± 0.14	0.87 ± 0.11
		G	2.8 ± 3.9	5.9 ± 2.8	2.24± 0.15	1.00 ± 0.11
2	0, 375, 563	K	12.1 ± 8.1	10.4 ± 5.1	1.77 ± 0.21	0.78 ± 0.12
		G	2.0 ± 10.2	5.6 ± 5.6	2.25 ± 0.24	1.01 ± 0.13
3	0, 563, 750	K	20.4 ± 14.7	14.8 ± 8.0	1.57 ± 0.29	0.68 ± 0.15
		G	0.8 ± 22.4	5.5 ± 9.9	2.24 ± 0.36	1.00 ± 0.16
4	0, 188, 375, 563	K	7.7 ± 2.5	8.3 ± 1.9	1.88 ± 0.08	0.82 ± 0.05
		G	2.8 ± 2.9	5.8 ± 1.9	2.24 ± 0.09	1.00 ± 0.06

Note. Rician noise was included for simulations with Non-Gaussian (K) and Gaussian (G) diffusion models. Data are means ± standard deviations. Perfusion fractions (f) are in percentages.

Fig. 4.

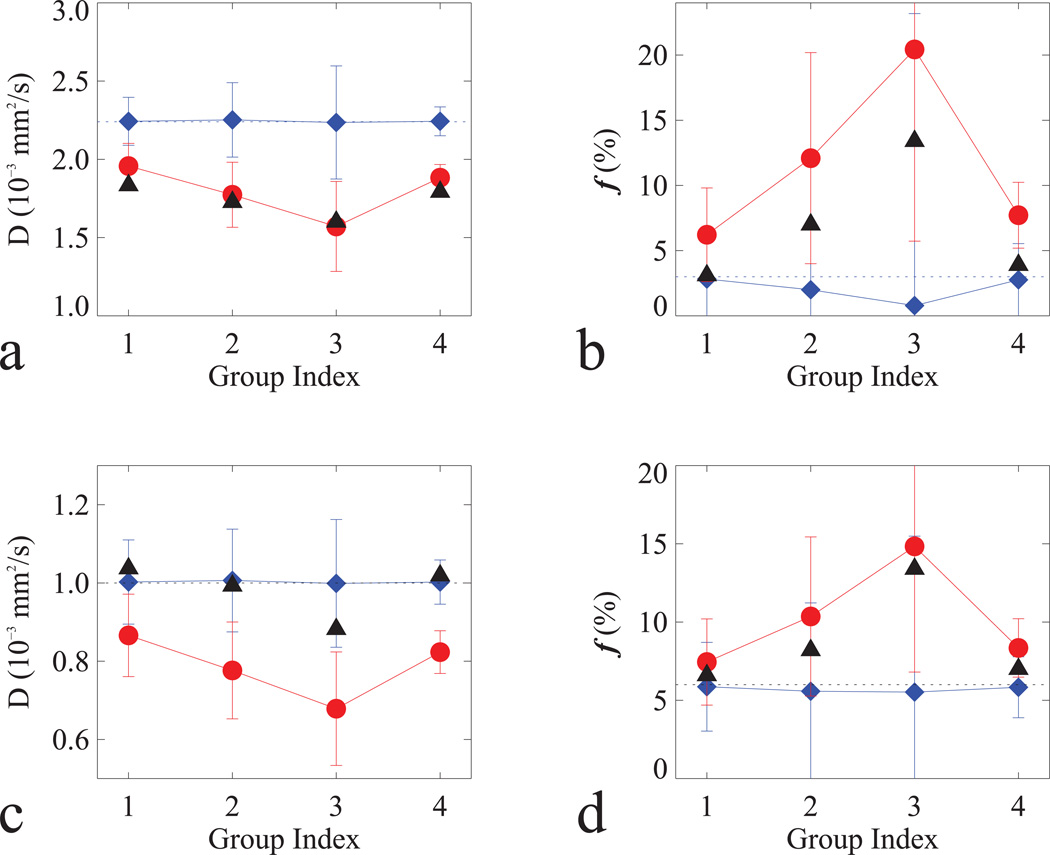
Simulated D (a, c) and f (b, d) in normal (a–b) and tumor (c–d) tissues with non-Gaussian (filled circle in red) and Gaussian (filled diamond in blue) models in Table 3. For comparison, measured D and f (filled triangle in black) were included; and horizontal dash lines were added to indicate the true values for the simulations.

Results

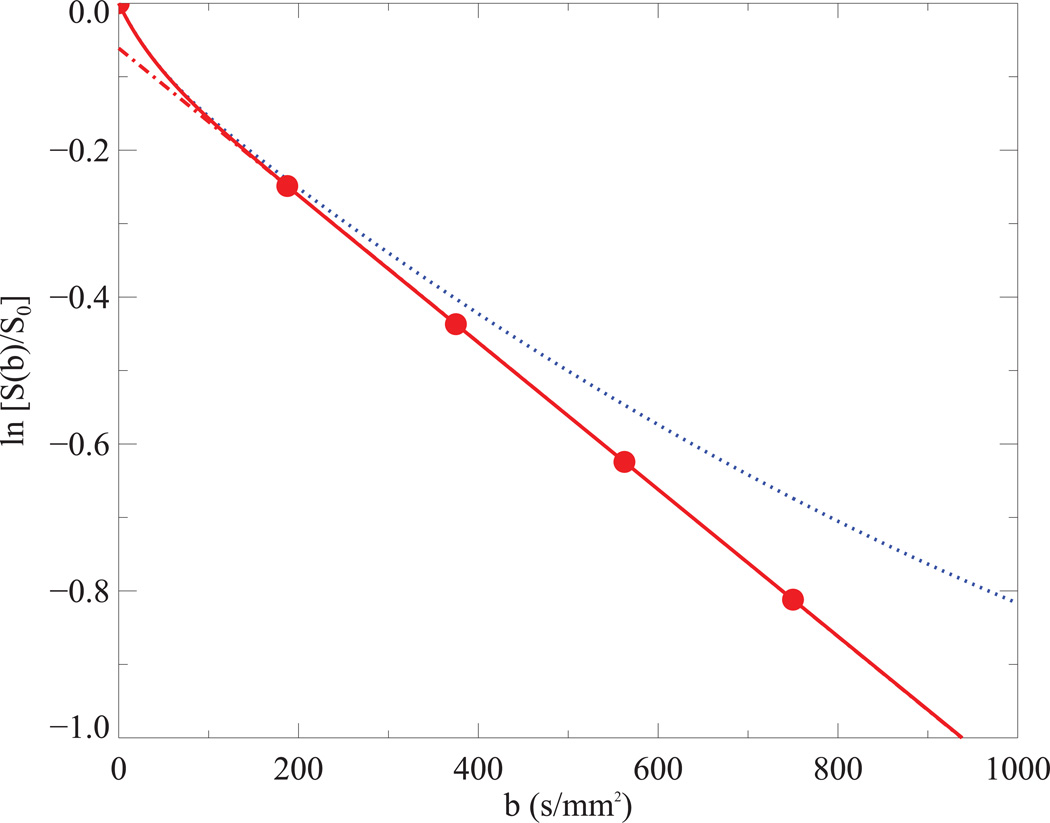
Simulated diffusion signals in tumor tissues with Eq. [1] were shown in Fig. 1, where the departure from the straight line (Gaussian diffusion) was clearly appreciable in a non-Gaussian diffusion model if b-values increased beginning from 400 s/mm² and above. An example of the measured and modeled diffusion signals from one patient is depicted in Fig. 2 where the curve fittings are performed using three b-values (188, 375, 563 s/mm²) with Eq. [4]. It clearly shows that D was relatively reduced, but f was relatively increased in tumor tissues (solid line); furthermore, the measured signals were apparently elevated in comparison to the predicted signals at the highest b-value.

Fig. 1.

IVIM simulations for tumor tissues using both Gaussian (solid line in red) and non-Gaussian (dot line in blue) diffusion model. Predicted signals (circle filled in red) at five b-values used in current study were depicted on the Gaussian diffusion model, from which a straight line (dash and dot in red) was fitted without b=0. The following parameters were used in the simulations (see Table 2): D = 1.0*10⁻³ mm²/s, D* = 25*10⁻³ mm²/s, f = 6% and K = 1.47 and 0 for non-Gaussian and Gaussian diffusion model, respectively.

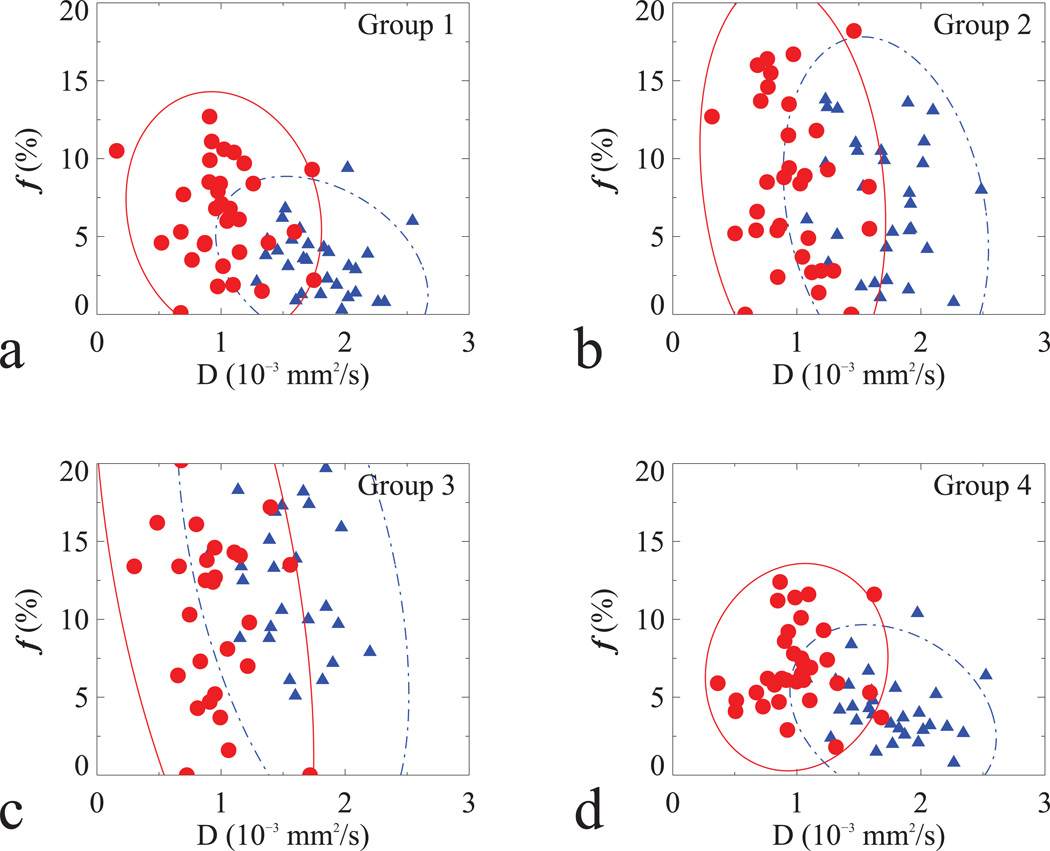
The descriptive statistics of D and f in normal and tumor tissues using different b-values from all 33 patients were listed in Table 1 and the corresponding scatter plots were in Figure 3. IVIM parameters from each subject were derived from the averaged diffusion signals of all pixels within the respective ROIs, with the averaged numbers of pixels of 46 ± 33 for normal and 34 ± 23 for tumor tissues. As can be seen, IVIM-derived parameters largely depended on the choice of b-values; for instance, f was significantly reduced when two non-zero b-values were set to 188 and 375 s/mm² (Group 1 in Table 1 and Fig. 3a), but it was indistinguishable when two non-zero b-values were set to higher than 375 s/mm² (Group 2–3 in Table 1 and Fig. 3b–c) in normal compared to tumor tissues. When three (188, 375 and 563 s/mm²) instead of two (188 and 375 s/mm²) non-zero b-values were used, the precision in D and f was slightly improved (Group 4 in Table 1), as shown by the relatively smaller areas of the error ellipses in Fig. 3d.

Fig. 3.

Scatter plots of D and f from 33 subjects in normal (filled triangle in blue) and tumor (filled circle in red) tissues, derived from b-values: (a) 0, 188, 375; (b) 0, 375, 563; (c) 0, 563, 750 and (d) 0, 188, 375, 563 s/mm².

The relevant parameters for IVIM simulations in normal and tumor tissues are listed in Table 2. The simulations on original IVIM data (i.e. K=0) with Gaussian noise (not shown) indicated that the precision of the derived parameters (D and f) was reduced when using higher b-values. The simulated results with Rician noise for both non-Gaussian and Gaussian models are tabulated in Table 3 and plotted in Figure 4 using the same combinations of b-values as in Table 1. It clearly shows that measured D and f were much better characterized by the non-Gaussian diffusion model; for instance, the measured f (see Table 1) increased in normal (332%) and tumor (103%) tissues when using b-values of 0, 563 and 750 s/mm² (Group 3) instead of 0, 188 and 375 s/mm² (Group 1); simulations (see Table 3) predicted comparable increases in normal (281%) and tumor (115%) tissues.

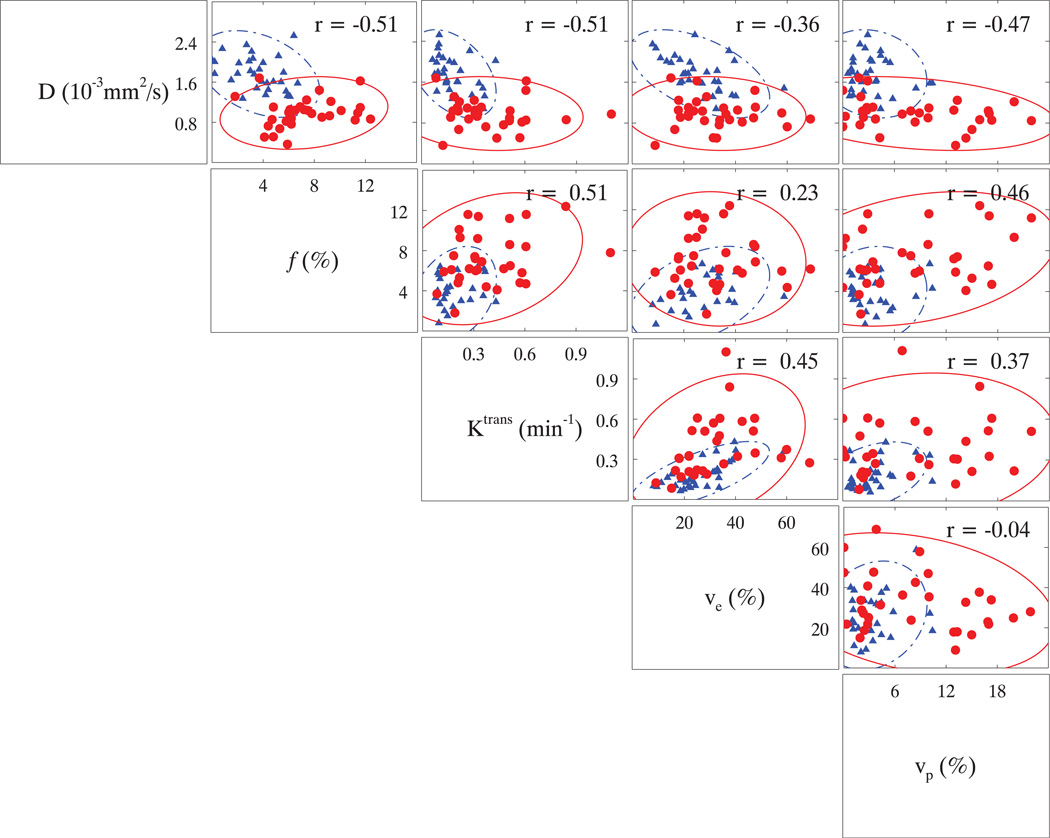
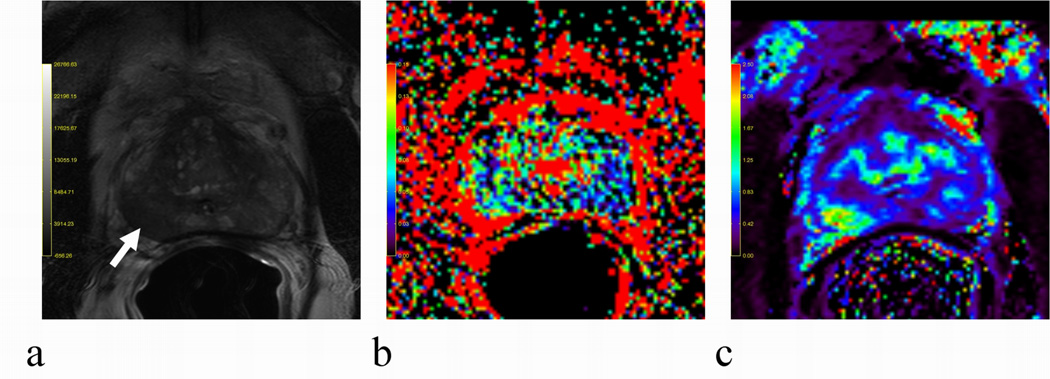
For comparison, the descriptive statistics of DCE-derived parameters from 31 subjects are shown in Table 4 along with the corresponding D and f obtained with Group 4 b-values (b=0, 188, 375, 563 s/mm²) (Table 1). Statistically, all parameters were significantly different between normal and tumor tissues; especially, f was almost twofold increased in tumor compared to normal tissues, correlating positively with K^trans and v_p with Pearson’s correlation coefficients (r) of 0.51 and 0.46, respectively. Furthermore, D and f were negatively correlated (r = −0.51). In Figure 5, a scatter-plot matrix was employed to depict the correlations among different measured parameters. To demonstrate a positive correlation, f and K^trans maps from one subject were depicted along with the corresponding T2W image in Fig. 6. The exemplary lesion is clearly recognized by a hyper-intense spot in the right PZ on both f (Fig. 6b) and K^trans (Fig. 6c) maps; by comparison, the same lesion is hypo-intense on the T2W image in Fig. 6a.

Fig. 5.

A scatter-plot matrix of measured IVIM and DCE parameters in normal (in blue) and tumor (in red) tissues. Pearson’s correlation coefficient (r) was included in each scatter-plot.

Fig. 6.

An example of a positive correlation between f (b) and K^trans (c) in tumor tissues. For comparison, the T2W image (a) was also included. The lesion located in lower right PZ indicated by a white arrow was hypo-intensity in (a) but hyper-intensities in (b–c).

In summary, IVIM-derived parameters depended heavily on the choice of b-values; particularly, the tumor perfusion fraction (f) could be either significantly elevated or indistinguishable from normal depending on the exclusion or inclusion of the higher b-values.

Discussion

DW-MRI has been accepted as an imaging biomarker of cancer and is regarded as a key tool for the detection and characterization of cancers, as well as a method for monitoring the effects of treatment (4). Traditionally, ADC was derived from the assumption that the observed water diffusion was simply a random molecular process, and was lower in prostate tumor compared to normal prostate (20). More importantly, ADC was correlated negatively with the degree of tumor aggressiveness as determined by the Gleason scoring system (34–37). Although similar correlations were observed in many studies, the reported ADC mean values were somewhat disparate even for the same GS. For instance, the values of 1.10 and 0.88*10⁻³ mm²/s were reported in two different studies on tumors with GS of 3+4 (36–37). As stated explicitly in one report (36), ADC values depended heavily on the choice of b-values, i.e. these values would decrease if derived from b-values of 0 and 1000 rather than 700 s/mm². This variability clearly demonstrates that the simple diffusion model for prostate ADC quantification is limited.

There has been a resurgent interest in recent years for measuring both diffusion and perfusion simultaneously in IVIM studies (18). Particularly, three prostate cancer MRI studies reported that f was paradoxically lower or indistinguishable in tumors (Table 5), which contradicts current theories about the initiation of angiogenesis within tumors and observations made on DCE-MRI (21–22). In the current study, we investigated the dependence of IVIM-parameters on b-values, where a pair of non-zero b-values was increasingly shifted towards the highest 750 s/mm² b value (see Table 1). Any deviations from simple mono-exponential diffusion decay would be manifested in variations in D and f. Furthermore, these findings in measurements were reinforced with the computer simulations using reported diffusion and perfusion parameters in prostate.

Table 5.

Prostate IVIM Parameters from Previous Reports

Study	b-values (s/mm2)	B0 (T)	f (%)		D (10−3 mm2/s)		D* (10−3 mm2/s)
			Normal	Tumor	Normal	Tumor	Normal	Tumor
Mazaheri et al. in Ref. [14]	0, 400, 700	1.5	20 (−3–41)	20 (−10–60)	1.38 (0.68–3.47)	1.05 (0.19–1.89)	n/a	n/a
Döpferta et al. in Ref. [15]	0, 50, 500, 800	3.0	21.3 ± 8.3	14.3 ± 7.1	1.21 ± 0.22	0.84 ± 0.19	6.8 ± 2.8	7.5 ± 4.8
Riches et al. in Ref. [16]	0, 1, 2, 4, 10, 20, 50, 100, 200, 400, 800	1.5	23 (6–53)	15 (3–77)	1.34 ± 0.28	0.82 ± 0.45	21.2 (3.89–110)	25.2 (0–122)

Note. Data are means ± standard deviations, or means followed by ranges (in parentheses). Not available ≡ n/a.

We found that f was significantly increased in tumors provided that b-values below 750 s/mm² were used. However, when high b-values were employed, f became lower (in simulation) or indistinguishable (in measurement) from normal corresponding to prior reports (14–16). Additionally, our findings most likely provide a sound explanation for another earlier observation in soft-tissue tumors using the highest b-value of 701 s/mm² where no significant difference in f was found between benign and malignant lesions (19). IVIM was originally formulated as a bi-exponential model, assuming one pseudo-diffusion and one molecular diffusion (5). However, the molecular diffusion was shown to depart from conventional random diffusion process at very high b-values due to the existence of barriers within cellular complex environments, leading to observed deviations from a simple mono-exponential diffusion decay (11). This non-Gaussian diffusion behavior is well documented for prostate (6–7). Therefore, it would not be appropriate to apply IVIM to diffusion data obtained with higher b-values where the contribution due to non-Gaussian diffusion was appreciable. Our finding in f obtained without the highest b-value is more in keeping with the known increases in perfusion within most prostate cancers based on DCE-MRI (21,38–39); that is f correlated positively with both K^trans and v_p.

It is worth noting that the kinetic model used in DCE-MRI is only valid for tissues containing small blood volumes (40); in other words, the DCE parameters reported here might not be accurate especially for high grade tumors with large vascular spaces. To be clear, v_p is a measure of the plasma fractional volume in blood (26), while f is the partial blood fractional volume in the capillary network (41) which typically demonstrates random orientations and segmentations from which flowing blood mimics the typical molecular diffusion process with distinct temporal and spatial scales (5). Therefore, it is not surprising that only a weak (r=0.46) correlation was found between f and v_p. Nonetheless, it is fascinating that comparable perfusion fractions could be derived from different MRI techniques based on two completely distinct mechanisms.

Our findings in D are comparable to published results (4, 20), in that it was significantly reduced in tumor compared to normal tissues regardless of variations in b-values. However, the absolute values of D in tumors were noticeably reduced (0.88 ± 0.35 vs. 1.04 ± 0.32 10⁻³ mm²/s) when derived from higher b-values (563 and 750 s/mm² Group 3 in Table 1) compared to lower ones (188 and 375 s/mm² Group 1 in Table 1), indicating that non-Gaussian diffusion had made noticeable contributions to these measured signals at higher b-values, which were well above the estimated noise-floor (see Fig. 2a). In case of insufficient SNR, the effect of non-Gaussian diffusion and of non-Gaussian noise on the measured diffusion signals could not be separated.

Among all discussed parameters, only D (derived without b-value of 750 s/mm² Group 4 in Table 1) was capable of differentiating high grade (0.85 ± 0.25 10⁻³ mm²/s) from low grade (1.13 ± 0.27 10⁻³ mm²/s) tumors, consistent with the literature (34–36). It is undeniable that accurate quantification of D would eventually translate into much more reliable diagnosis on tumor malignancy, which would have great clinical relevance for better patient managements.

There have been attempts to optimize the distributions of b-values in deriving more precise parameters based on the original IVIM model (42–43). These endeavors are probably helpful in designing studies on most perfused organs (i.e. kidney, liver and pancreas) where the perfusion contribution most likely overshadows the non-Gaussian diffusion effects at the b-values routinely used in clinical settings. However, when the non-Gaussian diffusion indeed makes a measurable contribution at higher b-values (given sufficient SNR), IVIM-derived parameters even with higher precisions would be largely biased based on abovementioned optimal b-values.

In a recent review (44), the contribution from non-Gaussian diffusion to IVIM signals has been acknowledged in the context of functional MRI, which supports this study’s findings. To extract both D and f from an IVIM study is of potential clinical relevance. One appealing feature of this data is that perfusion information might be obtained without the need for intravenous contrast media. This is especially relevant in patients with compromised renal function or severe allergies who cannot receive intravenous gadolinium-based contrast media. However, the inclusion of IVIM in addition to T2 weighting raises the possibility of a highly efficient, multi-parametric (T2, D, f) screening method that does not require gadolinium chelate injection. Moreover, use of IVIM with diffusion weighted imaging could shorten protocols while retaining the ability to characterize prostate lesions according their likelihood of containing cancer using a proven multi-parametric approach.

One limitation of our work is that we used MR-TRUS fusion guided biopsy results as a reference for validating our imaging as whole mount histopathology was not available in all patients. Criticisms of studies conducted using conventional TRUS biopsy are probably deserved since they are well known to be inaccurate. However, unlike conventional blind TRUS biopsies, these biopsies were guided by MR-TRUS fusion which allows direct sampling of each MRI positive lesion and assures that the lesion identified by MRI was the lesion evaluated by histology. This method has been previously validated and has been successfully used in over 100 patients (2, 45).

Conclusions

In this study, we have shown that IVIM measurements can be obtained in endorectal coil MRI studies of the prostate at 3T, and the diffusion and perfusion measurements depended heavily on the choice of b-values. Therefore, in order to obtain more accurate IVIM parameters, it is critical to select an appropriate range of b-values in prostate studies, or incorporate the non-Gaussian diffusion contribution in data modeling. IVIM measurements could be incorporated into the current multi-parametric paradigm for diagnosing prostate cancer with MRI and could reduce or eliminate the need for gadolinium enhanced DCE-MRI. Studies are underway to assess the impact of IVIM on the diagnostic performance of MRI for prostate cancer