Shear Wave Speed Measurement Using an Unfocused Ultrasound Beam

Abstract

Tissue elasticity is related to pathology and therefore has important medical applications. Radiation force from a focused ultrasound beam has been used to produce shear waves in tissues for shear wave speed and tissue elasticity measurements. The feasibility of shear wave speed measurement using radiation force for an unfocused ultrasound beam is demonstrated in this study with a linear and a curved array transducer. Consistent measurement of shear wave speed was achieved over a relatively long axial extent (z = 10-40 mm for the linear array, and z = 15-60 mm for the curved array) in 3 calibrated phantoms with different shear moduli. In vivo measurements on the biceps of a healthy volunteer show consistent increase of shear wave speed for the biceps under 0, 1, 2, and 3 kg loading. Advantages and limitations of unfocused push are discussed.

INTRODUCTION

Mechanical properties of tissues such as shear modulus (elasticity) are related to the state of tissue health (Sarvazyan et al. 1998). Assuming isotropy, incompressibility, and linearity, the shear modulus μ of an elastic tissue is related to its shear wave propagation speed c_s by

$$\mu =\rho c_s^2,$$ (1)

where ρ is density which can be assumed to be 1000 kg/m³ for all soft tissues (Yamakoshi et al. 1990). Eq. (1) neglects tissue viscosity and frequency effects, but generally is considered valid when the frequency of the shear wave is low and narrowband. Therefore, measurements of shear wave propagation speed can be used to estimate tissue elasticity.

Acoustic radiation force from a focused ultrasound beam can be used to generate shear waves within tissues (Sarvazyan et al. 1998; Bercoff et al. 2004; Palmeri et al. 2008; Chen et al. 2009). It is commonly assumed that the shear waves generated by the ultrasound radiation force at the focal region propagate within the transducer imaging plane in a direction perpendicular to the ultrasound beam axis (Parker et al. 2011). Therefore, tissue motion at several lateral positions along the shear wave propagation path at the push beam focal depth can be measured using pulse-echo ultrasound to calculate shear wave propagation speed based on the time-of-flight principle. However, a previous study shows shear wave speed measurements based on such a method suffer from bias that may be associated with the focused push beam shape (Zhao et al. 2011).

Some alternative push methods using ultrasound radiation force have been proposed. Bercoff, et al., proposed Supersonic Shear Imaging (SSI) which generates quasi-plane shear wave by marching multiple focused push beams at a supersonic speed (Bercoff et al. 2004). Hoyt, et al., reported an elasticity imaging method using shear waves generated by axicon focal beams (Hoyt et al. 2012). McAleavey, et al., introduced a spatially-modulated impulse acoustic radiation force (SMURF) imaging method which uses apodization function or intersecting push beams to generate shear waves with known spatial distribution (McAleavey et al. 2007).

In this study, we evaluate the feasibility of shear wave production in tissue with unfocused ultrasound for shear wave speed measurements based on the time-of-flight principle. The performance of the shear wave speed measurements is validated using both phantom and in vivo experiments. The advantages and limitations of the unfocused push are also discussed.

METHOD

Shear wave measurement technique

A Verasonics ultrasound system (Verasonics Inc., Redmond, WA) was used in this study to make shear wave speed measurements with a linear array transducer L7-4 or a curvilinear transducer C4-2 (Philips Healthcare, Andover, MA). A continuous segment of elements (8, 12, or 16 elements) at the center of each transducer was used to transmit the unfocused push beam at ±90 volts. There were no focusing delays applied between the transmitting transducer elements. A total of 2976 cycles of ultrasound were used in the push beam. This provided a 595 μs push duration for the L7-4 with a center frequency of 5 MHz, and 992 μs push duration for the C4-2 with a center frequency of 3 MHz. Propagation of shear waves was monitored for 15 ms at a pulse repetition frequency (PRF) of 4 kHz for the L7-4 using “flash” imaging. In flash imaging mode, the Verasonics ultrasound system transmits an unfocused ultrasound pulse (a “plane wave” compared to a traditional focused ultrasound “beam”) into the imaged medium and uses parallel channel processing to generate one complete two-dimensional (2D) ultrasound image from each transmission (Bercoff et al. 2004). To improve the signal-to-noise ratio (SNR) of detection for the C4-2, two steered flash imaging frames were used for angle compounding with an effective PRF of 4.85 kHz (Montaldo et al. 2009). The center frequencies used for imaging pulses were 3 MHz for the C4-2 and 5 MHz for the L7-4. Therefore, shear wave motion can be detected within a 2D region (with a pixel resolution of one ultrasound wavelength which was 0.51 mm for the C4-2 and 0.31 mm for the L7-4) at high PRF. The axial range of flash imaging was 3-72 mm for C4-2 and 2-46 mm for L7-4, which were much smaller than the maximum detectable range (150 mm for 4.85 kHz assuming c = 1540 m/s). Tissue velocity due to shear wave motion was calculated from in-phase/quadrature (IQ) data using one-dimensional (1D) autocorrelation method (Kasai et al. 1985) and averaged over 10 wavelengths (corresponding to an axial range of 5 mm for C4-2 and 3 mm for the L7-4) along the depth direction to improve SNR. Shear wave speed (group velocity) was then estimated from the arrival time (using time-to-peak) of the shear wave at different lateral distances from the push beam center through linear regression (Palmeri et al. 2008). The lateral range used for linear regression of shear wave speed was 3-18 mm for L7-4 and 4-18 mm for C4-2.

Intensity Field Simulation Using Field II

The simulation program Field II (Jensen and Svendsen 1992) was used to simulate intensity fields of the unfocused and focused beams generated by the L7-4 and C4-2.

For the L7-4, the simulated transducer has 128 elements with element size of 7 mm × 0.283 mm (height × width) and kerf width of 0.025 mm. The elevation focus is fixed at 25 mm depth. The center frequency of the transducer is 5 MHz. The spatial resolution is set to 0.5 mm. The excitation signal is 100 cycles of sinusoids (20 μs) oscillating at 5 MHz, the duration of which is long enough to be treated as continuous wave.

For the C4-2, the simulated curved array transducer has 128 elements with element size of 13 mm × 0.359 mm (height × width) and kerf width of 0.05 mm. The elevation focus is fixed at 70 mm depth. The convex radius is 41 mm. The center frequency of the transducer is 3 MHz. The spatial resolution is also 0.5 mm. The excitation signal is 100 cycles of sinusoids (33.3 μs) oscillating at 3 MHz.

The simulation sampling rate is set to be 100 MHz for both transducers. The pressure fields of the unfocused push (12 elements aperture for both L7-4 and C4-2) and focused push (64 elements aperture, focused at 25 mm for L7-4 and 40 mm for C4-2) were simulated, and the intensity field I is derived by

$$I=\frac{p^2}{\rho c}$$ (2)

where p is the pressure and ρ and c are the density and sound speed of the medium, respectively.

Phantom experiments

Three homogeneous elasticity phantoms (custom made by CIRS, Inc. Norfolk, VA) with different elasticity values were used in this study. Each phantom had a dimension of 10 × 10 × 8 cm³ (width × depth × height) and frequency dependent ultrasound attenuation of 0.43 dB/MHz/cm. The shear wave speed in each phantom was calibrated by Magnetic Resonance Elastography (MRE) and 1D Transient Elastography (TE) in a previous study (Zhao et al. 2011). The mean and standard deviations of shear wave speed measured at 100 Hz by MRE are 1.24 ± 0.01 m/s, 1.47 ± 0.02 m/s, and 1.80 ± 0.02 m/s for phantoms 1, 2, and 3, respectively. Results obtained from 1D TE (using one cycle of 100 Hz vibration) are close to those of the MRE tests: 1.23 ± 0.02 m/s, 1.48 ± 0.03 m/s, and 1.89 ± 0.07 m/s for phantom 1, 2, and 3, respectively.

Shear wave speed measurements using the unfocused push were made in each phantom using both L7-4 and C4-2. For each transducer, the aperture size used for unfocused push beam transmission was 8, 12, or 16 elements. For each of the setup combinations mentioned above, 3 repeated measurements were made by positioning the transducer at 3 different locations on the phantom surface. The locations were selected randomly near the center of each phantom to avoid potential influence of the boundaries for measurements. For each acquisition, shear wave speed was estimated for one region at the left side and one region at the right side of the push beam. Therefore, we have a total of 108 unfocused shear wave measurements in this phantom study (3 phantoms by 2 transducers by 3 aperture sizes by 3 repetitions by 2 sides). Shear wave measurements with focused push beams were also performed in all 3 phantoms to facilitate comparison with unfocused push. For the L7-4 transducer, the push beam had a center frequency of 5 MHz, duration of 198 μs, a 64-element aperture, and focal depth of 25 mm. For the C4-2 transducer, the push beam had a center frequency of 3 MHz, duration of 331 μs, a 64-element aperture, and focal depth of 40 mm.

Acoustic Output Measurements

The acoustic output of the L7-4 and C4-2 transducers (both focused and unfocused beams) in the phantom experiments was measured using a calibrated hydrophone (HGL-0200, Onda Corporation, Sunnyvale, CA) according to a procedure recommended by the American Institute of Ultrasound in Medicine (AIUM) (AIUM/NEMA 2009). The mechanical index (MI) and spatial peak pulse-average intensity (I_SPPA), and spatial peak time-average intensity (I_SPTA) were derated at 0.3 dB/cm/MHz based on the equations in (AIUM/NEMA 2009). The PRF for the push pulse to calculate I_SPTA was set to be 1 Hz. The maximum temperature increase was calculated based on the following equation (Palmeri and Nightingale 2004):

$$\Delta T=\frac{2\alpha I_{\mathit{SPPA}}}{c_v}t$$ (3)

where α is the ultrasound attenuation which was set to be 0.5 dB/cm/MHz, c_v is the heat capacity per unit volume (4.2 J/cm³/°C), and t is the duration of the push pulse. Equation (3) neglects cooling due to heat conduction and blood perfusion, and therefore provides a conservative estimation of heating in tissue.

In vivo tests

Elasticity of biceps brachii muscle under different loading was studied in a healthy volunteer. The study was approved by Mayo Institutional Review Board (IRB) and written consent was obtained. As illustrated in Fig. 1, the volunteer was seated upright with upper arm and forearm elevated to chest height and rested on a table. The L7-4 transducer was placed on the mid-section of the biceps and aligned with the muscle fiber direction through a custom made probe holder. The elbow angle was kept at 90° during the experiment. Muscle elasticity measurements were made at rest and then during isometric contractions at different loading levels (1, 2, and 3 kg) using the reading from a force scale as visual feedback. An unfocused push beam transmitted by 16 elements of the transducer with duration of 0.2 ms was used to generate shear waves. Propagation of shear waves was then detected using the same transducer for 15 ms at a PRF of 22.22 kHz with the axial range of 2-18 mm. Three angle compounding was used to improve the SNR of detection, leading to an effective frame rate of 7.41 kHz for detection. A high effective PRF for detection was necessary to capture the shear wave in muscle which propagated at a relatively high speed. Measurements were repeated 5 times for each loading level (with a resting time of about 1 minute between measurements).

Fig. 1.

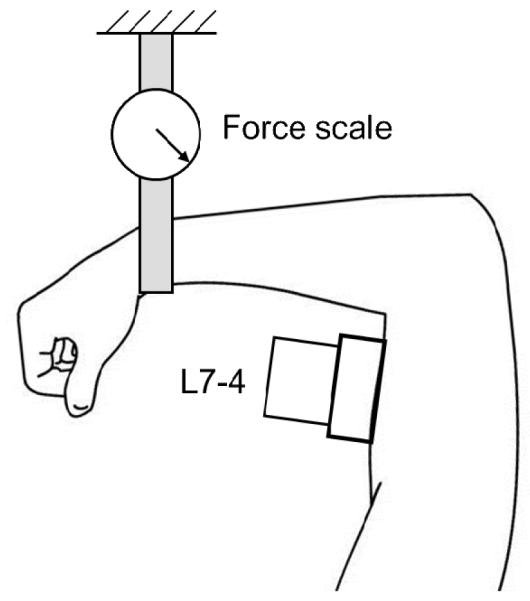
Illustration of the in vivo biceps muscle experiment

Statistical analysis

One-way ANOVA was used to test statistically significant differences among groups of shear wave speed results using unfocused, focused, and independent measurements. Student t-test (two-tailed) was used to test difference between two groups when ANOVA result was significant. Tests with a p value less than 0.05 was considered statistically significantly different.

RESULTS

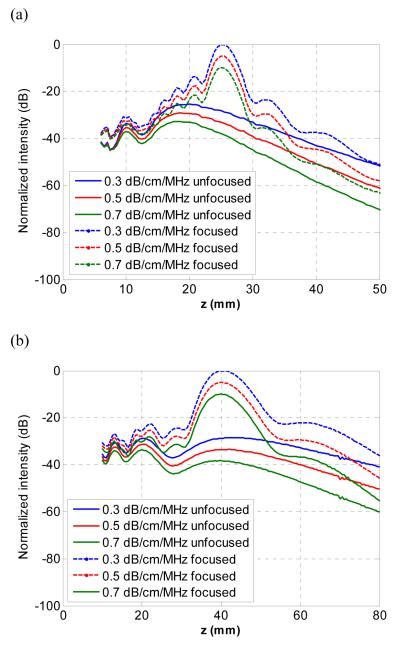
Fig. 2 shows the simulated intensity of the center axis of the focused and unfocused beams generated by the L7-4 (a) and C4-2 (b) transducers under attenuation levels of 0.3, 0.5, and 0.7 dB/cm/MHz. The intensity curves were normalized by the one with the highest magnitude for each transducer. According to the figure, focused beams generate higher intensity at the focal depths than unfocused beams. However, the unfocused beams have more consistent intensity over depth than focused beams.

Fig. 2.

Simulated acoustic intensity (normalized in dB) of the center axis of the unfocused and focused beams generated by (a) L7-4 and (b) C4-2 transducers under different levels of attenuation (0.3, 0.5, and 0.7 dB/cm/MHz)

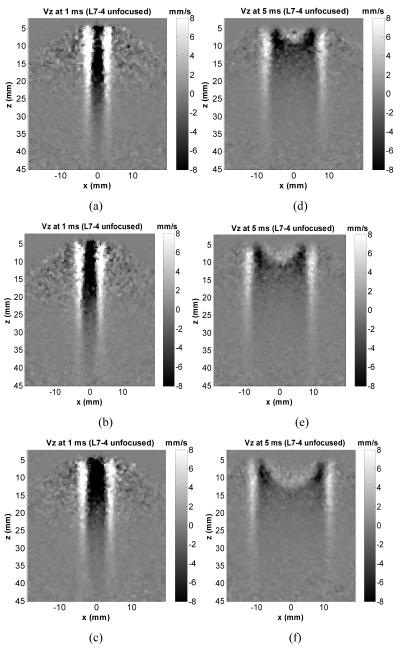
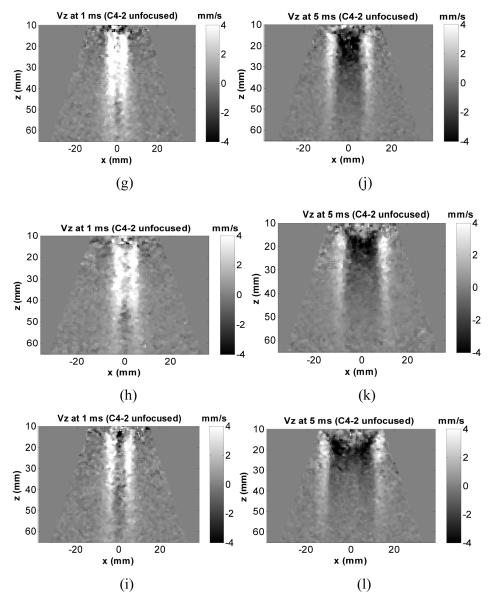
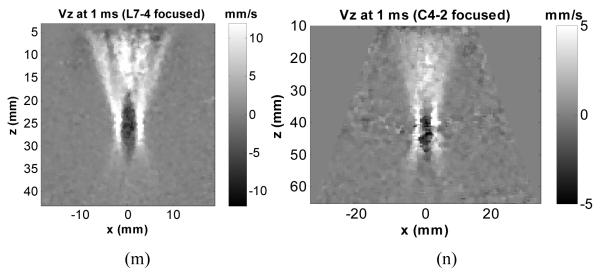
Fig. 3(a)-(c) and (d)-(f) show representative motion (particle velocity in axial direction) distributions in phantom 1, 2, and 3 generated by the L7-4 using a 12-element aperture at 1 ms and 5 ms after the push. Fig. 3(g)-(i) and (j)-(l) show motion distributions in 3 phantoms generated by the C4-2 using a 12-element aperture at 1 ms and 5 ms after the push. It can be observed that the shear wave fronts generated by L7-4 and C4-2 remain fairly vertical even when propagating to certain lateral distance, indicating consistent shear wave speed measurement can be achieved over a relatively large axial range. For comparison, Fig. 3(m) and (n) show motion in phantom 2 generated by L7-4 and C4-2 using a 64-element focused push at 25 mm and 40 mm depths, respectively. Except the small region near focal zone, the shapes of the wave fronts generated by focused push are more complicated, suggesting that shear wave speed measurement may not be consistent using data at depths out of the focal zone.

Fig. 3.

Motion (particle velocity in axial direction) distribution generated by unfocused push (12 elements) and focused push. Motion obtained by L7-4 at (a), (b), (c) 1 ms and (d), (e), (f) 5 ms after the unfocused push in phantom 1, 2, and 3, respectively. Motion obtained by C4-2 unfocused push at (g), (h), (i) 1 ms and (j), (k), (l) 5 ms after the unfocused push in phantom 1, 2, and 3, respectively. For comparison, motion obtained in phantom 2 at 1 ms after the L7-4 focused push at 25 mm depth (m) and after the C4-2 focused push at 40 mm depth (n).

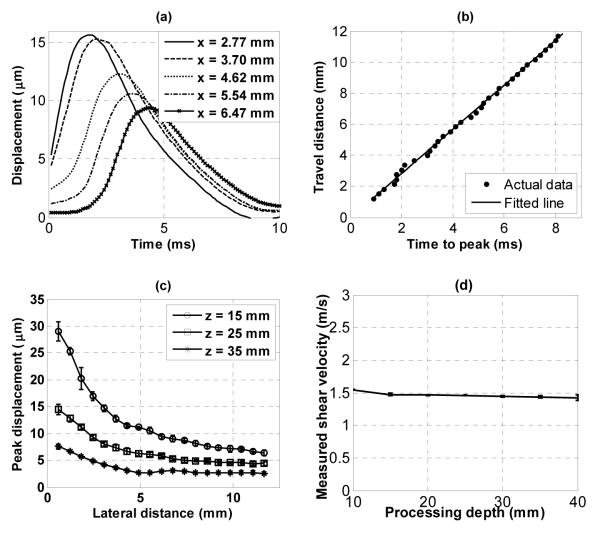
Representative results obtained with the L7-4 using a 16-element unfocused push beam in phantom 2 are shown in Fig. 4. Fig. 4(a) shows the displacement time curves at different lateral positions obtained at the depth of z = 15 mm from the transducer surface. The linear regression of the time-to-peak vs. lateral position at z = 15 mm is shown in Fig. 4(b). Fig. 4(c) shows the maximum displacements of the shear wave versus lateral positions measured at different depths. Error bars are standard deviations obtained from 6 independent measurements (3 random locations within the same phantom, each location with two sides: left and right). This figure reveals the magnitude of the displacement signal available for shear wave speed measurement. Fig. 4(d) shows the shear wave speed measured by processing echoes from different depths of the same acquisition. Error bars are standard deviations from 6 independent acquisitions. Each acquisition was processed to estimate shear wave speeds for all depths shown in Fig. 4(d).

Fig. 4.

Results in phantom 2 obtained with L7-4 (16 elements). (a) Shear wave at different lateral positions (at z = 15 mm depth from transducer surface). (b) Linear regression of time-to-peak. (c) Maximum displacement. (d) Shear wave speed measured at different depths.

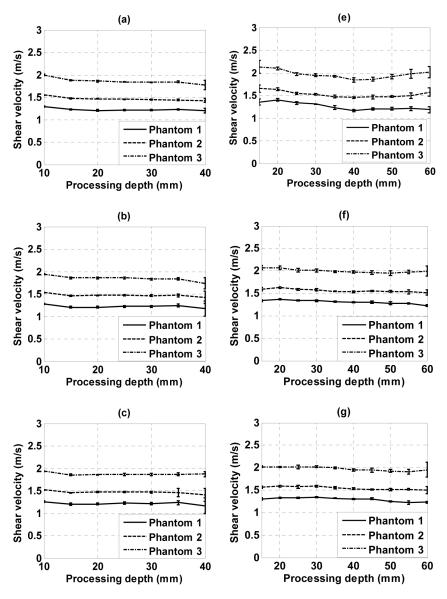
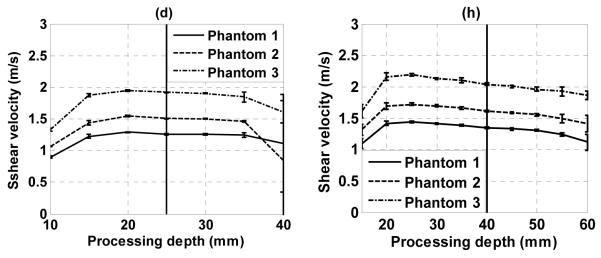
Shear wave speeds measured in all 3 phantoms are shown in Fig. 5. Fig. 5(a)-(c) are results obtained with the L7-4 using 16, 12, and 8 elements for unfocused push, respectively. Fig. 5(e)-(g) are results obtained with the C4-2 using 16, 12, and 8 elements for unfocused push, respectively. For comparison, Fig. 5(d) shows results obtained with the L7-4 using a 64-element focused push at 25 mm depth, and Fig. 5(h) shows results obtained with the C4-2 using a 64-element focused push at 40 mm depth. Compared to focused push, unfocused push produces more consistent results in the axial depth range shown in Fig. 5.

Fig. 5.

Shear wave speeds measured in 3 phantoms using (a) L7-4 with 16 elements unfocused push; (b) L7-4 with 12 elements unfocused push; (c) L7-4 with 8 elements unfocused push; (d) L7-4 with 64 elements focused push at 25 mm depth; (e) C4-2 with 16 elements unfocused push; (f) C4-2 with 12 elements unfocused push; (g) C4-2 with 8 elements unfocused push; (h) C4-2 with 64 elements focused push at 40 mm depth.

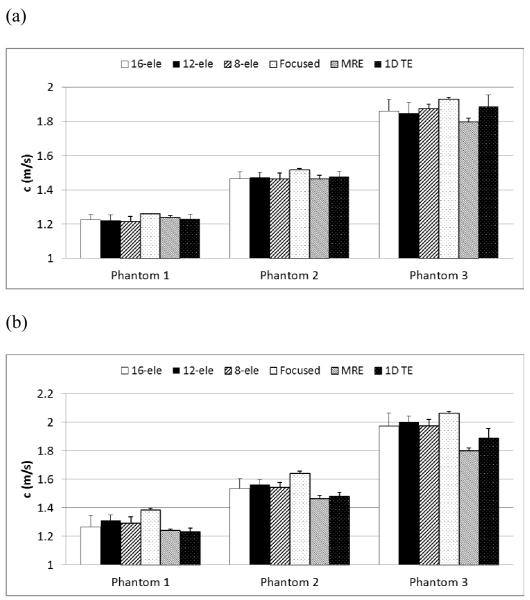
Shear wave speeds measured with unfocused push in all three phantoms are shown in Fig. 6 for comparison with focused push, MRE and 1D TE. Fig. 6(a) shows results for the L7-4 using 16, 12, and 8 elements for unfocused push and 64 elements for focused push at 25 mm depth. Error bars for the unfocused push measurements are standard deviations of mean shear wave speeds at different depths shown in Fig. 5. The mean and standard deviation values for focused push in each phantom are from 5 measurements at 5 random locations using data from the focal region. Fig. 6(b) shows results for the C4-2 using 16, 12, and 8 elements for unfocused push and 64 elements for focused push at 40 mm depth. No significant difference is found between unfocused and independent measurements (MRE and 1D TE) using the L7-4 in each phantom (p > 0.21). The results using focused push are significantly higher than unfocused and independent measurements (p < 0.047). For the C4-2, unfocused results are significantly higher (p < 0.014) than independent measurements. Results from the focused push are significantly higher than unfocused and independent measurements (p < 0.001). However, no significant difference is found among unfocused results using different push apertures (p > 0.22).

Fig. 6.

Shear wave speeds measured with unfocused push compared with focused, MRE, and 1D TE results in 3 phantoms. (a) L7-4 using 16, 12, 8 elements for unfocused push and 64 elements for focused push at 25 mm depth. (b) C4-2 using 16, 12, 8 elements for unfocused push and 64 elements for focused push at 40 mm depth.

Table 1 shows the acoustic output measurement results for the push beams used in this study. The MI and I_SPTA,0.3 used in this study are within the FDA safety limits (FDA 2008), and unfocused push has lower acoustic outputs than the focused push. Maximum heating in tissue due to a push beam is very low. Although the focused beam has higher I_SPPA than the focused beam, the maximum temperature rise in tissues are comparable for both push pulse types because the pulse duration for focused beams are shorter than (one third of) focused beams.

Table 1.

Acoustic output measurement results for the push beams used in this study

	L7-4 unfocused	C4-2 unfocused	L7-4 focused	C4-2 focused
MI0.3	0.75	0.83	1.46	1.66
ISPPA,0.3 (W/cm2)	100.8	72.7	455.8	327.6
ISPTA,0.3 (mW/cm2)	60.0	72.1	90.2	108.4
Temperature rise (°C)	0.005	0.006	0.007	0.009

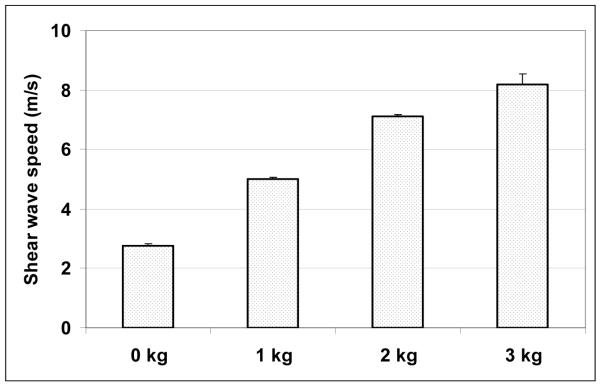
Fig. 7 is the shear wave speed measured at 14 mm depth (from the skin surface) along the muscle fibers of the biceps using the L7-4 (16-element unfocused push). The error bars are standard deviations of 5 repeated measurements at each of the loading condition: 0, 1, 2, 3 kg, respectively. The results are comparable with the phase velocities measured parallel to the biceps brachii muscle fibers under the same loading condition in (Gennisson et al. 2010).

Fig. 7.

Shear wave speeds of the biceps along muscle fibers measured with L7-4 under different loading levels.

DISCUSSION

Results in this study demonstrate that shear wave speed measurements with unfocused push beams are feasible. Fig. 2 shows ultrasound radiation force of unfocused beams has less peak magnitude, but also less variations over depth, compared to focused beams. Fig. 4(a) shows that sufficient shear wave motion can be produced for shear wave speed measurement using an unfocused push beam. As demonstrated in Fig. 5, shear wave speed can be estimated over a long axial extent with this method. Results are relatively consistent over the whole axial (depth) range studied. This may be a beneficial feature compared to shear wave speed measured with focused push beam, which can show relatively large variation with depth of measurement, especially in the transducer near field (Zhao et al. 2011). Results obtained with unfocused push are similar to those obtained with MRE and 1D TE in all 3 phantoms. Precision of in vivo measurements are very good, as demonstrated by the results in the biceps muscle at different loading levels.

For the L7-4 transducer, performance using 16, 12, and 8 elements is similar in this phantom study. We notice that using more elements gives more shear wave motion, which may increase the SNR of measurements for in vivo applications. For the C4-2 transducer, an unfocused push with 16 elements gives larger variation along depth, as demonstrated by Fig. 4(d). The C4-2 has a pitch of about 0.5 mm, so 16 elements account for about 8 mm aperture size, which may be too large for shear wave production. In addition, the unfocused beam spreads out along depth direction due to the curvature of the transducer surface. Therefore, it seems better to use fewer elements for the C4-2 in unfocused push mode. However, selection of push elements must be balanced with SNR because too few elements cannot produce sufficient shear wave motion for reliable measurements.

For shear wave speed measurements based on ultrasound radiation force, MI is usually the limiting factor. MI from a focused ultrasound beam can exceed the FDA limit for diagnostic ultrasound and therefore needs careful control and monitoring. However, as listed in Table 1, the MI for the unfocused push beam at maximum transmit voltage of the Verasonics system (±90 V) was less than 0.9 in this study, which is well below the FDA limit of 1.9 (FDA 2008). Using an unfocused push beam therefore will simplify both safety control on ultrasound outputs and acoustic output measurements because exhaustive calibrations of all possible focal points are not necessary.

Another issue common for radiation force based shear wave measurement is power droop of the transmission board during the long duration, high voltage push transmission. Unfocused push can help alleviate this issue because fewer transmit channels are used for unfocused beams compared to focused push beams: the total energy used for an unfocused push is less than a focused push. However, unfocused push produces less tissue motion at deeper regions from the transducer surface. To compensate for this effect, the duration of the unfocused push is usually longer than a focused push beam. This can stress the transducer elements and transmit circuit of the active channels used for unfocused push. Optimization of maximum penetration of the unfocused push method needs further investigation.

Compared with focused push methods (including single focus, Supersonic Shear Imaging, axicon focusing), shear waves produced by unfocused beams may have less motion amplitude and thus lower SNR, especially at deep regions far away from the transducer surface. Higher transmit voltage can be used to increase motion amplitude because the MI for unfocused push beams is well below the FDA safety limit (FDA 2008). In this study, the maximum transmit voltage of the Verasonics system (±90 V) is used. In addition, push pulses with longer duration can be used to produce stronger shear waves for unfocused pushes. However, transducer elements may be damaged if the high voltage transmission lasts too long. The push duration used in the experiments in this study produces shear waves adequate for reliable measurements in both phantoms and human biceps brachii muscle. Future investigations may be needed to optimize the performance of unfocused push methods and compare them with various focused push methods. Simulation methods such as those proposed by Nightingale, et al., (Nightingale et al. 2000) and Lee, et al., (Lee et al. 2012) will be useful in these future studies.

Compared to focused push, the shear waves produced by unfocused push are also wider than shear waves produced by focused push because of the wider push beams compared to the focused push beams at the focal region. This means shear waves generated by unfocused push may have narrower bandwidth, so that the frequency component of the shear waves change less as they propagate in dispersive media. Therefore, the group velocity measurement with unfocused push in dispersive media may be more consistent over the propagation distance than the measurement using focused push. Typically the time-of-flight method for shear wave speed measurement is applied to a lateral region outside the push beam. Spatial resolution of measurements is determined by the size of the lateral range used for time-of-flight calculation. Therefore, wider beam width from an unfocused push should not affect the spatial resolution of shear wave speed measurement.

Flash imaging is used in this study for motion tracking at a high frame rate. It uses unfocused “plane wave” for pulse-echo detection which may result in lower SNR compared to traditional focused beam pulse-echo detection. Therefore, angle compounding was used here to help improving SNR in detection of shear waves produced by both focused and unfocused push (Montaldo et al. 2009). Sufficient frame rate can still be achieved even after compounding because the PRF of a single frame flash imaging is very high. Compounding is not necessary if a traditional ultrasound scanner is used for shear wave detection.

In this study, in vivo biceps muscle is used to demonstrate the feasibility of the proposed method. The reason for choosing the biceps muscle is that it is superficial and easily accessible, which seems to be a good application for the unfocused push technology. The primary purpose is not to evaluate the function of the biceps, but to demonstrate the feasibility of the proposed technology. Therefore, only a single case study is shown here without a systematic study of multiple subjects. The measurement results show good precision and are comparable with the results reported in (Gennisson et al. 2010).

CONCLUSION

It is demonstrated in this study that shear wave speed measurements with an unfocused push beam are feasible. The unfocused push beam produces sufficient shear wave motion for reliable measurements. Shear wave speed can be measured over an axial extent of 10-40 mm using a linear array and over an axial extent of 15-60 mm using a curved array. Results obtained with this method in 3 elasticity phantoms are validated by MRE and 1D TE measurements. Precision of the method is also good, as demonstrated by in vivo measurements along the muscle fibers of the biceps under different loading conditions.