Abstract
Membranous nanostructures, such as nanovesicles and nanotubules, are an important pool of biological membranes. Recent results indicate that they constitute cell-cell communication systems and that cancer development is influenced by these systems. Nanovesicles that are pinched off from cancer cells can move within the circulation and interact with distant cells. It has been suggested and indicated by experimental evidence that nanovesicles can induce metastases from the primary tumor in this way. Therefore, it is of importance to understand better the mechanisms of membrane budding and vesiculation. Here, a theoretical description is presented concerning consistently related lateral membrane composition, orientational ordering of membrane constituents, and a stable shape of nanovesicles and nanotubules. It is shown that the character of stable nanostructures reflects the composition of the membrane and the intrinsic shape of its constituents. An extension of the fluid mosaic model of biological membranes is suggested by taking into account curvature-mediated orientational ordering of the membrane constituents on strongly anisotropically curved regions. Based on experimental data for artificial membranes, a possible antimetastatic effect of plasma constituents via mediation of attractive interaction between membranous structures is suggested. This mediated attractive interaction hypothetically suppresses nanovesiculation by causing adhesion of buds to the mother membrane and preventing them from being pinched off from the membrane.
Keywords: nanovesicles, nanotubules, nanotubes, microvesicles, exosomes, metastasis
Introduction
According to a World Health Organization report, cancer is a leading cause of death worldwide, and it was estimated that 7.6 million people died from cancer in 2008, with metastases being the major cause of death.1 More than 100 distinct types of human cancer have been described, while subtypes of tumors can be found within specific organs, leading to the conclusion that cancer is a highly complex disease, both in time and space.2 Due to the heterogeneity of hitherto revealed mechanisms, the hypothesis has been put forward that each tumor is unique, and the spectrum of biological changes determining tumors is highly variable.2 The question arises as to whether major underlying mechanisms exist that could be addressed in diagnosis and treatment.
In this work, a basic (bio)physical mechanism of biological membrane configuration is explored. Lateral redistribution of membrane constituents is connected with an increase in membrane curvature. Nanosized membrane buds are formed which may elongate into nanotubules, or be pinched off from the membrane to become nanovesicles. Nanotubules and nanovesicles reflect the composition of the membrane and the interior of the mother cell. Nanotubules may become attached to adjacent cells while nanovesicles travel within the circulation. Thereby, these nanostructures convey matter and information to other cells and represent cell-cell communication systems. Nanovesicles have been found to transfer surface-bound ligands and receptors,3–7 prion proteins,8–10 genetic material including RNA,11–14 and infectious particles15,16 between cells. It has also been suggested that in cancer they contribute to metastasis.17,18
Information on the presence of tumors could be obtained from cell-derived nanovesicles which are expected to be found in body fluids, such as blood, synovial fluid, ascites, pleural fluid, and cerebrospinal fluid.19,20 For example, it was recently demonstrated that tumors of various origin21 and various clinical outcomes22 can be classified by their micro RNA (miRNA) profiles. miRNAs are short (about 18–25 nucleotides long) noncoding RNAs, including small interfering RNA, ribosomal RNA, transfer RNA, and small nuclear RNA.23 Over 700 miRNAs have been identified in the human genome.24 It has been suggested that an miRNA profile is associated with prognostic factors and disease progression22,25 and that mutations in miRNA genes are frequent and may have functional importance,22 by either suppressing tumors or promoting their growth and proliferation.24 miRNA profiling has already been used to determine whether patients with chronic lymphocytic leukemia have slow-growing or aggressive forms of the cancer,21 while plasma samples collected from patients with early (stage II) colorectal cancer could be distinguished from those of healthy gender-matched and age-matched volunteers.26 Compared with current methods used to diagnose most malignancies, assessment of blood is advantageous because it is much less invasive. Nanovesicles can be considered as potentially relevant biomarkers for diagnosis, prognosis, and treatment of cancer, encouraging the study of the processes of membrane budding and nanovesiculation.
In studying cancer and its underlying mechanisms, extensive work has been devoted to chemical and biochemical methods involving specific molecules, reactions, pathways, and the binding of particles. Although substantial progress has been made, an essential unifying mechanism or mechanisms have not yet been revealed. Hitherto, the contributions of physics and biophysics cannot match those of chemistry and biochemistry, although physics essentially strives to reveal the relevant general mechanisms necessary to understand and manipulate cancer. Living creatures are commonly considered to be complex systems beyond the reach of physical methods which are effective in the description of simple systems.
However, even in highly complex living creatures, some relevant issues can be highlighted to simplify the system so that methods of theoretical physics can be applied. In this work, we focus on the curvature of the membrane connected to the redistribution of constituents, a field which is subject to the methods of statistical physics and thermodynamics. Using these methods, it is demonstrated that, to understand whether the membrane is likely to produce a nanotubule or a nanovesicle, it is enough to distinguish only one property of the diverse constituents, ie, their symmetry with respect to the axis perpendicular to the membrane, which may lead to energetically favorable ordering of membrane constituents in strongly anisotropically curved membrane regions. These theoretical predictions are supported by experimental evidence from membranous nanostructures. Further, orientational ordering of particles with an internally distributed charge provides an explanation for mediated attractive interaction between membranes which could prevent the bud being pinched off from the membrane, and is the basis of a suggested antimetastatic and anticoagulant effect of body fluid constituents.
Description of the cell membrane
Fluid mosaic model and its extension by function/curvature-related lateral inhomogeneities
The cell membrane is an important building element of the cell. Understanding the interdependence of processes which take place in cells seems impossible without understanding the features relevant to the cell membrane. Therefore, the cell membrane has been a subject of interest in many studies. After performing their thorough and inspired work, Singer and Nicolson in 1972 suggested a fluid mosaic model for the membrane,27 describing it in general as a lipid bilayer with embedded proteins and other large molecules. Within the physical implementation of the fluid mosaic model, the phospholipid bilayer shows the properties of a two-dimensional laterally isotropic liquid, while proteins and other large molecules are more or less free to move laterally in the membrane. Many experiments and theoretical studies performed during the last 40 years have established the fluid mosaic model as the standard model for description of the cell membrane.
After 25 years, the fluid mosaic model was upgraded by considering lateral inhomogeneities.28–30 According to the upgraded model, the membrane is a two-dimensional liquid with embedded microdomains of specific composition, called membrane rafts. Membrane rafts are small (10–200 nm), relatively heterogeneous, dynamic structures with an increased concentration of cholesterol and sphingolipids.31,32 From a biochemical point of view, membrane rafts are structures which resist solvation by detergents at low temperatures, while from a biophysical point of view, within the raft, increased ordering takes place due to interactions between the highly saturated fatty acids of sphingolipids. Fatty acids within the rafts have limited mobility with respect to the unsaturated fatty acids in other parts of the membrane. Dynamic accumulation of specific membrane constituents in rafts regulates the spatial and temporal dependence of signalization and transport of matter, thereby forming transient but vitally important signaling platforms.33
In membranes, there is an interdependence between structure and shape because the membrane constituents create the membrane geometry, ie, membrane curvature is determined by the shape of the membrane constituents and their interactions. The curvature of the raft is formed by accumulation of a specific type of constituent, and may be different from the curvature of the surrounding membrane. In other words, lateral sorting of membrane constituents may cause changes in local membrane curvature. Considering this interdependence, the fluid mosaic model was further modified, as described below.
Membrane as a composite two-dimensional surface
To make the system simple, it is considered that one of the membrane extensions (thickness) is much smaller than the other two extensions, so the membrane may be treated as a two-dimensional surface. The membrane is also viewed as being composed of a large number of particles (building units) which act one upon another.35 Taking into account the above, the membrane layer is described as a surface composed of building units (molecules, groups of molecules, membrane rafts, nanodomains), which attains a shape corresponding to the minimum of its free energy.
Cutting the surface at a chosen point by a plane through a normal to the surface defines a curve, known as the “normal cut”. The curvature of the normal cut is the inverse value of the radius of the circle which fits the curve at the chosen point, C = 1/R. An infinite number of possible normal cuts can be made through the normal. The cuts with the maximal and minimal curvatures, ie, C1 = 1/R1 and C2 = 1/R2, respectively, are called the principal curvatures, while the corresponding mutually perpendicular directions of the cuts are the principal directions (Figure 2).
Figure 2.
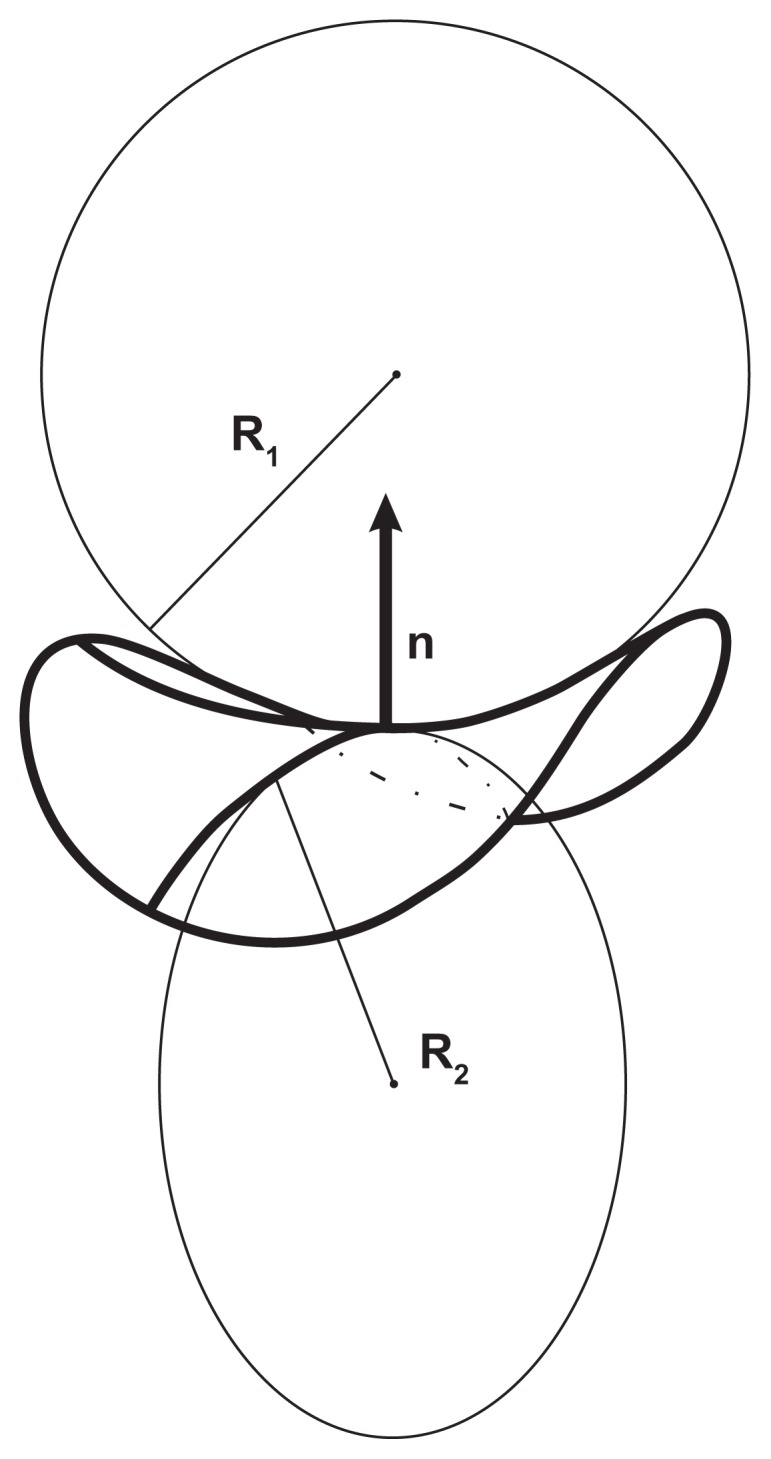
Curvature of the surface.
The diagonalized curvature tensor of the membrane surface at a given point is
| (1) |
A membrane can be imagined which would completely fit the constituent at a given point, in the sense that no energy would be needed to insert the constituent into the membrane. The curvature tensor of such a membrane is the intrinsic curvature tensor
| (2) |
where C1,m and C2,m are the intrinsic principal curvatures. Lying perpendicular to the membrane plane, the principal axes system of the membrane may be rotated with respect to the intrinsic principal axes system.
We now define the isotropic and anisotropic membrane constituents, whereby a constituent is called isotropic if C1,m = C2,m and anisotropic if C1,m ≠ C2,m.
Energy of a single membrane constituent
When assembled into the membrane, the constituents cannot all resume the most energetically favorable curvature (ie, intrinsic curvature). Namely, the shape corresponds to the minimal energy of the whole membrane. Also, constraints regarding the area and volume must be taken into account. Mismatch of the intrinsic and actual curvature at the site of the constituent is a source of the single constituent energy. In other words, the constituent deforms and rotates in the membrane plane for an angle ω in order to constitute the membrane.
The energy of a single constituent is given in terms of the mismatch tensor M,35
| (3) |
where R is the rotation matrix
| (4) |
| (5) |
so that
| (6) |
The energy of the constituent is given by a phenomenological expression subject to two invariants of the mismatch tensor, M, of the second order in curvatures. The trace and the determinant of the mismatch tensor are considered as fundamental invariants35
| (7) |
where K and K are constants.
It follows from expression (6) that
| (8) |
Taking into account the relationship between the trigonometric functions sin2ω = 1/2[1 − cos(2ω)] and cos2ω = 1/2[1 + cos(2ω)], after some rearranging, we obtain
| (9) |
and
| (10) |
where we have introduced the mean curvature of the membrane H
| (11) |
and
| (12) |
The corresponding intrinsic quantities are
| (13) |
and
| (14) |
A membrane constituent is characterized by Hm and Ĉm. For isotropic constituents Ĉm = 0.
The trace of the mismatch tensor (9) can be expressed by the invariants (traces) of the curvature tensors C and Cm. Further, it follows from Equations (11) and (12) that
| (15) |
so that the determinant of the mismatch tensor can also be expressed by invariants of the curvature tensors [(H, Ĉ) and (Hm, Ĉm), respectively],
| (16) |
Inserting the expressions (9) and (16) into Equation (7) yields the expression for the single constituent
| (17) |
or conveniently35
| (18) |
where
| (19) |
and
| (20) |
It can be seen from Equation (18) that the energy E depends on the angle ω multiplied by the difference between the two intrinsic curvatures (Ĉm). This means that for anisotropic building units, the orientation with respect to the coordinate system is important.
Local thermodynamic equilibrium of membrane monolayer
To ensure uniformity of the curvature field within the system which is being described by ensemble statistics, the monolayer area is imagined to be divided into small patches containing a large number of constituents. Let there be P kinds of membrane constituents in a chosen patch. All constituents of the i-th type are taken to be equal and independent. The lattice statistics approach is used, analogous to the problem of noninteracting magnetic dipoles in a magnetic field.36 Here, the curvature field takes the role of the magnetic field.
Considering a subset of constituents of the i-th type (i = 1,2, ..., P) it follows from (18) that the single-constituent energy attains a minimum when cos(2ωi) = 1, while the single-constituent energy attains a maximum when cos(2ωi) = −1. In the first case, the single-constituent energy is
| (21) |
whereas in the second case the single-constituent energy is
| (22) |
where
| (23) |
and
| (24) |
are the curvature deviator and the intrinsic curvature deviator, respectively. The states with ωi = 0, π and with ωi = π/2, 3π/2, respectively, are degenerate. We say that the ordering is quadrupolar.
We assume a simple model where we have Mi equivalent constituents in a patch. Each constituent is in one of the two possible states, ie, Ei, min and Ei, max, respectively (Equations (21) and (22), so that Ni constituents are in the state with the higher energy Ei, max while (Mi − Ni) constituents are in the state with the lower energy, Ei, min.
The partition function of a constituent of the i-th type in the lower energy state is36
| (25) |
while the partition function of a constituent of the i-th type in the higher energy state is
| (26) |
where
| (27) |
and k is the Boltzmann constant.
Constituents in the same energy state are treated as indistinguishable. For Ni constituents of the i-th type in the state with higher (maximal) energy and (Mi −Ni) constituents in the state with lower (minimal) energy, the number of possible arrangements is Mi!/Ni!(Mi − Ni)!. To calculate the partition function, we must consider that Ni can be any number from 0 to Mi; Ni = 0 means that all the constituents are in the state with the lower energy, Ni = 1 means that one constituent is in the state with the higher energy, while Mi − 1 constituents are in the state with the lower energy, …
The canonical partition function Qi(Mi, T, C) of Mi constituents in the membrane patch is
| (28) |
Considering Equations (25) and (26),
| (29) |
Using the binomial formula
| (30) |
where
| (31) |
We call the quantity di eff, the effective curvature deviator. After some rearranging, we obtain the canonical partition function of the constituents of the i-th type
| (32) |
Local ordering of constituents
The average number of constituents in each of the energy states representing the local ordering of the constituents is obtained using the local canonical partition function of the constituents of the i-th type, Qi. The average number of constituents with higher energy (Ei,max) is
| (33) |
while the average number of constituents with lower energy (Ei,min) is
| (34) |
An alternative definition can be used,
| (35) |
where
| (36) |
It follows from Equations (35) and (36) that
| (37) |
and
| (38) |
It can be seen from Equations (37) and (38) that at di,eff = 0, ie, when the principal curvatures are equal, both energy states are equally occupied (〈Ni〉/Mi = 〈Mi − Ni 〉/Mi = 1/2). The fraction of the number of constituents in the lower energy state increases with increasing di,eff to 1, while the fraction of constituents in the higher energy state decreases to 0.
Global equilibrium of a multicomponent membrane
Taking into account that there are P types of constituents which can be treated as independent, the partition function of the membrane patch is
| (39) |
were
| (40) |
and Qi is given by Equation (32). The free energy of the patch is
| (41) |
Taking into account Equations (32) and (41) yields
| (42) |
To calculate the free energy of the whole monolayer, the contributions of all the patches are integrated,
| (43) |
where
| (44) |
The integration is performed over the monolayer area A. In the equilibrium state the free energy attains its minimum
| (45) |
The total number of constituents of each kind in the monolayer (Mi,T, i = 1, 2, ..., P) is kept constant at minimization,
| (46) |
while a local constraint is applied by requiring that all sites in the patch are occupied
| (47) |
To perform the variation, a functional is constructed
| (48) |
where λ is a local Lagrange multiplier and λi, i = 1, 2, ..., P are global Lagrange multipliers. It is assumed that the average density of the constituents is uniform over the monolayer so that
| (49) |
where MT is the total number of sites in the monolayer. The variational problem is expressed by the Euler-Lagrange equations
| (50) |
and
| (51) |
It follows from Equations (48) and (50) that
| (52) |
while expression (48) and the Euler-Lagrange equation (51) yield the condition (47).
To determine the parameter λ, Equation (52) is inserted into Equation (47). The parameter λ is included in all terms of the sum and is independent of i, so it can be expressed as
| (53) |
Using Equations (52) and (53) gives
| (54) |
The global Lagrange multipliers λi are determined by fulfilling conditions (46),
| (55) |
Expression (54) represents the probability of finding a constituent in the state with a given curvature-dependent energy. Because the background is consistent with Boltzmann statistics (explicitly independent and indistinguishable constituents), expression (54) can be described as a modified Boltzmann distribution. The explicit independence of constituents in the derivation of the local thermodynamic equilibrium is complemented by introducing the excluded volume effect [the condition (47)] which is reflected in the denominator of Equation (54).
The equilibrium free energy is obtained by inserting distribution (54) into expression (43). After some rearranging, we obtain
| (56) |
One-component membrane. Comparison with Helfrich bending energy
If the monolayer is composed of equal constituents which occupy all sites in the lattice, it follows that
| (57) |
Taking into account the definition of q0 (27) and the above equation gives
| (58) |
The free energy of the bilayer is obtained by summing the contributions of both layers. It is taken into account that the principal curvatures in the inner layer are opposite in sign to the principal curvatures of the outer layer
| (59) |
The area densities of the constituents m are taken to be equal and constant over both layers. The outer and inner membrane areas are regarded as equal in integration. The contributions to the free energy which turn out to be constant are omitted. We obtain
| (60) |
Using relationship (15)
| (61) |
Equation (60) gives37,38
| (62) |
We compared the expression for free energy of the one-component membrane (62) with the acknowledged Helfrich local bending energy of a thin, laterally isotropic surface,39,40
| (63) |
where kc and kG are the membrane local and Gaussian bending constants, respectively. Expression (62) obtained by statistical mechanics recovers the Helfrich isotropic bending energy (63) if
| (64) |
and
| (65) |
and if the constituents are isotropic (Dm = 0).
Expression (62) is more general because it takes into account the possibility of in-plane orientational ordering of the constituents. The new term deriving from orientational ordering of the constituents [the third term in Equation (62)] is called the deviatoric elastic energy of the membrane, and is always negative. In other words, orientational ordering of the anisotropic constituents on the anisotropically curved membrane regions diminishes the free energy of the membrane, and therefore stabilizes shapes with anisotropically curved membrane regions. The orientational ordering of the constituents provides an additional degree of freedom which also proves relevant in other systems (eg, the electric double layer).41–43
For isotropic constituents, the membrane free energy can be equivalently expressed by either set of invariants of the curvature tensor C, ie, the trace and the determinant of the curvature tensor or the trace and the deviator of the curvature tensor. However, for anisotropic constituents, the orientational ordering of constituents can be described by the trace and the deviator of the curvature tensor and not by the trace and the determinant of the curvature tensor. Both cases can be described by the trace and the determinant of the mismatch tensor, M.
The variational problem for the one-component membrane considering orientational ordering of the constituents was expressed by a system of Euler equations and solved by numerical methods.38 It has been shown that the energies of the equilibrium shapes were considerably affected by ordering of the constituents in strongly anisotropically curved regions, but the shapes were only slightly different from shapes calculated by minimization of the isotropic bending energy. For convenience, the shapes calculated by minimization of membrane isotropic bending can therefore also be used when calculating energies taking into account the deviatoric terms. Good agreement between the predicted and observed structures44 demonstrates that the statistical mechanical description of the membrane is relevant and useful.
Equilibrium configuration of the two-component membrane
To illustrate the interdependence between equilibrium composition and shape of the membrane, we consider a two-component membrane. Two types of membrane constituents (first and second) are distinguished. The local constraint (47) is omitted and the concentration of the second type of constituents is expressed using the local conservation equation:
| (66) |
so the functional can be expressed by the concentration, m1
| (67) |
The Euler-Lagrange equation subject to m1 gives the local fraction of constituents of the first type,
| (68) |
Considering (66), we also obtain the local concentration of constituents of the second type,
| (69) |
Further, it is assumed that the concentration of constituents of the first type is much smaller than the concentration of constituents of the second type,
| (70) |
implying that 2q10 cosh (d1,eff/2) exp(−λ1/kT)/2q20 cosh (d2,eff/2) is small.
The global constraint
| (71) |
gives
| (72) |
Taking into account the approximation for small x, ln(1 + x) ≅ x and the definitions for qi0 (Equation (27) and di,eff (Equation (31)) yields, for the monolayer,
| (73) |
The first two terms of Equation (73) recover the elastic energy of the membrane composed of constituents of the second (abundant) type, while the third term describes the nonlocal effect caused by distribution and orientational ordering of constituents of the first (scarce) type.
To obtain the free energy of the bilayer membrane, the two monolayer contributions are summed. It is taken into account that the curvature tensor has different signs in the opposing monolayers (Equation (59)). Omitting the constant terms gives
| (74) |
The self-consistent solution of the variational problem based on a functional including the system free energy and relevant local and global constraints, yields equilibrium lateral and orientational distribution functions and the equilibrium free energy, all of which derive from the same principle of single-constituent energy.38
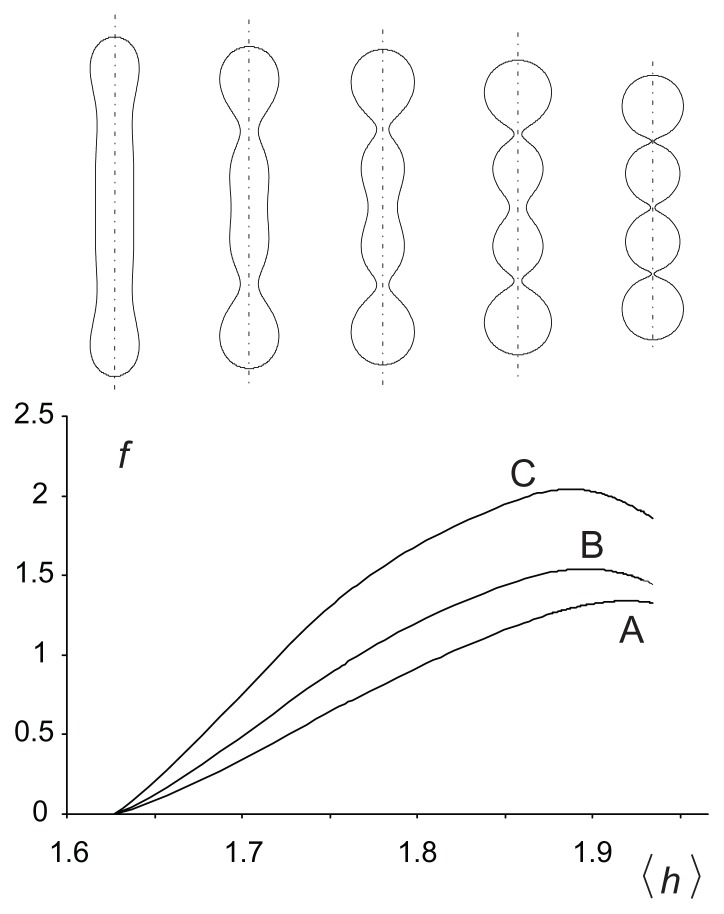
In solving the variational problem,38 dimensionless quantities are used, ie, h = HRs, d = DRs, hm = HmRs, and dm = DmRs, where . The equilibrium free energy of the nanovesicle membrane bilayer enclosing dimensionless volume V = (36πV2/A3)1/2, where V is the enclosed volume, as a function of the average mean curvature of the membrane 〈h〉 = ∫ hdA/4πRs2 is shown in Figure 3. Three interaction constants (ξ1/kTRs2) were considered. It can be seen that the energy increases with increasing 〈h〉 due to an increase in the isotropic bending energy. With increasing 〈h〉, the shape of the nanovesicle becomes undulated and the necks become narrow. Anisotropy of the curvature becomes high in the necks so the constituents undergo ordering. Redistribution and orientational ordering of the constituents diminish the free energy. For high enough interaction constants (ξ1/kTRs2), the free energy reaches a maximum and then decreases. In such cases, the energy dependence exhibits two local minima corresponding to the limit shapes (cylinders and spheres, respectively).
Figure 3.
Free energy of a two-component nanovesicle as a function of the average mean curvature of the membrane for three interaction constants, ξ1/2kTRs2 (A) 0.001, (B) 0.020, and (C) 0.040. It was taken that ξ1 = ξ1* and ξ2 = ξ2*.
Notes: The values of other model parameters were ξ1/2kTRs2 = 0.001, h1,m = 2, d1,m = 2, h2,m = 0, d2,m = 0, M1,T = 0.1 MT, v = 0.5. Five characteristic equilibrium shapes obtained by solving the system of Euler-Lagrange equations subject to isotropic bending energy are also depicted at the corresponding 〈h〉 values.
The shape corresponding to the minimum of the average mean curvature within the given class of shapes is composed of a cylinder with hemispherical caps, and the shape corresponding to the maximum of the average mean curvature is composed of quasispherical units connected by very thin necks. For the chosen parameters, the tubular limit shape corresponds to the minimum of the global energy (Figure 3).
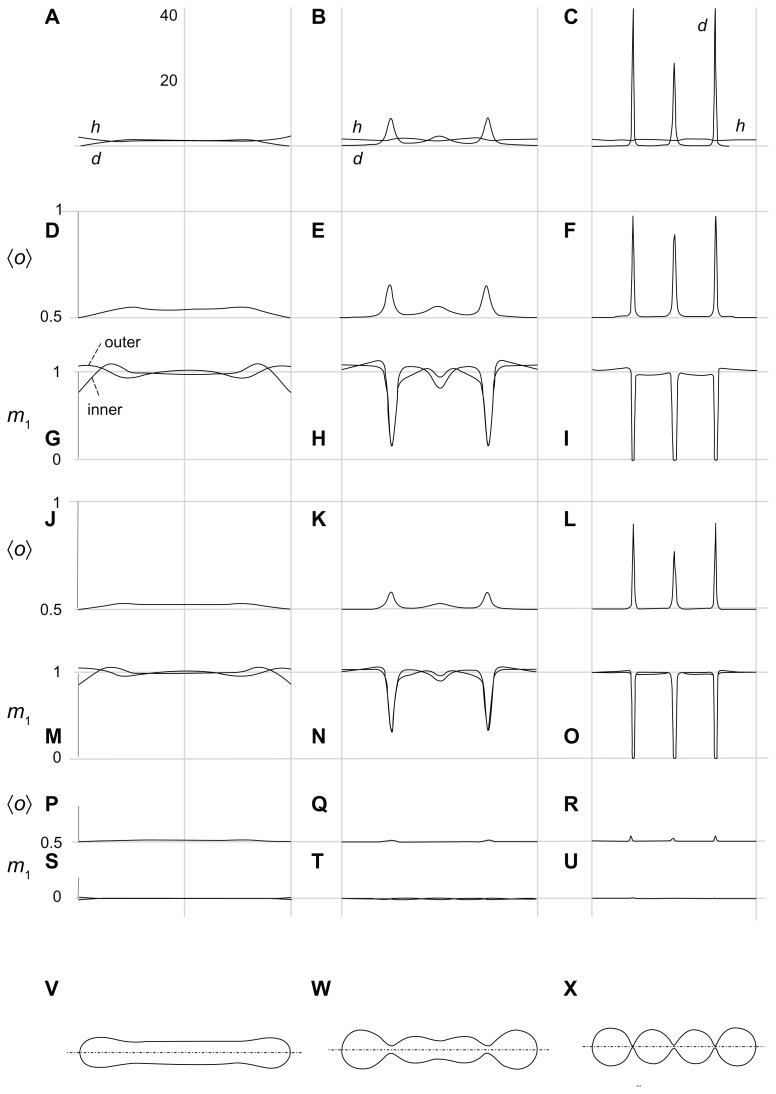
Figure 4 shows the mean curvature and the curvature deviator of the nanovesicle as a function of the coordinate along the long axis (A–C), ie, the average orientation of the anisotropic constituents 〈o〉 = 1/[1 + exp(−d1,eff)] which we describe as the average local number of constituents with the lowest energy of type 1 (scarce type) for the three interaction constants (ξ1/kTRs2) considered in Figure 3, (D–F, J–L, P–R), the equilibrium distribution of constituents of type 1 in both membrane layers (G–I, M–O, S–U) and the respective shapes (V–X), which are also considered in Figure 3. If the interaction constant (ξ1/kTRs2) is small, the constituents are uniformly distributed over both membrane layers in all shapes (S–U). There is almost no ordering of the constituents in the tubular shape (P), while weak ordering takes place in the necks (Q, R). For higher values of the interaction constant, deviations of the distributions from uniformity are small in the tubular shape (M) while they are strong in the necks (N, O), the effect being stronger if the necks are thinner. Type 1 molecules are depleted from the necks, but the ones that remain undergo substantial ordering (L, F). The values of the curvature deviator in the narrow necks may be rather high (up to 40 in panel C). Because the value of the normalized intrinsic deviator was taken as 2, constituents do not favor the necks. Figure 4 provides clarification of the free energy dependence depicted in Figure 3.
Figure 4.
Calculated equilibrium configuration of three characteristic shapes of a two-component nanovesicle. It was taken that ξ1 = ξ1* and ξ2 = ξ2*,ξ2/2kTRs2 = 0.001, h1,m = 2, d1,m = 2, h2,m = 0, d2,m = 0, M1,T = 0.1 MT, v = 0.5. (D–I)ξ1/2kTRs2 = 0.04, (J–O) ξ1/2kTRs2 = 0.02, (P–U)ξ1/2kTR s2 = 0.001. (V–X) the characteristic shapes and (A–C) the respective invariants of the curvature tensor.
It can be seen in Figures 3 and 4 that the nanotubule corresponds to the global minimum of free energy, so it could be considered as energetically the most favorable and therefore the most probable. However, if there is a process in the system that increases the average mean curvature of the membrane (such as integration of molecules into the outer membrane layer), the system may be driven towards the shape composed of spherical units.
Deviatoric elasticity may stabilize anisotropic nanostructures
Quadrupolar ordering of phospholipid molecules in a deviatoric field has been used to describe the stability of shapes with strongly anisotropically curved structures, such as nanotubular protrusions,37 tubular and spherical nanovesicles of the erythrocyte membrane,45 torocyte endovesicles,46 narrow necks of one-component phospholipid vesicles,38 two-component vesicles,34,47 peptidergic vesicles,48 nanotubules in astrocytes49 and urothelial cancer cells,50–52 flattened structures in Golgi bodies,53 inverse hexagonal lipid phases,54 and membrane pores.55,56 While it was previously acknowledged that membrane composition and shape are interdependent,34,57–59 the orientational ordering model provides a unified explanation of the above feature, and has been reviewed extensively elsewhere.37,45,60,61
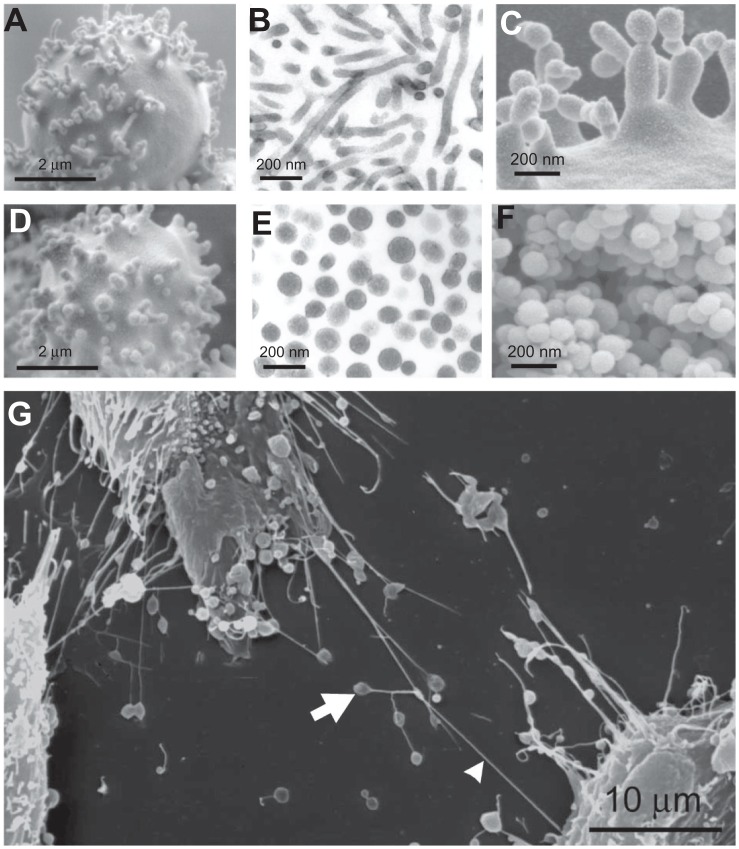
Figure 5 presents some of these nanostructures, with buds and nanovesicles of the erythrocyte membrane and nanotubules observed in urothelial cancer cells. Dilatations of the nanotubules are often present. These dilatations travel along the tube and discharge material when they reach the cell surface, so are called gondolae. Transport by gondolae is also observed in phospholipid vesicles.62
Figure 5.
Nanobuds and nanovesicles of the erythrocyte membrane and nanotubules connecting T24 cancer cells. In erythrocytes, budding and vesiculation was induced by adding a detergent. The type of detergent determines the character of the nanobuds and nanovesicles. (A) Scanning electron micrograph of echinocyte budding induced by dodecylmaltoside, (B) transmission electron micrograph of isolated tubular nanovesicles induced by dodecylmaltoside, (C) scanning electron micrograph of the budding erythrocyte membrane, (D) scanning electron micrograph of echinocyte budding induced by dodecylzwittergent, (E) transmission electron micrograph of isolated spherical nanovesicles, (F) scanning electron micrograph of isolated spherical nanovesicles, (G) nanotubules with dilatations connecting urothelial cancer cells. (A, B, D, E, and G) reproduced with permission of Schara et al63 and (C and F) reproduced from Sustar et al.64
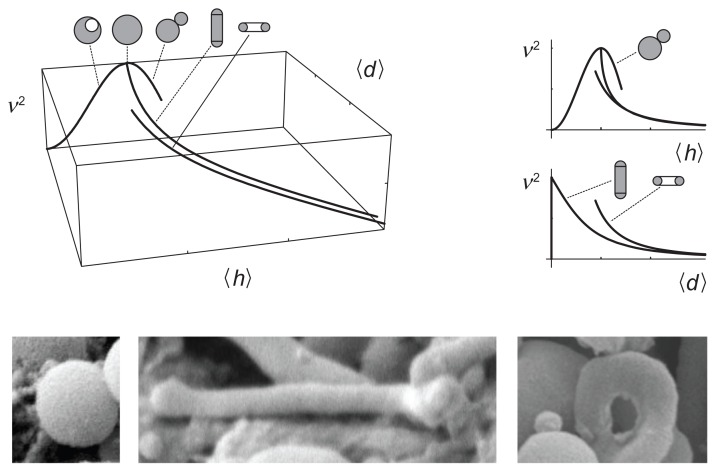
The proposed description is based on two invariants of the curvature tensor, ie, the trace (mean curvature) and the deviator. It seems natural that the average values of these two invariants would span a phase diagram of possible shapes
| (76) |
| (77) |
The third parameter which determines the shape is the relative volume, v. Therefore it is convenient to present the set of equilibrium shapes within the (v, 〈h〉, 〈d〉) coordinate system. Figure 6 shows a (v, 〈h〉, 〈d〉) phase diagram, with selected curves representing limit shapes composed of spheres, tubes, and tori. The predicted shapes are indeed observed in blood isolates (Figure 6).
Figure 6.
A (v, 〈h〉, 〈d〉) phase diagram with curves representing limit shapes (spheres, tubes, and tori) and characteristic shapes of microvesicles found in blood isolates (a sphere, a tube and a torus).
Clinical relevance of cell nanovesicles
It was reported early on that “platelet dust” existed in plasma.65 It was also observed that nanosized particles called microvesicles are shed from the membranes of erythrocytes during storage66–68 and from membranes of other cells, including cancer cells.69–72 These nanoparticles were connected to coagulopathies secondary to cancer.73–76 It has been suggested that they may play a role in the coagulation process inside blood vessels.77
Membrane asymmetry in nanovesicles is corrupted so that negatively charged phospholipid phosphatidylserine appears in the outer membrane layer, a process which is necessary to trigger formation of a blood clot. Further, the membrane of platelet-derived nanovesicles contains tissue factor, an integral membrane protein present in endothelial cells, platelets, and leukocytes. Tissue factor is the primary cellular initiator of the coagulation protease cascade, which leads to fibrin deposition and activation of platelets. Thus, the nanovesicle membranes contribute considerably to the catalytic surface needed for formation of blood clots. Aberrant tissue factor expression within the vasculature initiates life-threatening thrombosis in a number of diseases, including cancer. Also, recent studies have revealed a nonhemostatic role of tissue factor in the generation of coagulation proteases and subsequent activation of receptors on vascular cells, and this tissue factor-dependent signaling contributes to a variety of biological processes, including metastasis.78–80 Nanovesicles that are pinched off from cells interact with other cells81,82 and thereby mediate interactions between platelets, endothelial cells, and tumor cells which can be expressed by thromboembolism in cancer.83,84 Further, nanovesicles were shown to stimulate proliferation of cancer cells, mRNA expression for angiogenic factors, as well as adhesion to fibrinogen and endothelial cells85 and downregulation of antitumoral immune responses in the host.86
Clinical studies have shown that the concentration of nanovesicles isolated from blood in patients with a range of diseases is changed with respect to healthy subjects. For example, the concentration of nanovesicles was found to be increased in patients with lung cancer,74 dermatofibroma,87 dermatofibrosarcoma protuberans,87 carcinoma of the oral cavity,88 ovarian cancer,89 and gastrointestinal cancer.90,91 It was recently suggested that the material isolated from blood contains both nanovesicles and residual cells, and that residual cells, mostly platelets, are the origin of the nanovesicles found in isolates as an artifact of the isolation procedure.64 However, clinical studies show differences between concentrations of nanovesicles isolated from the blood of patients with cancer and from that from healthy subjects, suggesting that the properties of blood cells and plasma which determine the state of the isolate in cancer patients and in healthy subjects differ from each other.64
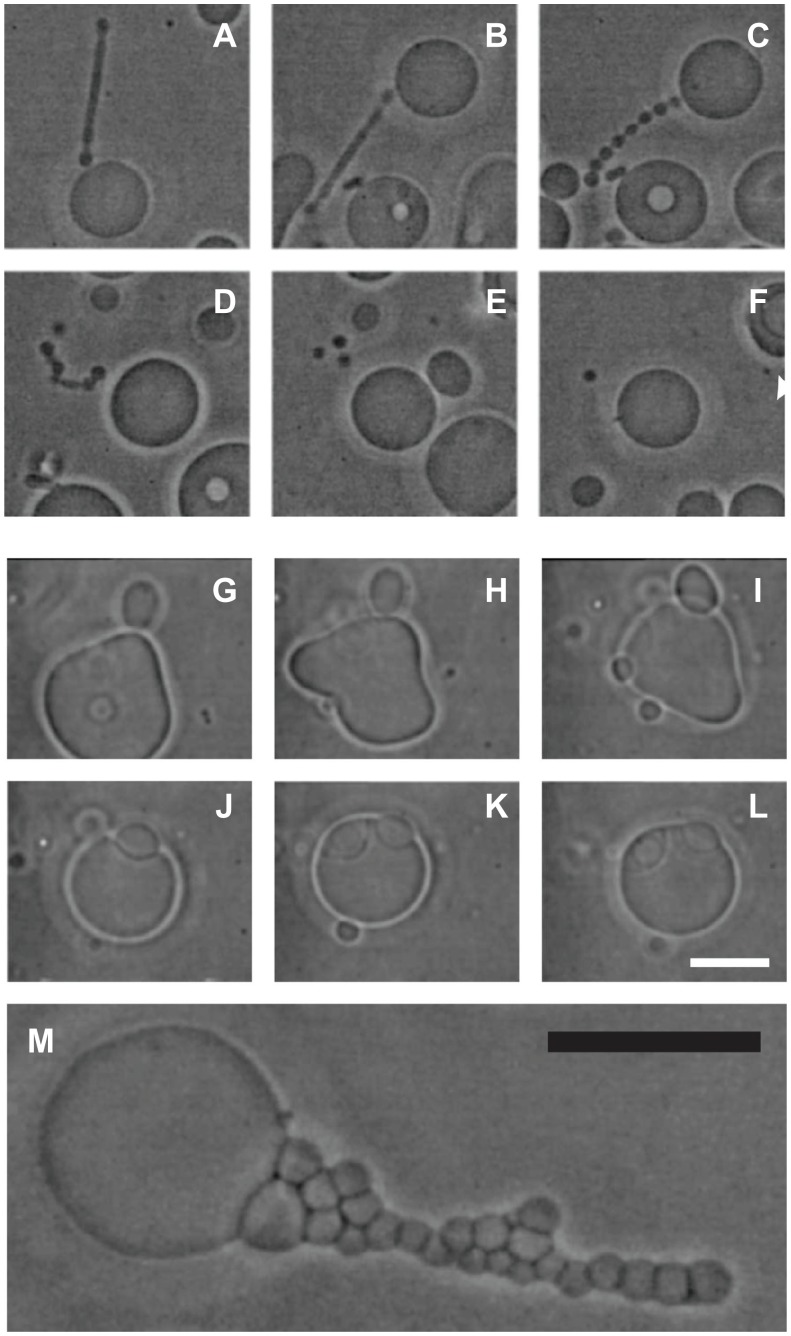
Given that nanovesicles are considered to be procoagulant and prometastatic, it could be beneficial to develop methods for suppression of nanovesiculation. To obtain an insight into the processes taking place during budding and pinching off from cells, studies were undertaken of giant phospholipid vesicles which are large enough to be observed directly by phase-contrast microscopy. Figure 7 illustrates the effect of the composition of the surrounding solution on budding of the giant phospholipid vesicle membrane. Budding was induced by raising the temperature of the sample. 92 When the tube was of sufficient length (Figure 7A), heating was discontinued and phosphate-buffered saline was added to the sample. The protrusion underwent beading (Figure 7B, C), substantial movement, followed by its detachment from the mother vesicle (Figure 7D), and finally decomposition into spherical vesicles (Figure 7E), which migrated away from the mother vesicle (Figure 7F). However, if molecules which mediate the attractive interaction between membranes (specific proteins) were present in the solution, the bud (Figures 7G and H) was attracted back to the mother membrane (Figure 7I) and remained bound to the surface of the mother vesicle (Figure 7J–L).
Figure 7.
(A–F) Vesiculation of a giant phospholipid vesicle. After addition of phosphate-buffered saline to a suspension of vesicles, the tubular bud (A) exhibited undulations (B and C), detached itself from the mother vesicle (D), and decomposed into separate spherical vesicles (E), which were free to migrate away from the mother vesicle (F). (G–L) show suppression of vesiculation. When molecules which mediate attractive interaction between membranes (proteins dissolved in phosphate-buffered saline) were present in the solution, the bud (G and H) was attracted back to the mother membrane (I) where it remained bound to the surface of the mother vesicle (J–L). (M) Bead-like structures forming a long bud adhered to each other due to the mediating effect of added proteins dissolved in phosphate-buffered saline.
Notes: Bars represent 10 μm.
Reprinted from Urbanija et al92 with the permission of Elsevier.
Observing this process inspired the hypothesis that molecules which mediate attractive interaction between membranes are both anticoagulant and antimetastatic.44,92,93 Blood plasma mediates this attractive interaction,94 indicating that molecules with the required properties are present in blood. Heparin (a common choice of anticoagulant prophylaxis and treatment) induces adhesion between phospholipid vesicles.44,93,94 Heparin is known to have an antimetastatic effect in some types of cancer,95 which supports the hypothesis of the anticoagulant and antimetastatic effect of plasma constituents based on suppression of nanovesiculation.44
Conclusion
It is now acknowledged that cell-cell communication may take place via nanotubules96–98 and nanovesicles,99 and that these processes are important in cancer.100 In order to manipulate membranous nanostructures, they should be better understood. Membrane properties that are the key to formation of tubules and vesicles can be subjected to the methods of theoretical physics.39,40,101
In addition to considering membrane nanodomains (rafts) as an acknowledged extension of the fluid mosaic model of the membrane,102 another major mechanism should also be acknowledged, ie, orientational ordering of membrane constituents on strongly anisotropically curved membrane regions. This mechanism provides an explanation for the stability of different types of membranous nanostructures, including nanotubules and nanovesicles, which are important in cell-cell communication and involved in cancer progression. This approach has led to prediction of transport by membranous nanotubules62 which was then found experimentally in cells.96 Also, the orientational ordering of mediating molecules is the basis of short-ranged attractive interactions involving membrane surface(s).103
It has been shown experimentally that there are some common properties in most biological membranes. Budding and vesiculation takes place in erythrocytes which lack a nucleus and cytoskeleton, and in cells with a nucleus and cytoskeleton. Moreover, these features can also be observed in artificial membranes composed of pure or mixed lipids, demonstrating that the phospholipid bilayer is indeed the backbone of the biological membrane. It is an essential feature of membranes that they create their own geometry, and furthermore, this geometry is the relevant field which determines their energy. The theoretical description of the system is based on the notion that the system seeks the state of lowest energy consistent with one of the most basic laws of nature, ie, it will attain the state that is the most probable.
This work focuses on a particular mechanism involved in metastasis (ie, cell-to-cell communication by nanovesicles), which does not exclude other mechanisms that were suggested previously (eg, crawling over a surface, phagocytosis, extension of pseudopodia). The experimental evidence indicates that nanovesiculation takes place in vitro and in vivo, but it is not yet certain to what extent it increases the probability of cancer spreading in vivo. It can be concluded that the stability of membranous nanostructures is a possible key mechanism of cancer progression.
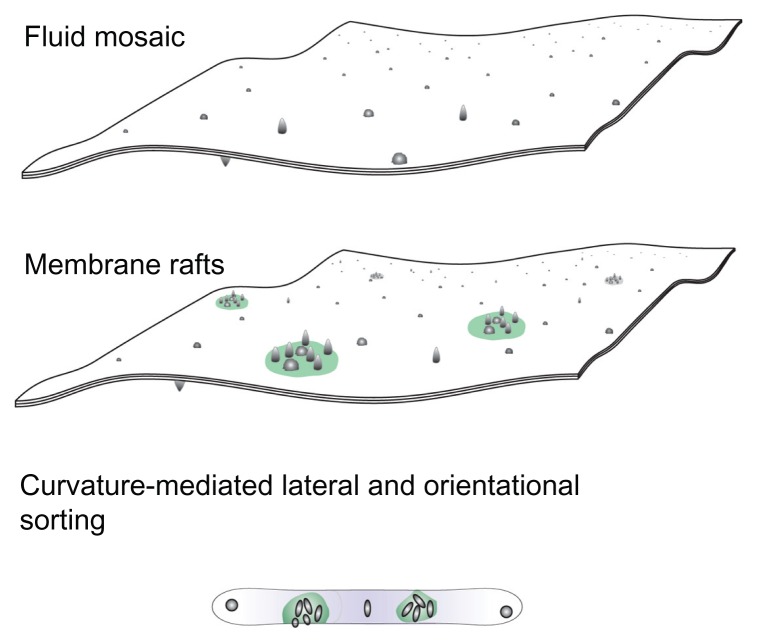
Figure 1.
A schematic representation of three models of the membrane, ie, the fluid mosaic model,27 the membrane raft model,28–30 and the curvature-mediated lateral and orientational sorting model.34,35
Note: Violet color indicates orientational ordering of lipid molecules in the tubular portion.
Acknowledgments
The author acknowledges support from the Slovenian Research Agency (projects J3-2120 and J3-4108), EUREKA grant IMIPEB, and Novartis International AG.
Footnotes
Disclosure
The author reports no conflicts of interest in this work.
References
- 1.World Health Organization Media Centre. Fact sheet 297. Feb 20, [Accessed April 9, 2012]. Available from: http://www.who.int/mediacentre/factsheets/fs297/en/
- 2.Grizzi F, Chiriva-Internati M. Cancer: looking for simplicity and finding complexity. Cancer Cell Int. 2006;6:4. doi: 10.1186/1475-2867-6-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ratajczak J, Wysoczynski M, Hayek F, Janowska-Wieczorek A, Ratajczak MZ. Membrane-derived microvesicles: important and underappreciated mediators of cell to cell communication. Leukemia. 2006;20:1487–1495. doi: 10.1038/sj.leu.2404296. [DOI] [PubMed] [Google Scholar]
- 4.Baj-Krzyworzeka M, Majka M, Pratico D, et al. Platelet-derived microparticles stimulate proliferation, survival, adhesion, and chemotaxis of hematopoietic cells. Exp Hematol. 2002;30:450–459. doi: 10.1016/s0301-472x(02)00791-9. [DOI] [PubMed] [Google Scholar]
- 5.Janowska-Wieczorek A, Majka M, Kijowski J, et al. Platelet-derived microparticles bind to hematopoietic stem/progenitor cells and enhance their engraftment. Blood. 2001;98:3143–3149. doi: 10.1182/blood.v98.10.3143. [DOI] [PubMed] [Google Scholar]
- 6.Rozmyslowicz T, Majka M, Kijowski J, et al. Platelet- and megakaryocyte-derived microparticles transfer CXCR4 receptor to CXCR4-null cells and make them susceptible to infection by X4-HIV. AIDS. 2003;17:33–42. doi: 10.1097/00002030-200301030-00006. [DOI] [PubMed] [Google Scholar]
- 7.Ratajczak J, Miekus K, Kucia M, et al. Embryonic stem cell-derived microvesicles reprogram hematopoietic progenitors: evidence for horizontal transfer of mRNA and protein delivery. Leukemia. 2006;20:847–856. doi: 10.1038/sj.leu.2404132. [DOI] [PubMed] [Google Scholar]
- 8.Fevrier B, Vilette D, Archer F, et al. Cells release prions in association with exosomes. Proc Natl Acad Sci U S A. 2004;101:9683–9688. doi: 10.1073/pnas.0308413101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Robertson C, Booth SA, Beniac DR, et al. Cellular prion protein is released on exosomes from activated platelets. Blood. 2006;107:3907–3911. doi: 10.1182/blood-2005-02-0802. [DOI] [PubMed] [Google Scholar]
- 10.Vella LJ, Greenwood DLV, Cappai R, et al. Enrichment of prion protein in exosomes derived from ovine cerebral spinal fluid. Vet Immunol Immunopathol. 2008;124:385–393. doi: 10.1016/j.vetimm.2008.04.002. [DOI] [PubMed] [Google Scholar]
- 11.Pisetsky DS. Microparticles as biomarkers in autoimmunity: from dust bin to center stage. Arthritis Res Ther. 2009;11:135. doi: 10.1186/ar2856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Reich CF, Pisetsky DS. The content of DNA and RNA in microparticles released by Jurkat and HL-60 cells undergoing in vitro apoptosis. Exp Cell Res. 2009;315:760–768. doi: 10.1016/j.yexcr.2008.12.014. [DOI] [PubMed] [Google Scholar]
- 13.Ardoin SP, Shanahan JC, Pisetsky DS. The role of microparticles in inflammation and thrombosis. Scand J Immunol. 2007;66:159–165. doi: 10.1111/j.1365-3083.2007.01984.x. [DOI] [PubMed] [Google Scholar]
- 14.Baj-Krzyworzeka M, Szatanek R, Weglarczyk K, et al. Tumour-derived microvesicles carry several surface determinants and mRNA of tumour cells and transfer some of these determinants to monocytes. Cancer Immunol Immunother. 2005;55:808–818. doi: 10.1007/s00262-005-0075-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pelchen-Matthews A, Raposo G, Marsh M. Endosomes, exosomes and Trojan viruses. Trends Microbiol. 2004;12:310–316. doi: 10.1016/j.tim.2004.05.004. [DOI] [PubMed] [Google Scholar]
- 16.Coltel N, Combes V, Wassmer SC, Chimini G, Grau GE. Cell vesiculation and immunopathology: implications in cerebral malaria. Microbes Infect. 2006;8:2305–2316. doi: 10.1016/j.micinf.2006.04.006. [DOI] [PubMed] [Google Scholar]
- 17.Ratajczak MZ. Enhancing effect of platelet-derived microvesicles on the invasive potential of breast cancer cells. Transfusion. 2006;46:1199–1209. doi: 10.1111/j.1537-2995.2006.00871.x. [DOI] [PubMed] [Google Scholar]
- 18.Janowska-Wieczorek A, Marquez-Curtis LA, Wysoczynski M, Ratajczak MZ. Enhancing effect of platelet-derived microvesicles on the invasive potential of breast cancer cells. Transfusion. 2006;46:1199–1209. doi: 10.1111/j.1537-2995.2006.00871.x. [DOI] [PubMed] [Google Scholar]
- 19.Junkar I, Sustar V, Frank M, et al. Blood and synovial microparticles as revealed by atomic force and scanning electron microscope. Open Autoimmun J. 2009;1:e50–e58. [Google Scholar]
- 20.Mrvar-Brecko A, Sustar V, Jansa V, et al. Isolated microvesicles from peripheral blood and body fluids as observed by scanning electron microscope. Blood Cells Mol Dis. 2010;44:307–312. doi: 10.1016/j.bcmd.2010.02.003. [DOI] [PubMed] [Google Scholar]
- 21.Lu J, Getz G, Miska EA, et al. MicroRNA expression profiles classify human cancers. Nature. 2005;435:834–838. doi: 10.1038/nature03702. [DOI] [PubMed] [Google Scholar]
- 22.Calin GA, Ferracin M, Cimmino A, et al. A microRNA signature associated with prognosis and progression in chronic lymphocytic leukemia. N Engl J Med. 2005;353:1793–1801. doi: 10.1056/NEJMoa050995. [DOI] [PubMed] [Google Scholar]
- 23.Metias SM, Lianidou E, Yousef GM. MicroRNAs in clinical oncology: at the crossroads between promises and problems. J Clin Pathol. 2009;62:771–776. doi: 10.1136/jcp.2009.064717. [DOI] [PubMed] [Google Scholar]
- 24.Patel N, Saute R. Body fluid micro(mi)RNA as biomarkers for human cancer. J Nucleic Acids Investig. 2011;2:e1. [Google Scholar]
- 25.White NM, Yousef GM. MicroRNAs: exploring a new dimension in the pathogenesis of kidney cancer. BMC Med. 2010;8:65. doi: 10.1186/1741-7015-8-65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nielsen BS, Jorgensen S, Fog JU, et al. High levels of microRNA-21 in the stroma of colorectal cancers predict short disease-free survival in stage II colon cancer patients. Clin Exp Metastasis. 2010;28:27–38. doi: 10.1007/s10585-010-9355-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Singer SJ, Nicolson GL. The fluid mosaic model of the structure of cell membranes. Science. 1972;175:720–731. doi: 10.1126/science.175.4023.720. [DOI] [PubMed] [Google Scholar]
- 28.Simons K, Ikonen E. Functional rafts in cell membranes. Nature. 1997;387:569–572. doi: 10.1038/42408. [DOI] [PubMed] [Google Scholar]
- 29.Brown DA, London E. Functions of lipid rafts in biological membranes. Annu Rev Cell Dev Biol. 1998;14:111–136. doi: 10.1146/annurev.cellbio.14.1.111. [DOI] [PubMed] [Google Scholar]
- 30.Brown DA, London EJ. Structure and origin of ordered lipid domains in biological membranes. J Membr Biol. 1998;164:103–114. doi: 10.1007/s002329900397. [DOI] [PubMed] [Google Scholar]
- 31.Pike LJ. Rafts defined: a report on the keystone symposium on lipid rafts and cell function. J Lipid Res. 2006;47:1597–1598. doi: 10.1194/jlr.E600002-JLR200. [DOI] [PubMed] [Google Scholar]
- 32.Simons K, Gerl MJ. Revitalizing membrane rafts: new tools and insights. Nat Rev Mol Cell Biol. 2010;11:688–699. doi: 10.1038/nrm2977. [DOI] [PubMed] [Google Scholar]
- 33.Melkonian KA, Ostermeyer AG, Chen JZ, et al. Role of lipid modifications in targeting proteins to detergent-resistant membrane rafts. Many raft proteins are acylated, while few are prenylated. J Biol Chem. 1999;274:3910–3917. doi: 10.1074/jbc.274.6.3910. [DOI] [PubMed] [Google Scholar]
- 34.Kralj-Iglic V, Heinrich V, Svetina S, Zeks B. Free energy of closed membrane with anisotropic inclusions. Eur Phys J B. 1999;10:5–8. [Google Scholar]
- 35.Kralj-Iglic V, Remskar M, Iglic A. Deviatoric elasticity as a mechanism describing stable shapes of nanotubes. In: Reimer A, editor. Horizons in World Physics. Hauppauge, NY: Nova Science Publishers; 2004. [Google Scholar]
- 36.Hill TL. An Introduction to Statistical Thermodynamics. Reading, MA: Adison Wesley; 1986. [Google Scholar]
- 37.Kralj-Iglic V, Iglic A, Gomiscek G, et al. Microtubes and nanotubes of a phospholipid bilayer membrane. J Phys A: Math Gen. 2002;35:1533–1549. [Google Scholar]
- 38.Kralj-Iglic V, Babnik B, Gauger DR, et al. Quadrupolar ordering of phospholipid molecules in narrow necks of phospholipid vesicles. J Stat Phys. 2006;125:727–752. [Google Scholar]
- 39.Helfrich W. Elastic properties of lipid bilayers – theory and possible experiments. Z Naturforsch C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 40.Seifert U. Configurations of fluid membranes and vesicles. Adv Phys. 1997;46:13–137. [Google Scholar]
- 41.May S, Iglic A, Rescic J, et al. Bridging like-charged macroions through long divalent rod-like ions. J Phys Chem B. 2008;112:1685–1692. doi: 10.1021/jp073355e. [DOI] [PubMed] [Google Scholar]
- 42.Gongadze E, Iglic A. Decrease of permittivity of an electrolyte solution near a charged surface due to saturation and excluded volume effects. Bioelectrochemistry. doi: 10.1016/j.bioelchem.2011.12.001. [DOI] [PubMed] [Google Scholar]
- 43.Gongadze E, van Rienen U, Iglic A. Generalized Stern models of an electric double layer considering the spatial variation of permittivity and finite size of ions in saturation regime. Cell Mol Biol Lett. 2011;16:576–594. doi: 10.2478/s11658-011-0024-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kralj-Iglic V, Sustar V, Hagerstrand H, et al. Suppression of membrane vesiculation: A possible anticoagulant, antimetastatic and antiinflammatory effect of heparin. In: Piyathilake DE, Liang RH, editors. Heparin: Properties, Uses and Side Effects. Hauppauge, NY: Nova Science Publishers; 2011. pp. 27–57. [Google Scholar]
- 45.Kralj-Iglic V, Iglic A, Hagerstrand H, Peterlin P. Stable tubular microexovesicles of the erythrocyte membrane induced by dimeric amphiphiles. Phys Rev E. 2000;61:4230–4234. doi: 10.1103/physreve.61.4230. [DOI] [PubMed] [Google Scholar]
- 46.Bobrowska-Hagerstand M, Kralj-Iglic V, Iglic A, Bialkowska K, Isomaa B, Hägerstrand H. Torocyte membrane endovesicles induced by octaethyleneglycol dodecylether in human erythrocytes. Biophys J. 1999;77:3356–3362. doi: 10.1016/S0006-3495(99)77167-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Iglic A, Babnik B, Bohinc K, et al. On the role of anisotropy of membrane constituents in formation of a membrane neck during budding of a multicomponent membrane. J Biomech. 2007;40:579–585. doi: 10.1016/j.jbiomech.2006.02.006. [DOI] [PubMed] [Google Scholar]
- 48.Jorgacevski J, Fosnaric M, Vardjan N, et al. Fusion pore stability of peptidergic vesicles. Mol Membr Biol. 2010;27:65–80. doi: 10.3109/09687681003597104. [DOI] [PubMed] [Google Scholar]
- 49.Gimsa U, Iglic A, Fiedler S, et al. Actin is not required for nanotubular protrusions of primary astrocytes grown on metal nanolawn. Mol Membr Biol. 2007;24:243–255. doi: 10.1080/09687860601141730. [DOI] [PubMed] [Google Scholar]
- 50.Veranic P, Lokar M, Schutz GJ, et al. Different types of cell-to-cell connections mediated by nanotubular structures. Biophys J. 2008;95:4416–4425. doi: 10.1529/biophysj.108.131375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kabaso D, Lokar M, Kralj-Iglic V, et al. Temperature and cholera toxin B are factors that influence formation of membrane nanotubes in RT4 and T24 urothelial cancer cell lines. Int J Nanomedicine. 2011;6:495–509. doi: 10.2147/IJN.S16982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kabaso D, Gongadze E, Elter P, et al. Attachment of rod-like (BAR) proteins and membrane shape. Mini Rev Med Chem. 2011;11:272–282. doi: 10.2174/138955711795305353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Iglic A, Fosnaric M, Hagerstrand H, Kralj-Iglic V. Coupling between vesicle shape and the non-homogeneous lateral distribution of membrane constituents in Golgi bodies. FEBS Lett. 2004;574:9–12. doi: 10.1016/j.febslet.2004.07.085. [DOI] [PubMed] [Google Scholar]
- 54.Mares T, Daniel M, Perutkova S, et al. Role of phospholipid asymmetry in the stability of inverted hexagonal mesoscopic phases. J Phys Chem B. 2008;8:16575–16584. doi: 10.1021/jp805715r. [DOI] [PubMed] [Google Scholar]
- 55.Fosnaric M, Kralj-Iglic V, Bohinc K, et al. Stabilization of pores in lipid bilayers by anisotropic inclusions. J Phys Chem B. 2003;107:12519–12526. [Google Scholar]
- 56.Kanduser M, Fosnaric M, Sentjurc M, et al. Effect of surfactant polyoxyethylene glycol (C12E8) on electroporation of cell line DC3F. Colloid Surfaces A. 2003;214:205–217. [Google Scholar]
- 57.Gozdz WT, Gompper G. Composition-driven shape transformations of membranes of complex topology. Phys Rev Lett. 1998;80:4213–4216. [Google Scholar]
- 58.Gozdz WT, Gompper G. Shapes and shape transformations of two-component membranes of complex topology. Phys Rev E. 1999;59:4305–4316. [Google Scholar]
- 59.Shlomovitz R, Gov NS, Roux A. Membrane-mediated interactions and the dynamics of dynamin oligomers on membrane tubes. New J Phys. 2011;13:1–25. [Google Scholar]
- 60.Iglic A, Kralj-Iglic V. Effect of anisotropic properties of membrane constituents on stable shape of membrane bilayer structure. In: Tien HT, Ottova-Leitmannova A, editors. Planar Lipid Bilayers (BLMs) and their Applications. Amsterdam, The Netherlands: Elsevier; 2003. pp. 143–172. [Google Scholar]
- 61.Iglic A, Babnik B, Gimsa U, Kralj-Iglic V. On the role of membrane anisotropy in beading transition of undulated tubular membrane structures. J Phys A Math Gen. 2005;38:8527–8536. [Google Scholar]
- 62.Iglic A, Hagerstrand H, Bobrowska-Hagerstrand M, et al. Possible role of phospholipid nanotubes in directed transport of membrane vesicles. Phys Lett A. 2003;310:493–497. [Google Scholar]
- 63.Schara K, Jansa V, Sustar V, et al. Mechanisms for the formation of membranous nanostructures in cell-to-cell communication. Cell Mol Biol Lett. 2009;14:636–656. doi: 10.2478/s11658-009-0018-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Suštar V, Bedina-Zavec A, Stukelj R, et al. Nanoparticles isolated from blood – a reflection of vesiculability of blood cells during the isolation process. Int J Nanomedicine. 2011;6:2737–2748. doi: 10.2147/IJN.S24537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Wolf P. The nature and significance of platelet products in human plasma. Br J Haematol. 1967;13:269–288. doi: 10.1111/j.1365-2141.1967.tb08741.x. [DOI] [PubMed] [Google Scholar]
- 66.Rumsby MG, Trotter J, Allan D, Michell RH. Recovery of membrane micro-vesicles from human erythrocytes stored for transfusion: a mechanism for the erythrocyte discocyte-to-spherocyte shape transformation. Biochem Soc Trans. 1977;5:126–128. doi: 10.1042/bst0050126. [DOI] [PubMed] [Google Scholar]
- 67.Greenwalt TJ. The how and why of exocytic vesicles. Transfusion. 2006;46:143–152. doi: 10.1111/j.1537-2995.2006.00692.x. [DOI] [PubMed] [Google Scholar]
- 68.Sens P, Gov N. Force balance and membrane shedding at the red-blood-cell surface. Phys Rev Lett. 2007;98:1–4. doi: 10.1103/PhysRevLett.98.018102. [DOI] [PubMed] [Google Scholar]
- 69.Black PH. Shedding from normal and cancer-cell surfaces. N Engl J Med. 1980;303:1415–1416. doi: 10.1056/NEJM198012113032411. [DOI] [PubMed] [Google Scholar]
- 70.Taylor DD, Chou IN, Black PH. Isolation of plasma-membrane fragments from cultured murine melanoma cells. Biochem Biophys Res Commun. 1983;113:470–476. doi: 10.1016/0006-291x(83)91749-7. [DOI] [PubMed] [Google Scholar]
- 71.Kralj-Iglic V, Batista U, Hagerstrand H, et al. On mechanisms of cell plasma membrane vesiculation. Radiol Oncol. 1998;32:119–123. [Google Scholar]
- 72.Taylor DD, Black PH. Neoplastic and developmental importance of plasma membrane vesicles. Am Zool. 1987;26:411–415. doi: 10.1007/978-1-4684-5050-7_3. [DOI] [PubMed] [Google Scholar]
- 73.Bastida E, Ordinas A, Jamieson GA. Identity of procoagulant and platelet aggregating activities in microvesicles from human glioblastoma cells. Thromb Haemost. 1983;50:218. [Google Scholar]
- 74.del Conde I, Bharwani LD, Dietzen DJ, et al. Microvesicle-associated tissue factor and Trousseau’s syndrome. J Thromb Haemost. 2007;5:70–74. doi: 10.1111/j.1538-7836.2006.02301.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Rauch U, Antoniak S. Tissue factor-positive microparticles in blood associated with coagulopathy in cancer. Thromb Haemost. 2007;97:9–10. [PubMed] [Google Scholar]
- 76.Tesselaar ME, Romijn FP, van der Linden IK, et al. Microparticle-associated tissue factor activity in cancer patients with and without thrombosis. J Thromb Haemost. 2009;7:1421–1423. doi: 10.1111/j.1538-7836.2009.03504.x. [DOI] [PubMed] [Google Scholar]
- 77.Muller I, Klocke A, Alex M, et al. Intravascular tissue factor initiates coagulation via circulating microvesicles and platelets. FASEB J. 2000;17:476–478. doi: 10.1096/fj.02-0574fje. [DOI] [PubMed] [Google Scholar]
- 78.Mackman N. Role of tissue factor in hemostasis, thrombosis, and vascular development. Arterioscler Thromb Vasc Biol. 2004;24:1015–1022. doi: 10.1161/01.ATV.0000130465.23430.74. [DOI] [PubMed] [Google Scholar]
- 79.Garnier D, Milsom C, Magnus N, et al. Role of the tissue factor pathway in the biology of tumor initiating cells. Thromb Res. 2010;125(Suppl 2):S44–50. doi: 10.1016/S0049-3848(10)70012-8. [DOI] [PubMed] [Google Scholar]
- 80.Lee TH, D’Asti E, Magnus N, et al. Microvesicles as mediators of intercellular communication in cancer – the emerging science of cellular “debris”. Semin Immunopathol. 2011;33:455–467. doi: 10.1007/s00281-011-0250-3. [DOI] [PubMed] [Google Scholar]
- 81.Prokopi M, Pula G, Mayr U, et al. Proteomic analysis reveals presence of platelet microparticles in endothelial progenitor cell cultures. Blood. 2009;114:723–732. doi: 10.1182/blood-2009-02-205930. [DOI] [PubMed] [Google Scholar]
- 82.Boilard E, Nigrovic PA, Larabee K, et al. Platelets amplify inflammation in arthritis via collagen-dependent microparticle production. Science. 2010;327:580–583. doi: 10.1126/science.1181928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Hron G, Kollars M, Weber H, et al. Tissue factor positive microparticles – cellular origin and association with coagulation activation in patients with colorectal cancer. Thromb Haemost. 2007;97:119–123. [PubMed] [Google Scholar]
- 84.Furie B, Furie BC. Cancer-associated thrombosis. Blood Cells Mol Dis. 2006;36:177–181. doi: 10.1016/j.bcmd.2005.12.018. [DOI] [PubMed] [Google Scholar]
- 85.Janowska-Wieczorek A, Wysoczynski M, Kijowski J, et al. Microvesicles derived from activated platelets induce metastasis and angiogenesis in lung cancer. Int J Cancer. 2005;113:752–760. doi: 10.1002/ijc.20657. [DOI] [PubMed] [Google Scholar]
- 86.Lima LG, Chammas R, Monteiro RQ, et al. Tumor-derived microvesicles modulate the establishment of metastatic melanoma in a phosphatidylserine- dependent manner. Cancer Lett. 2009;283:168–175. doi: 10.1016/j.canlet.2009.03.041. [DOI] [PubMed] [Google Scholar]
- 87.Dominguez-Malagon H, del Carmen Valdez-Carrillo M, Cano-Valdez M. Dermatofibroma and dermatofibrosarcoma protuberans: a comparative ultrastructural study. Ultrastruct Pathol. 2006;4:283–291. doi: 10.1080/01913120600820468. [DOI] [PubMed] [Google Scholar]
- 88.Kim JW, Wieckowski E, Taylor DD, et al. Fas-ligand positive membranous vesicles isolated from sera of patients with oral cancer induce apoptosis of activated T lymphocytes. Clin Cancer Res. 2005;11:1010–1020. [PubMed] [Google Scholar]
- 89.Abrahams VM, Straszewski SL, Kamsteeg M, et al. Epithelial ovarian cancer cells secrete functional Fas ligand. Cancer Res. 2003;63:5573–5581. [PubMed] [Google Scholar]
- 90.Jansa R, Sustar V, Frank M, et al. Number of microvesicles in peripheral blood and ability of plasma to induce adhesion between phospholipid membranes in 19 patients with gastrointestinal diseases. Blood Cells Mol Dis. 2008;41:124–132. doi: 10.1016/j.bcmd.2008.01.009. [DOI] [PubMed] [Google Scholar]
- 91.Baran J, Baj-Krzyworzeka M, Weglarczyk K, et al. Circulating tumour-derived microvesicles in plasma of gastric cancer patients. Cancer Immunol Immunother. 2010;59:841–850. doi: 10.1007/s00262-009-0808-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Urbanija J, Tomsic N, Lokar M, et al. Coalescence of phospholipid membranes as a possible origin of anticoagulant effect of serum proteins. Chem Phys Lipids. 2007;150:49–57. doi: 10.1016/j.chemphyslip.2007.06.216. [DOI] [PubMed] [Google Scholar]
- 93.Sustar V, Jansa R, Frank M, et al. Suppression of membrane microvesiculation. A possible anticoagulant and anti-tumor progression effect of heparin. Blood Cells Mol Dis. 2009;42:223–227. doi: 10.1016/j.bcmd.2009.01.012. [DOI] [PubMed] [Google Scholar]
- 94.Frank M, Sodin-Semrl S, Rozman B, et al. Effects of low-molecular-weight heparin on adhesion and vesiculation of phospholipid membranes – a possible mechanism for the treatment of hyper-coagulability in antiphospholipid syndrome. Ann N Y Acad Sci. 2009;1173:874–886. doi: 10.1111/j.1749-6632.2009.04745.x. [DOI] [PubMed] [Google Scholar]
- 95.Smorenburg SM, Hettiarachchi RJ, Vink R, Buller HR. The effects of unfractionated heparin on survival in patients with malignancy – a systematic review. Thromb Haemost. 1999;82:1600–1604. [PubMed] [Google Scholar]
- 96.Rustom A, Saffrich R, Markovic I, et al. Nanotubular highways for intercellular organelle transport. Science. 2004;303:1007–1010. doi: 10.1126/science.1093133. [DOI] [PubMed] [Google Scholar]
- 97.Watkins SC, Salter RD. Functional connectivity between immune cells mediated by tunneling nanotubules. Immunity. 2005;23:309–318. doi: 10.1016/j.immuni.2005.08.009. [DOI] [PubMed] [Google Scholar]
- 98.Vidulescu C, Clejan S, O’Connor KC. Vesicle traffic through intercellular bridges in DU 145 human prostate cancer cells. J Cells Mol Med. 2004;8:388–396. doi: 10.1111/j.1582-4934.2004.tb00328.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Mause SF, Weber C. Microparticles: protagonists of a novel communication network for intercellular information exchange. Circ Res. 2010;107:1047–1057. doi: 10.1161/CIRCRESAHA.110.226456. [DOI] [PubMed] [Google Scholar]
- 100.van Doormaal FF, Kleinjan A, Di Nisio M, et al. Cell-derived microvesicles and cancer. Neth J Med. 2009;67:266–273. [PubMed] [Google Scholar]
- 101.Canham PB. The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. J Theor Biol. 1970;26:61–81. doi: 10.1016/s0022-5193(70)80032-7. [DOI] [PubMed] [Google Scholar]
- 102.Mrowczynska L, Salzer U, Iglic A, Hgerstrand H. Curvature factor and membrane solubilisation, with particular reference to membrane rafts. Cell Biol Int. 2011;35:991–995. doi: 10.1042/CBI20100786. [DOI] [PubMed] [Google Scholar]
- 103.Gongadze E, Kabaso D, Bauer S, et al. Adhesion of osteoblasts to a nanorough titanium implant surface. Int J Nanomedicine. 2011;6:1801–1816. doi: 10.2147/IJN.S21755. [DOI] [PMC free article] [PubMed] [Google Scholar]