Does Gender Matter in Grant Peer Review?

Abstract

One of the most frequently voiced criticisms of the peer review process is gender bias. In this study we evaluated the grant peer review process (external reviewers’ ratings, and board of trustees’ final decision: approval or no approval for funding) at the Austrian Science Fund with respect to gender. The data consisted of 8,496 research proposals (census) across all disciplines from 1999 to 2009, which were rated on a scale from 1 to 100 (poor to excellent) by 18,357 external reviewers in 23,977 reviews. In line with the current state of research, we found that the final decision was not associated with applicant’s gender or with any correspondence between gender of applicants and reviewers. However, the decisions on the grant applications showed a robust female reviewer salience effect. The approval probability decreases (up to 10%), when there is parity or a majority of women in the group of reviewers. Our results confirm an overall gender null hypothesis for the peer review process of men’s and women’s grant applications in contrast to claims that women’s grants are systematically downrated.

The function of science is to produce knowledge. For conducting specialized research, “researchers formulate proposals for specific projects, which are submitted to funding bodies, where they are evaluated by peer review and awarded grants on the basis of their scientific merits” (Ziman, 2000, p. 75). A criterion that differentiates a judgment of merit in a peer review process from a simple preference is that a merit judgment is unbiased: “Deviations from true merit can come from at least one source other than random error. They can also come from one or more biases” (Thorngate, Dawes, & Foddy, 2009, p. 134). It is important for all research funding organizations to be concerned about possible biases (such as age or sex) and any resulting unfairness toward certain groups of applicants in their peer review process (Bornmann, Mutz, & Daniel, 2008). Findings by Martinson, Anderson, Crain, and de Vries (2006, p. 51) indicated that “when scientists believe they are being treated unfairly they are more likely to behave in ways that compromise the integrity of science. Perceived violations of distributive and procedural justice were positively associated with self-reports of misbehavior among scientists.”

Of the many types of biases discussed in connection with peer review, gender bias has been the most frequently named and investigated (Bornmann, 2011). One of the most frequently cited studies on gender bias analyzed peer review scores for postdoctoral fellowships at the Swedish Medical Research Council (Wennerås & Wold, 1997). The study found that “female applicants had to be 2.5 times more productive than the average male applicant to receive the same competence score as he” (p. 342). An audit of the Wellcome Trust’s decision making on grants demonstrated, however, “that there is no evidence of sex discrimination in the awarding of project grants, programme grants or Senior Research Fellowships in Basic Biomedical Science (SBBF)” (Wellcome Trust, 1997, p. 4). The results of the study of Wennerås and Wold (1997) could also not be confirmed by Ward and Donnelly (1998) on research fellowships awarded by the National Health and Medical Research Council (Australia) and by Bornmann and Daniel (2007a) on postdoctoral fellowships in biomedical research at the Boehringer Ingelheim Fonds.

Additionally, the first meta-analysis of studies on gender bias in grant peer review representing 353,725 proposals from eight countries demonstrated (Bornmann, Mutz, & Daniel, 2007; Marsh, Bornmann, Mutz, Daniel, & O’Mara, 2009), that 40 (of 66) studies did not find a statistically significant effect of gender on grant peer reviews. This lack of effect held across country, year of publication of the studies included in the meta-analysis, and disciplines ranging from physical sciences to the humanities. The study did, however, reveal very small – but statistically significant – gender differences in favor of men for the 26 sets of results that were submitted for fellowship applications. However, these fellowship results varied greatly between the individual studies within the analysis, indicating that they are not generalizable (Marsh & Bornmann, 2009). The results of the meta-analysis are in line with the results of the narrative literature overview published by Ceci and Williams (2011).

Beyond the empirical findings on gender differences in peer review, explanations for possible small gender differences are sought in the social psychology of gender (Rudman & Glick, 2008), especially the salience hypothesis: From a social psychological point of view, the salience of individual characteristics to group members or observers has an impact on their behavior (Marwell, 1963; Moreland & Levine, 2003, p. 372). Salience is strongly affected by the distribution of a characteristic (Voci, Hewstone, Crisp, & Rubin, 2008). The higher the variance, the more attention a characteristic (here: gender) attracts. This implies that the more divergent the proportions of male and females in a group of reviewers are, the more salient gender becomes (McGuire, McGuire, & Winton, 1979). Correspondingly, a heavy preponderance of females (or males) in a group of reviewers could enhance the probability of gender bias in the group’s funding decisions.

Our study evaluates the two-stage grant peer review process (external reviewers’ ratings and board of trustees’ final decision: approve or not approve for funding) of the Austrian Science Fund (FWF) with respect to gender. The FWF is Austria’s central funding organization for basic research. The body responsible for funding decisions at the FWF is the board of trustees, which consists of 26 elected reporters and 26 alternates (Fischer & Reckling, 2010). For each grant application, the FWF obtains at least two international expert reviews. The number of reviewers depends on the amount of funding requested. Expert review consists (among other things) of an extensive written comment and a rating providing an overall numerical assessment of the application. During the FWF board’s decision meetings, the written reviews and ratings of each application are presented by the reporters. The FWF does not enforce any quotas or specific budgets for individual disciplines, and as a result all applications from all fields and disciplines compete with one another at the five decision meetings held each year (Fischer & Reckling, 2010).

In a 2 × 2-factorial design this study tested whether the final decision of the board of trustees and the reviewers’ ratings are influenced by applicants’ and reviewers’ gender, respectively (Bornmann & Daniel, 2007b). The presence of a statistical interaction may provide some empirical evidence for the matching hypothesis that the congruence between applicant’s and reviewer’s gender has an impact on the final decision or rating, respectively.

Due to dependencies of ratings and decisions within disciplines, decision years, and/or reviewers (only ratings), cross-classified multilevel models were performed (Bornmann, Mutz, Hug, & Daniel, 2011; Jayasinghe, Marsh, & Bond, 2003).

Hypotheses

(1)Null hypothesis across main disciplines and year: There is much empirical evidence that women do not suffer from discrimination in the peer review procedure in science (Bornmann et al., 2007; Ceci & Williams, 2011; Hyde, 2005; Marsh et al., 2009). As a statistical null hypothesis, we adopt the assumption that there are no systematic gender differences in either the overall reviewers’ ratings of a proposal or the final decisions of the FWF board of trustees.

(2)Female reviewer salience hypothesis: The final decision of the board of trustees varies with the proportion of female reviewers among all reviewers of a proposal (salience). According to Jayasinghe et al. (2003) female reviewers rate a proposal more strictly than male reviewers in social sciences and humanities. Therefore, if there is an equal proportion of female and male reviewers (parity) or a majority of female reviewers among the reviewers of a proposal, there is a decreased probability that a proposal will be approved in the final decision by the board of trustees.

Methods

Data and Variables

The data for this investigation (see Table 1 ) consisted of 8,358 proposals (census) of individual research projects (about 60% of all FWF grants, Fischer & Reckling, 2010, p. 4) across all fields of research (22 main disciplines) from 1999 to 2009, which were rated on a scale from 1 to 100 (from poor to excellent) by 18,357 external reviewers (about 2 to 3 reviews for each proposal on average) in 23,977 reviews (Fischer & Reckling, 2010). The data were generated by the usual review procedure of the FWF. The two outcome variables that were used in the statistical analyses described in this paper are (1) the final decision of the FWF board of trustees (0 = rejected, 1 = accepted), and (2) the mean grade-point average of a proposal (mean overall rating) obtained by averaging across all of its external reviews.

Table 1. Summary description of the data (reviews, proposals).

Variable	Code	N	%	M	SD	Min-Max
I Reviews (N = 23,977)
Reviewer attributes
Gender
Male	0	20,817	86.4
Female	1	3,155	13.6
Overall rating		23,704		81.6	15.7	0–100
II Proposals (N = 8 358)
Proposal attributes
Gender
Male	0	6,877	82.3
Female	1	1,481	17.7
Age		8,345		46.7	9.8	23–87
Overall rating		8,358		81.3	11.9	0–100
Final decision
Not approved	0	4,591	54.9
Approved	1	3,767	45.1
Year of decision
1999	1	661	7.9
2000	2	611	7.3
…	…	…	…
2008	10	789	9.4
2009	11	858	10.3
Main disciplines
Mathematics	1	310	3.7
Informatics	2	315	3.8
…	…	…	…
Art research	21	197	2.4
Other humanities	22	139	1.7
Reviewer attributes
Gender
Only male (ref.)	1	5,817	69.6
Female minority	2	1,277	15.3
Female parity or majority	3	1,264	15.1

The categorical gender variables (e.g., applicant’s gender, reviewer’s gender) were dummy coded, with male gender as the reference group (=0). In the analysis of the proposals the gender of reviewer was summarized according to the concept of “salience” as follows: majority of male reviewers, minority of female reviewers, and parity or majority of female reviewers. For instance, if a proposal has two reviewers, there are the following possibilities: two male reviewers (male majority), one female reviewer (parity), or two female reviewers (female majority). In the case of three reviewers, there are the following possibilities: two or three male reviewers (male majority), one female reviewer (female minority), two female reviewers (parity), or three female reviewers (female majority) (a corresponding procedure was used in the case of more than three reviewers). Proposals with only one review (1.62%, N = 138) were excluded from the analysis. Besides gender, the age of the grant applicant was used as a covariate (grand-mean centered) as were the application’s discipline and the application year. Reviewers may attribute more status and influence to older applicants than younger applicants, based on their greater experience (track record). For this reason we assume that seniority of applicants will have an influence on the final decision but that this influence will not differ for male and female applicants.

We analyzed two data sets, one with the overall ratings of each reviewer as the basic units and one with the proposals as the basic units (for the evaluation of the board’s final decision). It should be mentioned that the data analyzed by Fischer and Reckling (2010) were corrected for misclassification of proposals in main disciplines (N = 106 proposals).

Statistical Analysis

As Jayasinghe et al. (2003, p. 284) outlined, peer review data have a hierarchical structure. The single rating of a reviewer is nested within a proposal; a proposal associated with a certain final decision is cross-classified within year of decision and main disciplines. Additionally, if one reviewer rated more than one proposal, the single rating is nested within the cross-classification of Reviewer × Proposal. If there are any intra-proposal correlations (i.e., the overall ratings are more reliable) or intraclass correlations within the main disciplines (i.e., more homogeneous decisions within a discipline), the results of single-level models are biased. First, the standard errors of parameters are too small (Hox, 2010, p. 4f). Second, the number of parameters increases dramatically, if certain covariates as the 22 main disciplines are included in a single-level model with their main effect terms and interaction terms with gender (e.g., for disciplines: 1 intercept + 21 main effects + 21 interaction effects = 43 parameters).

Considering the hierarchical data structure and reducing the number of estimated parameters including variance and covariance components, multilevel models are favored over single-level models. However, in the case of 18,357 proposals from 23,977 reviewers, even a multilevel analysis runs into serious statistical and computational problems. For one, the variance components cannot be accurately estimated due to sparse sample sizes of reviews (level-1) for each proposal. For another, the computer runs out of memory to perform the algorithm. Since 79.1% of all reviewers rated only one proposal, we abstained from using “reviewer” as a grouping variable and considered only “proposal.” To speed up the calculation, “proposals” serve as a subject factor, the levels of which identify the repeated overall ratings of a proposal (R-side of the model) in combination with a compound symmetry structure of the residuals (Littell, Milliken, Stroup, Wolfinger, & Schabenberger, 2006, p. 159). The combinations of “decision years” and “main disciplines” provide for the level-2 units of the multilevel model (G-side of the model).

This procedure not only enhances the statistical power of the random effects part of the multilevel model due to an increase in the number of level-2 units, that is, 11 years × 22 disciplines = 242 units combined with sufficient sample sizes of level-2 units (Hox, 2010, p. 233f), but also allows screening of gender effects simultaneously across “years of decision” and “disciplines” using random slopes for reviewer’s gender and applicant’s gender, respectively. In a simulation study, Maas and Hox (2004) found that with 100 groups, the operating alpha level amounts to 6%, which approximates the nominal alpha of 5%. Moineddin, Matheson, and Glazier (2007) recommended at least 100 groups with group size of 50 for a multilevel logistic regression. In the analysis of the final decision of the FWF board of trustees, the R-part of the model was eliminated. For “final decision” as outcome variable, a multilevel logistic regression model instead of an ordinary multilevel model was performed. Due to the fact that the level-1 variance is arbitrarily fixed to π²/3, any meaningful explanation of level-1 variance inevitably increases the level-2 variance components. Therefore, the parameters of the models are corrected to allow different models to be compared (Bauer, 2009). Full maximum likelihood instead of restricted maximum likelihood was used to estimate the parameters (Hox, 2010, p. 41). This estimation procedure allows the comparison of fixed and random effects models with information criteria like the Schwarz Bayesian information criterion (BIC). The multilevel analyses were performed with the SAS procedures “proc mixed” (overall ratings) and “proc glimmix” (final decision) (Littell et al., 2006). In the case of multilevel logistic regression, the likelihood function was estimated by numerical quadratures (10 quadrature points).

The gender hypothesis was tested following Jayasinghe et al. (2003) with a two-factor design, with “reviewer’s gender” as factor 1, “applicant’s gender” as factor 2. A statistically significant interaction between “applicant’s gender” and “reviewer’s gender” would confirm the matching hypothesis.

In the case of nonsignificant results (confirmation of the null hypothesis), the power p(reject H₀| H₀ is false) of the design is essential. Sun, Pan, and Wang (2011) found in simulation studies that observed power analysis (a posteriori) does not serve for additional information to the statistical test, “because (a) observed power for a nonsignificant test is generally low and, therefore, does not provide additional information to the test; and (b) a low observed power does not always indicate that the test is underpowered” (p. 81). We follow the recommendations of Sun et al. (2011) to report exemplarily confidence intervals and observed effect sizes to interpret nonsignificant results.

Results

Single Overall Ratings of a Proposal

In the first step, four multilevel models regarding the single overall ratings of a proposal were compared (see Table 2 ). The statistically significant variance components of the null model for “Year × Discipline” (12.35) and for “proposals” (51.73) show that single overall ratings of a proposal vary not only across proposals but also across the combinations of “year” and “main discipline.” The intraclass correlation coefficient for single ratings (sum of variance components except the residual component divided by the total variance) amounts to 0.26. That means that two single overall ratings of a proposal are correlated on the average of about 0.26 across all proposals. Five percent of the total variance in ratings is due to differences between the combination of “years” and “disciplines” and 21.1% due to variability across “proposals.” The amount of intraclass correlation makes it necessary to perform multilevel instead of single-level analysis to avoid biased statistical inference tests.

Table 2. Results for four multilevel regression models of the single overall rating of a proposal across Year of Decision × Main Disciplines.

		Null model			Random intercept + female reviewer/female applicant			Random intercept/slope + female reviewer/female applicant			Random intercept + female reviewer/female applicant + applicant’s age
Term	Est. Par.	Est.		SE	Est.		SE	Est.		SE	Est.		SE
Notes. Est. Par. = parameter, Est. = estimated parameter value, SE = standard error, −2LogL = deviance, BIC = Schwarz Bayesian information criterion; N = 23,977 reviews. *p < .05 (t-test; t-value and degrees of freedom are not reported), †p < .05 (Wald test).
Fixed effects
Intercept	β0	81.65*		0.27	81.86*		0.28	81.86*		0.28	81.79*		0.28
Female reviewer	β1				−0.34		0.33	−0.34		0.33	−0.34		0.33
Female applicant	β2				−1.08*		0.35	−1.08*		0.35	−0.96*		0.36
Female Reviewer × Female Applicant	β3				0.72		0.68	0.72		0.68	0.70		0.68
Applicant’s age	β4										0.04*		0.01
Applicant’s Age × Female Reviewer	β5										−0.001		0.03
Applicant’s Age × Female Applicant	β6										−0.01		0.04
Random effects
Year × Discipline u0j	σ2u0	12.35†		1.60	12.44†		1.61	12.44†		1.62	12.08†		1.59
u1j	σ2u1							0.00		–
u2j	σ2u2							0.00		–
u3j	σ2u3							0.00		–
Proposal εk(j)	σ2ε(j)	51.73†		2.08	51.55†		2.08	51.55†		2.08	51.40†		2.08
εi(j k)	σ2ε	181.41†		2.10	181.41†		2.10	181.41†		2.10	181.50†		2.10
−2LogL			194 566.6			194 556.4			194 556.4			194 286.0
BIC			194 588.6			194 594.8			194 594.8			194 340.9

The second model in Table 2 includes gender variables (“reviewer’s gender” and “applicant’s gender”) as fixed effects. There is neither an effect of “reviewer’s gender” nor an effect of the interaction “Female Reviewer × Female Applicant.” Fixed-effects parameters below 1 grade point (e.g., β₁ = −0.34) with high standard errors (e.g., 0.35 for β₁) and wide 95% confidence intervals (e.g., [−0.99, 0.31] for β₁) are clear indicators for trivial effects. The hypothesis positing specific effects if applicant’s gender and reviewer’s gender match cannot be confirmed. However, there is a small, statistically significant effect of “applicant’s gender.” Proposals submitted by female applicants are assessed about 1 rating point less favorably (1-100 scale) than proposals by male applicants. This effect remained constant across the models that follow in the table. However, the deviation (−2LogL) decreased only slightly in comparison to the null model; the BIC even increases.

To test whether there are different gender effects across the combinations of year and discipline, the third model was calculated, which does not show any differences regarding the deviation (−2LogL) and the BIC. Additionally, the variance components are zero, standard errors cannot be calculated (estimation and/or specification error). Thus, there are no specific gender effects in different years or different main disciplines.

In the last model in Table 2, applicant’s age and the interaction with applicant’s gender and reviewer’s gender were added. There is a statistically significant impact of age on the overall rating of a proposal in that proposals submitted by older applicants are rated more favorably (higher ratings) than proposals submitted by younger applicants and that this effect does not differ between applicant’s gender or reviewer’s gender. This result was additionally confirmed by a statistically significant likelihood ratio test between the last model and the second model, χ(3) = 9.98 p < .05. Only about (12.44 − 12.08)/12.44 = 2.9% of the variance between Year × Discipline and (51.55 − 51.40)/51.55 = 0.3% between proposals are explained by adding applicant’s age and the interactions as covariates.

Final Decision on Proposals

Table 3 shows the results for the final decision by the board of trustees using data summed over all reviews. A statistically significant variance component of 0.29 in the null model points out that the approval rates vary between the combinations of “years” and “main disciplines.” Eight percent of the total variance (rescaled parameter) is due to this variation, whereas 92% of the total variance was due to residuals and level-1 variance (within “year” and “discipline”), respectively. An intraclass correlation of 0.08 justifies the application of multilevel analysis.

Table 3. Results for five multilevel logistic regression models of the final decision of the board of trustees (N = 8,496 proposals).

		Null model			Random intercept + female reviewer, female applicant			Random intercept/slope + female reviewer, female applicant			Random intercept + female reviewer, female applicant + covariates			Final model
Term	Est. Par.	Est.	SE	Scal.	Est.	SE	Scal.	Est.	SE	Scal.	Est.	SE	Scal.	Est.	SE	Scal.
Notes. Est. Par. = parameter, Est. = estimated parameter value, SE = standard error, Scal. = rescaled parameter, −2LogL = deviance, BIC = Schwarz Bayesian information criterion. The variance of the residuals εji is fixed to 3.29. *p < .05 (t-test; t-value and degrees of freedom are not reported), †p < .05 (Wald test).
Fixed effects
Intercept	β0	−0.18*	0.04	−0.10	−0.12*	0.05	−0.06	−0.12*	0.05	−0.06	−1.10*	0.23	−0.20	−1.43*	0.10	−0.26
Female reviewer minority	β1				−0.13	0.07	−0.07	−0.13	0.08	−0.07	−0.14	0.15	−0.03
Female reviewer parity/maj.	β2				−0.21*	0.08	−0.11	−0.21*	0.08	−0.11	−0.60*	0.20	−0.11	−0.54*	0.18	−0.10
Female applicant	β3				−0.08	0.08	−0.04	−0.08	0.08	−0.04	0.76	0.55	0.14
Female Reviewer Minority × Female Applicant	β4				0.22	0.17	0.11	0.16	0.20	0.08	0.27	0.28	0.05
Female Reviewer Parity or Majority × Female Applicant	β5				−0.04	0.15	−0.02	−0.04	0.15	−0.02	0.05	0.27	0.01
Mean overall rating	β6										0.41*	0.01	0.07	0.41*	0.01	0.08
Female Reviewer Minority × Overall Rating	β7										0.006	0.02	0.00
Female Reviewer Parity or Majority × Overall Rating	β8										0.07*	0.03	0.01	0.06*	0.03	0.01
Applicant’s age	β9										−0.007	0.00	−0.00
Applicant’s Age × Female Applicant	β10										−0.01	0.01	−0.00
Random effects
Intercept u0j	σ2u0	0.29†	0.04	0.08	0.28†	0.04	0.08	0.28†	0.04	0.08	1.48†	0.20	0.05	1.46†	0.20	0.05
u1j	σ2u1							0.02	0.07	0.01
u2j	σ2u2							0.00	–	0.00
u3j	σ2u3							0.00	–	0.00
u4j	σ2u4							0.39	0.48	0.10
u5j	σ2u5							0.00	–	0.00
εji	σ2ε	3.29	–	0.92	3.29	–	0.92	3.29	–	0.92	3.29	–	0.11	3.29	–	0.11
−2LogL			11 240.6			11 225.6			11 224.3			5 044.7			5 062.2
BIC			11 251.6			11 264.0			11 273.7			5 110.6			5 089.6

The second model in Table 3 includes gender variables (“reviewer’s gender” and “applicant’s gender”) and its interactions as fixed effects. The deviation (−2LogL) and the BIC are slightly improved (i.e., decreased) in comparison to the null model; however, the variance components do not change. That means that the fixed effects do not explain much variance on the two levels. All parameters but one are not statistically significant, which confirms the overall gender null hypothesis. The found parameter value for female applicants (β₃ = −0.08), for instance, is rather trivial with a high standard error (SE = 0.08) and a wide 95% confidence interval of [−0.23, 0.07]. The estimated probability amounts to 0.45 for female applicants [p = exp(β₀ + β₃)/(1 + exp(β₀ + β₃))] and 0.47 for male applicants [p = exp(β₀)/(1 + exp(β₀))], respectively.

However, according to the female reviewer salience hypothesis the female reviewer parity or majority has a statistically significant effect on the final decision, which remains essentially unchanged constant across the models which follow. If there is parity or a majority of female reviewers in the group of reviewers of a proposal, the probability of approval of this proposal decreases. This result confirms the hypothesis of a female reviewer salience effect. We have additionally tested a model for separate subsets of cases, in which there is a majority of female reviewers, or, in which there is a parity of reviewers (2LogL = −11225.5, BIC = 11,274). The pure majority effect (−0.22) is quite similar to the pure parity effect (−0.19). Unfortunately, the pure majority effect is not statistically significant due to a small sample size of this subset (N = 340 female reviewers). However, strong support of the salience effect is found when the majority and the parity cases are combined to predict the final approval.

In the third model in the table the gender effects are allowed to vary across the combinations of “years” and “disciplines.” However, there are no statistically significant variance components except the intercept and residual variance components. Moreover, some variance components of the gender effect variables (female reviewer parity or majority, female applicant, female reviewer parity, or Majority × Female Applicant) and their standard errors cannot be estimated, because they are infinitesimally small or zero. In conclusion, the approval rates do not differ between male and female applicants and majority/parity of females and majority of males for certain combinations of “year” and “main discipline.” Regarding the deviation (−2LogL) and the BIC, the model becomes worse in comparison to the previous models.

In the fourth model the “applicant’s age” and the “rating over all reviews” or the grade-point average of a proposal, respectively, were added. The latter variable has a tremendous effect on the final decision in comparison to the second model. About (0.08 − 0.05)/0.08 = 37.5% of the variance of approval rates on the level Year × Main Disciplines, and (0.92 − 0.11)/0.92 = 88.0% of the level-1-variance (residuals) will be explained by the grade-point average. In spite of this huge effect, the female reviewer salience effect remains essentially unchanged. There is also a statistical interaction between “female reviewer parity or majority” and “overall ratings,” but there was no effect of “applicant’s age.” The significant interaction Female Reviewer Parity or Majority × Overall Rating (β₈ = 0.06 in the final model) shows that in cases where male and female reviewers give similar overall ratings, the approval rate slightly increases for a parity or majority of female reviewers. Eventually, the interaction modifies the relationship between the overall ratings and the final decision (main effect β₆ = 0.41) with a 0.06 points higher relationship for female reviewers (0.41 + 0.06 = 0.47). However, an interaction should not be independently interpreted from the main effects.

The final model in Table 3 includes all statistically significant effects of the models. Additionally, a one-level version of the last model of Table 3 was performed which was supplemented by “year of final decision” as categorical variable and its interactions with female reviewer parity or majority and mean overall rating, respectively (the results are not shown). No statistically significant interactions between “year” and “female reviewer parity or majority” or between “year” and Overall Rating × Female Reviewer Parity or Majority were found, that is, the female reviewer salience effect does not vary across years (all other effects are statistically significant). This finding replicates the result of the third model (Table 3) with variance components of main and interaction effects being infinitesimally small or zero (Main Discipline × Year of Decision). Eventually, the female reviewer salience effect remains statistically significant, even if the effect is controlled both for overall rating and final decision year.

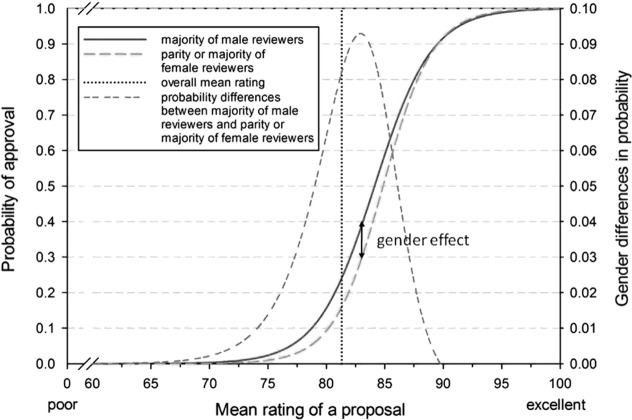
To better understand the relationship between the probability of grant approval and the grade-point average depending on the parity or majority of female reviewers, we simulated the relationship using the distribution of the data and the estimated parameters of the final model (Figure 1 ). The salience effects emerge in the range from 75 to 90 (grade-point average). Figure 1 shows a peak of the salience effect at the grade-point average of 83. At this point, the probability of approval decreases by almost 10%. In the procedure followed by FWF, the threshold between approving and not approving a proposal for funding lies at an average of about 85. This means that there was a salience effect mainly when the reviewers’ ratings do not clearly speak for or clearly speak against approving a proposal for funding.

Figure 1. Female reviewer salience effect.

Discussion

In line with the current state of research (Bornmann et al., 2007; Ceci & Williams, 2011; Marsh et al., 2009) and our first hypothesis, this study shows that the final decision of the board of trustees at FWF is not affected by applicant’s gender or by any correspondence between gender of applicants and of reviewers (matching hypothesis). Regarding the influence of applicant’s gender and reviewers’ gender on the reviewers’ ratings, we found a statistically significant effect of applicant’s gender but it is very small. Both results confirm the overall gender null hypothesis for the FWF peer review process.

In accordance with our second hypothesis, we found a female reviewer salience effect in the decision on grant applications: The probability of approval of a research proposal for funding decreases, when there is a parity or majority of female reviewers in the group of reviewers (instead of a majority of males). This effect remained constant also when further predictors – especially the grade-point average of the overall rating of a proposal, which explains a large part of the variance (37.5% on level 2, 88.0% on level 1) – were included in the model. This means that the effect can be called robust. We should point out that this phenomenon is found mainly in the middle range of ratings, where the overall ratings did not speak clearly for or clearly against funding a proposal.

Several studies have pointed out the risk of the influence of non-merit factors on the decision on grant proposals that are neither especially good nor especially bad. Kostoff (1995) wrote, for instance,

“While a peer review can gain consensus on the projects and proposals that are either outstanding or poor, there will be differences of opinion on the projects and proposals that cover the much wider middle range. For projects or proposals in the middle range, their fate is somewhat more sensitive to the reviewers selected” (p. 180).

Finally, it should be mentioned that the results of this study pertain to grant proposals for individual research projects (Stand-alone Projects, about 60% of all FWF grants) and not for other FWF research funding instruments (Priority Research Programs, Awards and Prizes, International Programs), which limits the generalizability of our results regarding the FWF.

As this is the first study to examine the female reviewer salience effect for grant peer review, further studies are needed to test whether this effect can be replicated at other research funding organizations. If that turns out to be the case, it will need to be studied in more detail. Is the salience effect due to female reviewers making milder judgments, or because their ratings are viewed as less valid than those made by male reviewers? Regardless, this effect was found for both men’s and women’s grant applications.