Mechanical Coupling between Myosin Molecules Causes Differences between Ensemble and Single-Molecule Measurements

Abstract

In contracting muscle, individual myosin molecules function as part of a large ensemble, hydrolyzing ATP to power the relative sliding of actin filaments. The technological advances that have enabled direct observation and manipulation of single molecules, including recent experiments that have explored myosin’s force-dependent properties, provide detailed insight into the kinetics of myosin’s mechanochemical interaction with actin. However, it has been difficult to reconcile these single-molecule observations with the behavior of myosin in an ensemble. Here, using a combination of simulations and theory, we show that the kinetic mechanism derived from single-molecule experiments describes ensemble behavior; but the connection between single molecule and ensemble is complex. In particular, even in the absence of external force, internal forces generated between myosin molecules in a large ensemble accelerate ADP release and increase how far actin moves during a single myosin attachment. These myosin-induced changes in strong binding lifetime and attachment distance cause measurable properties, such as actin speed in the motility assay, to vary depending on the number of myosin molecules interacting with an actin filament. This ensemble-size effect challenges the simple detachment limited model of motility, because even when motility speed is limited by ADP release, increasing attachment rate can increase motility speed.

Introduction

Muscle contraction is powered by the cyclical interaction of two contractile proteins, myosin and actin. While bound to actin, myosin undergoes a large conformational change (the power-stroke), which moves actin. When unbound (or weakly bound), myosin hydrolyzes ATP and reverses the power-stroke, thereby returning to its original state (1). Thus, myosin molecules in muscle transduce chemical energy into mechanical work, sliding thin (actin-containing) filaments past thick (myosin-containing) filaments and hydrolyzing ATP in the process. The recent development of single molecule measurements has allowed mechanical aspects of this process to be described in unprecedented detail (2–7).

Isolated actin filaments, when manipulated with a laser trap, can be used to measure both the duration of myosin binding (t₁) and the distance a single myosin molecule moves actin (d₁) (2–5). Varying the concentration of ATP in these experiments demonstrates that the duration of myosin binding to actin involves two kinetic steps (7,8). In the first step, myosin releases ADP; in the second step, myosin binds ATP, resulting in myosin detachment. Single-molecule experiments have explicitly demonstrated that ADP release, but not ATP binding, strongly depends on the force applied to myosin (6,7). Questions remain, however, about how to generalize these experimental results to the more physiologically realistic situation in muscle, where a large group (an ensemble) of myosin molecules interacts with actin.

Initial experiments suggested that measurements of single myosin molecules could be easily generalized to myosin ensembles by assuming that each molecule is independent (e.g., Uyeda et al. (9)). More recent experiments suggest that individual myosin molecules, when part of an ensemble, behave differently from isolated myosin molecules (10,11). For example, in vitro an ensemble of myosin moves actin faster than would be predicted from single-molecule measurements (10,11). Although this effect may be explained from thermodynamic arguments (10–12), a quantitative explanation based on a molecular model of myosin’s interaction with actin has yet to be developed. Such a molecular model is vital to connecting myosin’s molecular properties to larger scales of muscle contraction and a detailed understanding of myopathies.

Independent of these in vitro experiments, it might seem that for over 50 years (13) mathematical models have connected multiple scales of muscle contraction. Initially, steady-state (13) and later, transient (14) whole-muscle data were reproduced by simple phenomenological molecular models. These models were subsequently made consistent with both the laws of thermodynamics (15) and biochemical experiments (16). Subsequently, variations of these models were shown to be consistent with muscle fiber and whole-muscle experiments under different conditions (17–20). These models assume that chemical reaction rate depends on molecular extension, x, and mathematically convenient expressions for this x dependence are used. Model implementation therefore requires specification of phenomenological constants (e.g., the Huxley (1957) model (13) assumes piecewise linear functions, and one must define the slopes and the position of discontinuities). To give the models a physical basis, researchers have used nonequilibrium thermodynamics to connect model parameters to molecular mechanical properties (21–23). Such mechanical realism leads to less mathematically convenient models, so Monte Carlo simulations are often used in favor of differential equations (22,23). However, recent work shows that the connection between the molecular and cellular scales is not so straightforward as these models suggest (24–29).

Muscle contraction at the cellular level is very complex, requiring cellular-scale models to assume homogenous sarcomere lengths, noncooperative myosin binding, negligible actin compliance, and myosin’s interaction with actin being the primary means of contraction. Recent work has challenged each of these assumptions, and intersarcomere dynamics (24–26), actin elasticity (27), myosin-myosin cooperativity (28), and noncontractile proteins (29) play important roles in muscle contraction. Such complexities strongly limit the predictive power of these models.

As an alternative to these top-down approaches to modeling, where molecular details are inferred from fits to cellular data, single-molecule measurements can be used to predict experimental results at larger size scales. For example, the force-velocity relationship for a few myosin molecules as measured in the laser trap (30) is remarkably similar to that of whole-muscle (31) or muscle fibers (32,33). This agreement suggests that the simplified in vitro system recapitulates the key factors that dictate the force-velocity relationship of muscle. Furthermore, the simplicity of the in vitro experiments permits models that avoid the assumptions of top-down models, giving a greater level of predictive power and, potentially, a clearer connection between the molecular and cellular scales. A first step in this bottom-up approach is to connect single-molecule and ensemble in vitro measurements.

To understand if and how myosin force and motion generation in an ensemble differs from that produced by a single myosin, we develop a mechanochemical model based on single-molecule measurements, specifying as many parameters as possible from experimental data. Simulations of this model demonstrate that an ensemble of myosin cannot be viewed as a collection of independent motors, as the motors interact mechanically. Specifically, forces between myosin molecules accelerate ADP release and increase attachment distance when myosin is part of an ensemble.

Model

Single-molecule measurements suggest a simple kinetic scheme for smooth and skeletal muscle contraction (8,10), shown in Fig. 1. Unbound (or weakly bound) myosin with hydrolysis products (ADP and inorganic phosphate, P_i) in its active site transitions to a state where it strongly binds to actin. This transition includes the power-stroke and release of P_i from the active site. We assume that all of these events are well modeled as a first-order reaction of rate k_a. This assumption implies that there is a single rate-limiting step for myosin binding, but we make no assumptions about the identity of that step, or the order of the various steps. We allow myosin to bind actin with nonzero strain (see the Supporting Material for details). At the low P_i concentrations of the in vitro experiments we model, the reverse rate constant may be neglected.

Figure 1.

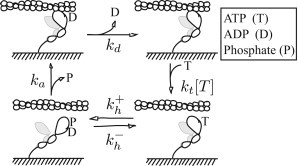
Kinetic scheme for the interaction of actin and myosin. (Starting at the lower left) Myosin releases phosphate, strongly binds to actin, and undergoes a power stroke (not necessarily in that order) at a rate k_a. It releases ADP at a rate k_d. Strong binding is terminated by the binding of ATP at a rate k_t[T], where [T] is the concentration of ATP. Hydrolysis of ATP reverses the power stroke and reprimes the head. Although both heads of myosin are pictured, we only consider the action of the unshaded head and do not imply anything about intramolecular head-head interactions.

Once strongly bound, myosin may release ADP. It does so in a force-dependent process consistent with Bell’s approximation (6,7,34):

$$k_d=k_d^0\text{exp}\left(-\frac{F{\delta }_x}{k_{\text{B}}T}\right),$$ (1)

where F is the force, $k_d^0$ is the rate in the absence of force, δ_x is a parameter that determines the force-dependence, and k_BT is Boltzmann's constant times absolute temperature. Although there is a conformational change and a small substep associated with this process (7,35), our simple model neglects this complexity (see the Supporting Material). In the absence of significant free ADP, as appropriate for the in vitro experiments we model, the reverse rate constant may be neglected.

Having released both ADP and phosphate, myosin’s nucleotide binding pocket is empty and the molecule is in the rigor state. Myosin may then bind ATP, and upon doing so, unbind from actin. This process occurs at an overall rate of k_t[ATP] (2,8,10,36). Because we consider ATP concentrations much greater than the myosin concentration, this process is assumed to be pseudo-first-order (i.e., [ATP] ≈ constant). This reaction is rarely reversed at the pH of the experiments we model (37).

Once ATP is bound and myosin has detached from actin, myosin may hydrolyze ATP and revert to a pre power-stroke conformation (1,38). This reaction is reversible (1,38). Upon hydrolysis, the molecule may strongly bind to actin and restart the mechanochemical cycle. This model is completely specified by eight parameters: the binding rate k_a, the ADP release rate in the absence of force $k_d^0$, the ATP binding rate k_t, the forward and backward hydrolysis rates $k_h^{+}$ and $k_h^{-}$, respectively, the force-dependent parameter δ_x, the power-stroke size d, and myosin’s assumed linear stiffness k. Some of these parameters may be estimated directly from previous experiments (see Table 1, and the Supporting Material); other parameters are more difficult to measure, so we must estimate them indirectly.

Table 1.

Parameter values (see the Supporting Material for experimental conditions)

Parameter	Smooth	References	Skeletal	References
ka (s−1)	6	(62)	40	(63,64)
k0d (s−1)	18	(6)	350	From fits
kt (μM−1 s−1)	1.2	(6,65)	2	(36)
k+h (s−1)	100	(66)	100	(66)
k−h (s−1)	10	(67)	10	(67)
δx (nm)	−2.60	(6,7)	−1.86	From fits
k (pN/nm)	0.3	From fits	0.3	From smooth
d (nm)	10	(5)	10	(5)

We use the model to fit force- and motion-generation data from both skeletal and smooth muscle myosin. For smooth muscle myosin, all parameters may be estimated from the literature except myosin stiffness, k. For skeletal muscle myosin, we must additionally estimate ADP release rate in the absence of force $k_d^0$ and the force-dependent parameter δ_x. Assuming smooth and skeletal muscle myosin have similar stiffness, we first estimated k from ensemble measurements of smooth muscle myosin and subsequently estimated skeletal myosin’s $k_d^0$ and δ_x from ensemble measurements of skeletal muscle myosin (see the Supporting Material for details).

Model validation

To test whether the model is consistent with both single-molecule and ensemble data, we simulated four different experiments spanning size scales from single isolated molecules, through small ensembles, to large ensembles:

• 1.Single-molecule step size and strong binding lifetime in the laser trap;
• 2.In vitro motility speed as a function of ATP concentration at high myosin surface density;
• 3.Actin filament length-dependent in vitro motility speed at low/intermediate myosin surface density; and
• 4.Force-velocity relationships for small myosin ensembles measured in the laser trap.

Data for smooth muscle myosin and skeletal muscle myosin were selected primarily from published literature of the Warshaw lab for internal consistency (see the Supporting Material for details). We used Monte Carlo simulations to model these four experiments and compared the results to measurements. In these simulations, we assume that myosin may bind anywhere on actin (26), and that actin is infinitely stiff (see the Supporting Material). We made an effort, when possible, to simulate experimental details and data analysis. We had at most two parameters to fit to the smooth muscle data: k, myosin’s stiffness and N, the number of myosin molecules interacting with the filament. For skeletal muscle myosin, we had at most three parameters: $k_d^0$, myosin’s ADP release rate in the absence of force, δ_x the force-dependent parameter, and N.

Single molecule

The three-bead laser trap assay has been used to measure properties of single myosin molecules interacting with single actin filaments (2). In this assay, actin filaments are manipulated via beads trapped with a laser and the position of actin is measured as a function of time (see Fig. 2 a). Myosin binding decreases the compliance of the system, resulting in a decrease in the variance of the bead’s position. Myosin binding is almost immediately followed by a translocation of actin caused by the power-stroke of myosin. Using various data analysis procedures (2–5), the unitary step size (d₁) and strong-binding lifetime (t₁) may be measured as a function of ATP. We performed explicit simulations of the single-molecule laser trap at variable ATP concentrations. We used a mean-variance analysis (5) to derive the step size (d₁) and attachment lifetime (t₁) (see the Supporting Material). Comparing this simulated data to previously published single-molecule measurements also using mean-variance analysis (5,6,8,37,39–43), we find reasonable agreement (see Fig. 2, b and c).

Figure 2.

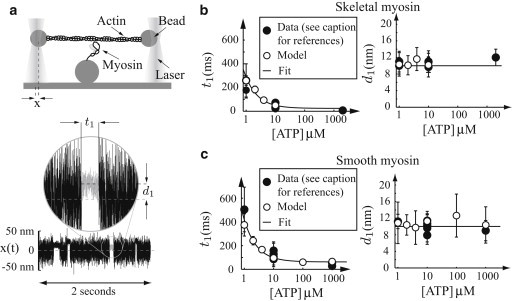
Model is consistent with single-molecule measurements in the laser trap. In all plots: (open circles) Simulated data; (solid circles) experimental data. (Error bars) Standard deviations. (a) A cartoon of a single-molecule experiment. Actin, manipulated by two beads trapped in lasers, is brought close to a myosin molecule that can then bind. The position of one laser-trapped bead x(t) is measured with a quadrant photodiode as a function of time, and the duration of binding (t₁) and myosin’s step size (d₁) may be measured. A typical simulated experiment is pictured (compare to Fig. 2 of Baker et al. (11)). (b and c) Same plots for skeletal muscle and smooth muscle myosin, respectively. (Left plot) Strong binding lifetime as a function of ATP. The simulated data are fit with an equation of the form t₁ = 1/$k_d^0$ + 1/k_t[ATP] (solid line). (Right plot) Unitary step size d₁ as a function of ATP. (Solid line) d₁ = 10 nm. Data are from the literature (5,6,8,39,40,43) for smooth muscle and the literature (2,5,37,41,42) for skeletal muscle myosin.

Motility at variable ATP

The in vitro motility assay measures properties of myosin ensembles interacting with single actin filaments. In this experiment, myosin is attached at high density to a flow cell, fluorescently labeled actin is added, and these actin filaments may be observed gliding across the myosin-coated surface (see Fig. 3 a). The average speed of these filaments is measured as a function of ATP concentration (e.g., Harris and Warshaw (44) and Debold et al. (45)). We performed Monte Carlo simulations of the motility assay at variable ATP. For skeletal muscle, simulations with 50 active myosin heads available to interact with the actin filament were in reasonable agreement with experimental measurements of Debold et al. (45) (see Fig. 3 b). For smooth muscle, the simulations differed from the experimental measurements of Harris and Warshaw (44) (see Fig. 3 c). In particular, although the maximum sliding speeds were similar, the K_m from the Michaelis-Menten fits differed (we predict K_m = 70.4 μM, whereas Harris and Warshaw (44) measured K_m = 46 μM). This discrepancy might be due to temperature differences between single-molecule and in vitro motility experiments (20 or 25°C for the former and 30°C for the latter), or experimental variation.

Figure 3.

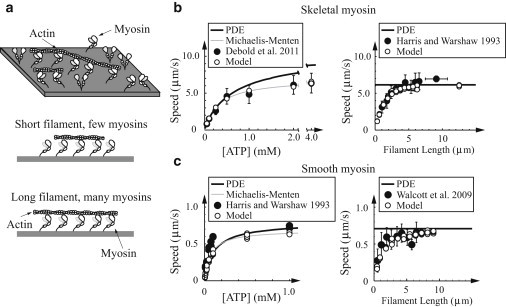
Model is consistent with small and large ensemble measurements in the absence of external force. (a) Cartoon of experimental setup. (Top) Motility assay, with free actin filaments moving across a bed of myosin. (Bottom) Number of myosin molecules interacting with actin depends on filament length. (b and c) Same plots for skeletal and smooth muscle myosin, respectively. In all plots: (open circles) simulated data; (solid circles) experimental data. (Error bars, when present) Standard deviations. (Solid) Numerical solution of the integro-partial differential equations (PDEs) that govern the model in the limit of large N. (Left) In vitro motility at high myosin density as a function of ATP. (Shaded line) Michaelis-Menten fits. Skeletal muscle simulations agree with the experimental measurements (45), given N = 50. The K_m of the smooth muscle fits differ from measurements (44) (70.4 μM and 46 μM, respectively). This difference might be due to temperature differences or experimental variation. (Right) In vitro motility speed at low myosin density as a function of filament length. The model is consistent with the data of Harris and Warshaw (44), given 16 active myosin heads/μm (skeletal) and Walcott et al. (43), given 11 active myosin heads/μm (smooth).

Actin filament length-dependent motility

In the motility assay at low myosin concentrations, shorter actin filaments (that interact with fewer myosin molecules) move more slowly than longer filaments (see Fig. 3 a) (9,43,44). Our simulations also predict this filament length-dependent motility (see Fig. 3, b and c). In particular, we can fit experimental data at low skeletal muscle myosin concentrations (44) assuming a myosin density of 16 active heads/μm of filament length, and data at low smooth muscle myosin concentrations (43), assuming a myosin density of 11 active heads/μm.

Small ensemble force-velocity

The motility assay, though an important ensemble measurement, does not directly probe myosin’s force-generating capacity. As a result, a tool for measuring myosin’s force-velocity relationship, one of the standard physiological assays of muscle function at cellular and larger scales (e.g., Hill (31)), was developed for small ensembles of myosin (30). In this experiment, the single-molecule laser trap is modified to have a higher concentration of myosin attached to the surface (see Fig. 4 a). Under these conditions, rather than seeing individual binding events, multiple myosin molecules work together to pull actin against the force of the laser trap. A feedback algorithm adjusts the laser position in real-time to apply a constant force on the system. Thus, as myosin pulls on actin, the force resisting this motion is dynamically adjusted through some specified range. This technique has been applied to skeletal (30) and smooth muscle (43). In all cases, even with relatively few molecules, smooth motion is observed and the resulting relationship between applied force and actin velocity is well-fit by the Hill force-velocity relation (31). We simulated these experiments with a physical model of the laser trap (see the Supporting Material). For skeletal muscle myosin, 11 molecules were sufficient to fit the experimental curves at both 100 and 30 μM ATP (see Fig. 4 b). For smooth muscle myosin, eight molecules were sufficient to fit the experimental curve (see Fig. 4 c).

Figure 4.

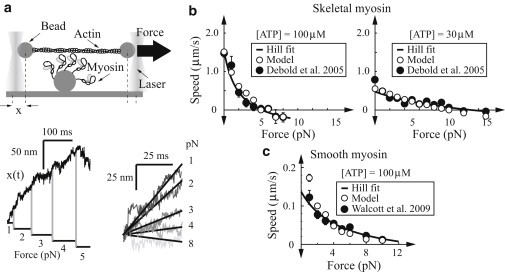
Model fits small ensemble force-velocity measurements. (a) Cartoon of experimental setup. (Top) Actin, manipulated by two beads trapped in lasers, is brought close to a small ensemble of myosin molecules that can then bind. The position of one laser-trapped bead is measured as a function of time x(t), and the position of the laser is dynamically adjusted to keep a constant force on the system. (Bottom left) Typical simulation of bead position versus time (compare to Fig. 1, B and C, of Debold et al. (30)). These simulations were for 11 active skeletal muscle myosin heads at 100 μM ATP. Applied force is shown below. (Right) Five position-versus-time simulations, aligned to emphasize how applied force slows actin speed. Force-velocity plots are shown for (b) skeletal and (c) smooth muscle myosin. (Solid circles) Data (30,43); (open circles) simulations. A quantity of 11 and 8 active myosin heads were simulated for skeletal and smooth myosin, respectively. (Error bars) Standard error. (Solid curves) Hill fits to the data (31).

In vitro mechanical data strongly support the model

By only adjusting a small number of parameters (k and N for smooth muscle, and $k_d^0$, δ_x, and N for skeletal muscle myosin), simulations of the kinetic model in Fig. 1 were consistent with experimental measurements at the single-molecule, small-ensemble, and large-ensemble level. Of particular interest is the model’s ability to quantitatively fit, for the first time to our knowledge, small-ensemble force-velocity data (30,43). To additionally support the model, we now show that several of our parameter estimates (N, k, and δ_x) are consistent with independent experimental measurements.

To fit the data, we varied the number of active myosin heads available to interact with a given actin filament, N. Based on measurements of NH₄-EDTA ATPase of myosin, Harris and Warshaw (44) provide an estimate of the surface density of myosin. This experimental technique identifies the total number of myosin heads per area (44). Assuming that only a single head of myosin may interact with an actin filament at a time (40,46), the actual number of available heads is half this value. Given an estimate of the distance over which myosin can reach and bind to actin (assumed to be 26 nm in Harris and Warshaw (44)), one may estimate N. These estimates of N agree with ours to within a factor of two (see Table 2), which is reasonable given the difficulty and uncertainty of the experimental measurement.

Table 2.

Estimates of myosin number

Experiment	Best-fit	Estimated value (44)
Skeletal motility (Fig. 3b)	33 heads/μM	54 heads/μM
Skeletal length-dependent motility (Fig. 3b)	16 heads/μM	9 heads/μM
Skeletal force-velocity (Fig. 4b)	11 heads	4–5 heads
Smooth motility	—	—
Smooth length-dependent motility (Fig. 3b)	11 heads/μM	13–17 heads/μM
Smooth force-velocity (Fig. 4c)	8 heads	9–12 heads

We estimate stiffness to be k ≈ 0.3 pN/nm. This value is the stiffness of all structures that connect actin to the rigid surface, including the myosin head, neck region, and the surface’s nitrocellulose coating. Myosin stiffness has been measured under variable conditions, with estimates ranging over several orders of magnitude (e.g., Kaya and Higuchi (47), Lewalle et al. (48), and Veigel et al. (49)). Our estimate is consistent with the measurements of Veigel et al. (49), who measured k = 0.69 ± 0.47 pN/nm with isolated skeletal muscle heavy meromyosin in the laser trap. This measurement is most appropriate for the experimental conditions we consider. Note that increased or nonlinear stiffness for myosin in filaments (47) might be responsible for the increased shortening rate seen in fibers and thick filaments compared to that seen in traditional in vitro motility (50,51).

For skeletal muscle, we estimate the force-dependent parameter δ_x = −1.86 nm. The value is consistent with the expectation that skeletal muscle myosin is less force-dependent than smooth muscle myosin (52). Our estimate is consistent with, though slightly larger than, the estimates of Capitanio et al. (35) of −1 to −1.3 nm. Thus, the kinetic model in Fig. 1, with only a few free physically based parameters, fits a wide range of experimental results from single molecule to large ensemble, both in the presence and absence of force (see Figs. 2–4).

Ensemble myosin behavior

The model correctly predicts that the speed of myosin in the motility assay is not simply equal to the unitary step size (d₁) divided by the attachment time (t₁), as would be predicted for an ensemble of independent motors (10,11). For example, for smooth muscle myosin at 1 mM ATP, based on simulated laser trap data of d₁ (10 nm) and t₁ (60 ms) one would predict a motility speed of d₁/t₁ = 0.167 μm/s, whereas simulated motility speed is 0.646 μm/s under these conditions, a nearly fourfold increase. Other aspects of myosin’s interaction with actin, such as the duty ratio (the ratio of strong binding time to total cycle time), vary with ensemble size (see the Supporting Material). Such results influence the interpretation of in vitro data, as calculations frequently assume that ensemble size does not affect myosin’s interaction with actin (9,43,44). To better understand these ensemble effects, we performed theoretical calculations in the limit of large ensembles.

Following the pioneering work of Huxley (13) and using the modifications of Lacker and Peskin (53), the kinetic model in Fig. 1 can be represented by a set of four integro-partial differential equations (PDEs) for the probability that myosin is attached to actin at a given extension. Such a representation requires a mean-field approximation, valid only for large ensembles. These PDEs can be numerically solved, and approach our Monte Carlo simulations as ensemble size becomes large (see Figs. 3 b and c, and 5). Two important results emerge from these equations: first, they predict that a single myosin molecule, when part of a large ensemble, moves actin a longer distance in a shorter time than when mechanically isolated; and second, the solution to the equations may be simply approximated. These solution approximations demonstrate that mechanochemical interactions between myosin are critical to ensemble function.

Figure 5.

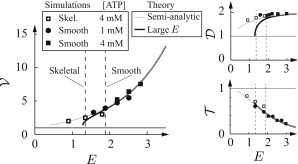
Comparison between theoretical calculations and simulations for actin speed ($\mathcal{V}$), myosin attachment time ($\mathcal{T}$), and attachment distance ($\mathcal{D}$), all normalized to the single-molecule values (single-molecule values are shown as a thin, solid line). These plots are shown as a function of the nondimensional mechanochemical coupling parameter E. Simulations were performed with large ensembles (N = 400) with kinetic parameters based on smooth muscle and skeletal muscle. The value E was varied by using different myosin stiffness values and/or force dependence. (Dashed lines) Our best estimate of E. Theoretical calculations, described in the text and the Supporting Material, agree with the simulations.

We may approximately solve the PDEs when steady-state is achieved (this approximation assumes that attachment occurs only when myosin is unstretched (54), that the external force on actin is zero and is valid only at high [ATP]). This solution, derived and discussed in the Supporting Material, is closed form but contains nonelementary functions (e.g., the exponential integral function), so we refer to it as “semianalytic”. We may use this solution to find semianalytic equations for three values of interest for myosin molecules in an ensemble relative to these values for isolated myosin:

• 1.$\mathcal{D}$ = d_∞/d₁, the average distance actin moves per myosin attachment. The expression d_∞ is this value for myosin in a large ensemble, and d₁ is this value for isolated myosin.
• 2.$\mathcal{T}$ = t_∞/t₁, the average time myosin strongly binds to actin. The expression t_∞ is this value for myosin in a large ensemble, and t₁ is this value for isolated myosin.
• 3.$\mathcal{V}$ = υ_∞/υ₁, actin’s average speed. The expression υ_∞ is this value for myosin in a large ensemble, and υ₁ = d₁/t₁ is this value neglecting myosin-myosin interactions.

Importantly, these semianalytic equations depend only on a single parameter that describes the mechanochemical coupling between myosin molecules, E = −kdδ_x/k_BT.

When E is large (>∼1.75, as we expect for smooth muscle myosin), we can write simple analytic expressions for the three above variables,

$$\begin{array}{c}\mathcal{D}\approx 1+\sqrt{1-\frac{{\pi }^2}{6E^2}},\\ \mathcal{T}\approx \frac{E\left(1+\sqrt{1-\frac{{\pi }^2}{6E^2}}\right)}{\text{exp}\left(\gamma +E\sqrt{1-\frac{{\pi }^2}{6E^2}}\right)},\\ \mathcal{V}\approx \frac{1}{E}\text{exp}\left(\gamma +E\sqrt{1-\frac{{\pi }^2}{6E^2}}\right),\end{array}$$ (2)

where γ = 0.5772… is the Euler-Mascheroni constant. Note that $\mathcal{D}$ > 1 so that free actin being moved by an ensemble of myosin moves further than d₁ every time myosin binds; $\mathcal{T}$ < 1 so that myosin in an ensemble stays strongly bound to actin for a shorter time than t₁; and $\mathcal{V}$ > 1 so that myosin-myosin interactions in an ensemble accelerate actin sliding speed (these results remain true when E is not large). These results are shown graphically, and the underlying assumptions validated in Fig. 5.

Discussion

Measurements of myosin’s single-molecule properties provided an unprecedented glimpse into muscle contraction at the molecular level (2). Previously, molecular properties could only be indirectly inferred from ensemble measurements in muscle (55). Reasonable agreement between these methods suggested that each myosin molecule is independent of all other myosin molecules (9). More recently, however, it was shown that single-molecule measurements strongly underestimate actin speed in the motility assay, implying that myosin-myosin interactions affect motility speed (10,11). Furthermore, recent theoretical and experimental work with nonmuscle molecular motors, such as kinesin, has demonstrated that motor-motor interactions are a critical aspect of ensemble function (56,57). Here, using detailed simulations of in vitro measurements at the single-molecule and ensemble level, we show that mechanochemical interactions between myosin molecules in an ensemble shorten strong binding lifetime (t_∞) and lengthen attachment distance (d_∞), thereby increasing actin speed. These results show that an ensemble of myosin is not equivalent to an ensemble of independent motors.

Relation to previous muscle models

The model discussed here is part of a large and growing group of models of myosin’s interaction with actin (e.g., (13–23,53,58,59)). Some of these models predict that intermolecular interactions occur in myosin ensembles (19,20,22,58,59), but none has made a clear connection between single-molecule and ensemble experiments. Duke (22), for example, analyzed a model where synchronization of myosin molecules explains nonhyperbolic force-velocity relations (33). Such synchronization occurs only near isometric force (22,26), and so does not explain ensemble-induced changes in unloaded actin speed (10,11). Pate and Cooke (59) analyzed the Huxley (13) model at variable ensemble size, showing that when two myosin molecules work together, each behaves differently than an isolated molecule. This effect is due primarily to their assumption that binding sites are sparsely distributed on actin and their assumption the actin filament’s Brownian motion is negligible (59). Both assumptions are violated in single-molecule measurements (60).

Separate from these predictions based on Monte Carlo simulations of specific kinetic models, thermodynamic arguments show that intermolecular forces can explain differences between ensemble and single-molecule myosin behavior (10–12). We provide additional evidence, based on a molecular model, that mechanochemical interactions occur between myosin molecules. Fitting only in vitro experiments both allows us to validate our model to a greater extent and makes the model’s predictions about those size scales more accurate than models fit to cellular-scale data (13–23,53,59). For example, we predict that myosin in an ensemble has a step size that is 1.8 times as far, and an attachment time that is half as long as isolated myosin (see Fig. 5). This result explains why ensembles of myosin move unloaded actin filaments four times faster than single-molecule measurements would predict (10,11). The model therefore connects single-molecule and ensemble in vitro measurements.

Myosin-induced myosin detachment

Simulations and theory show that increasing the number of myosin molecules interacting with a given unloaded actin filament decreases myosin’s average strong-binding lifetime. Theoretical calculations show that, at high ATP, myosin-induced myosin detachment depends on a single parameter E = −kdδ_x/k_BT (see Eq. 2). The meaning of the parameter E can be understood through a simple example. Suppose one myosin molecule is bound to actin with zero extension. Subsequently, a second myosin molecule binds (with zero extension) and undergoes its power stroke, thereby applying a force. The net force on actin is zero, so each myosin molecule exerts an equal and opposite force on the other. The initially bound myosin molecule experiences a force that accelerates ADP release (i.e., $k_d^{\mathrm{i}}$ > $k_d^0$); the second myosin experiences a force that slows ADP release (i.e., $k_d^{\mathrm{s}}$ < $k_d^0$). The parameter E is equal to the natural logarithm of the ratio of the ADP release rates, i.e., E = ln($k_d^{\mathrm{i}}$/$k_d^{\mathrm{s}}$). Thus, E determines the mechanochemical coupling between myosin molecules in an ensemble.

An increase in mechanochemical coupling, i.e., an increase in myosin stiffness (k) power-stroke size (d) and/or force-dependent ADP release (δ_x), decreases strong binding lifetime for myosin in an ensemble but has no effect on strong binding lifetime for isolated myosin. Increases in these mechanical parameters therefore lead to ensemble-induced decreases in attachment time. Changes in kinetic parameters (e.g., unloaded ADP release rate $k_d^0$) equally affect the strong binding lifetime of isolated myosin and myosin in an ensemble, leading to no ensemble-induced decrease in attachment time.

Myosin-induced increase in attachment distance

Simulations and theory show that increasing the number of myosin molecules interacting with an unloaded actin filament increases how far actin moves while a given myosin molecule is strongly bound. At high ATP, the size of this effect depends only on the mechanochemical coupling E (see Eq. 2). When mechanochemical coupling is weak (E ≪ 1), actin moves a distance d ≈ 10 nm each time myosin binds and then unbinds, i.e., actin moves 10 nm per ATP hydrolysis. Alternatively, when mechanochemical coupling is strong (E ≫ 1), actin moves nearly 2d ≈ 20 nm per ATP hydrolysis. Such myosin-induced myosin extension was proposed by Higuchi and Goldman (55) based on experimental observations in skinned muscle fibers; our model supports this interpretation of their data. Increases in attachment distance beyond 2d might occur with nonlinear myosin stiffness (47).

Myosin molecules, when part of a mechanically coupled ensemble, release ADP more rapidly and stay attached to actin for a longer distance than when mechanically isolated. Thus, individual myosin molecules in an ensemble behave differently from individual myosin molecules in the laser trap. This effect is most pronounced at high myosin densities, where intermolecular interactions occur most frequently, and at high ATP concentrations and/or high external resistive force, where actin filament motion is most limited by ADP release.

In this model, what does “detachment-limited” mean?

In the in vitro motility assay (and also in vivo), actin speed has been described as detachment-limited, meaning that, at high ATP concentrations, actin speed is limited by the rate at which myosin releases ADP (61). Under these conditions, average unloaded actin speed (υ_ens) is

$${\upsilon }_{ens}=\frac{d_{ens}}{t_{ens}},$$ (3)

where d_ens and t_ens are the attachment distance and time for myosin molecules in this ensemble. We have shown that, in general, d_ens ≠ d₁ and t_ens ≠ t₁. Further, these values vary as the average number of myosin molecules strongly bound to an actin filament vary. This ensemble size dependence implies that even when Eq. 3 is a good approximation, suggesting that motility is detachment-limited, actin speed can be increased by increasing the average number of myosin molecules strongly bound to actin, say by increasing attachment rate k_a (see the Supporting Material). Thus, detachment-limited motility is affected by attachment rate.

These ensemble size effects occur because, although the overall force on the actin filament is zero, internal forces between myosin molecules exist. These internal forces, which increase with ensemble size, increase attachment distance and decrease attachment time. For sufficiently large ensembles, however, this effect saturates (see the Supporting Material) and increasing or decreasing attachment rate has no effect. Because we assume this limit in our theoretical calculations, motility is completely independent of attachment rate if actin speed is well approximated by the curves in Fig. 5. Given our parameter estimates, such attachment-independent motility occurs in the absence of external force at ensembles of ∼100 myosin molecules.

Conclusions

Muscle is one of the best-studied systems in biology. Experimental data exist from size scales of single molecules to whole animals. However, major obstacles exist to bridging these scales. Here, for example, using a combination of simulation and theory we show that extrapolation from single molecule to ensemble is complex. Our simulations demonstrate that intermolecular forces increase ADP release and attachment distance when multiple myosin molecules work together, even when external force is zero. This effect causes a myosin molecule in an ensemble to behave differently from an isolated molecule, and must be included in discussions of the molecular basis of muscle contraction. The complexity of myosin’s interaction with actin under even simplified in vitro conditions suggests that a clear understanding of multiscale muscle contraction requires a combination of theory, simulation, and experiment.