Improved measurement of labile proton concentration-weighted chemical exchange rate (k_ws) with experimental factor-compensated and T₁-normalized quantitative chemical exchange saturation transfer (CEST) MRI

Abstract

Chemical exchange saturation transfer (CEST) MRI enables measurement of dilute CEST agents and microenvironment properties such as pH and temperature, holding great promise for in vivo applications. However, because of confounding concomitant RF irradiation and relaxation effects, the CEST-weighted MRI contrast may not fully characterize the underlying CEST phenomenon. We postulated that the accuracy of quantitative CEST MRI could be improved if the experimental factors (labeling efficiency and RF spillover effect) were estimated and taken into account. Specifically, the experimental factor was evaluated as a function of exchange rate and CEST agent concentration ratio, which remained relatively constant for intermediate RF irradiation power levels. Hence, the experimental factors can be calculated based on the reasonably estimated exchange rate and labile proton concentration ratio, which significantly improved quantification. The simulation was confirmed with Creatine phantoms of serially varied concentration titrated to the same pH, whose reverse exchange rate (k_ws) was found to be linearly correlated with the concentration. In summary, the proposed solution provides simplified yet reasonably accurate quantification of the underlying CEST system, which may help guide the ongoing development of quantitative CEST MRI.

1. Introduction

Chemical exchange saturation transfer (CEST) MRI provides an exchange-dependent contrast mechanism that enables measuring low concentration CEST agents and microenvironment properties (1–3). CEST MRI has been applied to study pH, temperature, metabolites and enzyme activities, and remains promising for a host of in vivo applications (4–12). For instance, pH-weighted amide proton transfer (APT) imaging, a form of CEST MRI that probes amide proton chemical exchange, has been translated to study ischemic tissue acidosis, an informative surrogate marker for altered tissue metabolism during acute stroke (13–18). Moreover, CEST imaging is sensitive to the labile proton concentration, which provides protein/peptide content-weighted image contrast for imaging cancer and multiple sclerosis (19–22). However, the experimentally measured CEST MRI contrast is complex, depending on not only the labile proton concentration and exchange rate, but also on experimental parameters including magnetic field strength, RF irradiation power, duration and scheme (23–25). There is a demonstrable need to develop quantitative CEST MRI for improved mechanistic understanding of the underlying CEST system.

Both numerical and empirical solutions have been developed to model CEST MRI contrast (17,23,26–29). Briefly, the CEST MRI contrast can be described as a multiplication of the simplistic CEST contrast and an experimental factor that includes the labeling coefficient and spillover factor (30). The labeling coefficient quantifies the saturation efficiency of the exchangeable protons, while the spillover factor calculates the direct RF saturation of the bulk water signal, which competes with the CEST effect. For typical diamagnetic CEST agents, the labeling coefficient improves with RF power, while the RF spillover factor degrades (3). For a given set of CEST agent properties, there is an optimal RF irradiation power that provides the maximal CEST MRI contrast, at which level the saturation of exchangeable protons and the RF spillover effect of bulk water signal are balanced (23). Therefore, proper estimation of the experimental factor is not only necessary to optimize CEST MRI experiments but also important to improve the accuracy of quantitative CEST imaging.

We postulated that the reverse chemical exchange rate (k_ws) could be derived from CEST MRI with reasonable estimation of the experimental factor. To evaluate the accuracy of quantitative CEST MRI, we first simulated CEST MRI contrast as a function of labile proton concentration ratio and chemical exchange rate under representative RF irradiation power levels. Because the experimental factor remains relatively constant across a broad range of CEST agent concentration ratio, the experimental factor can be estimated based on a reasonable guess of the CEST agent concentration ratio and exchange rate, permitting improved quantification of the CEST agent concentration ratio-weighted exchange rate (i.e., k_ws). The simulation was validated by using Creatine, a widely used experimental CEST agent with a single exchangeable amine proton (binary exchange model) of serially varied concentrations.

2. Results

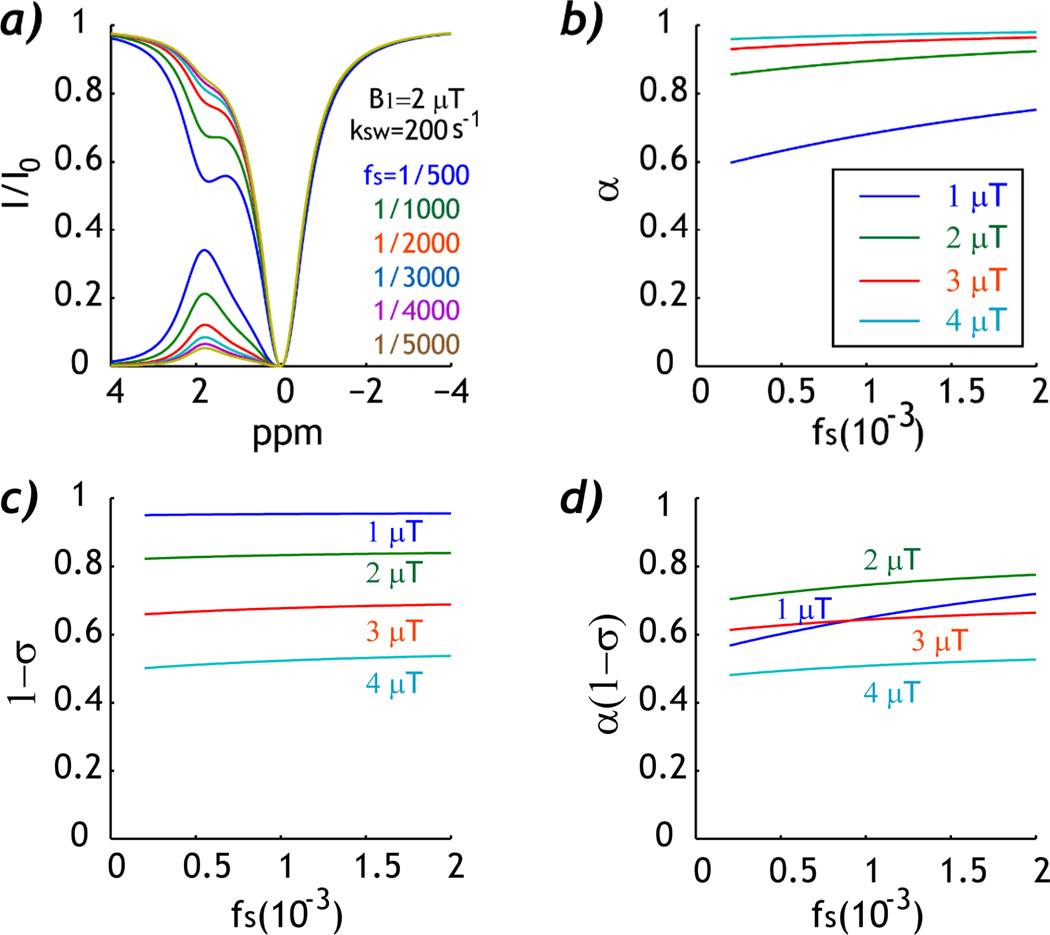
Fig. 1 summarizes the simulated experimental factor as a function of CEST agent concentration ratio. Fig. 1a shows Z-spectra and asymmetry spectra for six CEST agent concentration ratios, from 1:5000 to 1:500, for a representative exchange rate of 200 s⁻¹ and B₁ field of 2 µT. It shows that the CEST MRI contrast increases with CEST agent concentration. The labeling coefficient increases slightly with RF power, which remains relatively constant with respect to CEST agent concentration ratio for RF power above 2 µT (Fig. 1b). The RF spillover factor decreases with RF power, suggesting more concomitant RF spillover effect (Fig. 1c). In addition, the spillover factor shows relatively little change as a function of CEST agent concentration ratio while the experimental factor increases only slightly, at 0.65 ± 0.04, 0.75 ± 0.02, 0.64 ± 0.01 and 0.51 ± 0.01 for B₁ fields of 1, 2, 3 and 4 µT, respectively. Therefore, the experimental factor remains rather constant (within 2%) for intermediate B₁ field (2–4 µT).

Fig. 1.

Simulation of the experimental factor as a function of CEST agent concentration ratio. a) Z-spectra show increased CEST contrast at higher CEST agent concentration ratio. b). Labeling coefficient increases slightly with CEST agent concentration ratio. c) RF Spillover factor remains approximately constant as a function of CEST agent concentration ratio. d) The experimental factor shows relatively little change as a function of CEST agent concentration ratio when intermediate B₁ irradiation field is used (2–4 µT).

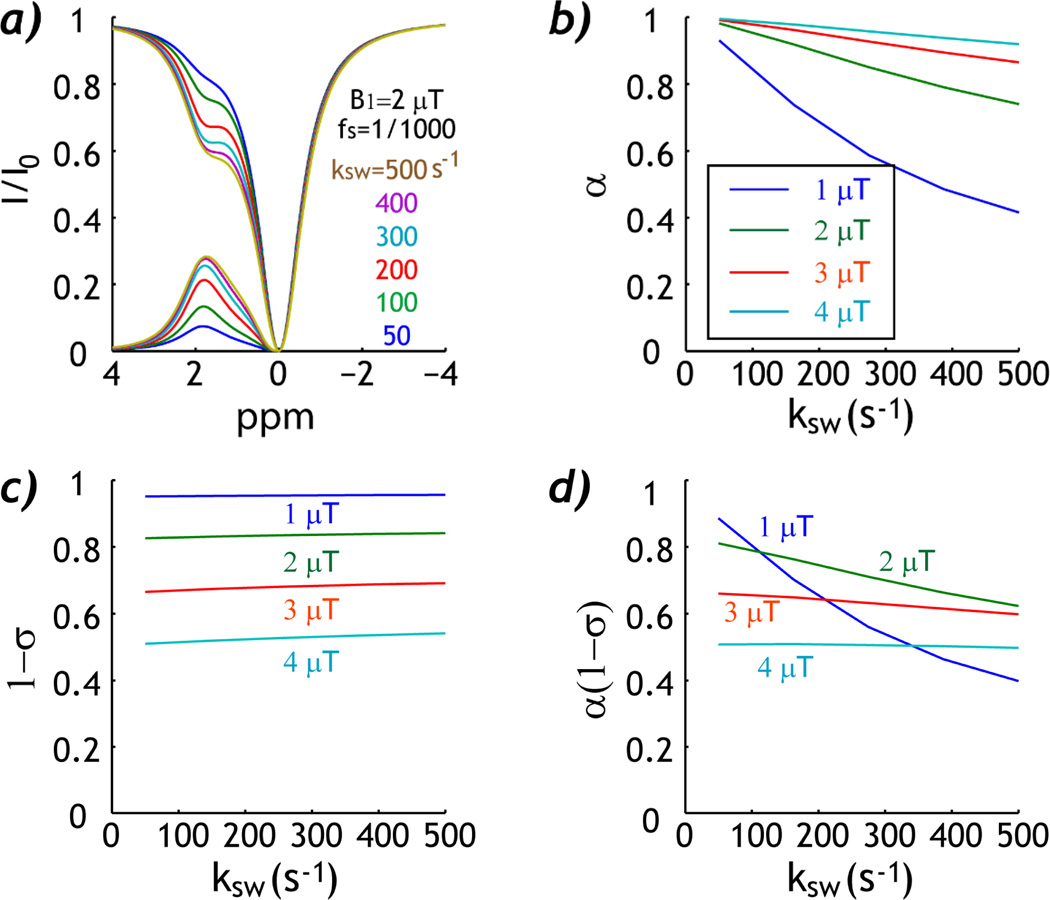
Fig. 2 shows the simulated experimental factor as a function of the chemical exchange rate. Fig. 2a shows Z-spectra and asymmetry spectra for six typical exchange rates, from 50 to 500 s⁻¹, for a representative labile proton concentration ratio of 1:1000 and B₁ field of 2 µT. Whereas the CEST MRI contrast increases with chemical exchange rate, the CEST MRI contrast plateaus at higher chemical exchange rate due to less efficient saturation. Indeed, Fig. 2b shows that the labeling coefficient quickly degrades with increasing exchange rate, particularly for low RF irradiation amplitude. Fig. 2c shows that the RF spillover factor decreases with RF power, as expected. More importantly, the spillover factor shows relatively little change as a function of exchange rate. The experimental factor was 0.60 ± 0.20, 0.71 ± 0.08, 0.63 ± 0.03 and 0.50 ± 0.00 for B₁ field of 1, 2, 3 and 4 µT, respectively. Whereas the experimental factor more strongly depends on the chemical exchange rate than labile proton concentration ratio, it remains reasonably constant (within 3%) as a function of exchange rate for intermediate B₁ field (3–4 µT).

Fig. 2.

Simulation of the experimental factor as a function of chemical exchange rate (k_sw). a) Z-spectra show increased CEST contrast at higher exchange rate. b) Labeling coefficient decreases with exchange rate. c) RF Spillover factor remains approximately constant as a function of exchange rate. d) The experimental factor decreases with exchange rate, yet remains relatively constant for intermediate B₁ irradiation field (3–4 µT).

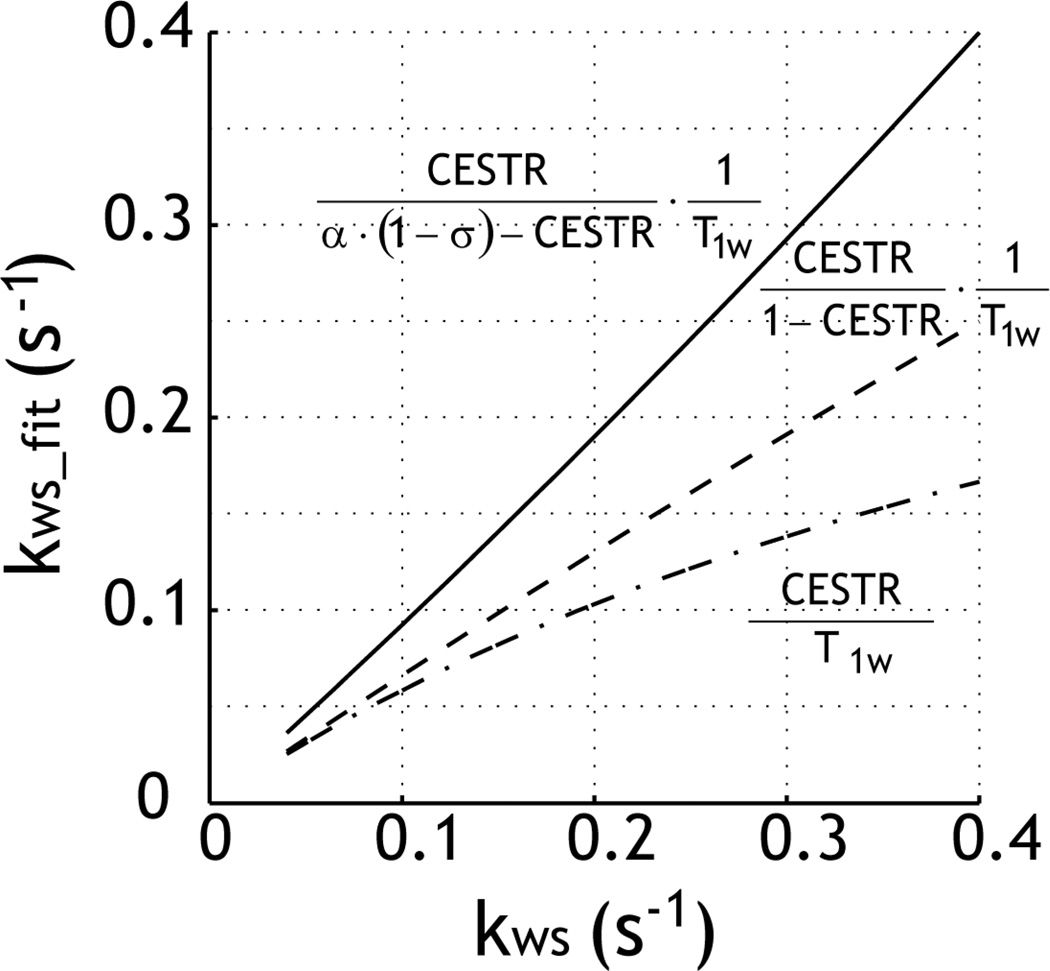
We postulated that k_ws could be reasonably derived from CEST MRI, provided that the experimental factor can be estimated and corrected for. Fig. 3a compares k_ws estimated by using the first-order approximation of the simplistic solution, the simplistic solution and the proposed experimental factor-corrected analysis (Eq. 2). The CEST labile proton concentration ratio with respect to bulk water protons was varied from 1:5000 to 1:500 for a constant exchange rate of 200 s⁻¹ and chemical shift of 1.875 ppm (B₁ = 2 µT). When the CEST MRI contrast becomes non-negligible, the first-order approximation of the simplistic solution appears to plateau at higher concentration ratio (dash-dotted line). The solution can be improved by the simplistic solution (i.e., CESTR/(1-CESTR)/T₁), which, however, still significantly underestimated the reverse exchange rate (gray dashed line). Because the simulation (Figs. 1 and 2) shows that the experimental factor remains relatively constant for typical CEST agent concentration ratio and exchange rate for intermediate RF irradiation power levels, we can reasonably estimate the experimental factor, assuming a median CEST concentration ratio (1:909) and exchange rate of 200 s⁻¹. Indeed, the proposed solution improved the calculation (solid line). This suggests that by correcting for the experimental factor, the accuracy of the quantitative CEST MRI can be significantly improved.

Fig. 3.

Evaluation of the precision of quantitative CEST solution. The reverse exchange rate was obtained using the first-order approximation of the simplistic solution (dash-dotted line), simplistic solution (dashed line), and the proposed experimental factor-compensated solution (solid line).

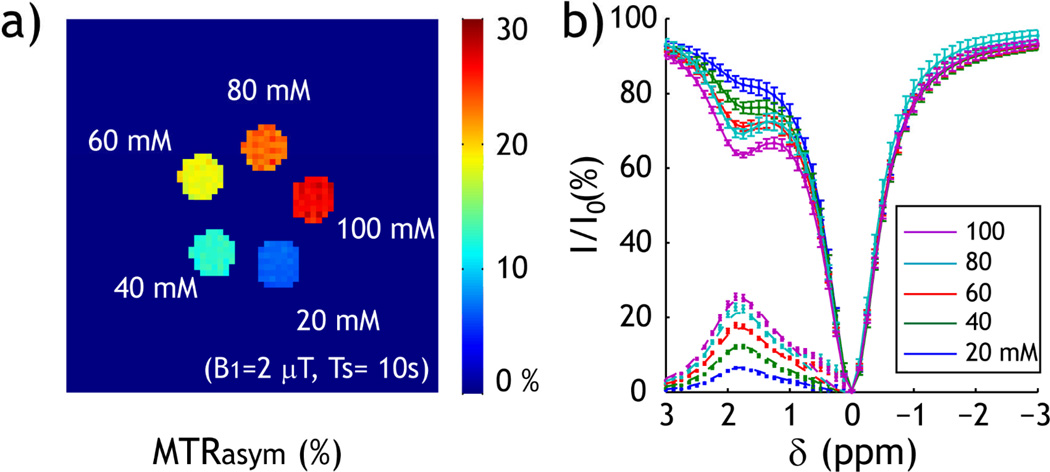
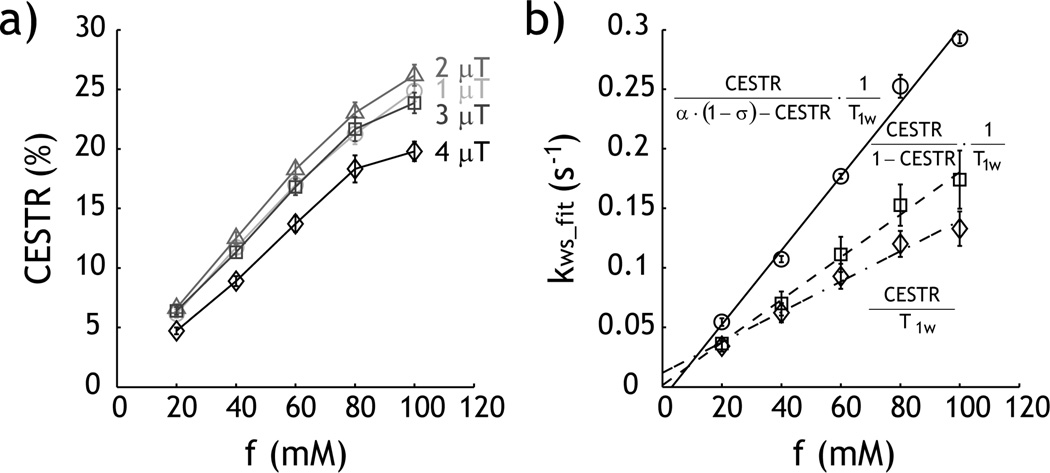
The proposed quantitative CEST MRI was validated by using a Creatine phantom, with a single exchangeable amine proton at 1.9 ppm from bulk water resonance. We prepared five compartments of serially varied Creatine concentration (20, 40, 60, 80 to 100 mM.) Fig. 4a shows that the CESTR increases with CEST agent concentration, obtained at B₁ field of 2 µT. Fig. 4b shows the corresponding CEST Z-spectra and asymmetry spectra of the multi-compartment CEST phantom, which clearly shows amine proton exchange-induced CEST contrast at 1.875 ppm. The B₀ map was obtained by acquiring four phase images with off-centered echo times (τ) of 1, 3, 5 and 7 ms. Because the B₀ of these five CEST agent compartments was very homogeneous (−1.6 ± 2.8 Hz), we did not conduct field inhomogeneity correction (30,31). The CEST asymmetry spectra were numerically fitted, using the Bloch-McConnell equation, from 1 to 3 ppm. We minimized the number of free parameters by fixing the relative CEST agent concentration of the multi-compartment phantom according to the Creatine concentration, and assumed four free parameters: exchange rate, CEST agent concentration ratio, T_1w, and T_2w. The exchange rate was determined to be 222 s⁻¹, and the labile proton concentration ratio with respect to the bulk water pool was 1:3999, 1:1999, 1:1333, 1:1000 and 1:800 for 20, 40, 60, 80 and 100 mM Creatine solution. Therefore, we have K_ws=0.0028 [C], where [C] is the Creatine concentration in mM. In addition, T_1w and T_2w were determined to be 1.91 s and 0.90 s, respectively.

Fig. 4.

Experimental measurement of CEST MRI. a) CEST map was calculated as MTR_asym (i.e. MTR_asym=(I_ref−I_label)/I₀). The CEST map shows that the CEST contrast increases with Creatine concentration (B₁=2 µT). b) Z-spectra and MTR_asym curve show exchangeable amine proton CEST contrast at 1.875 ppm.

T₁ was measured as 1.75 ± 0.03, 1.74 ± 0.03, 1.72 ± 0.03, 1.71 ± 0.03 and 1.70 ± 0.03 for 20, 40, 60, 80 and 100 mM Creatine solutions, respectively; the T₂ for each was 1.10 ± 0.12, 1.05 ± 0.12, 1.02 ± 0.08, 0.89 ± 0.06 and 0.91 ± 0.08 s. The R₁ and R₂ rates can be described by a linear regression relationship, with R₁= 0.0002*[C] + 0.5687 and R₂= 2.77*10⁻³[C] + 0.85, where [C] is the Creatine concentration in mM. Fig. 5a shows CEST contrast as a function of Creatine concentration, for four representative RF power levels of 1, 2, 3 and 4 µT. CEST contrast peaked when B₁ field was 2 µT. Notably, CEST MRI contrast appears to deviate from the linear relationship for highly concentrated Creatine compartment. Fig. 5b shows the calculated reverse exchange rate as a function of Creatine concentration. For the proposed experimental factor-corrected algorithm, the experimental factor was estimated assuming that k_sw was 200 s⁻¹ at labile proton concentration ratio of 1:2000. Moreover, we assumed T₁ and T₂ to be 1.76 and 1.18 s, respectively, from extrapolated T₁ and T₂ measurements. We repeated the calculations for RF powers of 2, 2.5, 3, 3.5 and 4 µT and the respective α values were 0.89, 0.93, 0.95, 0.96 and 0.97. In addition, the spillover factor correction (1-σ) was calculated to be 0.87, 0.80, 0.74, 0.67 and 0.60, respectively. The solution can be described by linear regression, where K_ws=0.0013 [C] + 0.0119, K_ws=0.0018 [C] + 0.0015 and K_ws=0.0031 [C] − 0.0097, for the first-order approximation of the simplistic solution (diamond), the simplistic solution (square), and the proposed solution (circle), respectively. The proposed solution is approximately equal to that obtained from the Bloch-McConnell numerical fitting (i.e. K_ws=0.0028 [C]), significantly improved from the results of the conventional solutions.

Fig. 5.

Evaluation of the proposed quantitative CEST MRI. a) The experimentally obtained CEST contrast initially increases with RF power from 1 to 2 µT, and decreases when higher RF power was used. b) Comparison of k_ws solution from the first-order approximation of simplistic solution (diamond), the simplistic solution (square), and the proposed experimental factor-compensated solution (circle).

3. Discussion

The proposed solution, by taking into account the experimental factor, significantly improves the measurement of the labile proton concentration ratio-weighted exchange rate (k_ws). Such simplified yet reasonably accurate quantification of k_ws augments the commonly used CEST-weighted MRI contrast, which is susceptible to confounding factors including relaxation time, chemical shift, magnetic field strength and RF irradiation power. Our results show that the experimental factor remains relatively constant for intermediate RF power levels, and hence can be properly estimated provided the range of labile proton concentration ratio and exchange rate can be reasonably estimated. The algorithm, in particular, is applicable to studying systems in which a change in CEST agent concentration is dominant while the k_sw exchange rate is relatively invariant during a comparative study, or a change in k_sw exchange rate is dominant while the CEST agent concentration is relatively invariant so the change in k_ws can be easily attributed to the dominant factor. This may require prior knowledge of the underlying CEST system, but only to the extent of reasonable approximations. On the other hand, the proposed method only derives the reverse exchange rate (k_ws) and cannot decouple the labile proton concentration ratio from chemical exchange rate. The exchange rate has to be independently measured in order to derive the absolute CEST agent concentration, or vice versa. Recently, it has been shown that by probing the RF power dependence of CEST MRI, the chemical exchange rate may be determined independent of ratio of CEST agent concentration to water proton concentration (f_s), which may complement the proposed algorithm for improved characterization of the underlying CEST system (32,33).

The proposed algorithm is based on the empirical solution developed for diamagnetic CEST (DIACEST) agents, which do not alter bulk water T₁ due to their slow to intermediate exchange rates. On the other hand, paramagnetic CEST (PARACEST) agents may affect bulk water T₁ and T₂ (34,35). Fortunately, for PARACEST agents with large chemical shifts, the direct RF saturation effect may be small and the experimental factor is dominated by the labeling coefficient (26). Indeed, Dixon et al. showed that the exchange rate of PARACEST agent could be derived independent of concentration by using the omega plot, which effectively described the labeling coefficient (32). Whereas the Bloch-McConnell equation can easily simulate CEST contrast and allow B₀ inhomogeneity correction, the reverse problem of numerically solving labile proton concentration and exchange rate from CEST contrast is technically challenging. Because multiple parameters are derived, including labile proton concentration, exchange rate, T₁ and T₂, the Bloch-McConnell fitting requires multi-parametric non-linear fitting, which may be subjected to non-negligible errors. In comparison, the proposed simplified solution provides reasonable measurement of the reverse exchange rate and is applicable under acceptable B₀ homogeneity. In addition, acquisition of Z-spectra is more time consuming when compared with the proposed solution.

It is helpful to compare the proposed algorithm and several quantification approaches of with transient solutions such as quantification of exchange rate with saturation time (QUEST) and ratiometric analysis (QUESTRA) (24,25). In the QUESTRA solution, multiple transient CEST contrast measurements are obtained to probe how they approach the steady state. The ratiometric solution complements the original QUEST solution by taking into account T_1ρ effect, T₁ relaxation under spin locking, for improved measurement of the reverse exchange rate (25). In addition, chemical exchange rate can be determined by studying its RF power dependency (23,24,33). The optimal RF power varies with chemical exchange rate, not the labile proton concentration (33). However, numerical fitting is often utilized in order to take the experimental factor into account. Moreover, it has been shown that off-resonance spin locking is sensitive to slow-exchanging protons, similar as CEST MRI (36). The exchange rate can be numerically solved following an spin locking mathematical model developed by Trott and Palmer (37). In comparison, the solution proposed in this study measures the steady state CEST contrast and directly calculates k_ws by estimating and correcting for the experimental factor. Because the steady state contrast is higher than that of transient state, the proposed solution should be of higher accuracy. To summarize, the proposed algorithm is simple to implement yet provides reasonably accurate quantification of the underlying CEST system, without using the complex approaches of multi-parametric non-linear fitting or transient solution.

4. Conclusions

Our study shows that the CEST MRI experimental factor remains relatively constant for a broad range of labile proton concentrations and exchange rates when an intermediate RF irradiation level is used. As such, the experimental factor can be reasonably estimated for quantitative CEST MRI, which significantly improves the accuracy of the reverse exchange rate (k_ws). The proposed solution provides more accurate measurement than the conventional CEST-weighted MRI contrast, which will thus further aid the development of quantitative CEST imaging.

5. Experimental

Phantom

We prepared a multi-compartment Creatine CEST phantom. Creatine (Sigma Aldrich, St Louis, MO) was added to gadolinium-doped (30 µM) phosphate buffered solution (PBS) and the Creatine concentration was serially varied from 20, 40, 60, 80 to 100 mM; pH was titrated to 6.75 ± 0.01 (EuTech Instrument, Singapore). The gadolinium doping reduced T₁ so that moderate repetition time (TR) can be used. In addition, the reduced T₁ value is closer to in vivo T₁. The solution was transferred into multiple centrifugal tubes, sealed and inserted into a phantom container. The container and an additional central tube were filled with 1% low melting-point agarose to secure the Creatine-PBS tubes.

Simulation

CEST MRI contrast was numerically simulated using the Bloch-McConnell 2-pool exchange model in Matlab 7.4 (Mathworks, Natick MA), as described previously (26,38). The longitudinal relaxation times were 2 s and 1 s for the bulk water and labile proton pools, respectively, and the transverse relaxation times were 60 ms and 15 ms for the bulk water and labile proton pools, respectively. We assumed a chemical shift of 1.875 ppm and a magnetic field strength of 4.7 Tesla. CEST MRI contrast is also calculated from the empirical solution (27),

$$\text{CESTR}=\frac{{\mathrm{k}}_{\text{ws}}}{{\mathrm{R}}_{1\mathrm{w}}+{\mathrm{k}}_{\text{ws}}}\cdot \mathrm{\eta }$$ (1)

where k_ws = f_s*k_sw, f_s is the labile proton concentration with respect to bulk water concentration, k_sw is chemical exchange rate, R_1w is the bulk water longitudinal relaxation rate, and η is the experimental factor. We have η= α *(1−σ), where α is the labeling coefficient and σ is the spillover factor (30). For slow chemical exchange, $\mathrm{\alpha }=\frac{{\mathrm{\omega }}_1^2}{\mathrm{p}\cdot \mathrm{q}+{\mathrm{\omega }}_1^2}$ and $\mathrm{\sigma }=1-\frac{{\mathrm{r}}_{1\mathrm{w}}}{{\mathrm{k}}_{\text{ws}}}\left(\frac{{\mathrm{R}}_{1\mathrm{w}}{\mathrm{r}}_{\text{zs}}{\text{cos}}^2\mathrm{\theta }+{\mathrm{R}}_{1\mathrm{s}}{\mathrm{k}}_{\text{ws}}\text{cos}\mathrm{\theta }{\text{cos}}^2(\mathrm{\theta }/2)}{{\mathrm{r}}_{\text{zw}}{\mathrm{r}}_{\text{zs}}-{\mathrm{k}}_{\text{ws}}{\mathrm{k}}_{\text{sw}}{\text{cos}}^2(\mathrm{\theta }/2)}-\frac{{\mathrm{R}}_{1\mathrm{w}}{\mathrm{r}}_{2\mathrm{s}}{\text{cos}}^2\mathrm{\theta }}{{\mathrm{r}}_{\text{zw}}{\mathrm{r}}_{2\mathrm{s}}-{\mathrm{k}}_{\text{ws}}{\mathrm{k}}_{\text{sw}}{\text{sin}}^2\mathrm{\theta }}\right)$, where $\mathrm{p}={\mathrm{r}}_{2\mathrm{s}}-\frac{{\mathrm{k}}_{\text{sw}}{\mathrm{k}}_{\text{ws}}}{{\mathrm{r}}_{2\mathrm{w}}}$, $\mathrm{q}={\mathrm{r}}_{1\mathrm{s}}-\frac{{\mathrm{k}}_{\text{sw}}{\mathrm{k}}_{\text{ws}}}{{\mathrm{r}}_{1\mathrm{w}}}$, r_zw = r_1w cos²θ/2 + r_2w sin²θ/2, r_zs = r_1s cos²θ + r_2s sin²θ, r_1w,s=R_1w,s+k_ws,sw, r_2w,s=R_2w,s+k_ws,sw and θ = tan⁻¹(ω₁ / Δω_s); here, ω₁=γB₁, Δω_s is the chemical shift of CEST labile proton, γ is the gyromagnetic ratio and B₁ is the amplitude of continuous-wave (CW) RF irradiation pulse.

It has been shown that the labeling coefficient strongly depends on the chemical exchange rate and RF irradiation power, while the spillover factor is dominated by labile proton chemical shift and RF power. Interestingly, labeling coefficient and spillover factor are relatively constant as a function of CEST agent concentration ratio, for intermediate RF irradiation power levels. In this case, the reverse exchange rate can be derived as

$${\mathrm{k}}_{\text{ws}}\approx \frac{\text{CESTR}}{\mathrm{\alpha }\cdot (1-\mathrm{\sigma })-\text{CESTR}}\cdot \frac{1}{{\mathrm{T}}_{1\mathrm{w}}}$$ (2)

For the simplistic case of complete labile proton saturation (α=1) and negligible RF spillover effects (σ=0), Eq. 2 can be simplified to $\frac{\text{CESTR}}{1-\text{CESTR}}\cdot \frac{1}{{\mathrm{T}}_{1\mathrm{w}}}$. If the CEST MRI contrast is small, the reverse exchange rate can be further simplified using its first order approximation, $\frac{\text{CESTR}}{{\mathrm{T}}_{1\mathrm{w}}}$.

MRI

MRI experiments were conducted using a 4.7 Tesla small bore Bruker MRI scanner (Bruker Biospin, Billerica, MA). Relaxation and CEST MRI was obtained with single-slice, single-shot echo planar imaging (EPI) (field of view: 76×76 mm², matrix: 64×64, slice thickness = 5 mm, acquisition bandwidth 200 kHz). Because the chemical shift of Creatine’s exchangeable amine proton is close to bulk water resonance, the reference scan is susceptible to non-negligible RF spillover effect so a 3-point CEST imaging was acquired. Specifically, I_ref, I_label and I₀ were acquired, where I_ref, I_label are the reference and label images, with RF irradiation applied at ±1.875 ppm (±375 Hz at 4.7 Tesla), in addition to I₀ (control scan) without RF irradiation (TR/echo time (TE)=20,000/28 ms, time of saturation (TS) =10,000 ms, number of signal average (NSA)=2). The RF power was varied from 1, 1.5, 2, 2.5, 3, 3.5 and 4 µT. In addition, the Z-spectrum was acquired with RF irradiation from −3 to 3 ppm, per 0.125 ppm (B₁=2 µT). T₁-weighted images were acquired using an inversion recovery sequence with eight inversion intervals (TI) ranging from 250 to 10,000 ms (TR/TE =12,000/28 ms, NSA=2). A T₂ map was derived from seven separate SE images, with TE ranging from 50 to 1,000 ms (TR=12,000 ms, NSA=2).

Image Processing

Images were processed in Matlab. The parametric T₁ map was obtained using least-squares mono-exponential fitting of the signal intensities (I) as a function of inversion time (I = I₀⎦1 − (1 + η)e^−TI/T₁⎦), where η is the inversion efficiency and I₀ is the equilibrium state. The T₂ map was derived by fitting the signal intensity as a function of echo time, I = I₀e^−TE/T₂. Moreover, CEST contrast was calculated from the 3-point CEST imaging as CESTR = (I_ref − I_label)/I₀.