Abstract
To provide mechanistic insight into the etiology of osteoporotic wedge fractures, we investigated the spatial distribution of tissue at the highest risk of initial failure within the human vertebral body for both forward flexion and uniform compression loading conditions. Micro-CT-based linear elastic finite element analysis was used to virtually load 22 human T9 vertebral bodies in either 5° of forward flexion or uniform compression; we also ran analyses replacing the simulated compliant disc (E = 8 MPa) with stiff polymethylmethacrylate (PMMA, E = 2,500 MPa. As expected, we found that, compared to uniform compression, forward flexion increased the overall endplate axial load on the anterior half of the vertebra and shifted the spatial distribution of high-risk tissue within the vertebra towards the anterior aspect of the vertebral body. However, despite that shift, the high-risk tissue remained primarily within the central regions of the trabecular bone and endplates, and forward flexion only slightly altered the ratio of cortical-to-trabecular load sharing at the mid-vertebral level (mean ± SD for n = 22: 41.3% ± 7.4% compression; 44.1% ± 8.2% forward flexion). When the compliant disc was replaced with PMMA, the anterior shift of high-risk tissue was much more severe. We conclude that, for a compliant disc, a moderate degree of forward flexion does not appreciably alter the spatial distribution of stress within the vertebral body.
Keywords: wedge fracture, forward flexion, finite element analysis, bone strength, osteoporosis
1. Introduction
Despite the frequent occurrence of vertebral wedge fractures in the aged (Eastell et al., 1991; Ismail et al., 1999), the etiology of these fractures remains uncertain (Adams and Dolan, 2011; Christiansen and Bouxsein, 2010). The morphology of the (anterior) wedge fracture provides an intuitive etiological link with forward flexion (Dall’Ara et al., 2010; Granhed et al., 1989; Osvalder et al., 1990). Presumably, forward flexion of the bone-disc motion segment increases stresses within the anterior portions of the cortical shell and trabecular bone. Indeed, cadaver testing of motion segments has confirmed that forward bending increases pressure in the anterior half of the intervertebral disc (Pollintine et al., 2004). However, the effects of this eccentric pressure distribution on the stresses within the underlying cortical and trabecular microstructure remain unclear due to the technical difficulty of measuring such stresses. With its ability to describe the bone microstructure at high spatial resolution and its inherently mechanistic nature, micro-CT-based finite element analysis is well suited to address this difficulty. Applied so far to human whole vertebral bodies to address cortical-trabecular load sharing (Eswaran et al., 2006; Homminga et al., 2004), locations of high-risk tissue (Eswaran et al., 2007), and mechanisms of endplate failure (Fields et al., 2010), this technique has not yet been applied using forward flexion loading conditions. Thus, to provide mechanistic insight into the etiology of osteoporotic wedge fractures, we used micro-CT-based finite element analysis on a cohort of elderly human cadaver vertebrae to compare tissue-level stresses throughout the vertebral body during both forward flexion and uniform compression loading conditions. We also used a simple beam-on-elastic-foundation model (Bartel et al., 2006; Hetenyi, 1946) to provide a more intuitive basis for understanding the effect of forward flexion loading conditions on the fundamental mechanism of load transfer from the disc through the endplate into the underlying bone.
2. Material and Methods
2.1 Specimen preparation and micro-CT scanning
Twenty-two fresh-frozen T9 human whole vertebral bodies were obtained from cadavers (n = 11 male; n = 11 female; age range: 53–97 years, mean ± SD = 81.5 ± 9.6 years) with no medical history of metabolic bone disorders. The posterior elements were removed and each isolated vertebral body was micro-CT scanned using a 30-μm voxel size (Scanco 80; Scanco Medical AG, Brüttisellen, Switzerland). To reduce computational cost, the scans were coarsened to a 60-μm voxel size before the hard tissue and marrow were segmented using a global threshold value, which was determined using the manufacturer’s software (Fields et al., 2010). The bone tissue was compartmentalized into the cortical shell, trabecular bone, endplates, and cortical rim (Eswaran et al., 2007).
2.2 Finite element modeling
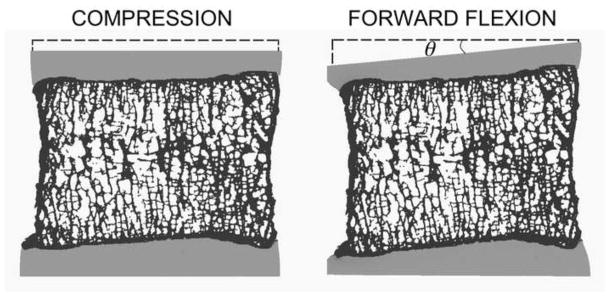
High-resolution “voxel” type finite element models of each vertebral body were created as described elsewhere (Eswaran et al., 2007; Van Rietbergen et al., 1995). All bone elements were assigned the same homogeneous and isotropic hard tissue material properties (elastic modulus of 18.5 GPa and Poisson’s ratio of 0.3 (Eswaran et al., 2007)), since the cortical shell is often described as condensed trabeculae (Roy et al., 1999; Silva et al., 1994). The disc was modeled using symmetry boundary conditions at its mid-transverse plane. Thus, element layers of nominal height 2.5 mm were added to the top and bottom of the vertebral body, which simulated a disc height of 5 mm (Middleditch and J., 2005) (Fig. 1). The disc elements were assigned homogeneous elastic and isotropic material properties (elastic modulus of 8 MPa (Duncan and Lotz, 1998) and Poisson’s ratio of 0.45 (Fagan et al., 2002)). The choice of 8 MPa was based on the compressive stress-strain curve at physiological strain rate from testing of the bone-annulus-bone segments (see Figure 6 of (Duncan and Lotz, 1998)). Those data show at strain of about 20%–25%, the stress is about 0.4–0.8 MPa, providing a secant modulus of about 8 MPa. This strain range was taken because it is consistent with the disc deformation in our models. Each model was analyzed with two different loading conditions (Fig. 1). For compression loading, an uniform apparent compressive strain 5% was applied to the top surface of each model; for forward flexion, the top surface of the superior disc layer was rotated by 5° in a mid-sagittal plane about the most superior-posterior point to simulate forward flexion over a single motion segment (Adams et al., 2006). The top surface of each model was displaced in the superior-inferior direction using roller-type boundary condition, allowing disc bulging, while the bottom surface was fixed using minimum frictionless constraints to prevent rigid body motion. We also performed simulations in which we replaced the disc with polymethylmethacrylate (PMMA) of elastic modulus 2.5 GPa and Poisson’s ratio 0.3, since this is a common configuration in cadaver studies (Buckley et al., 2009; Crawford et al., 2003; Dall’Ara et al., 2010; Mosekilde and Mosekilde, 1986).
Fig. 1.
Mid-sagittal slice (0.5 mm thick) of a vertebral body shows the imposed boundary conditions and the resulting deformation of the disc-bone-disc segment under uniform compression (5%) and forward flexion (θ = 5°).
Each FE model had up to about 80 million elements and was solved using a highly scalable, implicit finite element framework (Olympus) (Adams et al., 2004). All computations were performed on a Sun Constellation cluster supercomputer (Ranger; Texas Advanced Computing Center, Austin, TX, USA). Typical hardware requirements for a single analysis comprised up to 1024 processors in parallel and 4 TB of memory. The average CPU time required for each analysis was 115 hours. Altogether, 88 linearly elastic analyses were performed (22 vertebra, two load cases, disc and PMMA).
2.3 Beam-on-elastic-foundation analysis
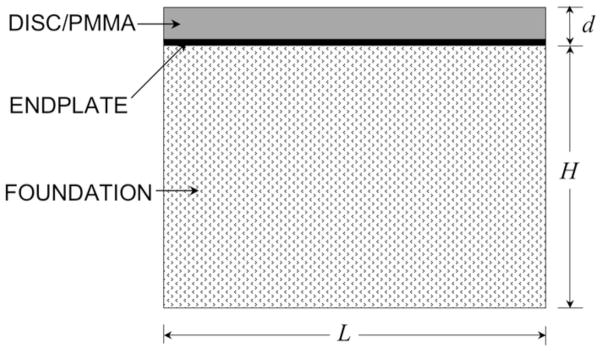
To provide a more intuitive insight into how the compressive force acting on vertebra is transferred to the underlying bone, we also performed a beam-on-elastic-foundation (BOEF) analysis (Bartel et al., 2006; Hetenyi, 1946) of the vertebral body (Fig. 2). The composite of the disc (or PMMA) and endplate is modeled as a straight uniform beam of length L, height d, depth (into page) b, elastic modulus E, and areal moment of inertia I, resting on a uniform elastic foundation of “foundation” modulus k of trabecular bone. The foundation modulus is given by k = Etb/H, for which Et is the apparent elastic modulus of the trabecular bone, taken as 200 MPa (Morgan et al., 2003). The stress in the trabecular bone was calculated as σ = vk/b, for which v is the displacement of the beam. The model was subjected to a compressive force of 1kN (Pollintine et al., 2010). Two different loading types were applied uniformly across the depth b of the beam: a distributed load along the length of the beam; and a resultant point-type load, applied at the center of pressure. Both load cases were based on the stress distributions as observed in the finite element models, for the disc and PMMA models.
Fig. 2.
Theoretical model used as the basis for the beam-on-elastic-foundation analysis. A composite of the disc/PMMA and endplate was considered as the beam, and the trabecular bone was considered as the foundation. The properties of the beam and the foundation were based on mean values of the measurements for the 22 vertebral bodies used in our finite element analysis: d = 5.5 mm (endplate thickness 0.5 mm (Fields et al., 2010)); L = 26 mm; depth (into page) b = 28 mm; and the effective height of the elastic foundation H = 28 mm.
2.4 Outcomes
The cortical load fraction was defined as the maximum value of the ratio of the axial compressive force acting on the cortical shell to the entire vertebra, computed at each transverse slice excluding the endplates (Eswaran et al., 2006). To identify locations of high-risk tissue, at centroid of each element we calculated the ratio of maximum and minimum principal stress to the respective tissue-level tensile (61 MPa) and compressive (150 MPa) yield stress (Bevill et al., 2006), and defined the tissue-level risk factor as the higher value, which also specified the tissue-level failure mode (tensile or compressive). The high-risk tissue was then identified as the top 10% of tissue in the model, ranked by tissue-level risk factor. To confirm that our forward flexion loading scheme indeed induced higher loads on the anterior half of the vertebral endplate (Pollintine et al., 2004), we also computed the reaction force acting on the anterior and posterior halves of the vertebral endplates. Mean responses for the different loading cases, and disc vs. PMMA, were compared using paired t-tests (JMP 8.0, SAS Institute, Cary, NC).
3. Results
Analysis of the total compressive force acting on the endplates confirmed that forward flexion increased loading locally on the endplates over the anterior half of the vertebra (Table 1). The center of disc pressure shifted (mean ± SD for n = 22) 3.0 ± 0.9 mm anteriorly when the loading was changed from compression to forward flexion. The net compressive force acting on the anterior half of the vertebra for forward flexion was 1.74 ± 0.45 times the force acting on the posterior half. For uniform compression, this ratio of anterior-to-posterior net compressive force was 0.71 ± 0.23, indicating that there was more load acting on the posterior half of the vertebral endplates.
Table 1.
Axial forces acting on the anterior and posterior halves of the superior endplate of the vertebral body loaded via a disc and a PMMA layer.
| Axial Force (N) | |||
|---|---|---|---|
| Anteriora | Posteriora | Anterior/Posterior | |
| Disc loading | |||
| Compression | 410 ± 77 | 590 ± 77 | 0.71 ± 0.23c |
| Flexion | 625 ± 62 | 375 ± 62 | 1.74 ± 0.45b,d |
| Flexion/Compression | 1.56 ± 0.17 | 0.63 ± 0.04 | |
| PMMA loading | |||
| Compression | 494 ± 72 | 506 ± 72 | 1.02 ± 0.31 |
| Flexion | 775 ± 54 | 225 ± 54 | 3.73 ± 1.24b |
| Flexion/Compression | 1.59 ± 0.14 | 0.44 ± 0.06 | |
Data given as mean SD for n = 22 vertebral bodies.
For both loading cases, applied forces were scaled linearly so that the overall axial force was equal to 1000 N, to facilitate comparison with reported experimental data (Pollintine et al., 2010);
p < 0.0001 vs. compression;
p < 0.005 vs. PMMA loading;
p < 0.0001 vs. PMMA loading.
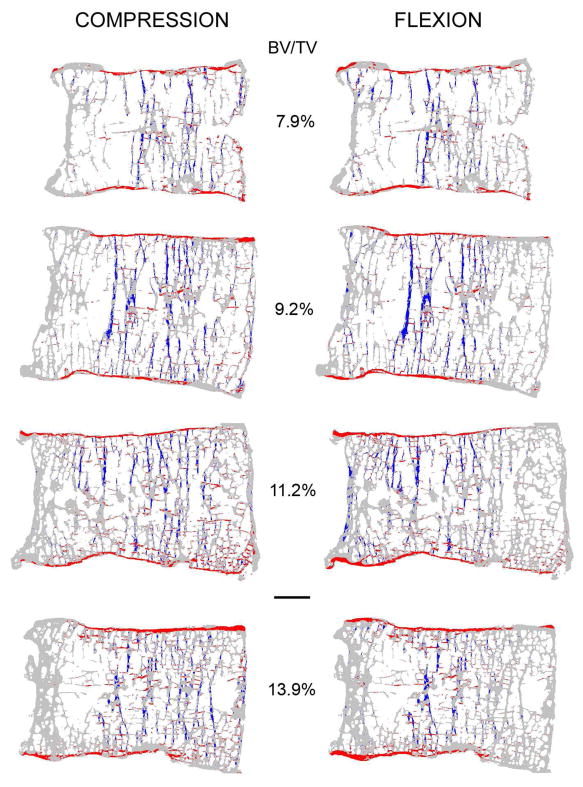
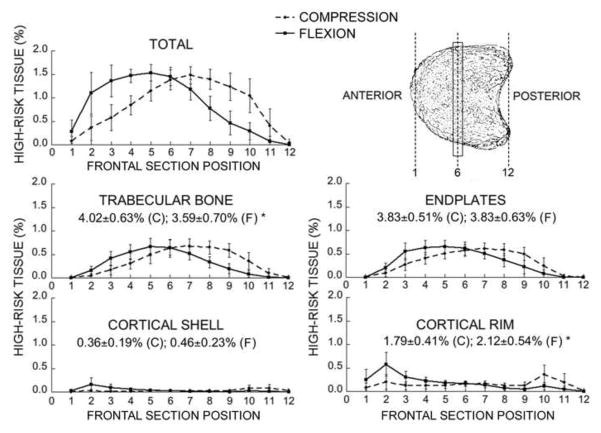
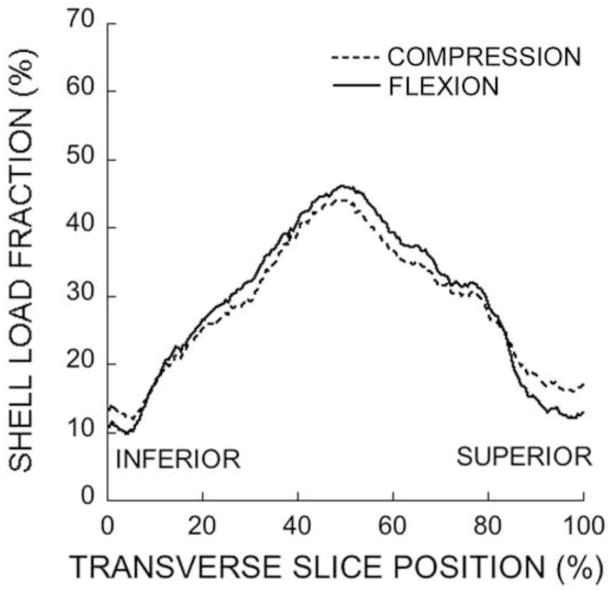
Regardless of the loading conditions, most of the high-risk tissue occurred in the central regions of the trabecular bone and endplates with minimal involvement of the cortical shell (Fig. 3 and Fig. 4). For both loading cases, the dominant tissue-level failure mechanism for the trabecular bone was compression, and for the endplates was tension. Compared to uniform compression, forward flexion — as expected — shifted the distribution of high-risk tissue towards the anterior aspect of the vertebral body, but this effect was only modest (Fig. 3 and Fig. 4). Forward flexion caused a small but statistically significant decrease (from 4.0% ± 0.6% to 3.6% ± 0.7%) in the amount of high-risk bone in the trabecular compartment and a small but statistically significant increase (from 1.8% ± 0.4% to 2.1% ± 0.5%) in the amount of high-risk bone in the cortical rim. Consistent with these trends, forward flexion caused no appreciable change in cortical-to-trabecular compressive load sharing at the mid-vertebral level (41.3% ± 7.4% for compression; 44.1% ± 8.2% for forward flexion; Fig. 5).
Fig. 3.
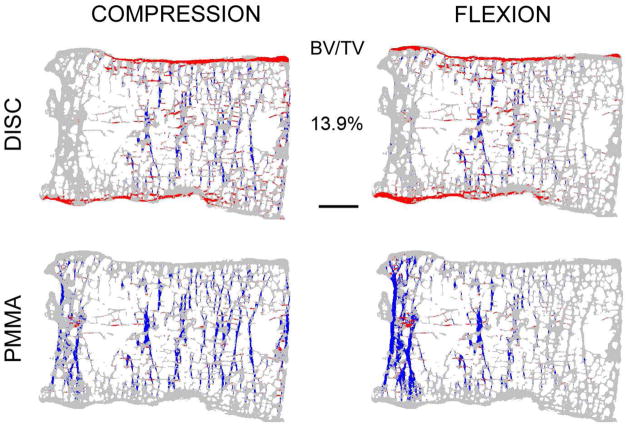
Mid-sagittal sections from four vertebrae with increasing bone volume fraction (BV/TV) from top to bottom showing the distribution of high-risk tissue (compressive tissue-level failure is blue and tensile tissue-level failure is red). Note that the trabeculae, cortical shell, endplates and cortical rim appear thicker than they actually are because all of the bone tissue in this 0.5 mm-thick section is projected onto a single plane. Scale bar: 5 mm.
Fig. 4.
Mean variation in the amount of high-risk tissue across frontal sections for the total vertebral bone and for each compartment. By definition, all values add up to 10% (see text). * Comparisons between compression (C) and flexion (F) were significantly different (p < 0.001 by paired t-test). Bars show ± 1 SD for n = 22 specimens.
Fig. 5.
Variation of the shell load fraction across transverse slices within a typical vertebral body loaded through a disc. The maximum degree of cortical load sharing occurs around the mid-transverse section.
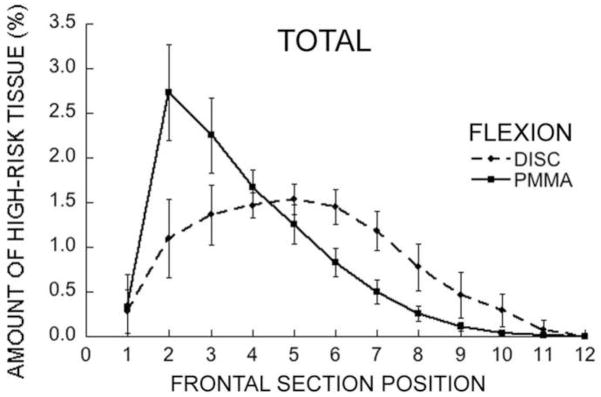
In contrast to these trends, for loading via the stiff layer of PMMA, forward flexion caused a severe shift of high-risk tissue towards the anterior aspect and a sharp concentration of stress in the anterior region (Fig. 6 and Fig. 7); almost no high-risk tissue was observed in the endplates for either flexion or compression (Fig. 6).
Fig. 6.
The distribution of high-risk tissue at a mid-sagittal section of a vertebra with relatively high bone volume fraction (BV/TV), for disc vs. PMMA loading (compressive tissue-level failure is blue and tensile tissue-level failure is red). Scale bar: 5 mm.
Fig. 7.
Mean variation in the amount of total high-risk tissue (for all vertebral compartments) across frontal sections of the vertebral body for forward flexion (disc vs. PMMA). Bars show ± 1 SD for n = 22 specimens.
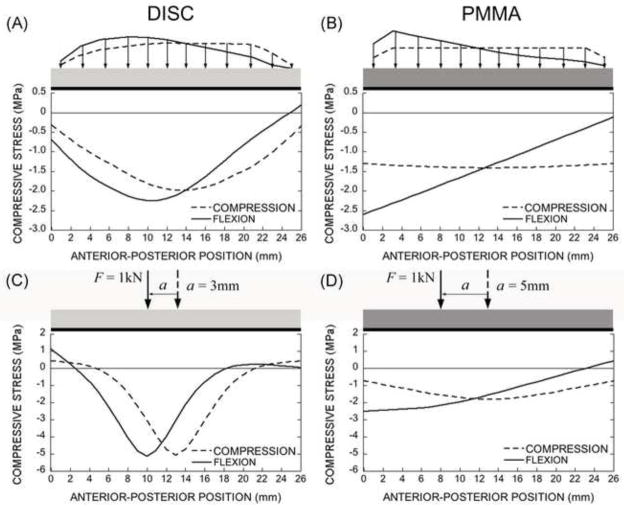
Consistent with these finite element results, in the BOEF analysis, when either a distributed load or a net resultant point load acting on the disc was shifted anteriorly, the highest compressive stresses in the underlying elastic foundation of trabecular bone remained concentrated in the central region (Fig. 8A and C). In contrast, for loading through a PMMA layer, there was an even distribution of stress in the underlying bone for compression but an anteriorly-increasing distribution for forward flexion that peaked at the most anterior aspect (Fig. 8B and D).
Fig. 8.
The distribution of the compressive stresses at the interface of the endplate and the trabecular bone along anterior-posterior direction for the distributed forces from the FE model (A and B) and the corresponding net resultant point forces (C and D). For loading via a disc, the composite behaves like a “flexible” beam on the elastic foundation (trabecular bone) with centrally distributed stresses (A and C). For loading via a PMMA layer, the composite behaves like a “rigid” beam on an elastic foundation with more uniform stresses (B and D).
4. Discussion
The motivation of this study was to gain mechanistic insight into the etiology of osteoporotic anterior wedge fractures. Here, we investigated how forward flexion changes the spatial distribution of stress within the underlying trabecular and cortical bone of the vertebral body. The increased anterior disc pressure that occurs as a result of forward flexion (Pollintine et al., 2004) suggests that forward flexion might overload the bone anteriorly. Consistent with observations from cadaver experiments, our models with the compliant disc showed increased anterior loading of the endplates for forward flexion. However, we found no appreciable anterior shift of high-risk tissue in the underlying cortical shell or trabecular bone or in the overall cortical-trabecular load sharing. Thus, in elderly vertebrae with compliant discs, it appears that a moderate degree of forward flexion does not appreciably alter the spatial distribution of stress within the vertebral body.
This insensitivity of the location of high-risk tissue within the vertebra to the nature of the applied loads (compression vs. forward flexion) has two sources. First, our BOEF analysis revealed that the endplate and disc together behave structurally as a “flexible” beam on an elastic foundation. Thus, maximum stresses in the supporting elastic foundation (the trabecular bone) occur beneath the center of pressure of the applied load, which for forward flexion is just slightly anterior to the center of the vertebral body. Second, because load is transferred through the elderly vertebral body primarily via a small number of the discrete load paths comprising of relatively thick but few vertically oriented trabeculae (Fields et al., 2011), this anterior shift in disc pressure is insufficiently large to shift those load paths from the central region of trabecular bone to the anterior cortical shell. Thus, the few vertically-oriented load paths in the central vertebral body that dominate load transfer under uniform compression loading in the elderly vertebra appear to also dominate load transfer under forward flexion.
These mechanisms apply to loading of the endplates via a compliant disc but do not apply for loading via the much stiffer PMMA. For that situation, the PMMA and endplate deform together as a single composite beam, and the resulting beam now behaves structurally as a “rigid” plate on an elastic foundation. In this case, maximum stresses in the foundation occur in the very most anterior bone for anterior loading. Whether or not any real disc — either shortened, collapsed, locally mineralized, severely dehydrated, or otherwise degenerated — ever approaches the structural behavior of the simulated PMMA is unclear and remains a topic of future research. However, for the patients who undergo artificial disc replacement (Auerbach et al., 2010) or spine fusion surgery (Steffen et al., 2000), or who otherwise have their disc space filled with a stiff material, the adjacent vertebral bodies may be at an elevated risk of wedge fracture due to over-loading of the anterior trabecular bone and cortical shell when there is a moderate degree of forward flexion.
Although we did not perform any experiments to validate our model predictions, our results are consistent with those from a number of experiments. Consistent with our simulations, experiments on spine motion segments have shown that initial failure occurred at the center of endplate and underlying trabecular bone for compression and 5° forward flexion loading conditions, regardless of disc age (Granhed et al., 1989). Other experiments under various amounts of forward flexion (~ 2–8°) have also shown that most fractures occurred in the endplates (Farooq et al., 2005; Hutton and Adams, 1982; Jiang et al., 2010; Zhao et al., 2009). By contrast, wedge fractures have been observed in some experiments that used a larger amount of forward flexion (≥~ 10°) (Adams and Hutton, 1982; Granhed et al., 1989; Luo et al., 2007). Together, these results suggest that wedge fractures may be related to the amount of forward flexion. Our findings are therefore only applicable to a moderate amount (~ 5°) of forward bending, and further work is required to understand failure mechanisms when the amount of flexion is much greater. Presumably in such cases, and perhaps depending on the state of disc degeneration and mineralization, the disc bottoms out and there is effectively bone-to-bone contact anteriorly, thus increasing anterior load transfer within the vertebral body — somewhat akin to our PMMA load case.
Despite the insight provided by this analysis, the precise etiology of anterior wedge fractures remains unclear. Adams (Adams et al., 2006) proposed that anterior unloading from erect standing can occur with disc narrowing as contact occurs at the facet joints and load is transferred more through the neural arch; such anterior unloading may lead to anterior stress shielding and adaptive bone loss, thus compromising the strength of the anterior bone for subsequent loading. Our analyses were performed on a sample of elderly bones which might have included some that had so adapted. Since we did not observe any evidence of anteriorly-placed high-risk tissue, either for compression or forward flexion, we suspect other factors are also at play, at least for initial failure.
One possibility, as noted above, is that wedge fractures only occur after for a large degree of forward flexion. Another possibility is that, even for the moderate flexion posture as simulated in our study, the lifting of heavy objects substantially increases the bending moment acting on the spine and thus the net compressive force acting on the vertebra (Dolan et al., 1994; Mannion et al., 2000), as dictated by static equilibrium considerations. Based on our results, such high axial loading, when superimposed with moderate flexion, would cause the central trabecular bone and endplates to fail first. It may be that, perhaps depending on vertebral morphology, damage then progresses anteriorly within the vertebra after such initial failure, eventually resulting in a wedge fracture. Study of such damage progression remains a topic for future research. It is also possible that some osteoporotic wedge fractures develop slowly over time, influenced by fatigue (Zioupos et al., 2008), creep (Pollintine et al., 2009; Yamamoto et al., 2006), or damage (Kopperdahl et al., 1999; Zysset and Curnier, 1996) behaviors, none of which were simulated in the present analysis. This too remains a topic for future research.
One limitation of this study is that the intervertebral disc was modeled as a homogeneous isotropic linearly elastic material when in fact its material behavior is much more complex and is altered by degeneration (An et al., 2004; Iatridis et al., 1998; O’Connell et al., 2012; Wagner and Lotz, 2004). The disc modulus of 8 MPa used in our simulation, consistent with measurements data from compression experiments on vertebra-disc-vertebra segments (Li et al., 1995; O’Connell et al., 2007; Pollintine et al., 2010), probably represents a lower bound on in vivo behavior. It remains to be shown how sensitive our current results are to variations in this modulus across a full physiological range, although a preliminary study in our lab found that the distribution of high-risk tissue was largely insensitive to the modulus values over the range of about 8–50 MPa (Yang et al., 2012). Despite the simplicity of our disc model, our models showed an anterior-to-posterior loading ratio for flexion (mean 1.74) that is comparable or even more than values observed in experiments (mean 1.45) (Pollintine et al., 2004). Further, our finding that the regions of initial failure were in the central endplate and trabecular bone agrees with the results from more sophisticated models of disc (Shirazi-Adl et al., 1986) and also with observations from experiments (Farooq et al., 2005; Granhed et al., 1989; Hutton and Adams, 1982; Jiang et al., 2010; Zhao et al., 2009). Together, these collective results suggest that our simple disc model was sufficient for exploring general trends regarding the role of loading conditions on the mechanisms of vertebral failure. Even so, future work is required to confirm our findings by integrating sophisticated modeling of both the bone and the disc, and by investigating the effects the variations in disc behavior on vertebral failure mechanisms (Homminga et al., 2001; Polikeit et al., 2004; Rohlmann et al., 2006).
There are some additional limitations. First, due to the computational cost, we used 60-μm voxel sizes. Clearly, very local measures of stress will be affected by resolution, but it is unlikely that the general stress distribution will be altered much since that is likely dominated by the overall trabecular topology, which appears to be well captured at 30-μm or 60-μm resolution (Eswaran et al., 2007). Second, although we only assessed T9 vertebrae, the consistency of our results with previous studies on lumbar vertebrae (Granhed et al., 1989; Hansson and Roos, 1981) suggests that our results also likely apply to lumbar vertebrae. As with many biomechanical analyses on scarce human tissue, use of a larger sample size would always be advantageous and would further help establish external validity. Finally, we did not include the posterior elements or account for any load transfer through the neural arch. However, cadaver experiments have shown that the posterior elements have little structural role for forward flexion loading regardless of disc quality, nor do they have an appreciable role for uniform compression for a healthy disc (Pollintine et al., 2004).
In summary, we found that the bone tissue with the highest risk of initial failure within the human vertebral body occurs in the central endplates and trabecular bone, for both compression and forward flexion. Thus, unless the disc behaves very stiffly, a moderate degree of forward flexion does not appreciably alter the spatial distribution of stress within the vertebral body.
Acknowledgments
Funding was provided by the National Institutes of Health (NIH AR43784) and the China Scholarship Council. Computational resources were obtained from the National Science Foundation through the TeraGrid program (TG-MCA00N019). Thanks to Arnav Sanyal for help in preparing the manuscript. TMK has a financial interest in O.N. Diagnostics and both he and the company may benefit from the results of this research.
Footnotes
All other authors have no conflict of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adams MA, Hutton WC. Prolapsed intervertebral disc. A hyperflexion injury 1981 Volvo Award in Basic Science. Spine (Phila Pa 1976) 1982;7:184–191. [PubMed] [Google Scholar]
- Adams MA, Pollintine P, Tobias JH, Wakley GK, Dolan P. Intervertebral disc degeneration can predispose to anterior vertebral fractures in the thoracolumbar spine. J Bone Miner Res. 2006;21:1409–1416. doi: 10.1359/jbmr.060609. [DOI] [PubMed] [Google Scholar]
- Adams MA, Dolan P. Biomechanics of vertebral compression fractures and clinical application. Arch Orthop Trauma Surg. 2011;131:1703–1710. doi: 10.1007/s00402-011-1355-9. [DOI] [PubMed] [Google Scholar]
- Adams MF, Bayraktar HH, Keaveny TM, Papadopoulos P. Ultrascalable implicit finite element analyses in solid mechanics with over a half a billion degrees of freedom. ACM/IEEE Proceedings of SC2004: High Performance Networking and Computing.2004. [Google Scholar]
- An HS, Anderson PA, Haughton VM, Iatridis JC, Kang JD, Lotz JC, Natarajan RN, Oegema TR, Jr, Roughley P, Setton LA, Urban JP, Videman T, Andersson GB, Weinstein JN. Introduction: disc degeneration: summary. Spine (Phila Pa 1976) 2004;29:2677–2678. doi: 10.1097/01.brs.0000147573.88916.c6. [DOI] [PubMed] [Google Scholar]
- Auerbach JD, Ballester CM, Hammond F, Carine ET, Balderston RA, Elliott DM. The effect of implant size and device keel on vertebral compression properties in lumbar total disc replacement. Spine J. 2010;10:333–340. doi: 10.1016/j.spinee.2010.01.008. [DOI] [PubMed] [Google Scholar]
- Bartel DL, Davy DT, Keaveny TM. Orthopaedic Biomechanics - Mechanics and Design in Musculoskeletal Systems. Pearson Prentice Hall; Upper Saddle River, NJ: 2006. [Google Scholar]
- Bevill G, Eswaran SK, Gupta A, Papadopoulos P, Keaveny TM. Influence of bone volume fraction and architecture on computed large-deformation failure mechanisms in human trabecular bone. Bone. 2006;39:1218–1225. doi: 10.1016/j.bone.2006.06.016. [DOI] [PubMed] [Google Scholar]
- Buckley JM, Kuo CC, Cheng LC, Loo K, Motherway J, Slyfield C, Deviren V, Ames C. Relative strength of thoracic vertebrae in axial compression versus flexion. Spine J. 2009;9:478–485. doi: 10.1016/j.spinee.2009.02.010. [DOI] [PubMed] [Google Scholar]
- Christiansen BA, Bouxsein ML. Biomechanics of vertebral fractures and the vertebral fracture cascade. Curr Osteoporos Rep. 2010;8:198–204. doi: 10.1007/s11914-010-0031-2. [DOI] [PubMed] [Google Scholar]
- Crawford RP, Cann CE, Keaveny TM. Finite element models predict in vitro vertebral body compressive strength better than quantitative computed tomography. Bone. 2003;33:744–750. doi: 10.1016/s8756-3282(03)00210-2. [DOI] [PubMed] [Google Scholar]
- Dall’Ara E, Schmidt R, Pahr D, Varga P, Chevalier Y, Patsch J, Kainberger F, Zysset P. A nonlinear finite element model validation study based on a novel experimental technique for inducing anterior wedge-shape fractures in human vertebral bodies in vitro. J Biomech. 2010;43:2374–2380. doi: 10.1016/j.jbiomech.2010.04.023. [DOI] [PubMed] [Google Scholar]
- Dolan P, Earley M, Adams MA. Bending and compressive stresses acting on the lumbar spine during lifting activities. J Biomech. 1994;27:1237–1248. doi: 10.1016/0021-9290(94)90277-1. [DOI] [PubMed] [Google Scholar]
- Duncan NA, Lotz JC. Computer Methods in Biomechanics and Biomedical Engineering. Gordon and Breach; 1998. Experimental validation of a porohyperelastic finite element model of the annulus fibrosus; pp. 527–534. [Google Scholar]
- Eastell R, Cedel SL, Wahner HW, Riggs BL, Melton LJ. Classification of vertebral fractures. J Bone Miner Res. 1991;6:207–215. doi: 10.1002/jbmr.5650060302. [DOI] [PubMed] [Google Scholar]
- Eswaran SK, Gupta A, Adams MF, Keaveny TM. Cortical and trabecular load sharing in the human vertebral body. J Bone Miner Res. 2006;21:307–314. doi: 10.1359/jbmr.2006.21.2.307. [DOI] [PubMed] [Google Scholar]
- Eswaran SK, Gupta A, Keaveny TM. Locations of bone tissue at high risk of initial failure during compressive loading of the human vertebral body. Bone. 2007;41:733–739. doi: 10.1016/j.bone.2007.05.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fagan MJ, Julian S, Siddall DJ, Mohsen AM. Patient-specific spine models. Part 1: Finite element analysis of the lumbar intervertebral disc - a material sensitivity study. Proc Inst Mech Eng [H] 2002;216:299–314. doi: 10.1243/09544110260216577. [DOI] [PubMed] [Google Scholar]
- Farooq N, Park JC, Pollintine P, Annesley-Williams DJ, Dolan P. Can vertebroplasty restore normal load-bearing to fractured vertebrae? Spine (Phila Pa 1976) 2005;30:1723–1730. doi: 10.1097/01.brs.0000171906.01906.07. [DOI] [PubMed] [Google Scholar]
- Fields AJ, Lee GL, Keaveny TM. Mechanisms of initial endplate failure in the human vertebral body. J Biomech. 2010;43:3126–3131. doi: 10.1016/j.jbiomech.2010.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fields AJ, Lee GL, Liu XS, Jekir MG, Guo XE, Keaveny TM. Influence of vertical trabeculae on the compressive strength of the human vertebra. J Bone Miner Res. 2011;26:263–269. doi: 10.1002/jbmr.207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Granhed H, Jonson R, Hansson T. Mineral content and strength of lumbar vertebrae - a cadaver study. Acta Orthopaedica Scandinavica. 1989;60:105–109. doi: 10.3109/17453678909150105. [DOI] [PubMed] [Google Scholar]
- Hansson T, Roos B. The relation between bone mineral content, experimental compression fractures, and disk degeneration in lumbar vertebrae. Spine. 1981;6:147–153. doi: 10.1097/00007632-198103000-00007. [DOI] [PubMed] [Google Scholar]
- Hetenyi MI. Beams on Elastic Foundation; Theory with Applications in the Fields of Civil and Mechanical Engineering. The University of Michigan Press; Ann Arbor: 1946. [Google Scholar]
- Homminga J, Weinans H, Gowin W, Felsenberg D, Huiskes R. Osteoporosis changes the amount of vertebral trabecular bone at risk of fracture but not the vertebral load distribution. Spine. 2001;26:1555–1561. doi: 10.1097/00007632-200107150-00010. [DOI] [PubMed] [Google Scholar]
- Homminga J, Van-Rietbergen B, Lochmuller EM, Weinans H, Eckstein F, Huiskes R. The osteoporotic vertebral structure is well adapted to the loads of daily life, but not to infrequent “error” loads. Bone. 2004;34:510–516. doi: 10.1016/j.bone.2003.12.001. [DOI] [PubMed] [Google Scholar]
- Hutton WC, Adams MA. Can the lumbar spine be crushed in heavy lifting? Spine (Phila Pa 1976) 1982;7:586–590. doi: 10.1097/00007632-198211000-00012. [DOI] [PubMed] [Google Scholar]
- Iatridis JC, Setton LA, Foster RJ, Rawlins BA, Weidenbaum M, Mow V. Degeneration affects the anisotropic and nonlinear behaviors of human anulus fibrosus in compression. J Biomech. 1998;31:535–544. doi: 10.1016/s0021-9290(98)00046-3. [DOI] [PubMed] [Google Scholar]
- Ismail AA, Cooper C, Felsenberg D, Varlow J, Kanis JA, Silman AJ, O’Neill TW. Number and type of vertebral deformities: epidemiological characteristics and relation to back pain and height loss. European Vertebral Osteoporosis Study Group. Osteoporos Int. 1999;9:206–213. doi: 10.1007/s001980050138. [DOI] [PubMed] [Google Scholar]
- Jiang G, Luo J, Pollintine P, Dolan P, Adams MA, Eastell R. Vertebral fractures in the elderly may not always be “osteoporotic”. Bone. 2010;47:111–116. doi: 10.1016/j.bone.2010.03.019. [DOI] [PubMed] [Google Scholar]
- Kopperdahl DL, Roberts AD, Keaveny TM. Localized damage in vertebral bone is most detrimental in regions of high strain energy density. J Biomech Eng. 1999;121:622–628. doi: 10.1115/1.2800864. [DOI] [PubMed] [Google Scholar]
- Li S, Patwardhan AG, Amirouche FM, Havey R, Meade KP. Limitations of the standard linear solid model of intervertebral discs subject to prolonged loading and low-frequency vibration in axial compression. J Biomech. 1995;28:779–790. doi: 10.1016/0021-9290(94)00140-y. [DOI] [PubMed] [Google Scholar]
- Luo J, Skrzypiec DM, Pollintine P, Adams MA, Annesley-Williams DJ, Dolan P. Mechanical efficacy of vertebroplasty: influence of cement type, BMD, fracture severity, and disc degeneration. Bone. 2007;40:1110–1119. doi: 10.1016/j.bone.2006.11.021. [DOI] [PubMed] [Google Scholar]
- Mannion AF, Adams MA, Dolan P. Sudden and unexpected loading generates high forces on the lumbar spine. Spine. 2000;25:842–852. doi: 10.1097/00007632-200004010-00013. [DOI] [PubMed] [Google Scholar]
- Middleditch AJO. Functional Anatomy of the Spine. Elsevier Ltd; Boston: 2005. [Google Scholar]
- Morgan EF, Bayraktar HH, Keaveny TM. Trabecular bone modulus-density relationships depend on anatomic site. J Biomech. 2003;36:897–904. doi: 10.1016/s0021-9290(03)00071-x. [DOI] [PubMed] [Google Scholar]
- Mosekilde L, Mosekilde L. Normal vertebral body size and compressive strength: relations to age and to vertebral and iliac trabecular bone compressive strength. Bone. 1986;7:207–212. doi: 10.1016/8756-3282(86)90019-0. [DOI] [PubMed] [Google Scholar]
- O’Connell GD, Johannessen W, Vresilovic EJ, Elliott DM. Human internal disc strains in axial compression measured noninvasively using magnetic resonance imaging. Spine (Phila Pa 1976) 2007;32:2860–2868. doi: 10.1097/BRS.0b013e31815b75fb. [DOI] [PubMed] [Google Scholar]
- O’Connell GD, Sen S, Elliott DM. Human annulus fibrosus material properties from biaxial testing and constitutive modeling are altered with degeneration. Biomech Model Mechanobiol. 2012;11:493–503. doi: 10.1007/s10237-011-0328-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osvalder A, Neumann P, Lovsund P, Nordwall A. Ultimate strength of the lumbar spine in flexion: An in vitro study. J Biomech. 1990;23:453–460. doi: 10.1016/0021-9290(90)90301-i. [DOI] [PubMed] [Google Scholar]
- Polikeit A, Nolte LP, Ferguson SJ. Simulated influence of osteoporosis and disc degeneration on the load transfer in a lumbar functional spinal unit. J Biomech. 2004;37:1061–1069. doi: 10.1016/j.jbiomech.2003.11.018. [DOI] [PubMed] [Google Scholar]
- Pollintine P, Dolan P, Tobias JH, Adams MA. Intervertebral disc degeneration can lead to “stress-shielding” of the anterior vertebral body: a cause of osteoporotic vertebral fracture? Spine. 2004;29:774–782. doi: 10.1097/01.brs.0000119401.23006.d2. [DOI] [PubMed] [Google Scholar]
- Pollintine P, Luo J, Offa-Jones B, Dolan P, Adams MA. Bone creep can cause progressive vertebral deformity. Bone. 2009;45:466–472. doi: 10.1016/j.bone.2009.05.015. [DOI] [PubMed] [Google Scholar]
- Pollintine P, van Tunen MS, Luo J, Brown MD, Dolan P, Adams MA. Time-dependent compressive deformation of the ageing spine: relevance to spinal stenosis. Spine (Phila Pa 1976) 2010;35:386–394. doi: 10.1097/BRS.0b013e3181b0ef26. [DOI] [PubMed] [Google Scholar]
- Rohlmann A, Zander T, Schmidt H, Wilke HJ, Bergmann G. Analysis of the influence of disc degeneration on the mechanical behaviour of a lumbar motion segment using the finite element method. J Biomech. 2006;39:2484–2490. doi: 10.1016/j.jbiomech.2005.07.026. [DOI] [PubMed] [Google Scholar]
- Roy ME, Rho JY, Tsui TY, Evans ND, Pharr GM. Mechanical and morphological variation of the human lumbar vertebral cortical and trabecular bone. Journal of Biomedical Materials Research. 1999;44:191–197. doi: 10.1002/(sici)1097-4636(199902)44:2<191::aid-jbm9>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- Shirazi-Adl A, Ahmed AM, Shrivastava SC. A finite element study of a lumbar motion segment subjected to pure sagittal plane moments. J Biomech. 1986;19:331–350. doi: 10.1016/0021-9290(86)90009-6. [DOI] [PubMed] [Google Scholar]
- Silva MJ, Wang C, Keaveny TM, Hayes WC. Direct and computed-tomography thickness measurements of the human, lumbar vertebral shell and end-plate. Bone. 1994;15:409–414. doi: 10.1016/8756-3282(94)90817-6. [DOI] [PubMed] [Google Scholar]
- Steffen T, Tsantrizos A, Aebi M. Effect of implant design and endplate preparation on the compressive strength of interbody fusion constructs. Spine (Phila Pa 1976) 2000;25:1077–1084. doi: 10.1097/00007632-200005010-00007. [DOI] [PubMed] [Google Scholar]
- Van Rietbergen B, Weinans H, Huiskes R, Odgaard A. A new method to determine trabecular bone elastic properties and loading using micromechanical finite element models. J Biomech. 1995;28:69–81. doi: 10.1016/0021-9290(95)80008-5. [DOI] [PubMed] [Google Scholar]
- Wagner DR, Lotz JC. Theoretical model and experimental results for the nonlinear elastic behavior of human annulus fibrosus. J Orthop Res. 2004;22:901–909. doi: 10.1016/j.orthres.2003.12.012. [DOI] [PubMed] [Google Scholar]
- Yamamoto E, Paul Crawford R, Chan DD, Keaveny TM. Development of residual strains in human vertebral trabecular bone after prolonged static and cyclic loading at low load levels. J Biomech. 2006;39:1812–1818. doi: 10.1016/j.jbiomech.2005.05.017. [DOI] [PubMed] [Google Scholar]
- Yang H, Jekir MG, Ruf SF, Keaveny TM. The influence of disc elasticity on the micromechanics of vertebral failure for forward bending. Proceedings of the 20th Annual Symposium on Computational Methods in Orthopaedic Biomechanics; Berkeley, CA. 2012. [Google Scholar]
- Zhao FD, Pollintine P, Hole BD, Adams MA, Dolan P. Vertebral fractures usually affect the cranial endplate because it is thinner and supported by less-dense trabecular bone. Bone. 2009;44:372–379. doi: 10.1016/j.bone.2008.10.048. [DOI] [PubMed] [Google Scholar]
- Zioupos P, Hansen U, Currey JD. Microcracking damage and the fracture process in relation to strain rate in human cortical bone tensile failure. J Biomech. 2008;41:2932–2939. doi: 10.1016/j.jbiomech.2008.07.025. [DOI] [PubMed] [Google Scholar]
- Zysset PK, Curnier A. A 3D damage model for trabecular bone based on fabric tensors. J Biomech. 1996;29:1549–1558. [PubMed] [Google Scholar]