Water-Exclusion and Liquid-Structure Forces in Implicit Solvation

Abstract

A continuum model of solvation is proposed to describe: i) long-range electrostatic effects of water exclusion resulting from incomplete and anisotropic hydration in crowded environments, and ii) short-range effects of liquid-structure forces on the hydrogen-bond interactions at solute/water interfaces. The model is an extension of the phenomenological screened Coulomb potential-based implicit model of solvation. The developments reported here allow a more realistic representation of highly crowded and spatially heterogeneous environments, such as those in the interior of a living cell. Only the solvent is treated as a continuum medium. It is shown that the electrostatic effects of long-range water-exclusion can strongly affect protein-protein binding energies and are then related to the thermodynamics of binding. Hydrogen-bond interactions modulated by the liquid structure at interfaces are calibrated based on systematic calculations of potentials of mean force in explicit water. The electrostatic component of the model is parameterized for monovalent, divalent and trivalent ions. The conceptual and practical aspects of the model are discussed based on simulations of protein complexation and peptide folding. The current implementation is ~1.5 times slower than the gas-phase force field and exhibits good parallel performance.

I. Introduction

Living cells contain high concentrations of solutes^1–3, including macromolecular complexes and assemblies that displace large amounts of water, thus removing part of the highly polar/polarizable medium that modulates electrostatic interactions. These water-exclusion effects depend mainly on the size and morphology of the water-excluding solutes. The internal components of the cell also form extensive solute/liquid interfaces; thus much of cell water is indeed interfacial². Aqueous interfaces display non-bulk behavior and can extend into the bulk a few Angstroms or several nanometers, depending on the surface size, topography, and charge distribution.^4–9 The behavior of molecules immersed in such regions can differ from those in the bulk solution as well.^10–16 As is the case in many surface-mediated phenomena, the microscopic origin of these effects is not well understood. Both electrostatic and liquid-structure effects at the interface have been invoked as possible mechanisms.

The amount of water in the interior of living cells that displays non-bulk behavior is still controversial^2,17,18, and many experiments have been conducted to elucidate it. Magnetic relaxation dispersion data^4,19 suggest that only water in the first hydration shell is substantially modified by the solutes (up to ~20% of the cell water content). In contrast, X-ray and neutron scattering^20,21, as well as diffusion data of endogenous probes^22–24, suggest a much larger fraction of non-bulk water (up to ~75% in some cell types). Given the heterogeneous nature of the subcellular environment, it is likely that the cell contains regions of water with substantial non-bulk behavior (e.g., in the intervening space between nearby proteins, or in confined spaces) and regions with bulk-like behavior (less crowded regions in the cytoplasm). Atomistic dynamics simulations show that small solutes can induce long-range water structure in the intervening space between polar or charged groups²⁵, a property likely to be amplified in the crowded and heterogeneous cellular milieu.

Regardless of the overall proportion of bulk/non-bulk water suggested by experiments, at the molecular level most biology ultimately happens at interfaces. Moreover, evidence suggests² that about half of biologically active molecules in the cell do not diffuse freely in the bulk medium despite their solubility, but are transiently bound, either specifically or non-specifically to one another, to membranes, or to the cytoskeleton. Therefore, a model of solvation for application in crowded environments requires special considerations of at least two main effects: the long-range electrostatic modulation resulting from incomplete and anisotropic hydration owing to the presence of water-excluding solutes, and the short-range forces induced by interfacial water, in particular the forces induced by the structure of the solute hydration shells in close proximity. Several simplified models of solvation, known as continuum or implicit solvent models (ISMs) have been proposed for simulations of macromolecules^26–33 that can speed up computation by several orders of magnitude in some cases. Millisecond-long dynamics simulations of small proteins using a fully-atomistic model of water are now possible with special-purpose computer architecture.^34,35 This implies that increasingly realistic cellular environments could soon be simulated over biological time scales, provided that a computationally efficient, complete ISM is available. ISMs commonly used in macromolecular simulation focus mainly on macroscopic electrostatic effects. They do not explicitly address the problems posed by the interfaces, neither dielectric nor structural effects, and water-exclusion effects are not given particular consideration or are treated in rather simplified ways. Although numerical solutions of the Poisson equation do account for water-exclusion effects quite naturally, they are computationally demanding, especially for large systems.

In this paper the screened Coulomb potential-based implicit solvent model (SCPISM)^36–39 is extended to account for the forces induced by exclusion of water from the environment of a solute and the forces induced by the structure of water in the hydration shells of closely-interacting solutes. The conceptual aspects of the model and its computational efficiency are discussed based on results from simulations of a peptide and a protein complex. Emphasis is on the physical meaning of the quantities that define the model.

II. Electrostatic effects in the SCPISM

Electrostatic modulation by an aqueous solution originates in the structural and dynamic response of the water molecules to the electric field created by the solute’s charge distribution. Bulk water is relatively simple to characterize and can be viewed as the reorientation and polarization of the water molecules subject to thermal fluctuations.⁴⁰ Closer to the solute the response is more complicated due to the competition between water-water and water-solute interactions. When compared to the bulk phase, the competing forces lead to changes in the structure and dynamics of the interfacial water, and bulk behavior is recovered only at a certain distance from the surface. These microscopic changes in the water response lead to two macroscopic (thermodynamic) effects^39,41: local variations in the water density and local changes in the dielectric response. Therefore, at least two basic elements are necessary in a continuum electrostatic model of solvation: a position-dependent water density, ρ(r), and a position-dependent scalar dielectric permittivity, ε(r). A model based on these local properties has been proposed³⁹, which is valid for any polar/polarizable solvent and solutes of arbitrary shape and charge distribution. A simplified expression for ε(r) based on the Lorentz-Debye-Sack (LDS) approximation was obtained previously for a point charge q in a homogeneous fluid, which is given by^42,43

$$\epsilon (r)=1+\frac{4\pi }{3}[\epsilon (r)=2]\frac{\alpha }{v}+\frac{4\pi \mu }{qv}{r}^2\epsilon (r)L\left\{\frac{q\mu [\epsilon (r)+2]}{[3kT+\mu R(r)]r^2\epsilon (r)}\right\}$$ (1)

where ν, α, and μ are the molecular volume (i.e., the inverse of the number density), polarizability, and dipole moment of the solvent molecule, respectively; T is the temperature, r is the distance from the charge, and R is the Onsager reaction field. The function L is the Langevin function obtained from the Boltzmann average over all molecular orientations^42,43. The relationships between the reaction, directing, local or microscopic, Maxwell or macroscopic, vacuum and cavity fields, and Debye and Lorentz fields, and their roles in determining ε(r) have been discussed in detail³⁹. Numerical solutions of Eq.(1) show that ε is sigmoidal in r due to saturation effects close to the source, with an asymptotic value ε₀ at large r; ε₀ is the static dielectric permittivity of the bulk solvent at the given temperature. In the limit of weak electric fields, or large r in this case, Eq.(1) converges to the Onsager equation³⁹, which relates ε₀ and μ². In the limit of high frequencies, Eq.(1) converges to the Lorenz-Lorentz relationship³⁹ between α and the optical permittivity ε_∞ (or the refractive index of the bulk solvent). Several expressions similar to Eq.(1) have been proposed^44–46 that differ in the rate of increase of ε with r, depending on the assumptions of the model. The dielectric screenings used in the SCPISM are based on solutions of Eq.(1). Since ε depends on q, or more generally on the macroscopic field E³⁹, using Eq.(1) as the basis of an ISM has potential advantages.^36,38 The screening can be adjusted if q changes, e.g., when a polarizable force field is used, or when protonation states change upon pK_a shifts. The dependence of ε₀ with T, as well as the values of α and μ are known for most solvents, facilitating the application of the model to different solvents and temperatures. Finally, the basis of the model is essentially the same as those used in ISMs for quantum chemical calculations⁴⁷, and both QM and MM methods of solvation could eventually be unified in a common framework.

In a solvent, the dielectric function ε damps the vacuum electric field E₀, while the screening function D modulates the vacuum potential φ₀. The relation between ε and D is given by the definition of electric potential⁴⁸, i.e., E₀(r)/ε(r) = −∇[φ₀(r)/D(r)] for spherical symmetry, or explicitly by rdD(r)/dr= D(r)[D(r)−ε(r)]/ε(r). The screening D is also sigmoidal in r with the same asymptotic value ε₀ at large distances.³⁸ For isolated charged calculations show³⁸ that one particular function (Boltzmann sigmoidal), given by⁴³

$$D(r)=\frac{(1+{\epsilon }_0)}{1+kexp(-\alpha r)}-1$$ (2)

with k = (ε₀ − 1)/2, allows a good fit of D(r) for several polar liquids using the single screening parameter α [not to be confused with the polarizability α in Eq.(1)]. This parameter reflects all the physics of the system embedded in Eq.(1), including the charge q, the properties of the solvent, and the temperature. Equation (2) is a solution of⁴⁹ dD(r)/dr = α[1 + D(r)][ε₀ − D(r)]/(1 + ε₀), which provides algebraic solutions for D(r) when ε(r) is known from theory [e.g., Eq.(1)] or experiments.

II.1. Total electrostatic energy and hydration free energy

The total electrostatic energy E_e of a molecule in a solvent can be partitioned into two terms, E_e = E_int + E_self, where E_int is the interaction energy and E_self is the self energy. Because this is a phenomenological proposition, any model based on this partitioning is necessarily phenomenological. Except in numerical solutions of the Poisson equation, this approach is the basis of most solvent models currently used in simulations of macromolecules, and is also used in the SCPISM. The electrostatic contribution to the Helmholtz free energy of solvation is given by⁵⁰ ΔF_e = ∫E·D − ∫ E₀·E₀, where E and D are the electric and the displacement fields in the solvent, and the integration is over all space. For a single charge q the simplest form of ΔF_e is given by the original Born model⁵¹ as ΔF_e = −q²(1−1/ε₀)/2R. Subsequent studies of ion hydration showed that the Born radius can be expressed as R = R_I + δ_± where R_I is the ionic radius and δ is an extension, different for anions and cations.^52,53 With this interpretation, ΔF_e could be reproduced for ions of different charges (−1e to +3e) and sizes without the need to empirically adjust R in each case. It was also shown^53–55 that saturation effects of the electric field had to be incorporated to reproduce both the enthalpy and entropy of ion hydration. Thus, a more general form of ΔF_e can be obtained for a fully-solvated charge q, in the form^36,48,

$$\mathrm{\Delta }{F}_e=\frac{q^2}{2R(q)}\left(\frac{1}{D[q,R(q)]}-1\right)$$ (3)

which depends on the screening D instead of the permittivity ε, and where both R and D depend on the magnitude of the charge q, and D also depends explicitly on R. The dependence of R on q, instead of its sign only, allows for partial charges, which are common in classical force fields. The SCPISM takes Eq.(3) as the self-energy of a partially-solvated atom i in a protein, but with an effective radius R_i ^36,37 and an effective screening D_i dependent on the protein structure, i.e.,

$$\mathrm{\Delta }{F}_{e,i}=\frac{q_i^2}{2R_i(q_i,\mathbf{r})}\left(\frac{1}{D_i[q_i,R_i(q_i,\mathbf{r}),\mathbf{r}]}-1\right)$$ (4)

where r ≡ {r₁, r₂,…, r_N} indicates the explicit dependence of R and D on the coordinates of all the atoms in the protein (see below). The total electrostatic energy of a solvated protein is then calculated as

$$E_e=\frac{1}{2}\sum _{i\ne j}^N\frac{q_i{q}_j}{r_{ij}{D}_{ij}(q_i,q_j,r_{ij},\mathbf{r})}+\frac{1}{2}\sum _{i=1}^N\frac{q_i^2}{R_i(q_i,\mathbf{r})}\left\{\frac{1}{D_i[q_i,R_i(q_i,\mathbf{r}),\mathbf{r}]}-1\right\}$$ (5)

where the first term is a sum of pairwise Coulomb interactions screened by effective screenings D_ij and the second term is a sum of the self-energies given by Eq.(4); r_ij is the distance between atoms i and j, and N is the total number of atoms in the system. The first summation in Eq.(5) contains N² screening functions D_ij, each depending explicitly on r_ij and on the positions r of all other atoms in the system. Each function D_ij also depends on the charges q_i and q_j, although this dependence is implicit through the corresponding screening parameters α_i and α_j defined in Eq.(2). The functions D_ij are expected to depend in general not only on q_i and q_j, but also on all other charges in the system, i.e., q ≡ {q₁, q₂,…, q_N}. This is so because the dielectric response of the liquid, which is reflected in ε and determines the total energy, depends on the macroscopic field E generated by the solute, not only on the field generated by the two charges³⁹. This generalization, however, is not introduced in the current model. Equation (5) also contains N screening functions D_i in the second term. As discussed above, these functions depend explicitly on R_i and r, and implicitly on q_i through α_i; here also a general dependence on q is expected. Finally, the effective radii R_i in Eq.(5) depend explicitly on both r and q. These radii appear only in the self-energy term and play no role in the interaction term. The dielectric permittivity is the only physical quantity that affects both interaction and self energy. Although phenomenological, the form E_e given by Eq.(5) contains all the basic ingredients of a complete electrostatic model of solvation. Non-local effects⁵⁶ and other electrostatic effects³⁹ known to affect the behavior of water at interfaces are not introduced explicitly in Eq.(5). In the current development, however, such effects are expected to be accounted for by a suitable parameterization, mainly by the behavior of D’s at solute/solvent interfaces.³⁹

The transfer free energy of a solute from the bulk of a solvent a to the bulk of a solvent b is obtained from Eq.(5) in each solvent, as $\mathrm{\Delta }{F}_e^{a\to b}=E_{e,b}-E_{e,a}$. If a is vacuum and b is water, $\mathrm{\Delta }{F}_e^{a\to b}$ is the electrostatic hydration energy ΔF_e, and E_e’s are ‘effective’ energies containing the potential energy of the solute and the free energy of the solvent³⁰. A simplified form of ΔF_e is used in the SCPISM, namely,

$$\mathrm{\Delta }{F}_e=\frac{1}{2}\sum _{i\ne j}^N\frac{q_i{q}_j}{r_{ij}}\left[\frac{1}{D_{ij}}-\frac{1}{D_v}\right]+\frac{1}{2}\sum _{i=j}^N{q}_i^2\left[\frac{1}{R_i}\left\{\frac{1}{D_i}-1\right\}-\frac{1}{R_{i,0}}\left\{\frac{1}{D_v}-1\right\}\right]$$ (6)

where, D_ij ≡ D_ij(q_i, q_j, r_ij, r), D_i ≡ D_i[q_i, R_i(q_i, r), r], and R_i ≡ R_i(q_i, r), and R_i,0 ≡ R_i,0(q_i, r) is the effective radius of atom i when the solute is in the vacuum. Equation (6) is valid for a solute that can be assumed to be spatially homogeneous in its dielectric properties, and characterized by a constant permittivity ε_v = D_v > 1. Experiments and simulations have shown that proteins are highly heterogeneous, with local dielectric variations.^57–60 Therefore, Eq.(6) is not adequate to estimate ΔF_e for such systems, and D_v must be replaced by the complete position-dependent D_v(r). As for any thermodynamic quantity, estimation of D_v(r) requires first a simulation of the protein dynamics, and then the calculation of the corresponding time average once adequate sampling and convergence are achieved^59,60. These calculations are computationally demanding, and the results depend on the quality of the protein force field. On the other hand, estimating D_v(r) simply from a rigid protein structure is conceptually more difficult and also beyond the scope of this paper. Because the parameterization of the SCPISM is based on hydration energies of small molecules,³⁶ the assumption of dielectric homogeneity is reasonable, and Eq.(6) can then be used.

II.2. Effective radii R and effective screenings D

In the SCPISM the dependence of R with r (protein conformation) in Eq.(5) is given by³⁶

$$R_i=R_{0,i}+{\delta }_{w,i}{\xi }_i+{\delta }_{p,i}(1-{\xi }_i)$$ (7)

where p and w indicate ‘protein’ and ‘water’, respectively. In this equation R_0,i + δ_w,i is the effective radius of the atom when it is fully hydrated, while R_0,i + δ_p,i is the radius when the atom is fully dehydrated, i.e., in the interior of an infinitely large generic protein. The dependence on the charge q is through δ_w,i and δ_p,i, and R_0,i is taken as the covalent radius of the atom³⁶. The function ξ_i is a measure of exposure of the atom i to water, which is approximated by the function³⁷

$${\xi }_i=1-\sum _{j\ne i}^N{A}_{i}exp(-B_{ij}{r}_{ij})$$ (8)

where A and B are parameters that determine the degree of exclusion of water by the protein. Complete hydration implies r_ij → ∞ for all atoms j, so ξ_i → 1. Complete dehydration, can be represented by i at the center of an infinitely large solvent-excluding cavity (e.g., a protein with N → ∞), where A and B are such that ξ_i → 0.

Depending on its position in a protein, an atom polarizes the solvent only partially and anisotropically. Since this is manifested in the dielectric response, the screening D must also depend on the degree of water exclusion. To account for the dependence of D on the protein structure, the screening parameter α depends on the proximity of the atom to the solvent, as ξ does in Eq.(8). If the particle is gradually transferred from water to vacuum, then D(r) must converge gradually to unity as the particle moves further away from the water interface. This condition requires α to vanish smoothly, i.e., α → 0, leading to D(r) → 1 for all r. A similar situation arises for an atom at the center of an increasingly large solvent-excluding cavity, as water moves away from the atom. The screening parameter of a fully hydrated atom i is here denoted by α_w,i. The corresponding parameter α_i for the atom in the protein can then be described by the perturbation

$${\alpha }_i={\alpha }_{w,i}+\delta {\alpha }_i$$ (9)

where δα_i < 0. In analogy with Eq. (8) the degree of solvent exclusion is approximated by

$$\delta {\alpha }_i=\sum _{j\ne i}^N{A^{\prime }}_{ij}exp(-{B^{\prime }}_{ij}{r}_{ij})$$ (10)

where δα_i → 0 for r_ij → ∞ (full hydration); and A′ and B′ are such that δα_i → −α_w,i when the particle is at the center of an infinitely large solvent-excluding cavity (complete dehydration). In the latter case, ΔF_e in Eq.(4) vanishes, although both R and D retain finite values: R → R₀, as δ = 0 in the vacuum [cf. Eq.(7)], and D → 1, as α → 0 [cf. Eq.(9)]. Thus, in the current extension of the SCPISM, both R and α contain information of the protein structure. Straightforward generalizations of the original Born model, e.g., so-called GB models,^27,33 account for solvent-exclusion effects by adjusting the size of the Born radius R to the appropriate value. In this case, R diverges as the protein becomes infinitely large. The approach used in the SCPISM, where both R and α can adjust to the environment is expected to better account for solvent exclusion effects in non-globular environments, such as peptides, membranes, and molecular interfaces, or in heterogeneous environments in general.

II.3. SCPISM implementation

II.3.1. Molecular solutes

The hydration energy of a charge q is given by³⁹

$$\mathrm{\Delta }{F}_e=-\frac{1}{2}{q}^2\underset{L\to \infty }{lim}\underset{R}{\overset{L}{\int }}\frac{\epsilon (r)-1}{r^2\epsilon (r)}dr$$ (11)

where ε(r) is given by solutions of Eq.(1). Equation (3) is an analytical solution of the integral of Eq.(11) obtained upon a suitable change of variable and after using the relation between ε and D derived in Section II.^36,48 Calculations show³⁹ that, as a function of the upper limit L, this integral increases rapidly within the first two hydration shells (accounting for 50–70% of the total hydration energy of single ions), and much slower at longer distances. Therefore, water-exclusion effects on electrostatics can be partitioned into a short-range and a long-range component. This is exploited in the SCPISM to speed up computation: the short-range dependence is introduced through the effective radii R, and the long-range dependence through the screening parameters α. The structure dependence of R is fine grained, and depends on the atomistic details of the protein within a certain distance d_c from the solute atom. This distance is chosen as d_c = 7.5 Å, enough to accommodate two hydration shells. In contrast, the structure dependence of α is assumed to be coarse grained, since water-exclusion effects due to a distant solute depend less critically on its internal atomic structure. This partitioning of the system into short-range/fine-grain and long-range/coarse-grain contributions allows for fast computation and efficiency that increases with system size.

The short-range dependence of R on the protein structure has been discussed³⁷, and is given by a simplification of Eq.(8), with N replaced by the number of atoms N_c within a sphere of radius d_c centered at i. The focus here is on the long-range effects of water-exclusion, which are represented by α in Eq.(9), and δα given by a simplification of Eq.(10), in the form

$${\alpha }_i={\alpha }_{0,i}+\sum _{J\ne I}^M{A}_{IJ}^{\prime }exp(-B_{IJ}^{\prime }{r}_{IJ})$$ (12)

where M is the total number of residues in the protein (or nucleotides, or any basic units in which the system can be conveniently divided), and r_IJ is the distance between the C_α atoms of residues I and J. In Eq.(12) the unperturbed parameter α_0,i determines the screening assigned to atom i in the fully-hydrated residue I, while α_w,i in Eq.(9) determines the screening assigned to the same atom when it is fully hydrated. Thus, α_0,i is itself a perturbation of α_w,i due to the exclusion of water by all other atoms (j ≠ i) of residue I. The perturbation of Eq.(12) then contains information on the additional water-exclusion effects due to all other residues (J ≠ I) surrounding I. For ions, clearly α_0,i = α_w,i. In the SCPISM the parameters α_0,i are the actual quantities used in the parameterization of the model through Eq.(6).³⁶

The parameters A′ and B′ in Eq.(12) quantify the strength of the long-range effects of solvent exclusion, like A and B in Eq.(8) quantify the corresponding short-range effects. In the current implementation A′ and B′ are independent of I and J. For a particle in the interior of an infinitely large solvent-excluding cavity, D → 1, thus setting 0 = α_0,i + δα_i the parameter A′ can be determined, and Eq.(12) can be re-written as

$${\alpha }_i={\alpha }_{0,i}-\frac{{\alpha }_{0,i}}{S(\sigma )}\sum _{J\ne I}^{M}exp(-r_{IJ}/\sigma )$$ (13)

where σ ≡ 1/B′. In Eq.(13), S(σ) is a summation over the volume of an idealized infinitely large generic protein (M → ∞), i.e.,

$$S(\sigma )=\sum _{J\ne I}^{\infty }exp(-r_{IJ}/\sigma )\approx \underset{p}{\overset{\infty }{\int }}\frac{4\pi }{v_r}{r}^{2}exp(r/\sigma )dr=3\left(\frac{\sigma }{p}+2\frac{{\sigma }^2}{p^2}+2\frac{{\sigma }^3}{p^3}\right)exp(-p/\sigma )$$ (14)

where the sum has been approximated by an integral using v_r = < V_P/n_P > = (183 ± 10) ų as the average volume per residue, and p = (3v_r/4π)^−1/3 ≈ 3.5 Å is a radius; V_P and n_P are the volume and the number of residues of a protein P, and the average <> is taken over all of the proteins in the PDB with more than 500 amino acids. Volumes were calculated numerically using a three dimensional mesh of cubic unit cells of 1 Å side length.

A similar procedure can be followed to estimate α_ij and the correction δα_ij of the interaction terms E_e,ij = q_iq_j/r_ijD_ij in Eq.(5). In the original SCPISM implementation³⁶ the parameter α_ij, which defines the two-particle screening function D_ij is given by ${\alpha }_{ij}^2={\alpha }_i{\alpha }_j$. This form is admittedly arbitrary and chosen only to preserve the symmetry of E_e,ij upon particle permutation. This restriction is relaxed here, although the symmetry is still preserved. The correction δα_ij can be obtained in terms of single-particle corrections δα′_i and δα′_j to first order, i.e.,

$${\alpha }_{ij}\approx {\alpha }_{0,ij}+\delta {{\alpha }^{\prime }}_i+\delta {{\alpha }^{\prime }}_j$$ (15)

where ${\alpha }_{0,ij}^2={\alpha }_{0,i}{\alpha }_{0,j}$ is the uncorrected parameter³⁶. The interaction energy of two particles i and j in the middle of an infinitely large solvent-excluding cavity requires D_ij → 1, i.e., E_e,ij → q_iq_j/r_ij. Thus, imposing 0 = α_0,ij + δα_ij, the perturbation δα′_i is given by

$$\delta {{\alpha }^{\prime }}_i=-\frac{{\alpha }_{0,ij}}{2S({\sigma }^{\prime })}\sum _{K\ne I}^{M}exp(-r_{IK}/{\sigma }^{\prime })$$ (16)

where S is also given by Eq.(14). The correction δα′_j for atom j is obtained from Eq.(16) by changing index I to J. In Eq.(13) and Eq.(16), σ and σ′ are the characteristic decay lengths of the long-range effects of water exclusion on the self-energy and the interaction terms, respectively. Since σ and σ′ can now be chosen independently, the exclusion of solvent can have different effects on the self-energy and the interaction terms. Therefore, the two terms in Eq.(5) are completely decoupled. The correct balance between these terms is discussed in Section IV.1. The calculations above show indeed that the larger the solvent exclusion, the smaller the values of α, as discussed in this section.

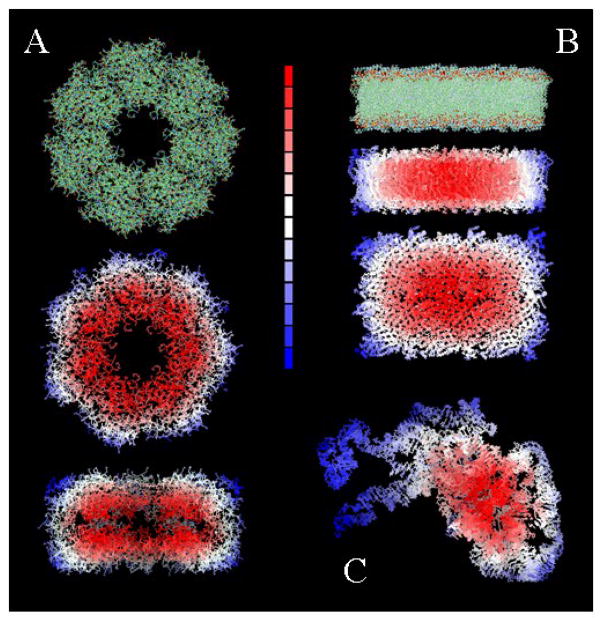
Both σ and σ′ are expected to be larger than d_c. The exact value of these parameters and their relation to the system thermodynamics is better discussed in the context of protein complexation (cf. Section IV.1). The effects of solvent exclusion on δα’s are illustrated in Fig. 1 for three different cases: a protein aggregate, a bundle of RNA, and a rectangular slice of lipid bilayer.

Figure 1.

Representation of water-exclusion effects for: (A) a multi-protein assembly; (B) a rectangular slice of lipid bilayer; and (C) a bundle of RNA. Regions more excluded from water are colored red [larger δα in Eq.(9)], and regions more exposed to water are colored blue (smaller δα). Similar behavior could be illustrated for δα′_i and δα′_j in Eq.(15).

II.3.2. Single charges

To obtain solvation parameters for a single charge q, ε(r) is first calculated numerically from Eq.(1), which requires the value of q, the temperature T, and the properties of the solvent molecules. From ε(r) the screening function D(r) is then calculated³⁸ (cf. Section II), and the screening parameter α is thus obtained from Eq.(2). This parameter is denoted by α_w and is also subject to the solvent-exclusion effects indicated by Eq.(9). Finally, the effective radius R is calculated from Eq.(3) using experimental values of ΔF_e. The radius can be further partitioned as³⁹ R = R_I + δ(q) and the extension δ obtained when the ionic radii R_I are known⁵³. The procedure just outlined combines the LDS theory [cf. Eq.(1)], the SCPISM self-energy [cf. Eq.(3)], and experimental ΔF_e data, and can be used to obtain parameters for other temperatures or solvents.

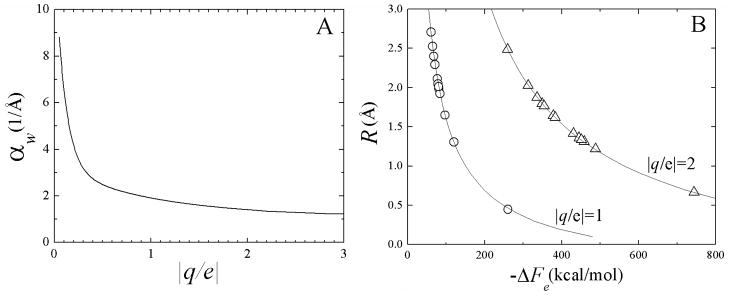
Figure 2A shows the dependence of α_w on q obtained from numerical solutions of Eq.(1). The values of α_w in Fig. 2A indicate that the dielectric behavior of bulk water is typically reached at r ~5 Å from the central ion, although other models^44,46 suggest much larger distances, in some cases beyond ~10 Å. Figure 2B shows the corresponding radii R versus ΔF_e obtained from a numerical inversion of Eq.(3). Experimental data for common monovalent and divalent ions are also shown (open symbols). The effective radii tend to fall in the range ~1–2.5 Å, with the exception Be²⁺ (R ~ 0.67 Å) which reduces its size upon double ionization, and H⁺ (R ~ 0.45 Å). Although Li⁺ has the same electronic configuration as Be²⁺ (1s²), its effective radius is twice as large (R ~ 1.31 Å) because of the reduced charge, i.e., reduced saturation effects. Quantum mechanical effects, although always present, do not in general lead to covalent bonds between the central ion and water, so the classical assumption of the LDS are quite appropriate. For H⁺, however, there are transient formations of valence bonds with nearest oxygen atoms, leading to (unstable) H₃O⁺ species. This is expected to decrease the average distance between the proton and the surrounding water, thus leading to slightly smaller effective radii than would be obtained if a purely classical treatment applies. This inconsistency is not expected to be a major concern here since the present development is aimed at developing parameters for biologically relevant cations, such as Na⁺ and K⁺ for use in classical simulations, for which these effects are less important.

Figure 2.

(A) Effective screening parameters α_w as a function of the charge q (e is the electron charge), and (B) effective radii R as a function of the electrostatic free energy of hydration ΔF_e. Theoretical curves in (B) from inversion of Eq.(3); experimental data (symbols) taken from ⁵³.

The optimization of the SCPISM for ions just outlined is only the first step prior to introducing explicit ions in an implicit solvent. A number of additional developments are needed before ions and other cosolutes can be used routinely in simulations. These include the estimation of the short-range liquid-structure effects^25,39, as done for amino acids in the next section, the optimization of Langevin parameters to reproduce experimental self-diffusion coefficients as a function of the ion concentration, and a computational algorithm to mimic anisotropic collisions with water in Langevin dynamics. These effects are important for all solutes, but are particularly critical for ions and small molecular species for which the granularity of the solvent becomes a significant challenge.

III. Liquid-structure effects in the SCPISM

Although the behavior of interfacial water is not yet fully understood, the first two hydration shells are known to be essential in modulating short-range intermolecular interactions. The structure of the liquid in these shells determines the characteristic shape of the intermolecular potentials of mean force (PMF), including the contact minimum, the desolvation barrier, and the solvent-separated minimum. The forces between closely-interacting solutes are influenced by the hydrogen-bond (HB) network of the surrounding water, which undergoes important changes as the hydration shells come into contact.^25,61 These liquid-structure forces are also known as solvent-induced forces^25,62–64 (SIF). At the microscopic level, hydrophobic and hydrophilic forces are different manifestations of SIF. These forces are known to play a role in the action of ions and cosolutes on protein denaturation, stabilization, precipitation, and self-assembly.^65,66 They also operate at the surface of proteins, e.g., between water-exposed side chains or during ligand binding. Although SIF have been studied extensively with computer simulations^25,61–64 and theories of non-homogeneous liquids^41,67, ISMs commonly used in macromolecular simulations have largely neglected their effects, except for simple treatments of the hydrophobic forces. Part of the challenge is that SIF cannot be described by a purely electrostatic model as they are not solely electrostatic in origin, although they are affected by the solute charge distribution. Therefore, an explicit treatment is needed to introduce the effects of SIF in a computationally efficient model of solvation, and the approach used in the SCPISM is described below.

III.1. Hydrogen bond interactions at protein interfaces

A hydrogen bond is characterized by its strength and its geometry⁶⁸. In the gas-phase, HB geometries are determined by the electron density at the donor and acceptor atoms, with a characteristic directionality provided by the orientation of the electron lone pairs. These gas-phase geometries can still be identified in the condensed phase, although they are perturbed by the specific environment. Thus, in the solid state the perturbation is provided by the crystal field; while in aqueous solutions the geometry is modulated by the SIF. The original SCPISM addressed the problem of SIF modulation on both HB strength and geometry.⁶⁸. It was shown that both HB features are important for correct structure prediction in Monte Carlo simulations of small peptides. For Langevin and molecular dynamics simulations, however, the algorithm that controls the HB geometry in the SCPISM has been removed.³⁷ This parallels the development of the molecular force field itself (in this case, CHARMM) which originally contained an explicit HB-geometry term that was subsequently removed for practical purposes. Because the HB geometry is mostly determined by the quantum mechanics of the interacting groups, it must be contained in the molecular force field in the first place, with the SIF only providing the additional perturbation to the basic gas-phase HB geometry. Therefore, this section deals only with an optimization of the HB strength in the SCPISM, i.e., the SIF modulation of the gas-phase energy.

Small hydrophilic molecules provide an ideal framework to quantify the effects of SIF and the resulting PMF at short intermolecular distances. A systematic study of the PMF in explicit water has been reported using a representative set of 42 amino-acid dimers containing polar and charged groups^61,69. These include the extreme cases of charge-charge interactions (i.e., ionic or salt-bridge), as well as charge-polar, polar-polar, and nonpolar-nonpolar (hydrophobic) interactions. The PMF is given by V(r) = φ(r) + V_w(r), where φ is the intermolecular potential energy in the gas phase and V_w is the intermolecular energy calculated from the forces exerted by the solvent. The ‘reaction coordinate’ r is assumed to be the distance between the acceptor atom and the proton shared by the acceptor (A) and the donor (D) atoms. Both φ(r) and V_w(r) vanish as r → ∞. A detailed discussion of the microscopic behavior of water as the monomers dissociate from close contact has been reported.⁶¹ The potentials show in all cases the usual desolvation barrier [V(r) = V_t at r = r_t] separating the close-contact (V_c at r_c) and the solvent-separated (V_ss at r_ss) minima. Additional, less pronounced maxima and minima appear beyond the water-separated distance, as a result of further restructuring of water in the intervening space between the monomers.^25,61 This restructuring, which is stronger for charged groups, can be visualized from the positions and relocation of the peaks of water density as the distance between the monomers varies.^25,39 An analysis of the contributions to the PMF made by bulk and non-bulk water shows the fundamental role of SIF in determining the form of V_w(r)⁶¹, in particular, the value V_c, which quantifies the ‘HB energy’ between the monomers in water-accessible regions. These HB energies are determined by the solvent, and must be accurately reproduced with an ISM. By contrast, the gas-phase HB is given by φ(r), which is accounted for by the parameterization of the protein force field, and is not the topic of this paper.

III.2. SCPISM implementation

The challenge here is to incorporate the effects of SIF between polar/charged groups into a computationally efficient algorithm that reproduces V_c at r_c. In the SCPISM the total energy E_SCP of a solute in a solvent is partitioned into a purely electrostatic contribution E_e, given by Eq.(5), and a short-range correction E_SIF due to the effects of SIF³⁹, i.e.,

$$E_{\mathit{SCP}}=E_e+E_{\mathit{SIF}}$$ (17)

In a non-polar solute E_e = 0 and then E_SCP = E_SIF, which in this case is simply a “hydrophobic” energy, typically modeled as a cavity term E_cav. For a polar solute E_e ≠ 0 and E_SIF is rather complicated, and depends on the solute topography and charge distribution. A physically complete ISM must reproduce the PMF for all values of r, including V_c (which controls thermodynamic equilibrium), V_t (kinetics), and V_ss. A numerical algorithm has been developed to achieve this goal with the SCPISM in the context of Langevin dynamics simulations.³⁹ A less demanding but highly efficient approach has been reported earlier⁶⁸, which is used here, and aims at reproducing V_c only. The method is based on an extension of Eq.(7) for polar hydrogen atoms,

$$R_i=R_{0,i}+{\delta }_{w,i}{\xi }_i+{\delta }_{p,i}(1-{\xi }_i)+{\delta }_{A,i}{\zeta }_i$$ (18)

where the fraction (1 − ξ_i) has been divided into a fraction ζ_i and a fraction (1 − ξ_i − ζ_i). As long as the proton i remains away from an acceptor A, then ζ_i = 0 and Eq.(18) is identical with Eq.(7). If the proton approaches A, then ζ_i measures the degree of exposure of the proton to A. The energy E_SCP of Eq.(17) is then approximated by

$$E_{\mathit{SCP}}\approx E_e+E_{\mathit{cav}}$$ (19)

where E_e is given by Eq.(5), using R_i of Eq.(18) if i is a polar proton, or Eq.(7) otherwise. Equation (19) represents the complete SCPISM as currently implemented, and yields the total energy of a solute in a solvent. The cavity term E_cav in Eq.(19) is calculated as E_cav = a + b S, where a and b are optimized parameters based on hydration energies of small non-polar molecules and S is the solvent-accessible surface area of the solute^36,70. In the original SCPISM implementation S was calculated numerically³⁶; in the current implementation an approximation similar to that in Eq.(8) is used instead, which allows analytical derivatives for the calculation of forces³⁷. In the current implementation this cavity term is the only source of hydrophobic forces between non-polar solutes, which is clearly a simplification. A better description of hydrophobic forces is clearly needed in the SCPISM. This is usually considered to be a conceptual and practical challenge; three theoretical approaches are currently being considered.^71–73

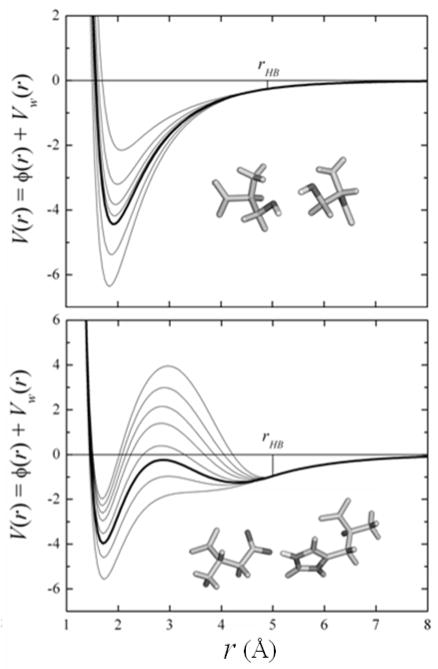
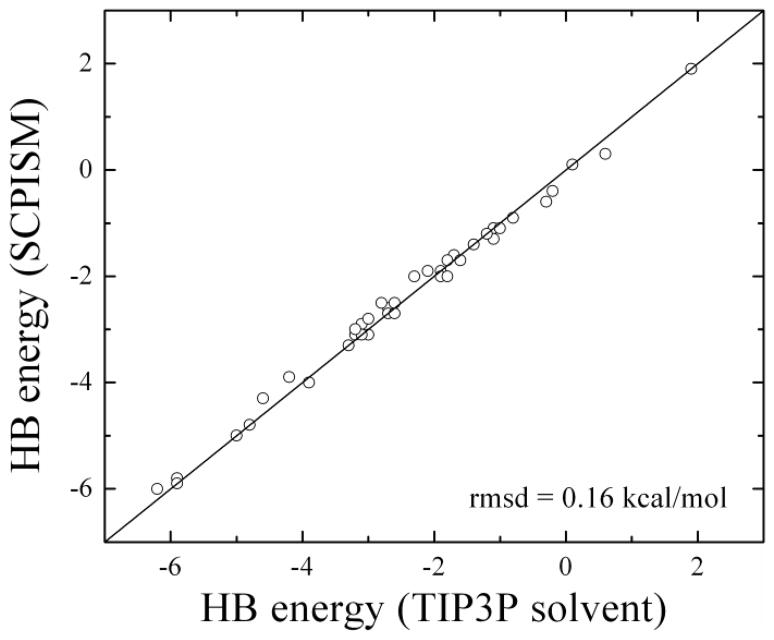
The parameter δ_A,i in Eq.(18) allows fitting to HB energies. To obtain δ_A,i for each amino acid pair the corresponding HB energies must be known, preferably experimentally. Such determination is difficult, although attempts have been reported. For example, HB energies in water-accessible regions of proteins have been estimated by site directed mutagenesis in enzyme-substrate complexes.⁷⁴ These studies showed that deleting a side chain that forms one HB between the enzyme and the substrate tends to weaken the free energy of binding by ~0.5 to ~4.5 kcal/mol, depending on the charge of the group left unpaired. During enzyme-substrate binding, the donor and acceptor atoms must break their HB with water molecules at the interfaces. Thus, these experiments measure the HB energies controlled by SIF.⁷⁴ The original implementation of the SCPISM^37,68 used these estimates to calibrate all the HB energies between amino acid pairs. In this case the δ_A values were adjusted individually for all possible side chain-side chain, side chain-backbone, and backbone-backbone interactions in proteins. The extensive calculations of the PMF previously reported⁶⁹ confirmed the overall range of HB energies determined experimentally. However, the relationship between the charge/polarity of the interacting groups and the HB strengths was less clear. Because of the limited number of HB studied experimentally, and because of the inherent difficulties in deriving individual HB interactions from kinetics data in protein complexes⁷⁴, the SCPISM is here recalibrated based on the systematic calculations of PMF using explicit water simulations.⁶⁹ Figure 3 shows the effects of δ_A on the HB energies in the case of two representative interactions. The thick lines show the optimized potentials that reproduce V_c and r_c obtained from the atomistic simulations. This potential is obtained with an optimized value of δ_A = δ^* in Eq.(18). The thin lines are the interaction energies for different values of δ_A, showing over-stabilization (δ_A < δ^*) and destabilization (δ_A > δ^*) of the dimers. Since the correction is effective only for r < r_HB, the long-range electrostatic forces described by Eq.(5) are not affected by δ_A. If the dimers are transferred to the interior of a protein, the SIF no longer play a role. In this case the modulation of HB energies become’s purely electrostatic problem, and is then addressed by the water-exclusion effects controlled by α. In the limit of complete exclusion (infinitely large solvent-excluding cavity) V_w → 0, and the PMF converges to the gas-phase interaction energy as given by the vacuum protein force field. Figure 4 shows the new HB calibration for the dimers reported in ⁶⁹, with V_c and r_c accurate to within the statistical errors of the simulations.

Figure 3.

Intermolecular energy V(r) (in kcal/mol) between Ser–Ser (left) and Asp⁻–Arg⁺ (right) as a function of the shared proton-acceptor atom distance r. Energy calculated with the SCPISM [Eq.(19)] and the all-atom CHARMM van der Waals potential. Thick lines correspond to the optimized HB energy based on PMF calculations in explicit water⁶⁹; thin lines illustrate the dependence of the HB energy with δ_A [Eq.(18)]. V_w(r) and φ(r) are the water-induced and the gas-phase intermolecular energies, respectively.

Figure 4.

Optimization of 42 representative HB interactions of amino acids pairs^68,69. All energies in kcal/mol. HB energies are calibrated within the statistical errors in explicit water simulations (~0.2–0.4 kcal/mol); HB distances are reproduced within the estimated errors (~0.2 Å).

The computational efficiency of the approximation described here stems from the relatively small number of shared protons for any given conformation of the system, and from the fact that ζ_i = 0 for proton-acceptor distance r > r_HB, where r_HB ~ 5 Å, the distance at which the first hydration shells begin to overlap.

IV. Applications

The SCPISM has been implemented in the CHARMM program⁷⁵ and was shown to be among the most computationally efficient ISMs currently available.⁷⁶ The developments reported in this paper add little computational cost. In the current implementation for dynamics, and only for practical purposes, the corrections δα’s in Eq.(9) and (15) are updated heuristically when any inter-residue distance r_IJ changes more than 0.5 Å from the last update. This screening-update protocol was motivated by the non-bonded list update method commonly used in macromolecular simulations, but may lead to energy conservation problems. The threshold 0.5 Å, however, was determined after substantial experimentation to keep energy-conservation errors small during each screening update. The current SCPISM implementation in CHARMM (version c36) is only ~1.5 times slower than the vacuum calculation. Its parallel performance is good, with a speedup of ~30 for 32 CPU cores using 48-core AMD Opteron 2.2 GHz machines, for 1000 dynamics steps of a ~6500-atom protein complex. To test and discuss the conceptual aspects of the model, two systems are considered: the complex of Barnase with its inhibitor protein Barstar, and the short peptide known as Trp-cage. Both systems are well characterized experimentally, and their conformations in aqueous solutions have been reported.

IV.1. Protein association

Barstar is a small protein (89 aa) that binds to barnase (110 aa) and inhibits its activity in vivo. The crystal structure of the complex (PDB code: 1BRS) has been resolved at 2 Å resolution⁷⁷. The proteins are commonly used as a paradigm for protein complexation.^77–82 Barnase and barstar associate mainly by electrostatic forces, and bind tightly to one another due to electrostatics and HB interactions. Recent studies have also suggested a role of interfacial water in the stability of the complex.⁸³ This protein system is thus well suited to discuss all aspects of the SCPISM developed in this paper. Chains A (barnase) and D (barstar) of the crystal structure were used. The calculations assume that the proteins are immersed in pure water, a common but imperfect assumption.⁶¹ Standard ionization states at neutral pH are used. Asp and Glu residues are assumed to be unprotonated, while Arg and Lys are protonated. There are three His residues in the complex, which are assumed to be protonated, as well. The complex is thus net neutral. H102 is located at the barnase/barstar interface and is known to shift its pKa upon complexation.⁷⁷ Calculations were repeated with a neutral H102, but the qualitative observations reported here were not affected.

The simulations consist of Monte Carlo (MC) annealing. The polar-hydrogen (param19) representation of the protein force field is used to speed up computation. Because the original SCPISM implementation in CHARMM was parameterized for the all-atom (param22) force field³⁶, these simulations required a parameterization of the model for param19. The HB energies were also calibrated for param19 as discussed in Section III.2. Two types of standard metropolis MC simulations were carried out. In “RBMC” runs, the proteins were treated as rigid bodies, while in “RBDMC” runs, selected dihedral angles at the protein surface were allowed to rotate in addition to rigid-body movements. Many proteins that form hetero-dimers are reasonably well represented as rigid bodies, since their backbone conformations change little from the uncomplexed to the complex forms. This is the case of barnase and barstar. RBMC moves consisted of rotation, translation, and rotation-translation of one of the proteins, chosen randomly with equal probability. Rigid body rotations were represented by quaternions. Both translations and rotations were generated randomly, with distances and angles taken from Gaussian probability distributions using the Box-Muller method. The acceptance rate λ was monitored on the fly at each temperature T, and the widths of the distributions were adjusted as needed to keep λ above a certain threshold (here, λ > 0.4) as T was decreased. In the RBDMC simulations, rotations, translations, roto-translations, and single-dihedral rotations were considered, each with equal probability. Dihedral angles were selected randomly and moved based on a Gaussian probability distribution with a variable width used to keep the acceptance rate above the threshold. The updates of the widths of the Gaussian distributions in both the RBMC and RBDMC violate detailed balance, which affects convergence to Boltzmann distributions unless proper corrections to the acceptance probability are introduced. Simulations were also carried out without λ-stabilization and the results reported here were similar. The goal was to find low-energy complexes, and no thermodynamic quantities were calculated from the ensembles generated in this study.

Initially, the proteins were distributed randomly in a spherical simulation cell of radius R_C. This radius can be selected heuristically or fixed based on the molar concentration of the proteins. The latter setup is more convenient when several types of proteins and ions are used to mimic realistic experimental setups. For the analysis intended here, the radius was set to R_c = 85 Å, which corresponds to a very low concentration and allows enough mobility of the proteins within the container. If the center of mass of a protein moved outside of the container during a translation, the protein is relocated in a random position inside the container. This is equivalent to imposing an infinitely repulsive potential outside the container. All the simulations were started at T = 3000 K and ended at T = 296 K (crystal growth temperature), and annealing was achieved through a logarithmic schedule in 20 temperature steps. A total of 2 × 10⁵ MC steps were performed per temperature for both RBMC and RBDMC simulations. This MC protocol was based on the authors previous experience but was not optimized. No cutoffs were used for the treatment of non-bonded interactions. For comparison, an additional RBMC simulation was carried out with a cutoff of 14 Å, which sped up computation by a factor of four, but the main results did not change and are not discussed. The widths of the distributions were initially set to 10 Å for the translations, and 180° for rigid-body and dihedral-angle rotations.

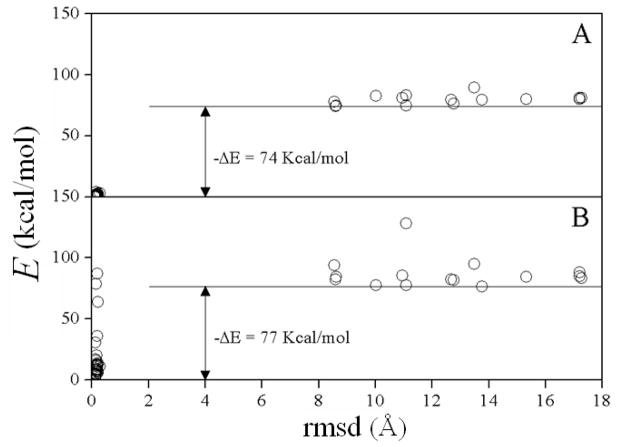
Each simulation consisted of fifty independent MC runs. Figure 5 summarizes the results for the RBMC simulation. Only the final structures in each run are shown (circles). About 75% of the runs identified the native population as the one with lowest energy (C_α-rmsd < 0.5 Å with respect to the crystal structure). The non-native conformations show no common structural features. All of the complexes were subsequently energy-minimized without restraints for 50 steps using an adopted basis Newton-Raphson algorithm, and the energies are plotted in Fig. 5B. The gap |ΔE| changes little, although the native conformations show a spread in energy due to internal structural relaxations.

Figure 5.

Results of the rigid-body Monte Carlo (RBMC) simulated annealing of barnase and barstar: Fifty complexes before (A) and after (B) energy minimization. Energy E is the sum of the CHARMM protein force field (param19) and the SCPISM energy E_SCP [cf. Eq.(19); parameterized for param19]. C_α–rmsd measured with respect to the crystal structure. ΔE’s are energy differences between the non-native and native complexes.

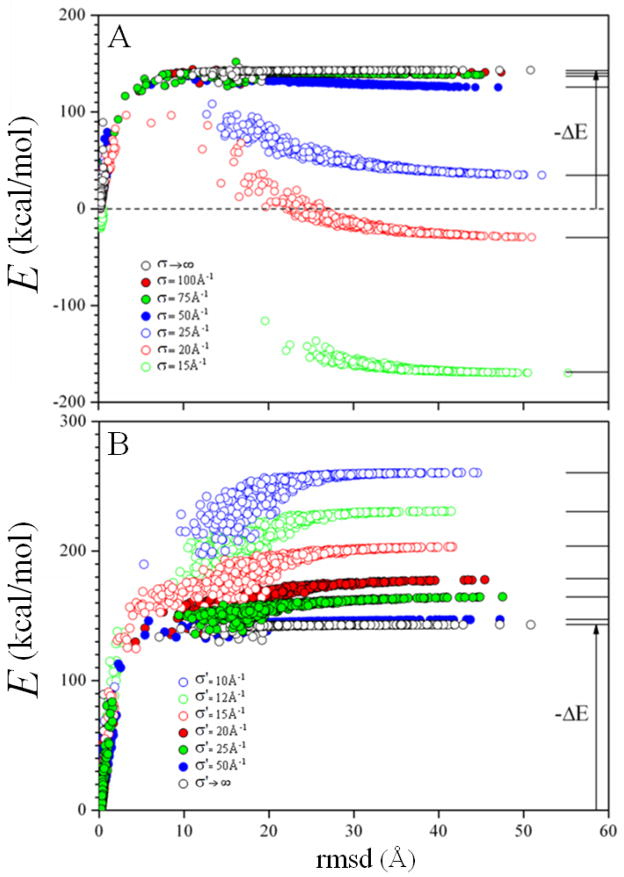
The simulations discussed above were carried out with σ → ∞ and σ′ → ∞ in Eq.(13) and (16), which means that the model neglected the long-range effects of water exclusion. The short-range effects are still accounted for through Eq.(8). However, long-range water-exclusion effects are large when two proteins come into contact, as there is a sudden exclusion of water at the protein/protein interface during complexation. Thus, protein association is an ideal process to gain insight into the long-range electrostatic effects described by the SCPISM. To carry out a systematic study of these effects, the dependences of the binding energy on the parameters σ and σ′ were analyzed. Here, the crystal structure was heated from T = 296 K up to 10³ K, generating a set of decoys which includes near-native structures and fully dissociated proteins. Simulations were performed as a function of σ and σ′, with each parameter varying in the interval [10 Å, ∞). Figure 6A shows the energies of the decoys as a function of the C_α-rmsd for selected values of σ and σ′ → ∞. By setting σ′ → ∞, only the effect of water exclusion on the self-energy is assessed. In this case |ΔE| is the binding energy, i.e., the energy difference between the native complex and the fully-dissociated proteins, and thus larger than |ΔE| in Fig. 5. Figure 6A shows that water-exclusion effects on the self-energy tend to decrease the binding energy. This result is physically correct for any polar solute, as association implies partial dehydration, which is energetically unfavorable for polar and charged groups. Binding can actually become unfavorable for small σ. In this case the proteins remain dissociated for σ < 22 Å, as confirmed with a set of RBMC simulations (not shown). Figure 6B shows the effect of water exclusion on the interaction energy, i.e., for σ → ∞. Here the trend reverses, and the smaller the value of σ′ the more favorable the binding energy. This reflects the fact that partial dehydration during complexation leads to stronger pair interactions at the protein/protein interface, which usually favors attraction.

Figure 6.

Long-range water-exclusion effects on the self-energy (upper panel) and interaction-energy (lower) terms of the total electrostatic energy E_e in the SCPISM [cf. Eq.(13)]. Decoys are generated from the crystal structure by heating. Characteristic lengths σ and σ′ are defined in Eq.(13) and Eq.(16). The limits σ → ∞ and σ′ → ∞ means that only short-range water-exclusion effects are accounted through Eq.(8) (original electrostatic description in the SCPISM^36,37). HB energies are based on systematic PMF calculations in explicit water⁶⁹. ΔE’s are energy differences between the fully-dissociated and the native complexes, i.e., binding energies). The right balance between σ and σ′ can be obtained from experimental binding energies or dissociation constants.

The qualitative behavior illustrated in Fig. 6 using the native complex holds for any of the non-native structures obtained in the MC simulation (not shown). The opposing trends in binding energy with σ and σ′ mean that for a given set of parameters (σ < ∞, σ′ < ∞) the resulting binding energy is a balance between the unfavorable and favorable effects of water exclusion on the different terms in Eq.(5). This observation provides a rationale to select values of σ and σ′ based on experimental thermodynamic measurements, such as binding affinities or dissociation constants (see below).

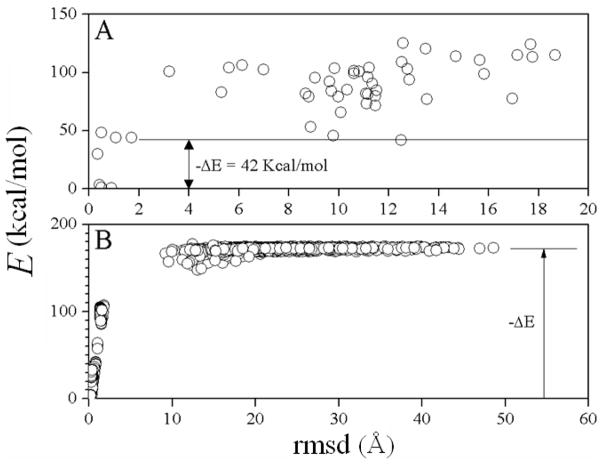
Similar analysis was carried out for the RBDMC simulations. Figure 7A shows the energies of the final structures as a function of the all-atom rmsd from the native complex. When compared to the RBMC simulations in Fig. 5, only four out of 50 structures are native, implying that better sampling is needed to accommodate the new degrees of freedom. Also, the binding energy decreased by ~30 kcal/mol, indicating that sampling of the dihedral space allowed the MC to find new conformations that were not allowed with the dihedral angles fixed at the crystal-structure values.

Figure 7.

(A) As in Fig. 5B, for the RBDMC simulation (interaction energy only); (B) as in Fig. 6, for the RBDMC simulation (interaction energy only) using short-range water-exclusion effects only (σ → ∞ and σ′ → ∞). The qualitative behavior of ΔE with σ and σ′ is the same as in Fig. 6 (not shown).

Figure 7B shows the results of the decoys obtained by heating the native complex in a RBDMC simulation, for σ → ∞ and σ′ → ∞. The same dependence with σ and σ′ observed in Fig. 6 is obtained in these simulations (not shown), as dihedral movements do not change the major effects of water-exclusion discussed above. As for the RBMC simulations, the binding energy is larger than |ΔE| in Fig. 7A, and for the same reasons. In addition, the binding energy in the RBDMC simulations is larger than the binding energy in the RBMC simulations, indicating that sampling the dihedral space helps find lower-energy conformations in the complex.

Three different approaches can be used to obtain values of σ and σ′ that yield a correct balance between the interaction and the self-energy terms in Eq.(5). One method, as mentioned above, is based on experimental data on the thermodynamics of protein-protein binding. A number of enzyme-inhibitor and antigen-antibody complexes, for which the rigid-body approximation is known to be reasonable, are well characterized thermodynamically, as in the case of barnase and barstar. This is the method of choice in the SCPISM, as the model has been parameterized in the past using experimental data only (excepting the new calibration of the HB energies reported here, which is based on data from atomistic dynamics simulations). The optimization of σ and σ′ based on thermodynamic data requires extensive calculations, and is not reported in this paper. It is possible, however, to obtain tentative values for these parameters using simpler methods, such as numerical solutions of the Poisson equation (PE). In general, solutions of the PE in peptides and proteins are known to be sensitive to the parameters used in the calculations, especially for charged atoms close to the solute/solvent interface.³⁸ For larger systems and buried atoms, i.e., away from the solute/solvent interface, solutions of the PE are however less sensitive to the parameters used.³⁸ These are the conditions required to probe long-range solvent-exclusion effects. Thus, the simplest method to evaluate σ and σ′ is to obtain effective screening functions D_ij and D_i and D_j for atoms i and j in a protein using a standard PE solver, and then to equate these PE-based effective screening functions with the corresponding ones in the SCPISM. From these calculations values of α_ij, α_i and α_j can be obtained from Eq.(2), and σ and σ′ can then be estimated from Eq.(13) and (15). Systematic calculations of PE-based screenings in proteins have been shown⁸⁴ to have sigmoidal behavior, similar to those used in the SCPISM (cf. Section II). It has also been shown⁸⁴ that solvent-exclusion effects modify the PE-based effective D’s in ways that are qualitatively similar to those proposed here (cf. Section II.2), i.e., the larger the exclusion, the smaller the value of α. An alternative method to evaluate σ and σ′ involves similar calculation of effective screenings but using atomistic dynamic simulation of water, preferably with a polarizable water model. This is more computationally demanding than solving the PE, but far more practical than using thermodynamic data of protein binding. Here, the PE based method will be used, but to avoid extensive PE calculations in proteins, an idealized spherical cavity of radius r_c centered at (0,0,0) is used instead. Two charges, q₁ = +1 and q₂ = −1 are located at positions (−r/2,0,0) and (r/2,0,0) respectively. The interparticle distance r is varied in the interval 2–10 Å, and for each value of r the radius r_c is changed in the 25–500 Å range. For a given r and r_c the PE is solved (ε_i =1 and ε_w = 78.4) and σ and σ′ are obtained as explained above. To evaluate the self-energy terms the charges are switched off, as needed. The procedure to obtain the interaction and the self-energy components from the PE solution was described.³⁶ It was shown that the SCPISM correlates well with solutions of the PE in small peptides with different conformations and charge distributions³⁶ and in decoys of small globular proteins⁴⁸. To use the SCPISM in this idealized system, the fully hydrated parameter α_0,i of Eq.(13) and α_0,ij in Eq.(15) are taken from Fig. 2 for a unit charge, and set to 2 Å⁻¹; the fully dehydrated radii in Eq.(7) is set to R_0,i + δ_p,i = 2 Å, which is a characteristic value in proteins. Also, the summations over r_IJ in Eq.(13) and Eq.(16) are performed numerically in the continuum, as done in Eq.(14), but with an upper limit of r_c, instead of ∞, i.e., M = (r_c/p)³. Although the exact values of σ and σ′ depends on which portion of the 25 Å < r_c < 500 Å interval the curves are fitted, in the limit of large r_c the calculations yield σ ~ 50 Å⁻¹ and σ′ ~ 75 Å⁻¹. These values are assumed to be the best estimates for the current implementation.

IV.2. Peptide folding

The original SCPISM has been used to predict the structure of small α-helix- and β-hairpin-forming peptides in solution.⁸⁵ To test the new implementation, and for comparison with other implicit solvent models^86–89, the 20-residue peptide NLYIQWLKDGGPSSGRPPPS known as Trp-cage is used here. The structure of this peptide has been determined⁹⁰ by NMR (PDB code: 1L2Y) at 282 K and pH 7. All residues are assumed to be neutral, except Lys⁺, Arg⁺, and Asp⁻. The NMR coordinates indicate standard NH₃⁺ and COOH⁻ termini, resulting in a total charge +1. In explicit-solvent simulations, charge neutralization is enforced by introducing a set of monovalent ions in the simulation cell. This strategy is usually avoided in implicit solvation where the excess charge is generally not removed. However, some implicit models enforce electric neutralization by effectively deleting the excess charge from the system, e.g., neutralizing all the charged side chains and termini in a protein. This approach is advantageous as charged groups are known to introduce strong local perturbations that can produce artifacts, especially in structure prediction. However, local charges are important modulators of biological function, and charge modification at specific sites and times, e.g., by proton transfer, or phosphorylation, can trigger specific dynamic responses. In Section II.3.2 the electrostatic component of the SCPISM was parameterized for multivalent ions. The system could then be neutralized by introducing a single Cl⁻ ion into the simulation cell. However, it was also mentioned that the physics of solvation for small solutes is more complicated than only electrostatic interactions, and that additional developments are needed prior to using explicit ions in an ISM simulation. Pending these developments the system here retains the +1 charge, and the simulations were carried out at zero ionic strength. The all-atom representation of the CHARMM force field was used, including the CMAP correction of the backbone dihedral energy terms.⁷⁶ Backbone rmsd from the NMR structure was calculated relative to the first model deposited in the PDB, excluding the first and last residues.

A Monte Carlo-minimization/annealing (MCMA) conformational search^86,91,92 was used to find low-energy minima in the Trp-cage energy landscape. Following biased, random changes in side-chain or main-chain dihedral angles, the energy is minimized before acceptance or rejection of the trial move. Occasionally, simulated annealing is performed prior to the energy minimization to increase acceptance of structures following relatively large conformational changes. Thus, MCMA is used to search for the global energy minimum, not to achieve Boltzmann sampling of a canonical ensemble.⁹²

Replica-exchange simulations (REx) were performed using N = 24 replicas, with each replica initiated using a structurally distinct low-energy conformation found by MCMA, as follows. The structure found using MCMA possessing the lowest energy was assigned to the lowest temperature, here 282 K (the NMR temperature). All other MCMA minima with backbone-rmsd within a cutoff distance of this first structure were assumed to belong to the same conformational family and were excluded from further consideration. Of the remaining structures, the lowest-energy structure was assigned to the second temperature, and structures within the cutoff distance of this structure were excluded. The process was repeated to produce 24 different starting structures of low energy. The cutoff distance was chosen to ensure inclusion of structures that were both low in energy and quite different from the lowest-energy structure. Temperatures of the replicas are given by T_n = int[282(1 + 19/282)ⁿ⁻¹ + 0.5] with n = 1,…,24, which produced a relatively uniform acceptance rate in the 0.3–0.4 range. Swaps of neighboring replicas were considered after 100 steps of Langevin dynamics, using a collision frequency of 2 ps⁻¹ for non-hydrogen atoms. The SHAKE algorithm was applied to bonds involving hydrogen atoms. The integration time step was 1.5 fs for T < 700 K and 1.0 fs for T ≥ 700 K. The relatively large number of replicas and the high temperatures (up to 1263 K) used represent a stringent test of the energy landscape.

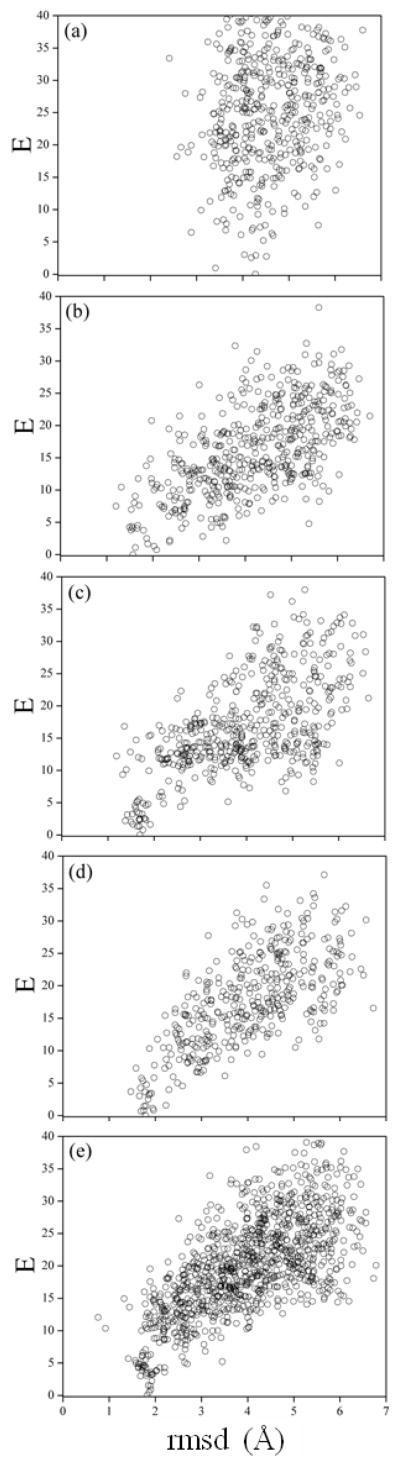
Results of the MCMA simulations are shown in Fig. 8. The lowest energy conformation found in vacuum (Fig. 8A) has a backbone-rmsd of ~4.2 Å with respect to the NMR structure, and all low-energy conformations have an rmsd above ~3 Å. Secondary structure elements resembling the NMR conformation were not observed in low-energy structures. The effect of entropy at 282 K, as evidenced by the REx simulation, further stabilizes these non-native structures (not shown), and none of the major conformational families are native-like. Thus, the MCMA/REx results confirm that the peptide does not adopt native-like structures in the gas-phase, at least with the CHARMM protein force field.

Figure 8.

Results from MCMA simulations of Trp-cage (all energies E in kcal/mol). (a) Gas-phase CHARMM force field (param22); (b) original SCPISM (HB energies based on experimental estimates; only short-range water-exclusion effects included); (c) as in (b) but with charges on the N- and the C-terminus switched off; (d) current SCPISM but with short-range water-exclusion effects only (HB interactions based on atomistic PMF calculations); to be compared with plot in (b); (e) as in (d) but with the complete SCPISM, including short- and long-range water-exclusion effects (σ = 75 Å and σ′ = 50 Å)

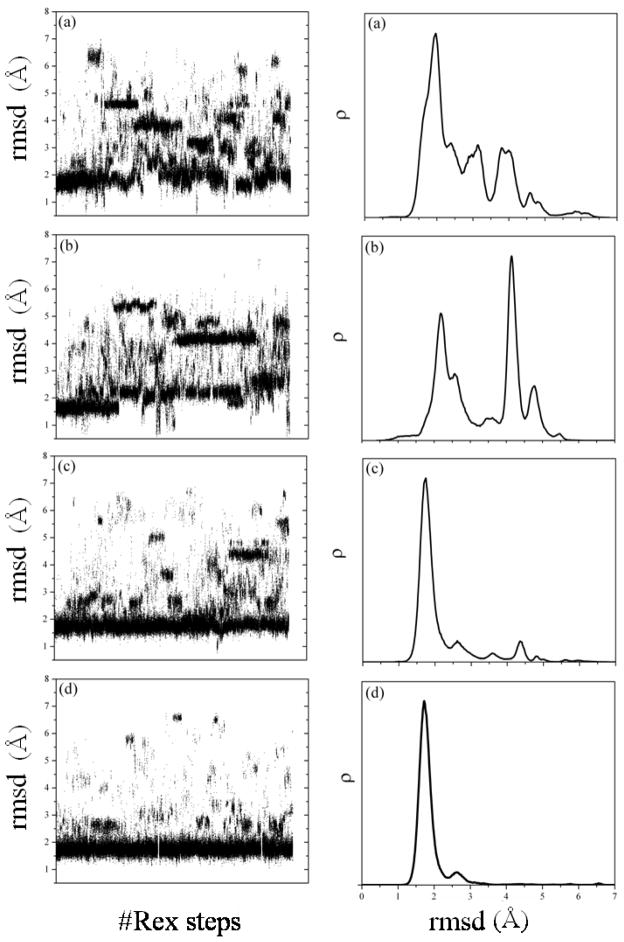
Figure 8B shows results for the original SCPISM. Only short-range effects of water exclusion are modeled, and the HB energies are calibrated based on enzyme-substrate data.^68,74 In contrast to protein complexation, long-range water-exclusion effects are not expected to play a major role for small systems. The lowest-energy structure is native-like with a backbone rmsd of ~1.5 Å. Several low-energy structures are non-native, some within ~3.5 kcal/mol from the NMR structure. Figure 9A shows the rmsd of structures sampled at 282 K (left panel), and the conformation histogram ρ as a function of the backbone rmsd (right panel). The distribution at 282 K suggests that the misfolded states are entropically favored, and the energy gap between the native and misfolded structures (inferred from Fig. 8B) is not wide enough to offset conformational entropy effects. From a predictive standpoint, however, the largest population is native-like, with a maximum located at rmsd ~1.75 Å, and some conformations reaching rmsd ~1.1 Å. The misfolded states detected at 282 K with REx, evidenced by the peaks in ρ, have not been discussed in the experimental literature and are apparently spurious. Simulations at lower temperatures (not shown) indicate that these misfolded states become less populated, as expected from the MCMA data in Fig. 8B. Inspection of the misfolded structures shows that they are stabilized by HB interactions of the charged termini with either the backbone or the charged side chains. In the original SCPISM the N– and C–termini are treated as Lys⁺ and Asp⁻ side chains in the HB energy calibration. To analyze the effects of these interactions, the excess charges in both termini were artificially removed. The corresponding MCMA data are plotted in Fig. 8C, showing a rather dramatic reshaping of the energy surface. The lowest-energy structure is still native like, with rmsd of ~1.7 Å, but the energy gap between lowest and misfolded states increased. Results of the corresponding REx simulation are shown in Fig. 9B. Although the uncharged termini play no role in stabilizing the misfolded structures, one conformational family with an rmsd of ~4.2 Å is now over-stabilized due to HB interactions involving other charged side chains. Structures very close to the NMR structure (rmsd close to ~0.5 Å) are also explored in the REx simulation, as evidenced by the distribution tail in Fig. 9B (right panel). Although there is a relatively large native-like population, this is insufficiently populated for successful blind structure prediction.

Figure 9.

Results from REx simulations of Trp-cage. Left column: backbone-rmsd as a function of the number of replica-exchange steps (maximum of ~10⁶). Right column: histogram ρ of conformations at 282 K (NMR temperature), as a function of the backbone rmsd. (a) Original SCPISM (HB energies based on experimental estimates and only short-range water-exclusion effects included); (b) as in (a) but with terminal charges switched off; (c) current SCPISM but with short-range water-exclusion effects only (PMF-based HB energies); (d) as in (c) but with short- and long-range water-exclusion effects included (σ = 75 Å and σ′ = 50 Å).

The above results confirm that charged groups can affect the proper folding but are also prone to engage in spurious local interactions that might over-stabilize non-native structures. This also shows why careful consideration must be given to the strength of HB interactions. Figure 8D shows results of the current implementation of the SCPISM. The original SCPISM calibration of the HB strength is here replaced by the new calibration shown in Fig. 4. Results in Fig. 8D are obtained with short-range water-exclusion effects only (σ → ∞ and σ′ → ∞), and the termini charges are restored, thus panel (D) can be compared with panel (B). The improvement is apparent, and all misfolded structures have now relatively large energies compared to the native structure. As shown in Fig. 9C the effects of conformational entropy are not sufficient to stabilize the misfolded state at 282 K. Some non-native families can still be detected, but a blind prediction could unambiguously identify native-like structures, with a maximum in the probability distribution located at rmsd ~1.75 Å. An analysis of the long-range effects of water-exclusion can also be made. Figure 8E shows the current implementation with σ = 75 Å and σ′ = 50 Å, values based on results from the protein complex discussed above. This simulation retains the current HB strength based on PMF calculations, and thus panel (E) can be compared directly to panel (D). Results are similar to those in panel (D), although a modest improvement is observed in the histogram of Fig. 9D. The native population can be identified, and misfolded structures have destabilized slightly, leading to negligible populations above rmsd ~3.0 Å. The backbone rmsd of the first 15 residues of the predicted native conformation is ~0.8 Å with respect to the NMR structure, and the main conformational differences appear in the last five residues, three of which are Pro residues. These last residues are bent with respect to the corresponding sequence in the NMR structure, and the Trp residue is then not properly packed in the predicted structure.

Conclusions

Highly crowded aqueous environments, such as the cytosol, are characterized by the presence of many solute/water interfaces, and large, non-uniform regions devoid of water. Such environments display unique properties that affect the structural and dynamic behavior of biomolecules, mainly due to electrostatic and liquid-structure forces not present in the bulk phase. Implicit models of solvation suitable for large-scale computer simulation of subcellular processes, for example, are necessarily phenomenological. However, careful design and parameterization can satisfactorily incorporate the most relevant physics of solvation. Such models are needed to study thermodynamic properties such as specific and non-specific binding, protein translocation, structural stabilization and denaturation, and other essential biological/biochemical mechanisms. In this paper, an extension of the SCPISM model of solvation is proposed to incorporate two of the most relevant effects observed in crowded environments: the long-range water-exclusion forces, and the effects of water-structure on the short-range forces between polar and charged groups. The model is parameterized on the basis of experimental data and on the strengths of HB interactions inferred from simulations in explicit water. The model provides a prescription to incorporate explicit ions and other cosolutes into the system.