Phasing of Many Thousands of Genotyped Samples

Abstract

Haplotypes are an important resource for a large number of applications in human genetics, but computationally inferred haplotypes are subject to switch errors that decrease their utility. The accuracy of computationally inferred haplotypes increases with sample size, and although ever larger genotypic data sets are being generated, the fact that existing methods require substantial computational resources limits their applicability to data sets containing tens or hundreds of thousands of samples. Here, we present HAPI-UR (haplotype inference for unrelated samples), an algorithm that is designed to handle unrelated and/or trio and duo family data, that has accuracy comparable to or greater than existing methods, and that is computationally efficient and can be applied to 100,000 samples or more. We use HAPI-UR to phase a data set with 58,207 samples and show that it achieves practical runtime and that switch errors decrease with sample size even with the use of samples from multiple ethnicities. Using a data set with 16,353 samples, we compare HAPI-UR to Beagle, MaCH, IMPUTE2, and SHAPEIT and show that HAPI-UR runs 18× faster than all methods and has a lower switch-error rate than do other methods except for Beagle; with the use of consensus phasing, running HAPI-UR three times gives a slightly lower switch-error rate than Beagle does and is more than six times faster. We demonstrate results similar to those from Beagle on another data set with a higher marker density. Lastly, we show that HAPI-UR has better runtime scaling properties than does Beagle so that for larger data sets, HAPI-UR will be practical and will have an even larger runtime advantage. HAPI-UR is available online (see Web Resources).

Introduction

Phased haplotypes are important for a number of applications in human genetics; these include genotype imputation,^1,2 identity by descent (IBD) detection,³ local-ancestry inference,^4–6 and methods that identify recent strong signals of positive selection.^7,8 For each of these applications, accurate haplotypes reflecting the true composition of alleles on each chromosome increase the accuracy of the inference. Many statistical and computational methods have been introduced for inferring haplotypes from genotypes, and although molecular methods for directly assaying haplotypes can in principle achieve near-perfect haplotype accuracy,⁹ indirect computational inference of haplotypes from genotypes is at present the most practical and economical approach for obtaining large numbers of haplotypes.

Considerable effort has been devoted to developing methods that infer haplotypes accurately,^1,2,10–13 but less attention has been given to the overall runtime and scalability of methods to very large sample sizes. The ability to phase large genotype data sets is important because (1) the accuracy of haplotypes inferred by statistical methods increases with sample size (see Results and Browning and Browning¹⁴), (2) genotype data sets continue to grow in size—individual data sets containing over 50,000 samples are now available (see Results) and larger data sets are soon to be available (see Risch et al.¹⁵ and the WTCCC2 data set in the Web Resources)—and (3) separately phasing large numbers of samples in smaller subsets results in errors that are correlated within each subset, and these errors reduce the utility of the haplotypes in subsequent applications. Several potential problems arise from using separately phased haplotypes. If one performs genotype imputation on prephased haplotypes that were phased in batches without being randomized with regard to trait status, false associations could arise from correlations between trait status and the batch. Even when a study randomizes phasing batches properly, the use of imputed genotypes from separately phased haplotypes is suboptimal and results in reduced power due to increased noise in the imputed genotype values. Besides association studies, applications such as IBD detection or identifying signals of selection might miss true signals when analyzing separately phased haplotypes.

The potential for phasing large cohorts arises in the context of individual large data sets generated at one institution (such as those from the Welcome Trust Case Control Consortium [WTCCC] and Children’s Hospital of Philadelphia [CHOP] data sets described in the Results), as well as from collections of samples from multiple sources. The opportunity exists for researchers to pool data sets through collaboration and obtain data from several genome-wide association study (GWAS) data sets available through the National Center for Biotechnology Information database of Genotypes and Phenotypes (dbGaP) and the European Genome-phenome Archive.

We present a method called HAPI-UR (haplotype inference for unrelated samples), which we developed to be both accurate and computationally practical for the application to large genotype data sets of unrelated and/or trio and duo samples. We demonstrate the speed and scalability of HAPI-UR on a data set containing 58,207 samples and show that running it on this large data set at a genome-wide scale is practical, even with access to modest computational power. We also show that phase accuracy increases when we include larger subsets of the cohort together. This data set contains individuals from multiple ethnicities, including European Americans, African Americans, Latinos, and East Asians, and we demonstrate that overall accuracy increases when we phase all samples together. We perform an empirical study that examines whether phasing individuals from multiple ethnicities separately or together increases accuracy, and our results are in line with related studies that demonstrate increased imputation accuracy with the use of reference haplotypes from multiple populations or ethnicities.^16–19 Our results suggest that, unless the proportion of ethnic groups is extremely skewed toward one group, the best practice is to phase all samples together regardless of ethnicity.

We compared the accuracy and runtime performance of HAPI-UR to those of Beagle,¹⁰ MaCH,² IMPUTE2 (Howie et al.¹), and SHAPEIT²⁰ on data sets of various sizes. The largest data set we used for comparison consisted of 386,353 SNPs for 16,353 samples from the WTCCC²¹ and HapMap²² (WTCCC1 + HapMap), and we also examined subsets (of 1,000, 3,000, or 5,000 samples) of the full WTCCC1 + HapMap data set. We examined phase accuracy by using the switch-error-rate metric.²³ A switch error occurs when a heterozygous site has phase switched relative to that of the previous heterozygous site. We calculated switch-error rates by comparing each method's results to the haplotypes of 88 trio parents for whom phase was separately inferred on the basis of trio relationships (we omitted the trio children from all evaluation data sets). On the data set with 16,353 samples, we show that HAPI-UR runs 18× faster than the other methods and also achieves comparable or lower switch-error rate. We also show that using consensus phasing from across three runs of HAPI-UR on the entire data set obtains lower switch error than the other methods do. When run serially, this approach is more than six times faster than the other methods, but it is also fully parallelizable to three processors.

To ensure that HAPI-UR is computationally efficient and accurate for data sets with a range of marker densities, we compared HAPI-UR to Beagle on a data set with a total of 755,008 SNPs from 5,353 samples combined from the WTCCC2 control samples²⁴ and HapMap²² (WTCCC2 + HapMap). In this comparison, HAPI-UR achieved speed advantages and accuracy comparisons similar to those exhibited in the WTCCC1 + HapMap data set.

An important factor for handling large data sets is how computational runtime scales with sample size. Whereas Beagle runs 156× slower when analyzing 16,353 samples than it does when analyzing a subset of 1,000 samples, the corresponding slowdown for HAPI-UR is 48×. MaCH scales linearly with sample size, and we conservatively assume that IMPUTE2 and SHAPEIT scale linearly as well (although in our experiments these methods scaled superlinearly). HAPI-UR and Beagle scale superlinearly but subquadratically; however, the overall runtimes of MaCH, IMPUTE2, and SHAPEIT are such that they remain more computationally expensive than HAPI-UR (see Results), and they also show higher error rates for large data sets. Because of the improved scaling factors and overall runtime of HAPI-UR, larger sample sizes will yield even greater speed-improvement factors for HAPI-UR than for Beagle, and we expect this runtime scaling to enable HAPI-UR to phase sample sizes of 100,000 individuals or more (see Results).

In the Material and Methods, we provide details of the algorithm implemented in HAPI-UR. In the Results, we compare the accuracy and runtime performance of HAPI-UR to those of other algorithms and evaluate its performance in phasing a large multiethnic data set. Finally, the Discussion analyzes phasing methodologies in the context of large data sets.

Material and Methods

The key feature differentiating HAPI-UR from other statistical phasing methods^1,2,10–12 is that although other methods construct states at each marker in their hidden Markov models (HMMs), HAPI-UR builds HMM states corresponding to nonoverlapping windows of adjacent markers. Instead of emitting an allele for the corresponding single marker, the states of the HAPI-UR HMM emit multiallele haplotype segments corresponding to the multiple markers that a window spans. Figure 1 shows the HMM states that PHASE¹² and HAPI-UR build for a set of three haplotypes. As Figure 1B shows, HAPI-UR builds states for each unique haplotype segment in each window. For the three haplotypes in the figure, HAPI-UR builds three states in the first window because all haplotype segments in that window are unique, but in the second window, HAPI-UR builds only two states because two of the haplotype segments in that window are identical. In contrast, PHASE builds one state for every haplotype at each marker, resulting in a total of 24 states compared to the five states that HAPI-UR builds (Figure 1A). Note that most methods other than PHASE produce fewer per-marker states than the total number of haplotypes available to the analysis,^1,2,10,11 so HAPI-UR is not unique in producing fewer states than the total number of haplotypes at each site.

Figure 1.

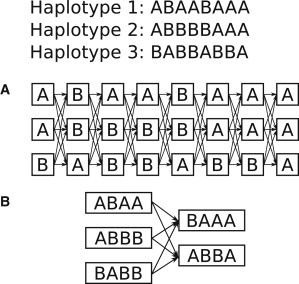
HAPI-UR Uses HMM States that Span Multiple Markers and Emit Haplotype Segments for Those Sites

Three example haplotypes and the HMM states that PHASE¹² and HAPI-UR generate. Boxes represent states, and the characters inside the boxes are the values that a state emits.

(A) PHASE and other statistical phasing algorithms build states corresponding to each marker and emit one allele corresponding to that site.

(B) HAPI-UR builds states that span multiple markers and emit a haplotype segment for those sites.

HAPI-UR employs several efficiency improvements that leverage its multimarker states. A by-product of the use of multimarker states is that HAPI-UR considers overall fewer states and only models state transitions at window boundaries rather than at each marker. Additional large efficiency gains come as HAPI-UR constructs individual-specific diploid HMMs that only contain states that are consistent with a given individual’s genotype. To efficiently construct these diploid HMMs, HAPI-UR stores an index of states and provides fast lookup of the haploid states that are consistent with a given genotype. HAPI-UR also makes use of a hash table to look up a specific haploid state that, for a given individual’s genotype, is complementary to another specific haploid state, enabling rapid formation of a complete diploid state consistent with a genotype.

HAPI-UR uses an iterative procedure that constructs a haploid HMM from the set of haplotypes for all individuals, randomly samples multiple haplotypes for each individual from the individual-specific diploid HMMs it builds, and then iterates by constructing a new haploid HMM based on these randomly sampled haplotypes.

This paper describes the approach that HAPI-UR uses to phase individuals; this approach includes emitting a multimarker haplotype from each state and utilizing a haploid-state index that enables state lookup on the basis of allelic values at each marker. The method SHAPEIT, which was published while this article was under review,²⁰ independently developed a phasing approach that, along with HAPI-UR, considers transitions among states only at window boundaries. IMPUTE2 (Howie et al.¹) constructs individual-specific HMMs that include the haplotypes that are most similar to the previous iteration’s estimated haplotypes for a sample, and HAPI-UR constructs individual-specific diploid HMMs conditional on an individual’s genotype. The local ancestry method HAPMIX described an optimized form of the Li and Stephens model²⁵ that contains an HMM state at each marker for all the unique haplotypes that occur in a given window around the marker. GERMLINE³ was the first to use hash tables to index haplotypes, and it uses this approach to efficiently detect IBD sharing among prephased haplotypes.

SHAPEIT has several similar properties to HAPI-UR but also differs from it in key respects. One difference is that it builds states at each marker and is therefore able to model mutations at each site, but this comes at a cost of computational overhead, and our results show that HAPI-UR is faster and more accurate than SHAPEIT for large data sets. SHAPEIT also constructs a fixed number of states at each marker, whereas HAPI-UR allows the number of states at a site to vary depending on the haplotype diversity and number of consistent haplotypes in a window. More specifically, SHAPEIT limits the number of possible haplotypes to be considered at any position on the basis of the number of heterozygous sites within a region in the individual; by default, it enumerates only eight possible haplotypes (corresponding to at most three heterozygous sites in a window) at any position. It is unclear how the choice of limiting the number of haplotypes in any position affects overall accuracy as sample size increases.

In the remainder of this section, we define the HMMs that HAPI-UR builds, describe our algorithm that phases individuals by iteratively constructing and sampling from individual-specific HMMs, provide details on the efficiency improvements that make HAPI-UR applicable to very large data sets, describe how HAPI-UR handles trios and duos as well as missing data, and discuss memory usage in HAPI-UR.

HMM Definition

To define the haploid HMM that HAPI-UR uses, we must specify the states it contains, the probabilities of the initial states, the emission probabilities, and the transition probabilities. Our algorithm constructs this HMM on the basis of a set of N complete haplotypes for a chromosome and generates a state for every unique haplotype segment that occurs in each window. To construct the HMM initially, we randomly assign phase to individuals at all heterozygous sites. The initial probability of a state in the first window is the frequency of the corresponding haplotype segment, so if s₁ is a state in the first window and N(s₁) is the number of occurrences of the corresponding haplotype segment, then the initial probability of s₁ is P(s₁) = N(s₁) / N. All states emit with probability 1 the unique haplotype segment to which they correspond; thus, HAPI-UR does not model genotyping errors or mutations because states that are inconsistent with a given individual’s genotype have an emission probability of 0. Note that Beagle also uses probability 0 for states that are inconsistent with a given individual’s genotype.¹⁰ We describe later how HAPI-UR leverages the fact that many states for a given sample have 0 probability in order to improve efficiency.

We define transition probabilities between states at adjacent windows by adapting the Li and Stephens model²⁵ by using a formulation related to an approximate Li and Stephens model implemented in HAPMIX.⁴ The transition probability between two states is defined as the sum of the probability of transitioning to the subsequent state without recombination and the probability of transitioning with recombination. The standard Li and Stephens model encodes a state at each marker for all N complete haplotypes, and a given state can only transition without recombination to the state at the next marker that models the same haplotype as the current state. In addition, the Li and Stephens model equally weights the probability (1/N) of recombining to any state because it uses exactly one complete haplotype to construct each state.

The HAPI-UR model produces states for every unique haplotype segment in a window, thus effectively merging a number of the original complete haplotypes into one state. Because one state models several original haplotypes, states can transition without recombination to one or more states at the subsequent window, and our model weights recombinations to a state by the frequency of the underlying haplotype segment.

Let N(s_w → s_w+1) denote the number of instances in which the haplotype segment corresponding to s_w at window w appears on the same original haplotype as the segment corresponding to s_w+1 at window w+1, and define N(s_w) and P(s_w) as above for states in the first window. The transition probability between s_w and s_w+1 is then

$$\mathrm{P}\left(s_w\to s_{w+1}\right)=\exp \left(\frac{-4N_e{g}_{w+1}}{N}\right)\frac{N\left(s_w\to s_{w+1}\right)}{N\left(s_w\right)}+\left(1\text{-}\exp \left(\frac{-4N_e{g}_{w+1}}{N}\right)\right)\mathrm{P}\left(s_{w+1}\right),$$

where N_e is the effective population size of the samples being phased and g_w+1 is the genetic distance between the centers of windows w and w+1. Here, the first term is the probability of not recombining multiplied by the frequency that state s_w occurs on the same haplotype as s_w+1, and the second term is the probability of recombining multiplied by the frequency of the haplotype segment underlying s_w+1.

Formation of a general diploid HMM based on the above haploid model is straightforward. The state space in each window is the cross product of the haploid states, and the initial probability of a diploid state is the product of the haploid probabilities, so for a diploid state in the first window (s_1a, s_1b), P((s_1a, s_1b)) = P(s_1a) P(s_1b). States emit with probability 1 an ordered pair containing the two haplotype segments underlying the haploid states. Transition probabilities are simply P((s_wa, s_wb) → (s_(w+1)a, s_(w+1)b)) = P(s_wa → s_(w+1)a) P(s_wb → s_(w+1)b). This is a generalized formulation of a diploid HMM, but HAPI-UR builds individual-specific diploid HMMs as we describe next.

Phasing Algorithm

To infer haplotypes, HAPI-UR first randomly initializes the phase of heterozygous sites in all individuals and then constructs haploid states from these random haplotypes as outlined above. Methods such as PHASE and MaCH construct a complete diploid HMM that applies to all individuals and genotypes and carry out computation on this general HMM. To improve efficiency, HAPI-UR constructs for each individual a diploid HMM conditioned on their genotype. The difference between these individual-specific diploid HMMs and a general diploid HMM is that the individual-specific HMMs omit diploid states that are inconsistent with the individual’s genotype because these have probability 0. Below, we describe the efficient computational techniques that we use to build these individual-specific diploid HMMs. Omitting states with probability 0 for an individual greatly improves the efficiency of our approach because many diploid states have probability 0 and would require construction and evaluation in a general diploid HMM. Beagle also uses 0 probability for states that are inconsistent with an individual’s genotype, and this improves its efficiency in a similar way to our approach in HAPI-UR.

During construction of each individual-specific HMM, we calculate the forward probabilities for all states—with standard HMM notation, these are the α_w((s_wa, s_wb)) values for all diploid states (s_wa, s_wb)—and then we randomly sample four haplotype pairs from the distribution implied by these probabilities and the HMM. The procedure for sampling from this distribution is conceptually simple, and the paper describing Beagle¹⁴ provides an explanation and example. In brief, we randomly sample a diploid state (s_wa, s_wb) at the last window with a probability proportional to α_w((s_wa, s_wb)). We then perform a recursive procedure that randomly samples from the previous window a state conditional on the chosen state in the current window.

After randomly sampling four haplotype pairs for all individuals, we iterate the procedure by constructing a new haploid HMM based on all sampled haplotypes. We then reconstruct individual-specific diploid HMMs and randomly sample haplotypes for each individual to complete an iteration. During the final iteration, rather than randomly sampling multiple haplotypes for all individuals, we use the maximum likelihood Viterbi decoding of each individual’s diploid HMM to provide the final haplotype solution.

Window sizes vary between iterations and start with a small window size of four markers in the first iteration and, in the last iteration, increase to the maximum window size that is specified as a parameter to execution. The algorithm performs two iterations for each window size and grows the windows by three markers after every two iterations. We experimented with other window-sizing strategies—including approaches that are inspired by the expected geometric distribution of length of IBD sharing—by using many small window sizes separated by only one marker initially and by using larger gaps between sizes as the windows grew larger. We empirically found that growth by three markers after two iterations achieves accuracy in line with these alternate approaches (data not shown) and can also be easily generalized to any maximum window size. We also experimented with a slower version of the algorithm by performing three or more iterations for every window size and increasing the window size by one marker after every set of iterations. We found that running HAPI-UR at least three times (with window sizes separated by three markers) and using consensus phase from among these runs produced more accurate results with a faster runtime than did running HAPI-UR once with window-size increases of one marker after multiple iterations.

Choosing the maximum window size depends on the marker density of a data set; we experimented with a range of window sizes for the data sets described in the Results, and we list suggested window sizes for the marker densities of these data sets in Table 1. For data sets with marker densities different than those listed, we advise a linear increase or decrease in maximum window size. Our experiments show that data sets with larger numbers of individuals benefit from increasing the maximum window size, so this table is a guideline, and we recommend increasing the maximum window size by small number of markers for larger data sets for improving accuracy.

Table 1.

Maximum Window Sizes Used for the Data Sets Evaluated in the Results

Data Set	Autosomal-Marker Density	Maximum Window Size
WTCCC1 + HapMap	386,353	64
CHOP	516,972	73
WTCCC2 + HapMap	755,008	90

For data sets with different marker densities, we suggest a linear increase or decrease in the maximum window size.

Because we use repeated iterations of the same window size in succession during phasing, we randomly vary the size of the first window on a chromosome to be between one marker long and the full window size used in the current iteration. For example, for an iteration with a window size of ten markers, the algorithm randomly chooses a size between one and ten markers long for the first window. To ensure a good mix of the locations of window boundaries, we add a constraint that prevents this first window from being close in size to the size of the first window in the previous iteration. Specifically, for an iteration with window size W, if the previous iteration’s first window size was l_p, we exclude the range [l_p – W/5, l_p + W/5] for the size of the first window in the current iteration. Randomizing the size of the first window and ensuring that this window is not close to the same size as in the previous iteration prevent the haplotypes from being too dependent on the locations of the window boundaries. Without this feature, switch errors might correlate with where window boundaries happen to fall on the chromosome.

Efficiency Improvements

Because diploid states that are inconsistent with an individual’s genotype have a probability of 0, HAPI-UR uses an approach that avoids spending compute time considering these states and instead builds individual-specific diploid HMMs by only constructing diploid states that are consistent with an individual’s genotype. To efficiently identify the set of states that are consistent with a genotyped individual, we construct an index of all haploid states. This index stores for each allele at each marker the set of haploid states that contain the indicated allele, as illustrated in Figure 2.

Figure 2.

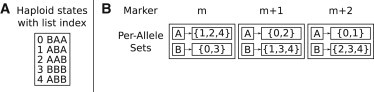
Index that Stores the Set of Haploid States that Have a Given Allele at a Given Marker

An example index for five haploid states that span a window of three markers numbered m through m+2.

(A) List of the five haploid states and list indexes for each state.

(B) The per-marker, per-allele index that stores the set of haploid states that have a given allele at a given marker. To identify the set of haploid states that are consistent with a genotype, HAPI-UR intersects the sets for alleles that are homozygous. In this example, a genotype that is homozygous for allele A at marker m and allele B at marker m+2 produces an intersected set of {2,4} and is therefore only consistent with these haploid states.

Figure 2A gives a list of five haplotypes that are each three markers long and that each correspond to a haploid state. To index these states, HAPI-UR constructs a set for every allele at every marker; for the haplotypes in this figure, each marker has two alleles, A and B. Figure 2B shows the sets that provide an index of these haploid states. There are three haploid states that contain an A allele at the first marker m—those with indexes 1, 2, and 4 in the state list—and the set for the A allele at marker m is thus {1,2,4}. The set for the B allele at marker m contains the states with this allele, i.e., the complement of the set with the A allele, and is thus {0,3}. The sets at markers m+1 and m+2 have the same properties as those at marker m, and the method constructs those sets on the basis of which haploid states contain the indicated alleles.

Our algorithm uses this index by leveraging the fact that a haploid state must contain the alleles at all homozygous markers in a window in order to be consistent with an individual’s genotype. Thus, for a given individual’s genotype, the method identifies all homozygous sites in a window and intersects the sets of states containing the homozygous alleles at those sites. As seen in the example in Figure 2, if an individual is homozygous for the A allele at marker m and homozygous for the B allele at marker m+2, the method intersects the sets {1,2,4} and {2,3,4} and obtains the set {2,4}, indicating that this individual is only consistent with those two haploid states. After this intersection procedure, we obtain a set containing all the haploid states that are consistent with the individual’s genotype.

To enable efficient set intersection operations with minimal space requirements, we use bit fields to store the sets of states that contain a given allele at a marker. Each bit maps to a particular haploid state, and the bit number (0 for the first bit, 1 for the second bit, 2 for the third bit, etc.) is the index in the corresponding list of haploid states. A bit value of 1 indicates that the corresponding state contains the allele that the set was built for, and with the use of bit-field encoding, computing set intersection is very efficient with the bit-wise AND operator. As an example, a bit field with value 00101 represents the set {2,4}.

Besides this per-marker, per-allele index of states, we store a hash table³ containing all haploid states in each window, enabling fast lookup of the complementary haplotype for a given haploid state and the subsequent formation of a consistent diploid state. Given the set of haploid states consistent with an individual’s genotype in a window, it is straightforward to deduce the complementary haplotype segment for each state on the basis of the individual’s genotype and to perform a hash-table lookup of this haplotype segment. Our implementation currently assumes that markers are biallelic and deduces the complementary haplotype segment by inverting the allele values at all heterozygous sites in the haplotype segment for the known haploid state. A more general alternative that does not require markers to be biallelic is to store genotypes as allele counts and subtract the known haplotype segment’s allele counts.

Combining our per-marker, per-allele index sets with a hash-table lookup for locating complementary states provides large efficiency gains key to HAPI-UR’s runtime performance. An alternative to using index sets for identifying consistent states is to perform a linear search over all haploid states. This approach scales poorly as window sizes increase because the number of haplotype segments in a window grows with the window’s size. In contrast, because we must perform set intersection at all homozygous markers regardless of window size, this part of the method runs in roughly constant time independent of window size; there is only a slight overhead for the intersection operation as the bit fields increase in size with the number of haploid states in a window. In addition, because the number of haploid states in a window grows with the sample size being phased, a linear search over all haploid states will slow as the sample size grows. In contrast, our index lookup continues to have roughly constant runtime regardless of sample size—larger bit fields again produce only minimal slowdown.

Trio and Duo Phasing

HAPI-UR can phase trio and duo family data, in addition to unrelated individuals. At sites where at least one member of a trio or duo is homozygous, Mendel’s first law implies which allele each parent transmitted to the child, and, ignoring a small number of recombination events, the phase of all the individuals is unambiguous across these sites. To handle trios, HAPI-UR first deduces the phase of each trio family member at unambiguous sites, and it imposes constraints on the parents’ phase so that the haplotypes it infers are consistent with this unambiguous trio phase and the child’s genotype. To enforce these constraints, HAPI-UR phases both parents simultaneously by constructing specialized states composed of two standard diploid states—one for each parent—and it ensures that the haplotypes in these states respect all constraints. As in other trio phasing methods, our approach does not directly phase trio children because the child’s two phased haplotypes are exactly those that contain the alleles that each parent unambiguously transmitted to the child. Our approach uses the per-marker, per-allele index to lookup haploid states that contain all alleles (including the homozygous alleles) that one parent (e.g., the father) unambiguously transmitted to the child. Given a set of haploid states that contain all unambiguously transmitted alleles for one parent, HAPI-UR next deduces for the other parent, for each of these states, the transmitted haplotype that is consistent with the child’s genotype. Next, it deduces complementary haplotypes for both parents on the basis of these two putatively transmitted haplotypes, and these four haplotypes form one specialized trio state. The probability of a specialized state is the product of the probability of their composite diploid states. HAPI-UR decodes the HMMs formed of specialized states in a fashion analogous to that of decoding its diploid HMMs, and it assigns phase to both parents on the basis of these specialized states.

Phasing duos is similar to phasing trios; duo specialized states contain two diploid states corresponding to haplotypes in the parent and the child, and these haplotypes respect the parent-child phase implied by Mendel’s first law. Because duos contain two copies of the same haplotype, HAPI-UR only incorporates one copy of the shared haplotype when constructing the haploid HMM at the start of each iteration.

Missing Data

HAPI-UR infers haplotypes at sites that are missing data—thereby imputing alleles at these sites—and it handles missing data during construction of both the haploid HMM and the individual-specific diploid HMMs. As outlined above, HAPI-UR uses the haplotypes unaltered from the previous iteration to construct the haploid HMM in windows where an individual has no missing data, and it adds a count of 1 to the N(s_w) value for the corresponding states s_w. If n is the number of sites where an individual is missing data in a given window, when 1 ≤ n ≤ 4, the algorithm only uses the previous inferred haplotype values at sites where the individual is not missing data. In these windows, the algorithm considers all possible allelic values at missing data sites; for biallelic markers, there are a total of 2ⁿ possible haploid states, and the method adds a value of 1/2ⁿ to N(s_w) for each such state s_w. This approach avoids dependence on the allelic values inferred at a missing data site in any iteration and equally weights all possible haplotypes at missing data sites. When n > 4, the method is the same as when n = 0 and reverts to using the alleles unaltered from the previous iteration, including at missing data sites, and adds a count of 1 to the N(s_w) value for the corresponding states s_w.

During the construction of individual-specific diploid HMMs, HAPI-UR builds diploid states by identifying for each haploid state the complimentary haplotypes that are consistent with the individual’s genotype. At sites that are missing data, there are multiple complementary haplotypes for a given haploid state. Again, if n is the number of sites where an individual is missing data in a window, for biallelic markers there are 2ⁿ complementary haplotypes for each consistent haploid state. If 1 ≤ n ≤ 3, HAPI-UR constructs all possible diploid states that are consistent with the individual’s genotype; the limit of n = 3 keeps the computational burden low for individuals or windows with extensive missing data.

When n > 3, HAPI-UR constructs a limited number of diploid states that are consistent with the individual’s genotype in the given window. The number of diploid states that HAPI-UR builds is bounded by a fixed proportion p multiplied by the total number of all haploid states in the window N_w (note that this is a proportion of all haploid states and not of the haploid states consistent with the individual’s genotype). The method builds diploid states in succession and starts by finding the haploid state s^∗ that has the highest frequency in the window and is consistent with the individual’s nonmissing genotypes. HAPI-UR next identifies the haploid state that has the highest frequency and that is complementary to s^∗ and constructs a diploid state for this pair. The algorithm proceeds by considering the most frequent haploid states in succession and finding the most frequent complementary state for each until it has built pN_w states or has constructed all possible consistent diploid states. To avoid constructing the same diploid state twice—given that HAPI-UR might have already built a state for a given pair—the method stores the diploid states it builds in a hash table and checks this table before diploid-state construction. Note that this approach will build many of the most likely diploid states, but it might miss the optimal, highest-likelihood states for two reasons. First, if a pair of moderately frequent states has an overall greater frequency than the highest frequency states and their highest frequency complements, the approach might miss these moderately frequent states. Second, this approach does not consider linkage across windows but only considers haplotype frequencies in the current window and thus might not find the diploid states that have the highest likelihood when accounting for linkage. Despite these limitations, this approach is likely to be effective for the small number of windows in which an individual has large amounts of missing data, and it should often provide diploid states that have high overall likelihood relative to that of any states that are omitted.

In order to efficiently identify states with the highest frequency in a window, before constructing the haploid HMM, the algorithm sorts all haploid states in each window by their frequency. This sorting places the highest frequency state first in the haploid-state list that accompanies the per-marker, per-allele index (see Figure 2).

The proportion p of states that HAPI-UR constructs when a window contains many missing data sites varies depending on the size of the window in the current iteration. We fixed p empirically as 1.5× the proportion of all haploid states contained in an individual-specific diploid HMM, averaged across individuals and windows, when HAPI-UR phased the WTCCC1 + HapMap data set described in the Results.

Memory Usage

For data sets with many samples, the largest memory requirements are for storing the haploid HMM, including its states and the transition probabilities between states. The number of haploid states in a window, regardless of window size, is bounded by N, the total number of haplotypes in the window. Let M be the number of markers on a chromosome and W be the window size in a given iteration. If HAPI-UR were to store transition probabilities from each state to all states in the subsequent window, its storage bound would be O(M/W·N²) in any iteration. Although our approach does have this theoretical bound, we use a sparser storage scheme for transition probabilities. Transition probabilities P(s_w → s_w+1) consist of one term for nonrecombinant transitions and a term for recombinant transitions, and our implementation only stores the probability of transitioning to a subsequent state s_w+1 if s_w has a non-zero term for transition to s_w+1 without recombination. Recombinant transitions to a given state s_w+1 have the same probability regardless of the starting state s_w, so it is not necessary to store information in every starting state related to subsequent states s_w+1 that can only be reached by recombination. Instead, our implementation only stores P(s_w → s_w+1) for states s_w+1 that s_w can reach without recombining. In practice, the total number of states reachable from any s_w without recombination is much less than N, and the total number of states in a window is also much less than N, so the actual memory usage is much less than the bound of O(M/W·N²).

The per-marker, per-allele index stores bit fields such that there is one bit for every haploid state in a window at every marker and for all alleles at a marker. If A is the maximum number of alleles at any marker (for biallelic markers, A = 2), the bound on memory required for storing this index is O(A·M·N) bits, but note that the number of haploid states will tend to be much smaller than N.

Besides storing all haploid states and the index of states, HAPI-UR stores a hash table to lookup haploid states by haplotype sequence, a haploid-state list that accompanies the index of states, and individual-specific diploid HMMs. The hash table containing haploid states and the list of haploid states each require space bounded by O(N). Individual-specific diploid HMMs exist only transiently while the method infers phase for a given individual, and they have an upper bound on memory use of O(M/W·N²). In practice, the number of diploid states that are consistent with an individual is much less than N², and the individual-specific diploid HMMs utilize a small amount of the total memory that HAPI-UR uses. A final memory requirement is storage of genotypes and haplotypes for each individual, and HAPI-UR stores these values by using bit fields, which have low space requirements and to which very efficient bitwise operations apply.

Results

This section describes experimental results from running HAPI-UR on three data sets and includes an analysis of phasing multiethnic groups of individuals. First, we show that HAPI-UR has a comparable or lower switch-error rate than do several existing phasing methods while also being more than an order of magnitude faster. For this comparison, we run each method on a data set containing more than 16,000 samples and run HAPI-UR and Beagle on another data set with a higher marker density and more than 5,000 samples. Second, we use HAPI-UR to phase a data set containing over 58,000 samples, and we inspect how the ethnicity of the individuals being phased affects accuracy; we show that the switch-error rate decreases with sample size even when we include diverse ethnicities. Finally, we consider the runtime scaling of HAPI-UR and other methods and examine their applicability to data sets with at least 100,000 samples.

Each data set that we analyze includes trio parents without their children, and we use separately inferred trio-phased haplotypes for these parents to identify switch errors. We consider the trio-phased haplotypes to be correct only at sites that have unambiguous trio phase, i.e., sites with at least one homozygous individual in the trio, and we omit other ambiguous sites from switch-rate calculations.

We report computational runtimes from 2.66 GHz Intel Core2 vPro machines that are not part of a compute cluster and are therefore not susceptible to timing bias due to the sharing of resources with other jobs. We report central-proccessing-unit (CPU) time rather than wall-clock time to avoid biases due to input/output overhead or interfering background processes. These computers have multicore processors, but we ran all programs single threaded (only SHAPEIT supports multithreading) and only executed one process at a time on any machine in order to prevent competition between runs.

Accuracy and Efficiency Comparisons to Existing Methods

We compared the switch-error rate and runtime of HAPI-UR to those of existing methods by using 17,000 samples from the WTCCC.²¹ We removed 735 samples that the WTCCC reported as having 3% or more missing data, as showing discordance with external genotyping, as having evidence of non-European ancestry, or as being duplicated. We retained 86 samples that the WTCCC detected as first- and second-degree relatives because most large studies will include some related individuals. We merged the resulting 16,265 WTCCC samples with 88 HapMap CEU (Utah residents with ancestry from northern and western Europe from the CEPH collection) samples²² that are unrelated parents in a set of 44 trios, but we did not include the offspring of these trios in the data set; we report the switch-error rate for these 88 samples. We removed 30,956 SNPs that the WTCCC filtered for quality control, and merged the WTCCC samples with HapMap data that were separately filtered for quality control;²² after merging, this data set contained 386,353 SNPs.

To thoroughly evaluate HAPI-UR in comparison to other methods, we examined the entire 16,353 sample WTCCC1 + HapMap data set, as well as subsets consisting of 5,000, 3,000, and 1,000 samples. These subsets included the 88 HapMap CEU samples and randomly chosen subsets of 4,912, 2,912, and 912 samples out of the total 16,265 WTCCC samples.

We ran Beagle 3.3.1, IMPUTE2 2.1.2, SHAPEIT 1.r415, MaCH 1.0.17, and HAPI-UR on the four sizes of WTCCC1 + HapMap data sets on chromosomes 19–22. The documentation for MaCH recommends running 50 rounds of phasing with 200 states, and we used these settings. We also used the recommended settings for IMPUTE2 by phasing the chromosomes in 5 Mb regions with a 500 kb overlap between adjacent regions and by using 80 states, 10 burn-in iterations, and 20 additional (30 total) iterations; the effective population size was set to 11,500. SHAPEIT has default parameters of 100 states, 10 burn-in iterations, 10 pruning iterations, and 50 main iterations and an effective population size of 15,000, and we used these default values in our tests. We ran HAPI-UR with a maximum window size of 64 markers and an effective population size of 10,000.

To obtain complete haplotypes from IMPUTE2, we combined the haplotypes from adjacent regions by using from each sample the heterozygous site that is closest to the center of the overlapping region to determine the relative phase between the regions. In our data set, chromosome 19 contains a large ∼5 Mb gap that contains no markers, and we merged the haplotypes on either side of the gap by using an arbitrary phase. This procedure might introduce a small number of switch errors across this gap, but these will impact the overall error rate only modestly; in the worst case of 88 switch errors, the total switch error across the four chromosomes we examined will increase by 0.017%.

Phasing of the full 16,353 sample data set on chromosome 20 for MaCH did not complete, so we calculated for this chromosome a switch-error rate relative to the rate for the 5,000 sample data set by using the same proportion as the average change on chromosomes 19, 21, and 22. Thus, the switch-error rate reported for MaCH is a normalized form of the rate for all chromosomes except for 20.

Figure 3A shows the switch-error rates of all methods for chromosomes 19–22 on the differently sized WTCCC1 + HapMap data sets; this plot is similar to one that Browning and Browning¹⁴ reported for chromosome 20 but is for a larger data set and also includes HAPI-UR and SHAPEIT. For the data set with 1,000 samples, SHAPEIT achieves the lowest switch-error rate, but this accuracy comes at a cost because SHAPEIT also has the second greatest runtime of all methods we considered (see below). For larger sample sizes, the switch-error rates of both SHAPEIT and MaCH stay roughly constant, whereas the error rates of other methods decrease; we consider the accuracy of each method as a function of sample size later in the Discussion.

Figure 3.

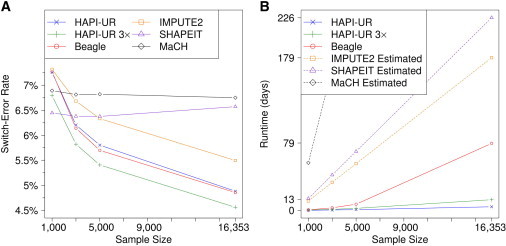
Switch-Error Rate and Runtime of HAPI-UR, HAPI-UR 3×, Beagle, IMPUTE2, SHAPEIT, and MaCH on the WTCCC1 + HapMap Data Set

(A) Switch-error rate on chromosomes 19–22 for 88 HapMap CEU trio parents from data sets containing 1,000, 3,000, 5,000, and 16,353 samples. The switch-error rates of HAPI-UR, HAPI-UR 3×, Beagle, and IMPUTE2 decrease with sample size, whereas the error rates of SHAPEIT and MaCH stay roughly constant with sample size. For 1,000 samples, SHAPEIT produces the most accurate phase. HAPI-UR has a similar but slightly higher switch-error rate than Beagle does, whereas HAPI-UR 3×, which computes phase by consensus on the basis of the output of running HAPI-UR three times, has a lower switch-error rate than Beagle does and is the most accurate method for the data sets with 3,000, 5,000, and 16,353 samples.

(B) Runtimes for HAPI-UR, HAPI-UR 3×, and Beagle and estimated runtimes for MaCH, IMPUTE2, and SHAPEIT for phasing all chromosomes on data sets with 1,000, 3,000, 5,000, and 16,353 samples. For the data set with 16,353 samples, HAPI-UR is 18.9× faster than Beagle, whereas running HAPI-UR 3× serially is 6.31× faster. Using the runtime for phasing 1,000 samples in IMPUTE2, SHAPEIT, and MaCH, we conservatively estimated total runtime by assuming linear scaling in both number of markers and number of samples for each method. Although both Beagle and HAPI-UR have superlinear scaling, our estimated runtime for HAPI-UR to phase 100,000 samples is lower than those estimated for IMPUTE2, SHAPEIT, and MaCH, and HAPI-UR will have much lower switch-error rate than any of these methods when they are run with their recommended number of states.

HAPI-UR and Beagle both have comparable and low switch-error rates for the data sets with 3,000, 5,000 and 16,353 samples, but HAPI-UR has a slightly higher switch-error rate than Beagle does on these data sets. To reduce switch-error rate further, we leveraged the randomized nature of HAPI-UR by running it three times and by performing consensus voting among the three results to decide the phase between successive pairs of heterozygous sites. We plot the results for this method in Figure 3 as “HAPI-UR 3×.” This approach achieves lower error and is also more than six times faster than all other methods (see below). Using consensus phasing based on multiple phasing runs also benefits other methods,^11,14 including Beagle. Note that each run of Beagle is slower than HAPI-UR, so for the same computational overhead, it is possible to execute a larger number of runs of HAPI-UR and perform consensus phasing among all these results. The switch error of IMPUTE2, SHAPEIT, and MaCH would also decrease if one ran them by using a larger number of states;¹⁴ however, increasing the number of states in these methods would also increase their computational burden. In general, an appropriate tradeoff between runtime and accuracy is necessary for phasing sizeable data sets (see Discussion).

We ran HAPI-UR, HAPI-UR 3×, and Beagle on all chromosomes for each of the data set sizes and obtained switch-error results that are consistent with those shown for chromosomes 19–22 in Figure 3A. For the full 16,353 sample data set, the switch error of Beagle is 3.08%, whereas HAPI-UR and HAPI-UR 3× obtain switch-error rates of 3.14% and 2.93%, respectively. Thus, for this WTCCC1 + HapMap data set, when 3,000 or more samples are phased and when each program is run with its recommended settings, HAPI-UR 3× provides low switch error and HAPI-UR provides a switch-error rate that is only slightly higher than that of Beagle.

We examined the runtimes on our noncluster computers for applying MaCH and IMPUTE2 to phase 1,000 WTCCC1 + HapMap samples on chromosomes 19–22, and we estimated their runtimes for all chromosomes from these values by assuming that their runtimes scale linearly in the number of markers; this scaling matches the scaling we observed on the four chromosomes. We further estimated the runtime of these methods for larger data sets by assuming that their runtimes scale linearly in the number of samples. We verified that runtime scales linearly for MaCH by running chromosome 20 with 3,000 samples. We also ran IMPUTE2 on chromosomes 19 and 22 with 3,000 samples and observed that it runs 3.98× and 3.55× slower for chromosomes 19 and 22, respectively, than it does with 1,000 samples for the same chromosomes; despite these results, we conservatively estimated IMPUTE2’s runtime as scaling linearly in sample size.

To estimate the runtime of SHAPEIT on the full WTCCC1 + HapMap data, we used it to phase 1,000 samples and 3,000 samples on chromosomes 19–22. We found that its runtime across chromosomes is not exactly linear in the number of markers on a chromosome; instead, we observed differing per-marker runtimes for phasing 1,000 samples on chromosomes 19–22. The average per-marker runtimes were 3.60 s, 3.10 s, 3.08 s, and 3.26 s for chromosomes 19, 20, 21, and 22, respectively. In order to provide an overall runtime estimate for the full data set, we assumed that the runtime per marker for phasing 1,000 WTCCC1 + HapMap samples with SHAPEIT on chromosomes 1–18 would be 3.08 s. SHAPEIT also showed slightly greater than linear scaling in runtime with sample size; phasing of 3,000 samples on chromosomes 19, 20, 21, and 22 ran, respectively, 3.36×, 3.27×, 3.28×, and 3.34× slower than did phasing of 1,000 samples for the same chromosomes. To provide a conservative estimate, we again assume that the runtime of SHAPEIT scales linearly in sample size. Note that because SHAPEIT constructs states with variable window boundaries that depend on the heterozygous sites of an individual, in practice it probably does not scale linearly in either number of markers or sample size, and our timing results are consistent with this.

We examined the runtime of HAPI-UR and Beagle on the four different-sized WTCCC1 + HapMap data sets and found that for the full data set, the total runtime across all chromosomes for HAPI-UR is 18.9× faster than that for Beagle and that HAPI-UR has a runtime on chromosome 1 of 8.36 hr compared to 151 hr (6.30 days) for Beagle. HAPI-UR 3× is fully parallelizable to three nodes, but when it is run sequentially, its runtime is 6.31× faster than Beagle’s runtime. Memory overhead is minimal for both HAPI-UR and Beagle: HAPI-UR requires less than 3.2 GB to phase the largest chromosome on the full data set, and Beagle requires less than roughly 4 GB.

Figure 3B plots the runtimes of HAPI-UR, HAPI-UR 3×, and Beagle and the estimated runtimes of IMPUTE2, SHAPEIT, and MaCH for all WTCCC1 + HapMap data set sizes we have examined. The estimated runtimes for MaCH to phase 3,000, 5,000, and 16,353 samples are, respectively, 167 days, 279 days, and 912 days, and we did not include these points in Figure 3B. Both HAPI-UR and HAPI-UR 3× show considerably lower runtimes than the other methods do; Beagle is the closest method to HAPI-UR in terms of runtime but is more than an order of magnitude slower than HAPI-UR for the full WTCCC1 + HapMap data set.

The results above examined a data set with a smaller marker density than that provided by most current genotype platforms. To explore HAPI-UR’s accuracy and runtime performance further, we obtained the WTCCC2 control samples,²⁴ which include 5,667 individuals, and analyzed the Illumina 1.2M genotypes for these samples. We removed all individuals that the WTCCC flagged for quality control (for aberrant missing data or heterozygosity rates and non-European ancestry, etc.) except for those reported as being related or with gender mismatches, and we separately detected and removed 11 sample duplicates. We also removed 227,160 SNPs that failed the WTCCC quality-control checks. We merged these samples with the same 88 HapMap CEU trio parents as in the WTCCC1 + HapMap data set, resulting in a final merged data set of 5,342 samples with 755,008 SNPs.

We ran Beagle, HAPI-UR, and HAPI-UR 3× on this WTCCC2 + HapMap data set; we ran HAPI-UR with a maximum window size of 90 markers and an effective population size of 10,000. The overall switch-error rate of Beagle on this data set is 1.86%, whereas HAPI-UR and HAPI-UR 3× obtain switch-error rates of 1.93% and 1.84%, respectively. Thus, HAPI-UR and HAPI-UR 3× again achieve comparable error rates to Beagle, and HAPI-UR has a slightly higher switch-error rate. (Note that it is incorrect to compare these switch-error rates with those from WTCCC1 + HapMap because higher marker densities produce lower switch-error rates¹⁴).

This WTCCC2 + HapMap data set has only 5,342 samples and shows speed gains that are similar to those of the 5,000 sample WTCCC1 + HapMap data set. HAPI-UR runs 9.79× faster than Beagle on this WTCCC2 + HapMap data set; this speed is slightly better than the speed gains of HAPI-UR on the 5,000 sample WTCCC1 + HapMap data set (9.28× faster than Beagle). These timing- and phase-accuracy results on the WTCCC2 + HapMap data set show that, for this data set (which has roughly double the marker density of WTCCC1 + HapMap), HAPI-UR remains extremely fast while also achieving accuracy that is comparable to that of other methods.

Phasing of Large, Multiethnic Data Sets

We ran HAPI-UR on a collection of 58,207 samples genotyped on the Illumina Infinium platform by the Center for Applied Genomics at CHOP.^26–29 These 58,207 samples remained after we removed sample duplicates and close relatives that showed identity by state (IBS) sharing totaling at least 1,200 cM (of a total 3,522 cM on autosomes) contained in stretches of IBS longer than 3 cM. We removed 3,456 SNPs with 5% or more missing data, resulting in a final data set containing 516,972 SNPs. The samples include population identifiers of European American, African American, Latino, or East Asian ancestry. We performed principal-component analysis³⁰ in ten separate batches to identify individuals with mislabeled populations. For the phasing runs in which we specifically analyzed European American and/or African American samples, we excluded samples that did not cluster with the European Americans or that were not on the gradient of African American ancestry. After filtering, the data contain 37,925 European American samples and 10,003 African American samples. This data set includes a total of 1,194 European American parents from 597 trios and 88 African American parents from 44 trios, and we report switch-error rates for these samples.

To inspect switch-error rates in data sets with varying sample size, ethnicity, and relative proportions of ethnic groups, we ran HAPI-UR with a maximum window size of 73 markers and an effective population size of 10,000 on all chromosomes for ten different subsets of the CHOP data set. We compared switch-error rates among the collections of phased samples, which were: (1) the full 58,207 sample CHOP data set, (2) all 37,925 European American and all 10,003 African Americans, (3) a random subset of 20,000 European Americans and all African Americans, (4) a further random subset from (3) of 10,000 European Americans and all African Americans, (5) a random subset from (4) of 5,000 European Americans and 5,000 African Americans, (6) all European American samples alone, (7) the same 20,000 European Americans as in (3) phased alone, (8) the same 10,000 European Americans as in (4) phased alone, (9) the same 5,000 European Americans as in (5) phased alone, (10) all African Americans alone, and (11) the same 5,000 African Americans as in (5) phased alone.

Figure 4A plots the switch-error rates for all chromosomes of the CHOP data set. We show switch-error rates for both European American (plotted as “European”) and African American (plotted as “African”) samples phased alone or combined with either the indicated numbers of African American or European American samples or the entire data set. The x axis lists the sample size of the combined data set and the number of African American and European American individuals included in the combined data set. We plot the switch-error rate for phasing the individual ethnic groups alone at the same x value as the larger combined data set to enable direct comparison of switch error for phasing a given ethnic group alone versus combined with multiple ethnicities.

Figure 4.

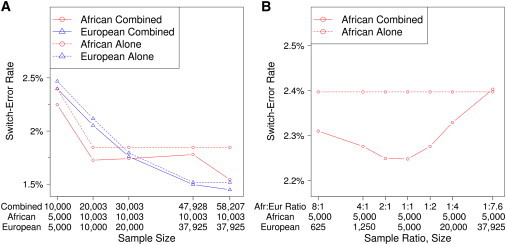
Switch-Error Rate for HAPI-UR Phasing on Several Subsets of the CHOP Data Set, Stratified by Ethnic Group and Sample Size

(A) Switch-error rate for 88 African American trio parents either phased combined with other ethnicities (“African Combined”) or alone (“African Alone”) and for 597 European American trio parents phased with other ethnicities (“European Combined”) or alone (“European Alone”). Switch-error rate decreases with sample size and also decreases when we include samples from multiple ethnicities in the phasing run. The full 58,207 data set contains African Americans and European Americans along with Latinos and East Asians, and the switch-error rate is lowest for both African Americans and European Americans with the use of this full data set.

(B) Switch-error rate for 88 African American trio parents in a data set of 5,000 African Americans phased either combined with differing proportions of European Americans (“African Combined”) or alone (“African Alone”). When the number of European American samples is equal to or less than the number of African American samples, the switch-error rate of the African Americans decreases relative to phasing alone. As the number of European American samples grows larger relative to the number of African Americans, the switch-error rate increases. When the ratio of African American to European American samples is 1:2 or 1:4, the switch-error rate remains lower for combined phasing than for phasing alone. For a ratio of 1:7.6 African Americans to European Americans, the switch-error rate of combined phasing is higher than for phasing alone.

The switch-error rate for European Americans always decreases with sample size when we phase these samples either alone or combined with African Americans or the full multiethnic data set. Switch error decreases for phasing larger numbers of European samples alone, but including additional samples from other ethnicities provides lower error than phasing alone.

When African Americans are phased alone, the switch-error rate again decreases with sample size, but because some data sets include proportionally more European Americans than African Americans, the switch-error profile for multiethnic phasing of African Americans is more complicated. The combined data sets containing 10,000 and 20,003 samples have equal proportions of European American and African American samples (5,000 and ∼10,000, respectively), and the switch-error rate of the African Americans decreases relative to that of phasing African Americans alone in both these cases. The data sets containing 30,003 and 47,928 samples both contain only 10,003 African Americans, and as the plot shows, the switch error of the African Americans phased in these data sets increases relative to that of the combined data set with 20,003 samples. Note that even when all the European American samples are phased with the African Americans, where the ratio of European American haplotypes to African American haplotypes is nearly 4 to 1, the switch-error rate for the African Americans remains lower (1.78%) than that for phasing these samples alone (1.85%). The switch-error rate of the African Americans is lowest (1.54%) when we phase the complete data set that includes Latinos and East Asians, and uneven ratios of ethnic groups might be less important when more than two populations are phased together.

To further explore the relationship between switch error and the ratio of sample ethnic groups, we phased 5,000 African Americans combined with different numbers of European American samples, and we show the switch-error rates in Figure 4B. The switch-error rate of the African Americans decreases considerably when we include even a relatively small number of European American samples. The lowest switch-error rates occur when the ratio of African American to European American samples is between 2:1 and 1:1, and the error rate is slightly lower for the ratio of 1:1. The switch-error rate for African Americans increases when the sample ratio is biased toward including more European American samples than African Americans but remains lower than phasing alone for ratios of 1:2 and 1:4. The largest sample ratio biased toward European Americans is 1:7.6, and in this extreme case, the switch-error rate of the combined phasing is higher than that of phasing the African American samples alone. These results suggest that, depending on the applications of the resulting haplotypes, it is typically best to phase all individuals together unless there is extreme bias in the ratios of ethnic groups. Alternatively, if one wishes to minimize the switch-error rate for only a single ethnic group rather than for an entire multiethnic collection of samples, including equal or lower numbers of samples from other ethnic groups will yield the lowest switch error for the group of interest.

Phasing of the entire CHOP data set required relatively modest compute resources despite its extremely large size. Chromosomes 1 and 2 had the highest memory requirements of 20.2 GB each. To inspect runtime across a range of sample sizes, we phased chromosome 22 on our noncluster computers, and we show the runtimes in Figure 5. Runtime increases with sample size and is again modest; phasing of the full data set on chromosome 22 completed in 26 hr (1.1 days). To determine runtime of larger chromosomes, we phased the data set with 5,000 African Americans on chromosome 1 and estimated the runtime for phasing all 58,207 samples on chromosome 1 to be 5.57 days. This estimate assumes that the time ratio required for phasing chromosome 1 compared to chromosome 22 for 5,000 African Americans is the same when the full data set is phased. We found that in the WTCCC1 + HapMap data set, estimating the runtime on the full 16,353 sample data set with the use of the runtime for 3,000 samples in this way overestimated the true runtime for the full data set by nearly 6%, and our estimated runtime for chromosome 1 is thus likely to be accurate or slightly conservative.

Figure 5.

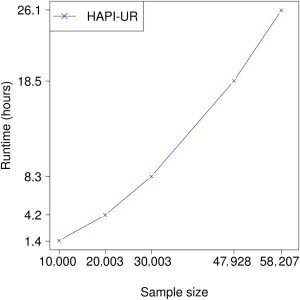
Runtime for Phasing Chromosome 22 on Various Subsets of the CHOP Data Set with HAPI-UR

Runtime increases with sample size and is tractable for the full 58,207 sample data set at 26 hr. We estimate the runtime for phasing chromosome 1 on the full data set to be 5.57 days.

Runtime Scaling with Sample Size

An important factor in evaluating algorithms that target large data sets is how quickly their runtime increases with sample size. An algorithm can be very fast for small sample sizes but scale poorly to larger data sets and be slower than some other algorithm with better scaling properties. Figure 6 compares the runtime scaling of Beagle to that of HAPI-UR and shows that Beagle runs 156× slower for 16,353 samples than for 1,000 samples. In contrast, HAPI-UR runs 48.1× slower for phasing 16,353 samples than for 1,000 samples. Thus, as sample sizes grow, the speed gains in HAPI-UR will become even larger than those in Beagle, making HAPI-UR especially practical for large data sets.

Figure 6.

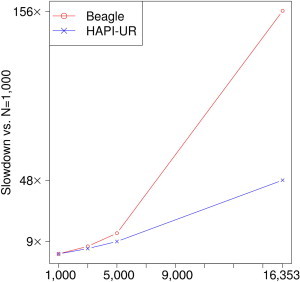
Runtime of Beagle and HAPI-UR for 3,000, 5,000, and 16,353 Samples Increases Relative to that for 1,000 Samples

Both Beagle and HAPI-UR scale superlinearly but subquadratically, and the precise scaling factors of both programs depend on the haplotype diversity of the data set being analyzed. The slowdown for analyzing 16,353 samples compared to 1,000 samples is 156× for Beagle and 48.1× for HAPI-UR.

The exact runtime scaling of HAPI-UR is not easily determined and depends on the haplotype structure and diversity of the data set. The empirically observed scaling for the WTCCC1 + HapMap data sets we have evaluated is superlinear but subquadratic (Figure 6). It might be that the scaling properties of HAPI-UR will improve in very large data sets because they might contain multiple copies of the same haplotype; in that case, fewer haploid states would be necessary for constructing an HMM, and the runtime scaling of HAPI-UR would tend more toward linearity.

We estimated how long HAPI-UR would take to run on data sets with 100,000 and 200,000 samples at the same marker density as the WTCCC1 + HapMap and CHOP data sets by using least-squares to fit quadratic functions to the observed runtimes and data set sizes for these two samples. These fits are conservative in that they assume that the runtime will continue to grow at a regular rate that we fit by a quadratic function even as more samples are added, whereas the true scaling might be smaller given that samples might contain duplicated haplotypes. Extrapolation based on the quadratic fit to the WTCCC1 + HapMap runtime shows that for chromosome 1, HAPI-UR is expected to take 8.64 days to phase 100,000 samples and 32.8 days to phase 200,000 samples at this marker density. Based on the runtimes we observe for phasing the CHOP data, the estimated runtimes to phase chromosome 1 at the CHOP marker density are 15.1 days for 100,000 samples and 56.6 days for 200,000 samples. Because the most computationally intensive part of the algorithm is constructing and sampling from the individual-specific diploid HMMs, parallelization of the algorithm across samples is feasible (although not yet implemented), and thus, for example, a parallelized run for phasing 200,000 samples at the CHOP marker density across eight processors should take slightly more than 7.08 days. It is also feasible to phase sections of chromosomes separately in parallel (and have some overlap across sections) and to combine the inferred phase across these sections to form complete haplotypes; this is the recommended approach for phasing with the use of IMPUTE2 and is how we performed phasing with IMPUTE2 in the results presented above.

For a fixed number of states, the runtime of MaCH scales linearly in sample size, and we have conservatively assumed that the runtimes of IMPUTE2 and SHAPEIT scale linearly. MaCH has a very high runtime and is not competitive with HAPI-UR on data sets with tens of thousands of samples. The estimated total runtime for HAPI-UR to phase all chromosomes for 100,000 samples at the WTCCC1 + HapMap marker density is 101.6 days (note that this is parallelizable across chromosomes and that the estimate for chromosome 1 reported above is 8.64 days). Using our conservative estimate of linear scaling for IMPUTE2 and SHAPEIT, their estimated runtimes to phase 100,000 samples at the WTCCC1 + HapMap marker density are 1,096 days and 1,382 days, respectively. This is the runtime for these methods with a fixed number of states, but our results suggest that in order to leverage the full benefit of large data sets, both these methods would need to be run with a larger number of states, and this would increase their runtime further.

Discussion

Low-cost SNP genotyping has permitted the collection of data from thousands of individuals at hundreds of thousands of SNPs, which in the last several years has resulted in the discovery of more than 1,300 common genetic variants associated with risk for common disease.³¹ Although these diploid genotype data have been extraordinarily powerful tools for medical genetics, the conversion of these data to phased haplotypes is likely to enable additional discoveries both in medical genetics through genotype imputation and in population genetics. Current algorithms require large computational resources to phase more than a few ten thousand samples simultaneously, yet data sets with up to 100,000 individuals genotyped on the same SNP array are now being generated (see Risch et al.¹⁵ and the WTCCC2 data set in the Web Resources). It is important to phase all individuals simultaneously so that haplotypes can be obtained with the highest overall accuracy and so that correlated errors do not result from separately phasing subsets of the samples.

HAPI-UR provides a method for efficiently phasing large data sets, and we have shown that HAPI-UR has similar accuracy to Beagle but is much faster and more scalable to very large data sets. We found that SHAPEIT and MaCH are considerably slower than HAPI-UR for phasing large data sets and that their switch-error rates stay roughly constant with increasing sample size (Figure 3). The HMMs of these methods have a fixed number of states in any run, and our results suggest that in the presence of a larger number of haplotypes, i.e., greater haplotype diversity, these methods are unable to represent the added information that all the samples provide. Thus, in order to benefit from all the information contained in larger data sets, both SHAPEIT and MaCH would need to be run with a larger number of states, but this would increase their computational overhead further from the runtimes reported in Figure 3B.

IMPUTE2 shows decreasing switch error with sample size (Figure 3A), and this is most likely due to the fact that it constructs an HMM for each individual by using the haplotypes in the data set that are most similar to estimated haplotypes for that individual. Thus, IMPUTE2 identifies the haplotypes that are most likely to provide useful information in order to phase a given individual. Despite the increased accuracy with sample size, IMPUTE2 does not benefit from large sample sizes as much as HAPI-UR and Beagle do, and using a larger number of states (and therefore a longer runtime) is most likely necessary for IMPUTE2 to take full advantage of the accuracy that can be achieved with larger data sets.

In general, phasing even a modest data set with, for example, 200 samples involves a tradeoff between runtime and accuracy. At the extreme of targeting the highest accuracy without regard to compute time, running PHASE—which implements the full Li and Stephens model²⁵ instead of an approximation as in IMPUTE2, SHAPEIT, MaCH, and HAPI-UR—would most likely produce the greatest phase accuracy among all the methods we have considered.³² However, PHASE would probably take several years to complete phasing a data set with 10,000 samples. On the other extreme, a phasing method that randomly assigns phase to an individual would require minimal runtime while producing extremely inaccurate and meaningless phasing results.

HAPI-UR and Beagle both occupy a space in the phasing landscape wherein the states they examine adapt, in a localized region, on the basis of the haplotype structure and diversity of the data. In regions with low haplotype diversity, both HAPI-UR and Beagle will include fewer states than they will in regions with higher diversity. This property might explain why, in contrast to methods that utilize fixed numbers of states, both of these methods have increased accuracy and efficiency when they examine a large number of samples. Running IMPUTE2, SHAPEIT, or MaCH with a very large number of states could probably produce haplotypes with greater accuracy than either HAPI-UR or Beagle could on large data sets, but this would also incur a large computational burden.

A phasing approach with a very different paradigm than HAPI-UR and the other methods we have considered is that of long-range phasing.¹³ Kong et al. applied long-range phasing in over 35,000 Icelanders and were able to identify many distant relatives for each sample and phase the individuals by identifying homozygous SNPs in one or more of their relatives. This approach works well for phasing Icelandic samples, but it is unclear whether this methodology would work in more outbred populations and, if so, what size of data set and/or marker density would be needed for it to work. It might be that, for example, European American data sets that include more than 1,000,000 samples and a sizeable marker density would benefit from long-range phasing, and this is an avenue worth exploring as data sets of this magnitude become available.

The results we have presented suggest that as sample size increases, phasing runtime must increase at a superlinear rate if one is to gain full advantage of the information contained in all samples, yet consideration of computational runtime is essential for practically leveraging large data sets. We have shown that HAPI-UR infers phase in large data sets with accuracies comparable to or better than existing methods and is also more than an order of magnitude faster. Because the number of states that HAPI-UR uses in any window is dependent on the haplotype structure and diversity in an individual, the method adapts to the nature of the data set, and we anticipate that it will perform well in the large data sets that now exist, as well as those that are being generated.

Web Resources

The URLs for data presented herein are as follows:

• HAPI-UR, http://code.google.com/p/hapi-ur/

• WTCCC2, http://www.wtccc.org.uk/ccc2/