Coupled motion in proteins revealed by pressure perturbation

Abstract

The cooperative nature of protein substructure and internal motion is a critical aspect of their functional competence about which little is known experimentally. NMR relaxation is used here to monitor the effects of high-pressure on fast internal motion in the protein ubiquitin. In contrast to the main chain, the motions of the methyl-bearing side chains have a large and variable pressure dependence. Within the core, this pressure sensitivity correlates with the magnitude of motion at ambient pressure. Spatial clustering of the dynamic response to applied hydrostatic pressure is also seen indicating localized cooperativity of motion on the sub-nanosecond time scale and suggesting regions of variable compressibility. These and other features indicate that the native ensemble contains a significant fraction of members with characteristics ascribed to the recently postulated “dry molten globule.” The accompanying variable side chain conformational entropy helps complete our view of the thermodynamic architecture underlying protein stability, folding and function.

INTRODUCTION

In principle, conformational entropy can potentially play a key role in the cooperative transitions that are vital for protein function^1,2. The states visited via fast sub-nanosecond motion potentially correspond to considerable conformational entropy³. Nuclear magnetic resonance (NMR) relaxation phenomena are quite sensitive to conformational fluctuations occurring on the sub-nanosecond time scale and have recently been developed as a quantitative experimental proxy for the underlying conformational entropy⁴. Thus, measures of fast internal motion can provide considerable insight into fundamental energetic components governing aspects of protein function. NMR relaxation studies suggest a highly heterogeneous distribution of the amplitudes of methyl-bearing amino acid side chain motion in proteins that resists explanation in terms of simple structural correlates⁵. Though few in number, experimental high resolution NMR studies of the temperature dependence of side chain motion emphasize the existence of several different classes of motion but fail to shed much light on the degree of coupling of motion within proteins^6,7.

Like temperature, pressure is a fundamental thermodynamic variable that is able to modify the free energy landscape of proteins. In contrast to temperature, high-pressure perturbation of proteins is often dissective and can reveal fundamental insights into local protein structure, dynamics, cooperativity and thermodynamics. LeChatelier's principle demands that the response of a protein solution to increasing pressure will be to shift towards the state(s) of lower system volume. However, the microscopic origins of this shift in the distribution of states are inherently complex and it is often difficult to disentangle contributions from the protein, the solvent and from protein-solvent interactions⁸. Indeed, as pointed out by Kauzmann⁹, there are fundamental inconsistencies between the simple hydrophobic models that are often invoked to explain protein stability and its observed pressure dependence. Clearly, atomic scale insight is necessary to resolve these and other issues critical to a fundamental understanding of the thermodynamic and dynamic aspects of proteins and their role in function¹⁰.

High-pressure NMR spectroscopy has a long history in physics, chemistry and biology^11-13. Advances in large active volume high-pressure NMR cell apparatus have enabled multidimensional NMR spectroscopy of proteins at kilobar pressures in otherwise unmodified NMR spectrometers and probes^14-17 and has culminated recently in the explicit introduction of pressure modulation within the NMR experiment itself¹⁸. These and related advances have allowed the application of state-of-the-art NMR spectroscopy to investigate details of fundamental properties of proteins such as the identification of minor conformers^19,20 and local structural transitions²¹, characterization of cooperative units of structure using native-state hydrogen exchange²², protein cold denaturation^23-25, characterization of folding intermediates and pathways^26,27 and details of molecular recognition mechanisms²⁸, aromatic ring dynamics^29,30, backbone dynamics by ¹⁵N relaxation methods and even the determination of protein structure to high resolution³¹. Here we present the first study of the pressure dependence of fast internal motion of protein methyl bearing side chains using deuterium NMR relaxation using ubiquitin as a model system. Pressure perturbation illuminates regions of variable compressibility and correlated motion in the protein and indicates that the native-state ensemble contains a significant fraction of protein molecules exhibiting the characteristics of the so-called “dry molten globule.”³²

EXPERIMENTAL SECTION

NMR relaxation experiments

¹⁵N labeled ubiquitin (0.8 mM) and ¹³C-55% ²H labeled ubiquitin (1.2 mM) samples were produced as described previously^33,34 and prepared as a mixture in 50 mM sodium acetate (pH* 5.0, uncorrected for the deuterium isotope effect), 50 mM NaCl, 0.02% (w/v) NaN₃, 10% D₂O. This allowed the characterization of backbone dynamics and macromolecular tumbling and methyl side chain dynamics with the same sample. The chemical shifts of the forty methyls and fifty-six amide sites were assigned by following the pressure induced chemical shift changes using the assignments at 1 bar for reference³³. Rotational diffusion tensors^35,36 and O²_NH parameters were determined from backbone T₁, T₂ and NOE ¹⁵N relaxation experiments³⁷ at 17.6 T and 14.1 T at 0.001, 0.4, 0.8, 1.2, 1.6 and 2.5 kbar. O²_axis parameters were determined from ²H T₁ and T_1ρ relaxation rates³⁸ measured under identical experimental conditions. All NMR experiments were carried out at 30 °C in a 2,500 bar rated 5 mm o.d./3 mm i.d. ceramic NMR tube connected to a high pressure Xtreme-60 pressure-stat syringe pump (Daedalus Innovations LLC, Philadelphia). Macromolecular tumbling parameters³⁵ and model-free parameters³⁹ were determined using a grid search approach³⁶ employing a quadrupolar coupling constant of 167 kHz^{ref. 40}, an effective N-H bond length of 1.04 Å^{ref. 41} and a consensus ¹⁵N chemical shift anisotropy tensor breadth of -170 ppm^{ref. 42}. The precision of the determined model-free parameters was estimated by Monte Carlo sampling of T₁ and T_1ρ based on errors estimated from replicate sampling.

NMR protein hydration experiments

Uniformly ¹⁵N, ²H labeled ubiquitin, prepared as described previously⁴³ in the abovementioned buffer, was used directly as a free aqueous protein solution or was encapsulated in AOT reverse micelles in liquid pentane (98%-d, Cambridge Isotopes, Cambridge MA) as described previously⁴⁴. Three-dimensional ¹⁵N-resolved NOESY spectra⁴³ were collected at 1 bar and at 2.5 kbar and the amide-water cross peaks were compared to determine pressure-dependent changes in ubiquitin solvent accessibility.

Statistical analysis

There are several occasions where multiple models needed to be distinguished. For instance, model-free analysis of relaxation data requires the explicit determination of rotational diffusion tensors of the protein molecule for isotropic, axially symmetric or completely anisotropic macro-molecular tumbling. For pressure sensitivity of fast side chain dynamics, first, second and third order polynomial models were considered. In the case of distribution of O²_axis parameters at various pressures, the best-fitting distribution function was chosen from random, single Gaussian, bi-Gaussian and tri-Gaussian models. In general, the fitting error decreases with an increase in the number of fitting parameters. To test whether such an improvement is statistically significant, pair wise comparisons were made using F-tests. The corresponding p-value was calculated in the standard way⁴⁵ using the F-value and the degrees of freedom of the corresponding two models. Pair wise comparisons with F-values that correspond to p ≤ 0.05 were considered to be significant.

Outlier analysis

An outlier analysis was carried out iteratively for Figure 4. All points were initially fitted by standard linear regression. The interquartile range (IQR)⁴⁶ of the differences between the fitted and experimental dO²_axis/dP (ΔdO²_axis/dP) were calculated. Methyls with a ΔdO²_axis/dP falling 1.5 IQR above the third quartile or below the first quartile were considered to be outliers and excluded until no further outliers were observed.

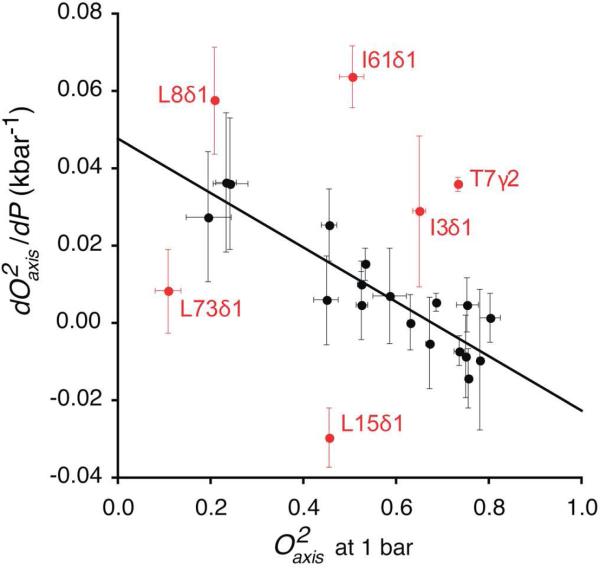
Figure 4.

Correlation of the pressure sensitivity of methyl bearing side chain motion in ubiquitin with their amplitude of motion at 1 bar. Only methyl groups showing a simple linear pressure dependence are shown. Methyls having a non-linear pressure dependence and/or residing in a region with significant pressure induced structural changes were excluded from the analysis (see text). Six outliers (red) were identified using the interquartile range method (see Methods). Linear regression of the remaining points gave a slope of -0.07 ± 0.01 kbar-1 and R of 0.9. This pressure response reflects a variable local compressibility of the protein.

Numerical grouping by k-means method

Using the k-means method^47-49, dO² /dP values and O²_{axis axis} parameters at ambient pressure for methyls with linear pressure response were grouped into k (4 and 3, respectively) different groups based on their closeness to k centroids calculated using the distribution of values within the given groups. For each possible combination of k groups, the centroids were iteratively optimized based on their closeness to the means until further iterations no longer changed the resulting groups (i.e. an equilibrium distribution was achieved). The final numeric sets with the least standard squared error (SSE) were selected, using

$$SS{E}_{numeric}=\sum _{i=1}^k\sum _{x\in C_i}{(C_i-x)}^2$$ (1)

These numeric groups plus an additional group containing those methyls having a non-linear pressure response were then tested for spatial clustering.

Visual inspection of the spatial distribution of groups with different pressure response within the molecular structure of ubiquitin (Figure 5, Figure S3 and Figure S4) is suggestive of spatial clustering but is potentially obscured by the limited number of methyl probes and their discontinuous distribution within the molecule. To determine the statistical significance of the spatial clustering of these reference groups, a new SSE was calculated to reflect distances between each methyl site in the crystal structure (PDB 1UBQ) using:

$$SS{E}_{distance}=\sum _{i=1}^k\sum _j{(x_j-{\stackrel{‒}{x}}_i)}^2+{(y_j-{\stackrel{‒}{y}}_i)}^2+{(z_j-{\stackrel{‒}{z}}_i)}^2$$ (2)

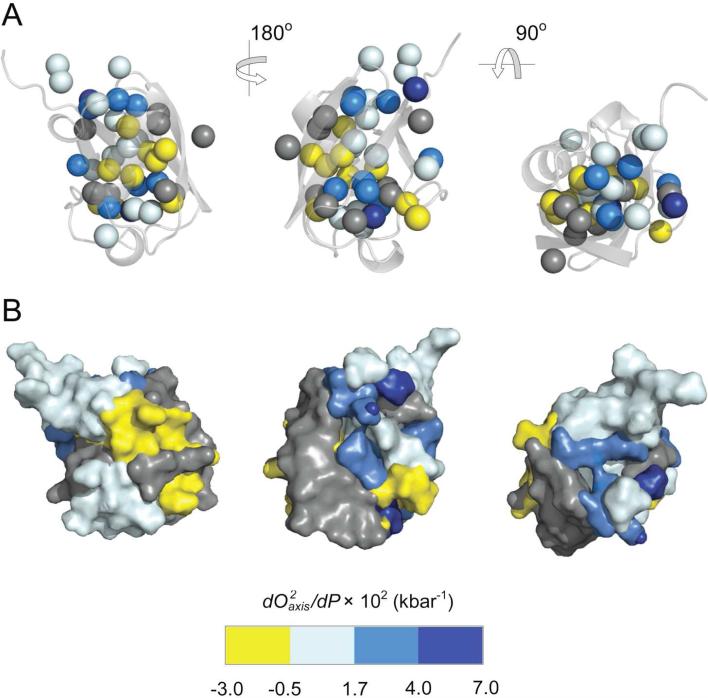
Figure 5.

Spatial distribution of the pressure sensitivity of fast methyl-bearing side chain motion in ubiquitin. (A) Different orientations of the crystal structure of ubiquitin⁵¹ (PDB 1UBQ) represented as a ribbon with side chain methyl carbons shown as spheres and colored according to their membership in the numeric groups derived from k-means clustering of (dO²_axis/dP) values (see Methods). Methyl groups showing a reduction in the amplitude of motion with increasing pressure (dO²_axis/dP > 0) are colored with a white-blue scheme while those having an increase in motion with increasing pressure (dO²_axis/dP <0) are colored yellow. Those methyls having a non-linear dynamic response to pressure were grouped separately and are colored gray. Statistical tests confirm the members of each numerical group (excluding T22γ2, L8δ1, L73δ2) of dO²_axis/dP values are also spatially clustered within the molecular structure (all p < 0.05), reflecting regions of variable compressibility. See Figure S4 also. These clusters of apparent compressibility are emphasized in (B) where each atom, including added hydrogens, was assigned to the cluster of the nearest methyl carbon probe. Hydrogen atoms were added and surface renderings were then made for each group and colored accordingly. Molecular images were generated using PyMOL (Schrödinger, Portland).

The statistical significance of the spatial distribution of the reference groups in space was calculated with a p-value obtained by exhaustive randomization⁵⁰. SSEs for randomly generated unique set of groups (groups with the same number of probes as found in the reference test groups) were determined. The p value was calculated as the ratio of the number of unique groups with SSE_distance below that of the SSE_distance of the reference groups to the total number of groups generated.

RESULTS

Ubiquitin is a small protein comprised of a mixed beta sheet against which are packed a long alpha helix and a short 3₁₀ helix⁵¹. The fast internal dynamics of ubiquitin in solution at ambient pressure are well-characterized^34,35,51,52. Importantly, the structure of ubiquitin at 3 kbar has been determined to high resolution by NMR-based methods³¹. In an attempt to study fast internal motions of ubiquitin at high pressure, we performed ²H methyl relaxation³⁸ and backbone ¹⁵N amide relaxation³⁷ experiments at 0.001, 0.4, 0.8, 1.2, 1.6 and 2.5 kbar at 303 K. To allow for detailed analysis of the pressure sensitivity of internal motion, the nature of the macromolecular tumbling of the protein was characterized directly using ¹⁵N-relaxation methods. This information was then used to separate the overall tumbling of the protein and internal motions of methyl bearing side chains and backbone amides. The magnitude of internal motion of side chain and backbone is described by the model-free squared generalized order parameter³⁹, as it applies to the methyl symmetry axis (O²_axis) or the backbone amide N-H bond (O²_NH). Recent re-evaluations of the model-free treatment of Lipari & Szabo reinforce confidence in its robustness with respect to highly asymmetric side chain motion^53,54. Spectral resolution was sufficient to allow the determination of rotational diffusion tensors and the pressure dependence of fifty-six O²_NH parameters of backbone amide N-H bond vectors. The O²_axis parameters of forty methyl side chains of ubiquitin were also determined to high precision at all six pressures ranging from 1 bar to 2,500 bar (Tables S1 and S2).

The pressure sensitivities of both the methyl-bearing side chain and backbone N-H motion within the protein are quite variable and their distributions are deceptively simple (Figure 1). Most probes of motion become more rigid with increasing pressure (i.e. increased order parameter), but some sites become more dynamic. In general, pressure has a greater effect on the apparent amplitude of motion of the methyl-bearing side chains than on that of the backbone amide

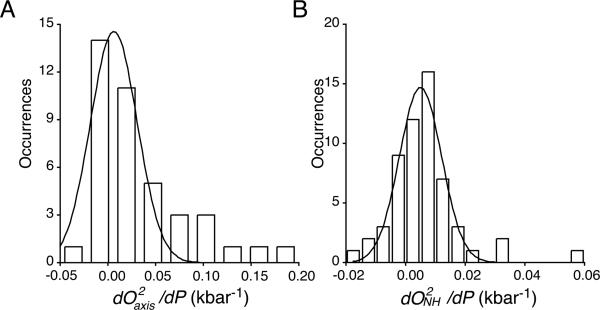
Figure 1.

Distribution of the linear response of methyl-bearing side chain motion (A) and backbone amides N-H motion (B) to pressure. For methyl-bearing side chains experiencing a nonlinear pressure response, dO²_axis/dP values were taken from the linear term of the fitted polynomial. The solid lines correspond to the best-fitted Gaussian distributions with widths of 0.035 ± 0.006 and 0.010 ± 0.001 kbar^-1, centers of 0.0063 ± 0.004 and 0.0050 ± 0.001 kbar^-1 and Pearson coefficients of correlation (R) of 0.91 and 0.97 for the dO²_axis/dP and dO²_NH/dP distributions, respectively.

N-H (Figure 1). There is no significant correlation between the pressure dependence of fast side chain and backbone motion (R < 0.03; see Figure S1). Further analysis is presented in the SI appendix. The decoupling of the dynamic responses of a protein to perturbation has been observed previously albeit in a somewhat different context⁵⁵ and emphasizes the need to consider changes in both the main chain and side chains.

As the O²_axis parameter arises from angular disorder on the nanosecond and faster time scales³⁹, it makes a direct connection to local volume fluctuations associated with motion of the side chain. The sensitivity of methyl bearing side chain motion to hydrostatic pressure is therefore a reflection of the effective local compressible volume sampled by the probe. Through this fundamental thermodynamic relationship, changes in relative volume fluctuations with pressure define the isothermal compressibility and are directly related to volume fluctuations^1,56. Thus, the variable pressure sensitivity of the motion of methyl bearing side chains effectively reflects a range of local compressibility within even this relatively small protein.

Pressure sensitivity of different types of motion

For methyl bearing side chains, a tri-modal distribution of O²_axis parameters arising from three distinct classes of motion is often illuminated by ²H NMR relaxation studies⁵. The motional origin of these classes, termed J, α and ω, has been well established⁵. The so-called ω-class is comprised of methyl groups with high O²_axis and whose motion is highly restricted within a single rotamer well. The J-class is centered at very low order parameter, which arises from extensive rotameric interconversion on a nanosecond or faster time scale. These cases are detected through the averaging of the corresponding scalar (J) coupling constants^6,57. The α-class is centered on intermediate O²_axis parameters and involves minimal rotameric interconversion and large amplitude motion largely restricted to within a single rotamer well.

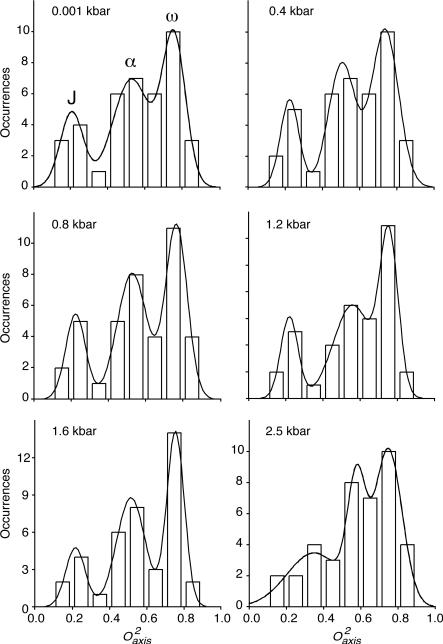
These three classes of motions are clearly observed for ubiquitin at 0.4, 0.8, 1.2 and 1.6 kbar and somewhat obscured at ambient pressure and 2.5 kbar (Figure 2). The fitting parameters of the tri-Gaussian distributions are summarized in Table S3 and Figure S2. At pressures up to 1.6 kbar, the populations of the motional classes are redistributed towards more restricted motion. Interestingly, there is a shift in the centers of the distributions above 1.6 kbar. The center of ω-class was not affected by pressure while centers of the J- and α-class shift to higher values above 1.6 kbar. The J-class distribution also significantly broadens (Figure 2).

Figure 2.

Pressure dependence of the distribution of the amplitude of methyl-bearing side chain motion. Shown are histograms of the distribution of squared generalized order parameter of the methyl symmetry axis (O²_axis) determined by deuterium relaxation at various applied hydrostatic pressures. The fitting parameters and statistics are listed in Table S3.

These observations provide important insight into what is typically thought of as the low-energy thermodynamic ground state of proteins. Within this ground state there are at least two distinct energetic states: a more compact state, wherein the side chains are tightly packed against one another, and a slightly expanded higher-entropy state, wherein the backbone is more or less constrained but the side chains have considerable freedom and, in many cases, are able adopt multiple conformations. It is this latter state that the present observations suggest is dominant at ambient pressure. This view is reinforced by the recent observation that low temperature crystal structures are “over packed” relative to structures obtained at room temperature⁵⁸.

Variable response of motion to pressure

The change in the free energy (ΔG) between low (P₀) and high-pressure (P₁) states can be expressed as

$$\Delta G=\Delta G^o+{\int }_{P_0}^{P_1}\Delta VdP$$ (3)

which is often recast as a Taylor series expansion

$$\Delta G=\Delta G^o+\left(\Delta V^o\right)\left(\Delta P\right)+\frac{1}{2}{\left(\Delta P\right)}^2\left(\frac{d\Delta V^o}{dP}\right)+\frac{1}{6}{\left(\Delta P\right)}^3\left(\frac{d^2\Delta V^o}{d{P}^2}\right)+\dots$$ (4)

where the zeroth order (ΔG°) and first order (ΔV°) terms represent the change in free energy and in specific volume between different states of ubiquitin at reference pressure (P₀), respectively. The second–order term (dΔV°/dP) arises from the pressure dependence of the isothermal compressibility. The third-order term (d²ΔV°/dP²) arises from the pressure dependence of the differential isothermal compressibility.

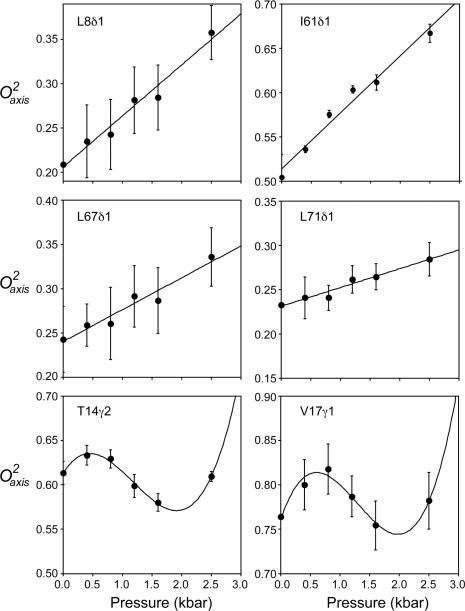
In some situations, a direct connection can be made between the pressure dependence of an observable and the underlying thermodynamics. Hydrogen exchange in the so-called EX2 condition is one such case²². Here, however, the obtained O²_axis parameters reflect a superposition of the ensemble. As pointed by Akasaka¹⁹, the general response of such an NMR parameter to pressure can be fitted with a general polynomial that is akin to the formal Taylor expansion of Equation 4. The pressure dependence of O²_axis parameter of each methyl group was fitted in such a manner. Nine out of the total forty sites required second or third order terms to be satisfactorily fitted (p < 0.05), implying a more complex pressure dependence of the structural context of the fluctuations. The remaining thirty-one methyls were best fitted with a simple linear response to pressure. The fitted parameters are listed in Table S4. Examples of both the simple linear and more complex pressure dependence of methyl-bearing side chain motion are shown in Figure 3.

Figure 3.

Pressure sensitivity of fast methyl-bearing side chain motion in human ubiquitin. Representative plots of the pressure dependence of the squared generalized order parameter of the methyl symmetry axis for methyl probes in ubiquitin. Examples include those showing a linear (L8δ1, I61δ1, L67δ1, L71δ1) or statistically significant higher order polynomial dependence (T14γ2, V17γ1) upon applied hydrostatic pressure. Fitted Taylor series parameters (Equation 4) and tests for statistical significance are summarized in Table S4. For those sites that have a linear dynamical response to pressure and are not involved in significant structural change (rmsd < 3 Å) (Table S5), the pressure dependence of the methyl dynamics (dO²_axis/dP) and the amplitude of motion (O²_axis) at ambient pressure are linearly correlated (Figure 4).

For those sites that have linear dynamical response to pressure and are not involved in significant structural change (rmsd < 3 Å, PDB 1UBQ and 1V81) (Table S5), the pressure dependence of the methyl dynamics (dO²_axis/dP) and the amplitude of motion (O²_axis) at ambient pressure are linearly correlated (Figure 4) except for six outliers iteratively identified using the interquartile range method (see Experimental). All of these outliers are within proximity (< 5 Å) of regions of the protein that show a non-linear pressure response and/or have significant pressure-induced structural change and are thus likely influenced more by the complex pressure response of their neighbors. The remaining eighteen sites show a linear relationship between dO²_axis/dP and O²_axis at ambient pressure (R = -0.9, slope = -0.07 ± 0.01 kbar^-1). These sites are sandwiched between the α helix and the β sheet of ubiquitin and are surrounded by the remaining twenty-two methyls. They are predominantly buried in the core of the protein and are spatially clustered (p < 0.01) (Figure S3).

Spatially correlated motion and its pressure sensitivity

In order to shed light on the spatial distribution of the observed variable pressure sensitivity of side chain motion, the dO²_axis/dP values and the O²_axis parameters at ambient pressure for the methyls having linear pressure response were numerically grouped into 4 and 3 sets (see Table S6), respectively, using the k-means algorithm (see Experimental). The O²_axis parameters seen at ambient pressure numerically segregate into three groups that have very similar membership to those identified using the dO²_axis/dP values. This echoes the correlation of O²_axis parameters and dO²_axis/dP (Figure 4). Those methyls having a non-linear response were placed in their own group. Visual inspection of the spatial distribution of these sets within the molecular structure of ubiquitin (Figures 5 and S4) is suggestive of spatial clustering but is potentially obscured by the finite number of methyl probes and their discontinuous distribution within the molecule. To objectively test for spatial clustering, exhaustive randomization of the numeric groups was carried out and confirmed a statistically significant spatial clustering for both the dO²_axis/dP values and the O²_axis parameter at ambient pressure within the molecular structure of ubiquitin (p < 0.05). Thus, although the pressure response is heterogeneous, it is not randomly distributed but is instead spatially clustered within the three dimensional structure of the protein. This is an unprecedented observation and points directly to regions of differing compressibility in the protein. There is no apparent correlation between the sign or magnitude of the pressure response and depth of burial. The heterogeneity of the pressure sensitivity of fast side chain motion is clearly complex and resists simple explanation. Finally, it should be emphasized, however, that a quantitative connection between the pressure dependence of dynamical parameters measured here and the underlying variation in the individual populations of protein species contributing to the average is currently elusive.

The interior of the ubiquitin is dry at 2.5 kbar

Molecular dynamics simulations of ubiquitin at a pressure somewhat above those used here (3 kbar versus 2.5 kbar) suggest that dozens of water molecules will penetrate to the core of the protein^59,60. The penetration of water has been proposed to facilitate pressure-induced global protein unfolding⁶¹. Clearly, penetration of water into the protein would greatly change the context within which changes in side chain motion should be interpreted. Though the solution structure of ubiquitin at 3 kbar has been determined to high resolution and reveals that the protein remains highly structured and closely similar to the structure at ambient pressure³¹, it is important to confirm the absence of significant water within the protein interior.

NOESY spectra of ubiquitin in free aqueous solution at ambient pressure show no long-lived NOE contacts between water and interior hydrogens^43,62. Additional NOEs between water and amide hydrogens are seen at 2.5 kbar but all of these involve surface interactions and apparently reflect subtle changes in the hydration of the protein with elevated pressure (Figure 7). The NOESY experiment is somewhat sensitive to the time scale of the interaction between the protein and an associated water molecule^63,64. We have recently demonstrated that encapsulation of a protein within the protective confines of a reverse micelle allows site-resolved quantitative assessment of protein hydration using solution NMR spectroscopy, in part by slowing the motion of hydration water and suppressing confounding hydrogen exchange chemistry⁴³. In effort to detect water molecules with too short residence times in the interior to provide detectable NOEs, we compared NOESY spectra of ubiquitin in AOT reverse micelles at 1 bar and 2.5 kbar. Again, there was no evidence for penetration and sustained residence of water at ambient or elevated pressure (Figure 6). Small differences in water hydration at the surface are largely consistent with the local rearrangement of the accessible surface area seen in the NMR-derived model for the structure of the protein at high-pressure³¹. Indeed, the quite subtle structural rearrangement involving Q49 seen in the high-pressure structure³¹ of ubiquitin in free solution results in the burial of the amide N-H of L50, which is manifested in the loss of the NOE contact with water (Figure 6). Thus, the interior of ubiquitin is apparently dry at pressures ranging up to 2.5 kbar and the linear correlation between the magnitude of the intrinsic side chain motion and the dependence on pressure shown by these eighteen methyl-bearing side chains that are isolated from solvent is likely a reflection of a basic property of structured proteins.

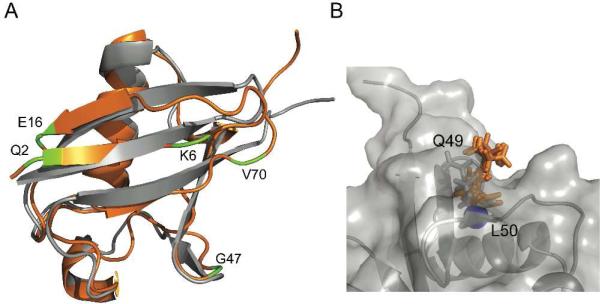
Figure 7.

Pressure effect on the hydration of ubiquitin. Panel A shows overlay of ribbon representations of the ambient pressure crystal structure⁵¹ (1UBQ) in gray and the 3 kbar solution structure³¹ (1V81) in orange. In free aqueous solution, the amide N-H of Q2, K6, E16, G47 and V70 show NOE cross peaks to water at high pressure but not at ambient pressure. They are located in regions that have the pressure induced structural change. Panel B shows a rendering of the surface of the ambient pressure crystal structure in gray, illustrating the surface pocket that exposes the amide hydrogen of L50 to solvent (shown as a blue sphere). The 3 kbar structure was aligned to 1UBQ and the side chain conformations of Q49 shown in stick representation for both 1UBQ (gray) and the 10 conformers in the 3 kbar structural ensemble (orange). This side chain undergoes a rearrangement at high pressure that fills the pocket, thereby burying the L50 amide hydrogen, consistent with the loss of an NOE from this site to the water measurements in the NOESY spectra shown in Figure 6.

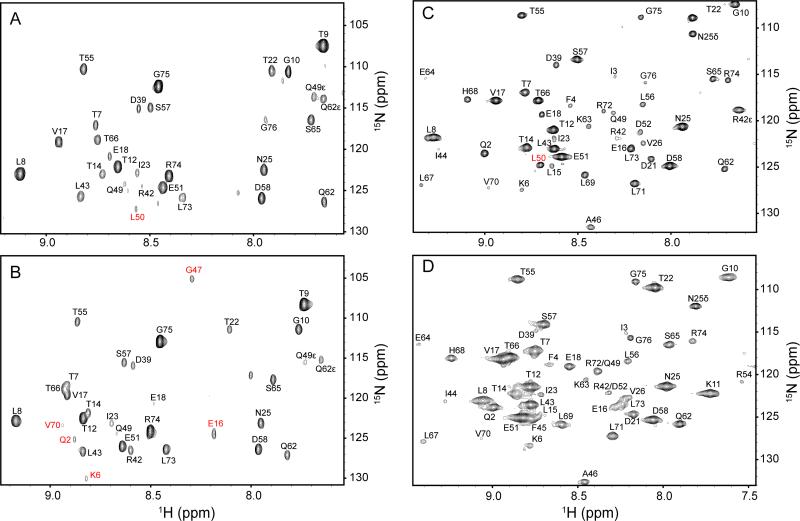
Figure 6.

The absence of water in the interior of the protein at high hydrostatic pressure. Indirect ¹H planes at the water resonance of three-dimensional ¹⁵N-resolved NOESY spectra of ¹⁵N, ²H-labeled ubiquitin in aqueous (4.7 ppm) and encapsulated in AOT reverse micelles in liquid pentane (4.5 ppm). Panels A and B are ubiquitin in free aqueous solution at 1 bar and 2.5 kbar, respectively. Panels C. and D are encapsulated ubiquitin in pentane at at 1 bar and 2.5 kbar, respectively. Differences in cross peak position result from pressure dependent changes in amide (¹H,¹⁵N) chemical shifts, while differences in linewidth arise from the increase in solvent viscosity with increasing pressure. Amide hydrogen-water cross peaks of L50 that disappear at high pressure both in aqueous and in encapsulated conditions are indicated in Panels A and C in red. The cross peaks of Q2, K6, E16, G47 and V70 that appear at high pressure only in free aqueous solution are indicated in B in red. There is no evidence for penetration of water into the protein at ambient or elevated pressure. Only amide hydrogens within NOE-detection distance of the surface of the protein show NOEs to the water resonance at either pressure.

DISCUSSION

The nature of the native-state ensemble

The observation that application of high pressure results in a measureable decrease in conformational fluctuations indicates that this lower energy pressure-sensitive state is a significant component of the native state ensemble and that the higher energy state is more compact, less dynamic and more akin to the static structures implied by low-temperature crystallography. The heterogeneous nature of the pressure response also relieves the incongruity noted by Kauzmann between the hydrophobic drop model for protein stability and the observed bulk pressure dependence for protein unfolding versus that of the solubility of non-polar molecules in water⁹. Particularly important is the significant presence of low energy states in the native ensemble that have dynamically activated side chains. These members of the ensemble have the critical characteristics ascribed to the “dry molten globule” that has recently been proposed to represent the penultimate species in the folding of a globular protein³². The pressure sensitivity of the dynamically activated side chains is found to be localized. The realization that the equilibrium between high and low volume states of ubiquitin is governed by localized changes has important implications. First, it begins to reveal the structural context and dynamical features of the coupling of motion within the protein matrix. As the ensemble of conformers visited by proteins represents considerable conformational entropy, the coupling of motion and its variation by perturbations such as the binding of ligands directly provides an important role for conformational entropy in protein function. Ligand binding by calmodulin^4,55,65 and the catabolite activator protein^66,67 appear to be such examples. The latter is especially interesting owing to the virtual absence of a change in structure associated with the binding event, which emphasizes the need to consider the ensemble of states rather than a single structure^68,69. This view does not require coherent localization of changes in motion (conformational entropy). Secondly, one can also envisage a role for conformational entropy in mechanisms of dynamically based allostery where changes in motion (conformational entropy) are channeled within the protein matrix. In this regard, Lee and coworkers have provided the first conclusive experimental evidence for such a mechanism in their study of the PDZ domain^70,71. The distinction between these two general mechanisms of allosteric regulation clearly rests on an apparent ability of a protein to balance the degree of motional coupling within its tightly packed matrix, i.e. the coupling must be localized and finite. The clustering of the pressure sensitivity of motion in ubiquitin suggests that this balance may be an inherent feature of proteins that can be manipulated by Nature. Future applications of high-pressure perturbation to probe protein motion that is potentially intimately connected to the contribution of conformational entropy and thereby to the energetics of protein function should therefore prove highly informative.

In conclusion, we have presented the first study of sub-nanosecond timescale side chain motion in a protein at kilobar pressures but well below the denaturation pressure. Only small changes in structure and backbone dynamics are introduced. In general, the amplitude of fast internal motion of the side chain methyls decreases with increasing pressure, suggesting a decrease in conformational entropy. Furthermore, there is an apparent linear relationship between the amplitude of motion at ambient pressure and the magnitude of the pressure sensitivity within the core of the protein. This is the pressure response anticipated for motion that is comprised largely of fluctuations about a mean structure and is directly related to the local compressibility of the protein. The pressure sensitivity also indicates that the native state ensemble contains a significant fraction of members that exhibit the characteristics of the dry molten globule and that the more compact, less dynamic and higher energy state populated at high pressure is more similar to the static compact structures emphasized by low temperature crystallographic structures of proteins. Importantly, the dynamic response to applied pressure is heterogeneous but spatially clustered, demonstrating localized and differential coupling of motion even within this relatively small protein. This behavior illuminates the raw material necessary for the participation of conformational entropy in the energetic transitions of proteins central to folding, stability and function.