Phenotypic plasticity and adaptive evolution contribute to advancing flowering phenology in response to climate change

Abstract

Anthropogenic climate change has already altered the timing of major life-history transitions, such as the initiation of reproduction. Both phenotypic plasticity and adaptive evolution can underlie rapid phenological shifts in response to climate change, but their relative contributions are poorly understood. Here, we combine a continuous 38 year field survey with quantitative genetic field experiments to assess adaptation in the context of climate change. We focused on Boechera stricta (Brassicaeae), a mustard native to the US Rocky Mountains. Flowering phenology advanced significantly from 1973 to 2011, and was strongly associated with warmer temperatures and earlier snowmelt dates. Strong directional selection favoured earlier flowering in contemporary environments (2010–2011). Climate change could drive this directional selection, and promote even earlier flowering as temperatures continue to increase. Our quantitative genetic analyses predict a response to selection of 0.2 to 0.5 days acceleration in flowering per generation, which could account for more than 20 per cent of the phenological change observed in the long-term dataset. However, the strength of directional selection and the predicted evolutionary response are likely much greater now than even 30 years ago because of rapidly changing climatic conditions. We predict that adaptation will likely be necessary for long-term in situ persistence in the context of climate change.

1. Introduction

All organisms undergo a sequence of life-history stages, and must time the transitions between these stages precisely to capitalize on favourable environmental conditions. In seasonal environments, plants must reproduce within a narrow timeframe each year. Individuals that emerge prematurely risk reduced fitness from frost damage to developing floral tissues [1], limited pollinator activity [2] or even intense herbivory [3]. Additionally, selection can favour increased size at maturity [4,5], and small individuals that flower early in the season could lack sufficient resources to maximize fecundity. At the same time, individuals that flower too late might not be able to complete their reproductive cycles prior to the onset of inclement conditions (e.g. winter or drought) [3,6].

Therefore, stabilizing selection should in many cases favour the evolution of intermediate optimal flowering times (figure 1a, also see [2,3,6–8]). Nevertheless, recent analyses have uncovered directional selection for=earlier flowering in many species [4,9,10]. In contemporary environments, plants are flowering earlier than ever before, owing to rising temperatures, altered precipitation regimes and elevated atmospheric CO₂ concentrations [11–14]. Widespread directional selection for earlier flowering could be symptomatic of rapidly changing climatic conditions (figure 1b), with increasing extinction risk as the rate of climate change exceeds the rate of adaptive phenotypic change (figure 1c).

Figure 1.

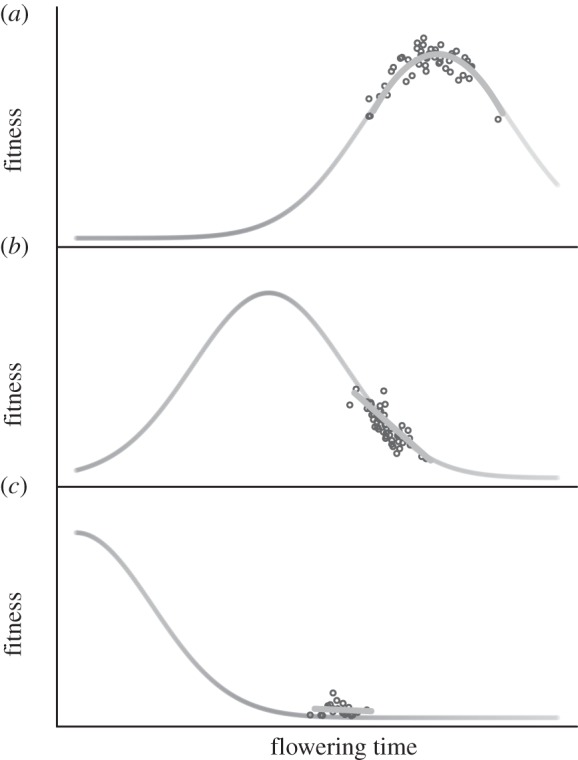
Conceptual model of natural selection on flowering phenology in the context of anthropogenic climate change. (a) Prior to industrialization: stabilizing selection could have favoured intermediate flowering time owing to seasonal constraints on growth and reproduction. (b) Contemporary conditions: climate change causes growing seasons to begin earlier, shifting the fitness landscape and resulting in directional selection for earlier flowering. (c) Future conditions: under continued warming, natural populations with limited genetic variation could fall far from the fitness optimum, have severely depressed fitness, and risk extinction. Further details are available in electronic supplementary material, S1.

Anthropogenic climate change will likely lead to local population declines and extirpation, range contractions and even extinctions [15]. Although some species will be capable of migrating to track-preferred environments [16], others will have to cope with climate change in situ through phenotypic plasticity and/or adaptive evolution [17]. We know virtually nothing about the relative roles of plasticity and adaptive evolution in the response of natural populations to ongoing climate change [11,18–22]. Plasticity will likely be crucial in the short term, but may be insufficient when species encounter novel future climates outside the range of historical variability. Adaptive evolution could enable population persistence in the long term [23]; however, sustained directional selection imposed by climate change could potentially deplete populations of the genetic variation needed for continued adaptation. It remains unclear whether adaptive evolution can keep pace with anthropogenic climate change [17–19,22].

This study integrates multiple lines of evidence to explore natural selection in the context of global warming. We quantified phenotypic and evolutionary changes in flowering time in the short-lived perennial forb Boechera stricta (Brassicaceae), which is native to undisturbed habitats in the US Rocky Mountains and reproduces primarily through self-pollination [4,24]. Montane species are especially vulnerable to climate change owing to short growing seasons and heightened projected temperature anomalies at higher elevations [1,25]. Many alpine species have already migrated upslope in response to elevated temperatures [26]. Our specific objectives were to: (i) assess long-term changes in the timing of flowering of B. stricta; (ii) quantify the statistical relationship between flowering phenology and key environmental conditions; (iii) examine selection on flowering phenology in experimental and observational studies; and (iv) estimate the potential for adaptive evolutionary responses to climate change.

2. Methods

(a). Study system

We conducted fieldwork at and around the Rocky Mountain Biological Laboratory (RMBL) in Colorado (38°57′ N, 106°59′ W, elevation: approx. 2900 m). In this subalpine environment, the growing season commences immediately after snowmelt, which is one of the primary environmental variables controlling flowering phenology [1]. Climate change is projected to increase temperatures, cause early snowmelt and reduce snowpack, and possibly augment drought stress in this region [25,27–29]. Data from this study have been deposited in Dryad (doi:10.5061/dryad.68mj4).

(b). Long-term study

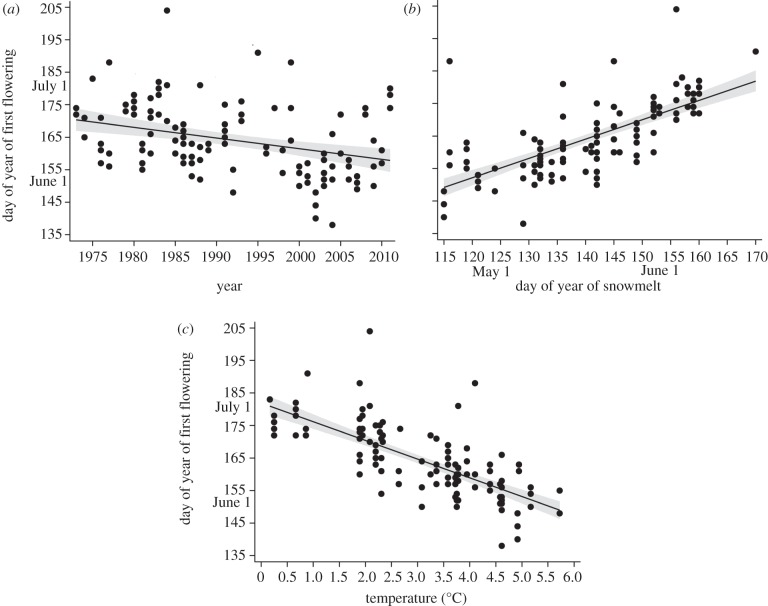
Detailed accounts of the long-term study are available elsewhere, including a map of plots [1]. Briefly, in 1973, D. Inouye and colleagues established a series of 2 m × 2 m plots in dry, mesic and wet habitats at RMBL, and have monitored flowering phenology of all species within the plots approximately every two days during the growing season since then (except 1978 and 1990). We used the total number of B. stricta flowers per plot at each census to determine dates of first flowering and peak flowering—the date with the maximum number of B. stricta flowers. Our analyses focus on seven dry rocky meadow plots (average elevation, 2962 m; range, 2927.5–2970.2 m) because B. stricta is abundant in this habitat, and for consistency with the quantitative genetics studies (see later text). Daily observations by B. Barr at RMBL from 1975 to 2012 determined the timing of snowmelt. Temperature values come from the Crested Butte NOAA weather station, approximately 9.5 km from RMBL (elevation: 2702 m). We excluded 1994 from analysis because first flowering was missed in some plots that year; models including 1994 produced similar results (not shown).

To investigate long-term changes in the entire flowering phenology curve [30], we analysed both the timing of first flowering and day of peak flowering. We regressed flowering phenology on: year, timing of snowmelt and average April and May temperature (hereafter: ‘temperature’) in mixed models that included a random effect for plot (Proc Mixed, SAS v. 9.3). Because the timing of snowmelt and temperature are correlated (Pearson correlation coefficient: −0.81, p < 0.0001), full models including all predictors could have problems with multicollinearity. Therefore, we also ran separate reduced models to determine the effect of each predictor in isolation on flowering phenology. Results were similar when the timing of first flowering was averaged across plots each year (see electronic supplementary material, S2).

To estimate long-term phenotypic rate of change in phenology, we regressed standardized first flowering date on the number of generations (following [31]), including a random effect for plot crossed with generation. This calculation from naturally recruiting individuals incorporates both genetic changes and phenotypic plasticity [31]. Traditionally, the rate of change in a trait is evaluated by dividing trait values by the s.d. for each generation [31]. We calculated the s.d. of flowering time across plots in 10-year increments because of limited numbers of observations each year, and used these values to standardize raw flowering time data. Boechera stricta is a short-lived perennial; throughout this study, we estimate generation time as 2 or 3 years.

We statistically estimated phenotypic plasticity in flowering time by calculating the residuals for separate regressions of first flowering time, temperature and snowmelt date on year. These residuals provide year-detrended estimates of flowering phenology and environmental conditions. We then regressed the detrended annual fluctuations in flowering time on detrended variation in snowmelt date and temperature. This analysis identifies variation in flowering time associated with environmental conditions that are decoupled from long-term trends caused by climate change. These time-independent associations likely represent phenotypic plasticity because an evolutionary response to selection would occur in subsequent generations (i.e. 2 or 3 years later), resulting in no significant regression in this analysis of residuals.

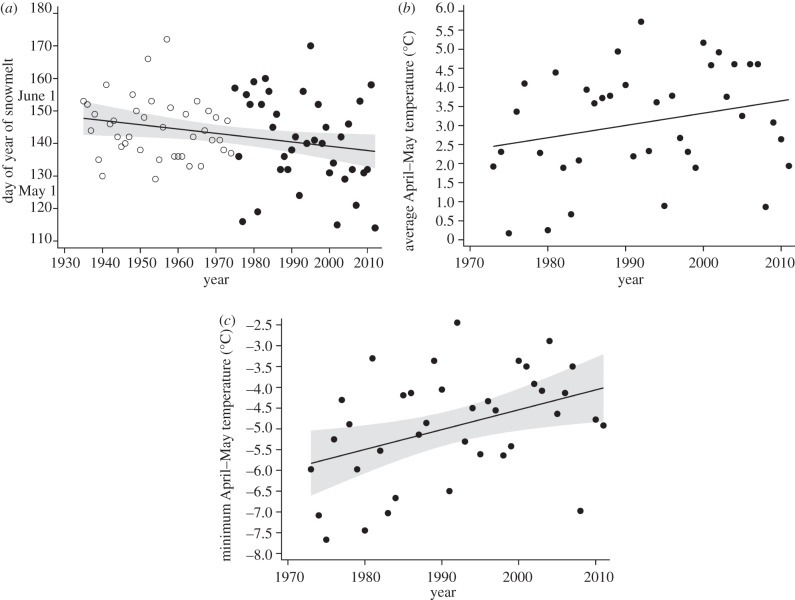
To quantify the rate of climate change, we regressed environmental conditions (averaged daily minimum and mean April–May temperatures, and snowmelt date) on year in separate analyses. Runoff in the nearby East River strongly predicts the timing of snowmelt (p < 0.0001, r² = 0.69; see electronic supplementary material, S3), and river runoff data date to 1935, allowing us to analyse snowmelt (calculated and observed) as a function of year from 1935 to 2012.

(c). Selection on flowering time (1): Recombinant inbred lines (RILs)

As part of a larger study to map quantitative trait loci (QTL) for flowering phenology and fitness, we planted F₆ recombinant inbred lines (RILs) into their parental environments in Colorado and Montana (see [4,32,33], for additional details about the generation of these RILs and the environments of the parental lines). Here, we focus on the Colorado garden (38°45′44′ N, 106°51′47′ W, elevation: 2530 m), which is 24 km from the long-term plots at the RMBL. The Colorado garden is located near an organic farm, in an intact undisturbed dry rocky meadow, dominated by sagebrush (Artemisia tridentata). This meadow has a robust endogenous Boechera population. The Colorado parental line was originally collected within 10 km of the garden, in a site with similar abiotic and biotic conditions and elevation (approx. 2480 m) [4,32,33]. This study allows us to estimate the potential for genetic responses in flowering time in B. stricta.

In September 2009, we planted 751 plants from 174 RILs (n = 1–5, average 4.35 individuals/RIL) and two parental lines (15 individuals/parental line) into the matrix of natural vegetation at 10 cm spacing in 10 experimental blocks in the Colorado field garden [33]. Planting in the fall allows juveniles to synchronize their life histories with local winters [4]. In spring 2010, 697 individuals remained alive, and were monitored every week over the growing season (seven censuses total from 4 June—19 July, 2010) for timing of first flowering and fruit production. Following Anderson et al. [4], we estimated the date of first flowering of individuals that flowered between censuses based on the daily rate of fruit elongation and flower production. Throughout this study, we used fruit number as our fitness component because it is tightly correlated with overall seedset in greenhouse studies of B. stricta (r² = 0.72, p < 0.0001, n = 103, A. Manzaneda 2008, unpublished data). Relative fitness was calculated by dividing an individual's fruit set by the population-level average. We recorded the density of naturally recruiting plant competitors within a 10×10 cm area centred on each transplant to include as a covariate in analyses.

We conducted linear and quadratic selection analysis using family means to assess relative fitness as a function of the day of first flowering, and plant size (leaf number and height at flowering) because selection can act on both age and stage at first flowering [4,9]. Significantly negative quadratic effects point to stabilizing selection, when optimal flowering times correspond with intermediate flowering times in the population [34]. In this analysis, we used family-level averages (LSMEANs) for fruit number, day of first flowering and plant size at flowering. These were estimated using mixed models (Proc Mixed, SAS v. 9.3) with block as a random effect, and two covariates: initial size and plant density. Phenotypes were standardized to a mean of 0 and a s.d. of 1 to facilitate comparison of traits measured using different units. A selection analysis on individual phenotypes (instead of family means), using a zero-inflated Poisson model, produced similar results (see electronic supplementary material, S4, including SAS code). In all cases, significant quadratic regression coefficients (and s.e.) were doubled to calculate quadratic selection gradients [35].

Finally, we directly estimated the potential per-generation response to selection as the genetic covariance between relative fitness and flowering time, following the Robertson–Price identity [36]. Here, we use broad-sense genetic (co)variance (instead of additive (co)variance, as in [36]), which is appropriate because six generations of selfing in the greenhouse minimizes maternal effects and because selection operates on total genetic variance in highly selfing species such as B. stricta [37]. Models using only data from the Colorado garden failed to converge because of limited statistical power, as only 152 plants (n = 97 families) successfully flowered. The strength of selection on flowering time was nearly identical in the Colorado garden (this study) and the Montana garden in 2009 [4]; so we estimated the Robertson–Price identity from a combined dataset of the same families of F₆ RIL and parental lines from: Colorado (2010, this study), Montana (2009 garden, previously published in [4]) and Montana (2010, unpublished). This combined dataset includes n = 689 individuals that flowered, from 164 RIL and two parental lines.

A full multivariate model evaluated covariance between relative fitness and: flowering time, height at flowering and leaf number at flowering. Traits were unstandardized to estimate selection responses in original units of measurement, rather than in s.d. We also investigated the covariance between relative fitness and flowering phenology in a reduced model that did not include plant size at flowering. In both models, we included fixed effects for site, planting year and plant density, and random effects for genotype and block crossed with site (SAS code available in electronic supplementary material, S5). We also used the univariate and multivariate breeder's equations to estimate the response to selection (calculations in electronic supplementary material, S5C). As with all studies of selection, unmeasured traits could influence the covariance between traits and fitness.

(d). Selection on flowering time (2): Local genotypes at Carpenter Meadow

We conducted an additional experiment designed to test for stabilizing selection at Carpenter Meadow, a rocky meadow site at the RMBL (38°57′48″ N, 106°59′15″ W; elevation: 2994 m), approximately 140 m from six of the long-term observational plots and 390 m from the remaining long-term plot. We generated four cohorts, each using 13 local seed families, to increase variance in flowering time relative to endogenous plants. We stratified seeds in the laboratory at Duke, and planted an average of 20 seedlings per family on 5 March, 12 March, 19 March and 25 March 2010. Seedlings were watered and fertilized as needed; in May, juveniles from all cohorts were vernalized in a cold room (4°C) for 4 weeks prior to transportation to the field, because vernalization is a requirement for flowering in B. stricta [4].

Individuals were planted in the field from 2 to 4 June 2010 (n = 748 individuals, average of n = 14.4 per cohort per family; see electronic supplementary material, S6 for details). At planting, we recorded data on initial plant size (leaf number). Flowering time and fitness were monitored until 27 August 2010 when autumnal conditions limited further growth. We estimated linear and quadratic selection on phenotypes and family means (see electronic supplementary material, S7). Cohort (planting date in the greenhouse) was considered a fixed effect. In contrast to the RIL experiments, heritability in this experiment is inflated by maternal effects; therefore, it is not appropriate to estimate the response to selection with these families.

(e). Selection on flowering time (3): Observational study at Carpenter Meadow

We quantified selection in the naturally recruiting population of Carpenter Meadow. From 8 to 10 June 2010, we established five transects, 4 m × 30 m, near our experimental garden, and tagged every B. stricta individual (2010: n = 265; 2011: n = 577). In each of 6 weeks during June and July in 2010 and again in 2011, we recorded plant size (height, leaf number), and reproductive status (number of flowers and fruits).

We conducted linear and quadratic phenotypic selection analyses separately for each year. To account for differences in plant size among naturally recruiting individuals, the analyses also included the following traits: maximum height, number of flowers and number of leaves at flowering, all standardized to mean of 0 and s.d. of 1. Residuals were heteroscedastic, even after log transformation of fitness. Poisson regression fit poorly. As heteroscedasticity can bias standard errors and significance tests [38], we used survey sample regression (Proc surveyreg), which calculates robust standard errors to compensate for non-constant error variance. We incorporated a cluster term (similar to a random effect) for transect.

3. Results

(a). Long-term flowering phenology and climate change

From 1973 to 2011, the timing of first flowering of B. stricta advanced by 0.34 days per year, and this effect was still significant in the multivariate model, indicating that environmental conditions do not fully account for shifts in phenology over time (table 1, figure 2a). First flowering increased significantly with snowmelt day (table 1, figure 2b), and decreased with temperature (table 1, figure 2c). The results presented in table 1 use data from 1975 to 2011 because snowmelt data are not available before 1975. A separate univariate analysis shows nearly identical advancement in the timing of first flowering from 1973 to 2011 (β = −0.34 ± 0.08, F_1,26 = 18.3, p < 0.0001). From 1973 to 2011, the phenotypic change in the timing of flowering (s.d. per generation) was moderately high (−0.25 ± 0.04 and −0.37 ± 0.06 haldanes, respectively, for generation times of 2 and 3 years; F_1,6 = 45.2, p = 0.0005).

Table 1.

Long-term flowering phenology records indicate that the timing of first flowering advanced significantly from 1975 to 2011, and flowering phenology is tightly associated with the timing of snowmelt and temperature. The significance of the random effect (plot) was determined via likelihood ratio tests of models with and without this effect (1 d.f.). Plot was non-significant for the reduced models (p-values were 0.25, 0.12, 0.058, respectively, for separate models of year, snowmelt date and temperature).

	full model				each predictor independently
	β	F1,119	p-value	partial r2	β	F1,121	p-value	r2
year	−0.22 ± 0.05	16.5	<0.0001	0.19	−0.34 ± 0.08	16.6	<0.0001	0.098
snowmelt day	0.32 ± 0.07	19.5	<0.0001	0.23	0.56 ± 0.04	154.6	<0.0001	0.53
temperaturea	−2.95 ± 0.7	18.2	<0.0001	0.22	−5.7 ± 0.45	162.5	<0.0001	0.54
plot		χ2 = 7.5	0.006

^aAverage April and May temperature.

Figure 2.

Long-term trends in flowering phenology in Boechera stricta. (a) The timing of first flowering has advanced significantly since 1973, and (b) is tightly related to the timing of snowmelt and (c) late winter temperatures. Grey bands represent 95% CI.

Plasticity represents a major component of this phenotypic change, as year-detrended fluctuations in flowering time vary significantly with detrended fluctuations in the timing of snowmelt (β = 0.66 ± 0.06, F_1,32 = 128.8, p < 0.0001, r² = 0.79) and temperature (β = −5.8 ± 0.6, F_1,34 = 81.1, p < 0.0001, r² = 0.70).

The timing of first flowering was strongly correlated with the timing of peak flowering (Pearson's correlation coefficient: 0.72, p < 0.0001). Peak flowering advanced by 0.32 days per year in a univariate model (p = 0.0035), and 0.20 days per year in a multivariate model that included temperature and snowmelt date (p = 0.03; see electronic supplementary material, S8 and S9).

The timing of snowmelt advanced significantly from 1935 to 2012 (β = −0.13 ± 0.06 days/year, F_1,76 = 5.13, p = 0.026, r² = 0.04, figure 3a), but only marginally from 1975 to 2012 (β = −0.34 ± 0.2, F_1,36 = 2.84, p = 0.10). Average April–May temperature increased marginally from 1973 to 2011 (β = 0.03 ± 0.02°C/year, F_1,36 = 2.48, p = 0.12, figure 3b). During the same period, minimum April–May temperature rose significantly (β = 0.043 ± 0.02, F_1,34 = 5.41, p = 0.026, r² = 0.11, figure 3c).

Figure 3.

Environmental change through time. (a) The timing of snowmelt has advanced significantly from 1935 to 2012 (open circles are estimated values from river runoff, 1935–1974; closed circles are observed data from 1975 to 2012). (b) Average April and May temperature increased only marginally from 1973 to 2011. (c) Minimum April and May average temperatures increased significantly from 1973 to 2011.

(b). Selection on flowering time (1): Recombinant inbred lines (RILs)

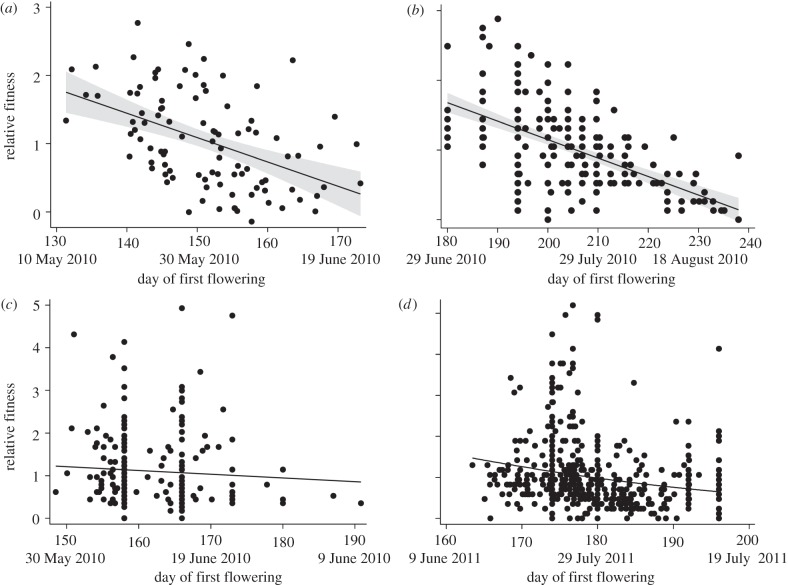
There was significant directional selection for flowering early in the growing season (table 2, figure 4a), with a slightly positive quadratic effect in family-level multivariate analyses, but not in univariate (table 2) or individual-level (see electronic supplementary material, S4) analyses. We found no evidence for negative quadratic effects of flowering time; thus, stabilizing selection does not appear to favour intermediate flowering dates (figure 4a). Selection also favoured increased height at flowering, but leaf number at flowering did not significantly affect fitness (table 2). Individual-level analyses (see electronic supplementary material, S4) produced qualitatively similar results. Relative fitness decreased by 3.6 per cent for every day delay in flowering in univarate analysis of unstandardized data (0.036 ± 0.007 relative fitness units per day; F_1,95 = 26.1, p < 0.0001).

Table 2.

Standardized selection gradients (β′) and differentials (S′) for multivariate and univariate analyses of family-level data of the RILs (recombinant inbred lines). Bold text indicates significance.

	multivariate analysis			univariate analyses
	β′	F1,93	p-value	S′	F1,95	p-value
day of first flowering: linear effect	−0.24 ± 0.1	5.45	0.0217	−0.48 ± 0.09	26.1	<0.0001
day of first flowering: quadratic effect (γ′)	0.42 ± 0.2	F1,92 = 4.3	0.04	0.32 ± 0.2	F1,94 = 2.2	0.14
height at first flowering	0.43 ± 0.1	20.29	<0.0001	0.54 ± 0.08	43.6	<0.0001
number of leaves at flowering	0.06 ± 0.09	0.49	0.49	−0.046 ± 0.1	0.19	0.66

Figure 4.

(a) Selection on flowering time: in recombinant inbred lines; (b) experimental population at Carpenter Meadow; and endogenous population at Carpenter Meadow in (c) 2010 and (d) 2011. All datasets show significant directional selection for earlier flowering (see text). Analyses were conducted using phenotypic data standardized to a mean of 0 and a s.d. of 1, but figure panels present unstandardized flowering time data.

The Robertson–Price identity predicted a response to selection on flowering time of −0.517 days per generation in the univariate model (χ² = 6.1, p = 0.0135) and −0.519 in the multivariate model (G matrix in electronic supplementary material, S5B). The breeder's equation predicted a slightly slower response to selection: −0.35 and −0.23 days/generation in the Colorado dataset, and −0.2 and −0.24 days/generation in the combined Colorado and Montana dataset (univariate and multivariate results, respectively; see electronic supplementary material, S5C for calculations). Over 38 years (equivalent to 1973–2011), these estimates would advance flowering time by 2.6–6.5 days, or 3.8–9.7 days (generation time of 3 or 2 years, respectively). If this predicted response to selection remained constant over the course of the long-term study, adaptive evolution would represent 20–50% (3 year generation time) or 30–75% (2 year generation time) of the observed advancement in flowering time (0.34 days/year×38 years = 12.9 days since 1973 in univariate analysis).

(c). Selection on flowering time (2): Local genotypes at Carpenter Meadow

Close to 30 per cent of experimental individuals successfully flowered (224 of 748). The timing of flowering varied with planting date (F_3,120 = 3.3, p = 0.023), indicating that flowering phenology was successfully altered in these cohorts. Consistent with the RILs, we found significant directional selection for earlier flowering in individual (β′ = −0.36 ± 0.04, F_1,112 = 71.9, p < 0.0001, figure 4b) and family-level analyses (β′ = −0.45 ± 0.08, F_1,15 = 34.9, p < 0.0001; see electronic supplementary material, S7). The quadratic effect of day of first flowering (γ′) was non-significant in phenotypic selection analysis on individuals (p = 0.4), but was significantly positive for family means (F_1,15 = 4.75, γ′ = 0.18 ± 0.08, p = 0.045; see electronic supplementary material, S7), indicating slight curvature in the relationship between flowering time and fitness. Neither analysis suggests that stabilizing selection favours an intermediate flowering time. We found no effect of cohort age (p = 0.64) or initial size (p = 0.49) on fecundity. Similar to the RILs, relative fitness declined by approximately 3 per cent for every day delay in flowering (−0.026 ± 0.003 relative fitness units/day, F_1,112 = 71.9, p < 0.0001). Broad-sense heritability was 0.27 (χ² = 43.6, p < 0.0001), but is inflated by maternal effects.

(d). Selection on flowering time (3): Observational study at Carpenter Meadow

In both 2010 and 2011, 90 per cent of naturally recruiting B. stricta individuals flowered. The two years of this study differed markedly in the timing of snowmelt (12 May 2010 versus 7 June 2011) and average day of first flowering (11 June 2010 versus 29 June 2011). This pattern is opposed to the overall acceleration in flowering in the long-term dataset, owing to unusually late snowmelt in 2011. Nevertheless, our analyses detected significant directional selection for earlier flowering in both years (table 3, figure 4c,d). In multivariate models, relative fitness increased with: maximum plant height, number of leaves at flowering (2010 only) and number of flowers (table 3). We found no evidence for stabilizing selection on flowering time (table 3, figure 4). Flowering time was significantly correlated across years for the individuals that flowered in both 2010 and 2011 (p = 0.0015; n = 122); however, the weak correlation coefficient (0.28) suggests that plastic responses to temporally varying conditions strongly influence flowering. In multivariate models of unstandardized data, relative fitness decreased by 1.5 per cent for every day delay in flowering (2010 dataset: β = −0.015 ± 0.002 relative fitness units/day, t = −7.7, p = 0.0015; 2011 dataset: β = −0.015 ± 0.005, t = −3.25, p = 0.03). The intensity of selection was slightly weaker in endogenous populations than in the experimental plantings.

Table 3.

Phenotypic selection analyses of traits on relative fitness in five transects through endogenous populations of Boechera stricta in 2010 and 2011. There were four denominators d.f. for t-tests. Parameter estimates represent standardized selection gradients, β′, and selection differentials, S′. Significant t-values are highlighted in bold. *p < 0.05; **p < 0.01; ***p < 0.0001.

	2010				2011
	β′	t-value	S′	t-value	β′	t-value	S′	t-value
day of first flowering: linear effect	−0.074 ± 0.023	−3.27*	−0.055 ± 0.06	n.s.	−0.14 ± 0.04	−3.54*	−0.19 ± 0.1	n.s.
day of first flowering: quadratic effect (γ’)	−0.03 ± 0.028	n.s.	−0.046 ± 0.34	n.s.	0.09 ± 0.02	3.47*	−0.12 ± 0.14	n.s.
maximum plant height	0.42 ± 0.031	13.6**	0.57 ± 0.046	12.4**	0.29 ± 0.006	44.9***	0.26 ± 0.05	5.39**
leaf number at flowering	0.41 ± 0.032	13.1**	0.57 ± 0.026	21.7***	0.14 ± 0.08	n.s.	0.41 ± 0.17	n.s.
number of flowers	0.21 ± 0.038	5.63**	0.48 ± 0.03	17.7***	0.37 ± 0.08	4.66**	0.45 ± 0.12	3.79*

4. Discussion

Long-term records clearly demonstrate that the day of first flowering has advanced significantly since the mid-1970s (table 1, figure 2), at a rate similar to recent phenological changes in birds, butterflies, amphibians and other plant species [12,14,39–43]. Flowering phenology was highly responsive to local environmental conditions, such as snowmelt date (figure 2b) and late winter temperatures (figure 2c). Furthermore, under controlled conditions, B. stricta families showed significant flowering time plasticity in response to temperature and vernalization (the length of winter) [4]. Thus, phenotypic plasticity has likely played a prominent role in the long-term acceleration of flowering. However, earlier flowering could also have a genetic component, which is crucial for adaptive responses to climate change. Directional selection in contemporary conditions favours earlier flowering in observational and experimental studies in Colorado (figure 4) and Montana [4]. Strong selection, along with moderate heritability, could result in rapid adaptive evolution of flowering phenology. Indeed, evolution can proceed quickly in response to selection imposed by anthropogenic climate change [11,17,18,21,44].

Our studies of selection in the recombinant inbred lines (RILs) allowed us to estimate the potential evolutionary responses to selection. Under current conditions, we predict 0.2 to 0.5 days acceleration in flowering time per generation. If the strength of selection and the extent of flowering time heritability remained constant over the course of 38 years (equivalent to the duration of the long-term records), our quantitative genetic results suggest a 2.6–9.7 day acceleration in flowering phenology, depending on whether generation time is 2 or 3 years (see Results). As a point of comparison, the timing of first flowering advanced 12.9 days from 1973 to 2011 in univariate analysis of the long-term observational records. Thus, the predicted genetic response to selection would account for 20–75% of the long-term observed acceleration. This large range is due to uncertainty in the exact generation time, and discrepancies between estimates from the Robertson–Price identity and breeder's equation, which could result from environmental bias or other factors [36]. Nevertheless, it seems possible that adaptive evolution could have contributed to the observed phenotypic change in flowering phenology. Similarly, Franks et al. [11] documented rapid adaptive change in flowering time in the annual mustard Brassica rapa over only seven generations in response to contemporary drought.

These estimates of the genetic response to selection should be treated cautiously and likely account for closer to 20 per cent rather than 75 per cent of the long-term change in flowering time. For one, genetic variation among the RILs is probably greater than variation in primarily selfing natural populations [24], which would inflate the predicted response to selection. Most importantly, extrapolating our quantitative genetic results back to the mid-1970s assumes that the covariance of relative fitness and flowering time in modern populations is representative of the past 38 years. However, both the intensity of selection and heritability can vary in space and time [45], which may be especially true over the timeframe of our study, as global temperatures have increased dramatically since the 1980s [46] and snow is melting earlier (figure 3). Contemporary analyses likely overestimate the magnitude of selection for earlier flowering compared with selection on this life-history trait in the recent past (i.e. the 1970s), as outlined below.

(a). Natural selection in the context of climate change

We hypothesize that stabilizing selection favoured the evolution of intermediate flowering times prior to anthropogenic global warming, because flowering too early or too late in the growing season can be disadvantageous [6]. Yet, our studies in contemporary environments did not support stabilizing selection on flowering time, as might be expected under equilibrium conditions (figure 1a). Rather, we found compelling evidence that directional selection favours early flowering (tables 2 and 3, figure 4), consistent with our previous field study of B. stricta [4] and a recent meta-analysis [9]. In our system, individuals that flower early produce flowers throughout the entire growing season, thus maximizing fitness compared with late-flowering individuals, which have only a short time to flower prior to the onset of drought or winter. As the climate warms, growing seasons are beginning earlier (figure 3), and this represents an ongoing shift in the adaptive landscape favouring earlier reproduction (figure 1b). As such, climate change may explain recent observations of directional selection for accelerated flowering in many species [9]. Long-term directional selection could deplete genetic variation for flowering time and correlated traits, thereby limiting adaptive potential. Species that fail to respond quickly to a shifting optimum could ultimately face extinction (figure 1c).

(b). Phenotypic plasticity

Our field results (this paper) and laboratory studies [4] suggest that plasticity has played a prominent role in phenotypic change since the mid-1970s [17–19]. Plants exhibit substantial variation in flowering time in response to environmental cues such as photoperiod, precipitation, ambient temperature, exposure to winter temperatures (vernalization) and snowmelt (reviewed in [47]). Plasticity is an important strategy for coping with temporal and spatial heterogeneity. In our study, flowering accelerated by  approximately 13 days from the 1970s to the present, and fitness declined by  approximately 3 per cent for each day that flowering was delayed; a perfectly plastic genotype capable of altering the timing of flowering by 13 days would have a fitness advantage of  approximately 40 per cent (approx. 13 days × 3% per day), relative to potential non-plastic genotypes. Increased temporal variability projected under climate change could favour plastic genotypes that are capable of sensing and responding to a wide variety of conditions [44]. However, current levels of plasticity might be insufficient for populations to reach new optima, if climate change dramatically increases variation in environmental conditions beyond historical levels. In that case, genetic adaptation in flowering phenology or flowering time plasticity will be essential for in situ population persistence.

(c). Conclusions and future directions

Given our extensive understanding of the molecular basis of flowering phenology (reviewed in [48]), continued monitoring of selection on this ecologically relevant trait in natural populations will reveal the extent to which climate change can disrupt the evolutionary trajectories of plants that differ in life-history strategy and mating system. Annual and short-lived perennial species that harbour sufficient genetic variation will undoubtedly evolve more quickly in response to climate change than longer-lived species. To determine whether climate change is altering the form (stabilizing to directional) or strength of selection will require long-term studies of individuals of known genotype under changing conditions, or manipulative experiments comparing selection under contemporary climates versus simulated climate change.

Altered climatic conditions could impose novel selection on phenology and traits that confer stress tolerance; yet we know very little about the evolutionary ramifications of anthropogenic climate change [17–19,22]. In our study, the long-term trend for advancing flowering corresponds with current directional selection for earlier flowering. It seems likely that phenotypic plasticity and adaptive evolution both contribute to recent shifts in flowering phenology. Our quantitative genetics studies suggest that B. stricta populations may be able to adapt their flowering phenology in response to continued climate change. However, we do not know whether adaptive evolution will allow populations to reach new phenotypic optima rapidly enough to keep pace with climate change.