Kin selection, not group augmentation, predicts helping in an obligate cooperatively breeding bird

Abstract

Kin selection theory has been the central model for understanding the evolution of cooperative breeding, where non-breeders help bear the cost of rearing young. Recently, the dominance of this idea has been questioned; particularly in obligate cooperative breeders where breeding without help is uncommon and seldom successful. In such systems, the direct benefits gained through augmenting current group size have been hypothesized to provide a tractable alternative (or addition) to kin selection. However, clear empirical tests of the opposing predictions are lacking. Here, we provide convincing evidence to suggest that kin selection and not group augmentation accounts for decisions of whether, where and how often to help in an obligate cooperative breeder, the chestnut-crowned babbler (Pomatostomus ruficeps). We found no evidence that group members base helping decisions on the size of breeding units available in their social group, despite both correlational and experimental data showing substantial variation in the degree to which helpers affect productivity in units of different size. By contrast, 98 per cent of group members with kin present helped, 100 per cent directed their care towards the most related brood in the social group, and those rearing half/full-sibs helped approximately three times harder than those rearing less/non-related broods. We conclude that kin selection plays a central role in the maintenance of cooperative breeding in this species, despite the apparent importance of living in large groups.

1. Introduction

The forces selecting for the evolution of cooperative breeding in vertebrates, where individuals provide care to the offspring of conspecifics, are currently contentious [1–6]. On the one hand, evidence for kin selection, where individuals benefit indirectly by helping to increase the productivity of relatives [7], appears overwhelming. For example, most cooperative vertebrates live and help in family groups [1,6] and both experimental [8] and meta-analytical [9] studies have shown that cooperative vertebrates are more likely to help kin than non-kin. However, the pre-eminence of kin selection in the evolution of vertebrate cooperative breeding systems has been questioned on a number of grounds [2,3,5,10,11]. Kin selection cannot easily explain cooperation among non-kin. Nor does it obviously account for systematic variation in contributions to cooperation by helpers of equivalent relatedness to recipients [12,13] or the common lack of variation in contributions by individuals differing in relatedness [2,9,11]. Such observations have led to the suggestion that direct benefits more commonly select for cooperative breeding in vertebrates than is assumed, and that helping kin might often be an incidental effect of living in family groups, rather than a selected consequence of indirect benefits [2,5,10,11].

Primary among the hypotheses competing with kin selection for the main evolutionary route to cooperative breeding in vertebrates is group augmentation [14,15]. This hypothesis proposes that individuals are selected to help rear the offspring of other group members when the resulting increase in productivity leads to their increased future survival, through the recruitment of additional group members (passive benefits), or future breeding success, through the recruitment of additional helpers (active benefits) [15]. Thus, both kin selection and group augmentation predict that helping increases group productivity, but only group augmentation predicts that helpers increase the productivity of their recipients because doing so increases their own future direct survival and/or reproductive success. Evidence in support of the first prediction is widespread [16,17], but evidence in support of the second is ambiguous [1,2,5,6,11]. Indeed, despite group augmentation being commonly invoked as an important, even dominant [2], selective force in vertebrate cooperative breeding systems, few direct tests of this hypothesis exist ([18], but see [12,13]).

Group augmentation has been implicated as the key pressure selecting for helping behaviour in obligate cooperative breeders where reproduction without helpers is rarely successful [2]. The rationale is that, in such species, group-living is so vital that the future direct benefits of helping to increase group size exceed the costs of contributing to cooperation [19] and any accruable indirect benefits [7]. Individuals are not selected to cheat because doing so reduces augmentation to group size and hence the potential future benefits to survival and/or reproduction [15]. The group augmentation hypothesis predicts that, all else being equal and irrespective of their level of relatedness to recipients, group members should: (i) decide whether to help based on their ability to increase future group size; (ii) given a choice, choose to help at the nest where they can have the greatest impact on future group size; and (iii) show significant reductions in their contributions to cooperation with increasing group size, where benefits of increasing future group size show diminishing returns. By contrast, under kin selection, group members should be selected to: (i) decide whether to help based on their relatedness to breeders; (ii) given a choice, choose those breeders to which they are most related; and (iii) contribute more to rearing kin than non-kin. To test these opposing predictions, one needs an obligate cooperative breeder, where individuals have a choice of helping groups that vary in size and degree of kinship and where the effect of helping on productivity is nonlinear, such that helpers can have different impacts on productivity in breeding units of different sizes.

Such an opportunity arises in the cooperatively breeding chestnut-crowned babbler (Pomatostomus ruficeps), a 50 g passerine bird endemic to semi-arid and arid regions of southeastern Australia [20]. Chestnut-crowned babblers can be classed as obligate cooperative breeders because breeding without helpers is rare (mean = 6% of units per year, n = 371 breeding unit-years), only occurs when part of a larger social group and is commonly unsuccessful [21]. During the non-breeding season (December–June), babblers forage and roost in cohesive social groups numbering three to 23 individuals (mean = 10, n = 91 social group-years), of which approximately 30 per cent are immigrants [21]. However, approximately 70 per cent of these social groups disband into an average of two units (maximum four units) for breeding (mean = six individuals per unit, range = 2–15). Breeding units from the same social groups overlap by approximately 40 per cent in their foraging ranges but nest hundreds of metres apart and remain virtually distinct during breeding: seldom foraging together [22] and never roosting together (A. F. Russell 2005, unpublished data). Despite units re-amalgamating after breeding, the composition of breeding units is highly repeatable between years (89 per cent of non-breeding helpers present in social groups were found in the same breeding unit between 2007 and 2008). Finally, a previous study found the heaviest nestlings present in units of intermediate size, suggesting a nonlinear relationship between unit size and productivity [21]. Given that social groups disband into units of differing relatedness and size, this system provides a unique opportunity to test directly the role of kin selection versus group augmentation on decisions of whether, where and how often to help.

First, we investigate the function of the relationship between breeding unit size and productivity, measured as annual fledgling numbers. Second, we test the causality of any such relationship using a brood size manipulation experiment aimed at varying unit : brood size ratios [23,24]. Third, we use the results generated from the function of the above relationship to generate predictions of whether and where non-breeding babblers should help if group augmentation explains such decisions. We can expect babbler helpers to have the potential to accrue both passive and active benefits through group augmentation [15]. Both predation risk [25] and thermoregulation costs (M. A. Chappell, W. A. Buttemer & A. F. Russell 2009, unpublished data) decline with increasing group size, suggesting that, by helping to raise future recruits, helpers can gain passive survival benefits. In addition, because there is inter-annual repeatability of unit composition, helpers can also rear a potential future workforce in their unit, meaning that active reproductive benefits are also accruable. Fourth, we test the role of kinship in decisions of whether and where to help in social groups. Finally, we investigate whether kin selection or group augmentation best accounts for quantitative variation in the magnitude of helper contributions to nestling provisioning.

2. Material and methods

(a). Study population and sampling

The study was conducted from 2006 to 2008 (July–December) on a colour-ringed population of chestnut-crowned babblers in a 56 km² area of the University of New South Wales Arid Zone Research Station, at Fowlers Gap in far-western New South Wales, Australia (31°05′ S, 141°43′ E). This population has been monitored since 2004 [21,22]. The climate is arid with low, unpredictable annual rainfall (approx. 100–200 mm). Ground vegetation is sparse and largely comprises chenopod shrubland, with stands of trees (principally Casuarina pauper) populating the drainage lines where the birds spend the majority of their time [22]. Babblers were captured using mist-nests (post-fledging) or as nestlings, uniquely colour and numerically banded (Australian Bird and Bat Banding Scheme issue), and injected subcutaneously alongside the flank with a 2×12 mm passive integrated transponder (PIT-tag). Whether, where and how often non-breeding group members contributed to provisioning nestlings were determined in 2007 and 2008 by monitoring the visit rate of PIT-tagged birds at the nest using automated electronic readers (LID650, Trovan Ltd, UK) [26]. Babblers breed in domed nests and must pass through the entrance hole to access the nest cup. By fitting an electromagnetic coil around the nest entrance, all PIT-tagged birds entering the nest could be recorded automatically, along with the date and time. This technique accurately measures individual provisioning rates (measurement repeatability of provisioning rates using decoders versus cameras, R = 0.94, 95% CI: 0.92, 0.95; n = 238 nest observations, 26 nests), and provisioning rate is the best predictor of prey biomass fed to nestlings in this species [26].

A blood sample (approx. 100 µl) was taken by brachi-venipuncture from each individual for molecular sexing [27] and genotyping [28,29]. All breeders (those gaining maternity or paternity) at each nest were identified with precision using a combination of behavioural and molecular data [29]. Non-breeding group members were then categorized as yearling (born previous year) or adult (born before previous year) and natal or immigrant. Natal birds were those ringed as nestlings within their current social group or whose parent(s) were revealed as current breeders through molecular analyses. Immigrants were those that had dispersed into the focal social groups, identified using a combination of observational and molecular data [29]. Using reconstructed pedigrees, we categorized the relatedness of non-breeding group members to the nestlings being reared in their social group. We assigned relatedness values of 0.5 to first-order relatives, 0.25 to second-order relatives and 0 to more distant relatives. This zero category likely includes a range of relatedness values from 0 to approximately 0.125, but we could not be confident of more fine-scale resolution owing to insufficient pedigree information and the problem of discerning distant from non-relatives on the basis of molecular data alone [29].

(b). Breeding unit size and productivity

Breeding activity was monitored using standard methods [21]. Clutch size in this species ranges from two to six eggs, brood sizes vary from one to six nestlings and fledging occurs after 21–25 days (this study, [21]). We recorded the total number of fledglings arising from all breeding attempts by 106 breeding females in 90 breeding units and 58 social groups during 2006–2008. Productivity was defined as the total annual production of fledglings from each breeding female. Breeding unit size (number of yearlings and adults) was determined by weekly counts throughout the breeding season and was used as a measure of the number of available carers in the unit (mean = 6, range = 2–15).

We investigated the effect of breeding unit size on productivity using linear mixed effects models with normal errors fitted using the R [30] package lme4 [31]. We used Akaike's information criterion (AIC) [32] to select the best of three candidate models: (i) no effect of unit size on productivity; (ii) linear unit size effect; and (iii) nonlinear (asymptotic) unit size effect (per unit size). The model with the lowest AICc (corrected for small samples) score was selected as best fitting the data. No model fell within two ΔAICc of the best model, circumventing the need for model averaging [32]. Year, social group and breeding female identity were fitted as random intercepts to account for non-independence of data. We followed steps for model selection outlined in Grueber et al. [33] using the R package MuMIn [34].

(c). Testing the causality of unit size effects

In order to establish causality, we manipulated the number of available carers per nestling (unit : brood size ratio) by experimentally changing brood size and monitoring the rate at which nestlings were fed. Previous evidence suggests that the primary effect of helpers is to reduce nestling starvation [21], and therefore this experiment is appropriate for investigating helper effects in this system. This approach [23,24] examines the influence of effective group size (carers per nestling) on helper care, while removing potential confounds of group size because the natural correlation between unit size and unit : brood size ratio is eliminated (natural Pearson's correlation: r = 0.66, n = 65, p < 0.001 versus experimental Pearson's correlation: r = 0.19, n = 15, p = 0.50). We can infer a causal relationship between unit size and productivity if the experimentally altered unit : brood size ratio: (i) is positively related to the rate at which each nestling receives food and (ii) the function of this relationship mirrors that between unit size and productivity. Furthermore, comparable relationships between unit : brood size ratio and nestling provisioning rates, and between unit size and productivity suggests the effect of helpers on productivity is, at least partly, mediated by provisioning young.

We conducted brood size manipulation experiments at eight nests in 2008 encompassing a broad range of natural brood (2–4, mean = 3) and unit (3–13, mean = 8) sizes, with mean unit : brood size of 2.5 : 1 (range = 1.5–3.3 : 1). Manipulations were achieved via reciprocal nestling swaps between broods of similar ages (±2 days) when nestlings were 7–14 days old (mean = 10 days). Comparisons of provisioning rates conducted on natural brood sizes, before and after manipulations, provided little evidence of brood age effects over the 2 days of the experiment (Mann–Whitney U test: U = 16, p = 0.16). Nevertheless, manipulations were generated by sequentially reducing (by 1–3) then increasing (by 1–2) brood sizes, or vice versa, at random, with each treatment lasting for approximately 24 h. On experimental days, broods contained a random mixture of nestlings from each brood and never exceeded natural variation of 1–6 (reduced = 1–3, mean = 2; enlarged = 3–6, mean = 5). Unit : brood size ratios for reduced and enlarged broods were 2.7–6.5 (mean = 4.8 : 1) and 1–2.3 (mean = 1.6 : 1), respectively. Broods were transported in bird bags between 09.00 and 12.00 h after having been provisioned for at least 3 h, no nests were left empty, nestlings never remained out of the nest for more than 45 min and all survived to fledging.

Provisioning rate was recorded throughout the entire length of the 4 days using the automated system described above. For each treatment at each nest, the total number of nest visits by all group members was recorded and converted into a per capita nestling provisioning rate per hour by dividing the total number of feeds by the daylight hours between the first and last feed of each treatment and then by the size of the brood. Nestling provisioning rate was fitted as the response term in a linear mixed model with normal errors in lme4 [28], manipulated unit : brood size ratio was fitted as the explanatory term and nest identity was fitted as the random intercept to block reduced and enlarged treatments within nests. We used the same AIC approach described above to investigate the linear versus nonlinear effects of unit : brood size ratio on per capita nestling provisioning rates.

(d). Non-breeder decisions to help: when, where and how often

The roles of group augmentation and/or kin selection in accounting for whether, where and how often non-breeding group members contributed to feeding nestlings were determined in 2007 and 2008 using records of PIT-tagged birds visiting the nest (see above). Overall, we collected 5182 h of provisioning data (mean = 10.8 h d⁻¹, range = 4.1–14.1 h d⁻¹) over 481 nest-days (mean = 8.3 observation-days per nest, range = 2–18). Using these data, we observed 144 decisions by 120 non-breeding group members (24 individuals were observed during two breeding seasons) of known pedigree (see above) at 58 nests from 40 breeding females in 38 breeding units and 27 social groups. To test specific predictions, this sample of individuals had to be restricted (see §3).

Decisions, by non-breeding group members to provide help within their social group and where helpers directed care when they had a choice of where to help within their social group, were analysed using a combination of χ², binomial and Fisher's exact tests. In each analysis, we asked whether decisions of whether or where to help were influenced by the size of breeding units available and/or by the degree of relatedness between the non-breeding group members and available broods. Decisions of whether and where to help based on group augmentation should be sensitive to the size of the breeding units available while those based on kin selection should be sensitive to the relatedness between potential donors and recipients of care.

Helper contributions to cooperation were investigated for all natal and immigrant non-breeders observed to contribute to nestling provisioning, irrespective of whether they had a choice of where to help within their social group. We collected data from 96 helpers observed over 481 days at 58 nests in 27 social groups. We analysed daily individual feeding rates (feeds per hour; n = 1293 measures) by fitting generalized linear mixed models using a Laplace approximation with Tweedie compound Poisson errors (see electronic supplementary material, table S2 for further details) and a log-link function using the tweedie [35], cplm [36] and lme4 [31] packages in R v. 2.14.1 [30]. Our primary predictors of interest were unit size and helper relatedness to the brood. In addition, we fitted a unit size × relatedness interaction to test whether helpers contribute according to potential group augmentation benefits when kin-selected benefits are low. The duration of the observation period (results not shown), brood size, helper sex and age category were fitted as potentially confounding variables. Finally, brood identity nested within social group and individual identity were fitted as random intercepts to account for repeated sampling of each. Tweedie distributions are not yet compatible with model-averaging procedures [34] in R. For this reason, we assessed the significance of each predictor variable against the minimal model using likelihood ratio tests [37].

Data from this study have been deposited in Dryad (doi:10.5061/dryad.ff868).

3. Results

(a). Unit size effects: offspring production and provisioning

Breeding units successfully fledged an average of one brood per breeding season (range = 0–2). The number of offspring fledged per breeding unit per season ranged from 0 to 9 (mean = 3 ± 2 s.d.). The size of the breeding unit had a substantial bearing on annual fledgling production, although an asymptotic function fitted the data better than a linear one (see figure 1a; electronic supplementary material, table S1a). For every additional member of a breeding unit, annual increments to fledgling production increased by an average of 0.85 in units of three and four individuals, 0.28 in units of five and six, 0.14 in units of seven and eight and 0.07 in units larger than eight. Thus, additional unit members were associated with considerable increases in annual breeding success in small units, but in those over eight, further increments to unit size had negligible effects on productivity.

Figure 1.

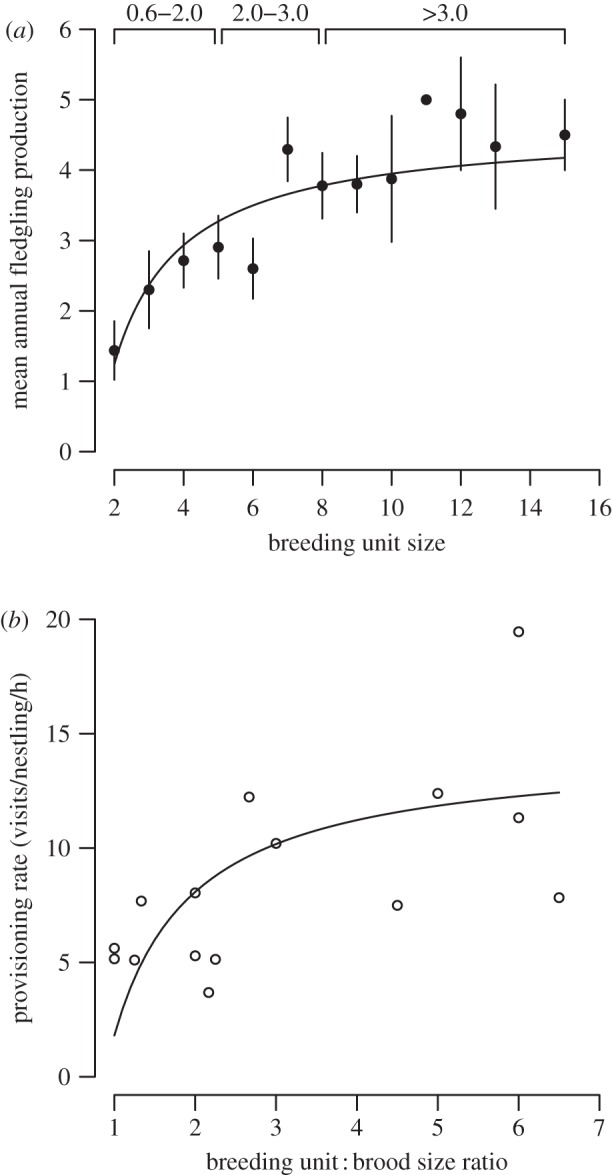
Breeding unit size effects. (a) Increasing breeding unit size was associated with an asymptotic increase in annual fledgling productivity (see electronic supplementary material, table S1a: y = 4.63–6.77x⁻¹; n = 125 measures, 106 breeding females, 3 years); and (b) Manipulating unit : brood size ratio led to a similar asymptotic relationship on the per capita rate at which nestlings received food (see electronic supplementary material, table S1b: y = 14.36–12.55x⁻¹; n = 15 measures (one data point is missing due to equipment failure), eight nests). Points show (a) raw means (±s.e.) and (b) raw values for each nest-treatment combination. Lines are generated from the best models. Brackets show naturally occurring range of unit : brood size ratios for the given range of unit sizes.

An asymptotic function also best explained the relationship between manipulated unit : brood size ratio and per capita nestling provisioning rates (see figure 1b; electronic supplementary material, table S1b). The rate at which each nestling in a brood received food increased steeply in unit : brood size ratios of up to 2 : 1, increased more slowly in ratios of between 2 : 1 and 3 : 1, and then effectively levelled off thereafter. Importantly, the experimentally created unit : brood ratios generating the steep, intermediate and flat functions describing nestling feeding rates (figure 1b), occurred naturally in unit sizes associated with steep, intermediate and flat functions describing fledgling production (figure 1a). These results suggest that helpers are sensitive to brood demand and that the unit size–productivity relationship was mediated, at least partly, by the differential effects of breeding unit size on the rate at which nestlings are fed.

(b). Whether and where to help: testing group augmentation and kin selection

The nonlinear effect of unit size on productivity generates predictions regarding whether and where members should help within a social group under group augmentation. Such predictions should be clearest for individuals helping for the first time, since their current actions cannot be confounded by previous ones. If group augmentation has a dominant effect on decisions to help, we would expect that: (i) immigrant and natal individuals will be similarly likely to help; (ii) that they will be more likely to help when units of fewer than eight individuals are available; and (iii) given the choice of helping non-kin in a breeding unit with fewer than eight versus kin in a unit of greater than eight, they should direct their efforts towards the former, because again only here can they enhance productivity. These predictions assume that first-time helpers do not simply follow a rule-of-thumb: live (and help) in the largest unit possible. If this were true, we would predict that in cases where the available choices are restricted to groups of fewer than eight (where helpers enhance productivity), they would always chose to help in the largest unit possible, even if kin are present in the smaller one. Alternatively, if there is a secondary influence of group augmentation on helping decisions, helpers should choose units of fewer, over larger, than eight when their relatedness to all potential recipients is equivalent.

We found no evidence for a dominant role of group augmentation on individual decisions to help. Of 52 individuals that could have helped for the first time in a given social group, approximately 75 per cent decided to do so, but new immigrants were 72 per cent less likely to help than natal yearlings (Fisher's exact test; p < 0.001; figure 2a, left bars). In addition, we found little evidence to suggest that individuals make decisions about whether to help based on the availability of breeding unit sizes in which they can affect productivity. Group members with the opportunity of helping for the first time in a given social group were no more likely to help when breeding units of below versus above eight were available (Fisher's exact test: p = 0.66; figure 2a, middle bars). Finally, in cases where first-time helpers could choose between breeding units of fewer versus more than eight, none chose to help in the smaller unit where they would have had a positive effect on productivity, but where kin were lacking (n = 12 individuals, eight social groups; one-sample binomial test; p < 0.001, 95% CI: 0, 0.26: figure 2a(i)). Similarly, when the choice of where to help was restricted to those in which all breeding units within a social group were of fewer than eight individuals, none chose to help at the largest unit, where the beneficial effects of group living are likely to be highest, but again where kin were absent (n = 8 individuals, five social groups; one-sample binomial test; p = 0.016, 95% CI: 0, 0.41: figure 2a(ii)).

Figure 2.

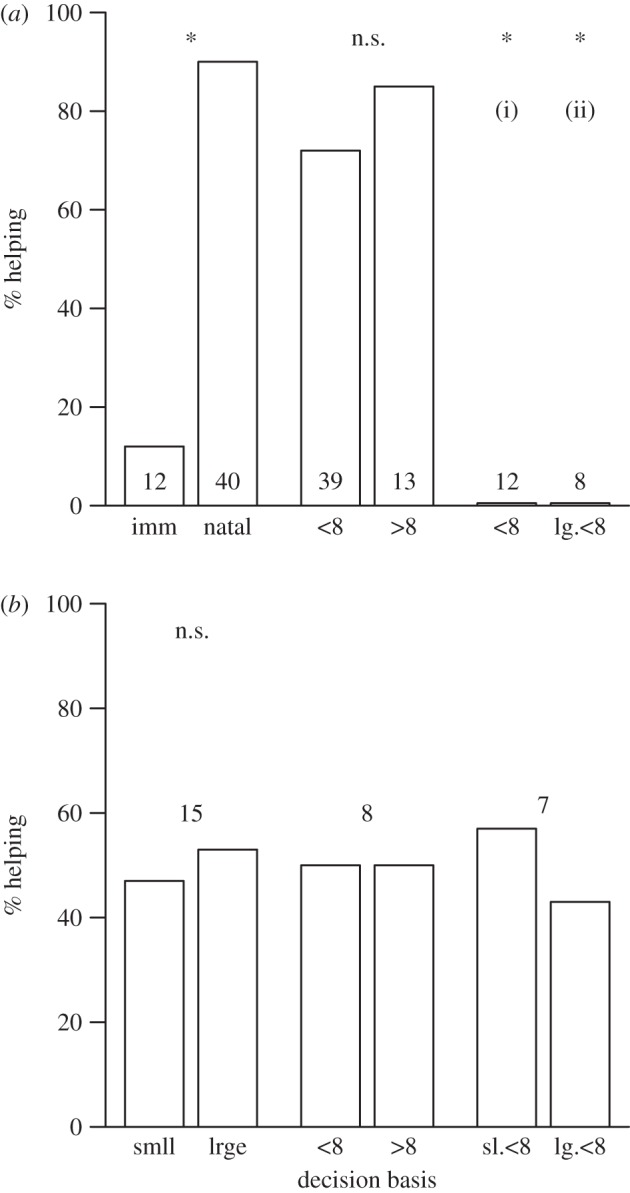
Decisions to help based on group augmentation for (a) first-time helpers and (b) helpers equally related to potential recipients. (a) Left bars: % immigrants (imm) versus natals helping; middle bars: % individuals helping in units less than eight individuals (where they could increase productivity) versus more than eight (where they could not); right bars: two specific predictions from group augmentation that are opposed by kin selection: (i) helpers choosing units less than eight with kin absent instead of more than eight with kin present; (ii) helpers choosing to help the largest unit when all available units are less than eight and kin are present in the smaller unit. (b) Left bars: % individuals choosing to help at the smaller (smll) versus larger (lrge) of two units available; middle bars: % individuals choosing to help at units less than eight versus more than eight where this was the only choice; right bars: % individuals choosing to help at the smaller versus larger unit where choice was restricted to units less than eight. In all cases, sample sizes are provided in the bars when specific to that bar, or between bars when specific to the comparison. Differences are shown as significant (*, p < 0.05) or non-significant (n.s., p > 0.05).

Moreover, we failed to detect a secondary effect of group augmentation on helper decisions. There was no systematic bias in the size of breeding units chosen to help, even when relatedness did not differ between donors and potential recipients within the social group. Of the 15 individuals that had a choice of helping in breeding units of different size, but where recipients were similarly related, 53 per cent chose to help at the larger unit while 47 per cent chose to help the smaller unit (one-sample binomial test; p = 0.99, 95% CI: 0.27, 0.79; figure 2b, left bars). The ambivalence of unit choice in such cases was also evident when we compared decisions to help in units of greater, versus fewer, than eight and in small versus large units of fewer than eight, although sample sizes for each were small (figure 2b, middle and right bars).

Taken together, the results above provide compelling evidence against a role of group augmentation in helper decisions for non-breeders, but suggest kin selection is important. To test the influence of kin selection, we investigated whether: (i) the presence of related broods affected the decision to a become helper and (ii) whether those with a choice of helping close-kin (0.25 ≤ r ≤ 0.5) versus distant/non-kin (0 ≤ r ≤ 0.125) chose to help kin over non-kin. Non-breeders (n = 120) showed a 232 per cent increase in their probability of helping if broods of close kin were present in their social group (χ² = 49.56, p < 0.001; figure 3a). In addition, in social groups where individuals had a choice of helping breeding units differing in kinship, 100 per cent helped the unit to whose offspring they were most related (χ² = 39.00, d.f. = 1, p < 0.001; figure 3b).

Figure 3.

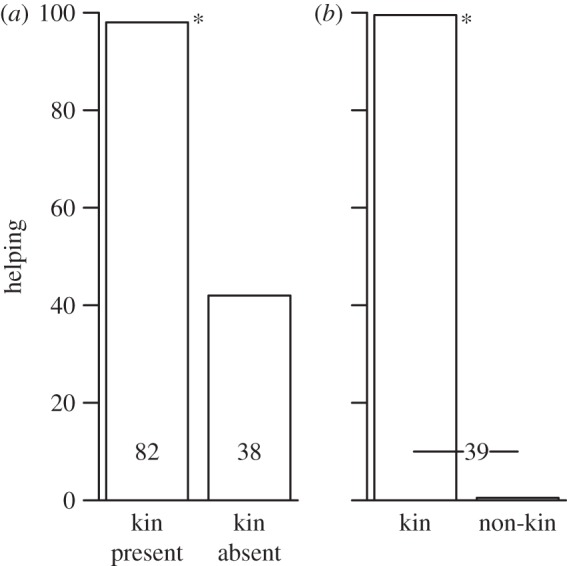
Decisions to help based on kinship. (a) % individuals that provided care when kin were present versus absent in their social group. (b) % individuals choosing to help at the nests of kin versus non-kin where the choice was available. Sample sizes are provided in the bars when specific to that bar, or between bars when specific to the comparison. Differences are shown as significant (*, p < 0.05) or non-significant (n.s., p > 0.05).

(c). Unit size and kinship effects on nestling provisioning rates

Immigrant and natal individuals that helped at the nest fed nestlings at an average rate of 2.1 times per hour (range = 0–8.3; see electronic supplementary material, table S2 for parameter estimates of predictors). Adult helpers fed nestlings more frequently than did yearlings, although there was no difference between the feeding rates of male and female helpers. Provisioning rates were positively associated with brood size and increased quadratically with chick age. After controlling for such effects, we found no evidence to suggest that unit size affected helper provisioning rates (unit size: L = 0.54, d.f. = 1, p = 0.46; unit size²: L = 1.16, d.f. = 1, p = 0.28), even under different levels of relatedness to the brood (unit size × relatedness interaction: L = 3.07, d.f. = 2, p = 0.22). By contrast, we found that relatedness had a significant effect on the rate at which helpers fed nestlings (figure 4; L = 76.61, d.f. = 2, p < 0.001): feeding rates were approximately three times higher when individuals were directing care to first- and second-order relatives compared with more distant/non-kin.

Figure 4.

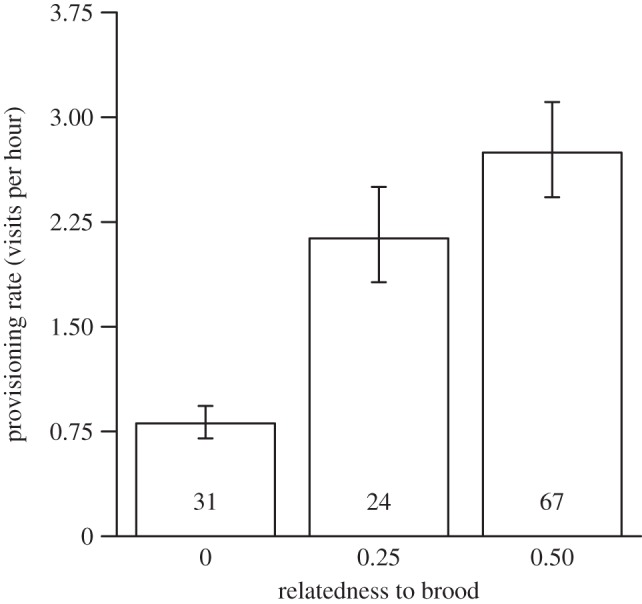
Relatedness to brood and helper provisioning. Relatedness had a significant effect on the rate at which immigrant and natal helpers fed young. Bars show means ± s.e. predicted by the model shown in electronic supplementary material, table S2, with other parameters set to their mean values. The number of individual-years in each category is shown at the base of each bar. Further sample sizes are given in electronic supplementary material, table S2.

4. Discussion

Group augmentation has been proposed as a particularly pervasive force selecting for cooperation in obligate cooperative breeders, in which reproductive attempts by pairs are rare and commonly unsuccessful. The chestnut-crowned babbler is an obligate cooperative breeder in which helpers have the potential to gain significant passive and active benefits from augmenting group size. Despite this, we found no support for predictions of group augmentation and considerable support for those of kin selection, at least in the ways tested here. Group augmentation failed to account for decisions of whether, whom and how often to help, while kinship explained all three measures. To our knowledge, this study represents the first attempt to examine directly the significance of group augmentation on decisions by group members to help, and one of the very few [12,13] to examine the predictions of group augmentation in the context of helper contributions.

Our predictions of group augmentation were largely based on the potential impact of helping on productivity in breeding units of variable size. Such a basis might be challenged for a number of reasons. For example, apparent helper effects on productivity can be non-causal [10,16]; so our predictions might not reflect true helper benefits from helping in groups of varying sizes. Group size manipulations [38] do not resolve this problem because only reductions are possible and they necessarily alter grouping benefits and disrupt social dynamics, making it difficult to verify that reductions in provisioning rates are caused by reductions in helper numbers [11]. Therefore, we used brood size manipulations which can circumvent the above problems [23,24]. Our experiment not only revealed that helpers are sensitive to varying brood demand, but also suggested why the effect of helpers on productivity asymptotes in breeding unit sizes above eight. The experimentally created unit : brood ratios that generated the steep, intermediate and flat functions describing nestling feeding rates (figure 1b) occurred naturally in unit sizes associated with, respectively, steep, intermediate and flat functions describing fledgling production (figure 1a). This suggests that the asymptotic relationship between unit size and productivity arises, at least partly, owing to a plateau in the amount of food nestlings received, presumably due to brood satiation.

Nevertheless, our predictions from group augmentation regarding whether, where and how often group members should help might be further challenged. First, helpers might gain greater group augmentation benefits by reducing the workload, hence increasing the survivorship of other carers, than by increasing offspring production. This is unlikely because we found little evidence that unit size influenced individual provisioning rates but substantial evidence that it increased annual productivity. Second, decisions of where to live and whether to help will depend not only on the future benefits of increased productivity, but also the current costs of living and helping in a given unit. For example, because breeding units function largely independently during breeding, a helper might gain higher survivorship benefits from living (and helping) in the largest breeding unit available in its group; outweighing the lesser effect it has on productivity in that unit. However, we found no evidence to suggest that helpers preferred to live in large units, independently of kinship.

The lack of evidence for the group augmentation hypothesis in this study cannot be explained by an absence of grouping benefits in this species. Large babbler groups are less likely to be attacked by predators, and calculations suggest that individuals continue to gain advantages through reduced predation in groups of up to approximately 20 birds [25]. In addition, we have detected substantial energetic savings from communal roosting, up to group sizes of at least eight (M. A. Chappell, W. A. Buttemer & A. F. Russell 2009, unpublished data). Thus, rearing additional group members would be expected to have significant survival benefits. Furthermore, helping to rear offspring might be expected to lead to significant active group augmentation benefits, since there is inter-annual repeatability in breeding unit composition. Thus, helping would appear to increase the work-force in a given breeding unit. Nevertheless, neither of these explanations accounts for helping by apparent non-relatives, and we can only speculate on the adaptive function of such helping. Analysis of non-feeding and false-feeding rates [39] have failed to reveal support for either social prestige [40] or pay-to-stay [41,42]. However, it would be premature to rule out either of these hypotheses at this stage, or a possible role of acquiring parenting skills [43].

Group augmentation is commonly invoked to explain several phenomena: (i) helping by non-kin; (ii) a lack of correlation between kinship and level of cooperation; (iii) greater cooperation by the philopatric sex; and (iv) a positive correlation between level of help and probability of becoming a breeder in the group. We caution that claims of support for the group augmentation hypothesis are ambiguous in all four cases. First, helping by non-kin is not itself evidence for group augmentation; low incidences of helping by non-kin are common [2,5,11], and in this study approximately 17 per cent of natals helped rear broods in the 0 relatedness category and 25 per cent of immigrants helped. Although further work is required to clarify helping by non-kin, we found no evidence for a role of group augmentation because unrelated individuals did not direct their care to groups where they could increase productivity and none of the immigrants that did help became breeders by the following breeding season. By contrast, 98 per cent of those with the chance of helping kin did so, and 100 per cent chose to help rear the more related brood. Second, while we found that helpers contributed more when helping kin than non-kin, they contributed similarly when rearing first- versus second-order relatives. Many studies have failed to find a relationship between relatedness and levels of care provided [9]. However, the absence of such a relationship does not necessarily counter predictions of inclusive fitness theory [7], provided that the opportunity to help more closely related individuals is not likely to arise in the future, and/or the long-term costs of contributing are low [19]. Third, a greater probability and level of helping by the philopatric sex are common features of cooperative societies [11], irrespective of whether augmenting group size is likely to be beneficial. An alternative explanation for sex differences are sex-specific differences in the costs of helping and/or the relative impact of helping costs for philopatric versus dispersive strategies [44]. Finally, positive correlations between levels of care and probability of breeding can be confounded by condition/quality. For example, condition is likely to have a positive effect on both helping effort and the likelihood of breeding [12,45], thereby creating a spurious relationship between the probability of breeding and propensity to help. We suggest that greater consideration of the potential confounding sources of variation is required before group augmentation is confirmed as the likely explanation of the above observations.

In conclusion, we provide convincing evidence for kin selection in an obligate cooperative breeder. Natals were the most common category of helpers, they virtually always helped when related broods were available, always chose close kin over distant/non-kin and provisioned such kin more frequently. Despite social groups containing a mix of kin and non-kin [29], the majority (82%) of natal helpers cared for full (57%) or half (25%) siblings, thereby increasing the survival of those siblings, suggesting that significant kin-selected benefits are accrued by the majority class of helper. These results are consistent with the emerging pattern in more facultative species [9], suggesting that kin selection is a general and powerful pressure selecting for cooperative breeding in vertebrates. Furthermore, we found no evidence for a primary or secondary selective role of group augmentation, at least as tested here. Group members did not base decisions of whether or where to help on their ability to enhance productivity and unrelated immigrants rarely helped. While it would be premature to rule out some role of group augmentation in the evolution or maintenance of cooperative breeding in this species, the available evidence suggests that it does not represent an important selective force. We urge future studies to be more cautious in inferring support for the group augmentation hypothesis without verification and due consideration of alternative possibilities.