Regional Variations in Mechanical Strain in the Posterior Human Sclera

Abstract

Purpose.

The goal of this study was to establish sectorial and regional variability in the mechanical strain of peripapillary and mid-peripheral sclera in normal eyes from elderly human donors.

Methods.

Ten pairs of normal eyes from human donors aged 57 to 90 years old were mechanically inflation-tested within 48 hours post mortem. The intact posterior scleral shells were pressurized from 5 to 45 mm Hg while the full-field three-dimensional displacements of the scleral surface were measured using laser speckle interferometry. The displacement field was fit to continuous and differentiable analytical functions, from which the full strain tensor of the outer scleral surface was calculated. Mean maximum principal (tensile) strain was computed for eight circumferential sectors (45° wide) within the peripapillary and mid-peripheral regions surrounding the optic nerve head (ONH).

Results.

Overall, the peripapillary sclera exhibited significantly higher tensile strain (1.2%) than mid-peripheral sclera (0.95%) for a 40 mm Hg IOP elevation (P < 0.00001). In the peripapillary region, the inferotemporal sector exhibited the highest tensile strain (1.45%) while the superior sector had the lowest (1.19%; P < 0.00001). Mid-peripheral scleral strains were lower but exhibited a similar sectorial pattern.

Conclusions.

Human posterior sclera exhibits complex regional mechanical behavior in response to acute IOP elevations from 5 to 45 mm Hg. Results indicate 1) the peripapillary sclera is subjected to significantly higher tensile strain than the adjacent mid-peripheral sclera, and 2) strains are significantly higher in the temporal and inferior quadrants of the peripapillary sclera, which may contribute to the increased prevalence of glaucomatous damage associated with these regions of the ONH.

When subjected to experimental inflation testing, human peripapillary sclera exhibits significantly higher tensile strain than the sclera further away from the scleral canal. Peripapillary scleral strains are highest in the temporal and inferior quadrants.

Introduction

Glaucoma is the second leading cause of blindness in the world after cataracts. The mechanism of damage to the retinal ganglion cell axons in glaucoma is not well understood, but it is hypothesized that IOP-driven biomechanics of the optic nerve head (ONH) and peripapillary sclera play a role.^1,2 The preponderance of evidence indicates that glaucomatous damage to retinal ganglion cell axons occurs at the ONH, a structure through which the axons pass out of the eye on their path to the brain. Evidence also suggests that the ONH is particularly susceptible to the effects of IOP, as it is less resistant to IOP-related mechanical stress than the other regions of the ocular coats.³ The sclera surrounds the ONH, and transmits IOP-related forces and deformations to the ONH at the scleral canal wall. Hence, scleral biomechanics are inseparably intertwined with ONH biomechanics.⁴

Sigal et al. determined that variations in scleral thickness, radius of the eye, laminar stiffness, and scleral thickness have the greatest influence on the biomechanical response of the ONH using computational models based on axisymmetric idealized geometries.⁵ A follow-up study using more accurate estimates of the ranges of laminar and scleral material properties indicates that laminar structural stiffness also plays a prominent role in determining laminar biomechanics.⁴ In a computational study, Norman et al. showed that the peripapillary sclera adjacent to the ONH is a particularly important factor in laminar biomechanics.⁶ Grytz et al. showed that the collagen architecture of the peripapillary sclera and the lamina cribrosa have a significant impact on the IOP-induced deformation response of the lamina cribrosa using computational modeling.⁷ These studies demonstrate that variation in both the material properties and geometries of the sclera and lamina, which combine to govern the overall structural stiffness of the posterior pole, are important determinants of the mechanical environment in the ONH.

Despite the importance of the sclera in determining ONH biomechanics, surprisingly few studies have been designed to accurately assess the sclera's mechanical behavior in human eyes. Studies have shown that the elastic properties of the sclera of various species are nonlinear^8,9 (stiffens as it stretches), anisotropic^9,10 (resists deformation more in certain directions), stiffens with age,^9,11 and remodels in response to chronic elevated IOP exposure.^12,13 Eilaghi et al.^14,15 confirmed the nonlinear behavior of the stress-strain relationship in human sclera using planar biaxial testing of small scleral patches excised near the ONH, although there was large variability among donors that resulted in a wide range of reported material properties. None of these studies report scleral strain values across the full peripapillary region in human eyes for physiologic loading conditions.

An inflation test setup employing precisely controlled pressure loading, coupled with an electronic speckle pattern interferometer (ESPI), allows us to capture three-dimensional full-field displacements for the entire surface of the posterior scleral shell with the high spatial resolution and sub-micrometer measurement precision necessary for local strain calculations. Inflation testing maintains the posterior eye in its natural geometry while the scleral shell is exposed to physiologic loading conditions, and full-field displacement measurements allow scleral strain calculation over the entire posterior third of each eye. Inflation testing of the posterior scleral shell to estimate global scleral material properties under physiologic loading conditions has been performed in murine,¹⁶ rabbit,¹⁷ bovine,¹⁸ nonhuman primate,¹³ and human eyes.⁸ However, only two of these studies used measurement techniques with sufficient spatial resolution to accurately determine local scleral mechanical strain (local tensile stretch, compression, and shear), and those studies were done in nonhuman primates.¹⁰

The principal aim of this work was to assess regional variations in the IOP-induced mechanical strain in the posterior human sclera for both the peripapillary and mid-peripheral regions using mechanical inflation tests. Regional variations in peripapillary strains could contribute to the focal structural and functional defects typically seen in glaucoma patients. This study was designed to test the hypothesis that regional variations in peripapillary scleral strain are significant, and to determine the ranges of strain present in the peripapillary and mid-peripheral posterior sclera subjected to experimental tests that mimic physiologic IOP loading. The results of these studies will serve as important inputs for future biomechanical modeling studies, and also provide accurate strain ranges for in vitro studies of the response of scleral cells to mechanical deformation.

Materials and Methods

Human Donor Specimens

Ten pairs of eyes from normal human donors aged 57 to 90 years old (average age: 78.5 years) were obtained from the Lions Eye Bank of Oregon in Portland, Oregon and the Alabama Eye Bank in Birmingham, Alabama. Donor eyes were deemed normal by next-of-kin questionnaire; donors with a history of glaucoma, severe myopia, or diabetes were excluded. All specimens were tested within 48 hours post mortem as follows.

Inflation Testing of Human Posterior Scleral Shells

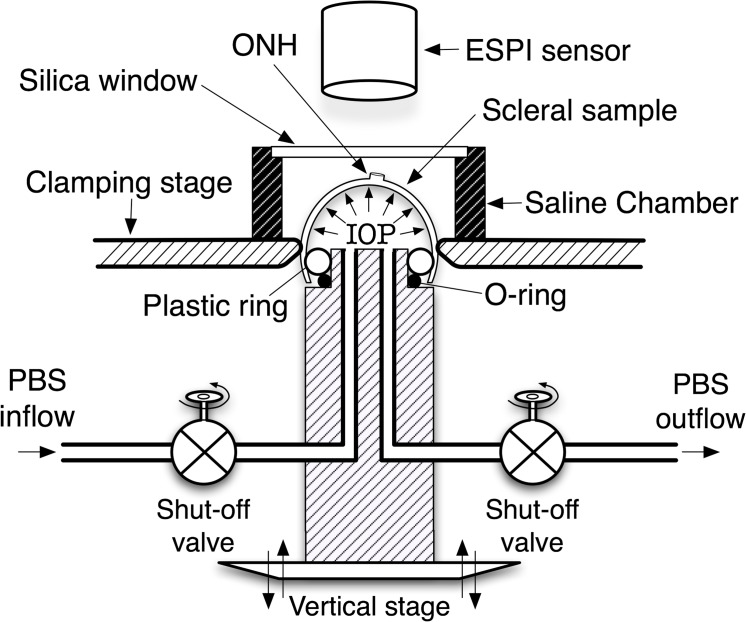
The custom scleral inflation testing apparatus and general protocol used in this work has been described in previous studies.¹⁰ Briefly, the scleral inflation testing apparatus consists of a clamping stage that allows the posterior third of the eye to be sealed and pressurized while preventing non-inflation induced motion (Fig. 1). A sealed chamber with a silica window was fitted atop the clamping stage, which allows the inflation testing to be performed with the specimen immersed in physiologic phosphate buffered saline solution (PBS) while measuring displacements optically through the window. An automated motorized lift stage connected to a manometer bottle was used to pressurize each scleral shell with PBS solution at precisely controlled pressure steps. Feedback for the pressure loading system was provided through a high-precision, in-line digital manometer with a serial data output (model XPi; Crystal Engineering, San Luis Obispo, CA).

Figure 1.  .

Pressurization apparatus for mechanical inflation test of spherically-shaped specimens. Reproduced with permission from Girard MJ, Suh J-KF, Bottlang M, Burgoyne CF, Downs JC. Scleral biomechanics in the aging monkey eye. Invest Ophthalmol Vis Sci. 2009;50:5226–5237.

Each eye was pressurized at room temperature from 5 to 45 mm Hg in small steps of 0.01 to 0.2 mm Hg while scleral surface displacements were recorded using a commercial laser speckle interferometer (ESPI; Q-100, Dantec Dynamics A/S, Denmark). After each pressure step, displacements were allowed to reach equilibrium before they were recorded, and pressure step size was carefully controlled via computer feedback during the testing protocol to ensure displacement steps of similar size. A starting pressure of zero could not be used since the posterior scleral shell does not maintain its shape at that pressure. So, we began testing at an internal pressure of 5 mm Hg, which was assumed to be a zero load condition for the purposes of strain calculation.

Soft tissue mechanical behavior is affected by preconditioning loads,^19,20 but the physiologic effects of preconditioning on soft tissues are not well understood. All sclera shells were subjected to the same preconditioning loading protocol, consisting of 20 pressurization cycles from 5 mm Hg to a maximum of 30 mm Hg at a rate of 5 mm Hg per second, and then allowed to recover for 15 minutes. The preconditioning and final inflation test protocols were applied in series at room temperature while the tissues were fully immersed in PBS solution to maintain tissue hydration, which has been shown to be important when testing biologic tissues.²¹

Measurement Accuracy and Uncertainty

Uncertainty of our displacement measurement system was assessed by measuring surface displacement of a spherically-shaped rubber specimen that was mounted and pressurized on the apparatus shown in Figure 1. The rubber test specimen was preconditioned as described above, pressurized to 25 mm Hg, then 10 additional cyclical pressure loadings of 0.5 mm Hg were applied. This test was repeated with the specimen immersed in air and then in PBS. A very small pressure load step was used to ensure a linear elastic response of the rubber specimen, which also ensures that the resulting deformation is solely a function of the pressure difference between internal and external surfaces of the rubber. Mean displacement measurement uncertainty was ±16 nm at the 95% confidence level,²² which is of sufficient resolution to accurately measure local scleral strains reported herein. Furthermore, ESPI possesses extremely high spatial resolution, as it measures displacements pixel-by-pixel.

B-Spline Based Displacement Fitting

Noise in the ESPI phase maps affect accuracy²³ and repeatability²⁴ of the measurements. Filtering phase maps before the unwrapping procedure introduces systematic errors that reduce the spatial resolution of the measurement system.²³ To avoid these problems, we used a strategy wherein phase maps were unwrapped with an algorithm robust to noise²⁵ and B-splines were then fit to the absolute phase maps with the aim of preserving a high spatial displacement resolution. This approach results in continuous and differentiable analytical functions that define the three-dimensional displacement field over the entire posterior third of the scleral surface.

The strategy used to build the B-spline system is conceptually based on the formulation proposed by Bruno,²⁶ where a set of functions based on the B-spline formulation is linearly combined to define the entire fitted domain. Incorporation of the numerical compensation²² and the customized B-spline fitting allows reconstruction of the local continuous deformation field at the nanometer-scale, which is necessary to quantify the point-to-point surface deformation associated with mechanically inhomogeneous, anisotropic, and hyperelastic tissues such as sclera. The customized B-spline fitting method that was used to analytically express the specimen shape and displacement field is a flexible tool that can fit noisy experimental data. In addition, using the same functional form to describe specimen shape and displacement allows direct surface deformation analysis and local strain calculation without any intermediate finite element modeling.

Eye-Specific Shape Reconstruction

Following inflation testing, the shape of each eye was acquired using a 3D digitizer with a nominal resolution of ∼ 0.2 mm (MicroScribe G2X, Immersion, San Jose, CA). Three-dimensional coordinates of ∼ 2500 points on the outer surface of the posterior sclera were acquired while the shell was pressurized to 10 mm Hg with PBS. To perform a transformation from Cartesian to spherical coordinate systems, a least squares nonlinear optimization was used to fit the digitizer point cloud to a sphere (eye-radius, and global coordinate-system location). This fitting resulted in a function sphere (θ, φ) that was used to describe the outer shape of the sclera of each eye as a sphere for all subsequent analyses. The B-spline based system described above was also used to obtain a continuous and differentiable function shape (θ, φ) that described the actual shape of the outer surface of each eye derived directly from the digitizer points, but the small difference between the best-fit sphere and the actual shape (<3% deviation at any point) made the additional computational cost of calculating the strains using the actual eye shape unnecessary.

Strain Calculations

The IOP-induced displacement field was measured using ESPI for each eye as described above, then processed to calculate the engineering strain tensor (ε(θ, φ), Equation 1) for the outer surface of each eye as follows. We based these calculations on small deformation theory because the 45 mm Hg pressure loading we applied engendered scleral strains that were generally below 5%. The linearized strain tensor accounts for the first-order infinitesimal displacement variations, which are generally accurate for strains up to of approximately 10%.

1. ESPI displacements in Cartesian space were filtered and fit to continuous, differentiable, analytical functions as described above, and then transformed into the best-fit spherical coordinate system sphere (θ, φ) for each eye.

2. Analytical differentiation of the resulting displacement function υ(θ, φ) = {u_θ(θ, φ), u_φ(θ, φ), u_r(θ, φ)], which defines the displacement field over the domain defined by the meridional [θ, 0, π/2] and circumferential [φ, 0, 2π] directions, was performed to reconstruct 5 out of 9 components (ε_θθ, ε_θφ, ε_φφ, ε_rφ, ε_rθ) of the full strain tensor (Equation 2) for the outer surface of each eye.

   

   where²⁷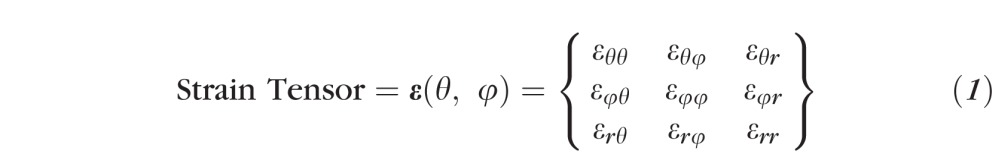

   
3. Three additional strain tensor components, ε_φθ, ε_φr, and ε_θr, were computed by strain compatibility equations (Equation 3) that ensure strain tensor symmetry,²⁷ and a single-valued continuous displacement field:

   

   (with i, j, k, l being indices varying from 1 to 3).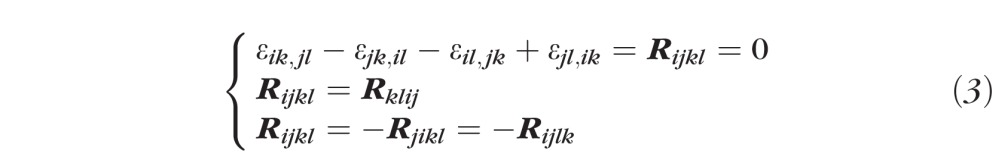

4. The one unknown component of the strain tensor, ε_rr, was computed by assuming tissue incompressibility, thereby imposing det[ε +I] = 1 (where I is the Identity Matrix).

Maximum principal tensile strain (ε_I, Equation 4) was computed over the entire scleral surface by computing eigenvalues of the full strain tensor:

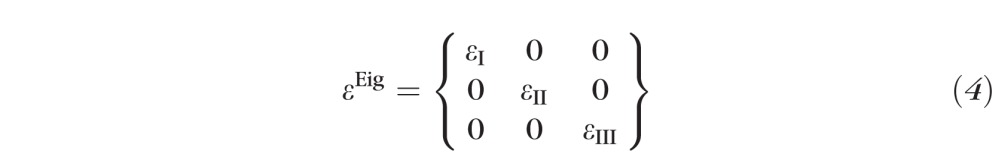Von Mises Equivalent Strain (${\epsilon }_{\text{VM}}=\sqrt{\frac{\text{2}}{\text{3}}{\epsilon }_{\text{ij}}^{\text{Eig}}{\epsilon }_{\text{ij}}^{\text{Eig}}}$), and Normalized Strain Energy Density (${\epsilon }_{\text{NSED}}=\sqrt{(Iiso{c}^2-3)}$, where Iisoc = tr(ε^Eig + I)) were also computed from the strain tensor eigenvalues.

The full strain tensor is made up of nine components as shown in Equation 1. It is difficult to interpret the local mechanical state of the material when it is expressed in terms of a tensor, so several methods have been developed to quantify local strain as a single scalar value with physical meaning. One such approach is the calculation of failure criteria for ductile materials, which are commonly used in analysis of damage mechanics (e.g., von Mises equivalence criteria or Normalized Strain Energy Density). A second is maximum principal strain (ε_I, the first eigenvalue of the strain tensor), which represents the local tensile strain. Maximum principal strain is believed to have direct influence in tissue growth and remodeling, and studies have shown it to be a driving force for the growth-direction of collagen fibers in bones (the well-known Wolff's law) and skin²⁸ (direction of Langer's lines). Collagen is the dominant load-bearing constituent of the sclera, so we chose to present our results primarily in terms of local maximum principal strain. We also present limited results for von Mises equivalent strain, which includes all three independent eigenvalues (Equation 4) and therefore represents the full three-dimensional mechanical state of the tissue. In addition, fibrillar load-bearing tissues exhibit nonlinear (or hyperelastic) material behavior, that is, they stiffen as they stretch. Normalized Strain Energy Density better represents the energy state of these hyperelastic materials, so we chose to present limited results for this measure as well. To calculate this, we used a strain energy density function chosen from among the several formulations available in the literature.

Regionalization and Strain Sampling

Mean maximum principal (tensile) strain, von Mises equivalent strain, and Normalized Strain Energy Density were computed overall and for eight circumferential sectors (45° wide) of equal surface area within both the peripapillary and mid-peripheral regions surrounding the ONH. The peripapillary region was defined as a ∼ 10 degree-wide-band adjacent to the ONH (approximately 2.2 mm wide) and the mid-peripheral region was defined for each eye such that it had the same surface area as the peripapillary region. Previous studies have shown that the peripapillary sclera adjacent to the ONH is a particularly important factor in laminar biomechanics^6,7 so we focused our measurements in this region.

Statistical Analysis

For each strain parameter in turn, strain at 46 equally-spaced sample points per sector were compared between the eight 45° sectors, first within the peripapillary region and then within the mid-peripheral region. In each case, a linear mixed effects model was used to determine whether sector was a significant predictive factor, accounting for the fact that there are multiple measurements within each sector and multiple sectors within each eye. A two-dimensional first-order autoregressive correlation structure was used to account for the fact that scleral strains at locations close to each other will be better correlated than locations further apart. Analyses of variance (ANOVA) were used to assess whether strains in the sectors within each region were significantly different from one another, and whether overall strains in the peripapillary and mid-peripheral regions (all sectors combined) were significantly different from one another.

Results

Regional Mechanical Strain Variation

Regional Differences.

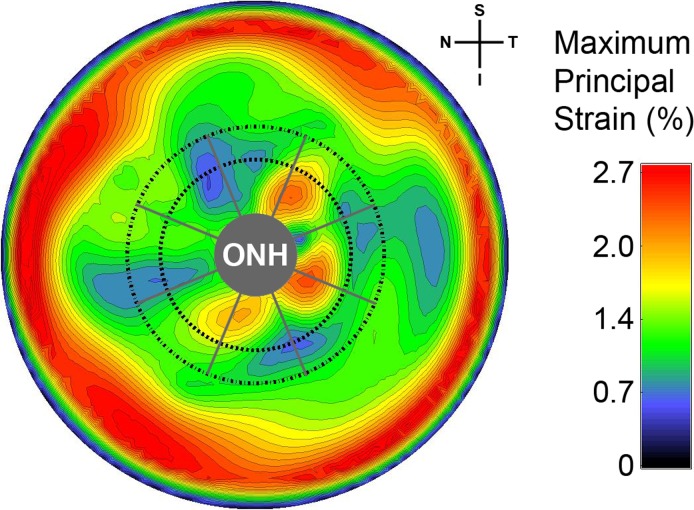
A contour map of tensile strain for a representative human scleral specimen is presented in Figure 2. On average, the peripapillary sclera exhibited significantly higher tensile strain (1.28%) than the mid-peripheral sclera (0.98%) for a 40 mm Hg IOP elevation (P < 0.00001). The von Mises equivalent strain (1.8% vs. 1.52%) and normalized strain energy density (0.31% vs. 0.26%) were also significantly higher in the peripapillary versus the mid-peripheral regions (P < 0.00001).

Figure 2.  .

Contour plot showing the maximum principal (tensile) strain for the posterior third of the intact scleral shell of a representative human eye for an IOP elevation from 5 to 45 mm Hg. The boundaries of the peripapillary and mid-peripheral regions surrounding the ONH are shown by the inner and outer dashed lines, respectively. The boundaries of the 45-degree-wide sectors are shown with radial gray lines. The spatial complexity and steep gradients of the strain around the ONH (3.3 mm in diameter in this eye) indicate that only techniques with extremely high spatial resolution and displacement measurement accuracy are appropriate for displacement and strain calculation in scleral shells subjected to inflation testing.

Sectorial Differences.

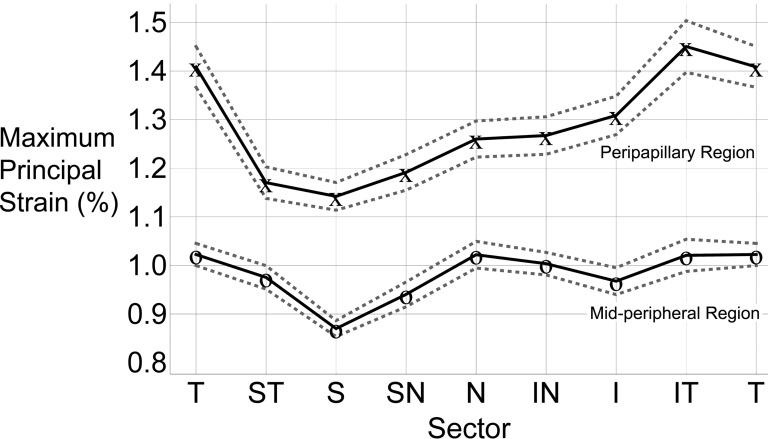
Regional differences in maximum principal (tensile) strain are presented in Figure 3 (assuming zero deformation at 5 mm Hg and a 40 mm Hg IOP elevation). In the peripapillary region, the tensile strains were generally highest in the temporal sectors and lowest in the superior sectors.

Figure 3.  .

TSNIT plot of the mean maximum principal strain for the eight circumferential sectors at 45 mm Hg (assuming zero deformation at 5 mm Hg and a 40 mm Hg IOP elevation) in the peripapillary and mid-peripheral regions averaged for all 20 eyes. The 95% confidence limits of the sector means are indicated by dotted lines. On average, the inferotemporal sector of the peripapillary sclera showed the highest tensile strain, while the superior sector had the lowest strain. In the mid-peripheral region, the temporal sector had the highest tensile strain, and the superior sector exhibited the lowest. Peripapillary sclera is subjected to significantly higher tensile strain than the mid-peripheral sclera. T, temporal; S, superior; N, nasal; I, inferior.

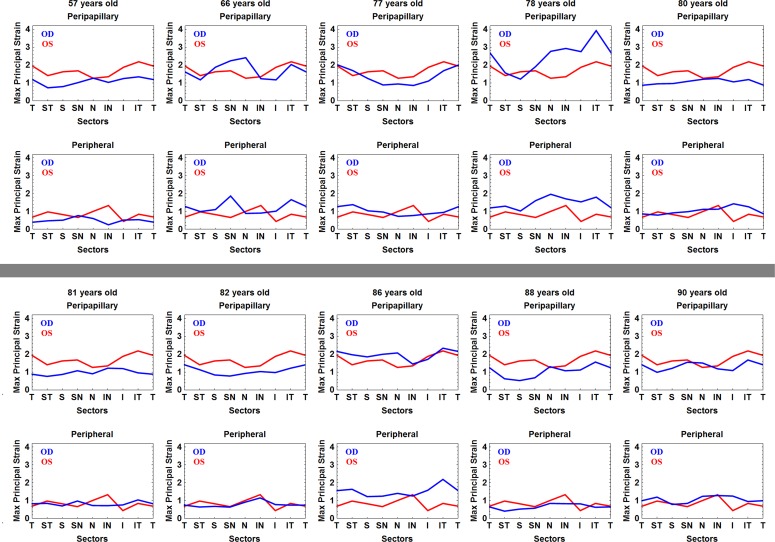
In the mid-peripheral region, the temporal sector had the highest tensile strain (1.02%) while the superior sectors exhibited the lowest strains. Sectorial variations were less pronounced in the mid-peripheral sclera compared to the peripapillary sclera. Superior sectors exhibited the lowest strains and strains in the temporal sectors were among the highest in both regions. In individual eyes, sector means for tensile strain ranged from 4.58% to 0.12%, inclusive of both regions (Fig. 4). This indicates that while the sectorial and regional variability followed a similar pattern within eyes, some eyes exhibited much higher strain levels than others (Fig. 4). The von Mises equivalent strain and normalized strain energy density exhibited the identical sectorial distribution as that shown for the tensile strain (Table).

Figure 4.  .

TSNIT plot of the mean maximum principal strain for the eight circumferential sectors at 45 mm Hg (assuming zero deformation at 5 mm Hg and a 40 mm Hg IOP elevation) in the peripapillary and mid-peripheral regions for all 20 individual eyes from 10 human donors. Confidence limits of the sector means are not shown, because the autocorrelation function applied to the sample point data in the overall analysis is not appropriate for application to data from individual eyes. T, temporal; S, superior; N, nasal; I, inferior.

Table.  .

Regional and Sectorial Values for Strain Averaged across all 20 Human Donor Eyes in the Study

Region / Sector	Maximum Principal Strain (%)	von Mises Equivalent Strain (%)	Normalized Strain Energy Density (%)
Peripapillary	Mean = 1.28	Mean = 1.80	Mean = 0.31
T	1.41	1.94	0.34
ST	1.17	1.68	0.29
S	1.14	1.61	0.28
SN	1.19	1.69	0.29
N	1.26	1.77	0.31
IN	1.27	1.80	0.31
I	1.31	1.89	0.33
IT	1.45	2.07	0.36
Peripheral	Mean = 0.98	Mean = 1.52	Mean = 0.26
T	1.02	1.56	0.27
ST	0.98	1.49	0.26
S	0.87	1.41	0.24
SN	0.94	1.45	0.25
N	1.02	1.55	0.27
IN	1.00	1.57	0.27
I	0.97	1.54	0.27
IT	1.02	1.59	0.28

Figure 2 shows how strain values are particularly pronounced in the peripheral sclera near the clamp. The nature of inflation testing of quasi-spherical specimens requires that the radial displacement component (u_r) is zero at the clamp ring; this forces a steep gradient in the radial displacements near the clamp and induces a large shear deformation (ε_rθ in Equation 2). All three strain measures reported herein include this shear component, so the outer boundary of the studied regions were located sufficiently distant from the clamping ring such that the clamp-induced shear deformation was approximately zero.

Summary and Discussion

Summary

The main finding of this work is that human posterior and peripapillary sclera exhibits complex regional and sectorial mechanical behavior in response to an acute IOP elevation from 5 to 45 mm Hg. Our results indicate (1) the peripapillary sclera is subjected to significantly higher tensile strain than the adjacent mid-peripheral sclera, and (2) peripapillary scleral strains are significantly higher in the temporal and inferior quadrants, which may contribute to the increased prevalence of glaucomatous damage associated with these regions of the ONH. Finally, mean scleral tensile strains in ostensibly normal eyes from elderly human donors were in a reasonable range (0.87% to 1.41%) that is likely to be well tolerated by resident cell populations. However, there is a wide range of behaviors in individual eyes, and sector tensile strains were as high as 4.58% in one eye and as low as 0.12% in another. This indicates that while there is a similar pattern of sectorial and regional variation in tensile strain, some eyes exhibited much higher strains overall than others. Hence, some eyes may be subjected to strains at elevated IOPs that are well outside the homeostatic range of the resident scleral fibroblasts and myofibroblasts, which could induce a scleral remodeling response.¹³ The regional and sectorial variations in strain reported herein were consistent across three separate strain formulations (Maximum Principal Strain, Normalized Strain Energy Density, and von Mises Equivalent Strain), which indicates that the reported results are robust in terms of representing the overall mechanical strain state of the tissues.

Limitations

This work should be considered with the following limitations in mind. First, there is some displacement error at the outer edge of the specimen due to ESPI phase map reconstruction difficulties. This is unavoidable for cap sphere geometries such as this, but it does create considerable uncertainty at the edges of the posterior scleral shell near the clamp boundary. To minimize the effect of these errors, we positioned the ONH and peripapillary sclera at the center (apex) of the posterior scleral specimen when clamping it in the pressurization apparatus. This positioning, coupled with analyzing strains in a relatively narrow band around the ONH, ensures that the reported measurements are accurate and reliable.²² Second, the pinhole model assumption underlying the ESPI compensation methodology used in this work²² could be a source of error that limits the presented method's capabilities. However, our measurement uncertainty²² of ±16 nm should be more than sufficient to capture scleral deformations with the displacement measurement precision and spatial resolution required for the sectorial and regional strain analyses presented herein. Third, we assumed that the sclera is incompressible to calculate one of the nine strain tensor components necessary for our analyses. Human sclera is composed of approximately 70% water,²⁹ which should result in only slight compressibility. Furthermore, this assumption is unlikely to lead to significant errors in the reported strain values since it affects computation of only one of the nine strain tensor components that form the strain values reported. Fourth, we assumed that the sclera is at a zero-strain state at 5 mm Hg IOP, so the strain values we report are likely lower than the true strain. Computational methods exist to estimate the pre-existing strains³⁰ at 5 mm Hg, but we did not apply them in this study because the regional and sectorial strain distributions that are the focus of this report should be unaffected by this assumption. Fifth, we assumed that the donor eyes were normal without confirming normality through an ophthalmic exam performed while the patient was living. This could prove crucial for studies on cellular activity or neural tissues, or those that are designed to detect differences due to treatments or disease states such as glaucoma. However, there are relatively few pathologies that are likely to significantly impact scleral biomechanics we report for ostensibly normal eyes, and these were broadly excluded based on next-of-kin questionnaire. Finally, we performed our scleral inflation testing at room temperature, which could affect the biomechanical response of the tissues. We could not heat the specimen bath, because the ESPI displacement measurement system we used is so sensitive that thermal convection currents in heated PBS induce measurement errors. The strain values we measured are reasonable and several previous studies have performed scleral testing at room temperature.^10,31 In any case, regional and sectorial strain variations we report should not be affected by testing temperature because all specimens were tested under identical conditions.

Discussion

This study is the first to report regional and sectorial variations in mechanical strain in the peripapillary sclera around the ONH in human eyes subjected to inflation testing. Using PBS to pressurize the intact posterior scleral shell, coupled with full-field displacement measurements made while the specimen is fully immersed in PBS, allows testing to be performed in physiologically mimetic conditions that cannot be achieved with uni- or bi-axial mechanical testing of excised tissue strips or patches. Mechanical testing of strips or patches has some advantages, such as independent control of the loading direction, but these approaches also engender artifact by requiring that the sclera be flattened from its naturally curved shape for testing. In addition, uni- and bi-axial testing cannot capture strains due to stress concentrations around the scleral canal, or measure strains over the full posterior pole of an eye.

The optimized ESPI technique we used allows scleral strain analyses that are not possible with other measurement methods. First, to calculate strain accurately in structurally inhomogeneous tissues such as the sclera, one must accurately measure differential displacement of adjacent locations, and the maximum distance between these measurement locations is dependent on the degree of structural inhomogeneity. The peripapillary sclera exhibits a high degree of structural inhomogeneity resulting from both geometric factors (the sclera varies in thickness and surrounds a relatively compliant ONH) and material factors (scleral collagen fibril orientation varies by location). Accurate characterization of the resulting strain concentrations and steep strain gradients seen in Figure 2 requires displacement measurement techniques like ESPI that possess extremely high spatial resolution, high accuracy, and low measurement uncertainty (error). Calculations of strain (change in length/original length) require that one measure the differential displacement between adjacent points. The width of the low-strain area in the temporal sector of the peripapillary region is approximately 200 μm. To calculate the 0.5% strain in this low strain area, one must measure the differential displacement between points on the area boundaries, which requires displacement measurement spatial resolution of < 200 μm, a displacement measurement accuracy on the order of 500 nm (two points moving 500 nm apart is equivalent to a 1 μm differential displacement, and hence 0.5% strain). In this case, the displacement measurement uncertainty of ±16 nm we have shown for our ESPI system²² implies up to a 3.2% error in the differential displacement measurements and reported strain calculations.

Second, to capture the smallest statistically significant inter-sector strain differences (on the order of 0.05%) reported in the Table, the measurement technique must possess the spatial resolution, measurement accuracy, and measurement uncertainty capable of distinguishing between the mean displacements of different sectors. The arc length of each sector is ∼ 1300 μm near the ONH, and detecting a difference of 0.05% in linear deformation (strain) between two sectors would require a displacement measurement uncertainty or error of less than 650 nm. Finally, the sclera is hyperelastic, but that does not necessarily mean that the scleral deformations are large, especially for relatively small pressure loads used in this study. We have reported strain for an IOP load of 5 to 45 mm Hg, but to characterize the hyperelastic (nonlinear) mechanical response of the sclera, one must measure the small, step-wise displacements between 5 and 45 mm Hg, for example, 5 to 7.5 mm Hg, 7.5 to 10 mm Hg, 10 to 15 mm Hg, …etc. Small pressure steps and the accurate measurement of correspondingly small displacements are necessary to capture the variable curvature of the sclera's stress-strain response and hence calculate hyperelastic material properties. We have shown that our ESPI system is capable of displacement measurements well within the sub-micrometer tolerances required for these three different situations.²²

Other commonly used non-contact optical measurement methods, such as 3D DIC, lack the spatial resolution³² and/or measurement accuracy and uncertainty³³ necessary to accurately capture peripapillary scleral deformations during mechanical inflation tests. Cirello and Pasta directly compared the ability of ESPI and DIC to detect small deformations around a circular hole in a metal plate subjected to tensile loading, a mechanical condition similar to the scleral canal and ONH. This study showed that the ESPI technique accurately measured the steep deformation gradient around the hole, but DIC was unable to properly resolve the deformation field due to its lack of spatial resolution.³⁴ These results show that DIC cannot measure steep deformation gradients or local strain variations in specimens with mechanical discontinuities or inhomogeneities like those present in scleral shells subjected to inflation loading. However, DIC is appropriate for relatively homogeneous deformation fields, and its fast acquisition time makes it ideal for time-dependent deformation measurements.

The detailed regional and sectorial distributions of scleral strain are important, as they inform us about the strains that scleral tissues and the resident cells actually experience when IOP is elevated, both acutely and chronically. We measured scleral tensile strains that were significantly higher in the peripapillary sclera compared to the adjacent mid-peripheral sclera. IOP-related stress is concentrated in the peripapillary sclera around the ONH,³⁵ but these stress concentrations are resisted by a reinforcing, circumpapillary ring of collagen fibers.^7,36–38 To the authors' knowledge, this is the first study to report local strains in human peripapillary sclera that are the direct result of the interplay between IOP-induced stress concentrations and the resistance provided by the circumpapillary ring of collagen. Deformation of the peripapillary sclera relative to the mid-peripheral sclera has been observed in nonhuman primates after acute IOP elevation from 10 to 30 or 45 mm Hg using both histomorphometry³⁹ and in vivo OCT imaging,⁴⁰ and the higher peripapillary strains we report herein for human eyes are consistent with those observations.

Our previous study using uniaxial testing of sclera strips from nonhuman primates reported no significant sectorial differences in peripapillary scleral strain in the 0% to 2% range, but we did report that the equilibrium modulus (stiffness) of the sclera in the temporal quadrant was the lowest of the four tested quadrants, although that finding did not achieve statistical significance.⁴¹ Several modeling studies have estimated strain values in the peripapillary sclera but none have used material property models that incorporate circumpapillary collagen fibril anisotropy, so these estimates are likely unreliable. Thus, the reported sectorial and regional scleral strain values reported herein can serve as benchmarks for validation of future computational models as well as define the appropriate strain ranges for applying mechanical deformations to scleral cells and tissues in vitro.

A similar pattern of sectorial and regional variation in tensile strain was found in all eyes, but some eyes exhibited much higher strains overall than others (range: 0.12%–4.58%). This wide range of strain between different eyes may relate to variations in the distribution of scleral components such as collagen, elastin, or crosslink density. Furthermore, the sclera is a living tissue that may remodel and grow in response to different stimuli including IOP-induced mechanical strain. Hence, the variation in strain might relate to different IOP loading and remodeling histories of each eye.^13,42

It is interesting that the high strains in the inferotemporal sector we report (Fig. 2) correspond to the regional distribution of neuroretinal rim area loss rates seen in a recent longitudinal study in glaucoma patients and normal age-matched controls.⁴³ This suggests the possibility that the variation in strain reported herein is either a risk factor associated with the pathogenesis of glaucoma, or secondary to a remodeling response seen in both aging eyes and those with glaucoma. While we do not fully understand the extent to which peripapillary scleral strain is transmitted to the ONH and lamina cribrosa or how laminar strain induces axonal damage, it is plausible that high regional peripapillary strains induce high strains in the adjacent lamina cribrosa, and those strains contribute to focal glaucomatous axon loss. Further work should be done to elucidate the mechanistic relationships between peripapillary scleral strains, laminar strains, and glaucomatous vision loss.