Grid inhomogeneous solvation theory: Hydration structure and thermodynamics of the miniature receptor cucurbit[7]uril

Abstract

The displacement of perturbed water upon binding is believed to play a critical role in the thermodynamics of biomolecular recognition, but it is nontrivial to unambiguously define and answer questions about this process. We address this issue by introducing grid inhomogeneous solvation theory (GIST), which discretizes the equations of inhomogeneous solvation theory (IST) onto a three-dimensional grid situated in the region of interest around a solute molecule or complex. Snapshots from explicit solvent simulations are used to estimate localized solvation entropies, energies, and free energies associated with the grid boxes, or voxels, and properly summing these thermodynamic quantities over voxels yields information about hydration thermodynamics. GIST thus provides a smoothly varying representation of water properties as a function of position, rather than focusing on hydration sites where solvent is present at high density. It therefore accounts for full or partial displacement of water from sites that are highly occupied by water, as well as for partly occupied and water-depleted regions around the solute. GIST can also provide a well-defined estimate of the solvation free energy and therefore enables a rigorous end-states analysis of binding. For example, one may not only use a first GIST calculation to project the thermodynamic consequences of displacing water from the surface of a receptor by a ligand, but also account, in a second GIST calculation, for the thermodynamics of subsequent solvent reorganization around the bound complex. In the present study, a first GIST analysis of the molecular host cucurbit[7]uril is found to yield a rich picture of hydration structure and thermodynamics in and around this miniature receptor. One of the most striking results is the observation of a toroidal region of high water density at the center of the host's nonpolar cavity. Despite its high density, the water in this toroidal region is disfavored energetically and entropically, and hence may contribute to the known ability of this small receptor to bind guest molecules with unusually high affinities. Interestingly, the toroidal region of high water density persists even when all partial charges of the receptor are set to zero. Thus, localized regions of high solvent density can be generated in a binding site without strong, attractive solute-solvent interactions.

INTRODUCTION

Hydration plays a central role in aqueous molecular recognition, because the binding of two solutes necessarily entails displacement of water from their surfaces. The properties of this surface water are directly related to the surface energy and entropy of the solute-water interfaces and hence influence the overall thermodynamics of binding. Computational tools for gaining insight into the thermodynamic properties of water at molecular surfaces are thus of considerable interest, and also have important practical applications, due to the importance of molecular recognition in supramolecular chemistry and biomedicine. However, the development of such tools still poses practical challenges and conceptual conundrums.

In the setting of structure-based drug-design, for example, it is often unclear on structural grounds whether the optimal strategy for designing a high affinity ligand will involve displacing crystallographic water molecules, using them as bridges between the ligand and the protein, or avoiding contact with them altogether.^{1, 2, 3, 4, 5, 6, 7} It may even be unclear how to rigorously pose such questions, as a crystallographic water is actually a site of high water density, with water molecules exchanging in and out on some time-scale; and the consequences of extending the ligand into such a site must depend not only on the nature of the site but also on the ligand group that comes to occupy it. Although binding-site regions with a water density lower than that of bulk water will not be highlighted crystallographically, they, too, may have implications for ligand optimization;⁸ and some binding pockets favor more complex multi-water structures that can affect ligand binding affinities.⁹ Thus, although crystallographically identified waters are of great interest, they are only the tip of the iceberg, because the rest of the water in a binding pocket also is perturbed relative to bulk, in a manner determined by the shape of the local protein surface and its patterning of hydrophilic and hydrophobic groups.

Continuum solvent models^{10, 11, 12} can capture key aspects of hydration, notably the consequences of water's high dielectric constant^{13, 14, 15, 16, 17, 18} and the hydrophobic effect,^{19, 20, 21, 22, 23} but they do not capture the consequences of the finite size of water molecules and the directionality of their hydrogen-bonds. Although one may supplement a continuum model with a few strategically placed explicit water molecules, it is not clear how to treat the thermodynamics of such a mixed model rigorously. Molecular simulations with explicit water account for the molecular, rather than continuum, nature of water, but do not in themselves provide much insight into the local properties of water in a binding pocket. For this, further analysis tools are needed. One important approach involves using thermodynamic integration (TI) or related methods to compute the work of extracting an isolated water molecule from a binding pocket.^{24, 25, 26, 27, 28} However, it may be difficult to apply this approach in settings of partly occupied water sites or sites where a removed water molecule would immediately be replaced by another from the bulk.

Several groups have addressed these challenges by using a statistical thermodynamic approach called inhomogeneous solvation theory^{29, 30, 31} (IST) to extract local thermodynamic information from molecular dynamics (MD) trajectories and thus provide insight regarding the thermodynamics of crystallographic waters^{32, 33, 34, 35} and other highly occupied water sites.^{8, 9, 36, 37, 38, 39} Thus, the pioneering WaterMap^{9, 37} and solvation thermodynamics of ordered water (STOW)³⁵ methods use MD simulation data to evaluate the entropy of the water occupying specific hydration sites, as well as the mean energetic interaction of this water with the rest of the system. This approach has provided valuable insight into the role of specific water sites in molecular recognition. For example, application to the binding pocket of streptavidin revealed five high-occupancy water sites with energetics similar to that of bulk water but with geometric restrictions that lead to greatly reduced orientational and translational entropy.⁹ The large entropic gain when these waters are ejected into the bulk presumably helps account for the remarkably high affinity of streptavidin for the small molecule biotin.⁴⁰ In another scenario, the water in a highly occupied site cannot form its full complement of hydrogen bonds,^{9, 36} and it has been estimated that ejecting even a single such frustrated water molecule into the bulk can yield a biologically significant contribution to the free energy, up to several kilocalories per mole.^{8, 36, 41, 42, 43, 44} Such phenomena are not accounted for well by continuum solvent models yet are important determinants of binding affinity.

Nonetheless, implementations of IST to date still have significant limitations. Of particular concern is that they have been restricted to analysis of high-occupancy, single-water hydration sites, so they do not provide information on larger high-density regions, weakly occupied sites or regions where the water density is low, rather than high, relative to bulk.⁴¹ In addition, it is not clear how the results of site-based IST implementations relate to standard treatments of solvation thermodynamics, such as continuum models or thermodynamic integration with explicit solvent, and this lack of connection to solvation free energies has made the results of IST difficult to interpret or assess rigorously. Thus, there is still a need for a clear conceptual framework, coupled with practical tools, for thinking about, modeling, and taking advantage of the structure and thermodynamics of water in protein binding pockets.

Here, we seek to address this need with grid IST (GIST), an implementation of IST which overcomes the limitations, noted above, of prior implementations. The chief innovation of GIST is that it discretizes the spatial integrals which appear in IST's entropy and energy expression onto a three-dimensional (3D) grid, thus avoiding any need to define hydration sites or water clusters within a binding pocket, or to use a separate theory for water-depleted regions. The present study, details the GIST methodology and describes a first application to cucurbit[7]uril (CB7),⁴⁵ a small, synthetic receptor. This model system is of particular interest because it binds guest molecules in water with extraordinarily high affinities normally associated only with much larger biomolecules.^{46, 47} It has been argued that these high affinities result from the preorganization of this host molecule and its guests, combined with their high degree of chemical complementarity.⁴⁸ However, it is also possible that something special about the structure and thermodynamics of the water in and around this unique host molecule helps it to achieve such high binding affinities. The present GIST analysis focuses in particular on the structure and thermodynamics of water within the rounded, hydrophobic central cavity of this pumpkin-shaped⁴⁸ receptor.

THEORY AND METHODS

The solvation entropy of a flexible solute may be written as

$$\int p\left(\mathbf{q}\right)\Delta S_{solv}\left(\mathbf{q}\right)d\mathbf{q},$$

where q represents the internal coordinates of the solute, p(q) is the Boltzmann probability density over these coordinates, and ΔS_solv(q) is the solvation entropy the solute would have if it were constrained in conformation q.⁴⁹ Analogous expressions apply for the solvation energy and free energy. Here, as in prior applications of IST, we consider the solvation of a solute in a given conformation, or in a narrow range of conformations, although one could, at some computational cost, explore solvation over a range of conformations by applying IST to each one separately. For simplicity, we will refer to ΔS_solv(q) as the solvation entropy and write ΔS_solv instead of ΔS_solv(q), and will proceed analogously for the solvation energy and free energy. Given a solute in a conformation of interest, then, GIST uses multiple solvent configurations sampled from a canonical distribution to evaluate leading terms in the multi-body expansions of solvation entropy and energy provided by IST. This is done by discretizing the analytic expressions of IST onto a 3D grid that is fixed in the reference frame of the solute and extends several solvation layers into solution around the solute. Subsections 2A, 2B, 2C review the required theory, describe the approach taken to discretization, and detail the present simulations and their analysis.

Inhomogeneous solvation theory

Like other liquid theories,⁵⁰ IST transforms integrals over the coordinates of all solvent molecules to integrals over distribution functions, leading to expressions for thermodynamic quantities that are expressed in terms of one-water, two-water, and higher order distribution functions.^{29, 51, 52, 53, 54} Here, we focus on the lower order terms, as these are relatively tractable computationally and are expected, based in part on prior applications of IST (see Introduction), to capture much of the physics; higher order terms will be examined in future studies. Subsections 2A1, 2A2 briefly review IST in order to define notation and provide a basis for the discretization methodology.

Solvation entropy

The solvation entropy, ΔS_solv, of a solute in a given conformation may be decomposed as,^{30, 31, 55}

$$\Delta S_{solv}=\Delta S_{sw}+\Delta S_{ww},$$ (1)

where ΔS_sw accounts for solute-water correlations and ΔS_ww for water-water (ww) correlations. Here, we limit attention to the solute-water term,

$$\Delta S_{solv}\approx \Delta S_{sw}\equiv -k_B\frac{{\rho }^o}{8{\pi }^2}\int g_{sw}(\mathbf{r},\omega )d\mathbf{r}d\omega ,$$ (2)

where the approximation reflects the single body truncation of the entropy expansion, so that it accounts for only solute-water correlations; k_B is Boltzmann's constant; ρ^o is the number density of bulk solvent; g_sw(r, ω) is the solute-water pair-correlation function in the solute frame of reference, where r may be defined as the location of a water oxygen relative to the solute and ω may be defined by Euler angles in the solute frame of reference; and the factor of 1/(8π²) normalizes the orientational integrals. The form of the integrand resembles the −ρlnρ form of the Gibbs/Shannon entropy. However, because g_sw(r, ω) is unity for bulk density and a uniform orientational distribution, the first-order solvation entropy appropriately goes to zero for bulk. In addition, because solute-solvent correlations are short in range, the function g_sw(r, ω) approaches unity with increasing distance from the solute, the integrand decays to zero, and ΔS_solv may be approximated by a local integral around the solute.³⁰

The solute-water entropy term, ΔS_sw, is without approximation broken into intuitively meaningful and computationally tractable translational and orientational terms⁵⁶ by rewriting g_sw(r, ω) as the product of a translational distribution function and an orientational one conditioned on the position, r: g_sw(r, ω) = g_sw(ω|r)g_sw(r) so that,

$$\begin{array}{ccc}\hfill \Delta S_{sw}& =& \Delta S_{sw}^{trans}+\Delta S_{sw}^{orient},\hfill \\ \hfill \Delta S_{sw}^{trans}& \equiv & -k_B{\rho }^o\int g_{sw}\left(\mathbf{r}\right)\ln g_{sw}\left(\mathbf{r}\right)d\mathbf{r},\hfill \\ \hfill \Delta S_{sw}^{orient}& \equiv & {\rho }^o\int g_{sw}\left(\mathbf{r}\right)S^{\omega }\left(\mathbf{r}\right)d\mathbf{r},\hfill \\ \hfill S^{\omega }\left(\mathbf{r}\right)& \equiv & \frac{-k_B}{8{\pi }^2}\int g_{sw}\left(\omega \right|\mathbf{r})\ln g_{sw}\left(\omega \right|\mathbf{r})d\omega ,\hfill \end{array}$$ (3)

where g_sw(r) ≡ ρ(r)/ρ^o and $g_{sw}\left(\omega \right|\mathbf{r})\equiv \rho \left(\omega \right|\mathbf{r})/{\rho }_{\omega }^o=8{\pi }^2\rho \left(\omega \right|\mathbf{r})$. The quantity S^ω(r) is a local orientational entropy relative to that of bulk solvent, and ρ^o∫g_sw(r)S^ω(r)dr is the local orientational entropy density. It is also possible to write S^ω(r) in terms of orientational densities,⁵⁷

$$S^{\omega }\left(\mathbf{r}\right)=-k_B\int \rho \left(\omega \right|\mathbf{r}\left)\ln \rho \right(\omega \left|\mathbf{r}\right)d\omega +k_B\int {\rho }_{\omega }^o\ln \left({\rho }_{\omega }^o\right)d\omega .$$ (4)

It is worth noting that, although the solute-water entropy is sixth-order in the sense that it represents an integral over six translational and orientational degrees of freedom, (r, ω), it is a one-water term. As a consequence, its contribution to the solvation entropy from a region of interest, R, such as part of a protein binding pocket, is obtained simply by limiting the spatial integrals in Eq. 3 to R, yielding regional values of the translational and orientational entropy, $\Delta S_{sw}^{R,trans}$ and $\Delta S_{sw}^{R,orient}$. (The sum of these two terms for a small region corresponding to a highly occupied water site corresponds to the quantity S^e in prior work related to the WaterMap method⁵⁶). Dividing these quantities by n^R, the mean number of water molecules in R, yields normalized (per water) quantities, $\Delta S_{sw}^{R,trans,norm}$ and $\Delta S_{sw}^{R,orient,norm}$, which are useful for comparing water properties between regions. The next term in the entropy expansion, the pairwise water-water contribution, is more difficult to evaluate, and prior IST implementations lacking this term have proven to be highly informative (see Introduction). Therefore, we reserve its analysis for future work.

Solvation energy

For the solvation energy, the solute-water and water-water terms are readily computed,

$$\begin{array}{ccc}\hfill \Delta E_{solv}& =& \Delta E_{sw}+\Delta E_{ww},\hfill \\ \hfill \Delta E_{sw}& =& {\rho }^o\int g_{sw}\left(\mathbf{r}\right)\Delta E_{sw}\left(\mathbf{r}\right)d\mathbf{r},\hfill \\ \hfill \Delta E_{sw}\left(\mathbf{r}\right)& \equiv & \frac{1}{8{\pi }^2}\int g_{sw}\left(\omega \right|\mathbf{r})U_{sw}(\mathbf{r},\omega )d\omega ,\hfill \\ \hfill \Delta E_{ww}& =& {\rho }^o\int g_{sw}\left(\mathbf{r}\right)\Delta E_{ww}\left(\mathbf{r}\right)d\mathbf{r},\hfill \\ \hfill \Delta E_{ww}\left(\mathbf{r}\right)& \equiv & {\left(\frac{1}{8{\pi }^2}\right)}^2{\rho }^o\int g_{sw}\left(\omega \right|\mathbf{r})\hfill \\ & & \times [g_{sw}({\mathbf{r}}^{\prime },{\omega }^{\prime })g_{ww}(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })\hfill \\ & & -g_{ww}^o(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })]\hfill \\ & & \times U_{ww}(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })d\omega d{\mathbf{r}}^{\prime }d{\omega }^{\prime }.\hfill \end{array}$$ (5)

Here, g_ww(r, ω, r′, ω′) is the pair distribution function between water molecules with spatial and orientational coordinates (r, ω) and (r^′, ω^′) in the neighborhood of the solute, $g_{ww}^o(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })$ is the corresponding quantity for bulk water, U_sw(r, ω) is the solute-water interaction potential, and U_ww(r, ω, r′, ω′) is the water-water potential. Note that both $g_{ww}^o(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })$ and U_ww(r, ω, r′, ω′) could be rewritten in terms of the relative water-water coordinates. The first line of Eq. 5 is an equality because for commonly used water models, such as SPC/E⁵⁸ or TIP4PEW,⁵⁹ where the interaction potentials include only the pairwise-additive Lennard-Jones and Coulombic terms, the full IST expansion of the solvation energy⁵⁰ conveniently terminates with the two-water term. Force fields that include higher order terms, such as that arising from electronic polarization, will lead to non-zero higher order terms in the IST expansion. As for the entropy integrals, above, the energy integrands decay with distance from the solute, so the solvation energies can again be approximated by local spatial integrals. In addition, as for the solute-water entropy (above), the contribution of a region R to the solute-water energy, $\Delta E_{sw}^R$, can be readily determined by simply limiting the spatial integral in line 2 of Eq. 5 to the region of interest, and the normalized (per water) solute-water energy of the region is simply $\Delta E_{sw}^{R,norm}=\Delta E_{sw}^R/n^R$.

However, it is not straightforward to assign the contribution from a region of interest to the pairwise water term, ΔE_ww, because the integral of ΔE_ww(r) over the region includes interactions with water molecules outside the region. This means that the contributions from two different regions, R₁ and R₂, will not sum to the contribution of their union, due to double-counting of interactions between the two regions. We introduce two accounting methods to address this issue. The first method is for use when one is interested in the energy cost of displacing the waters from a region of interest to the bulk. The second is for use when one is interested in comparing the properties of water molecules that are located in different regions. These accountings are as follows.

Water displacement

In the first method, a regional water-water interaction energy is defined to include all interactions of all waters in the region R and corrects for any double-counting within the region,

$$\begin{array}{ccc}\hfill E_{ww}^{R,corr}& =& {\left(\frac{{\rho }^o}{8{\pi }^2}\right)}^2{\int }_R{g}_{sw}(\mathbf{r},\omega )d\mathbf{r}d\omega \left[\int g_{sw}({\mathbf{r}}^{\prime },{\omega }^{\prime })\right.\hfill \\ & & \times g_{ww}(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })U_{ww}(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })d{\mathbf{r}}^{\prime }d{\omega }^{\prime }\hfill \\ & & -\frac{1}{2}{\int }_R{g}_{sw}({\mathbf{r}}^{\prime },{\omega }^{\prime })g_{ww}(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })\hfill \\ & & \left.\times U_{ww}(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })d{\mathbf{r}}^{\prime }d{\omega }^{\prime }\right].\hfill \end{array}$$ (6)

The first integral in the square brackets extends over all volume, while the second extends only over the region R, and its subtraction corrects for the first integral's double-counting of water-water interactions within R. We now consider displacement of the water from R into the bulk phase, such as by binding of a ligand in R. The change in water-water interaction energy then is simply

$$\Delta E_{ww}^R=n^R{E}_{ww}^{bulk}-E_{ww}^{R,corr},$$ (7)

where n^R is the average number of water in region R and $E_{ww}^{bulk}$ is the mean (Boltzmann averaged and averaged over all waters) water-water interaction energy for bulk water:

$$\begin{array}{ccc}\hfill E_{ww}^{bulk}& =& \frac{1}{2N_w}{\left(\frac{{\rho }^o}{8{\pi }^2}\right)}^2\int g_{ww}^o(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })\hfill \\ & & \times U_{ww}(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })d\mathbf{r}d\omega d{\mathbf{r}}^{\prime }d{\omega }^{\prime },\hfill \end{array}$$ (8)

where N_w is the number of water in a pure water system. The quantity $E_{ww}^{bulk}$ is ∼−11 kcal/mol for TIP4PEW water. It is important to note that the change in energy $\Delta E_{ww}^R$ does not account for any relaxation of the waters around the region R after the waters within it have been removed. For this, an additional simulation would be needed.

Normalized water properties

On the other hand, if one wishes to compare the properties of water in different regions, the water-displacement energy just presented can be misleading. The problem with using the water-displacement energy for this purpose may be understood by considering two regions, R₁ and R₂, both far from the solute and hence with essentially bulk water properties. If the first region, R₁, is so small that it only ever contains a single water molecule, its energetics will result entirely from interactions with waters outside the region, and its regional water-water energy, $E_{ww}^{R_1}$, will be about −22 kcal/mol for the TIP4PEW water model. Thus, from Eq. 7, its regional displacement energy will be about $\Delta E_{ww}^{R_1}=$ (−11 − (−22)) = +11 kcal/mol. Now, if region R₂ is large, so that its energetics are dominated by water-water interactions within R₂, then its regional water-water energy, $E_{ww}^{R_2}$, will amount to about −11 kcal/mol/water, and its displacement energy, $\Delta E_{ww}^{R_2}$, will be essentially zero. In summary, although the water is bulk-like in both regions R₁ and R₂, the per-water-displacement energies of the two regions will be very different: +11 and 0 kcal/mol/water, respectively. This difference in the per-water energy of the two regions clearly does not stem from a difference in the properties of the water they contain, since both regions are in bulk solvent. Rather, it is a consequence of the different counting of water-water interactions within a region versus interactions between water molecules inside and outside of it. Here, we address this problem by defining a normalized measure of water-water interactions in a given region, which does not depend upon the volume of the region,

$$\begin{array}{ccc}\hfill E_{ww}^{R,norm}& =& \frac{1}{n^R}{\left(\frac{{\rho }^o}{8{\pi }^2}\right)}^2{\int }_R{g}_{sw}(\mathbf{r},\omega )d\mathbf{r}d\omega \int g_{sw}({\mathbf{r}}^{\prime },{\omega }^{\prime })\hfill \\ & & \times g_{ww}(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })U_{ww}(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })d{\mathbf{r}}^{\prime }d{\omega }^{\prime }.\hfill \end{array}$$ (9)

Because this expression does not correct for any double-counting of water-water interactions within R, it provides the mean (Boltzmann-averaged and averaged over waters in R) interaction energy of the water in R with all other waters in the system, including those also in R. For bulk-like water, the value of $E_{ww}^{R,norm}$ goes to $2E_{ww}^{bulk}$, no matter what the volume of the region. We therefore reference this quantity to its bulk value,

$$\Delta E_{ww}^{R,norm}=E_{ww}^{R,norm}-2E_{ww}^{bulk}.$$ (10)

This quantity is zero for bulk water and will typically be positive for water near a solute, because displacement of water by the solute leads to a loss of water-water interactions.

Note that, if WaterMap defines a water cluster at a site that is always occupied by exactly one water, then the world energy,⁹ or system-interaction energy,⁶⁰ computed by WaterMap will correspond to GIST's $\Delta E_{sw}^R+E_{ww}^{R,norm}$ for the small region occupied by the cluster. Furthermore, under these circumstances, we have that $E_{ww}^{R,corr}=E_{ww}^{R,norm}$.

Discretization of inhomogeneous solvation theory on a 3D grid

In GIST, the spatial integrals in the IST expressions are replaced by discrete sums over the boxes, or voxels, of a three-dimensional grid, where the quantities on the grid are computed from the stored frames of an MD simulation. More specifically, a spatial region G, which may include both solute and solvent, is discretized into voxels indexed by k, centered at locations r_k and having volumes V_k. In general, this grid may be non-uniform and even adaptive, based on the specifics of the molecular system to be studied. Here, however, we use a uniform cubic grid, where each voxel has the same volume. The approximations inherent in this discretization become exact in the limit V_k → 0 and are clearly more accurate for smaller voxels, given adequate sampling of solvent configurations. Subsections 2B1, 2B2, 2B3, 2B4 describe the discretization of the specific IST terms discussed above.

Translational entropy

The total translational solvation entropy contributed by a region R within the gridded region G is given by

$$\begin{array}{ccc}\hfill \Delta S_{sw}^{R,trans}& \approx & \sum _{k\in R}\Delta S_{sw}^{trans}\left({\mathbf{r}}_k\right),\hfill \\ \hfill \Delta S_{sw}^{trans}\left({\mathbf{r}}_k\right)& \equiv & -k_B{\rho }^o{\int }_{k}g\left(\mathbf{r}\right)\ln g\left(\mathbf{r}\right)d\mathbf{r}\hfill \\ & \approx & k_B{\rho }^o{V}_{k}g\left({\mathbf{r}}_k\right)\ln g\left({\mathbf{r}}_k\right),\hfill \\ \hfill g\left({\mathbf{r}}_k\right)& \equiv & \frac{N_k}{{\rho }^o{V}_k{N}_f},\hfill \end{array}$$ (11)

where a k subscript on an integral sign means the integral's domain is voxel k, N_k is the number of waters within voxel k summed across all frames, and a water molecule is considered to lie in voxel k if the center of its oxygen atom is in the voxel. The approximation here results from treating g(r) as uniform within each voxel. By analogy with the normalized water-water energy discussed above, we also characterize the water in region R by its normalized (per water) entropy,

$$\Delta S_{sw}^{R,trans,norm}\equiv \frac{\Delta S_{sw}^{R,trans}}{n^R}.$$ (12)

Orientational entropy

Similarly, we write the orientational entropy in a region R as a sum over the voxels, k, it contains,

$$\begin{array}{ccc}\hfill \Delta S_{sw}^{R,orient}& \approx & \sum _{k\in R}\Delta S_{sw}^{orient}\left({\mathbf{r}}_k\right),\hfill \\ \hfill \Delta S_{sw}^{orient}\left({\mathbf{r}}_k\right)& \equiv & {\rho }^o{\int }_{k}g\left(\mathbf{r}\right)S^{\omega }\left(\mathbf{r}\right)d\mathbf{r}\hfill \\ & \approx & {\rho }^o{V}_{k}g\left({\mathbf{r}}_k\right)S^{\omega }\left({\mathbf{r}}_k\right),\hfill \\ \hfill S^{\omega }\left({\mathbf{r}}_k\right)& \equiv & \frac{-k_B}{V_{k}8{\pi }^2}{\int }_{k}d\mathbf{r}\int g\left(\omega \right|\mathbf{r}\left)\ln g\right(\omega \left|\mathbf{r}\right)d\omega .\hfill \end{array}$$ (13)

Here, $\Delta S_{sw}^{orient}\left({\mathbf{r}}_k\right)$ is the density-weighted orientational entropy associated with voxel k, and the approximation is that the density is uniform over the voxel k. The normalized (per water) orientational entropy for region R (see above) is defined as

$$\Delta S_{sw}^{R,orient,norm}\equiv \frac{\Delta S_{sw}^{R,orient}}{n^R}.$$ (14)

We used a nearest neighbor method^{61, 62, 63} to compute the orientational entropy associated with each voxel k, i.e., S^ω(r_k), from water simulation data. This provides substantially better convergence properties than a uniform histogram method we initially tried. The calculation begins by computing the Euler angles, (ϕ, cos θ, andψ)_i, in the solute frame of reference, for each water molecule i in voxel k in any trajectory frame. (Note that a uniform distribution of water orientations will yield uniform distributions in ϕ, cos θ, and ψ.) For each of the N_k waters, one finds the shortest angular distance, Δω_i, to any other water in the voxel, where the angular distance between water molecules i and j, for example, is

$$\Delta {\omega }_i\equiv {\left[{\left({\varphi }_i-{\varphi }_j\right)}^2+{\left(\cos {\theta }_i-\cos {\theta }_j\right)}^2+{\left({\psi }_i-{\psi }_j\right)}^2\right]}^{1/2}.$$ (15)

The value of the orientational distribution function at water i is approximated as

$$\begin{array}{c}{\displaystyle g\left({\omega }_i\right|{\mathbf{r}}_k)=\frac{8{\pi }^2}{V_i^{\omega }},}\hfill \\ \\ {\displaystyle V_i^{\omega }=\frac{4\pi {\left(\Delta {\omega }_i\right)}^3}{3}.}\hfill \end{array}$$ (16)

(Note that this density can also be estimated from the distance to the mth nearest neighbor, rather than the first nearest neighbor as currently implemented.) The orientational entropy is then estimated as

$$S^{\omega }\left({\mathbf{r}}_k\right)=\frac{-k_B}{N_k}\left(\gamma +\sum _{i=1}^{N_k}\ln g\left({\omega }_i\right|{\mathbf{r}}_k)\right),$$ (17)

where Euler's constant, γ, compensates for an asymptotic bias in the naïve entropy estimator.⁶¹

Energy

The total solute-water interaction energy in region R is readily decomposed into a sum over voxels, k, as follows:

$$\begin{array}{c}\Delta E_{sw}^R=\sum _{k\in R}\Delta E_{sw}\left({\mathbf{r}}_k\right),\hfill \\ \Delta E_{sw}\left({\mathbf{r}}_k\right)\equiv {\int }_k\Delta E_{sw}\left(\mathbf{r}\right)d\mathbf{r}.\hfill \end{array}$$ (18)

In practice, the value of ΔE_sw(r_k) is computed as the total solute interaction energy, according to the simulation force field, of all water molecules in voxel k, averaged over all simulation frames. The normalized (per water) solute-water interaction in the region R is computed as:

$$\Delta E_{sw}^{R,norm}=\frac{\Delta E_{sw}^R}{n^R}.$$ (19)

The water-water energy associated with region R is decomposed as follows. First, we define the water-water interaction energy of voxel k as

$$\begin{array}{ccc}\hfill E_{ww}\left({\mathbf{r}}_k\right)& =& {\rho }^o{\int }_k{g}_{sw}\left(\mathbf{r}\right)E_{ww}\left(\mathbf{r}\right)d\mathbf{r},\hfill \\ \hfill E_{ww}\left(\mathbf{r}\right)& \equiv & {\left(\frac{1}{8{\pi }^2}\right)}^2{\rho }^o\int g_{sw}\left(\omega \right|\mathbf{r})g_{sw}({\mathbf{r}}^{\prime },{\omega }^{\prime })\hfill \\ & & \times g_{ww}(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })U_{ww}(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })d\omega d{\mathbf{r}}^{\prime }d{\omega }^{\prime },\hfill \end{array}$$ (20)

and the water-water interaction of voxels k and l as

$$\begin{array}{ccc}\hfill E_{ww}\left({\mathbf{r}}_{k,}{\mathbf{r}}_l\right)& \equiv & {\left(\frac{{\rho }^o}{8{\pi }^2}\right)}^2{\int }_{V_k}{g}_{sw}(\mathbf{r},\omega )d\mathbf{r}d\omega {\int }_{V_l}{g}_{sw}({\mathbf{r}}^{\prime },{\omega }^{\prime })\hfill \\ & & \times g_{ww}(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })U_{ww}(\mathbf{r},\omega ,{\mathbf{r}}^{\prime },{\omega }^{\prime })d\mathbf{r}d\omega .\hfill \end{array}$$ (21)

In practice, these quantities are computed as mean water-water interaction energies for the water molecules in the respective voxels, based on the simulation frames. The water-displacement energy for region R becomes,

$$E_{ww}^{R,corr}=\sum _{k\in R}{E}_{ww}\left({\mathbf{r}}_k\right)-\frac{1}{2}\sum _{k\in R}\sum _{\underset{l\in R}{l\ne k}}{E}_{ww}({\mathbf{r}}_k,{\mathbf{r}}_l).$$ (22)

Here, as in Eq. 6, the second term corrects for double-counting of interactions within the region by the first term. Finally, the normalized water-water interaction energy is discretized as

$$E_{ww}^{R,norm}=\frac{{\sum }_{k\in R}{E}_{ww}\left({\mathbf{r}}_k\right)}{n^R}.$$ (23)

Free energy

One may furthermore estimate a local, density-weighted free energy of solvation, ΔG(r_k) for voxel k,

$$\begin{array}{c}\Delta G\left({\mathbf{r}}_k\right)=\Delta E_{total}\left({\mathbf{r}}_k\right)-T\Delta S_{sw}^{total}\left({\mathbf{r}}_k\right),\hfill \\ \Delta E_{total}\left({\mathbf{r}}_k\right)\equiv \Delta E_{sw}\left({\mathbf{r}}_k\right)+\Delta E_{ww}\left({\mathbf{r}}_k\right),\hfill \\ \Delta S_{sw}^{total}\left({\mathbf{r}}_k\right)\equiv \Delta S_{sw}^{trans}\left({\mathbf{r}}_k\right)+\Delta S_{sw}^{orient}\left({\mathbf{r}}_k\right),\hfill \end{array}$$ (24)

where T is absolute temperature. The normalized (per water) free energy of region R can also be written as

$$\begin{array}{ccc}\hfill \Delta G^{R,norm}& =& \Delta E_{sw}^{R,norm}+\Delta E_{ww}^{R,norm}-T\Delta S_{sw}^{R,trans,norm}\hfill \\ & & -T\Delta S_{sw}^{R,orient,norm}.\hfill \end{array}$$ (25)

The change in solvation free energy on displacing the water from a region into bulk without allowing the remaining water to relax, and the normalized (per water) solvation free energy, is computed by similarly assembling the corresponding energy and entropy terms.

Computational methods

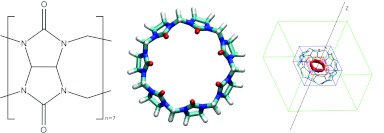
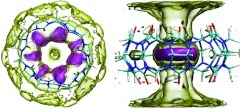
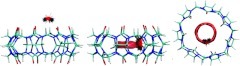
MD simulations of the synthetic host molecule CB7 (Figure 1) in explicit water⁵⁷ were carried out with the program AMBER11.⁶⁴ In order to study the role of electrostatics in solvation, we ran one simulation with regular partial charges on the host molecule and another in which the partial charges of all host atoms were set to zero; this system will be referred to as the nonpolar host, as opposed to the regular host. The GIST methodology was implemented on a rectangular 3D grid of dimensions 22 Å × 22 Å ×14 Å (green in Figure 1), centered on the host, with the grid's xy plane defined to hold the glycoluril carbon atoms and with the z axis along to the host's C₇ axis of rotational symmetry. The coordinates of each MD frame were registered to the grid by repositioning the host's center of mass to the origin and removing rotations of the host by minimizing the root-mean-square deviation from the first frame; water molecules and their images were translated accordingly. The grid spacing was 0.5 Å along each axis, as this was found to provide a detailed representation and good convergence of local water density. A water molecule is considered to reside in a voxel if its oxygen coordinates are within it, and its orientation is specified by Euler angles.⁵⁷ In some analyses, voxels were grouped into two regions (torus and cavity, Figure 1) to enable comparative analysis of water thermodynamics in and around the host.

Figure 1.

Cucurbit[7]uril, a symmetric ring of seven glycouril units. Right-hand graphic includes rectangular prisms showing the size and position of the GIST grid (green), and the computational definitions of the torus (red), and cavity (blue) regions used in the quantitative solvation studies (Results). The torus region of high water density is shown with a red contour.

RESULTS

We begin by presenting GIST visualizations of hydration structure and thermodynamic components, for both the regular cucurbit[7]uril host, and a computationally modified form of the same host in which all partial charges have been set to zero to test the role of electrostatics in the hydration of this solute. We then present a quantitative analysis of the same data for both the regular and nonpolar host.

Visualization of water structure and thermodynamics

Regular host

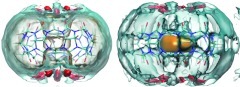
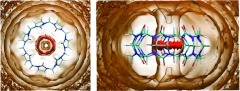
Translational entropy and water density

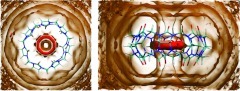
Figure 2 plots three-dimensional contours of the local translational entropic contribution to solvation free energy ($-T\Delta S_{sw}^{trans}\left({\mathbf{r}}_k\right)$) in and around CB7. This quantity is simply related to the local water density (Eq. 11), so these contours of translational entropy directly correspond to water density contours. In particular, the tan contours at zero entropy correspond to bulk water density, while the red contour corresponds to a density of 4ρ^o. The most striking feature in this plot is the sharply defined red toroidal region of unfavorable translational entropy, and correspondingly high water density, in the middle of the CB7 cavity. Note that, this torus lies between the first and second zero entropy contours, which is where the first peak of the water distribution function is located. Thus, it may be regarded as a local enhancement of the density peak of the first solvation shell. The first-order translational entropy gained from displacing water from this region is larger than for displacement of water from other regions, where the translational entropy is more favorable.

Figure 2.

Contour plots of $-T\Delta S_{sw}^{trans}\left({\mathbf{r}}_k\right)$, the first-order translational entropy contribution to solvation free energy, for top (left) and side (right) views of CB7. Red: 0.1 kcal/mol/ų. Tan: 0.0 kcal/mol/ų. Note that this quantity is referenced to bulk water. Molecular graphics generated with Visual Molecular Dynamics (VMD).⁶⁵

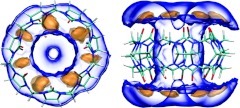
The layering pattern in the zero entropy (bulk density) contours clearly shows that the perturbation from bulk properties induced by the solute (CB7) extends for several solvation shells. Somewhat unexpectedly, we found no obvious peaks in the solvent density relating to water's hydrogen-bonding interactions with the host's carbonyl oxygens. However, a contour plot of the density of water hydrogen atoms (Figure 3) shows a flower-like pattern at the portals of the cavity. The localization of hydrogen density is clearly due to hydrogen bonding interactions with the host carbonyls. These observations suggest that, while the water hydrogens are often placed in the petals of the flower, the oxygens bonded to those hydrogens move relatively freely within the constraints of the hydrogen placement and the H−O bond length.

Figure 3.

Local density of water hydrogen atoms in and around CB7, contoured at bulk density.

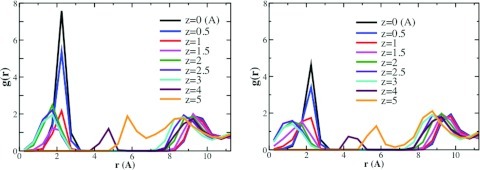
Further detail regarding the spatial distribution of water density is provided in Figure 4 (left), which plots g(r), the mean density relative to bulk as a function of distance r from the z axis at various z-levels. The high-density torus is manifest in the tallest peaks at r = 2 for z = 0 and z = 0.5, with densities that reach about eight times the bulk value. At higher values of z, the corresponding peaks are shorter, with values of about twice the bulk density, which is similar to the peaks at the outer surface of the host (r ≈ 9); they also shift to somewhat smaller values of r, presumably because of the inward curve of the host's walls with increasing z. Along the host's axis of symmetry, (r = 0), the solvent density near z = 0 is essentially zero. Given that this locus lies within the cavity, it is evident that the absence of solvent there is a packing effect; i.e., a consequence of steric exclusion by the first solvent peak near r = 2. The two extra peaks near r = 4.5 and r = 6, for z = 4 and z = 5, respectively, also appear to result from shape and packing interactions, because they are also present when all the partial charges of the host are set to zero (Figure 4, right, and text below).

Figure 4.

Radial distribution functions in the x-y plane of regular CB7 (left) and nonpolar host (right) at multiple values of z (Å). Densities were computed for planar layers of thickness 0.5 Å and averaged circumferentially to yield g(r), the water density as a function of distance from the z axis. The equator of the host is at z = 0 and the carbonyl oxygens are at about z = 3.1.

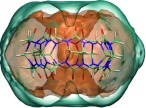
Orientational entropy

Figure 5 plots the local free energy contribution of orientational entropy per mole of water; i.e., −TS^ω (left-hand panel). The most orientationally ordered water molecules are found above and below the host, at its polar portals (violet contours). This ordering results from hydrogen bonding between water molecules and the host's carbonyl oxygens. Moderately oriented water (yellow) is also observed at the host's surface and in the interior toroidal region. Note that the seven low-entropy (violet) petals at the portals are not particularly densely occupied by water (Figure 2) and, in particular, are not occupied simultaneously by seven tightly bound water molecules. Thus, although this is the region where water is most highly oriented, it is not the region where, on a per-voxel basis, the orientational entropy makes the strongest contribution to solvation. To evaluate this, one needs to examine the density-weighted contribution of orientational entropy, or $-T\Delta S_{sw}^{orient}$. Contours of this quantity (Figure 5, right-hand panel) show that the high-density toroidal region (above) is the strongest contributor, due to its combination of moderately reduced orientational entropy and extremely high water density.

Figure 5.

Contributions of orientational entropy to solvation free energy in and around CB7. Left: orientational entropy (−TS^ω) contours at 1.5 kcal/mol/water (violet) and 0.5 kcal/mol/water (yellow). Right: contours of orientational entropy density ($-T\Delta S_{sw}^{orient}$), at 0.15 kcal/mol/ų (violet) and 0.05 kcal/mol/ų (yellow).

Total solvation energy

Figure 6 plots contours of normalized (per water; left) and density-weighted (right) total solvation energy in and around CB7; all values are referenced to bulk water. There are three key features in the per-water energies (left). First, there is energetically favorable water interacting with the polar carbonyls at the upper and lower portals of the host. These locations correspond to the low orientational entropy locations seen above, indicating water molecules that are low in both energy and entropy, as might be expected, given the common, though debated, phenomenon of entropy-enthalpy compensation.^{66, 67, 68, 69, 70, 71} Second, there is a shell around the entire host comprising water molecules that have unfavorable energies because of their interactions with the host's repulsive Lennard-Jones wall. However, this shell is lightly populated, so water molecules in this region do not significantly contribute to the overall energy of solvation. Third, the highly populated toroidal region which appeared in the entropy figures (above) is also apparent here as a region of energetically unfavorable solvation. (Note that we characterize this as unfavorable in the sense that the average energy of interaction with the system as a whole of a water molecule located in this region is higher (less negative) than that of a water molecule located in bulk water.) The density-weighted energy contours (Figure 6, right) highlight that the toroidal region makes a particularly strong net contribution to the solvation energy. Thus, although water molecules in the toroidal region have energetically unfavorable interactions with their surroundings, relative to bulk, and are also entropically unfavorable due to their orientational and translational ordering, the voxels in this region have the highest populations found in our simulations. It is also interesting to note that the properties of the water in the toroidal region show a clear breakdown of entropic-enthalpic compensation, in contrast with the portal waters, as it is less favorable both energetically and entropically than bulk water.

Figure 6.

Contours of total solvation energy. Left: per-water values, ΔE_sw(r_k) + ΔE_ww(r_k), where $\Delta E_{ww}\left({\mathbf{r}}_k\right)=E_{ww}\left({\mathbf{r}}_k\right)-2E_{ww}^{bulk}$, at 1.8 (tan) and 0.3 (cyan) and −1.0 (red) kcal/mol/water. Right: density-weighted values (ρ^og(r_k)(ΔE_sw(r_k) + ΔE_ww(r_k))) at 0.0125 (orange), 0.001 (cyan), and −0.006 (red) kcal/mol/ų.

Host-water and water-water interaction energies

The total energy of the water in each voxel can also be broken down into solute-water and water-water interactions. One broad observation is that the numerical magnitudes of these terms are much greater than those of the total water energies (above and see Table 1), indicating strong balancing compensation between solute-water and water-water interactions in and around the host molecule. Focusing now on the solute-water energy, i.e., the average interaction between the host and the water molecules found in each voxel, we observe that the strongest water-host interactions are found at the carbonyl groups of the two portals (orange, Figure 7), and these solute-water energy contours resemble the orientational entropy contours in Figure 5 (left). These results are consistent with the fact that waters in these regions can form hydrogen bonds with the host. Somewhat surprisingly, the water molecules inside the cavity have significantly stronger interactions with the host than those on its exterior surface. We attribute this to a greater van der Waals contact with the internal surface, due to the concavity of the interior as opposed to the convexity of the exterior, as well as to favorable electrostatic interactions with the carbonyl oxygens both above and below. Due to the inward curvature of the host, the carbonyl oxygens are closer to the internal water molecules (at the same z level) than those hydrating the exterior of the host. In a ligand binding context, we believe that information on solute-water interaction usefully maps out regions where the ligand must make hydrophilic contacts if it is to reach high affinity, as it must compensate for the solute-water interactions that will be lost in these regions upon binding.

Table 1.

Normalized water properties in four regions in and around regular (top) and nonpolar (bottom) CB7 (kcal/mol). $\Delta E_{total}^{R,norm}=\Delta E_{sw}^{R,norm}+\Delta E_{ww}^{R,norm}$. Mean number of waters in region: n^R.

	nR	$-T\Delta S_{sw}^{R,trans,norm}$	$-T\Delta S_{sw}^{R,orient,norm}$	$\Delta E_{total}^{R,norm}$	$\Delta E_{sw}^{R,norm}$	$\Delta E_{ww}^{R,norm}$	ΔGR, norm
Regular host
Cavity	6.7	0.53	1.0	1.0	−6.9	7.9	2.6
Torus	3.6	0.70	1.22	1.8	−7.1	8.9	3.6
Cavity surf	36.1	0.25	0.35	−0.2	−2.0	1.8	0.44
Torus surf	12.3	0.27	0.35	−0.2	−2.1	1.9	0.44
Nonpolar host
Cavity	5.2	0.34	0.39	3.2	−2.8	6.0	3.9
Torus	2.8	0.46	0.37	4.3	−3.3	7.6	5.1
Cavity surf	35.9	0.24	0.23	−0.02	−0.82	0.80	0.45
Torus surf	12.2	0.26	0.24	−0.08	−0.79	0.71	0.42

Figure 7.

Contours of solute–water interaction energy ($\Delta E_{ww}\left({\mathbf{r}}_k\right)=E_{ww}\left({\mathbf{r}}_k\right)-2E_{ww}^{bulk}$) in and around CB7. Orange: −8.5 kcal/mol/water. Blue: −4.0 kcal/mol/water.

Contour plots of water-water interaction energetics (Figure 8) show, not surprisingly, that the presence of the host leads to water-water interactions that are weakened relative to bulk. This results largely from the simple excluded volume of the host, which reduces the numbers of neighbors around each water molecule. This effect is particularly pronounced in the cavity of the host. In addition, the host forms hydrogen bonds with water molecules at the portals, thereby preventing them from forming hydrogen bonds with other waters. This second effect presumably accounts for the bumps in the orange contours above and below the portal carbonyls.

Figure 8.

Contours of water–water interaction energy (ΔE_ww(r_k)) in and around CB7. Orange: 8.0 kcal/mol/water. Cyan: 3 kcal/mol/water.

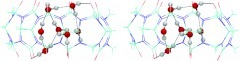
Water configurations

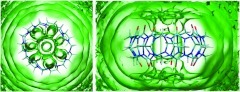
Visual examination of the water trajectories revealed that water molecules freely exchange between the cavity of CB7 and the surrounding bulk, as also reflected by the rapid fluctuations of the number of water molecules in the cavity (Figure S2 of the supplementary material⁵⁷). Nonetheless, the GIST analysis indicates significant reductions in orientational entropy relative to bulk in certain regions, and one may gain some insight into the types of conformations the water adopts by examining snapshots from the simulation. Thus, Figure 9 illustrates conformational preferences of water molecules in two interesting voxels, one, near two portal carbonyl oxygens where the water has a particularly low orientational entropy (left), and the other in the toroidal region of high water density (middle and right). The marginal probability density functions of the Euler angles for these voxels (Figure S3 of the supplementary material⁵⁷) have particularly tight distributions for the low-entropy portal water, and more complex, multimodal distributions for the torus water. Two typical snapshots are shown in Figure 10, one with three (left) and the other with four (right) water molecules in the high-density toroidal region. Somewhat unexpectedly, the torus water molecules tend not to hydrogen bond with each other, but instead with other waters situated above and below this equatorial feature that tend to form additional hydrogen bonds with the host's carbonyl oxygens.

Figure 9.

Overlays of 200 water coordinates in a low orientational entropy (per water) voxel near two carbonyl groups at one portal of CB7 (left), and a highly occupied voxel in the toroidal region of high water density (middle and right).

Figure 10.

Two representative snapshots of water conformations within the cavity of CB7. Hydrogen bonds, based on geometric criteria (oxygen–oxygen distance <3.0 Å and O−H···O angle >155^°), are shown as black dotted lines.

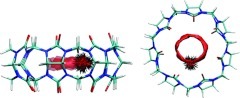
Nonpolar host

We investigated the degree to which the ordering of water observed in and around CB7 is a consequence of polar solute-water interactions by simulating an artificial version of the cucurbit[7]uril host, in which all of the host molecule's partial charges were set to zero, while leaving all other parameters the same. The translational entropy contours of the nonpolar host (Figure 11) strongly resemble those of the regular host (Figure 2). In particular, the highly occupied torus is still present. Although the density of this feature is lower in the nonpolar host (Figure 4, right vs. left panels), it still reaches more than twice the density of the peak in g(r) at the outer surface of the host (i.e., atr ≈ 9Å). We thus conclude that the formation of the torus feature is driven by packing more than by polar interactions. The lowering of this density peak corresponds to a reduction in the mean number of waters within the nonpolar cavity, as evident from the time-course of water occupancy (Figure S2 of the supplementary material⁵⁷). The lowered water occupancy is consistent with expectation for this artificially hydrophobic host molecule. Interestingly, for the exterior of the host, turning off attractive interactions has little effect on the density and the corresponding translational entropies. This insensitivity of local density to attractive forces is an instance of a more general result of perturbation theory for dense homogeneous liquids.⁷² However, although this homogenous liquid result holds for the exterior of the cavity, it clearly does not for the interior, where turning the attractions on or off has a significant effect on the local density. The persistence of the peaks near r = 4 and r = 6 for the nonpolar host (Figure 4, right) indicates that these do not result from hydrogen bonding with the host carbonyls, but from shape and packing, as noted above. However, neutralization of this host eliminates the flower-like structure of the distribution of water hydrogens that was observed for regular CB7 (data not shown).

Figure 11.

Contour plots of the translational entropy contribution to free energy, for top (left) and side (right) views of nonpolar CB7. Red: 0.008 kcal/mol/ų. Tan: 0.0 kcal/mol/ų.

The water in and around the nonpolar host is subject to a considerably smaller penalty in orientational entropy, relative to regular CB7 (contours not shown). For example, reduced orientational ordering is evident in the smoother distribution of Euler angles for a voxel in the high-density torus (Figure S3 of the supplementary material⁵⁷) and in the corresponding conformational overlays (Figure 12); the reduction in ordering is even more marked near the carbonyls, as they are now unable to accept hydrogen bonds. It is perhaps not surprising that packing considerations seem to play a proportionally greater role in translational ordering, while electrostatics is more important for orientational ordering.

Figure 12.

Overlays of 200 water coordinates in a highly occupied voxel in the toroidal region of high water density, for the nonpolar host.

Quantitative analysis of local contributions to solvation

This section examines local contributions to the hydration thermodynamics of the CB7 receptor, taking advantage of GIST's ability to analyze regions of arbitrary size and shape. Two regions of interest within the host receptor are examined, the toroidal region of high water density discussed above (torus), and the entire binding cavity of the receptor (cavity). In practice, these are defined here with rectangular prisms (Figure 1). Two corresponding regions outside the receptor, termed the torus surface and cavity surface, are also examined. These are annular regions at the outer surface of the receptor, having the same extents along the receptor's z axis as the torus and cavity, respectively, and comprising the first peak of the radial distribution function (RDF) at the outer surface of the receptor, i.e., the right-most peak in Figure 4.

Regular CB7

Normalized thermodynamic properties of hydrating water

We first discuss the normalized (per water) thermodynamic properties of water in each region, referenced to their corresponding bulk values. Table 1 lists these quantities for the four regions defined above; all are well-converged within 30 ns or less of simulation time (Figure S4 of the supplementary material⁵⁷).

For all four regions, the data in Table 1 show the same qualitative pattern of unfavorable translational and orientational entropy, implying greater ordering than bulk water; less favorable water-water interactions than in bulk, as expected given that the host occupies space that would otherwise be filled with water; and favorable water-host interactions that partly balance the unfavorable entropic and water-water terms. The net effect is one of positive changes in the normalized free energy, ΔG^{R, norm}. In this sense, the water molecules in these regions are thermodynamically unstable relative to the bulk phase. However, nontrivial reference state issues discussed later in this section and in Discussion, must also be kept in mind when interpreting such results.

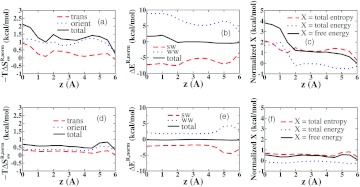
Further analysis of these normalized water properties is provided in Figure 13, which plots their values for successive slabs of thickness 0.5 Å normal to the z axis (Figure 1), with z = 0 at the receptor's equator. In the top row of Figure 13, the slabs are restricted to the interior of the receptor, and in the bottom row, the slabs include only the first external peak of the RDF. As shown in Figure 13a, the orientational entropy penalty exceeds the translational entropy penalty everywhere within the receptor. Both entropy penalties are maximal in the torus region, which lies between z = 0 and z = 1 Å. Smaller peaks are evident at about z = 2 Å, and the orientational entropy shows a broad peak near z = 4 Å, which corresponds to the ordering of water near the carbonyls of the receptor's portal (Figure 5). The solute-water interaction energy (Figure 13b) is most favorable deep within the receptor (near z = 0), and also becomes favorable near the carbonyls. Interestingly, however, except at the middle of the cavity (z = 0–1.5 Å), this term is quite precisely balanced by the water-water energy, leaving the total solvation energy near zero in most of the interior of the receptor. Analogous graphs of the net energy, entropy, and free energy (Figure 13c) show that entropy and energy each provide about half of the free energy penalty in the torus region, but elsewhere the unfavorable free energy is primarily entropic in nature, due to cancellation of the water-water and solute-water energies. Analogous plots for the first hydration shell at the outer surface of the host (Figure 13, bottom row) show less overall thermodynamic perturbation, but are similar in that they also reveal near-cancellation of the water-water and solute-water energies, energy bumps near the carbonyls, and a primarily entropic contribution to the mildly unfavorable free energy.

Figure 13.

Normalized thermodynamic quantities, as labeled, on the interior (top row) and exterior (bottom row) of the regular CB7 receptor, as a function of distance along the z axis.

Thermodynamics of water displacement

The consequences of removing all the water molecules from the cavity and torus regions and transferring them to bulk are addressed in Table 2. These are the non-normalized regional quantities defined in the Methods section. Like the results of other IST approaches, they do not account for the thermodynamics of reorganization of the remaining water. (See Discussion for more on this topic.) Note, too, that these thermodynamic quantities equal simply the mean number of water molecules in the region, n^R, times the corresponding normalized quantities except in the case of the water-water energy and hence also ΔG. The reason for this difference is that simply multiplying $\Delta E_{ww}^{R,norm}$ by the average number of waters in a region, such as the torus, would double-count the interactions of pairs of waters within the region. The non-normalized quantity reported here does not double-count, and it is also referenced to the mean water-water interaction energy in the bulk phase, which is about −11 kcal/mol for TIP4PEW. These changes in accounting lead to the change in sign for ΔG^R vs. ΔG^{R, norm}.

Table 2.

Water-displacement thermodynamics for the toroidal region of high water density as well as the entire receptor cavity, for regular (top) and nonpolar (bottom) CB7 host molecule (kcal/mol). $-\Delta E_{sw}^R$(VDW): solute–water van der Waals interactions. Note that the solute-water energies for the nonpolar host are purely van der Waals in nature. See text for other definitions. Note the sign changes relative to Table 1.

	$T\Delta S_{sw}^{R,trans}$	$T\Delta S_{sw}^{R,orient}$	$-\Delta E_{sw}^R$	$-\Delta E_{sw}^R\left(\mathrm{VDW}\right)$	$-\Delta E_{ww}^R$	−ΔGR
Regular host
Cavity	−3.6	−6.9	45.9	15.5	−19.8	15.7
Torus	−2.5	−4.1	25.3	11.3	−2.9	15.8
Nonpolar host
Cavity	−1.8	−2.0	14.7	14.7	−2.1	8.9
Torus	−1.3	−1.0	9.2	9.2	2.2	9.1

As shown in Table 2, we observe net entropic driving forces of about −10 kcal/mol for displacing all water from the receptor's cavity and about −7 kcal/mol for displacing all waters from just the torus region. About two thirds of these changes are orientational and one third translational, consistent with the normalized water properties (Table 1). Water displacement to the bulk is also predicted to lead to considerably more favorable water-water interactions, but at the cost of losing strong solute-water interactions. In the torus, the total solute-water interaction is partitioned about equally between van der Waals and electrostatics, while electrostatics plays a proportionally larger role for the full cavity region. This is physically reasonable, given that some water molecules in the cavity region are near the receptor's carbonyl groups, unlike the water in the torus region.

The substantial losses in energy and the moderately compensating gains in entropy lead to free energy penalties of about 15 kcal/mol for displacement of water from both the cavity and the torus regions, despite their different sizes. In effect, once the torus waters are displaced, there is little thermodynamic consequence of displacing the rest of the waters to completely empty the cavity. Thus, the torus waters arguably play a dominant role in determining the work of emptying the cavity. The similarity in the free energy change upon displacement of water from the cavity and the torus traces to the larger energetic penalty for displacing waters from the cavity (26.1 vs. 22.4 kcal/mol), balanced by a greater entropic gain (‑10.5 vs. −6.6 kcal/mol).

The positive free energy of water displacement in Table 2 might suggest that binding of a guest molecule would be thermodynamically unfavorable. However, the guest will establish its own energetic interactions with the host molecule, and these may be similar in magnitude to that of the displaced waters. In the present case, this would lead to a thermodynamic balance of −45.9 ($\Delta E_{sw}^R$) + 15.7 (ΔG^R) = −30.2 kcal/mol for binding in the cavity region. Prior calculations of host-guest binding for this host yielded roughly −30 kcal/mol of van der Waals interaction energy for a small neutral guest molecule that is adequate to fill the cavity.⁷³ Combining this energetic gain with the water-displacement free energy of 15.7 kcal/mol (Table 2) leads to a driving force for binding of −14.3 kcal/mol, even before including possible electrostatic host-guest interactions.

Artificially nonpolar CB7

Analogous results are provided in Tables 1, 2 for a model of the same host molecule in which all partial charges have been artificially set to zero. The numerical convergence of these data is similar to that observed for the regular host (data not shown).

Normalized thermodynamic properties of hydrating water

The nonpolar host shows the same overall pattern of unfavorable entropy, favorable water-host energy, and unfavorable water-water energy for all four regions (Table 1). Although the magnitudes of the individual solvation terms are smaller, the net effect is that the normalized water free energies are more unfavorable here than for the regular host. The differences trace primarily to less favorable solute-water interactions, due to the lack of favorable electrostatics interaction present in the nonpolar host. The water-water interactions are slightly more favorable in the nonpolar host, presumably because the waters are no longer locked into electrostatic interactions with the host molecule; by the same token, it is reasonable that the entropic penalties are lower for this nonpolar model. Note, however, that the entropies presented here do not account for two-particle correlations, which might be stronger for the nonpolar host than for the regular one.

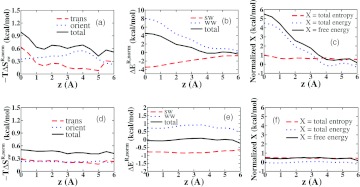
Detailed analyses of water properties in layers along the host's z axis are shown in Figure 14. The translational entropy graph is similar to that for the regular host, consistent with the persistence of the torus feature in the nonpolar host (above). However, the orientational entropy is higher (lower −TΔS) for the nonpolar host, consistent with the absence of the ordering polar interactions with the host. The energy profiles of the nonpolar host (Figure 14b) differ substantially from those of the regular host. Although there is again a large loss in water-water energy near z = 0, consistent with the sequestration of water molecules in the host interior, this energy penalty is no longer balanced by the favorable solute-water interactions present in the regular host, due to the absence of electrostatic water-host interactions. The net effect is a substantial energetic penalty for water molecules within the nonpolar host. Graphs of overall energy, entropy, and free energy (Figure 14c) highlight the significance of the energy as a determinant of unfavorable solvation free energy in this model system. Outside the host (Figure 14, bottom row), the thermodynamic profiles are quite similar to those of the regular host, except for the near-absence of features in the proximity of the portal carbonyls, which makes sense since these are now treated as neutral.

Figure 14.

Normalized thermodynamic quantities, as labeled, on the interior (top row) and exterior (bottom row) of the artificial nonpolar receptor, as a function of distance along the z axis. The regions R analyzed here are successive layers normal to the z axis.

Thermodynamics of water displacement

Consistent with the analysis of normalized water properties, above, the water displacement analysis (Table 2) indicates a significant smaller free energy penalty for displacing waters from the nonpolar host, at about 9 kcal/mol vs. 15.5 kcal/mol for the regular host. This is consistent with expectation for a hydrophobic molecule and, all other things being equal, would create a tendency toward stronger binding of guest molecules to the nonpolar host.

DISCUSSION

GIST

Simulation studies dating back at least to 1978 (Ref. ⁷⁴) have provided insight regarding the structure and energetics of water solvating biomolecules and other solutes. More recently, the development of IST (Refs. ³⁰ and ³¹) has provided a framework for innovative computational tools^{9, 36, 35} that use explicit water simulations to generate valuable thermodynamic information regarding hydrating water, including its entropic contributions and its implications for ligand binding.^{32, 34, 36, 38, 39, 41, 55} To date, such tools have focused on discrete, highly occupied hydration sites, but water distributions are not always readily partitioned into discrete sites, and low-occupancy regions in a binding pocket may have their own implications for ligand binding. The grid implementation of IST described here (GIST) addresses these and other issues by discretizing the same leading terms of IST onto a three-dimensional grid, which may cover a large region of interest, as illustrated in the present study of the small receptor molecule CB7. This approach enables both visualization and thermodynamic interpretation of solvation thermodynamics anywhere in the region of interest. In particular, because GIST is not site-based, it is directly applicable to regions of high, medium, or low density, providing a smooth representation of solvation structure and thermodynamics. The local water properties converge well within about 30 ns of simulation time for the system studied here. One reason for this favorable result is that, although the orientational entropy contribution, in particular, has the potential to require extensive sampling to reach useful convergence, its contribution to the overall entropy is proportional to the local solvent density. As a consequence, the least sampled voxels are also the ones that matter least. We also find that a nearest-neighbor entropy estimator yields dramatically faster convergence than an initial naïve histogram method.

The GIST method should be useful for elucidating the roles of solvation structure and thermodynamics in molecular recognition, with applications to proteins, nucleic acids, and surfaces. We anticipate in particular that GIST can be a tool for guiding the design of potent ligands. Like prior IST implementations, GIST should help identify high-occupancy locations where a ligand can profitably displace water; and it should be equally capable of identifying regions of intermediate or low density, which would be favorably occupied by ligand atoms. Also, because GIST does not require that water density be partitioned into discrete sites, it can be used to analyze larger solvation structures, such as the torus region of high solvent density observed in the present study. GIST's ability to separate and visualize regional solute-water and water-water energetics (ΔE_sw and ΔE_ww) enable further insight. For example, visualization of ΔE_sw can highlight locations where water's strong interactions with a protein must be replaced by compensating ligand interactions in order to reach high affinity. Separate visualization of van der Waals and electrostatic contributions to ΔE_sw might also be useful and would be straightforward to implement.

Hydration of CB7

This small, symmetric receptor displays a surprisingly intricate pattern of solvation structure and thermodynamics and yields insights that are expected to hold more generally. A particularly prominent feature of the solvation structure is the torus region of high water density within the receptor's binding site. The water molecules in this region are translationally and orientationally ordered. They are also energetically disfavored by about 2 kcal/mol relative to waters in bulk, as they have lost nearly 9 kcal/mol of water-water interaction energy while gaining about −7 kcal/mol of water-host interaction energy. The water molecules in the entire binding site (termed cavity in the tables) have similar thermodynamic properties, but are somewhat less perturbed relative to bulk. Despite the perturbation of the water in these regions, the free energy of displacing the water molecules from the torus or cavity regions is unfavorable by about 16 kcal/mol (Table 2). This result is physically reasonable, given that the cavity is, in fact, continuously occupied by water molecules during the simulation (Figure S2 of the supplementary material⁵⁷). It is also important to recognize that this result does not account for any relaxation of the remaining water molecules subsequent to displacement (see below), and hence will tend to overestimate the cost of displacement.

Although the unfavorable normalized properties of the water in the torus and cavity, relative to bulk, are not strong enough to cause spontaneous dewetting, they can still enhance the binding affinity of guest molecules. This may be understood by recognizing that the only term in Table 2 that in net opposes the displacement of water to bulk is the solute-water interaction energy, which will be offset by the interactions of a suitable guest molecule with the host. For example, it has been estimated that bicyclo[2.2.2]octane has an interaction energy with this host of about −28 kcal/mol,⁷³ more than enough to overcome the computed free energy penalty for displacing the perturbed waters. If the displaced water were not entropically disfavored by about 14 kcal/mol, relative to bulk (Table 2), binding of this guest could become thermodynamically unfavorable. Moreover, a ligand that replicated the full water-host interaction energy for waters in the cavity region (about −46 kcal/mol, Table 2) would potentially achieve extremely high affinity. Perhaps, then, the instability of the water within this small receptor molecule is part of the reason it is able to achieve exceedingly high binding affinities for some guest molecules.⁷³ Note, however, that a full accounting of the binding free energy must include additional factors, such as the desolvation of the guest, changes in configurational entropy on binding,⁷⁵ and the reorganization of water upon binding.

In order to study the role of polar interactions in the solvation of CB7, we also applied GIST to a computationally modified form of this host with the partial charges of all atoms artificially set to zero. (The water model was kept the same.) The individual entropic and energetic solvation terms for the water molecules within the resulting nonpolar binding site are less perturbed in all respects than those in the regular binding site (Table 1), but their net effect is, nonetheless, to make these water molecules less stable than those in the regular host. Accordingly, the estimated free energy of displacing the water is only about 9 kcal/mol, rather than 16 kcal/mol (Table 2), and the average number of water molecules resident in the binding site is also reduced (Table 1 and Figure S2 of the supplementary material⁵⁷). These results are consistent with expectations for solvation of a hydrophobic molecule versus a polar one. Examination of the specific solvation terms reveals a picture of trade-offs between water-host energetic interactions versus water-water interactions and entropy terms. This pattern is physically reasonable: the stronger interactions of water molecules with the polar over the nonpolar host reduce their entropy and prevent them from interacting optimally with other waters.

It was somewhat unexpected that a well-defined toroidal region of high-density water would appear in the nonpolar host as it had in the regular host. The presence of this feature in the nonpolar host, albeit at somewhat lower density (Figure 4), suggests that it results in large part from packing geometry, rather than specific attractive forces between the water and the hosts. In fact, it may be considered an enhancement of the first solvation shell of the host, since it lies between the two innermost zero-crossing contours of the translational entropy density. One may speculate that the torus results in part from constructive interference of an oscillatory g(r) defined at the two portals of the host. If this is valid, then a host of similar shape but with a longer distance between its portals might contain a toroidal region of low, rather than high, solvent density, in its center. Another contributing factor to formation of the torus may be that water molecules in this region have particularly favorable van der Waals interactions with the incurving walls of the host. The reduced orientational ordering of water molecules in the torus region for the nonpolar versus the regular host is also of interest. Sample water configurations in the regular host (Figure 11) suggest that the orientational ordering of water in the torus results in part from interactions with bridging water molecules in the cavity region above and below the torus, which in turn form hydrogen bonds with the host's carbonyl oxygens.

More broadly, the present results highlight the importance of confinement as a determinant of water structure and thermodynamics. This emerges clearly from comparison of water at the z = 0 level in the interior of CB7 and hence in the torus, with water at z = 0 in the first solvation shell around the exterior of the host. At both locations, water molecules are unable to form hydrogen bonds with the host, so standard scoring functions would treat the host-guest contacts in these regions as hydrophobic. However, these locations are still quite different: the surface of the host is concave in the interior and convex on the exterior; waters in the interior are confined, while those in the exterior are exposed to successive layers of solvent molecules; and the interior water molecules are somewhat closer to the host's carbonyl oxygens and hence interact more strongly with them. These three factors cause the interior and exterior water properties to differ significantly, and indeed, the present data clearly show that the interior water is significantly more structured, both translationally and orientationally, than the exterior water. In addition, the energies of the interior waters are significantly less favorable than those at the exterior. Turning off the charges of the host molecule to form the nonpolar host makes the interactions of water with the carbonyl oxygens irrelevant, while leaving the other two factors unchanged. It is thus striking that, although the removal of the charges from the system lowers the entropic ordering in the interior of the host, the interior remains the most translationally structured region in the system. Similarly, whereas the water molecules on the exterior are able to compensate for the loss of favorable energetic interactions with the host by forming stronger interactions with their neighboring water molecules, the interior water molecules are unable to adjust to the loss of favorable interactions with the host, and become more energetically unfavorable in net. These results suggest that the confinement and concavity of the interior is largely responsible for the strikingly unfavorable energetic and entropic properties of the water found in the interior toroidal region, and in particular, for the observed break down of enthalpy-entropy compensation there. In brief, waters within the receptor cavity have lost favorable interactions with other waters, and their interactions with the receptor are not strong enough to fully compensate for this energetic penalty; at the same time, they are more ordered than bulk water, and hence lower in entropy.

The present results also illustrate the general concept that local water density is not a reliable readout of water stability, local chemical potential, or local free energy. (Indeed, these are not necessarily well-defined quantities.) Thus, in the torus region of the regular host, water reaches about 8 times bulk density, even though water molecules in the torus are destabilized, relative to bulk, by elevated orientational entropy and less favorable energetic interactions with their surroundings. Similarly, water may be present at high density near a nonpolar surface, despite the positive surface energy (surface tension). Conversely, one may imagine experiments showing that highly stabilized waters need not be at particularly high density. Consider, for example, immersion of a small parallel plate capacitor in a large volume of water, such that water molecules may freely exchange between the capacitor and the bulk. Imposing a high voltage across the plates will stabilize the waters in the capacitor, but will produce little increase in water density there relative to bulk, due to the low compressibility of liquid water.

Interpreting inhomogeneous solvation theory

We now discuss conceptual issues important for the interpretation of solvation calculations based upon IST. A central point is that, when one uses a single GIST calculation to evaluate the thermodynamics of displacing water molecules from a binding pocket to the bulk, the results do not account for any relaxation or reorganization of the rest of the system in response to the displacement. The rest of the water molecules in the simulation retain their original interactions with each other and with the solute, and their low-order entropy is also left unchanged. The same holds for other methods based on IST, such as WaterMap and STOW. Furthermore, allowing the remaining waters to reorganize in response to the removal of the displaced waters can only reduce the free energy of the system. Therefore, one may expect that such an estimate of water-displacement thermodynamics will tend to overestimate the thermodynamic cost of displacement. The actual free energy of reorganization will of course depend upon the nature (e.g., the polarity) of the ligand that is doing the displacing. On the other hand, the reorganization free energy could be minimal, such as when one adds a methyl group to a ligand and thereby displaces a single water molecule that had been trapped between the ligand and the protein: because this water molecule was isolated from the rest of the solvent, its displacement is not expected to lead to significant reorganization. In any case, if one wishes to account for solvent reorganization, then a second, post-displacement, simulation and IST calculation is required. The only exception is if one considers removal of all water molecules from the solute, in which case, a single GIST calculation provides an estimate of the solvation free energy, as discussed below. It is worth noting that a cavity-formation term recently introduced as an adjunct to the WaterMap approach in order to treat sites where water is at particularly low density⁸ has a different reference state than that of IST. The cavity term provides the reversible work of creating a cavity of a desired radius at a site of interest, and this work implicitly includes the consequences of solvent reorganization in response to cavity formation.

It is also important to be aware of the thermodynamic accounting issues which stem from two-water terms, such as ΔE_ww and ΔS_ww. Because these are integrals over two positions, denoted r and r^′ in the Theory section, they are intrinsically non-local. Therefore, unlike the one-water terms, ΔE_sw and ΔS_sw, they cannot be immediately rendered as three-dimensional scalar fields in r. The natural step is to integrate over one of the positions, say r, in order to generate a scalar field, such as ΔE_ww(r). However, if one then integrates such a quantity over r^′ in a region R in order to determine the region's contribution to solvation, one will double-count any pairwise contributions within R. In the present study, we correct for any double-counting by subtracting the mean water-water interaction energy within R. The analogous issue can arise in the site-oriented WaterMap and STOW methods, because they both assign the full water-water interaction energy to the water in each site. (WaterMap adds this to the solvent-water interaction energy to form what is termed the world energy⁹ or the system energy.⁶⁰) As a consequence, if one sums the WaterMap energies of removing the water molecules from two neighboring sites, one will presumably double-count the interactions of the removed waters with each other. If these interactions are favorable, as expected, say, for the five water sites in streptavidin's binding pocket,⁹ one will overestimate the energetic cost of expelling water from the region. Analogous bookkeeping considerations will apply to two-body and higher order entropy terms.

Two-water terms also generate issues regarding the choice of the bulk water reference state. If one is interested in local water properties and therefore computes the normalized water-water interaction energy defined in Methods, then the corresponding bulk quantity is the mean interaction energy of one water molecule in bulk with all other water molecules, or 2$E_{ww}^{bulk}$, where $E_{ww}^{bulk}$ is the mean, net water-water interaction energy of the bulk phase. However, the sum of this quantity over all water molecules in the bulk phase would double-count the total water-water interaction energy. As a consequence, if one is interested in the thermodynamic consequences of displacing water from a binding site into the equilibrated bulk phase, the appropriate reference energy for each water molecule is simply $E_{ww}^{bulk}$. Once again, analogous considerations will apply to pairwise and higher order entropy terms in IST.

Finally, in the present study, we have referenced the single-body translation and orientational entropy terms to their values in bulk water. This approach has the appeal of making the reported entropy difference terms go to zero for bulk water. However, one might instead take the view that the sum of these one-body translational and orientational entropy represent approximations to the full partial molar entropy of bulk TIP4PEW water, including the consequences of pairwise and higher order correlations. If so, then one would use the full entropy of bulk water as the Ref. 34.

Estimation of solvation free energy with GIST

It is interesting and potentially useful that GIST could be used to estimate solvation free energies by considering the removal of all water in and around the solute. Removal of all water molecules, rather than just those in a local region, eliminates the requirement of accounting for the reorganization of the remaining water molecules. In the future, formal tests of such GIST solvation calculations should compare GIST with matched TI or free energy perturbation results generated with the same explicit solvent model; e.g., TIP4PEW. Such studies will be informative regarding the consequences of the approximations in GIST, notably the restriction to low-order terms in the IST expansion. Success in such tests would support applications where GIST is used to propose a change in a lead compound aimed at improving affinity. In this setting, running a pair GIST calculations could provide computationally inexpensive end-point estimates of changes in the solvation contribution to binding free energy. Thus, an initial MD calculation of a system in state A (initial ligand) would be used to compute a “before” estimate of the total solvation free energy via IST, ΔG_{solv, A} = ΔE_{solv, A} − TΔS_{solv, A}. A second simulation of the system in state B (modified ligand) would then be used to compute an “after” estimate of the total solvation free energy ΔG_{solv, B} = ΔE_{solv, B} − TΔS_{solv, B}. The change in solvation free energy for the two states is then estimated simply as ΔG_IST = ΔG_{solv, B} − ΔG_{solv, A}. We anticipate that such solvation free energy differences will converge much faster than the total solvation free energy, due to the relatively small volume of water that is differentially perturbed. The central benefit of such a study is that it would account for the consequences of solvent reorganization due to the change in the ligand.