Abstract
Many biochemical networks have complex multidimensional dynamics and there is a long history of methods that have been used for dimensionality reduction for such reaction networks. Usually a deterministic mass action approach is used; however, in small volumes, there are significant fluctuations from the mean which the mass action approach cannot capture. In such cases stochastic simulation methods should be used. In this paper, we evaluate the applicability of one such dimensionality reduction method, the quasi-steady state approximation (QSSA) [L. Menten and M. Michaelis, “Die kinetik der invertinwirkung,” Biochem. Z 49, 333369 (1913)] for dimensionality reduction in case of stochastic dynamics. First, the applicability of QSSA approach is evaluated for a canonical system of enzyme reactions. Application of QSSA to such a reaction system in a deterministic setting leads to Michaelis-Menten reduced kinetics which can be used to derive the equilibrium concentrations of the reaction species. In the case of stochastic simulations, however, the steady state is characterized by fluctuations around the mean equilibrium concentration. Our analysis shows that a QSSA based approach for dimensionality reduction captures well the mean of the distribution as obtained from a full dimensional simulation but fails to accurately capture the distribution around that mean. Moreover, the QSSA approximation is not unique. We have then extended the analysis to a simple bistable biochemical network model proposed to account for the stability of synaptic efficacies; the substrate of learning and memory [J. E. Lisman, “A mechanism of memory storage insensitive to molecular turnover: A bistable autophosphorylating kinase,” Proc. Natl. Acad. Sci. U.S.A. 82, 3055–3057 (1985)]10.1073/pnas.82.9.3055. Our analysis shows that a QSSA based dimensionality reduction method results in errors as big as two orders of magnitude in predicting the residence times in the two stable states.
INTRODUCTION
Virtually all cell functions from metabolism through cell division and up to synaptic plasticity, the cellular basis of learning and memory, are achieved via networks of interacting molecules. Progress in molecular biology has led to identification of many elements of these networks, and these often turn out to be quite complex. In order to better understand and predict the actions of such networks mathematical models are essential.3 An understanding of such molecular networks will enable us not only to understand how these cell function normally, but also the source of their pathology in various disease states.
Mechanistic modeling of even a moderately large biochemical network can be quite a complex high dimensional problem. Simulating such networks can be numerically challenging and time consuming,4 and it is often difficult to gain an intuition into their function as well. Thus, it is worthwhile to explore methods for dimensionality reduction. Such methods have been explored for over 100 years, and one well known method is the quasi-steady state approximation (QSSA).1 However, such methods were developed for the deterministic mass action approach while molecular interactions are inherently stochastic because they are determined by collisions and bimolecular interactions that depend on thermal energy and on the orientations of the interacting molecules. In this paper, we test the accuracy of the QSSA approach within the stochastic framework.4
One of the approaches to mechanistic modeling, the mass action approach, assumes that molecular reactions can be characterized by the concentrations of the different molecular species. This approach describes the dynamics of a molecular network via a set of coupled ordinary differential equations (ODEs). Such an approach is usually a good approximation when the molecular system is well mixed, and when the number of molecules is large, so that relative fluctuations from the mean are typically small.
Many biological systems have a small number of molecules that determine cell function, among them are gene expression processes that govern cell fate.5 Such processes that include transcription are outside the scope of this paper, where we are primarily considering post-translational processes. One biological system in which stochastic fluctuations play a crucial role is synaptic plasticity—the molecular substrate of learning and memory. The synaptic strength between neurons is modulated by enzymatic reactions taking place in the small volume of a neuronal spine, a volume much smaller than that of a typical cell. At such a small volume, a small number of molecules are involved in the reaction such that the stochastic fluctuations may be responsible for determining the synaptic state. Various studies have examined the impact of such stochastic fluctuations during the induction6, 7, 8, 9, 10, 11 and maintenance phases.12, 13 Stochastic fluctuations might be of importance not only when the actual size of compartments are small, but also when systems are not well mixed and as a result, have effective microdomains in which relative fluctuations are significant.
There is a long history of methods for reducing the dimensionality of biochemical reaction networks. This set of approximations called the QSSA is based on the assumption that some of the molecular reactions are fast, and can therefore be assumed to quickly reach their steady state. Therefore, some of the dynamical variables can be eliminated by replacing them with their steady state values.4 Different variants of this approach have been proposed over the years.14
When analyzing stochastic molecular systems the aim is not to characterize only the mean molecular concentrations, but also to characterize the distribution of the molecular numbers. The dynamics of these distributions are characterized by the so-called chemical master equation.15 Often the only practical way to estimate the joint distributions of the different chemical species is by using numerical Monte Carlo methods. The most commonly used method is the exact stochastic simulation method proposed by Gillespie.16 However, in complex networks this method is likely to be very slow. This is especially the case when molecular networks include a mix of slow and fast reactions. While simulating the fast reaction uses most of the computational time, the slow reactions often determine the primary shape of the dynamics, and the magnitude of the stochastic fluctuations. For example, in the case of the simple enzyme catalyzed reaction most of the computational power and run time is devoted to calculating the binding and unbinding of the substrate to the enzyme, while the property of interest is likely to be the product being formed in the reaction; a computation that takes only a small fraction of the computational power.17 Therefore, it is appealing to try and reduce dimensionality by using the QSSA in order to simplify the stochastic molecular networks, and speed up the calculations of the distributions. Such an approach was proposed by Rao and Arkin,18 who showed that such an approximation can produce a reasonable approximation of the dynamics of the mean concentration. Another advantage of dimensionality reduction is that at lower dimensions it is sometimes possible to obtain analytical solutions to the master equation.15
The focus of the current paper is whether the QSSA approach can approximate well not only the means of the distributions of the dynamical variables, but also their fluctuations, or more generally the complete distributions. We will test this in two different molecular networks over a wide range of parameters. The two examples we have examined are: a simple enzyme reaction with a basal rate of reversal of product back to substrate and a kinase-phosphatase bistable switch similar to the one suggested by Lisman in 1985.2 In our analysis, we have found in general that the QSSA based reduction scheme fails to capture the distribution of substrate concentration around the mean as obtained from the full model. Also, we found no significant relationship between accuracy of a QSSA based reduction method in predicting the deterministic transients and the accuracy of such a reduction method in predicting the stochastic fluctuation at steady state. Using linear noise approximation (LNA) we found the narrow conditions under which QSSA does approximate well the distribution of the full stochastic system. For the bistable reaction system, we found that a QSSA based reduction method made significant errors in the prediction of residence times in each stable state by about two orders of magnitude.
ENZYME REACTIONS
The quasi-steady state approximation has been applied to a standard two-stage enzyme mediated catalysis reaction to obtain the Michaelis-Menton kinetics. Consider the following set of reactions:
The first reaction indicates the reversible binding of the enzyme (E) and substrate (S) to form the enzyme-substrate complex (C). The enzyme-substrate complex either dissociates back to free enzyme and free substrate or a product molecule (P) is formed and released from the enzyme. The second reaction represents an irreversible conversion of products back to substrate via a separate independent process. The addition of the second reaction ensures that, at equilibrium, the substrate concentration is not equal to zero. This is especially important because we are interested in the distribution around steady state for stochastic simulations and such a distribution exists only for a non-zero steady state. This additional process is of direct interest since in networks of enzymatic reactions, individual dynamics of a particular substrate may be affected by a background rate of conversion of products back to substrate.
Using a mass action approach, a three-dimensional system of differential equations describes the kinetics of the full model
| (1) |
| (2) |
| (3) |
| (4) |
The QSSA assumes that the time scale at which the substrate is being consumed (or product is being formed), the concentration of enzyme-substrate complex is essentially not changing. Hence, the dimensionality of the set of differential equations, that govern the kinetics of the first reaction, can be reduced, by setting the time derivative of the enzyme-substrate complex to zero. The QSSA results in a one-dimensional ODE that describes the kinetics of the reduced model4
| (5) |
| (6) |
| (7) |
where km = (k−1 + k2)/k1.
The initial conditions are set such that the mass balances S + C + P = ST and E + C = ET are satisfied. ST and ET are the total substrate and enzyme concentrations, respectively. Since C*(t) is now a function of S(t), not all initial conditions choices appropriate for Eqs. 1, 2, 3, 4 can be imposed in the reduced system. Here we start from the maximum allowed value of S, which is set at the initial condition by solving the mass balance equation: ST = S(0) + C*(0) + P(0) with P(0) = 0. For comparison purposes, the initial conditions of the full model used in our simulations are identical to the reduced model.
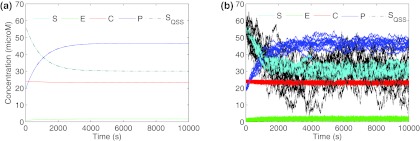
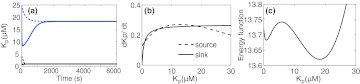
Figure 1a (solid lines) shows the numerical solution of the system ODEs for the full model. Overlaid on the same plot is also the numerical simulation for the 1D ODE for time evolution of substrate in the reduced model (dashed line). In the example shown, the parameters are chosen such that the following condition for validity of QSSA is satisfied:14
| (8) |
Hence, the substrate trace for the reduced model is reasonably close to the substrate trace for the full model. Note that both the full model and the reduced model settle down to the same steady state.
Figure 1.
(a) Quasi-steady state approximation. Comparison of deterministic solution of the complete enzymatic system and the reduced system with the quasi-steady state assumption. The dashed line is the substrate trace for the 1D equation with quasi-steady state assumption. For the chosen parameters that satisfy the QSSA validity criterion, the dashed line is reasonably close to the substrate trace for the full model. The substrate trace for both the full and the reduced model settle down to the same steady state (parameters: k1 = 0.01 [1/(sec* μM)], k−1 = 0.02, k2 = 0.002, k3 = 0.001 [1/sec], ET = 25 μM, ST = 100 μM). (b) Stochastic simulation of the chemical master equation for the complete set enzymatic reactions using the Gillespie algorithm. Overlaid on top, is the reduced stochastic simulation by implementing a Gillespie-like algorithm for the reduced chemical master equation, using the quasi-steady state assumption (Eq. 17). The mean of the stochastic simulation is well approximated by the deterministic simulation. The distribution of substrate concentration for the reduced stochastic simulation is different than the distribution obtained for the full stochastic model. The volume of the reaction mixture is 10−17 l.
The main interest in this paper is not the deterministic solution to the ODEs governing the dynamics of the system. Instead, our focus here is the stochastic simulation. Formally, the joint distribution of the number of free substrate molecules (nS) and number of complex molecules (nC) in a stochastic system is given by the following chemical master equation:
| (9) |
where is the number of free product molecules plus the total number of substrate molecules in bound and free form, and the total number of E molecules in bound and free form.
It is usually not possible to obtain analytical solutions of the master equation. Instead, a numerical solution to Eq. 9 can be obtained by implementing the stochastic simulation algorithm suggested by Gillespie.16 Figure 1b shows the result of fifteen runs of Gillespies algorithm for the same set of parameters as that in Figure 1a. Note that the Gillespie algorithm simultaneously solves for the number of molecules of all the species in the reaction mixture. Also note that in Figure 1b, for comparison with Figure 1a, the output of the Gillespies algorithm has been suitably scaled with reaction volume, V, and Avagadros number, Na, to represent concentrations instead of numbers of molecules.
For the stochastic system the aim of QSSA is to reduce the dimensionality of the two-dimensional master equation as described in Eq. 9 to a one-dimensional master equation of the form
| (10) |
where r(n) and g(n) are the sink and source functions, respectively. In such an equation, the sink function and the probability function must be subject to the following boundary conditions:
| (11) |
| (12) |
In fact, for this kind of chemical master equation, there is a general recursive analytical solution of the form15
| (13) |
This provides the solution as a function of ρ(0), and the full solution is obtained by the condition that the probabilities sum to 1.
A method for reducing dimensionality of the system of chemical master equations for stochastic simulation (Eq. 9), in order to obtain an explicit expression for g and r, was proposed by Rao and Arkin,18 where it was suggested that the equation derived from law of mass action in a deterministic system (Eq. 7) can be used to directly write a reduced chemical master equation for stochastic evolution of the substrate molecule. The idea is to take the reduced differential equation obtained from a QSSA based reduction and identify the sink and the source terms to construct a reduced chemical master equation. The process is outlined more clearly underneath.
We first rewrite Eq. 7 in terms of number of molecules instead of concentrations by replacing concentration values (c) with molecule numbers (n) using the relationship c = n/(NaV), where Na is Avogadros number and V is the volume of the reaction mixture. The following equation is obtained:
| (14) |
| (15) |
| (16) |
Subsequently, the origin of each term in Eq. 16 is identified as a source or sink term, in order to write the following chemical master equation:
| (17) |
where sink and source functions are identified as following:
| (18) |
where and nP are defined by Eqs. 14, 15.
Algebraic simplification of Eq. 16 can give rise to another possibility for the choice of r(n) and g(n) as follows:
| (19) |
where and . There is no clear reason to prefer one choice of r(n) and g(n) over another. As long as the boundary conditions of the system are satisfied, theoretically, any choice of r(n) and g(n) should suffice. It is interesting to note though that any reasonable choice of r(n) and g(n) preserves the mean of the stationary stochastic distribution, the specific choice, however, significantly affects the variance around this mean. This implies that the choice of a reduced master equation is not unique, and indeed there is an infinite number of reduced master equations that are all consistent with the same mass-action equation.
Equation 17 can be solved either analytically or by using the numerical Gillespie algorithm.18 In Figure 1b the results of fifteen runs of the reduced stochastic simulation (black) are overlaid on the traces the full stochastic simulations (cyan). The reduced stochastic simulation in this figure is for the choice of rn and gn as in Eq. 18. The mean of the stochastic simulations (Fig. 1b) is quite close to the deterministic simulation (Fig. 1a) for both the reduced and full stochastic simulation.
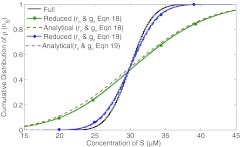
In this paper our focus is on the fluctuations of the distributions around the mean. To simplify this task we concentrate on the distributions at steady state. This is done by running the full and reduced model stochastic simulations for a long time and comparing the distribution of the full and reduced models at steady state. We use the part of the substrate trace where the deterministic counterpart has already reached steady state (t ⩾ 6000 s in the example) and calculate the probability of a certain concentration of substrate when the system is in overall equilibrium. The cumulative distribution of this probability is plotted in Figure 2. The Kolmogorov Smirnov test shows that the distribution for the complete reaction system is significantly different from that for the reduced system. We have also plotted the analytical solutions of the master equations using Eq. 13 in this figure.
Figure 2.
Comparison of the cumulative distribution of probability of a certain concentration of the substrate in the reaction volume after the corresponding deterministic simulation has reached steady state. The cumulative distribution for the numerical solution of the chemical master equation for the complete reaction system has same mean (full: 29.92, reduced (Eq. 18): 30.66, reduced (Eq. 19): 29.88, reduced analytical (using Eqs. 13, 19): 30.12) as that of the reduced system but a different standard deviation (full: 2.60, reduced (Eq. 18): 8.36, reduced (Eq. 19): 3.21, reduced analytical (using Eqs. 13, 19): 3.16). The Kolmogorov Smirnov test shows that the three distributions are significantly different. The analytical and the numerical solution of the reduced chemical master equation (Eq. 17) yield identical results.
The significant difference obtained in the distribution around mean between the full stochastic model and the reduced model suggests that constructing a reduced chemical master equation from deterministic equations reduced by QSSA may not always yield desired accuracy in stochastic simulations, even though the traditional condition for validity of quasi-steady state approximation (Eq. 8) is satisfied.
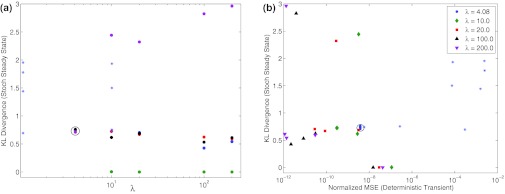
One could hypothesize that a good approximation of the deterministic transient would produce a good approximation of the distribution at steady state in stochastic simulation. The condition for the validity of the QSSA is described by Eq. 8. We define λ = (km + ST)/ET as a parameter quantifying the QSSA approximation, the larger λ the better is the approximation in the deterministic case. We quantified how well the quality of the reduced stochastic simulation by the Kullback-Leibler (KL) divergence between the steady state distributions of the full and reduced models (See Appendix). In Figure 3a, we plotted the KL divergence as a function of λ. Each different color in this plot corresponds to the same steady state value, but with different parameters that are still consistent with this steady state. Here we see no obvious relationship between the fidelity of the deterministic simulations, as quantified by λ, and the fidelity of the stochastic simulations. It is possible that such negative results arise from λ not faithfully quantifying the fidelity of the deterministic simulations. Therefore, we directly measured the fidelity of the deterministic simulations during their transient phase using a normalized mean squared error (NMSE), as described in the Appendix. In Figure 3b, we show the KL divergence as a function of the NMSE. The different colors here code for different values of λ. These results, as those in Figure 3a, show no apparent dependence between the fidelity of QSSA in stochastic simulations during steady state and deterministic dynamics during the initial transient.
Figure 3.
Relationship between the accuracy of the quasi-steady state approximation in predicting the deterministic transients and the accuracy of the reduced stochastic model to predict steady state distributions. (a) The accuracy of the stochastic simulations quantified by the KL divergence between the full and reduced models as a function of the parameter λ which quantifies the QSSA approximation in the deterministic case. The points denoted by (*) are consistent with the data points in the paper by Barik et al..17 The circle is around the data point from the example in the previous figures. (b) The accuracy of stochastic simulations quantified as in (a) by the KL distance, as a function of the actual accuracy of the deterministic simulation. Here the accuracy of the deterministic simulations is quantified by the average normalized mean distance (NMSE) between the full and reduced models (see Appendix).
In order to gain insight into why the QSSA fails in this case, we have developed a LNA of this model.15, 20, 21 The LNA approximation is typically applicable to mesoscopic systems. The approximation allows us to gain simple expressions for the variance; an expression from which we can gain insight. We have used this approach both for the full two-dimensional system and for the reduced one-dimensional system as defined in Eqs. 17, 18. In order to obtain the variance of LNA one has to solve the algebraic system of equations
| (20) |
where J is the Jacobian of the system of the differential equations evaluated at the steady state, B the diffusion matrix of this system, and Ω is the volume of the system.15, 20 In this equation σ is the covariance matrix in terms of the number of particles, and has to be rescaled if it is used to calculate the concentration of particles.
For the complete two-dimensional system at steady state these take the form
| (21) |
| (22) |
From these expressions one obtained that the LNA approximation for the variance of the substrate (σ11) is
| (23) |
where Kn = (k−1 − k3)/k1.
We can also use the reduced QSSA equations (Eqs. 17, 18) to obtain the variance using the LNA. This results in
| (24) |
where jqss = j11 − j12j21/j22.
In order to analytically compare the variance using the LNA approximation for the full system (Eq. 23) and the system reduced by QSSA (Eq. 24) we use a time scale separation following the approach outlined in Thomas et al..21
For the system defined here, the time constant of the substrate is: τs = (k1E + k3)−1 and the time constant of the complex is: τc = (k1S + k−1 + k2)−1. The ratio of the two time constants, defined as γ = τs/τc, should be large when the QSSA approximation holds. For the full system γ = (S + Km)/(E + k3/k1). Using the definition of γ in Eq. 23 we obtain
| (25) |
The two terms on the left are negligible for γ ≫ 1 and the term on the right becomes equivalent to . This leaves us with the third term, which is the difference between the variance of the full system using an LNA approximation and the reduced system using the standard QSSA method used for deterministic systems. This difference does not vanish even under the conditions of time scale separation, as defined by the condition γ ≫ 1.
The relative error of the QSSA equation can then be defined as
| (26) |
where . Note that the relative error vanishes (ɛr ≪ 1) only when Km ≫ S and Km ≫ Kn. Taken together with the time scale separation constraint, this implies that QSSA would produce a good approximation of the variance only when Km ≫ E as well. These conditions lead to a narrow set of conditions under which the QSSA is appropriate for estimating noise in enzymatic reactions.21
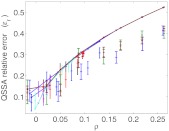
The generality of the analysis outlined here might be limited by the use of the LNA, and these results might not be valid when the LNA fails. To test this we carried out simulations for the complete 2D system, and the reduced system using the Gillespie algorithm to numerically estimate ɛr. In Figure 4 we plotted the numerically estimated ɛr as a function of ρ. The results show that the relative error increases monotonically with ρ; qualitatively very similarly to the analytical prediction (solid lines).
Figure 4.
The dependence of the relative error between the variance of the full system and the variance of the system reduced using the QSSA approach. Solid lines are the analytical results using the LNA approach (Eq. 26), and symbols with error bars are obtained directly from simulations. Different colors represent different parameters sets. In each parameter set all parameters are fixed, except for k1 which is varied, to obtain different values of ρ.
A BISTABLE KINASE-PHOSPHATASE MOLECULAR SWITCH
Stochastic fluctuations have a significant impact in bistable systems, where these fluctuations determine the transitions between the two stable fixed points. A simple example of such a bistable system was proposed by Lisman.2 Lisman's original model did not explicitly describe the reaction scheme. We have postulated a reaction scheme which is qualitatively consistent with Lisman's original model. This results in the following reaction scheme:
The phosphorylated form of kinase molecule, KP, is active while the dephosphorylated form of kinase K is inactive. In the first reaction, an active kinase molecule phosphorylates an inactive kinase molecule. This process is called autophosphorylation. In the second reaction, an active kinase molecule is dephosphorylated by binding to a phosphatase molecule. The third reaction represents the basal level of phosphatase activity that converts an active kinase molecule to an inactive kinase molecule. This reaction is not in Lisman's original model but we added it to avoid an absorbing state. Note that here the enzyme and the substrate are different states of the same molecular species; making it difficult to obtain a validity condition for the QSSA.
The “full” deterministic model for the above set of reactions, obtained by applying the of law of mass action, is
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
where K is the concentration of the free dephosphorylated kinase, KP is the concentration of the free phosphorylated kinase, P is the concentration of free phosphatase, C1 is the concentration of the kinase autophosphorylation complex, and C2 is the concentration of the kinase dephosphorylation complex. KT and PT are total kinase and total phosphatase concentrations, respectively. The initial conditions are C1(0) = C2(0) = 0, P(0) = PT, K(0) = KT for low steady state and KP(0) = KT for high steady state. This set of equations has two stable equilibrium solutions. This means that even with the same set of parameters, starting from various initial conditions will lead to one of two different stable steady states. Such a system of equations is said to represent a bistable system. Figure 5a (solid lines) shows the result of numerical simulation of Eqs. 27, 28, 29, 30, 31 for two initial conditions. When KP(0) = 25 μM, the steady state concentration of KP is 18.4 μM and when KP(0) = 4 μM, the steady state concentration of KP is 0.8 μM.
Figure 5.
(a) Deterministic simulation for the kinase-phosphatase switch showing bistability. The solid lines are obtained from the simulation of the full system. The dashed lines are from simulations with QSSA. Blue lines are for initial condition KP(0) = 25 μM and black lines are for initial condition KP(0) = 4 μM. (b) The source and sink terms for the quasi-steady state reduced model as a function of phosphorylated kinase concentration. The points of intersection of the solid and dashed lines are the fixed points of the system. (c) Potential energy wells for the fixed points in the reduced model. Note that the fixed points of the reduced model are identical to the fixed points of the full model. (Parameters: r1 = 0.001 [1/(sec* μM)], r−1 = 0.002, r2 = 0.02 [1/sec], r3 = 0.08 [1/(sec* μM)], r−3 = 0.001, r4 = 0.0539, r5 = 0.00212 [1/sec], KT = 60 μM, PT = 5 μM.)
Applying the quasi-steady state assumption ( and ) to Eqs. 27, 28, 29, 30, 31, we obtain a one-dimensional ODE for the concentration of phosphorylated kinase that describes the kinetics of the reduced model (Eq. 32)
| (32) |
This QSSA equation is now analogous to Lisman's model though it quantitatively differs from it. Numerical simulations of Eq. 32 are shown as dashed lines in Figure 5a. Fixed points of the system can be obtained analytically by setting the left hand side of Eq. 32 to zero. Note that the fixed points (steady states) of the reduced 1D system are identical to the fixed points of the full model of Eqs. 27, 28, 29, 30, 31.
In order to construct a chemical master equation, the origin of each term in Eq. 32 is taken into account to define the source and sink terms as follows:
Note that here again, different possible choices of source and sink terms can be formulated keeping the steady state the same. Figure 5b shows the source and sink terms plotted separately as a function of KP. The points of intersection of the solid and the dashed lines are the fixed points of Eq. 32. Figure 5c shows the potential energy wells for the two steady states for the given set of parameters (See Appendix). Stochastic fluctuations between the two stable steady states in the 1D reduced model are seen as transitions between the the two energy minima.
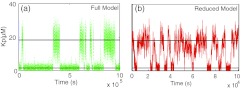
Stochastic simulations for the kinase-phosphatase switch are carried out by implementing the Gillespie algorithm for the reaction scheme described above. Figure 6a shows a stochastic simulation of the complete reaction system. The solid lines represent the fixed point of the system. Note that the mean of the stochastic fluctuations in a given stochastic equilibrium well approximates the deterministic steady state (solid lines). Also note that a large fluctuation is enough to tip the system into the other stable state. This switching of states is very sensitive to the magnitude of stochastic fluctuations around the mean. To reduce the dimensionality of the stochastic simulation, a scheme similar to that employed in the previous section is used. Equation 32 written in terms of number of molecules instead of concentration is
| (33) |
where
Similar to Eqs. 17, 18, the following one-dimensional chemical master equation is obtained:
| (34) |
where
| (35) |
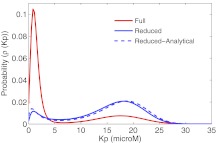
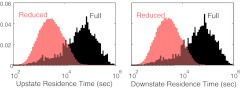
Equations 34, 35 can be solved using a Gillespie like algorithm.18 Figure 6b shows the results of the numerical simulation of Eq. 34. The switching is much faster in the reduced system (note the different time scale). This is because the variance of KP is larger in case of the reduced stochastic simulation. Figure 7 shows the stationary distribution of the probability density of a particular concentration of KP for the full model and the reduced model. An analytical expression for such a stationary distribution is also obtained using Eq. 13. Notice that the probability density functions for the reduced model is very different from that for the full model. The bimodal representation in the two cases is due to the bistable nature of the system. Another statistic that characterizes this system is the characteristic dwell time at or near each of the stable states. To do this calculation we set an upstate threshold and a downstate threshold. We count the time after the system goes below the downstate threshold until it hits the upstate threshold as “downstate residence time” and the time after the system goes above the upstate threshold until it hits the downstate threshold as “upstate residence time.” We set the same threshold for the full and the reduced model. For a simulation run over a long time (5 × 108 s), there are many transitions between the states, with a different residence time for each transition; resulting in a distribution of the residence times. In our observation, we found that the mean of both “upstate residence time” and “downstate residence time” were significantly different between the full and reduced models (Fig. 8). Specifically, the full model predicts much longer residence times in both the ‘up” and “down” states. This trend is consistent with the results in Figure 6 that show a smaller level of fluctuations in the full model, since it is these fluctuations that drive the transitions between the states.
Figure 6.
Stochastic switching between bistable states. (a) Green line is the stochastic simulation of the complete reaction system using the Gillespie algorithm. The initial conditions are set to the upper steady state value. The black horizontal line indicates the two stable steady state concentration levels for each species. Note that the mean of the stochastic fluctuations within an equilibrium state is close to the steady state concentration. (b) The red line is the stochastic simulation using the reduced master equation and a Gillespie-like algorithm. Note the difference in the scale of x axis in the plots on the left and right.
Figure 7.
Histogram showing difference in upstate and downstate distribution for the full model and quasi-steady state model for stochastic simulations. Kp > 5.7 μM is classified as upstate and Kp < 5.7 μM is classified as downstate.
Figure 8.
Distribution of residence times in the upstate and downstate for the full model and QSSA model. The total simulation time over which this histogram is calculated is 5 × 108 s. The mean upstate residence time for the full model is 2.70 × 104 s while that for reduced model is 4.93 × 103 s. The mean downstate residence time for full model is 3.25 × 104 s while that for reduced model is 4.70 × 103 s.
DISCUSSION
Chemical reactions involving small number of reacting molecules are essentially stochastic in nature. The mass action approach to obtain a deterministic approximation works well in estimating the mean concentrations of reacting species over time, when the system is well mixed and the number of molecules is large. In certain reaction systems, where the stochastic fluctuations are large, the distribution around the mean is of interest. Most protein networks are quite complex, even in their deterministic limit, and their complexity and computational cost increase significantly once stochastic fluctuations are taken into account. For many years a dimensionality reduction technique, the quasi-steady state assumption, has been applied to deterministic models, and recently it has been suggested that similar techniques can be useful when applied to stochastic systems as well.17, 18 Whether this approach yields precise results is the question addressed by this paper.
In this paper, we have shown two examples where a QSSA based reduction when applied to stochastic dynamics leads to significant errors in the distribution of stochastic fluctuations around the mean. The first example we examined is closely related to the simple catalytic reaction scheme, with one additional reaction that avoids a trivial fixed point. For this reaction we show that applying the QSSA results in large errors in the distribution of the substrate. We show this both using an analytical solution of the master equation, and by performing stochastic simulations of the full and reduced models. Surprisingly we find that the reduced model has much higher variance than the original model. This is the case even though we tested the model in the regime where the QSSA should be valid.
In order to gain insight as to why the system reduced by QSSA provides inexact estimates of the distribution even though the traditional conditions for the QSSA hold, we carried out a linear noise approximation of the system.15, 20 Such an approximation, which is valid for monostable mesoscopic systems, can provide a simple expression for the variance for both the full and reduced systems. When comparing the variance for the reduced system with the variance of the full system we find that they do not fully coincide even under the time scale separation conditions where the QSSA should be valid. Instead, we describe a set of much narrower constraints under which the reduced system can capture the variance of the full system. Using simulations we show that these conditions are not limited by the validity of the LNA. These results are qualitatively consistent with results obtained recently for an open biochemical network.21
The other example analyzed here is a bistable autophosphorylation loop, inspired by a model proposed by Lisman in 1985, to account for the stability of memory. The model differs from the original model in having an additional constitutive kinase activity to avoid an absorbing state2 at the low fixed point, and in that we systematically applied the QSSA approximation to reduce the full model to a 1D system. The stochastic simulations of both the full and reduced models show spontaneous transitions between a “down” and an “up” state. For both the full and reduced models these states have the same value. However, here too the distributions of the states in the reduced model are significantly different than the distributions obtained for the full model. Most significantly the residence times in both the “down” and “up” states in the reduced model are two orders of magnitude shorter than the residence times of the full model. This result implies that such reductions might not be useful if the statistic of biological significance is the residence time.
The canonical technique for simulating stochastic chemical reactions is the exact stochastic simulation algorithm proposed by Gillespie in 1977. This algorithm can be very computationally expensive. Various approximations have been proposed to speed it up, one such approach is the QSSA approach18 analyzed here, and a related partial equilibrium approach.18, 19 The QSSA assumes that intermediate complexes have quick relaxation and can be assumed to be at equilibrium, given the other variables, while the partial equilibrium methods assume that fast reactions are at equilibrium.22 Often, but not always, these two approaches are practically identical. Rao and Arkin18 have shown that such methods significantly reduce computational costs, and at the same time produces good estimates of the means of full models. The errors in predicting the mean with this Gillespie-like algorithm mirror the errors that the QSSA produces in deterministic simulations. However, Rao and Arkin did not examine if this Gillespie-like approach estimates well other properties of the distribution of the chemical species.
Another approach for dimensionality reduction in chemical reactions is the total quasi-steady state approach.14 This approach when applied to a simple catalytic reaction preforms a change of variables, and assumes a time scale separation not between the original reactions, but for the transformed set of reactions. For deterministic cases this approach extends the range over which the quasi-steady state assumptions can be applied, at the cost of producing more complex equations that do not have an intuitive closed form. Recently this approach was extended to stochastic systems, by using again a Gillespie-like algorithm directly for the equations produced by the total QSSA.17 Applying this approach to various monostable and bistable systems produced results that seem very close to those produced by the full system. We did not examine here the impact of the total QSSA approximation, and this should be carried out in subsequent work. However, our results are qualitatively both similar and different from the results of using total QSSA approach for dimensionality reduction in stochastic simulations. First, in our simple enzymatic reaction we added an additional step, not included by the Barik et al.’s paper.17 Therefore, our system has an additional parameter. Nevertheless, we have simulated the catalytic reaction system with all parameters except for one being identical to those on Barik et al.17 (Figure 3—star symbols). For few of those simulations (i.e., for few values of our parameter k3 in Eq. 7) we indeed find a relatively good agreement between the full and reduced models, even without applying directly the total QSSA approach. For other choices of k3, the agreement between full and reduced stochastic distributions is not good. In our simulations of the bistable system we find a big difference in the residence times between the full and reduced models, and indeed this is consistent with results obtained for some sets of parameters for the different bistable system modeled by Barik et al. (Figure 10 in Barik et al.).17 In a sense it is not surprising that the biggest differences between the full and reduced models are obtained for the residence time statistics. Transitions between these two states can be thought of as jumps between two energy minima, triggered by stochastic fluctuations. Stochastic transitions between these states can be viewed as being triggered by the tails of distribution of these two states, and the mass of such tails can indeed be significantly different even if the parameters of the distribution are only moderately different, resulting in a large difference in the residence time statistics.
Several other approaches have been suggested for accelerating stochastic simulations. One well known approach, the tau-leap, was proposed Gillespie and co-workers.23, 24 Related techniques are various reduction methods such as slow-scale stochastic simulation algorithm19 and accelerated stochastic simulation algorithms. The reader is redirected to Gillespie25 and Gillespie et al.26 for a review of these algorithms. According to such approaches reactions are partitioned into fast and slow, fast reactions are simulated with deterministic or fast approximate stochastic techniques, whereas slow reactions still use the complete exact stochastic scheme. The slow-scale algorithms are related to the partial equilibrium assumptions as the fast reactions reach partial equilibrium quickly and once it is reached their means or distributions can be quickly assessed given the slow variables, and thus they no longer need to be explicitly simulated until the slow species change significantly. Different variants of this framework have been proposed. One variant suggests that the means of fast species, given the slow species, can be estimated using algebraic techniques;19, 22 a method which can produce good approximation if the fluctuations of the fast species are primarily driven by the fluctuations of the slow species. Alternatively the distribution of the fast species cab be estimated by direct stochastic simulations, which can be terminated when partial equilibrium is attained.27, 28, 29 Such algorithms can speed up run times, and reportedly produce reasonable approximations for large time scale separations. Another related approach has lead to hybrid simulation algorithms,30, 31 which also can produce decent approximations and speed up simulation times. Our results strictly apply just to QSSA as the alternative reduction techniques are typically more complex, and therefore might produce more faithful numerical approximations. However, in light of our results the ability of such methods to capture the complete distributions should be carefully analyzed as well. Our methodology is based on the observation that it is easier to assess complete distributions for systems that are in a non-trivial steady state, rather than systems that are still dynamically evolving. We also find it useful to quantify how well distributions are approximated by the reduced models rather than to graphically observe the distributions. A quantitative test of these approximations allows us to to test and display how the validity of the approximation depends on the system parameters.
The traditional QSSA approach not only speeds up simulations times. It also has the advantage of producing reduced dimension models that have an explicit closed form and may therefore provide analytical solutions and a better intuition for the systems function. We have given two examples here; one of the catalytic reaction and another of a simple bistable system based on autophosphorylation. Both systems can be reduced to a 1D model for which we have an analytical solution of the master equation, and intuition about the origin of the behavior; for example, bistability in the autophosphorylation system. Such simplifications are harder to obtain with alternative dimensionality reduction methods, including total QSSA.14, 17 However, the results of this paper question the validity of the QSSA approach when applied to stochastic systems.
ACKNOWLEDGMENTS
We would also like to thank our anonymous reviewers for suggestions that have considerably improved this paper, and R. Grima for sharing with us some of his methods. A.A. was supported by the UT graduate initiative, H.Z.S. was partially supported by NIH Grant No. 1RO1DA034970-01, and G.C.C. would like to acknowledge the Fondazione CarisBO.
APPENDIX A: MATHEMATICAL METHODS
Energy function
The QSSA based reduction of the deterministic system gives us the 1D equation
The energy function for this equation as a function of KP is given by
| (A1) |
The energy function in Figure 5 is generated by symbolic integration of the right hand side of Eq. 32.
Normalized mean square error function
Figure 3 shows the comparison between the accuracy of the quasi-steady state approximation for deterministic simulations and the reduced chemical master equation for the stochastic simulations. On the x axis is a measure of the accuracy of quasi-steady state approximation of the deterministic approximation. This measure is the mean-square error between a deterministic simulation implementing quasi-steady state and a deterministic simulation of the full model during the transient, i.e., before the steady state is reached (the error is zero after the steady state is reached). The mean-square error is normalized by the time taken for the transient to reach the steady state. This ensures that the measure is invariant to the rate of convergence the steady state. The error is measured relative to the concentration of the full model. This ensures that the measure is scale invariant. Mathematically it takes the form
| (A2) |
where tN is the time it takes for a particular trial to reach the steady state, and are the intrapolated x vectors on an equispaced time grid from 0 to tN for full and reduced deterministic simulations, respectively. This error in transients is averaged over a hundred trials with randomized initial conditions. Smaller NMSE values mean that the deterministic quasi-steady state transient better approximates the deterministic full model transient for a particular set of parameters.
Kullback-Leibler divergence
On the y axis of Figure 3 is the Kullback-Leibler divergence between the substrate distribution at steady state for the complete reaction system and the reduced model. The KL divergence is used as a measure of difference between the stochastic distributions of substrate in the full and reduced models. The KL divergence is given by the following formula:
| (A3) |
where pfull(x) is the probability density of the substrate distribution for the full model and preduced(x) is the probability density of the substrate distribution for the reduced model.
References
- Menten L. and Michaelis M., “Die kinetik der invertinwirkung,” Biochem. Z 49, 333369 (1913). [Google Scholar]
- Lisman J. E., “A mechanism of memory storage insensitive to molecular turnover: A bistable autophosphorylating kinase,” Proc. Natl. Acad. Sci. U.S.A. 82, 3055–3057 (1985). 10.1073/pnas.82.9.3055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Riel N. A. W., “Dynamic modeling and analysis of biochemical networks: Mechanism based models and model-based experiments,” Briefings Bioinf. 7(4), 364–374 (2006). 10.1093/bib/bbl040 [DOI] [PubMed] [Google Scholar]
- Segel L. A., “On the validity of steady state assumption of enzyme kinetics,” Bull. Math. Biol. 6, 579–593 (1988). [DOI] [PubMed] [Google Scholar]
- Cai L., Friedman N., and Xie X. S., “Stochastic protein expression in individual cells at the single molecule level,” Nature (London) 440, 358–362 (2006). 10.1038/nature04599 [DOI] [PubMed] [Google Scholar]
- Yeung L. C., Castellani G. C., and Shouval H. Z., “Analysis of the intraspinal calcium dynamics and its implications for the plasticity of spiking neurons” Phys. Rev. E 69, 011907 (2004). 10.1103/PhysRevE.69.011907 [DOI] [PubMed] [Google Scholar]
- Shouval H. Z. and Kalantzis G., “Stochastic properties of synaptic transmission affect the shape of spike time-dependent plasticity curves,” J. Neurophysiol. 93, 1069–1073 (2005). 10.1152/jn.00504.2004 [DOI] [PubMed] [Google Scholar]
- Cai Y., Gavornik J. P., Cooper L. N., Yeung L. C., and Shouval H. Z., “Effect of stochastic synaptic and dendritic dynamics on synaptic plasticity in visual cortex and hippocampus,” J. Neurophysiol. 97, 375–386 (2007). 10.1152/jn.00895.2006 [DOI] [PubMed] [Google Scholar]
- Keller D. X., Franks K. M., Bartol T. M. J., and Sejnowski T. J., “Calmodulin activation by calcium transients in the postsynaptic density of dendritic spines,” PLoS One 3, e2045 (2008). 10.1371/journal.pone.0002045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng S. and Holmes W. R., “The effect of noise on CaMKII activation in a dendritic spine during LTP induction” J. Neurophysiol. 103, 1798–1808 (2010). 10.1152/jn.91235.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubota Y. and Waxham M. N., “Lobe specific Ca2+-calmodulin nano-domain in neuronal spines: A single molecule level analysis” PLoS Comput. Biol. 6, e1000987 (2010). 10.1371/journal.pcbi.1000987 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller P., Zhabotinsky A. M., Lisman J. E., and Wang X. J., “The stability of a stochastic camkii switch: Dependence on the number of enzyme molecules and protein turnover,” PLoS Biol. 3, e107 (2005). 10.1371/journal.pbio.0030107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graupner M. and Brunel N., “STDP in a bistable synapse model based on CaMKII and associated signaling pathways,” PLoS Comput. Biol. 3, e221 (2007). 10.1371/journal.pcbi.0030221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borghans J. A., de Boer R. J., and Segel L. A., “Extending the quasi-steady state approximation by changing variables,” Bull. Math. Biol. 58, 43–63 (1996). 10.1007/BF02458281 [DOI] [PubMed] [Google Scholar]
- Van Kampen N. G., Stochastic Processes in Physics and Chemistry, 3rd ed. (North Holland Public Library, 2007). [Google Scholar]
- Gillespie D. T., “Exact stochastic simulations of coupled chemical reactions,” J. Phys. Chem. 81, 2340–2361 (1977). 10.1021/j100540a008 [DOI] [Google Scholar]
- Barik D., Paul M. R., Baumann W. T., Cao Y., and Tyson J. T., “Stochastic simulations of enzyme-catalyzed reactions with disparate timescales,” Biophys. J. 95, 3563–3574 (2008). 10.1529/biophysj.108.129155 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao C. V. and Arkin A. P., “Stochastic chemical kinetics and the quasi-steady-state assumption: Application to the Gillespie algorithm,” J. Chem. Phys. 118, 4999–5011 (2003). 10.1063/1.1545446 [DOI] [Google Scholar]
- Cao Y., Gillespie D., and Petzold L., “The slow-scale stochastic simulation algorithm,” J. Chem. Phys. 122, 014116 (2005). 10.1063/1.1824902 [DOI] [PubMed] [Google Scholar]
- Elf J. and Ehrenberg M., “Fast evolution of fluctuations in biochemical networks with linear noise approximation,” Genome Res. 13, 2475–2484 (2003). 10.1101/gr.1196503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas P. Straube A. V., and Grima R., “Limitations of the stochastic quasi-steady-state approximation in open biochemical reaction networks,” J. Chem. Phys. 135, 181103 (2011). 10.1063/1.3661156 [DOI] [PubMed] [Google Scholar]
- Cao Y., Gillespie D., and Petzold L., “Multiscale stochastic simulation algorithm with stochastic partial equilibrium assumption for chemically reacting systems,” J. Comput. Phys. 206, 395–411 (2005). 10.1016/j.jcp.2004.12.014 [DOI] [Google Scholar]
- Gillespie D. T., “Approximate accelerated stochastic simulation of chemically reacting systems,” J. Chem. Phys. 115, 1716–1733 (2001). 10.1063/1.1378322 [DOI] [Google Scholar]
- Cao Y., Gillespie D. T., and Petzold L. R., “Efficient stepsize selection for the tau-leaping simulation method,” J. Chem. Phys. 124, 044109 (2006). 10.1063/1.2159468 [DOI] [PubMed] [Google Scholar]
- Gillespie D. T., “Stochastic simulation of chemical kinetics,” Annu. Rev. Phys. Chem. 58, 35–55 (2007). 10.1146/annurev.physchem.58.032806.104637 [DOI] [PubMed] [Google Scholar]
- Gillespie D. T., Cao Y., Sanft K. R., and Petzold L. R., “The subtle business of model reduction for stochastic chemical kinetics,” J. Chem. Phys. 130, 064103 (2009). 10.1063/1.3072704 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samant A. and Vlachos D., “Overcoming stiffness in stochastic simulations stemming from partial equilibrium: A multiscale Monte Carlo algorithm,” J. Chem. Phys. 123, 144114 (2005). 10.1063/1.2046628 [DOI] [PubMed] [Google Scholar]
- Salis H. and Kaznessis Y., “Equation-free probabilistic steady-state approximation: dynamic application to the stochastic simulation of biochemical reaction networks,” J. Chem. Phys. 123, 214106 (2005). 10.1063/1.2131050 [DOI] [PubMed] [Google Scholar]
- E W., Liu D., and Vanden-Eijnden E., “Nested stochastic simulation algorithm for chemical kinetic systems with disparate rates,” J. Chem. Phys. 123, 194107 (2005). 10.1063/1.2109987 [DOI] [PubMed] [Google Scholar]
- Haseltine E. and Rawlings J., “Approximate simulation of coupled fast and slow reactions for stochastic chemical kinetics,” J. Chem. Phys. 117, 6959–6969 (2002). 10.1063/1.1505860 [DOI] [Google Scholar]
- Mattheyses T. and Simmons M., “Hybrid simulation of cellular behavior,” Bioinformatics 20, 316–322 (2004). 10.1093/bioinformatics/btg409 [DOI] [PubMed] [Google Scholar]