Effects of arterial oxygen tension and cardiac output on venous saturation: a mathematical modeling approach

Abstract

OBJECTIVES:

Hemodynamic support is aimed at providing adequate O₂ delivery to the tissues; most interventions target O₂ delivery increase. Mixed venous O₂ saturation is a frequently used parameter to evaluate the adequacy of O₂ delivery.

METHODS:

We describe a mathematical model to compare the effects of increasing O₂ delivery on venous oxygen saturation through increases in the inspired O₂ fraction versus increases in cardiac output. The model was created based on the lungs, which were divided into shunted and non-shunted areas, and on seven peripheral compartments, each with normal values of perfusion, optimal oxygen consumption, and critical O₂ extraction rate. O₂ delivery was increased by changing the inspired fraction of oxygen from 0.21 to 1.0 in steps of 0.1 under conditions of low (2.0 L.min^-1) or normal (6.5 L.min^-1) cardiac output. The same O₂ delivery values were also obtained by maintaining a fixed O₂ inspired fraction value of 0.21 while changing cardiac output.

RESULTS:

Venous oxygen saturation was higher when produced through increases in inspired O₂ fraction versus increases in cardiac output, even at the same O₂ delivery and consumption values. Specifically, at high inspired O₂ fractions, the measured O₂ saturation values failed to detect conditions of low oxygen supply.

CONCLUSIONS:

The mode of O₂ delivery optimization, specifically increases in the fraction of inspired oxygen versus increases in cardiac output, can compromise the capability of the “venous O₂ saturation” parameter to measure the adequacy of oxygen supply. Consequently, venous saturation at high inspired O₂ fractions should be interpreted with caution.

INTRODUCTION

The ultimate goal of hemodynamic support is to provide enough oxygen delivery (DO₂) to guarantee tissue oxygen needs and avoid organ dysfunction (1,2). Under normal conditions, DO₂ exceeds oxygen consumption (VO₂) to an extent that makes consumption independent of delivery (3,4). However, during regional low delivery, oxygen consumption becomes supply dependent (3-5). Oxygen delivery depends on the hemoglobin concentration (Hb), hemoglobin oxygen affinity, arterial partial pressure of oxygen (PaO₂), and cardiac output (CO). It is possible to achieve comparable changes in DO₂ by manipulating these variables within physiological limits, although the impact on VO₂ might depend on what parameter is modified (6).

Measuring oxygen consumption at the bedside is complex. Therefore, surrogates of the adequacy of oxygen delivery, such as lactate concentration, venous partial pressure of oxygen (PvO₂), and mixed (SvO₂) or central venous oxygen saturation, are commonly used during routine patient care (1,5,7). Venous oxygen saturation is part of the current guidelines for early resuscitation during sepsis (7). Nevertheless, SvO₂ can respond differently to changes in DO₂ if the changes are obtained through changes in different component of the DO₂ equation (8), even when these changes lead to similar VO₂ values. In this paper, we developed a mathematical model to investigate whether the type of DO₂ optimization, specifically increases in the arterial partial pressure of oxygen versus increases in cardiac output, would have different effects on SvO₂.

METHODS

The mathematical model was created based on the lungs and on seven peripheral compartments. Lung blood flow was divided into shunted and non-shunted areas. The peripheral compartments, each with its own perfusion, optimal VO₂, and critical oxygen extraction rate, were created to simulate the behavior of the flow to organs. Having multiple peripheral compartments in the model was important to simulate the heterogeneity of the oxygen supply/demand in different organs and tissues to reproduce the complex relationship between mixed venous oxygen saturation and oxygen delivery.

In all of the following notations, “x” represents venous (“v”), lung capillary (“c”) or arterial blood (“a”).

Hemoglobin oxygen saturation (SxO₂) was calculated according to equation 1 (9):

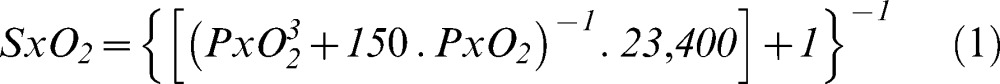Blood oxygen content (CxO₂) was calculated according to a standard formula (equation 2) (9):

Lungs: The alveolar partial pressure of oxygen was calculated using the alveolar gas equation (equation 3) and used as an approximation of the capillary partial pressure of oxygen (10):

As mentioned, the lungs were composed of shunted and non-shunted areas. Solving Berggren's shunt equation for CaO₂ gives the following equation (where Fshunt is the pulmonary shunt fraction):

DO₂ and VO₂ in the peripheral compartments: We used seven compartments to simulate blood flow to the brain, heart, kidneys, muscles, splanchnic (liver), skin, and ‘others', each with normal values of perfusion fraction, extraction rate, and optimal oxygen consumption (VO_2optimal) (11). Because the arterial oxygen content was the same for all compartments, differences in oxygen supply from one compartment to the other occurred through differences in regional perfusion. For each compartment, the oxygen consumption was calculated according to equation 5:

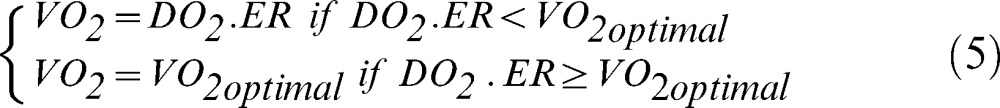The mathematical model: The input variables for the model included global values of cardiac output, pulmonary shunt fraction, pH, arterial carbon dioxide tension, Hb, and fraction of inspired oxygen. Additionally, we supplied hemodynamic variables for each compartment, including its perfusion fraction, its critical oxygen extraction rate and optimal VO₂.

In the first run of the model, mixed venous oxygen saturation and mixed venous content were calculated according to equation 1 using an arbitrary initial mixed venous oxygen partial pressure of 40 mmHg. Pulmonary capillary oxygen content was obtained through equations 2 and 3, and arterial oxygen content was estimated according to the pulmonary shunt fraction (equation 4). Oxygen delivery to each compartment was subsequently calculated by multiplying the compartment perfusion fraction by the global oxygen delivery.

A new venous oxygen content value for each compartment was then calculated using equation 6, and the global mixed venous oxygen content was obtained from a perfusion-weighted average of the local venous contents (equation 7).

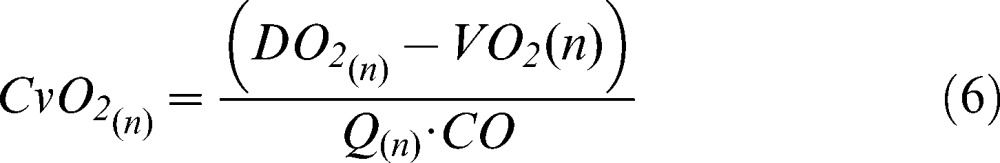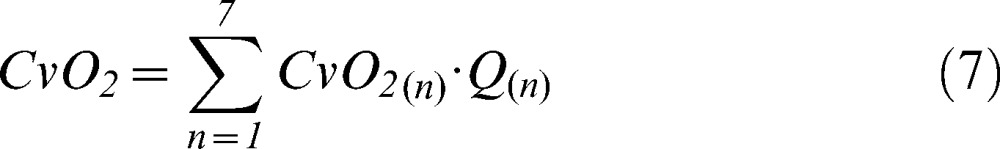The mixed venous partial pressure of oxygen was determined from the mixed venous oxygen content by solving equations 1 and 2 to an acceptable error of 1:1,000 using the Newton-Raphson method. The new calculated value of the mixed venous partial pressure of oxygen was then reentered into the model, replacing the initial guess. We repeated these calculations until the difference between successive approximations of the mixed venous partial pressure of oxygen values was less than 1:1,000 of the previous value. The model outputted compartment and global final values of both the arterial and venous partial pressures of oxygen and saturation values.

The model was designed using The R Project for Statistical Computing (www.r-project.org) with the rootsolve package.

RESULTS

In all simulations, we maintained the following constant global values: Hb 14 g/dL, PaCO₂ 40 mmHg, pH 7.40, and a pulmonary shunt fraction of 0.1. Normal values of the perfusion fraction, which were critical for the oxygen extraction rate and optimal oxygen consumption, were also provided for each peripheral compartment (11).

We modeled two different states: normal-high and low oxygen delivery. For each of these states, we varied the oxygen delivery by changing the FiO₂ with a fixed CO and changing the CO with a fixed FiO₂. The first step was to obtain increasing DO₂ values by changing the FiO₂ from 0.21 to 1.00 in steps of 0.10 (with the exception of the first step = 0.09) with two values of cardiac output: 1) CO = 2.0 L.min^-1 (low oxygen delivery) and 2) CO = 6.5 L.min^-1 (normal-high oxygen delivery). In the next step, with a constant fraction of inspired oxygen (0.21), we chose cardiac output values to match the DO₂ obtained in the previous step. In the normal-high delivery state, oxygen demands were always met (VO₂≥197 mL.min^-1), whereas in the low delivery state, the oxygen supplies were insufficient to meet the oxygen demands (VO₂<197 mL.min^-1).

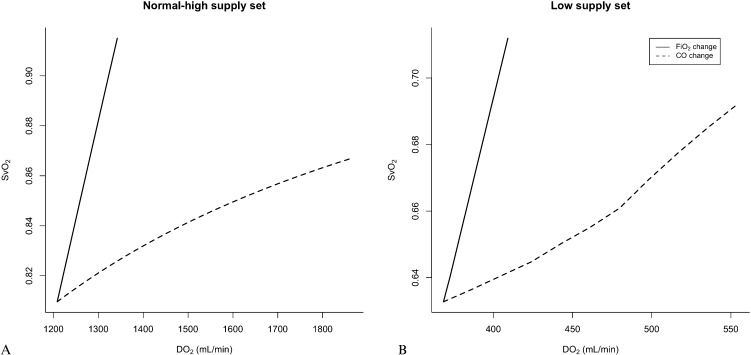
Normal-high supply set under this set of conditions, we simulated increases in DO₂ under optimal oxygen consumption to all compartments (Table 1). The increase in CO caused a proportional increase in DO₂, as expected. Conversely, DO₂ could only be increased by 11% by nearly quintupling FiO₂ from 0.21 to 1.0. This increase led to a change in SvO₂ from 81 to 92%; in contrast, when the same increase in DO₂ was accomplished by increasing CO, the SvO₂ only increased from 81 to 83%. In fact, even a 50% increase in DO₂ (Figure 1A) accomplished through augmenting CO alone only increased SvO₂ to 86%. Of note, for this set of conditions, the peripheral compartments could have been easily lumped together with no loss of information because VO₂ was constant among the different conditions simulated.

Table 1.

Effect of increasing the oxygen delivery on oxygen venous saturation by manipulating either the inspired fraction of oxygen or the cardiac output.

			Changes in FiO2 with fixed CO			Changes in CO with fixed FiO2
	DO2	VO2	FiO2	CO	SvO2	FiO2	CO	SvO2
	(mL.min-1)	(mL.min-1)		(L.min-1)	(%)		(L.min-1)	(%)
Normal-high supply set	1,208	197	0.21	6.50	81	0.21	6.50	81
	1,238	197	0.3	6.50	83	0.21	6.66	81
	1,256	197	0.4	6.50	85	0.21	6.75	82
	1,271	197	0.5	6.50	86	0.21	6.84	82
	1,286	197	0.6	6.50	87	0.21	6.91	82
	1,300	197	0.7	6.50	88	0.21	6.99	82
	1,315	197	0.8	6.50	89	0.21	7.07	82
	1,329	197	0.9	6.50	90	0.21	7.15	82
	1,344	197	1	6.50	92	0.21	7.22	83
Low supply set	368	125	0.21	2.00	63	0.21	2.00	63
	377	128	0.3	2.00	65	0.21	2.05	63
	383	129	0.4	2.00	66	0.21	2.08	64
	387	130	0.5	2.00	67	0.21	2.10	64
	392	131	0.6	2.00	68	0.21	2.13	64
	396	133	0.7	2.00	69	0.21	2.15	64
	401	134	0.8	2.00	70	0.21	2.18	64
	405	135	0.9	2.00	70	0.21	2.20	64
	410	136	1	2.00	71	0.21	2.22	64

CO: cardiac output; DO₂: oxygen delivery; FiO2: inspired fraction of oxygen; SvO₂: venous oxygen saturation; VO₂: oxygen consumption.

Figure 1.

Panel A: Effect of increasing DO₂ on the SvO₂ through changes in the inspired fraction of oxygen (FiO₂, solid line) or cardiac output (dashed line) under normal and high oxygen supply conditions sufficient to attain optimal oxygen consumption in all peripheral compartments. Panel B: Effect of increasing DO₂ on the SvO₂ through changes in the inspired fraction of oxygen (FiO₂, solid line) or cardiac output (dashed line) under low oxygen supply conditions that caused the oxygen consumption to be supply limited.

Low supply set

When VO₂ was supply limited, the relation between DO₂ and SvO₂ became more complex as a consequence of the critical extraction rates being reached at different DO₂ values (Table 1 and Figure 1). Interestingly, the modest 11% increase in DO₂ produced by augmenting FiO₂ markedly increased SvO₂ to values above 70%, masking the 31% deficit of VO₂ present at an FiO₂ of 1.0 (Table 1). In contrast, increasing DO₂ by the same amount by improving CO led to an SvO₂ of 64%, indicating insufficient oxygen supply.

DISCUSSION

In this paper, we showed that when oxygen supply was increased by the same amount by increasing either FiO₂ or CO, the resulting SvO₂ was higher when DO₂ was increased by manipulating FiO₂. Of note, we found that under conditions of low oxygen supply, high values of the fraction of inspired oxygen could increase the mixed venous saturation to normal levels, masking states of insufficient oxygen supply.

Mixed venous saturation has long been used as a surrogate for adequate perfusion to tissues during resuscitation (5). Low levels of SvO₂ are associated with poor prognosis for several clinical scenarios, and currently, guidelines suggest targeting SvO₂ at 70% during the early phase of sepsis resuscitation, which is associated with a reduction in mortality (7). Nowhere in those guidelines, however, do the authors comment on the FiO₂ at which the central venous blood gas should be collected.

One strength of the theoretical modeling approach is that it is possible to compare the effects of FiO₂ and CO on the mixed venous saturation at precisely the same oxygen supply/demand conditions, i.e., equal VO₂ and DO₂. Ho et al. have previously shown that in humans with shock, high levels of PaO₂ can increase SvO₂ levels (8). From their data, however, it was not possible to determine whether the increase in SvO₂ was indeed reflecting a better oxygen supply/demand relationship or whether the SvO₂ represented a false marker of the adequacy of such a relationship. Our findings of increases in SvO₂ to levels considered normal caused by increasing the FiO₂ in the setting of insufficient oxygen supply support the latter hypothesis.

The mechanism by which increased values of FiO₂ cause a steeper increase in SvO₂ than that caused by increases in CO can be explained by the conservation of mass. When manipulating the FiO₂ at fixed values of CO and oxygen consumption, the arteriovenous difference in oxygen content (CaO₂ – CvO₂) must remain constant because oxygen consumption is equal to the product of cardiac output and the arteriovenous difference in oxygen content. Thus, in this scenario, increases in arterial oxygen content will be followed by equal increases in venous oxygen content, explaining the roughly linear relationship between SvO₂ and DO₂ shown in Figure 1. Conversely, when manipulating CO while keeping arterial oxygen content and oxygen consumption constant, the increase in CO will be compensated for by an increase in the venous oxygen content proportional to the arteriovenous difference in oxygen content such that at high CO values, the venous oxygen content approaches the arterial oxygen content. For example, using the Fick principle, if one assumes a hypothetical initial arterial oxygen content of 16 mL/dL and a venous oxygen content of 12 mL/dL, a 25% increase in the DO₂ by increasing the arterial oxygen content to 20 mL/dL will cause an increase in venous oxygen content by the same amount (from 12 to 16 mL/dL), causing venous saturation to increase from 62 to 83%. The same 25% increase in DO₂ caused by increasing CO will only decrease the arteriovenous difference in oxygen content from 4.0 to 3.2 mL/dL, thus increasing the venous oxygen content from 12 to 12.8 mL/dL. The result would be a modest increase in the central venous oxygen saturation from 62 to 66%.

Our study has several limitations. We kept the values of pH and the arterial partial pressure of carbon dioxide, variables known to be affected by the hemodynamic condition, constant during all simulations. Although the model could accommodate changes in these variables, we decided to keep them constant to isolate the effects of the fraction of inspired oxygen and cardiac output. Additionally, for similar reasons, we ignored potential changes in the perfusion fraction that could be caused by the local control of blood flow during regional hypoxemia. Blood flow to tissues is usually driven by local metabolic demands to match supply and demand. Therefore, this model does not take into account changes in the local oxygen consumption that may occur after changes in the local partial pressures of oxygen and carbon dioxide.

In conclusion, we showed that the type of DO₂ optimization, specifically increases in FiO₂ versus increases in CO, could affect the capability of venous oxygen saturation to measure the adequacy of oxygen supply. Interpreting venous saturation at high arterial partial pressures of oxygen values should be performed with caution.