A Hierarchical Bayesian Model for Calibrating Estimates of Species Divergence Times

Abstract

In Bayesian divergence time estimation methods, incorporating calibrating information from the fossil record is commonly done by assigning prior densities to ancestral nodes in the tree. Calibration prior densities are typically parametric distributions offset by minimum age estimates provided by the fossil record. Specification of the parameters of calibration densities requires the user to quantify his or her prior knowledge of the age of the ancestral node relative to the age of its calibrating fossil. The values of these parameters can, potentially, result in biased estimates of node ages if they lead to overly informative prior distributions. Accordingly, determining parameter values that lead to adequate prior densities is not straightforward. In this study, I present a hierarchical Bayesian model for calibrating divergence time analyses with multiple fossil age constraints. This approach applies a Dirichlet process prior as a hyperprior on the parameters of calibration prior densities. Specifically, this model assumes that the rate parameters of exponential prior distributions on calibrated nodes are distributed according to a Dirichlet process, whereby the rate parameters are clustered into distinct parameter categories. Both simulated and biological data are analyzed to evaluate the performance of the Dirichlet process hyperprior. Compared with fixed exponential prior densities, the hierarchical Bayesian approach results in more accurate and precise estimates of internal node ages. When this hyperprior is applied using Markov chain Monte Carlo methods, the ages of calibrated nodes are sampled from mixtures of exponential distributions and uncertainty in the values of calibration density parameters is taken into account.

Since Zuckerkandl and Pauling (1962) put forth their hypothesis describing molecular evolution as a clock-like process, such that nucleotide or amino acid substitutions occur at a constant rate over time, researchers have integrated data from the fossil record with molecular sequence data to date lineage divergence events on the tree of life. Recently developed methods for accommodating variation in rates of substitution among lineages make it possible to relax the assumption of a global molecular clock and can provide robust estimates of relative species divergence times (Hasegawa et al. 1989, Kishino and Hasegawa 1990, Sanderson 1997, Sanderson 2002, Thorne et al. 1998, Huelsenbeck et al. 2000, Kishino et al. 2001, Yang and Yoder 2003, thorne05, Drummond et al. 2006, Lepage et al. 2006, Rannala and Yang 2007, Drummond and Suchard 2010, Heath et al. 2012). Consequently, when combined with carefully applied node age constraints based on reliable date estimates from geological data, relaxed-clock divergence time analyses can also produce more accurate estimates of the absolute ages of ancestral nodes.

When used to calibrate relaxed-clock phylogenetic analyses, age constraints are typically assigned to nodes representing known most-recent-common ancestors (MRCA) of living taxa present in an alignment of molecular sequence data. Although it is possible to calibrate an analysis using known substitution rates, biogeographical event dates, or inferred node age estimates from previously published studies, age estimates of fossil organisms are the primary and (typically) most reliable source for time calibration (Marshall 2008, Kodandaramaiah 2010). However, numerous challenges arise when calibrating molecular phylogenies with fossil age estimates (Graur and Martin 2004, Gandolfo et al. 2008, Ho and Phillips 2009). Disparity in fossilization and preservation, geographical distribution, and fossil recovery biases are all factors influencing the availability of adequate fossil calibrations for certain clades (Benton and Ayala 2003, Lloyd et al. 2012). Moreover, new fossil discoveries must be carefully identified, described, analyzed, dated, and curated; endeavors both challenging and labor intensive. It is also no small undertaking to identify the phylogenetic placement of a fossil. Ideally, this is done by conducting thorough phylogenetic analyses of homologous morphological characters from both extant and fossil taxa (e.g., Brochu 1997, Feng et al. 2009, Magallón 2009, Ruane et al. 2010, Wiens et al. 2010). However, combined phylogenetic analyses become increasingly difficult depending on the completeness of available fossils and the availability of morphological data for extant species. As a consequence, fossil age constraints are often assigned to putative ancestral nodes based on taxonomy or other criteria, which can lead to inaccurate node age estimates if the fossil is truly older than its presumed ancestor (Benton and Ayala 2003, Graur and Martin 2004, Hug and Roger 2007, Marshall 2008). In spite of such challenges, fossil and geological data are practically essential for estimating the absolute ages of lineage divergences.

With reliably dated and identified fossil taxa in hand, further consideration must be taken when applying age constraints and calibrating divergence times. The approach to incorporating calibration dates can significantly impact node time estimates throughout the tree (Graur and Martin 2004, Benton and Donoghue 2007, Hug and Roger 2007). The ages of fossil taxa can only provide reasonable minimum age estimates for calibrating internal nodes (Benton and Ayala 2003, Marshall 2008). For this reason, applying a point calibration by assuming the fossil date is an error-free age estimate of the age of the MRCA of the clade to which it is assigned can result in erroneous branching time estimates and is not recommended (Graur and Martin 2004, Hedges and Kumar 2004, Ho 2007). This pitfall can be circumvented without difficulty when prior densities are applied to calibrated nodes in a Bayesian framework.

The fossil record provides prior information about the ages of certain nodes in the tree of life, and dates obtained from fossil taxa are easily incorporated in Bayesian inference methods for divergence time estimation (Kishino et al. 2001, Drummond et al. 2006, Yang and Rannala 2006, Benton and Donoghue 2007, Ho 2007, Ho and Phillips 2009). The common practice in Bayesian phylogenetic dating methods is to apply parametric distributions as prior densities on the ages of calibrated nodes (Fig. 1). The prior density placed on a calibrated node is typically offset by the minimum age estimate obtained from the fossil specimen. Parameterization of the node age prior can accommodate uncertainty about the timing of the divergence event in relation to its calibration time. In their thorough review, Ho and Phillips (2009) describe different approaches to applying calibration dates for divergence time estimation and explicitly discuss the use of calibration priors for Bayesian inference, highlighting the importance of judicious application of calibration prior densities.

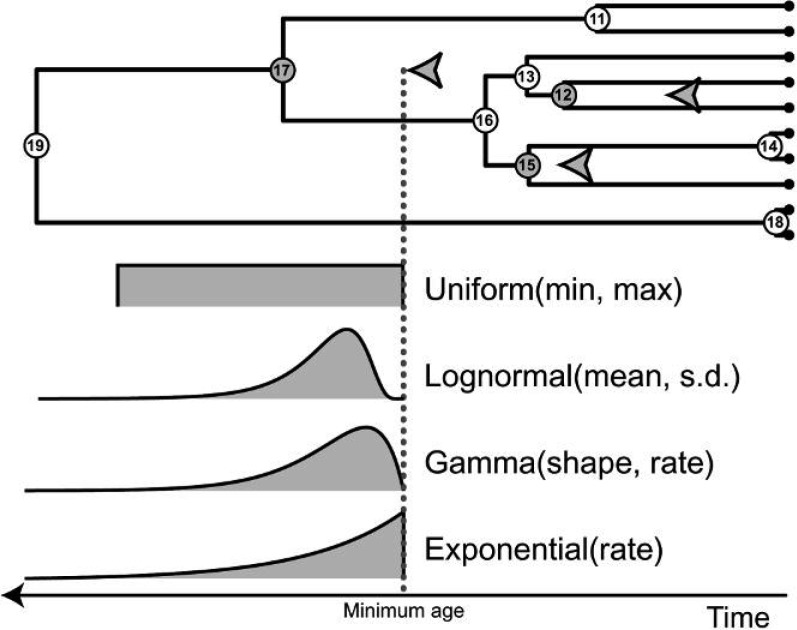
Figure 1.

Examples of four different types of probability densities and associated hyperparameters commonly used as priors on the ages of calibrated nodes when provided a minimum age estimate. The ages of the N = 10 tips (a₁,a₂,…,a₁₀) are known and indicated with black circles. The internal nodes are labeled N + 1,…,2N − 1 in postorder sequence. For the majority of empirical data sets, it is not possible to place a reliable age constraint on most internal nodes (white circles: a₁₁,a₁₃,a₁₄,a₁₆,a₁₈,a₁₉) and a general prior on branching times is assumed for uncalibrated internal nodes (e.g., birth–death process or uniformly distributed node times). Geological data can provide information that can be used to calibrate certain nodes (gray circles: a₁₂,a₁₅,a₁₇). Typically, a node is calibrated by placing a minimum age obtained from the oldest known descendant fossil taxon (gray arrows). Provided that the phylogenetic placement of the fossil is correct, the age of the calibrated node is assigned a prior distribution. This example shows four different prior densities for the age of calibrated node number 17 (separate priors can be specified for nodes 12 and 15 in the same manner). The gray dotted line indicates the minimum age constraint placed on the age of node 17 by the fossil descendant (gray arrow). Commonly used parametric distributions are offset by the minimum age provided by the fossil and each requires that hyperparameter values (in parentheses) be specified prior to analysis.

In Bayesian inference, parameters describing a prior distribution are called hyperparameters, thus distinguishing them from parameters estimated as part of the likelihood model. Figure 1 illustrates some of the parametric distributions often used as priors on fossil-calibrated nodes. When specifying a prior density and the values of its associated hyperparameters (such as the shape and rate of the gamma distribution), the user must make assumptions about the expected age of each calibrated node relative to the external constraint. If prior data regarding the age difference between the fossil and ancestral node or a maximum age bound are unavailable, the parameter values of the prior distribution must be set so that the prior on the calibrated node age is not overly informative (Yang and Rannala 2006). An excessively informative prior implies explicit knowledge about the true age of the ancestral node in relation to the age of its fossilized descendant. If a highly informative prior is erroneously specified, posterior samples of node ages throughout the tree may be biased, potentially leading to inaccurate divergence time estimates. Conversely, a vague prior signifies equivocal knowledge about the age of the calibrated node, giving higher relative probability to a greater range of values compared with an overly informative prior. In some cases, an uninformative prior can result in estimates similar to those produced by frequentist methods. It is also important to note that an overly disperse prior may lead to problematic estimates of parameter values if significant probability is assigned to unrealistic values and if there is insufficient signal in the data to inform inference, though this will be reflected in the relevant credibility intervals resulting from the Bayesian analysis.

Although, in most cases, prior knowledge of the true node age is unavailable and specifying a vague prior is the preferred approach, selecting parameter values that lead to a sufficiently vague prior density for each calibrated node can be challenging. Recently, Dornburg et al. (2011) presented a multiple-step method that identifies a set of “consistent” fossils and discards “inconsistent” node calibrations that may result in biased, excessively young node age estimates. Additionally, they parameterize prior distributions on calibrated nodes based on the bracketing approach developed by Marshall (2008). This novel approach attempts to account for disparity in fossil preservation, whereby the probability of fossilization and recovery is higher for younger lineages (Marshall 1990). Because researchers using fossil data to calibrate divergence time estimates often find themselves in need of clear methods for parameterizing prior distributions on calibrated nodes, the approach described by Dornburg et al. (2011) is a worthwhile contribution to the field, providing a repeatable and direct method for specifying prior densities on nodes calibrated by information from the fossil record. Additionally, it is of vital importance that molecular biologists conducting studies employing data from the fossil record evaluate and understand each fossil specimen included in their analyses, and calibration–validation methods provide a means for researchers to familiarize themselves with relevant geological data (Near et al. 2005, Hugall et al. 2007, Rutschmann et al. 2007, Marshall 2008, Dornburg et al. 2011, Warnock et al. 2012). There are, however, potential drawbacks to discarding fossil calibrations that are (assumed) correctly placed on the tree since previous studies have indicated that the placement and number of fossil calibrations may impact estimates of node ages (Hug and Roger 2007, Rutschmann et al. 2007, Moreau and Bell 2011, Lukoschek et al. 2012). Moreover, the approach of Dornburg et al. (2011) specifies the hyperparameters of calibration densities based on the fossil ages, which can potentially lead to overly informative prior distributions, particularly for younger fossils. Such informative priors can, in turn, result in biased underestimates of species divergence times. To overcome these challenges, a hierarchical Bayesian approach can provide a repeatable method for integrating fossil data to calibrate relaxed-clock analyses of molecular data sets.

Estimation in a hierarchical Bayesian framework allows for inference under richer classes of models that are better at reflecting our statistical understanding of the distribution of ancestral node ages in relation to fossil calibrations. In addition, such methods diminish the difficulty of specifying hyperparameter values that lead to adequate prior distributions on calibrated nodes. In Bayesian inference, an additional prior distribution can be placed on a hyperparameter of a prior distribution (Fig. 2). These second-order priors are called hyperpriors and are very useful for incorporating uncertainty in the hyperparameters (e.g., rate, shape, scale, or location parameters) of a prior distribution (Carlin and Louis 2000). A generic hierarchical Bayesian model is illustrated in Fig. 2, where a lognormal prior density is assigned to the parameter of interest (χ), and the standard deviation hyperparameter (σ) of that lognormal distribution follows a gamma distribution:

where s and β are the shape and rate parameters of the gamma-distributed hyperprior, respectively, and μ is the mean of the lognormal prior distribution describing χ. Thus, generating values of χ under this model involves first drawing an instance of the hyperparameter, σ, from the gamma hyperprior distribution (Fig. 2a), then an instance of χ is sampled from the prior density: Lognormal(μ,σ) (Fig. 2b); and this entire procedure is repeated for each occurrence of χ sampled from the lognormal prior density. Namely, in the field of Bayesian phylogenetic inference and divergence time estimation, when lineage-specific substitution rates are assumed to be independent draws from an underlying lognormal distribution in the program BEAST (Drummond and Rambaut 2007), separate hyperpriors are typically applied to the mean and standard deviation hyperparameters of that distribution (Drummond et al. 2006). As a result, the lineage-specific rates are sampled by Markov chain Monte Carlo (MCMC) from a mixture of lognormal distributions, even though the uncorrelated lognormal model is not a true mixture model. Bayesian methods employing hierarchical models provide additional information in the form of posterior estimates of hyperparameter values. In the case of divergence time analysis in BEAST, estimates of the variance parameter of the lognormal distribution can indicate deviation from or conformity to a strict molecular clock. Furthermore, applying hyperpriors frees the user from the responsibility of specifying the values of hyperparameters, and uncertainty regarding the parameterization of a prior distribution is taken into account.

Figure 2.

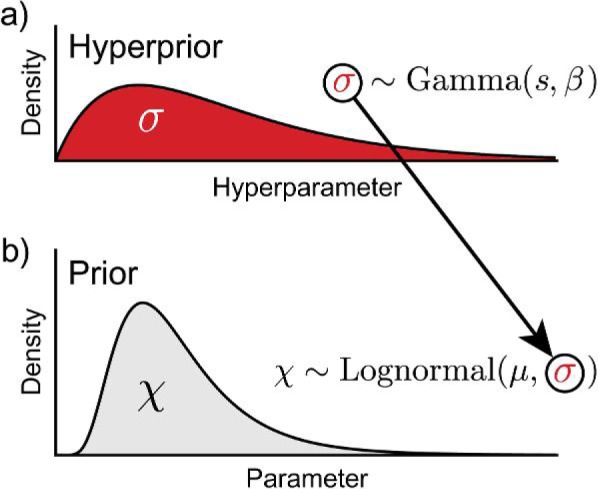
A generic example of a hierarchical Bayesian model. Hyperparameter values are sampled from the hyperprior (a) and used to parameterize the prior density assigned to the parameter of interest χ (b). In this example, χ follows a lognormal distribution with a mean (μ) and standard deviation (σ). A gamma distribution with shape (s) and rate (β) parameters is the hyperprior and describes the standard deviation hyperparameter (σ) of the lognormal prior on χ.

Calibration ages can rarely be assigned to nodes of a tree without error, and much of the information associated with geological dates is lost when the fossil record of a clade is represented as a single time estimate applied to a single internal node. Because of the considerable uncertainty associated with calibration dates, it is necessary to accommodate this in priors placed on calibration node ages. In this study, I considered a mixture model, the Dirichlet process prior, for use as a hyperprior on the rate parameters of offset exponential distributions applied as prior densities on the ages of calibrated nodes. This hyperprior is useful for analyses employing multiple age constraints to calibrate divergence time analyses, and when combined with numerical methods, such as MCMC, calibrated node ages are sampled from mixtures of exponential distributions.

MATERIALS AND METHODS

Bayesian Divergence Time Estimation

The objective of Bayesian divergence time estimation methods is to calculate the joint probability density of the following parameters:

conditioned on observed data (X) for N species (Thorne and Kishino 2005, yang06). Assuming a known rooted tree topology, with the tips labeled 1,…,N and the internal nodes labeled N + 1,…,2N − 1 (in postorder sequence so that the root is labeled 2N − 1), the joint conditional distribution is:

where f(X∣r,a,θ_r,θ_a,θ_s) is the likelihood and f(r,a,θ_r,θ_a,θ_s) is the joint prior probability density over the parameters and hyperparameters. The difficulty of calculating the marginal probability of the data, f(X), is conveniently eliminated with the application of MCMC algorithms (Metropolis et al. 1953, Hastings 1970).

Note that the probability of the sequence data depends on the node ages and the rates of sequence evolution, but the process of sequence evolution is independent of the process that generates these ages and rates, such that

Furthermore, it is assumed that the process governing the ages of nodes operates independently of processes governing mutation, and that the process governing the total rates of substitutions is independent from the mutational parameters that determine relative rates of different substitutions:

After enforcing these assumptions, the posterior distribution of the parameters and hyperparameters can be expressed as:

A number of researchers have focused their attention on the development of models that capture variation in rates of molecular evolution. Therefore, f(r|θ_r) can represent any of a number of priors on branch rates, including, but not limited to, the molecular clock (Zuckerkandl and Pauling 1962), local molecular clock models (Hasegawa et al. 1989, Kishino and Hasegawa 1990, Yoder and Yang 2000, Yang and Yoder 2003, Drummond and Suchard 2010), autocorrelated rate models (Thorne et al. 1998, Kishino et al. 2001, Lepage et al. 2006), models accounting for stepwise rate changes along branches (Huelsenbeck et al. 2000), and uncorrelated rate models (Drummond et al. 2006, Heath et al. 2012). For example, if all lineages are assumed to evolve under a strict molecular clock, with a single substitution rate drawn from a gamma distribution with a shape parameter (s) and a rate parameter (β), then r = (r,r,…,r) and f(r∣θ_r) = f(r∣s,β).

Prior Density on Node Ages

In the absence of external calibration ages, node time prior densities, f(a∣θ_a), can be characterized by nonbiological parametric distributions such as the Dirichlet distribution (Kishino et al. 2001) or uniform distribution (Lepage et al. 2007), or by branching processes describing lineage diversification, including the Yule model (Yule 1924, Sanderson 1997, Thorne et al. 1998) and the birth–death process (Yule 1924, Kendall 1948, Nee et al. 1994, Rannala and Yang 1996, Gernhard 2008). None of these priors provide much precision about the absolute ages of nodes in the tree, however, and usually, some information from fossils is introduced to provide a timescale for the tree.

The ideal approach to accommodating fossil information would be to treat the ages of fossils as data. Thus, rather than inferring the values for parameters conditional on the sequence data, the inference is conditioned on having observed the sequence data and the set of fossils. In principle, every fossil would be used, and uncertainty about the phylogenetic position of fossil taxa would be incorporated during inference. Such an approach has been carefully explored by Ronquist et al. (2012) in their investigation of the diversification of Hymenoptera. Their work and the studies by Lee et al. (2009) and Pyron (2011) present methods for accounting for uncertainty in the placement of fossil taxa and represent exciting, new developments in divergence time estimation methods, although further work is required to determine sufficient tree priors that account for fossilization and sampling probabilities of fossil lineages for combined datasets (Wilkinson et al. 2011; Ronquist et al. 2012). Despite such advancements, combined analysis is not feasible for many taxonomic groups as it requires extensive knowledge of fossil taxa, morphological characters for both extinct and extant species, as well as an understanding of the processes that affect the probability of the fossilization and recovery of ancient lineages.

If the fossil record is viewed as primarily providing minimum bounds on the ages of clades, then the analysis can be simplified by using only the dates that are associated with the oldest fossil assigned to each group. Such an approach would capture most of the minimum age information from fossil taxa without requiring exhaustive treatment of the fossil record. Each clade in the tree can be identified with an internal node (which represents the speciation event at the end of the lineage that is the MRCA of the clade). For each internal node i, there is a parameter value that represents the age of the node (a_i). Data on the age of the oldest fossil associated with the group can be represented by C_i. The variable H_i can serve as an indicator variable that assumes the value 0 if node i has no fossils associated with it and 1 if node i does have a calibration fossil. This would then lead to:

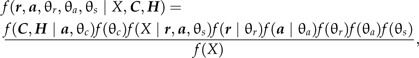where θ_c is a set of parameters related to the probability of fossilization, fossil discovery, and diagnosis of the fossil as a member of a specific clade. Treating the fossilization events as independent for each clade would allow one to calculate a probability density for fossil calibrations for the entire tree as the product of the event that a fossil is assigned to a clade, Pr(H_i∣a_i), and a probability density for the time lag between the node i and the oldest fossil:

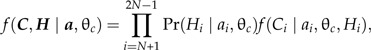where

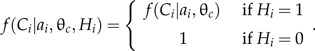Modeling Pr(H_ia_i,θ_c)f(C_i∣a_i,θ_c,H_i) in a biologically plausible fashion would be difficult. The probability of the discovery of a fossil which represents a particular clade on the tree (and which is not assignable to one of the “daughter clades”) would depend on the amount of time associated with ancestral lineages, the rate of evolution for diagnostic morphological traits, the probability of preservation of such traits, the completeness of the fossil record, and other factors.

Treating the dates associated with the oldest fossils for a clade as data merits further investigation. However, this detailed modeling of fossilization processes is beyond the scope of this study. Presumably, the main effect of a rigorous model for f(C_i∣a_i,θ_c,H_i) would be a preference for small differences in time between C_i and a_i. The precise functional form of the probability density for this difference would depend on the wide variety of factors mentioned above. But fundamentally, the probability density should reflect a waiting time; specifically, the time between the speciation event and the creation of the oldest assignable fossil. Thus, in place of a full model, it seems reasonable to assume that the calibration difference, a_i − C_i, can be described by a probability function that is similar to an exponential distribution. Strictly speaking, an exponential distribution would only be appropriate if the rate of creation of the oldest assignable fossil was constant after the clade was formed.

For the purposes of the present study, I have used a very simple model for the presence of a fossil being assigned to any clade of age a_i:

for all nodes regardless of their age. Furthermore, f(C_i|a_i,θ_c,H_i = 1) is assumed to have a simple functional form that only depends on a_i − C_i. This is essentially equivalent to following the common practice in Bayesian divergence time estimation of placing prior densities on calibrated nodes, offset by fossil dates. When assuming an offset prior density on a calibrated node i, the age of the node (a_i) must be older than the age of the fossil (C_i). This rough sketch of a model about the probability for the lag between speciation and oldest fossilization (the calibration difference) can be incorporated into divergence time analysis. Typically, the prior density assigned to a calibration difference is combined with a general prior on node times, such as the birth–death prior. This “multiplicative” approach assumes that the process responsible for generating the node times is independent of process describing the calibration difference and disregards some rules of probability theory (Heled and Drummond 2012). Nevertheless, applying calibration priors in this way is the convention in Bayesian inference methods.

In this study, I am addressing the prevailing practice for applying calibrating information in Bayesian divergence time estimation and parameterization of densities applied to multiple calibrated nodes on a fixed topology. A birth–death process is assumed as a general prior on speciation times (Gernhard 2008). This prior formulation differentiates the ages of nonroot internal nodes in the set ℐ from the age of the root of the tree (ω). Using the tree in Fig. 1 as an example, ℐ = (11,12,13,14,15,16,17,18) and ω = a₁₉. Under the birth–death prior, the probability of a is conditional on a speciation rate (b) and an extinction rate (d), such that f(a∣θ_a) = f(ω)f_BD(a_ℐ∣b,d,ω), where a_ℐ represents the ages of nodes in set ℐ. Thus, using the formula in Gernhard (2008), the probability density for the ages of the interior nodes (excluding the root), a_ℐ, is:

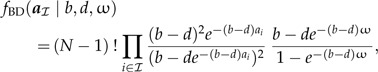where N is the number of species in the tree (also see Stadler 2009, Stadler 2010). With the addition of minimum age constraints from the fossil record, the prior density on the ages of internal nodes is also conditional on the calibration priors (Yang and Rannala 2006). Thus, the observations of fossil ages must be considered and the ages of the calibrated nodes are identified, ℋ = (12,15,17), along with the minimum age constraints provided by the fossil record for those nodes, C = (C₁₂,C₁₅,C₁₇) (Fig. 1). With these additional parameters, the density associated with a becomes: f(a,C∣θ_a) = f(ω)f_BD(a_ℐ∣b,d,ω)f(C∣a_ℋ), with a_ℋ denoting the ages of the calibrated nodes. This “multiplicative” approach assumes that the birth–death branching process is independent of the fossil data (Heled and Drummond 2012).

The exponential distribution is convenient for calibrating internal node ages because it is described by a single rate parameter (λ) and does not require specification of a maximum bound (Fig. 3). Under an offset exponential distribution, the greatest prior weight is placed on ages equal to the minimum age constraint. However, nonzero probability is given to node ages ranging to infinity, and the relative probability of older node ages changes as the rate parameter is increased or decreased. As a prior on node age, the exponential distribution is offset by age of the fossil, and the expected difference between the ancestral node age and the fossil age is equal to λ ^{− 1}. Accordingly, for very large values of λ, the prior places very low probability density on node ages significantly older than the minimum age provided by the fossil calibration, resulting in a strongly informative prior. The exponential prior distribution becomes less informative as the rate parameter decreases (Fig. 3). For any calibrated node, j∈ℋ (where ℋ is the set of all calibrated nodes), I use the unnormalized density of the exponential distribution in the calculations,

because MCMC eliminates the need to calculate normalization constants. Thus, the unnormalized probability density is over a and C used here is

where λ is the vector containing the exponential rate parameters of the calibrated nodes. Note that, because the model simply assigns a probability of 0.5 to the event that H_i = 1 regardless of the age of the node or other parameters, that constant factor can be dropped from the unnormalized probability calculations.

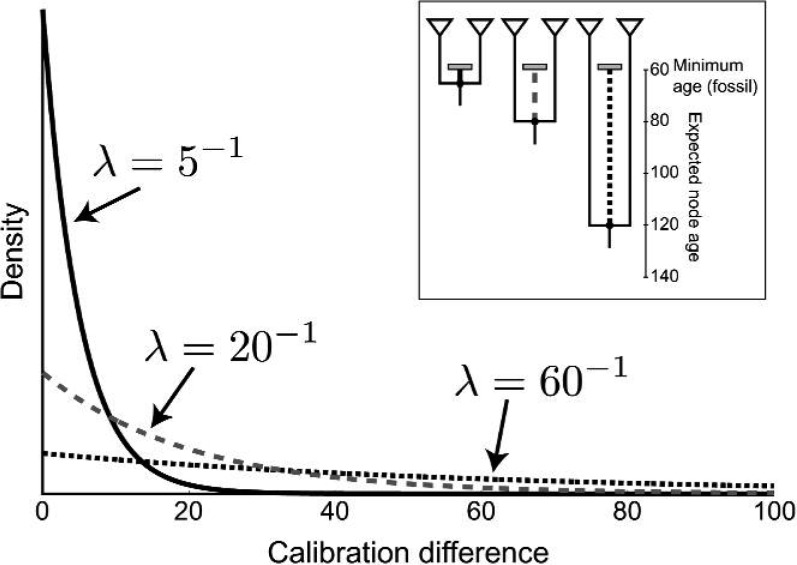
Figure 3.

Examples of exponential distributions on the age difference between the calibrated node and its descendant fossil (calibration difference). The three probability densities are parameterized so that the expected calibration differences are equal to 5 (black solid line), 20 (gray dashed line), and 60 (black dotted line) time units, respectively. For exponentially distributed variables, the expected value is equal to the inverse of the rate parameter: E(x) = λ ^{− 1}. The inset figure shows an example of the expected node ages under the three different exponential distributions if the minimum age provided by the fossil is 60 time units. Under the most informative prior, the expected node age is equal to 65 (black line). Reducing λ results in less informative exponential prior distributions, and the expected node ages under these are 80 (gray dashed line) and 120 (black dotted line).

Applying the exponential distribution as a prior on calibrated nodes requires careful consideration of the time duration from the divergence event to the date of the fossil calibration (Ho and Phillips 2009). When using multiple fossil calibrations, it is possible that some fossil constraints are close in age to their calibration nodes, whereas others may be a great deal younger than their putative ancestral node. Thus, in such cases, it is inappropriate to use a single rate parameter for all prior distributions on calibrated nodes.

Hyperprior Density on Calibration Node Priors

Although a number of different distributions may be appropriate as hyperpriors on calibration densities, for the purposes of this study, I assume a Dirichlet process prior probability distribution on the rate parameters of offset exponential priors on calibrated node ages. Under this construction, the rate parameters are distributed such that λ∼DPP(α,G₀). This stochastic process assumes that discrete variables are distributed among an array of distinct parameter classes (Ferguson 1973, Antoniak 1974) and has been applied to a number of problems in phylogenetics (Lartillot and Philippe 2004, Huelsenbeck et al. 2006, Ané et al. 2007, Huelsenbeck and Suchard 2007, Heath et al. 2012) and population genetics (Huelsenbeck and Andolfatto 2007). As a hyperprior on λ-hyperparameters, each calibrated node is assigned an exponential prior distribution, and the individual rate parameters of those exponential priors are distributed according to a Dirichlet process. By choosing the Dirichlet process prior, an explicit assumption is made that there are latent (not yet observed) categories of λ-hyperparameters and that within a category, prior densities share the same rate value.

The Dirichlet process hyperprior (DPP-HP) is described by two parameters, a concentration parameter (α) and a generating distribution (G₀). The concentration parameter controls the degree to which the rate parameters are clustered into different categories. As a consequence, large values of α lead to greater partitioning among the data and more parameter classes relative to small values of α, which indicate greater homogeneity. Under the Dirichlet process prior, the exponential rate parameters are partitioned among different rate categories and the number of rate classes (k) and the assignment of calibration priors to those rate classes are random variables under this model. Furthermore, the probability of the number of categories depends on the concentration parameter and the number of fossil-calibrated nodes (F = ∑_i∈ℋH_i):

where c(·,·) is the Stirling number of the first kind. For each rate category, the value of λ is drawn from the base distribution, G₀, which, for the purposes of this study, is a gamma distribution. With the addition of the hyperprior on λ and the specification of the other prior parameters (b,d,α, and G₀,), the quantity proportional to the posterior density is

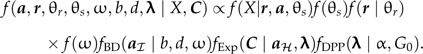The DPP-HP on calibration node ages was implemented in the C++ program DPPDiv and is available at http://cteg.berkeley.edu/software.html (for further details, see Heath et al. 2012). This program uses MCMC to estimate divergence times on a fixed rooted tree topology. As the Markov chain proceeds, samples of the marginal posterior distributions of exponential rate parameters are obtained using the proposal mechanism described by Neal ( 2000, Algorithm 8). This algorithm updates the partitioning of λ-hyperparameters into rate categories using Gibbs sampling with auxiliary rate classes (also see Huelsenbeck and Suchard 2007, Heath et al. 2012). The implementation of the hyperprior model on calibrated nodes, as well as priors on all other parameters, were evaluated by carrying out numerous independent runs on alignments without data and assessing the marginal distributions of the various parameters, using the program Tracer (Rambaut and Drummond 2009) when sampling only from prior densities.

Simulations: Data Generation

I used simulated data sets to evaluate the performance of the DPP-HP. One hundred ultrametric tree topologies and branching times were simulated under a birth–death process (b = 0.02, d = 0.01) using the general sampling approach described by Hartmann et al. (2010) and Stadler (2011). Each simulated tree topology contained 20 extant taxa, and the average root age was equal to 205 time units (ranging from 75.02 to 537.5). The branching times were scaled by a single clock rate, which, for each simulation replicate, was drawn from a gamma distribution with a mean of 0.5 and variance of 0.0625: Gamma(4.0,8.0). This substitution rate was used to transform the entire tree, producing branch lengths proportional to the number of expected substitutions per site; trees consistent with a strict global molecular clock.

Molecular data sets of 1000 nucleotides were simulated on each model tree using the program seq-gen (Rambaut and Grassly 1997). For each simulation replicate, parameter values for the general time reversible model with gamma-distributed rate heterogeneity (GTR + Γ; Tavaré 1986, Yang 1994) were drawn from the following parametric distributions: π = (π_A,π_C,π_G,π_T)∼Dirichlet(5, 5, 5, 5), θ = (θ_AC,θ_AG,θ_AT,θ_CG,θ_CT,θ_GT)∼Dirichlet(2, 2, 2, 2, 2, 2), and γ∼Gamma(8,16), where π is the vector containing each of the four nucleotide frequencies, the relative rates of substitution between two nucleotides are contained in the vector θ, and γ is the shape parameter of the mean-one gamma distribution on among-site rate variation.

The objective of this study was to evaluate the performance of divergence time estimation under the DPP-HP on calibrated nodes in the presence of variation in the distances of the fossil ages to the true ages of nodes to which they are assigned. To address this, four sets of calibration ages for each simulated tree were generated (Fig. 4). For each tree, a set containing 10 calibration nodes was assembled by selecting the root and 9 internal nodes randomly drawn from the set of divergence times with ages greater than 4.0 time units. The sets of calibration ages differed in the distribution of the calibration differences (δ), which is the time duration between the true MRCA age (A_T) and the fossil age (A_F): δ = A_T − A_F. The different sets of calibrating fossils are shown in Fig. 4. The first set of fossil ages, set A, were all equally distant from the true times of the calibrated nodes (δ₁ = δ₂ = δ₃ = ⋯ = δ₁₀). For each tree, the age of the youngest calibrated node was multiplied by 0.5 and δ_A was set to this value. Then, the calibration ages in set A were all fixed to δ_A, so that there was no variation in the true node age to fossil age distances, representing a single category of minimum ages (Fig. 4a). A second category was introduced for calibration set B. In this case, two randomly chosen calibration nodes from those used in set A were assigned fossil ages that were 6δ_A time units younger than the true node time, whereas all the other calibration nodes were assigned the same minimum ages as in set A. Both altered fossil ages were used to make calibration set B (Fig. 4b). Calibration set C was created by altering three of the calibration nodes from set B so that five fossils were δ_A time units younger than the true node time, two were 6δ_A time units younger, and three minimum ages were 3δ_A time units younger (Fig. 4c). Thus, in calibration set C, there were three categories of fossil age to node age distances. Finally, the calibration ages in set D were generated for each of the 10 nodes by drawing minimum age values from a uniform distribution on the interval U(A_T − 6δ_A,A_T), where the minimum value was equal to the true age of the node minus 6δ_A and the maximum value was equal to A_T, and the node calibrations did not cluster in distinct categories (Fig. 4d).

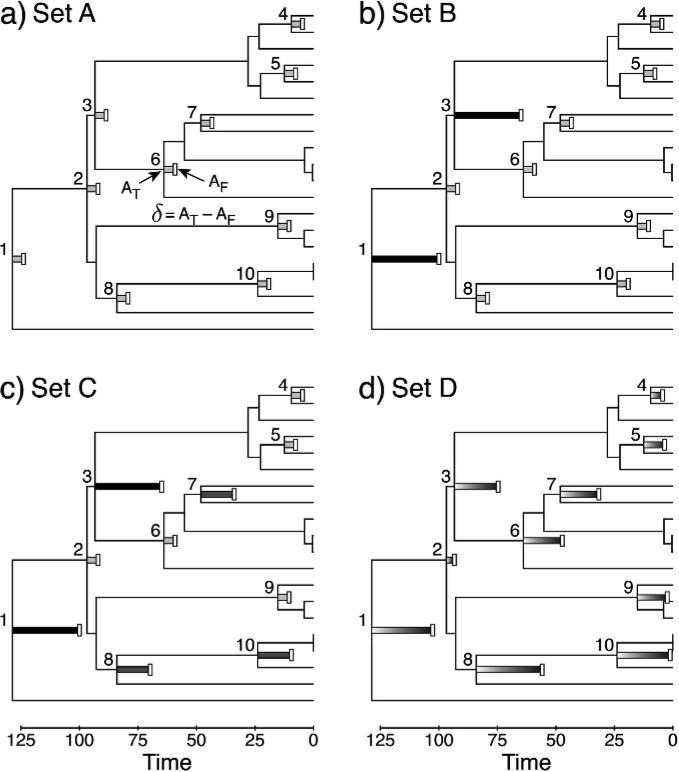
Figure 4.

The four sets of minimum node ages used to calibrate simulated data sets, shown with a single simulation replicate. In trees A through D, minimum ages provided by “fossils” (A_F; white vertical bars) were used to calibrate 10 different internal nodes. The differences (δ) between the true node ages (A_T) and the ages of their fossil descendants are represented by shaded horizontal bars (δ = A_T − A_F). (a) For each simulated phylogeny, a set of nodes were selected for calibration and assigned minimum age calibrations. The fossil ages in set A (1 category) were all equidistant from their respective calibration nodes (nodes 1–10, light gray bars). (b) A second fossil category was created by randomly selecting two calibration points from set A and altering them so that the minimum ages were 6 times that of the other fossils (nodes 1 and 3, black bars). (c) Calibration set C was created by altering three fossils from set B that had not yet been changed (nodes 7, 8, and 10; dark gray bars) so that the distance between the fossil and calibrated nodes was 3 times that of the calibration ages used in set A. (d) For the set of calibrations in D, each fossil minimum age was drawn from a uniform distribution with a minimum value equal to the true node age minus 6 times the calibration age difference from set A (A_T − 6δ_A) and a maximum value equal to the true node age (A_T). The calibration differences in set D did not fall into distinct clusters (nodes 1–10, gradient shaded bars).

Simulations: Analysis

I compared the performance of divergence time estimates under the DPP-HP with two alternative prior parameterizations on calibration node ages. The alternative priors fixed the rate of the offset exponential prior distribution on each calibrated node time based on the fossil age: λ_V imposed a relatively vague (noninformative) prior on the node age compared with λ_I, which resulted in a strongly informative prior on the difference between the fossil age and the true node age (Fig. 5). The exponential rate values were respectively set to:

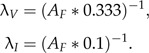Under an exponential prior on calibrated nodes, the expected age of the calibrated node is equal to A_F + λ ^{− 1}. Figure 5 provides an example of the two fixed parameter priors on calibrated nodes. If the minimum age bound provided by the fossil is equal to 80, then λ_I = 0.125 and λ_V = 0.0375, and as a result, the expected ages of the node calibrated by this fossil under the fixed priors are 88.0 and 106.67, respectively (Fig. 5). Thus, it is apparent that the informative prior (λ_I) places strong prior weight on node ages that are very close to the fossil age and there is a low probability of sampling much older node times. Under the vague prior (λ_V), the offset exponential distribution has a much fatter tail and higher probability of sampling older dates compared with the informative prior. This fixed hyperparameter approach results in a range of rate values for each set of calibration node prior distributions, and the scale of the minimum age provided by the fossil impacts the expected node age. Therefore, if the fossil age is very close to the present, the rate parameter of the exponential prior distribution will be greater than for nodes calibrated by older fossils. Potentially, this can lead to very precise prior densities for recent fossils, which may or may not be a desirable affect. This approach is similar to the prior distribution parameterization used by Dornburg et al. (2011), where they fixed the hyperparameters of each calibration prior distribution so that the 95% of the probability was less than the 0.95 confidence level given by Marshall (2008), which is the age of the fossil divided by 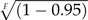, where F is equal to the total number of fossils. Under the DPP-HP, however, the age of the fossil does not influence the exponential density in the same way since a very young fossil and an ancient fossil can be assigned to a single λ-rate category.

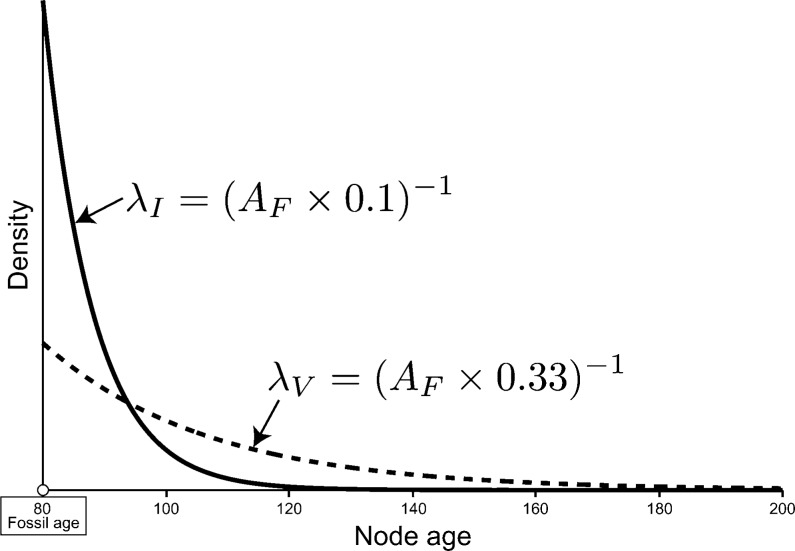
Figure 5.

Fixed calibration priors. This figure illustrates the two alternative prior parameterizations used to estimate node times. If the fossil age (A_F: white circle) is equal to 80 time units, the rate parameter for the offset exponential distribution on the calibrated node was fixed at λ_I = (A_F*0.1) ^{− 1} = 0.125 for the strongly informative prior (solid line) and λ_V = (A_F*0.333) ^{− 1} = 0.0375 for the vague prior (dashed line). For example, if the true age of the calibrated node was 110, or 30 time units older than the fossil age, the informative prior would place very little prior weight on the true divergence time, whereas under the vague prior, the Markov chain is more likely to sample the true node age.

Estimates of divergence times produced by analyses using fixed vague priors and fixed informative priors were compared with node times resulting from analyses under the DPP-HP. The DPP-HP requires the initialization of additional parameters: the concentration parameter (α) and the parameters of the base distribution (G₀; in this case, a gamma distribution) from which exponential rates are drawn. For each analysis, I specified a concentration parameter of α = 1.052, which results in a prior mean of, approximately, three λ-rate categories. The λ values for each category were drawn from a gamma distribution with a shape equal to 2.0 and a rate proportional to the initial age of the root of the tree. Specifically, the expected value of G₀ was equal to (0.07ω_t0) ^{− 1}, where ω_t0 is the starting value for the depth of the tree; this ensures that the λ values drawn from G₀ are within an appropriate range for a given data set.

In total, 12 analyses were performed for each simulated data set. The three different calibration prior parameterizations (DPP-HP, Fixed-λ_V, and Fixed-λ_I) were applied separately to each of the four sets of fossil minimum ages (A, B, C, and D). Divergence times were estimated under a strict molecular clock, with a gamma-distributed prior on the clock rate, such that r∼Gamma(4.0,8.0). The tree topology was fixed to the true tree and all analyses assumed a GTR + Γ model of sequence evolution (the true model) with the following prior densities: π∼ flat Dirichlet probability, θ∼ flat Dirichlet probability, and γ∼ Exponential(2) prior. The MCMC analyses were all run for 2 million generations with 1 million generations discarded as burn-in. Convergence assessment, although critical for any Bayesian analysis, was only feasible for a subset of the 1200 MCMC runs, this was done by comparing the marginal densities and effective sample sizes of relevant parameters and hyperparameters sampled by independent Markov chains in the program Tracer v1.5 (Rambaut and Drummond 2009).

The results of each analysis were analyzed so that the relative success and power of node time estimates could be compared. For each estimate of node age, I computed the 95% credible interval (CI) across all analyses of simulated data sets. The 95% CI serves as an approximation for the 95% highest posterior density interval and was used to quantify power and compute the coverage probability of each estimator. The coverage probability is the proportion of time the true value is found within the 95% CI. From a frequentist perspective, a robust unbiased estimator is expected to have a coverage probability of 0.95, and in a Bayesian framework, high coverage probabilities are preferred. However, even with high coverage probabilities, an analysis may have low power, and this was measured by assessing the widths of the 95% CIs.

Biological Application: Turtles

The DPP-HP on calibration node prior densities was applied to a data set comprised of 23 DNA sequences, each representing a single genus, spanning the diversity of the turtle phylogeny (for GenBank accession numbers, see Near et al. 2005). This biological data set has been analyzed in several studies evaluating methods for calibrating divergence time estimation methods (Near et al. 2005, Marshall 2008, Dornburg et al. 2011). The sequences in this alignment included a single mitochondrial gene (cytochrome-b) and two nuclear markers, recombination activating gene 1 (RAG-1) and intron 1 of the RNA fingerprint protein 35 (R35).

In their recent study, Dornburg et al. (2011) presented 14 fossil ages for calibration that were assumed to be correctly assigned to clades in the turtle phylogeny (Table 1). Of the 14 fossil calibrations, they found 10 consistent fossils using their approach for assembling a set of calibration ages. In Table 1, the consistent calibrations are assigned to nodes labeled 1 through 10 and were used to calibrate the divergence time analyses presented in the Dornburg et al. (2011) paper. The fossils descending from nodes 11, 12, 13, and 14 were deemed inconsistent based on the scaling factors estimated using their method. The inconsistent fossils also provide the youngest age constraints and it has been suggested that such fossils can potentially lead to biased underestimates of speciation times (Marshall 2008, Dornburg et al. 2011).

Table 1.

The fossil minimum ages and taxon names used for calibrating turtle divergence times (partially reproduced from Table 1 of Dornburg et al. 2011)

	Node	Minimum age (myr)	Fossil taxon name
Consistent fossils	1	100	Aspideretes maortuensis
	2	110	Cearachelys placidoi
	3	110	Araripemys barretoi
	4	71	Yaminuechelus gasparinii
	5	65	Hoplochelys
	6	50	Baltemys
	7	90	Lindholmemydidae
	8	52	Hadrianus majusculus
	9	50	“Ocadia” crassa
	10	34	Chrysemys antiqua
Inconsistent fossils	11	18	Pelusios rusingae
	12	11.6	Chelus
	13	15	Chelodina and Elsaya
	14	5	Trachemys inflata

Notes: Dornburg et al. (2011) identified 10 consistent fossils (1–10), which were used for calibrating divergence time analyses. The four inconsistent fossils (nodes 11–14) were not used to calibrate their node age estimates.

In the present study, I conducted two separate analyses estimating turtle divergence times; both assuming a DPP-HP on calibration prior densities. The first analysis used only the consistent calibrations (Table 1; nodes 1–10) and the second applied all 14 fossils to calibrate the estimates of divergence times. Node ages were estimated on a fixed rooted tree topology for all analyses that matched the phylogeny found by Dornburg et al. (2011). The phylogenetic relationships of turtles in this tree were congruent with the phylogeny presented in Near et al. (2005) with the exception of the placement of the root. Although the placement of the root of the Testudines tree is still an open question (Barley et al. 2010), the root found by Dornburg et al. (2011) was maintained in this study for comparing node age estimates. This root places species in the superfamily Trionychia (soft-shelled turtles, represented by the genera Carettochelys, Lissemys, and Apalone in this data set) as the sister group to all other turtles.

Two independent MCMC runs of 3 million iterations were carried out for each set of fossil calibrations. Additionally, for each set of fossil calibrations, independent Markov chains were run on “empty” data sets, providing samples from the joint prior densities. I applied a separate Dirichlet process prior on lineage-specific rates to relax the assumption of the molecular clock (Heath et al. 2012). This model assumes that the substitution rates associated with each branch in the phylogeny are distributed according to a Dirichlet process, with a clustering parameter, α_r, and a base distribution, G_0r (category-specific rates are drawn from a gamma distribution with a shape of 2.0 and a rate of 4.0, parameters chosen to cover a range of rate values with an expected value of 0.5), and has been shown to produce robust estimates of relative divergence times (Heath et al. 2012). The clustering hyperparameter (α_r) of the Dirichlet process prior on branch rates was sampled from a gamma-distributed hyperprior with an expected value of 1.24, so that the prior density on the vector of lineage-specific substitution rates (r) was:

where s and β represent the shape and rate parameters of the hyperprior density applied to α_r. The values of the shape and rate parameters of the gamma-distributed hyperprior were fixed to 2.0 and 1.613, respectively.

The DPP-HP on the fossil calibrated nodes was applied in each analysis. For the set of calibrations containing just the 10 consistent fossils, the concentration parameter of the hyperprior was equal to 1.05, which corresponds to an expectation of approximately three exponential rate categories. The value of the concentration parameter for analyses applying all 14 fossils was set to 0.86, which also leads to an expectation of three parameter classes.

For each divergence time analysis, I assessed convergence of the two independent Markov chains by evaluating the marginal distributions and the effective sample sizes of the various parameters and hyperparameters using Tracer v1.5 (Rambaut and Drummond 2009). The first 1 million generations were discarded as burn-in and the remaining samples were combined. The trees were summarized by computing average branching times and node height 95% CIs and annotated using the tools available in DendroPy (Sukumaran and Holder 2010). The average estimates of node ages from the analysis under the 10 consistent fossils were compared with the average estimates resulting from the analysis under all 14 fossil calibration constraints.

RESULTS AND DISCUSSION

Simulations

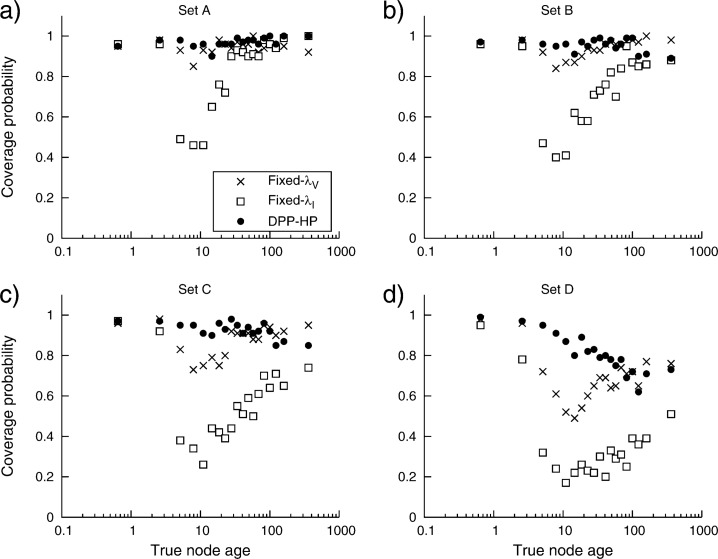
The coverage probabilities for estimates of node times produced by three different prior parameterizations on calibrated nodes (DPP-HP, Fixed-λ_V, and Fixed-λ_I) when provided each of the sets of calibration points (A, B, C, and D) are summarized in Table 2. Overall, these results show that as the variation in distances between the fossil age and node age increases, the accuracy of node time estimates under the three calibration priors decreases. These simulation results suggest that assuming a strongly informative prior (Fixed-λ_I), with considerable prior weight on node ages close to that of the fossil age, produces less accurate estimates of divergence times compared with choosing a less informative prior (Fixed-λ_V). Therefore, in the absence of prior knowledge of the true node to fossil age differences, it is advisable to assign a vague prior distribution to calibrated node ages. However, choosing a hyperparameter value that leads to a sufficiently uninformative prior is not a simple task, and it is preferable to accommodate uncertainty in the values of hyperparameters and treat them as random variables. For this reason, placing a hyperprior on such parameters can provide better estimates. Node age estimates under the DPP-HP have higher coverage probabilities, on average, compared with calibration priors fixed to precise values for each of the sets of fossils in these simulations (Table 2).

Table 2.

The node age coverage probabilities for the three separate analyses performed on each of the fossil calibration sets

Calibration set	DPP-HP	Fixed-λV	Fixed-λI
A (one category)	0.970	0.946	0.831
B (two categories)	0.955	0.941	0.734
C (three categories)	0.926	0.877	0.566
D (uniform distribution)	0.811	0.689	0.354

Notes: The coverage probability is the proportion of nodes (across all simulation replicates) where the true node time was contained within the 95% CI. The simulations were analyzed under four different calibration sets described in Fig. 4.

These results were examined further by evaluating coverage probability as a function of node age (Fig. 6). The true node ages, across all simulated trees, were binned so that each bin contained 100 nodes and each within-bin coverage probability was computed. Figure 6 shows the change in coverage probability as the true node age increases. Generally, these results show that as the variation in the distances between the fossil minimum ages and the true calibrated node ages increases, divergence time estimates under all three priors become less accurate. When all calibrated nodes are assigned very informative prior distributions (Fixed-λ_I), very poor coverage rates are observed for nodes at intermediate ages. However, when the analysis employed a much less informative prior (Fixed-λ_V) or the DPP-HP, a greater proportion of the true node times fell within the 95% CIs. On average, coverage probabilities under the DPP-HP are higher than under the fixed vague prior. However, in the presence of variation in the calibration differences, the simulation results indicate a decrease in coverage of estimates of older node ages when using the DPP-HP (Fig. 6c,d). This effect is due to the fact that the rate parameters of the exponential prior distributions are not scaled by the fossil ages under the hyperprior. Thus, the prior density on a very young node can, over the course of the Markov chain, be identical to the prior density on a much older calibrated node. For example, an exponential distribution with λ ^{− 1} = 20 (i.e., λ = 0.05) may be an equivocal prior density on a calibrated node with a minimum age constraint of 5 and, at the same time, it can be an overly precise prior density on a node calibrated by a fossil age of 200; given that there is typically more uncertainty associated with older fossils. In contrast, under the vague fixed prior, intermediate node age estimates are less successful (compared with older nodes) for fossil sets with greater variation in the node-to-fossil age differences. In this case, the prior density on the node age is parameterized based on the age of the calibrating fossil, thus λ_V = (A_F×0.33) ^{− 1} may result in a relatively informative prior when applied to a node with a fossil age equal to 10, where λ ^{− 1} = 3.3, or a very imprecise prior density can be placed on a node with a minimum age of 300, λ ^{− 1} = 99. These results are also evident when the widths of the CIs are compared with the true node ages.

Figure 6.

The change in coverage probability as node age increases. The node ages were binned so that each bin contained 100 true node depths and the coverage probability was calculated for each bin. Each graph plots the within-bin coverage probability against the average bin age (on the log scale). (a) shows the coverage rates when the single category calibration set (A) is used to calibrate divergence time analyses when assuming a DPP-HP (•) on calibrated node times and when vague (Fixed-λ_V: ×) or informative (Fixed-λ_I: □) fixed priors are used. These results are also shown for calibration sets B (b, two node time to fossil age distance categories), C (c, three categories), and for calibration set D (d, calibration ages sampled from a uniform distribution) (Fig. 4).

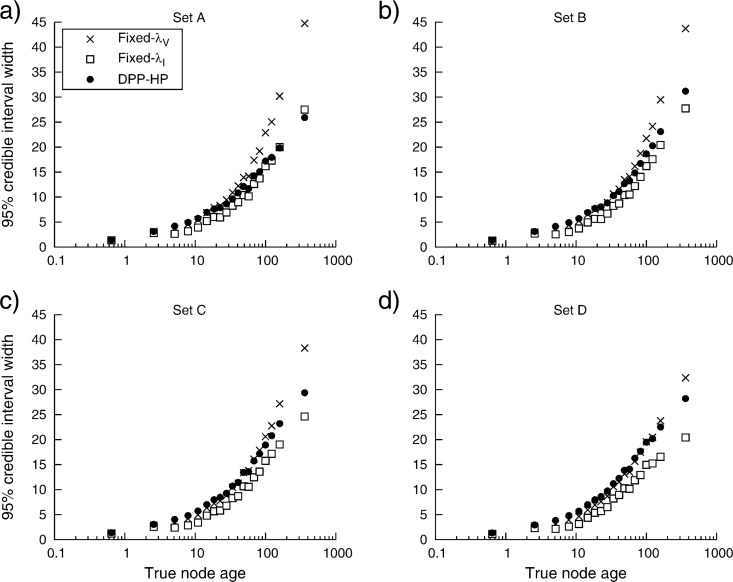
The widths of the 95% CIs were measured and compared with the true node ages for each of the three different calibration priors (DPP-HP, Fixed-λ_V, and Fixed-λ_I) and for each of the four calibration sets (Fig. 7). For the results presented in Fig. 7, the true node ages were binned so that each bin contained 100 values, then the average 95% CI width was calculated for each bin. This figure shows only slight differences in the precision of most node age estimates resulting from the three different calibration priors, and the greater accuracy of the DPP-HP is not accompanied by a loss in power for most node age estimates. However, there is a difference in the 95% CI widths for relatively old nodes. When the data were analyzed under a fixed vague prior (λ_V), the 95% CIs were larger compared with estimates resulting from the DPP-HP. Therefore, the high coverage probabilities of age estimates of relatively old nodes is the result of larger 95% CI widths and reduced power when applying the fixed-vague prior.

Figure 7.

The change in the size of the node age 95% CIs as node age increases. The true node ages were binned (each containing 100 node depths) and the average 95% CI width was calculated for each bin. Each plot compares the within-bin average 95% CI size with the average bin age (on the log scale). The results are shown for analyses using calibration sets A, B, C, and D (Fig. 4) when a DPP-HP (•) is applied to calibrated node times and when vague (Fixed-λ_V: ×) or informative (Fixed-λ_I: □) fixed priors are used.

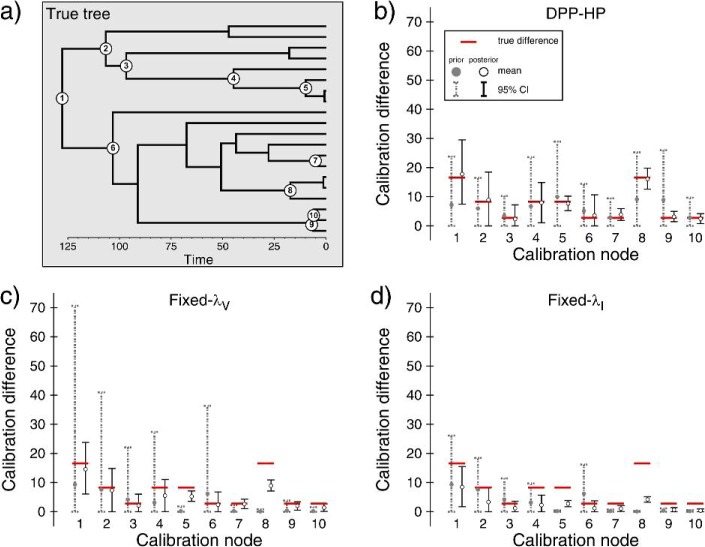
In general, I found that the prior density applied to calibrated node ages can have a strong effect on the accuracy of divergence time estimates. Using a single simulation replicate, Fig. 8 illustrates the effect of the prior distributions on estimates of node ages from analyses under the three types of priors on nodes calibrated by calibration set C (three categories). The sensitivity of node age estimates to offset exponential prior distributions is evident when comparing the marginal posterior estimates of the calibration differences (δ), where δ = A_T − A_F, to marginal densities sampled only from the priors (Fig. 8b–d). In this example, there were three categories of fossils, such that the calibration difference (δ_i) for each calibrated node i took one of the following values (Fig. 8a):

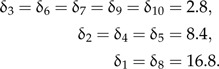Figure 8.

An example of the results from a single simulation replicate when a calibration set with three categories of fossils (set C; Fig. 4c) was used to estimate divergence times. The true tree topology and divergence times are shown in (a), and the 10 calibrated nodes are numbered. In this figure, graphs (b), (c), and (d) show the average (white circles) and 95% CIs for estimates of the calibration difference (δ = A_T − A_F) between the calibrated node age and the fossil age for each of the 10 fossil constraints (black vertical lines). The gray dotted lines indicate the 95% CIs under the prior. The true age differences are shown using horizontal bars. The results are shown for analyses under the DPP-HP is used (b), the fixed vague prior on calibrated nodes (c: Fixed-λ_V), and the fixed informative prior (d: Fixed-λ_I).

This figure shows that the DPP-HP had the advantage in this comparison since the generation of the calibration set matched the assumptions of the model (Fig. 8b). When a fixed exponential prior is assigned to calibrated nodes (Fig. 8c,d), the prior densities are overly informative for young fossils (e.g., nodes 5, 7, 8, 9, and 10) because the exponential rate parameters are scaled by the age of the fossil. This behavior can be particularly problematic when the fossil specimen is a great deal younger than the node to which it acts as a minimum age constraint. In particular, the fossil assigned to node number 8 (Fig. 8) is 16.8 time units younger than the node it calibrates, and the marginal posterior estimates of δ₈ under both of the fixed priors (Fixed-λ_V and Fixed-λ_I) indicate that although there is a strong signal in the data, the prior densities on node 8 are overwhelming the likelihood. In comparison, the DPP-HP leads to a much more diffuse prior density on the age of node 8 (Fig. 8b; gray dotted lines) and does not result in a biased estimate. Conversely, the prior densities on older nodes can be very diffuse when applying fixed vague priors (Fig. 8c; nodes 1 and 2). Thus, these results show that parameterizing a fixed prior distribution based on the age of the fossil can lead to both informative and vague prior densities on calibration differences depending on the age of the fossil. A hierarchical Bayesian approach like the DPP-HP, however, accounts for uncertainty in the hyperparameter values and can flexibly accommodate calibrations from a range of fossil ages. Ultimately, our understanding of the precision of ancient fossils as node calibrations is quite equivocal, and a hierarchical Bayesian model that also accounts for the age of the fossil in the same manner as the fixed vague prior is worthy of investigation.

Biological Application: Turtles

When calibrating molecular divergence time analyses with an array of fossil age estimates, applying a hyperprior to parameters of calibration densities is a practical approach to incorporating data from the fossil record. Provided the assumption that the fossils are correctly placed on the tree is met, this approach does not require the researcher to discard potentially important age constraints. The multistep method described by Dornburg et al. (2011) identified four calibrating turtle fossils that could potentially lead to biased age estimates. These inconsistent age constraints were removed from their subsequent analyses, and Bayesian divergence time estimates were calibrated with only the 10 oldest fossil taxa. Under certain calibration prior densities, it is quite likely that very young fossils can lead to biased, overly young node age estimates if the prior densities are very informative. However, if flexible prior distributions are applied to calibrated nodes, such an approach can allow for the inclusion of all available fossil calibrations.

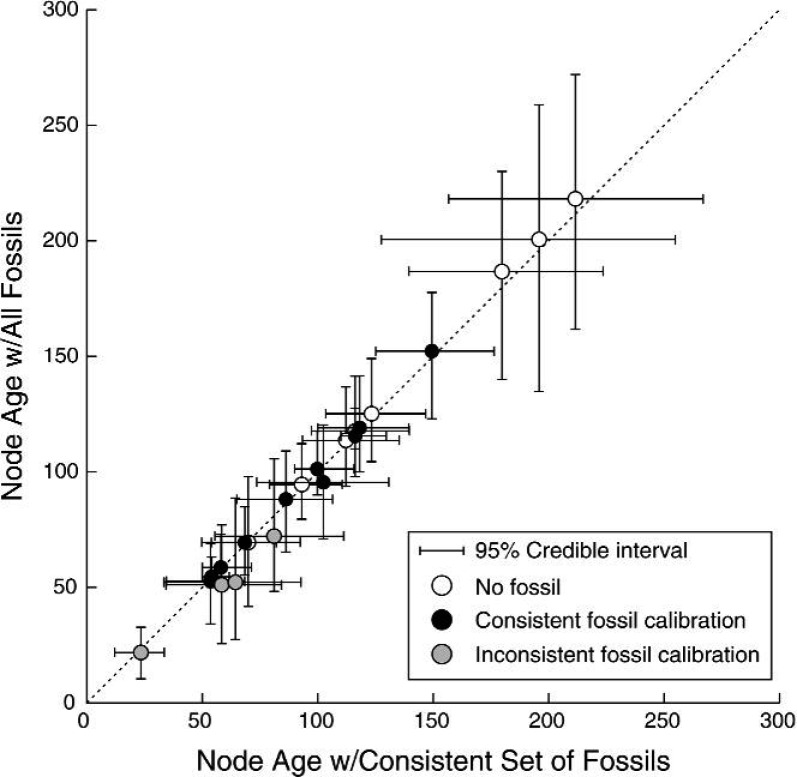
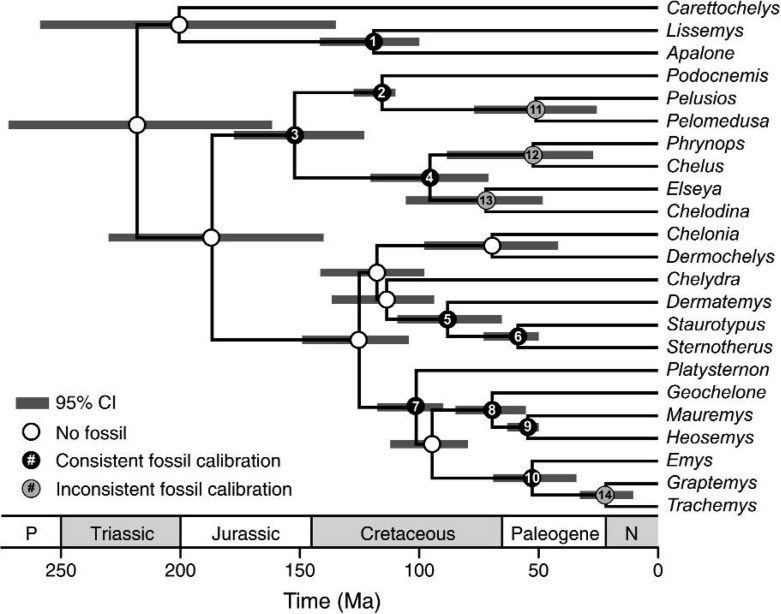
The DPP-HP on calibration densities was applied to a data set of turtles, using two overlapping sets of fossils. Figure 9 shows a comparison of the node age estimates resulting from two separate analyses; one analysis included all 14 fossils (Table 1) and the other was calibrated with only the 10 consistent fossils. These results show that there is no significant difference in the estimates of node ages. Specifically, inclusion of the four youngest, putatively inconsistent, calibration ages did not lead to biased age estimates that were excessively young compared with analyses that omitted those fossils (Fig. 9).

Figure 9.

A comparison of node age estimates produced by analyses using the DPP-HP on calibrated nodes. On the horizontal axis, the average age estimates and 95% CIs are plotted for an analysis that used only the consistent set of fossils (calibrations 1–10) identified in the study by Dornburg et al. (2011). The y-axis indicates the mean node ages and 95% CIs estimated when all the putatively accurate fossils are used (calibrations 1–14). Estimates of node ages without fossil calibrations are shown with white circles, the nodes calibrated by consistent fossils identified by Dornburg et al. (2011) are represented with black circles, and the nodes with inconsistent fossils discarded by the previous study are shown with gray-shaded circles.

In general, node age estimates under the DPP-HP using the complete set of calibration ages were consistent with the divergence times presented in Dornburg et al. (2011), in that the 95% CIs from the hierarchical analysis overlapped with the mean estimates resulting from the previous study (Table 3; Fig. 10). However, the mean estimated ages of calibrated nodes in the Dornburg et al. (2011) study (when assigned exponential calibration densities) were all younger than the ages estimated using the DPP-HP (Table 3). This result is, most likely, due to the fact that the exponential distributions applied in their study were specified with fixed λ-rate hyperparameters (Dornburg et al. 2011). These prior distributions were more informative than the calibration densities under the hierarchical Bayesian model. Additionally, in spite of the potential for “inconsistent” fossils to result in excessively young node age estimates, the estimated ages of nodes calibrated by these fossils under the DPP-HP were, in actuality, older than the estimates resulting from the Dornburg et al. (2011) analyses that did not include the four youngest fossils. In particular, when the calibration on node 14 was ignored, as was done by Dornburg et al. (2011), the node height 95% CI they reported covered the minimum fossil age (Table 3). Thus, it is more likely that the prior densities on calibration differences have a greater influence on the estimates of node ages compared with the inclusion of relatively young or potentially inconsistent fossil age estimates.

Table 3.

The mean calibrated node age estimates and 95% CIs under the DPP-HP with all 14 fossils and the estimates published in the paper by Dornburg et al. (2011) which used fixed exponential prior densities and a subset of fossil calibrations that were identified as consistent fossils

		All fossils (1–14)		Consistent fossils (1–10)
Node	Fossil Age (Ma)	DPP-HP	DPP-HP prior	Fixed exponential
1	100	119.0 (100, 141.6)	108.5 (100, 129.6)	106 (100, 118.4)
2	110	115.6 (110, 127.5)	114.6 (110, 126.2)	113.5 (110, 120.6)
3	110	152.2 (123.1, 177.6)	125.2 (110, 156.3)	143.8 (129, 160.4)
4	71	95.5 (71, 120.4)	80.3 (71, 103.4)	78.5 (71, 91.6)
5	65	88.1 (65.4, 109.7)	71.9 (65, 88.8)	71.7 (65, 82.4)
6	50	58.7 (50, 73.1)	56.1 (50, 67.8)	51.9 (50, 55.6)
7	90	101.3 (90, 117.6)	101.6 (90, 130.7)	94.5 (90, 103.1)
8	52	69.4 (55.4, 84.8)	60.6 (52, 77.8)	59 (52.7, 66.1)
9	50	54.6 (50, 63.2)	53.8 (50, 62.6)	51.7 (50, 54.9)
10	34	52.8 (34.2, 69.1)	42.7 (34, 63.6)	36.2 (34, 40.4)
11	18	51.7 (25.7, 77.0)	28.0 (18, 54.8)	43.2 (21.4, 67.5)
12	11.6	52.3 (27.2, 88.4)	21.1 (11.6, 45.4)	43 (25.4, 61.6)
13	15	72.2 (48.3, 105.6)	24.3 (15, 48.5)	60.8 (36.8, 80)
14	5	21.8 (10.4, 32.8)	12.9 (5, 30.9)	13.1 (4.55, 23.8)

Notes: Dornburg et al. (2011) identified 10 consistent fossils (nodes 1–10) and four inconsistent fossils (nodes 11–14); their results for estimates under exponential calibration priors are reproduced here (their estimates resulting from lognormal priors were not included). The minimum age estimates of the fossil taxa are expressed in units of millions of years. Mean age estimates are shown for two separate analyses (in units of millions of years) and the 95% CIs are presented in parentheses.

Figure 10.

Estimates of node ages for 23 turtle species, resulting from an analysis applying a DPP-HP on calibration densities, with the complete set of 14 fossils. The branch lengths are in proportion to the mean estimated branching times and the gray horizontal bars represent the 95% CIs of node age. The numbered nodes correspond to the fossil taxa used for calibration (Table 1). Calibrated nodes 1 through 10 (indicated with black circles) were identified as consistent fossil calibrations by Dornburg et al. (2011). The inconsistent fossils (11–14; nodes indicated with gray circles) were ignored in the previous study (Dornburg et al. 2011) but included in the analyses presented here.

Because of the uncertainty involved in applying fossil calibrations in Bayesian divergence time estimation methods, placing hyperpriors on calibration densities is preferable to specifying arbitrary fixed hyperparameter values. However, the Dirichlet process model, as applied in this paper, does warrant further investigation into its suitability as a hyperprior on the hyperparameters of calibration prior densities since it does not necessarily represent an explicit biological model. Incidentally, a hierarchical Bayesian approach to calibration priors is not limited to the Dirichlet process prior or the software presented in this paper. Although such analyses have not been explicitly described and may not be trivial to implement, in the popular divergence time analysis program BEAST (Drummond and Rambaut 2007), hyperpriors can be applied to any hyperparameter defined in the XML input file.

CONCLUSIONS

The results of this study indicate that calibrating divergence time analyses in a hierarchical Bayesian framework is a sensible approach to incorporating fossil age constraints in conventional methods for dating species phylogenies. By placing hyperpriors on calibration densities, uncertainty in values of hyperparameters is accounted for and ages of calibrated nodes are sampled from a mixture of prior distributions. When an array of calibrating information from the fossil record is available, the hyperprior approach described here allows for inclusion of all applicable fossils, regardless of their relative age and reduces the difficulty of specifying the parameters of calibration prior densities. This is in contrast to fossil validation methods that result in the removal of potentially accurate calibrating information (Near et al. 2005, Hugall et al. 2007, Rutschmann et al. 2007, Marshall 2008, Dornburg et al. 2011). Thus, in the absence of prior knowledge of the waiting time between the node age and the minimum age constraint provided by the fossil record, this hierarchical model is preferable to specifying fixed hyperparameters. It remains important to state, however, that applying hyperpriors to calibration densities does not also free the user from carefully considering and understanding the fossil and geological data applied in his or her divergence time analyses. Moreover, it is highly recommended that researchers applying Bayesian divergence time estimation methods evaluate and report the marginal prior distributions on calibrated nodes chosen for their analysis, regardless of the approach to including calibration data (Heled and Drummond 2012, Warnock et al. 2012). This can be done by sampling (via MCMC) from the joint prior probability density over the model parameters and hyperparameters. When the marginal prior densities on parameters and hyperparameters are compared with their expected distributions, problematic or unexpected results caused by misspecified or poorly constructed priors may be revealed (Heled and Drummond 2012).

As our understanding of the fossil record and the properties of lineage fossilization, preservation, and sampling continues to develop, these elements can be incorporated into descriptive biological models of lineage diversification. With such models, data from fossil taxa can be included in divergence time analyses in a more rigorous way, allowing for inclusion of all available fossil specimens instead of reducing the information from the fossil record to a single minimum age constraint (Wilkinson et al. 2011). This will lead to robust, combined analyses of fossil and extant taxa while accounting for uncertainty in the tree topology and placement of extinct lineages (Ronquist et al. 2012) and uncertainty in the ages of fossil specimens (Shapiro et al. 2011). Moreover, in cases where combined approaches are not possible, realistic macroevolutionary tree priors can allow for better and more statistically sound approaches to calibrating divergence times with fossil age estimates (Heled and Drummond 2012).

FUNDING

This research was supported by a National Science Foundation (NSF) postdoctoral fellowship in biological informatics [DBI-0805631] and NSF [DEB-0918791] and National Institutes of Health [GM-069801 and GM-086887].