The influence of saddle-shaped annuloplasty on leaflet curvature in patients with ischaemic mitral regurgitation

Abstract

OBJECTIVES

Reports indicate that repair procedures for ischaemic mitral regurgitation (IMR) are less durable than previously thought. Repair failure has been shown to be stress related. Leaflet curvature is the major determinant of valve stress. Theoretical and animal experiments have shown that saddle-shaped annuloplasty optimizes leaflet curvature when compared with standard flat ring annuloplasty. Despite this, the influence of the ring shape on leaflet curvature has not been described in patients with IMR. This study uses real-time three-dimensional echocardiography (rt-3DE) to assess the influence of the ring shape on leaflet curvature.

METHODS

Rt-3DE was performed in 21 patients with IMR after placement of either a flat (n = 10, CE-Physio, Edwards) or saddle-shaped (n = 11, Profile 3D, Medtronic) annuloplasty ring. A combination of commercially available and customized software was used to measure multiple leaflet curvature parameters across all regions of the mitral valve.

RESULTS

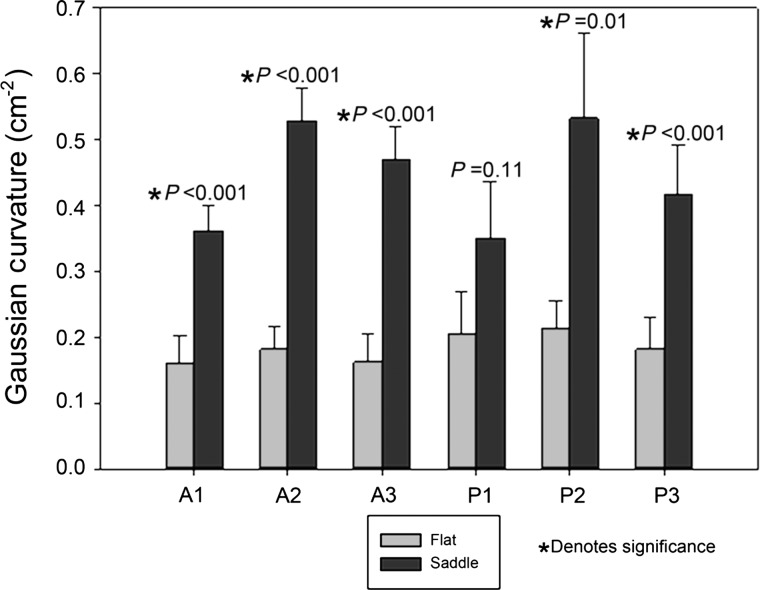
Independently of the shape of the annuloplasty ring, all patients were subject to the same degree of annular undersizing. Patients who received saddle-shaped annuloplasty rings had greater leaflet curvature in all six mitral valve leaflet regions (A1 = 0.36 ± 0.10, A2 = 0.53 ± 0.13, A3 = 0.47 ± 0.13, P1 = 0.35 ± 0.23, P2 = 0.53 ± 0.34, P3 = 0.42 ± 0.20 cm⁻²) compared with patients who received flat annuloplasty rings (A1 = 0.16 ± 0.11, A2 = 0.18 ± 0.09, A3 = 0.16 ± 0.11, P1 = 0.20 ± 0.17, P2 = 0.21 ± 0.11, P3 = 0.18 ± 0.13 cm⁻²). These differences were statistically significant in all regions except the P1 region.

CONCLUSIONS

Saddle-shaped annuloplasty rings increase leaflet curvature compared with flat rings in patients with IMR. As a result, saddle-shaped annuloplasty may decrease leaflet stress and potentially increases the durability of the repair in patients with IMR.

INTRODUCTION

For patients with ischaemic mitral regurgitation (IMR), valve repair with undersized ring annuloplasty, typically performed in conjunction with coronary artery bypass grafting, has become the preferred treatment [1, 2]. The majority of these repairs have been performed with flat annuloplasty rings. Despite its wide acceptance, this therapeutic approach is associated with a 30% recurrence rate of IMR at 6 months after surgery, with 3 to 5-year rates of recurrence approaching 60% [3–8].

Laboratory [9–11] and clinical studies [12, 13] have demonstrated that post-infarction left ventricular remodelling causes IMR by three distinct anatomical distortions: annular dilatation, annular flattening and leaflet tethering. While the standard flat undersized ring annuloplasty is effective in treating annular dilation, it tends to potentiate both annular flattening [14, 15] and leaflet tethering [5, 16].

The influence of the annular shape on leaflet curvature has been studied in detail in experimental and theoretical models. Previous work by our group has demonstrated that the natural mitral annular saddle shape acts to optimize leaflet curvature and minimize peak leaflet stress. In an ovine model, flat annuloplasty has been shown to decrease leaflet curvature and increase leaflet stress [15, 17, 18]. This increase in leaflet stress likely increases chordal loading and the force between the annulus and annuloplasty ring. As a result, it is not surprising that IMR repair failure has been associated with both progressive leaflet tethering [5, 7, 16, 19] and frank annuloplasty ring dehiscence [20, 21].

This experimental work suggests that saddle annuloplasty may improve the durability of repair for IMR by optimizing valve geometry and stress profiles. Although the concept is compelling, the influence of the shape of the annuloplasty ring on leaflet geometry has never been demonstrated in patients with IMR. The current study uses real-time three-dimensional echocardiography (rt-3DE) and novel imaging software to evaluate the influence of the shape of the annuloplasty ring on leaflet curvature in patients undergoing repair procedures for IMR.

MATERIALS AND METHODS

Patients and image acquisition

Twenty-one patients with severe IMR underwent mitral valve repair with ring annuloplasty. In 10 patients a Carpentier-Edwards Physio Annuloplasty Ring (flat ring) was used and in 11, a Medtronic Profile 3D Annuloplasty System (saddle ring). Ring selection was made at the discretion of the surgeon. Real-time 3D transoesophageal echocardiography was performed at the time of cardiac surgery. All patients underwent imaging before and after mitral valve repair. Pre-repair imaging data sets were acquired in the operating room after induction of general anaesthesia and before sternotomy. Post-repair imaging data sets were acquired after sternal closure and prior to leaving the operating room.

Images were acquired through a mid-oesophageal view with a Philips ie33 (Andover, MA, USA) ultrasound system equipped with a 2–7 MHz X7-2t TEE matrix transducer. Electrocardiographically gated full-volume images were acquired over four cardiac cycles at a frame rate of 17–30 frames/s. This study was approved by the University of Pennsylvania Institutional Review Board.

Image segmentation

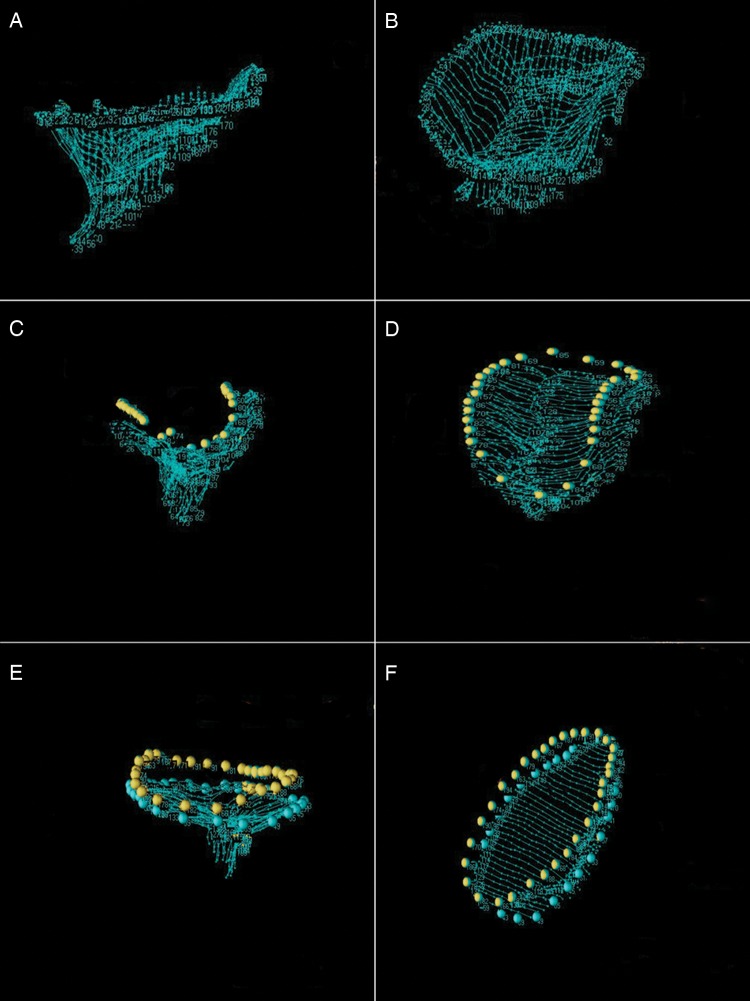
Each full-volume data set was then exported to an Echo-View 5.4 (Tomtec Imaging Systems, Munich, Germany) software workstation for image analysis. The highest quality data set was selected for each subject. Analysis was performed at mid-systole. The plane of the mitral valve orifice was rotated into a short-axis view. The geometric centre was then translated to the intersection of the two corresponding long-axis planes, which then corresponded to the intercommissural and septolateral (SL) axes of the mitral valve orifice. A rotational template consisting of 18 long-axis cross-sectional planes separated by 10° increments was superimposed on the three-dimensional echocardiogram. Two annular points intersecting each of the 18 long-axis rotational planes were then identified by means of orthogonal visualization of each plane; the 2 points were marked interactively. The anterior and posterior commissures were defined as annular points at the junction between the anterior and posterior leaflets. For post-repair images, the ring was marked in a similar fashion. Once the annular geometry was established, annular planes were marked at fixed 1-mm intervals along the entire length of the intercommissural axis. Free-hand curves for each two-dimensional (2D) annular plane were traced along the atrial surface delineating the anterior and posterior leaflets as well as the coaptation zone. Data sets of 600–1200 points were created for each valve (Fig. 1). The Cartesian coordinates of each assigned point were then exported to MatLab (The Mathworks, Inc., Natick, MA, USA).

Figure 1:

Annular and leaflet modelling. (A) and (B) demonstrate a lateral and oblique view of a data point cloud in a patient with ischaemic mitral regurgitation. The annulus appears flattened and dilated prior to repair. (C) and (D) depict a lateral and oblique view of the same patient after repair with a saddle-shaped annuloplasty ring. The three-dimensional ring (marked by yellow points) helps to restore non-planarity of the annulus and reduce the annular area. (E) and (F) show a second patient after repair with a flat annuloplasty ring (marked by yellow points) for comparison. Although the undersized ring reduces the annular area, the flat ring fails to restore annular non-planarity.

Annular analysis

Using custom MatLab algorithms and orthogonal distance regression, the least-squares plane of the data point cloud for the annulus was aligned to the x–y plane. Under these geometric conditions, the annular height for each point (z_n) was plotted as a function of rotational position on the annulus. A number of anatomical landmarks were identified. The septum (S) was identified as the anterior horn of the annulus at the aortic valve. The lateral annulus (L) was identified in the middle of the posterior annulus circumference. The SL diameter was defined as the distance between these two points, respectively. With the annular model rotated such that the commissures were aligned along the y-axis, the maximum and minimum y-values of the annulus were identified as the anterolateral and posteromedial annular points. Annular height was defined as the z_max − z_min. Commissural width (CW) was defined as the three-dimensional distance between the two commissures. The annular height to the CW ratio (AHCWR) for a given annular data set was defined as AH/CW × 100%. Mitral annular area (MAA) was defined as the area enclosed by the 2D projection of a given annular data set onto its least-squares plane. Mitral valve transverse diameter was defined as the distance separating the AL annulus and the PM annulus. The degree of annular undersizing post-repair was calculated as the change in the annular area (post-MAA—pre-MAA) divided by the pre repair MAA and expressed as a percentage.

Leaflet surface area and leaflet curvature analysis

The leaflet point clouds representing the anterior and posterior leaflets were then transformed such that their geometric centre coincided with the origin and their least-squares-fit plane lay on the x–y plane. All coaptation points were subsequently added to both data sets. Separate meshed grids, with boundary conditions determined by the given data set extremes, were created for the anterior leaflet and posterior leaflet data sets. Smoothing splines were constructed separately for the anterior and posterior leaflets using the MatLab spline TPAPS function for evenly spaced points separated by 0.1 mm in the x and y directions. The area of each triangle described by three adjacent mesh points was calculated continuously across the leaflet mesh grids. The anterior surface area (SA_AL) was defined as the sum of the triangular areas across the anterior leaflet. The posterior surface area (SA_PL) was defined as the sum of the triangular areas across the posterior leaflet. The total surface area (SA_Total) was defined as the sum of the SA_AL and the SA_PL. The ratio of the total leaflet surface area to the annular area was calculated as a measure of relative leaflet redundancy.

The two-dimensional intercommissural curvature (K_IC) and SL leaflet curvatures (K_SL) were then calculated. Intercommissural curvature was computed for each point on the mesh for each leaflet by determining the inverse of the radius of curvature of the circle formed by each mesh point and its two closest neighbours in the y-direction. This process was repeated in the x-direction to determine the SL curvature. The three-dimensional Gaussian leaflet curvature (K) was then computed for every meshed point on each leaflet as follows:

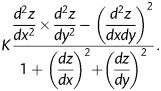For purposes of data analysis, the intercommissural axis of each mitral valve data curvature set was then subdivided into equal thirds. Each mesh point in a given data set was subsequently assigned to one of six leaflet zones—A1, A2, A3, P1, P2 and P3. Regional averages for the intercommissural, SL and Gaussian curvatures were grouped by the leaflet zone.

Statistical analysis

All continuous data are presented as mean ± standard deviation. Student's unpaired t-tests were used to compare parameters between annuloplasty cohorts. All statistical analysis was performed using SPSS software (SPSS, Inc., Chicago, IL, USA) A P-value <0.05 was considered to be statistically significant.

RESULTS

Patient characteristics

Preoperative patient characteristics are presented in Table 1. Patients were similar between groups for all measures of disease severity including the degree of MR, ejection fraction and left ventricular dimensions. Patients in the flat group tended to be slightly younger than patients in the saddle group in a significant fashion.

Table 1:

Baseline patient characteristics

	Flat ring	Saddle ring	P-value
Age (years)	59.2 ± 10.3	69.9 ± 11.0	0.03*
Women (%)	50.0%	18.2%	0.06
Body mass index	31.8 ± 3.0	30.9 ± 5.2	0.67
Ejection fraction (%)	34.5 ± 19.4	32.3 ± 15.6	0.78
MR grade, 0–4 scale	3.1 ± 1	2.8 ± 1	0.52
LVED diameter	6.0 ± 0.8	5.9 ± 1.2	0.77
LVES diameter	4.9 ± 0.8	4.7 ± 1.4	0.72

*Significance.

Annular geometry and leaflet surface area

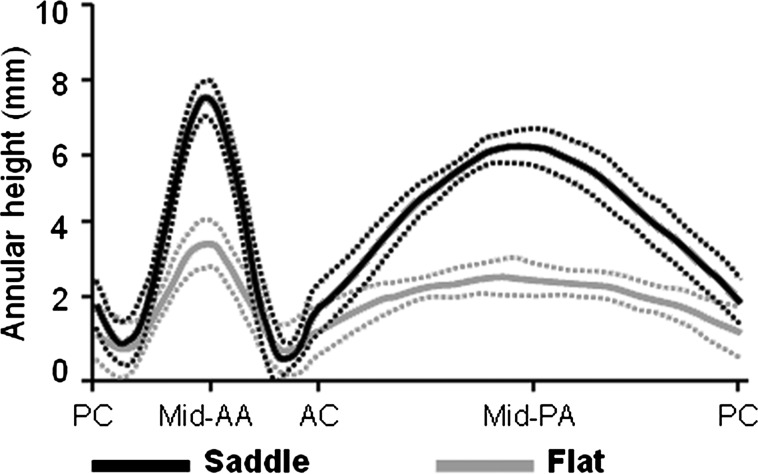
Measured and derived annular and leaflet surface area parameters are summarized in Table 2. The degree of annular undersizing was similar between groups (−46.6 ± 14.6 vs. −46.4 ± 15.7%, P = 0.98). Measures of post-repair annular size, including MAA, SL and CW, were also similar between the flat and saddle-shaped annuloplasty cohorts. Patients undergoing repair with a saddle-shaped annuloplasty ring had greater annular height after repair compared with patients who received a flat ring (7.4 ± 0.8 vs. 3.3 ± 1.1 mm, P < 0.0001) (Fig. 2). The non-planarity of the annulus, as determined by AHCWR, also showed a statistically significant difference between the two groups with the post-repair saddle group demonstrating increased non-planarity compared with the flat group (24.5 ± 1.9 vs.10.8 ± 3.7, P < 0.0001). Anterior and posterior leaflet surface areas, as well as total leaflet surface areas, were not statistically significant between the two groups after implantation of the annuloplasty device. Additionally, the degree of leaflet redundancy, as determined by the ratio of SA_Total to the MAA, showed no statistical significance between the flat and saddle-shaped annuloplasty cohorts after repair.

Table 2:

Annular and leaflet surface area parameters

Annular and leaflet parameters	Flat ring	Saddle ring	P-value
Post-repair annular height (mm)	3.3 ± 1.1	7.4 ± 0.8	<0.0001*
Post-repair commissural width (mm)	30.4 ± 3.4	30.6 ± 3.0	0.84
Post-repair annular height to commissural width ratio	10.8 ± 3.7	24.5 ± 1.9	<0.0001*
Post-repair septolateral dimension (mm)	24.9 ± 24.4	23.2 ± 2.3	0.28
Pre-repair mitral annular area (mm2)	1115.8 ± 339.6	1056.3 ± 221.4	0.67
Post-repair mitral annular area (mm2)	590.8 ± 126.6	584.4 ± 70.0	0.89
Annular undersizing (%)	−46.4 ± 15.7%	−46.6 ± 14.6%	0.98
Post-repair anterior leaflet surface area (mm2)	536.2 ± 179.3	494.7 ± 106.3	0.53
Post-repair posterior leaflet surface area (mm2)	226.5 ± 155.9	210.0 ± 55.8	0.76
Post-repair total surface area (mm2)	762.7 ± 325.4	704.7 ± 147.2	0.61
Post-repair total surface area to mitral annular area ratio	1.2 ± 0.2	1.2 ± 0.1	0.55

*Significance.

Figure 2:

Comparison of annular height. Average annular height (thick lines) with standard error of the mean (dotted lines) is plotted along the entire circumference of the annulus after repair with a flat or saddle-shaped annuloplasty ring. Patients repaired with saddle-shaped rings demonstrate greater annular height at the mid-anterior annulus (Mid-AA) and the mid-posterior annulus (Mid-PA) compared with patients repaired with flat rings. PC: posterior commissure; AC: anterior commissure.

Leaflet geometry

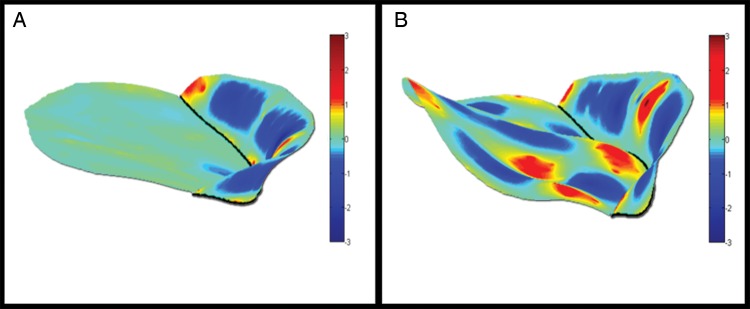
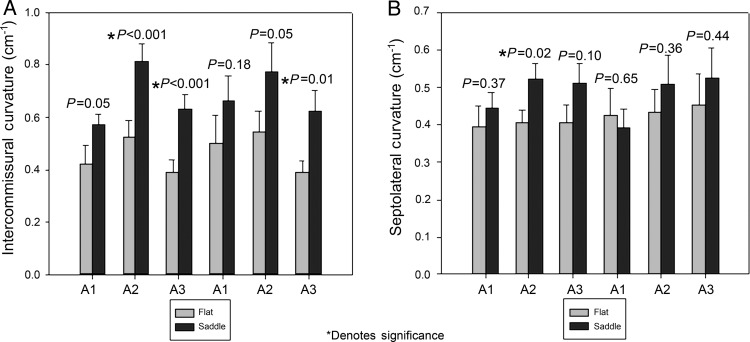
Regional mean values ± SEM are presented for the Gaussian curvature in Fig. 3. Patients who received a saddle-shaped annuloplasty ring had greater leaflet Gaussian curvature in all six mitral valve leaflet regions compared with patients who received a flat annuloplasty ring. These differences were statistically significant in all regions except the P1 region. Figure 4 illustrates the differences in Gaussian curvature patterns for an example patient repaired with a flat ring compared with an example patient repaired with a saddle ring. Regional mean values ± SEM are presented for SL curvature and intercommissural curvature in Fig. 5. Patients who received a saddle-shaped annuloplasty ring demonstrated statistically significant increases in intercommissural curvature in the A2, A3 and P3 regions. The saddle-shaped cohort also demonstrated significant increases in SL curvature in the A2 leaflet region (Fig. 6).

Figure 3:

Leaflet Gaussian curvatures after mitral valve repair. Average Gaussian curvature with standard error are presented for each leaflet region (A1-P3) for patients repaired with flat or saddle-shaped annuloplasty rings. Patients repaired with saddle-shaped rings show increases in the Gaussian curvature compared with patients repaired with flat rings. These differences are significant in all regions except the P1 region.

Figure 4:

Three-dimensional renderings of the leaflet Gaussian curvature. (A) (flat ring). (B) (saddle-shaped ring). Colour contouring represents leaflet Gaussian curvature. The patient repaired with the saddle-shaped ring (B) demonstrates increased Gaussian curvature compared with the patient repaired with the flat ring (A).

Figure 5:

Intercommissural and septolateral curvature after mitral valve repair. (A) Average intercommissural curvature with standard error for each leaflet region. (B) Average septolateral curvature with standard error for each leaflet region. Significant increases in the intercommissural and septolateral curvature are noted in the saddle group for multiple leaflet zones.

Figure 6:

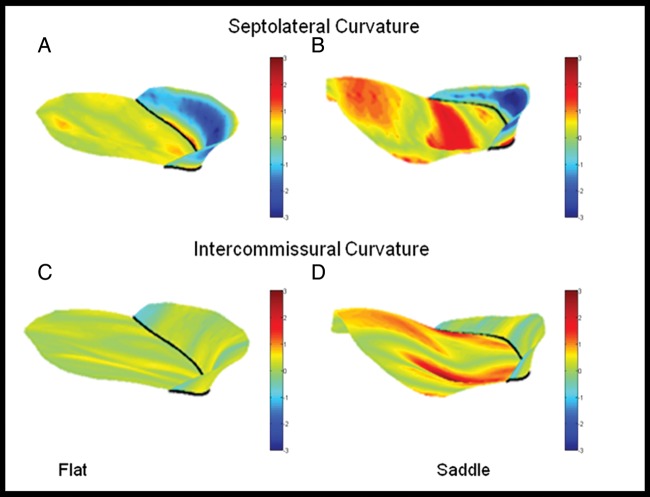
Three-dimensional contour maps of septolateral and intercommissural curvature. (A) (flat ring) and (B) (saddle ring) represent colour contoured maps for leaflet septolateral curvature. The patient repaired with the saddle ring (B) demonstrates increased septolateral curvature, especially notable in the A2 region, compared with the patient repaired with the flat ring (A). (C, flat) and (D, saddle) represent colour contoured maps for leaflet intercommissural curvature. The patient repaired with the saddle-shaped ring (D) demonstrates increased intercommissural curvature in multiple leaflet zones compared with the patient repaired with the flat ring (C).

DISCUSSION

Our results demonstrate that saddle-shaped annuloplasty increases leaflet curvature, as measured by several quantitative indices, when compared with flat annuloplasty in patients undergoing valve repair for IMR. These clinical findings corroborate previous animal and theoretical work describing the influence of the shape of the annuloplasty ring on leaflet geometry.

In the present human study, patients undergoing repair with a saddle-shaped ring demonstrated restoration of the annular height (7.4 ± 0.8 mm) into the previously described normal human range of 7.5 mm [22], while patients treated with flat annuloplasty rings had annular heights of approximately half that value (3.3 ± 1.1 mm).

It is interesting to note that both post-repair annular size and leaflet surface area were similar in both groups. These findings are important because it has been shown that both leaflet billowing and annular shape contribute to leaflet curvature and valve stress profile [18]. Annular area and leaflet surface area are both determinants of leaflet billowing. IMR is the ideal model to study the effects of annular shape on leaflet geometry, as there is no leaflet resection or plication as is commonly performed in the repair of regurgitant myxomatous valves. The fact that both annular and leaflet surface area were similar in both groups gives reasonable assurance that the difference in leaflet curvatures measured between the two groups was a function of annular geometry alone in this pathology.

In the previous work, our group has quantitatively described normal leaflet curvature using both echocardiography and sonomicrometry array localization studies [23, 24]. Tibayan et al. augmented this discussion by quantifying the radii of curvature in an ovine model at baseline and after IMR [25]. In their work, they noted that the anterior leaflet in normal mitral valves assumes a compound curvature in the SL direction. This hyperbolic surface in the mid-anterior (A2) region is diminished as the valve and left ventricle remodel in IMR. Additionally, they noted that the radii of curvature also increased (diminished curvature) in the posterior leaflet with IMR. In an ovine model, looking at the effects of annuloplasty ring geometry on leaflet curvature, we confirmed these findings and noted that implantation of a saddle-shaped ring in naïve sheep augmented SL curvature in multiple zones [15].

Despite the fact that all patients (regardless of ring type) underwent similar SL shortening in the current study, significant differences in SL curvature profiles in the A2 region were noted between groups. It follows that saddle-shaped annuloplasty rings may help to restore compound curvature, thereby reducing leaflet stress.

IMR repair failure continues to be a significant clinical problem. Failure mechanisms seem to be, at least partially, attributable to leaflet stress. As a result, procedures and devices designed to optimize leaflet geometry may have a significant impact on long-term repair durability. This study shows, for the first time, that saddle-shaped annuloplasty can augment leaflet curvature in patients with IMR and as a result may have an influence on reducing leaflet stress.

Despite these compelling results, further investigation is necessary to correlate post-repair curvature indexes with actual stress distributions, and to follow the long-term outcomes of patients with IMR treated with flat vs. saddle annuloplasty rings.

Funding

The study was funded in part by an investigator-initiated grant from Medtronic, Minneapolis, MN as well as research grants HL70321 and HL63954 from the National Heart Lung and Blood Institute of the National Institutes of Health, Bethesda, MD, USA.

Conflict of interest: This study was funded in part by an investigator-initiated grant from Medtronic, Minneapolis, MN.

APPENDIX. CONFERENCE DISCUSSION

Dr M. Mariani (Groningen, Netherlands): You conclude by talking about clinical durability, but you do not indicate in either your presentation or in the paper, the duration of your clinical follow-up, or whether you have any echocardiographic data that supports this basic data which translates into clinical advantage, such as less recurrence of mitral regurgitation at follow-up. This is the clinical part of my question.

And then I have a more specific question for the future. I have to make some notes, because it is quite a difficult study for me, too. How do you plan to correlate the post-repair curvature indices with actual stress distribution?

Dr Vergnat: Related to the first question about clinical results, you are absolutely right, that is the most important aspect, but the study presented is much more towards basic science, with very small numbers. So it doesn't make sense to draw any clinical conclusions based on such a small cohort. Therefore I don't expect any difference in terms of recurrence among our small number of patients. That is the first point. Secondly, the Gormans have studied a lot of ischaemic mitral regurgitation and we strongly believe that annuloplasty is not enough. It is part of the treatment, but you also have a lot to do with a leaflet procedure. We did a very basic science study that shows in humans what we had shown in animals. Now we need a lot more patients in order to be able to speak about clinical results.

Dr Mariani: How do you plan to correlate the post-repair curvature indices with the stress situation?

Dr Vergnat: These are theoretical studies that showed that leaflet stress results from leaflet billowing and annular non-planarity that has been demonstrated with a computational model. So if you want to prove that, you have to do a measure of leaflet stress and leaflet curvature at the same time, which has never been done in an animal study. That is a very interesting study. But that has been proven theoretically.

Dr Ž. Jonjev (Novi Sad, Serbia): I have a question that might have an influence on the overall impression about this. We all know that, according to the model of Torrent-Guasp, the heart is made of one muscle that is twisted around itself and makes two different chambers that are connected together. So if we wish to have an excellent surgical result with ischaemic mitral regurgitation, we should observe the heart as a functional unit of these two chambers together. So whoever wants to have a good result should do tricuspid annuloplasty at the time of mitral valve reconstruction.

Do you believe that that concept is acceptable, and how many patients in your hands had tricuspid reconstruction at the same time as mitral reconstruction was performed?

Dr Vergnat: I have to admit that my experience with ischaemic mitral regurgitation repair is quite limited, I’m sorry, and our presentation was not about this. Do you feel that is connected to what I presented?

Dr Jonjev: I believe that treating the heart as a functional unit is extremely important in every kind of mitral valvuloplasty.

Dr Vergnat: I cannot answer that question precisely based on what I did.

Dr V. A. Subramanian (New York, NY, USA): I think it is important for us to understand leaflet stress, and also I wonder whether you can tell me how you can quantitate some of the chordal tension, especially the strut chordae and the marginal chordae, because that is going to be a unit which plays a tremendous role in the durability of this leaflet stress. Our future should be looking at completely different principles of mitral repair, either a percutaneous or a surgical device. I think one is a saddle shape, and it clearly has been shown, at least in the Mayo Clinic, that most of the patients with a myxomatous degenerated valve already have a flattened annulus. Even if you put in a saddle-shaped ring, it doesn't really bring it to the normal level. So the question is, should we pay more attention to the chordal tension? And so you need to have a different type of mentality to use a new surgical repair device, either percutaneous or surgical. So can you at least tell me about how you measure the strut chordal tension or the marginal chordal tension, which is going to be extremely important if you want to have a durable repair. Do you have anything in your lab to tell us?

Dr Vergnat: You are absolutely right. Actually, there are two working perspectives in the lab. We work with clinical people who obtain the echo data in the hospital and then we work with that. The Gormans found that it was easier to study curvature than to do a leaflet stress computational model of these studies obtained in the hospital. So now we just use curvature to assess stress; it is a surrogate for stress. We work with the clinics and in the research lab with basic research, studying stress. They have a model for stress measuring, using real-time 3D echo and a real-time model, because, as you know, most of the models for stress calculation are based on an idealistic mitral valve, and we know that geometry is a major component for stress analysis. So what we do is to include realistic geometry in this leaflet stress calculation, and we also incorporate chordae. It is easy to locate the papillary muscle in 3D echo but it is much more difficult to locate the chordae. So we use idealistic chordae based on cadaver studies.