Abstract
Current MRI methods for myocardial motion and strain quantification have limited resolution because of Fourier space spectral peak interference. Methods have been proposed to remove this interference in order to improve resolution; however, these methods are clinically impractical due to the prolonged imaging times. In this paper, we propose total removal of unwanted harmonic peaks (TruHARP); a myocardial motion and strain quantification methodology that uses a novel single breath-hold MR image acquisition protocol. In post-processing, TruHARP separates the spectral peaks in the acquired images, enabling high-resolution motion and strain quantification. The impact of high resolution on calculated circumferential and radial strains is studied using realistic Monte Carlo simulations, and the improvement in strain maps is demonstrated in six human subjects.
Keywords: MRI, HARP, tagging, cardiac motion, strain quantification
Measuring cardiac motion and strain plays a major role in research related to heart diseases (1,2) and is becoming increasingly important in standard clinical practice (3–8). MRI based on tagging (9–12) and stimulated echo (13,14) is the gold standard for making these measurements (15), yet limitations remain. In particular, existing methods exhibit well-known tradeoffs between strain resolution, artifacts, and imaging time. Fast imaging methods (11–14,16,17) typically suffer in resolution or contain artifacts, while methods that have few artifacts and high strain resolution (18,19) are associated with long imaging times. The present work provides a new operating point in the tradeoff by demonstrating high-resolution artifact-suppressed motion and strain quantification using a single breath-hold imaging protocol.
Current methods using MR tagging with harmonic phase (HARP) MRI (11) or displacement encoded stimulated echoes (DENSE) (14) can be described in a common framework (20) by either referring to spectral peaks or echoes that are present in the Fourier transform or signal data yielding the acquired image sequences. In particular, harmonic peaks (stimulated echoes) and conjugate peaks (conjugate echoes) contain information about motion, while the DC peak (T1 echo) does not contain any information related to motion. When acquiring data for HARP or DENSE, interference from other spectral peaks or echoes can be reduced by changing pulse sequence parameters to spread the peaks or echoes apart (20) or by band-pass filtering during post-processing (11,14). The former approach reduces the SNR of the acquired data and the latter approach reduces the functional resolution of the resulting motion and strain images, where functional resolution refers to the spatial resolution of the filtered images that are used to generate the motion and strain images. Spectral peak interference can also be reduced through use of inversion recovery (21,22) or a through-plane dephasing gradient (23). The use of inversion recovery is not compatible with the acquisition of cine sequences and through-plane dephasing can cause signal loss due to through-plane strain (16). For these reasons, neither of these techniques is considered in this paper.
Complete removal of the DC peak can be accomplished by using two complementary acquisitions—e.g., complementary spatial modulation of magnetization (CSPAMM) (24–27). CSPAMM requires four acquisitions for two-dimensional strain estimation, two (e.g., the original and complementary acquisitions) for each orientation (e.g., vertical and horizontal). Conventional HARP and DENSE processing (cf., (11,14)) uses a single band-pass filter to extract a single peak in each orientation, while peak-combination HARP (28) extracts both peaks to reduce phase errors. In both cases, the peaks are separated using band-pass filters, which does not perfectly isolate their spectra (even though the DC peak is absent). In fact, the harmonic peaks or echoes still interfere with each other, which requires one to choose between either a medium-resolution strain map containing artifacts or a low-resolution strain map with fewer artifacts.
Epstein and Gilson (19) introduced the CANSEL method to completely isolate spectral peaks in DENSE MRI, and we note that it is also applicable to tagging methods and HARP processing (29). CANSEL can be thought of as an extension of CSPAMM in that it acquires both cosine and – cosine modulations as in CSPAMM, as well as sine and – sine modulations. With these four acquisitions, a spectral peak can be completely isolated. Another four acquisitions are required for the second orientation (to yield both horizontal and vertical displacements) and a phase reference acquisition is also required (for DENSE processing). In total, nine acquisitions of image sequences are required to implement the CANSEL method, which is very costly in terms of imaging time. Generally, in order to maintain high resolution, this process cannot be accomplished in a single breath-hold.
This paper presents a single breath-hold MRI tagging methodology for the total removal of unwanted harmonic peaks (TruHARP). Although TruHARP is in the spirit of CANSEL, the key advantage of TruHARP over CANSEL arises from the recognition that data acquired from both horizontal and vertical directions can be processed together, rather than separately, as in CANSEL. As a result, TruHARP requires only five acquisitions of image sequences and is implemented in a single breath-hold protocol requiring just 16 heartbeats. All spectral peaks are isolated using a simple algebraic combination of the acquired data, and HARP processing can be readily carried out on the isolated peaks. In the absence of spectral interference, the resolutions of the motion and strain profiles are limited by noise and acquired image resolution, rather than the spacing between spectral peaks. In the following sections, we describe the TruHARP pulse sequence and its post-processing procedures, present simulations demonstrating improved resolution, and explore the tradeoffs between resolution and noise. Improvements in strain quantification are then demonstrated in six normal subjects.
THEORY
TruHARP Peak Extraction
The image intensity of a horizontally-tagged image sequence acquired using the 1-1 SPAMM pulse sequence shown in Fig. 1 is given by
| (1) |
where ρ(x) is the effective spin density and ω is the sinusoidal tagging modulation frequency. By the CSPAMM convention (24), ω = 2π/(tag period) and the tag period is twice the tag spacing defined as the distance between zero crossings of the tag pattern in the modulus magnitude image. P(x, t) is the reference map (position of three-dimensional spatial point x at the reference time), φ(x, t) is the displacement-encoding phase resulting from tagging, φe(x, t) is the phase resulting from inhomogeneity and other magnetic field non-idealities, and t is the time from tag application to image acquisition. Adc(x, t) and Ahp(x, t) depend on the imaging parameters and represent the effect of T1 on, respectively, the spectral peak in the center of k-space and the harmonic peaks. Typically, Adc(x, t) increases with time due to T1 while Ahp(x, t) decreases with time due to tag fading (24). A ramped flip-angle excitation (30) strategy is typically used to keep Ahp(x, t) constant over the cardiac cycle. Using an analogous explanation, it follows that the image intensity of a vertically-tagged 1-1 SPAMM image sequence is given by
| (2) |
FIG. 1.
Tagging building unit for TruHARP. The values of , , Gx, and Gy are shown in Table 1.
IAh and IAv in Eqs. 1 and 2 can be represented as the following combinations of five separate images Idc, , , , and :
| (3) |
| (4) |
where,
| (5) |
| (6) |
| (7) |
Equations 3 and 4 constitute a linear system of two equations with five unknown variables. Since this system of equations is underdetermined, in conventional HARP analysis the displacement-encoded images corresponding to harmonic peaks I+h and I+v cannot be extracted directly, and an explicit k-space band-pass filtering (11) is necessary to separate the spectral peaks. To eliminate this requirement, TruHARP also acquires the following image sequences
| (8) |
| (9) |
| (10) |
From these five image sequences, the x and y displacement-encoded images corresponding to harmonic peaks ( and ), as well as their conjugate peaks (I−h and I−v), are extracted as follows without band-pass filtering, which was previously necessary for isolating spectral peaks.
| (11) |
| (12) |
| (13) |
Scaled displacement-encoded harmonic phase (HARP) images φx and φy obtained from the phase component of the complex results as follows:
| (14) |
| (15) |
where the symbol * is the complex conjugate operator and the symbol ∠ is an operator for the phase of complex number. Since the phase operator only finds angles in the range [ −π, π], the resulting angles are wrapped versions of the true harmonic phases as follows:
| (16) |
| (17) |
where W is the wrapping operator defined in Osman et al. (11). As in conventional HARP and DENSE analyses, the wrapping of these phases poses no significant challenge in post-processing since the phases can be globally or locally unwrapped as needed.
Single Breath-Hold TruHARP Pulse Sequence
The modified 1-1 SPAMM tagging sequence with ramp flip-angle acquisition, as shown in Fig. 1, is repeated five times with different tagging parameters to obtain the tagged image sequences described in Eqs. 1, 2, and 8–10. Table 1 shows the values of flip-angle θ and initial phase ϕ of the first and second tagging radiofrequency (RF) pulses ( and ) and the tagging gradients (Gh and Gv) used to generate these five image sequences. A ramped flip-angle strategy (30) is used during data acquisition in order to have constant tagging contrast Ahp over the cardiac cycle. A segmented spiral k-space data acquisition (30) with three spiral interleaves is used to acquire each of the five image sequences. Five datasets are acquired in the order given in Table 1 with one dummy heartbeat in the beginning of a 15-heartbeat scan, therefore acquiring a complete dataset in a single 16-heartbeat breath-hold.
Table 1.
Tagging Parameters for the TruHARP Pulse Shown in Fig. 1
| Scan order | Gx | Gy | Tagging | |||
|---|---|---|---|---|---|---|
| 1 | IAh | 0 | G | cos (ωy) | ||
| 2 | IAv | G | 0 | cos (ωx) | ||
| 3 | IBh | 0 | G | −cos (ωy) | ||
| 4 | ICh | G | 0 | sin (ωx) | ||
| 5 | ICv | 0 | G | sin (ωy) |
TruHARP Motion and Strain Resolution
Even though there is no interference present after separation of the displacement-encoded spectral peaks using TruHARP, a k-space filter is still required to correct for asymmetric data acquisition around the displacement-encoded spectral peaks and to reduce the impact of noise that becomes dominant at higher spatial frequencies. This filter is applied to the four TruHARP-separated displacement-encoded spectral peaks before peak combination. The k-space data are acquired over a disk centered at the origin of k-space, and the separated spectral peaks are centered at ±ω mm−1. Therefore, the acquired k-space data are asymmetric around the spectral peak with missing data at the complex conjugate k-space location, producing artifacts in motion and strain estimation. The distance between the nearest edge of acquired k-space and the spectral peak is rs = 1/2Δ–ω mm−1, where Δ is the in-plane resolution of the tagged image slice. To reduce the artifacts arising due to the asymmetrically sampled spectral peak and noise, a Kaiser-Bessel filter (31) centered at the spectral peak with full width at half maximum (FWHM) of at most 2rs in Fourier space is applied, thereby restricting the resolution of the filtered image associated with any of the separated spectral peaks to 1/2rS = Δ/(1 – 2ωΔ) mm. While a smaller will decrease the error due to noise and increase the error due to low resolution, a larger FWHM will increase the error due to both noise and asymmetric sampling and decrease the error due to resolution. Therefore, the choice of optimal filter size depends on both the amount of noise and the pattern of k-space sampling. Finally, HARP processing (11) is applied on image sequences corresponding to the separated spectral peaks to estimate the Eulerian strain profile and to track points over the imaged slice.
Noise Characteristics
The effect of noise can be studied by considering the case when each 1-1 SPAMM-tagged image in the datasets for TruHARP, 1-1 SPAMM, and CSPAMM is acquired with the same acquisition time and is corrupted by additive white Gaussian noise with variance σ2. Therefore, the total acquisition time for TruHARP and CSPAMM datasets will be 2.5 and 2 times the time for 1-1 SPAMM dataset acquisition, respectively. Using Eqs. 11–13, the variance of the noise in TruHARP-separated images of horizontal and vertical displacement-encoded spectral peaks is given by 0.5σ2 and 0.75σ2, respectively. Following similar derivations, the unseparated harmonic peak images from SPAMM and CSPAMM has noise variances of σ2 and 0.5σ2, respectively. Although 1-1 SPAMM has the highest SNR and CNR efficiency (SNR and CNR per unit scan time) and CSPAMM has highest CNR and SNR, the spectral peaks separated using 1-1 SPAMM or CSPAMM are corrupted by interference from the conjugate spectral peaks, an additional source of error not considered by the above noise computations.
Since harmonic peaks and their conjugate peaks are completely isolated and extracted for every displacement direction in TruHARP, peak-combination HARP (28) is employed (Eqs. 14 and 15) to eliminate off-resonance and magnetic field inhomogeneity artifacts. In addition to this, averaging of the harmonic phase of conjugate peaks during peak combination further reduces the influence of independent noise.
MATERIALS AND METHODS
Simulation
Monte Carlo simulations were performed to study the effects of spectral peak interference, noise, and resolution (filter FWHM) on the accuracy of strain quantification from image sequences acquired by CSPAMM and TruHARP, using HARP analysis. In CSPAMM, the spectral peaks are affected by both noise and interference, while in TruHARP the spectral peaks are only affected by noise. Complex-valued CSPAMM and TruHARP image sequences were simulated for a contracting annular region in a stationary background, mimicking the incompressible contraction of the left ventricle during systole. The annular region with inner radius Ri and outer radius Ro was contracted radially such that a layer with an original radius R shrank to a smaller radius Rε according to the formula,
| (18) |
where ε is the maximum radial thickening occurring at endocardium (Ri). In this simulation, Ri = 18 mm, Ro = 28 mm, and ε = 0.3 were chosen to produce maximum radial thickening of 30% and maximum circumferential shortening of 40% at the endocardium. The simulated images were of size 256 × 256 pixels, field of view (FOV) of 280 mm, and tag spacing of 7 mm, generating spectral peaks that are spread out from the center of the k-space by ±20 pixels (0.0714 mm−1) in k-space. Tags were generated in the initial time instant, simulating conventional tag application at end-diastole.
HARP analysis was applied to the CSPAMM and TruHARP datasets by varying the amount of additive white Gaussian noise to achieve CNR 5 and 15 for 1-1 SPAMM-tagged images during data acquisition, and varying the FWHM of the filter in k-space. The relationship between the filter FWHM and the Fourier resolution of the filtered image Δf is given by
| (19) |
The filter FWHM was varied from 16 pixels to 80 pixels, which corresponds to Fourier resolutions from 17.5 mm to 3.5 mm. Peak-combination HARP (28) was also employed for the CSPAMM datasets.
Another simulation was performed to study the impact of increased Fourier resolution on strain estimation across an infarcted tissue. Similar to the previous Monte Carlo simulation, a tagged contracting annular region was simulated with different contractions in left and right half of the annulus. This contraction pattern generates two interfaces located at top and bottom of the annular region, mimicking the interface between the normal and infarcted tissue. A TruHARP-tagged dataset was obtained by contraction of the left and right half of the annulus to produce maximum radial thickening of 30% and 18% and maximum circumferential shortening of 40% and 22%, respectively, at the endocardium. HARP analysis was performed using filter FWHMs of 32, 48, and 64 pixels, which corresponds to Fourier resolutions of 8.75, 5.83, and 4.37 mm, respectively.
In Vivo Single Breath-Hold Experiments
Six healthy human subjects of ages 24 ± 4 years with no history of heart disease were scanned. The experiments were approved by the Institutional Review Board of Johns Hopkins Medical Institutions. Informed consents for scanning and participation were obtained from all subjects. The study was Health Insurance Portability and Accountability Act compliant. The pulse sequence was implemented on a clinical Philips 3.0-T Achieva MRI scanner (Philips Medical Systems, Best, The Netherlands) equipped with a six-channel cardiac phased-array surface coil. Channels were distributed equally between the anterior and posterior sides of the chest in each subject. Four ECG leads were placed on the subjects’ chests for triggering the pulse sequence at the R-wave of the ECG. The subjects were positioned head first and supine.
The scans were performed using a VECG-triggered, segmented k-space, spiral acquisition with spectral-spatial excitation and a ramped flip-angle (30,32). Twenty short-axis systolic cine frames at midcavity, with a temporal resolution of 30 ms, were acquired from end-diastole to end-systole (from 11 ms to 611 ms after the R-wave of the ECG). The TruHARP dataset was acquired using three spiral readouts per image, each with a 14-ms acquisition window. Acquired images had FOV = 280 mm, spatial resolution = 2.5 × 2.5 mm2, slice thickness = 8 mm, TR = 30 ms, and tag spacing = 7 mm. Each scan was completed in a single breath-hold comprising 16 heartbeats.
CSPAMM datasets were acquired separately, using nine spiral readouts per image, each with a 10-ms acquisition window. Acquired images had FOV = 300 mm, resolution = 2 × 2 mm2, slice thickness = 8 mm, TR = 30 ms, and tag spacing = 7 mm. The four datasets for CSPAMM = processing were acquired in two breath-holds of 19 heartbeats each, including one dummy heartbeat in the beginning of each breath-hold.
Statistical Analysis
The myocardium was divided into six sectors (anterior (A), anteroseptal (AS), inferoseptal (IS), inferior (I), inferolateral (IL) and anterolateral (AL)), and three layers (endocardium, midwall, and epicardium), producing 18 segments in total. A Student’s t test with unequal variances was performed to compare the estimated radial and circumferential strains in each of these segments for filter FWHM = 32 pixels and filter FWHM = 64 pixels, which are equivalent to Fourier resolutions of 8.75 mm and 4.37 mm, respectively. Two-sided Student’s t test was chosen to test the hypothesis if the uses of larger filter FWHM lead to a significant increase or decrease in strain values. The Welch-Satterthwaite equation (33) was used to compensate for the spatial smoothing due to filtering by regulating the degrees of freedom in the t test. The end-systolic radial and circumferential strains (peak strains) were compared for six subjects over the myocardium.
RESULTS
Simulation
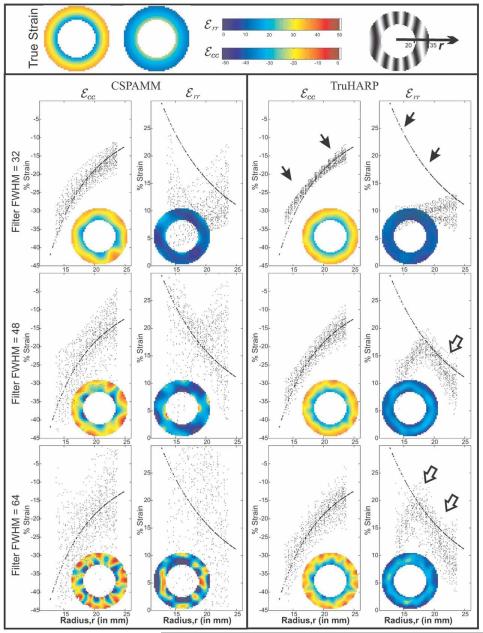
True and estimated Eulerian circumferential and radial strains over the annular region mimicking myocardium for one of the 50 Monte Carlo simulations are shown in Fig. 2. The figure also shows scatterplots between the calculated strain values at the myocardium and their radial distance r from the center of myocardium. True strain values (shown as dark points) are uniform along the circumference of the myocardium and increase (in absolute value) transmurally from epi- to endocardium (solid arrows). The strain results are shown for a filter FWHM of 32 pixels, which is equivalent to a Fourier resolution of 8.75 mm (a typical HARP filter FWHM when the spectral peaks are located at ±20 pixels in k-space) and also for FWHM = 48 pixels and FWHM = 64 pixels, which are equivalent to Fourier resolutions of 5.83 mm and 4.37 mm, respectively.
FIG. 2.
Eulerian circumferential and radial strains for CSPAMM and TruHARP with filter FWHMs given by 32, 48, and 64 pixels. Inset pictures show the estimated strain. The plot shows the scatter diagram of estimated strain and true strain (marked by hollow arrows) over the circumference of myocardium at a given radius within myocardium. Radial strain is underestimated and approaches its true value (dark arrow) at larger filter FWHM.
For a typical HARP filter size of FWHM = 32 pixels, both TruHARP and CSPAMM had similar strain profile distributions (Fig. 2). However, when the filter size was increased to FWHM = 48 pixels and 64 pixels, both circumferential and radial strain maps calculated using CSPAMM were adversely affected, as demonstrated by the large variations in strain values at certain radii along the circumference of the myocardium. In TruHARP, there was no significant change in the circumferential strain with the increase in filter size, which could be due to the presence of a constant strain profile in the circumferential direction. Radial strain is underestimated for filter FWHM = 32 pixels but increases in value with an increase in filter size, approaching its true value first at the midwall (marked by hollow arrows) for the filter FWHM = 48 pixels and then at the epicardium (marked by hollow = arrows) for the filter FWHM = 64 pixels. Radial strain remains underestimated at the endocardium for filter FWHM = 64 pixels due to the presence of a maximum amount of strain within the myocardium at endocardium and low and noisy strains outside the myocardium. As expected, the effect of noise was more pronounced at larger filter sizes, which is apparent from the increase in variation of the estimated radial and circumferential strains at certain radii along the circumference of myocardium.
The root mean square (RMS) error between the true and the estimated radial and circumferential strains over the myocardium was computed in multiple Monte Carlo simulations. Fifty Monte Carlo simulations were performed, beyond which there was no significant difference in the statistics (average and standard deviation) of the RMS error. The average RMS errors over the Monte Carlo simulations are shown in Fig. 3 for CSPAMM and TruHARP as a function of FWHM of the filter at CNR = 5 and 15. As the filter size increases, the RMS error first decreases (dotted arrows) then, beyond a certain filter size, the error increases at a higher rate for CSPAMM than for TruHARP (solid arrows). The FWHM corresponding to the minimum RMS error in circumferential and radial strains with TruHARP (~50 pixels is higher than that with CSPAMM (~32 pixels). Furthermore, for TruHARP the increase in error is smaller, and the range of filter FWHM is wider for which the error in strain is minimal, indicating a greater robustness to noise and interference than CSPAMM.
FIG. 3.
Average RMS error over the Monte Carlo simulation in estimated radial and circumferential strain estimated using TruHARP (gray curves) and CSPAMM (black curves) by varying the FWHM of the filter. The RMS error is shown for acquisition CNR of 5 (dashed curves) and 15 (solid curves) and tag spacing of 7 mm. Dotted arrows mark similar error for both CSPAMM and TruHARP at smaller filter sizes. Solid arrows mark increase in error due to spectral peak interference for CSPAMM compared to TruHARP at larger filter size. The filter FWHM is related to spatial resolution as given in Eq. 19.
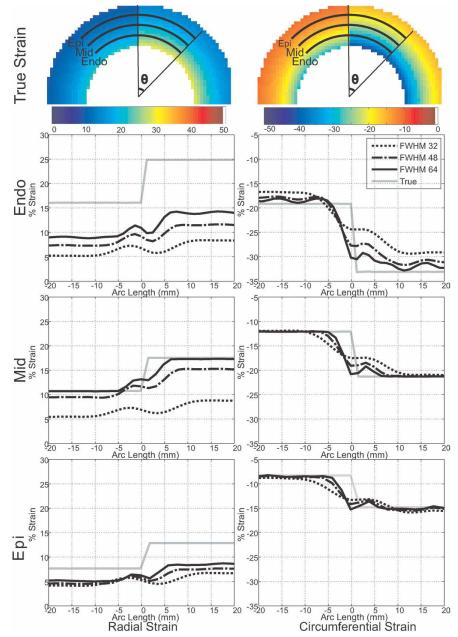
Results from the simulated infarction are shown in Fig. 4. True and estimated radial and circumferential strain profiles along the epicardium, midwall, and endocardium at the top interface of the annulus region are plotted for filter FWHM = 32, 48, and 64 pixels. In agreement with the Monte Carlo simulation, the calculated circumferential strain at filter FWHM = 32 pixels is only well estimated at locations away from the interface. Although the exact relationship between the filter FWHM and strain resolution is not straightforward due to the tensor nature of the strain and is rarely studied (34), the width of the transition between the two different circumferential strain levels decreases with the increase in filter size, indicating improvement in resolution. Radial strain is underestimated for small filter sizes and approaches its true value as the filter size is increased. Radial strain reaches its true value at the midwall, while it is still underestimated at endo- and epicardium for a filter FWHM = 64 pixels. Although underestimated, the width of transition of the radial strain from one strain level to another decreases with increase in filter size, which indicates an improvement in strain resolution.
FIG. 4.
Radial and circumferential strain along the three arcs (at the endocardium, midwall, and epicardium) over the myocardium, passing from infarct (left) to normal (right) myocardium.
In Vivo Single Breath-Hold Experiments
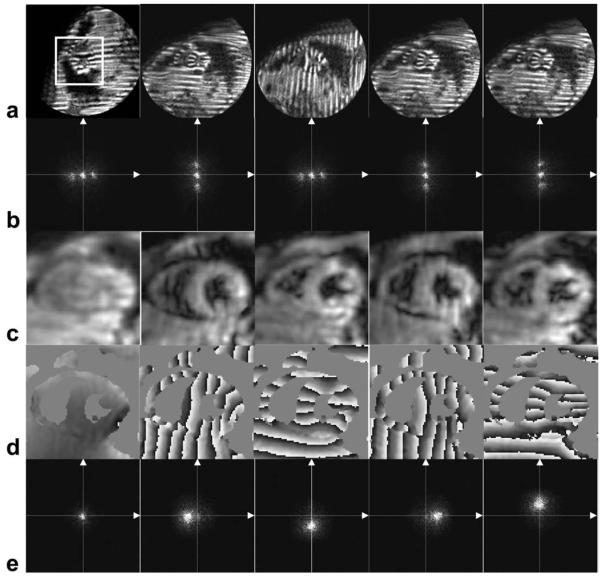
All six subjects were successfully scanned. CNR of 12 ± 2 was observed for TruHARP datasets when averaged over the myocardium at end-systolic time frame. Figure 5a and b shows the magnitudes and Fourier transforms, respectively, at an end-systolic time frame, of the five datasets acquired using TruHARP for one of the six human subjects. The Fourier transforms of these datasets have one DC and two spectral peaks due to the modified 1-1 SPAMM-generated sinusoidal tagging. The four harmonic peaks and DC peak were separated from these datasets using the TruHARP formulation. The magnitudes, phases, and Fourier transforms of the separated and filtered harmonic peaks and DC peak over the portion of image marked by white bounding box in Fig. 5a are shown in Fig. 5c, d, and e, respectively. A filter of FWHM of 64 pixels is used, which is less than the maximum filter size of 2rs = 72 pixels that can be used with the acquired images while avoiding artifacts due to asymmetric sampling of spectral peaks.
FIG. 5.
TruHARP-tagged dataset (a) and their Fourier transforms (b). c: Magnitude, (d) phase, and (e) spectrum of the DC and the four x and y displacement-encoded filtered (FWHM = 64 pixels) spectral peaks separated using the TruHARP formulation described in Eqs. 5–7 over the portion of image containing heart, marked by white bounding box in (a). Fourier spectra in (b) and (e) are accentuated by clipping the data at one fourth of the maximum value.
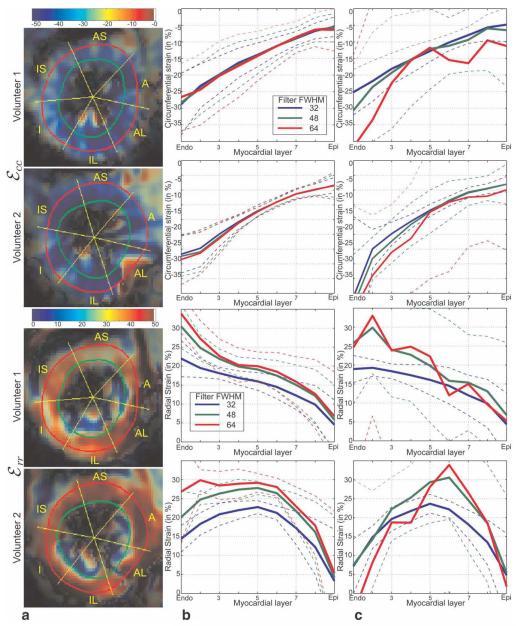
Figure 6a shows the circumferential and radial strains calculated using TruHARP for two subjects at end-systole using Kaiser-Bessel filter with FWHM = 64 pixels. The myocardium is divided into six sectors and each sector is divided into nine layers from endocardium to epicardium (as marked in Fig. 6a). Figure 6b and c shows the calculated circumferential and radial strains at end-systole averaged over the anteroseptal sector of myocardium with the filter FWHM = 32, 48, and 64 pixels, when calculated using TruHARP and CSPAMM, respectively. For TruHARP, the circumferential strain does not change with the increase in filter size, while radial strain first increases at all the layers and then converges at midwall and endocardium. With further increase in filter size, radial strain increases at the epicardium. For CSPAMM, the calculated circumferential and radial strains are similar to those of TruHARP at filter FWHM = 32 pixels; however, when the filter FWHM increases, the calculated strain gets distorted and yields physiologically impossible strain values due to the artifacts arising from interference from the conjugate spectral peak.
FIG. 6.
Estimated circumferential and radial strain for two subjects at an end-systolic time frame. a: Spatial profile of strain estimated using TruHARP for filter FWHM of 64. Transmural strain profile over anteroseptal (AS) segment in myocardium estimated using (b) TruHARP and (c) CSPAMM, when averaged over nine myocardial layers from endocardium to epicardium, for filter FWHM of 32, 48, and 64 pixels. The dashed line are plotted to show mean ± standard deviation levels for various strain values.
The P values from the two-sided Student t test for rejecting the null hypothesis that the strains calculated using TruHARP for filter FWHM = 32 pixels are similar to filter FWHM = 64 pixels are shown in Table 2. Since myocardium is subdivided into 18 segments and although these segments are not completely independent due to spatial smoothing, most aggressive Bonferroni correction was done and a P value of 0.00278 = 0.05/18) was used when establishing statistical significance with P value of 0.05. It is observed that 14 out of 18 segments have shown statistical significant difference, while only one sector (at the endocardium) has shown statistical significance for circumferential strain.
Table 2.
P Values for Two-Sided Student’s t test Comparing Radial and Circumferential Strain Obtained Using Filter FWHM = 64 Pixels Is Greater Than Filter FWHM = 32 Pixels Over Six Sectors and Three Layers in Myocardium*
| Sectors |
|||||||
|---|---|---|---|---|---|---|---|
| Strain | Myocardial layer | AS | A | AL | PL | P | PS |
| Err | Endo | <0.0001 | <0.0001 | 0.8785 | 0.0017 | 0.8532 | <0.0001 |
| Mid | 0.0002 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | |
| Epi | 0.0014 | 0.3122 | <0.0001 | <0.0001 | 0.0026 | 0.0161 | |
| Ecc | Endo | 0.5061 | 0.0216 | 0.1950 | 0.0021 | 0.0083 | 0.4259 |
| Mid | 0.0013 | 0.2443 | 0.9192 | 0.1225 | 0.1124 | 0.5421 | |
| Epi | 0.8389 | 0.8455 | 0.3177 | 0.3723 | 0.6896 | 0.5005 | |
Entries with a P value less than 0.0028 (= 0.05/18) are marked by shaded boxes.
DISCUSSION
TruHARP combines data from both horizontal and vertical motion-encoding directions for high-resolution artifact-suppressed myocardial motion and strain calculation using datasets comprising only five image sequences as compared to nine in CANSEL (19). Both TruHARP and CANSEL separate the spectral peaks by linear combination of the acquired image sequences; therefore, any imperfection in the data acquisition will lead to unwanted residual spectral peaks in the isolated peaks. The artifacts due to residual conjugate spectral peak will be similar to those observed in CSPAMM at larger filter sizes. To reduce the likelihood of such imperfections that readily arise due to misregistration in multiple breath-hold acquisitions (standard in CANSEL), a single 16-heartbeat breath-hold, TruHARP imaging protocol was implemented and tested using a clinical MR scanner.
The proposed TruHARP MR imaging protocol was shown to generate strain images free from artifacts arising due to the spectral peak interference at a 4.37 mm functional resolution in a single breath-hold MR scan. Standard DENSE-based techniques readily produce results at high functional resolution using stronger motion-encoding gradient or, equivalently, smaller tag spacing. However, this practice leads to a reduction in SNR (19). Through-plane dephasing (23) can also reduce the impact of unwanted harmonic peaks; however, the choice of through-plane dephasing gradient is critical as large gradient values may lead to signal nulling due to tissue strain in the slice-selection direction (16). As well, the benefits from peak combination (28) such as removal of the phase due to magnetic field inhomogeneity are not available as only one harmonic peak is imaged. Although both TruHARP and CANSEL can isolate spectral peaks from which displacement can be computed, TruHARP acquisition can be carried out more quickly (almost half the time) and the resulting datasets are less prone to misregistration errors.
The tag spacing of 7 mm, which is commonly used in MR tagging literature (35), is used in simulation and in vivo scans. Larger tag spacing will lead to a decrease in sensitivity of harmonic phase to motion (19,20). Although smaller tag spacing leads to an improvement in the results from CSPAMM due to greater peak separation, it also leads to an increase in intravoxel dephasing due to through-plane rotation (36) and a corresponding decrease in SNR. More important, since TruHARP directly separates the spectral peaks, the use of a smaller tag spacing does not reduce spectral peak interference for TruHARP; however, it does lead to an overall greater k-space occupation due to both motion modulation at high systolic strains and spectral peak separation. Longer spiral acquisitions are required to cover a greater amount of k-space within a single breath-hold, which leads to lower SNR and increased distortions due to off resonance and magnetic field inhomogeneity. On the other hand, use of multiple breath-holds leads to misregistration across multiple breath-holds, which significantly interfere with the ability of TruHARP to successfully cancel the peaks. A tag spacing of 7 mm was found to be the smallest tag spacing that could be reliably imaged in one breath-hold within the desired acquisition specifications.
The TruHARP MR imaging protocol acquires five datasets with only one dummy heartbeat in the beginning of first dataset. Given the RR-interval (~1000 ms) and T1 of the heart wall (~1100 ms) at 3 T, one might expect to observe artifacts arising from the residual tagged magnetization present in the previous heartbeat. However, we did not observe noticeable artifacts. This may be due to an additional decrease of the tagged longitudinal magnetization by the RF excitations with ramped flip-angle used for imaging.
Monte Carlo simulations were performed to study the effect of removal of interference from conjugate spectral peaks and noise in strain calculation at higher spatial resolution. A conventional tradeoff in error between noise and the partial-volume effect was observed with the increase in spatial resolution/filter size. At small filter size, the error is primarily due to the low-resolution/partial-volume effect, which decreases with the increase in filter size. However, beyond a certain filter size, the error increases due to noise (for both CSPAMM and TruHARP) and interference (for CSPAMM). The rate of increase in error due to interference is much higher than that due to noise, leading to larger filter size corresponding to minimum strain error for TruHARP than for CSPAMM. Furthermore, even larger filter sizes can be used with TruHARP, with minimal increase in error, which indicates the feasibility of higher resolution and robustness to error with the removal of interference. SNR analysis showed that the noise variance in TruHARP is comparable to that of SPAMM and CSPAMM.
Monte Carlo simulations revealed that radial strain is underestimated at a conventional HARP/DENSE filter size and increases to its true value as the spatial resolution of the filtered spectral peak increases. On the other hand, for the contraction of a healthy heart the calculated circumferential strain is accurate even for a small filter FWHM and does not improve further with the increase in filter FWHM. However, during infarction, delineation between normal and infarcted tissue using both radial and circumferential strains improves with the increase in spatial resolution. This suggests that the higher resolution provided by TruHARP in a single breath-hold data acquisition may have significant clinical relevance over conventional methods such as HARP and DENSE.
The findings from the simulations were consistent with the in vivo study involving six healthy adult human subjects. A significant increase in radial strain was observed in 14 out of 18 (six sectors in three myocardial layers) segments while only one out of 18 segments showed a significant decrease in the value of circumferential strain. Furthermore, similar artifacts due to the noise and the numerical limitations of strain tensor computation were present in strain maps generated for in vivo images. Although this experiment does not constitute independent confirmation of improvement against a gold standard measurement, it is consistent with the effects of poor resolution that were demonstrated in our Monte Carlo experiment.
The proposed TruHARP framework can be applied to DENSE when it is used with only in-plane displacement encodings (i.e., no through-plane dephasing gradient). This is because TruHARP framework combines the data acquired for both horizontal and vertical displacements to decrease the number of image sequence acquisition from nine in CANSEL to five. The mathematical conditions for this reduction will not hold when DENSE is used with any through-plane encoding or through-plane dephasing (23). It is not yet known how methods that encode through-plane displacements such as DENSE and SENC could take advantage of the TruHARP framework.
TruHARP can be extended to the zHARP framework (37) with an additional image sequence acquisition (i.e., six instead of five). The TruHARP framework acquires cosine, – cosine, and sine-tagged image sequences for horizontal displacement direction and cosine and sine-tagged image sequences for the vertical displacement direction. The T1 (DC) spectral peak estimated from the horizontal displacement direction is used to remove the T1 peak from the dataset of vertical displacement direction. In zHARP, this cannot be done as the T1 peak will have different z-encodings between the DC peaks of two displacement directions. However, if an additional image sequence, – cosine-tagged, is acquired in vertical direction, then the peaks can be isolated. This extension will yield three-dimensional displacement and three-dimensional surface strain over a single slice in a breath-hold of 16 heartbeats and can be extended to three-dimensional strain measurements using two or more acquired slices (38).
CONCLUSION
TruHARP, a single breath-hold MR tagging protocol and post-processing framework in which spectral peaks in tagged MR images are isolated and high-resolution motion and strain are computed, has been described. Similar to CANSEL, TruHARP permits motion and strain resolution that is limited by the resolution and SNR of the acquired images instead of being limited by the proximity of conjugate peaks or echoes. Moreover, with TruHARP, a two-dimensional strain resolution of 4.37 mm was demonstrated in vivo in a clinically feasible single 16-heartbeat long breath-hold acquisition, therefore avoiding any artifacts due to misregistration between multiple breath-holds. Simulations have shown that the removal of interference from other spectral peaks leads to higher resolution and more accurate strain maps. Simulations also showed that while the strain values are underestimated when computed using low-resolution harmonic peaks, they approach their true values when higher-resolution harmonic peaks are used for calculations. These findings were experimentally demonstrated, and statistical significance was established in six in vivo human studies.
ACKNOWLEDGMENTS
The authors acknowledge Dr. Bennett Landman for helpful comments regarding the data analysis and graphical presentation of results.
Grant sponsor: NIH/NHLBI; Grant number: R01HL47405.
REFERENCES
- 1.Wu KC, Lima JA. Noninvasive imaging of myocardial viability: current techniques and future developments. Circ Res. 2003;93:1146–1158. doi: 10.1161/01.RES.0000103863.40055.E8. [DOI] [PubMed] [Google Scholar]
- 2.Bax JJ, De Roos A, Van Der Wall EE. Assessment of myocardial viability by MRI. J Magn Reson Imaging. 1999;10:418–422. doi: 10.1002/(sici)1522-2586(199909)10:3<418::aid-jmri25>3.0.co;2-c. [DOI] [PubMed] [Google Scholar]
- 3.Fernandes VR, Polak JF, Edvardsen T, Carvalho B, Gomes A, Bluemke DA, Nasir K, O’Leary DH, Lima JA. Subclinical atherosclerosis and incipient regional myocardial dysfunction in asymptomatic individuals: the Multi-Ethnic Study of Atherosclerosis (MESA) J Am Coll Cardiol. 2006;47:2420–2428. doi: 10.1016/j.jacc.2005.12.075. [DOI] [PubMed] [Google Scholar]
- 4.Fernandes VRS, Polak JF, Cheng S, Rosen BD, Carvalho B, Nasir K, McClelland R, Hundley G, Pearson G, O’Leary DH, Bluemke DA, Lima JAC. Arterial stiffness is associated with regional ventricular systolic and diastolic dysfunction: the Multi-Ethnic Study of Atherosclerosis. Arterioscler Thromb Vasc Biol. 2008;28:194–201. doi: 10.1161/ATVBAHA.107.156950. [DOI] [PubMed] [Google Scholar]
- 5.Korosoglou G, Lossnitzer D, Schellberg D, Lewien A, Wochele A, Schaeufele T, Neizel M, Steen H, Giannitsis E, Katus H. Strainencoded cardiac MRI as an adjunct for dobutamine stress testing: incremental value to conventional wall motion analysis. Circulation. 2009;2:132. doi: 10.1161/CIRCIMAGING.108.790105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Amundsen BH, Helle-Valle T, Edvardsen T, Torp H, Crosby J, Lyseggen E, Stoylen A, Ihlen H, Lima JAC, Smiseth OA, Slordahl SA. Noninvasive myocardial strain measurement by speckle tracking echocardiography: validation against sonomicrometry and tagged magnetic resonance imaging. J Am Coll Cardiol. 2006;47:789–793. doi: 10.1016/j.jacc.2005.10.040. [DOI] [PubMed] [Google Scholar]
- 7.Stuber M, Scheidegger MB, Fischer SE, Nagel E, Steinemann F, Hess OM, Boesiger P. Alterations in the local myocardial motion pattern in patients suffering from pressure overload due to aortic stenosis. Circulation. 1999;100:361–368. doi: 10.1161/01.cir.100.4.361. [DOI] [PubMed] [Google Scholar]
- 8.Nagel E, Lehmkuhl HB, Bocksch W, Klein C, Vogel U, Frantz E, Ellmer A, Dreysse S, Fleck E. Noninvasive diagnosis of ischemiainduced wall motion abnormalities with the use of high-dose dobutamine stress MRI: comparison with dobutamine stress echocardiography. Circulation. 1999;99:763–770. doi: 10.1161/01.cir.99.6.763. [DOI] [PubMed] [Google Scholar]
- 9.Zerhouni EA, Parish DM, Rogers WJ, Yang A, Shapiro EP. Human heart: tagging with MR imaging—a method for noninvasive assessment of myocardial motion. Radiology. 1988;169:59–63. doi: 10.1148/radiology.169.1.3420283. [DOI] [PubMed] [Google Scholar]
- 10.Axel L, Dougherty L. MR imaging of motion with spatial modulation of magnetization. Radiology. 1989;171:841–845. doi: 10.1148/radiology.171.3.2717762. [DOI] [PubMed] [Google Scholar]
- 11.Osman NF, Kerwin WS, McVeigh ER, Prince JL. Cardiac motion tracking using CINE harmonic phase (HARP) magnetic resonance imaging. Magn Reson Med. 1999;42:1048–1060. doi: 10.1002/(sici)1522-2594(199912)42:6<1048::aid-mrm9>3.0.co;2-m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Osman NF, McVeigh ER, Prince JL. Imaging heart motion using harmonic phase MRI. IEEE Trans Med Imaging. 2000;19:186–202. doi: 10.1109/42.845177. [DOI] [PubMed] [Google Scholar]
- 13.Aletras AH, Balaban RS, Wen H. High-resolution strain analysis of the human heart with fast-DENSE. J Magn Reson. 1999;140:41–57. doi: 10.1006/jmre.1999.1821. [DOI] [PubMed] [Google Scholar]
- 14.Aletras AH, Ding S, Balaban RS, Wen H. DENSE: displacement encoding with stimulated echoes in cardiac functional MRI. J Magn Reson. 1999;137:247–252. doi: 10.1006/jmre.1998.1676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.McVeigh E. Measuring mechanical function in the failing heart. J Electrocardiol. 2006;39(4 suppl):S24–27. doi: 10.1016/j.jelectrocard.2006.05.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Osman NF, Sampath S, Atalar E, Prince JL. Imaging longitudinal cardiac strain on short-axis images using strain-encoded MRI. Magn Reson Med. 2001;46:324–334. doi: 10.1002/mrm.1195. [DOI] [PubMed] [Google Scholar]
- 17.Sampath S, Osman NF, Prince JL. A combined harmonic phase and strain-encoded pulse sequence for measuring three-dimensional strain. Magn Reson Imaging. 2009;27:55–61. doi: 10.1016/j.mri.2008.05.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pelc NJ, Herfkens RJ, Shimakawa A, Enzmann DR. Phase contrast cine magnetic resonance imaging. Magn Reson Q. 1991;7:229–254. [PubMed] [Google Scholar]
- 19.Epstein FH, Gilson WD. Displacement-encoded cardiac MRI using cosine and sine modulation to eliminate (CANSEL) artifact-generating echoes. Magn Reson Med. 2004;52:774–781. doi: 10.1002/mrm.20232. [DOI] [PubMed] [Google Scholar]
- 20.Kuijer JP, Hofman MB, Zwanenburg JJ, Marcus JT, van Rossum AC, Heethaar RM. DENSE and HARP: two views on the same technique of phase-based strain imaging. J Magn Reson Imaging. 2006;24:1432–1438. doi: 10.1002/jmri.20749. [DOI] [PubMed] [Google Scholar]
- 21.Aletras AH, Wen H. Mixed echo train acquisition displacement encoding with stimulated echoes: an optimized DENSE method for in vivo functional imaging of the human heart. Magn Reson Med. 2001;46:523–534. doi: 10.1002/mrm.1223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Aletras AH, Arai AE. Meta-DENSE complex acquisition for reduced intravoxel dephasing. J Magn Reson. 2004;169:246–249. doi: 10.1016/j.jmr.2004.05.008. [DOI] [PubMed] [Google Scholar]
- 23.Zhong X, Spottiswoode BS, Cowart EA, Gilson WD, Epstein FH. Selective suppression of artifact-generating echoes in cine DENSE using through-plane dephasing. Magn Reson Med. 2006;56:1126–1131. doi: 10.1002/mrm.21058. [DOI] [PubMed] [Google Scholar]
- 24.Fischer SE, McKinnon GC, Maier SE, Boesiger P. Improved myocardial tagging contrast. Magn Reson Med. 1993;30:191–200. doi: 10.1002/mrm.1910300207. [DOI] [PubMed] [Google Scholar]
- 25.Kim D, Gilson WD, Kramer CM, Epstein FH. Myocardial tissue tracking with two-dimensional cine displacement-encoded MR imaging: development and initial evaluation. Radiology. 2004;230:862–871. doi: 10.1148/radiol.2303021213. [DOI] [PubMed] [Google Scholar]
- 26.Abd-Elmoniem KZ, Stuber M, Osman NF, Prince JL. ZHARP: three-dimensional motion tracking from a single image plane. Inf Process Med Imaging. 2005;19:639–651. doi: 10.1007/11505730_53. [DOI] [PubMed] [Google Scholar]
- 27.Kuijer JP, Jansen E, Marcus JT, van Rossum AC, Heethaar RM. Improved harmonic phase myocardial strain maps. Magn Reson Med. 2001;46:993–999. doi: 10.1002/mrm.1286. [DOI] [PubMed] [Google Scholar]
- 28.Ryf S, Tsao J, Schwitter J, Stuessi A, Boesiger P. Peak-combination HARP: a method to correct for phase errors in HARP. J Magn Reson Imaging. 2004;20:874–880. doi: 10.1002/jmri.20186. [DOI] [PubMed] [Google Scholar]
- 29.Abd-Elmoniem KZ, JL P. QuickCANSEL: reduced scan time CANSEL to eliminate artifact-generating echoes in cardiac MRI. Proceedings of the 13th Annual Meeting of ISMRM; Miami Beach, Florida. 2005. p. 1648. [Google Scholar]
- 30.Ryf S, Kissinger KV, Spiegel MA, Bornert P, Manning WJ, Boesiger P, Stuber M. Spiral MR myocardial tagging. Magn Reson Med. 2004;51:237–242. doi: 10.1002/mrm.10688. [DOI] [PubMed] [Google Scholar]
- 31.Harris FJ. Use of windows for harmonic-analysis with discrete Fourier-transform. Proc IEEE. 1978;66:51–83. [Google Scholar]
- 32.Meyer CH, Pauly JM, Macovski A, Nishimura DG. Simultaneous spatial and spectral selective excitation. Magn Reson Med. 1990;15:287–304. doi: 10.1002/mrm.1910150211. [DOI] [PubMed] [Google Scholar]
- 33.Neter J, Wasserman W, Kutner M. Applied linear statistical models. Richard D. Irwin. Inc; Homewood, IL: 1974. p. 842. [Google Scholar]
- 34.Parthasarathy V, Prince J. Strain resolution from HARP-MRI. Proceedings of the 12th Annual Meeting of ISMRM; Kyoto, Japan. 2004. p. 1797. [Google Scholar]
- 35.Atalar E, McVeigh ER. Optimization of tag thickness for measuring position with magnetic resonance imaging. IEEE Trans Med Imaging. 1994;13:152–160. doi: 10.1109/42.276154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Stuber M, Fischer SE, Scheidegger MB, Boesiger P. Toward high-resolution myocardial tagging. Magn Reson Med. 1999;41:639–643. doi: 10.1002/(sici)1522-2594(199903)41:3<639::aid-mrm31>3.0.co;2-4. [DOI] [PubMed] [Google Scholar]
- 37.Abd-Elmoniem KZ, Osman NF, Prince JL, Stuber M. Three-dimensional magnetic resonance myocardial motion tracking from a single image plane. Magn Reson Med. 2007;58:92–102. doi: 10.1002/mrm.21267. [DOI] [PubMed] [Google Scholar]
- 38.Abd-Elmoniem KZ, Stuber M, Prince JL. Direct three-dimensional myocardial strain tensor quantification and tracking using zHARP. Med Image Anal. 2008;12:778–786. doi: 10.1016/j.media.2008.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]