Dynamic Origin of the Stereoselectivity of a Nucleophilic Substitution Reaction

Abstract

A nucleophilic substitution on a dichlorovinyl ketone was studied experimentally and computationally. A mixture of products is observed experimentally, but a conventional computational analysis does not account for the formation of the minor stereoisomer. Instead, the product mixture is predicted accurately from a dynamic trajectory study on a bifurcating energy surface. The dynamic origin of the stereoselectivity of the reaction is discussed.

Many forms of nucleophilic substitution reactions are intrinsically stereospecific, in that their products are defined in their mechanisms by the stereochemistry of the starting materials. Others are stereoselective, in that their product stereochemistry is defined by the choice among pathways leading to stereoisomeric products. The normal implicit assumption in the latter case is that any kinetic stereoselectivity is understandable from transition state theory (TST) and is determined by the free energies of competitive transition states (TSs) leading to the products. Theoretical studies have long recognized that this assumption need not be correct on complex energy surfaces,^1,2 and our work has focused on the experimental evidence for such energy surfaces in ordinary organic reactions and their experimental consequences.^3,4,5,6,7,8 We describe here an experimental, standard computational, and dynamic trajectory study of a nucleophilic substitution at an sp² carbon in which the stereoselectivity is not decided by TS energies, but rather is decided dynamically on the downhill slope of a “bifurcating energy surface.”⁴

The conventional mechanism for nucleophilic substitution at sp² carbons involves a stepwise addition-elimination process proceeding through a tetrahedral intermediate. ⁹ In some reactions, however, experimental and computational studies have supported concerted substitutions, particularly when the reaction involves good leaving groups. Williams showed that nucleophilic substitution reactions at acyl carbons can occur via a concerted mechanism,¹⁰ and a series of experimental studies by Castro and Santos have shown that a variety of acyl substitutions can occur in a concerted fashion.^11,12,13 A theoretical basis for concerted mechanisms was established by Guthrie using multidimensional Marcus theory, and he particularly defined structural conditions under which substitutions are likely to be concerted.¹⁴ Schlegel and Bach studied nucleophilic substitutions on vinylic chlorides in the gas phase and established the viability of a concerted mechanism, though they suggested that the presence of electron-withdrawing groups could favor a stepwise process.¹⁵ Indeed, with activation by multiple electron-withdrawing groups, there has long been strong evidence for intermediates in vinylic substitutions. ^16,9

We considered that the concerted mechanism could lead to an intriguing phenomenon in the nucleophilic substitution reactions of electrophiles containing two leaving groups, such as carbonates or vinylic dihalides. When there are two leaving groups in a stepwise mechanism, the selectivity between leaving groups is decided by the relative energies of the competing TSs for loss of the leaving groups. For a concerted process, however, it seemed possible that the reaction could involve only a single TS that is passed through before the structural “decision” has been made as to which of the two leaving groups will be lost. In such a circumstance, the selectivity between leaving groups, and the product selectivity, could be decided by dynamic effects on the slope of the potential energy surface beyond the TS.

To explore this possibility, nucleophilic substitution on the 4,4-dichloro-3-buten-2-one¹⁷ (1) was chosen for study. In 1, the good chloride leaving groups should promote a concerted mechanism, based on the ideas of Guthrie. In addition, reactions of 1 exhibit a stereoselectivity that is readily observable. The particular reaction of 1 with sodium p-tolylthiolate is convenient, occurring rapidly and cleanly in dry ethanol at 25 °C.¹⁸

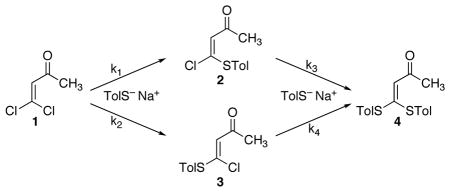
The determination of the stereoselectivity in this reaction was complicated by the susceptibility of the initial products 2 and 3 to further reactions affording the disubstituted product 4. Due to the rapidity of the reaction, the complete kinetic modeling of the reaction including the absolute rate constants was not feasible. However, we were able to determine the kinetic selectivity between 2 and 3 as well as the relative rates of their conversion to 4 by analyzing the product mixture versus conversion on adding successive aliquots of sodium p-tolylthiolate. The relative amounts of 1-4 were obtained at a series of conversions by the ¹H-NMR analysis of worked-up aliquots, based on the integrations of the vinylic peak for each compound, located in d₆-benzene at δ 6.24, 6.37, 5.87, and 5.63 for 1, 2, 3, and 4, respectively. The ratio of 2 to 3 changed little, less than the scatter of repeat measurements, in mixtures obtained from reactions using 0.2 to 1.4 equivalents of thiolate, interestingly suggesting that 2 and 3 are equally reactive (k₃ ≈ k₄, within 20%). Allowing for the scatter in the measurements and extrapolating to zero conversion, the ratio of k₁ to k₂ was 4.2 ± 0.3. This preference for formation of 2 over 3 in an 81 (±1.5) : 19 ratio is consistent with previous observations of nucleophilic substitution reactions of 1 and related compounds.^18,19,20,21

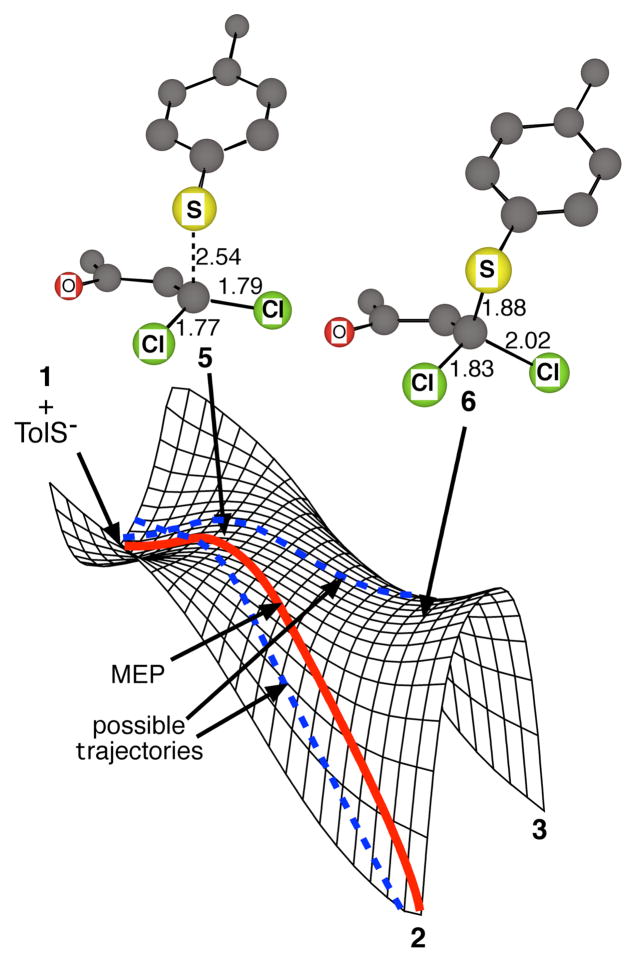
The unusual observation here is that 3 is formed at all, as a conventional computational study does not account for its formation. The reaction of 1 with p-tolylthiolate anion was studied systematically in B3LYP/6-31+G**/PCM(ethanol) and M06-2X/6-31+G**/PCM(ethanol) calculations. For each DFT method, a series of six TSs were located for the nucleophilic addition process, arising from a combination of s-cis and s-trans conformations of the enone and three different modes of approach of the p-tolylthiolate. Structure 5 was the lowest-energy TS with each method; the higher-energy structures are given in the Supporting Information. The preference for 5 was 0.9 kcal/mol in the B3LYP calculations including zero-point energy.

Three features of the calculational results were striking. The first is that no intermediates could be located. There is some question whether a PCM solvent model would be satisfactory for locating intermediates in reactions of this type, but the concerted process would also fit with the general expectations of these reactions as outlined by Guthrie due to the high nucleofugality of the chlorides. Exploration of a simplified model reaction in CCSD(T)/6-31+G**/PCM calculations also supports the absence of an intermediate (see the Supporting Information). The second feature is that at TS 5, no clear structural decision has been made regarding which chloride will be displaced. The bond lengths of the two C-Cl bonds in 5 are nearly equal, differing by less than 0.02 Å. The third and most striking feature is that only TSs leading to 2 were locatable. Despite extensive effort, no substitution TS leading by intrinsic reaction coordinate (IRC) analysis to 3 could be found in any of the calculations with either DFT method.

For each of the six possible 1/p-tolylthiolate orientations, the energy surfaces include a second saddle point in which the carbon-sulfur bond has fully formed. IRC analyses indicated that these structures were formally TSs for the interconversion of 2 and 3 by a process of chloride addition/conformational rotation/loss of chloride passing over a single potential energy barrier. The ‘rotational TS’ 6 corresponding to 5 is shown in Figure 1; the others are given in the Supporting Information.

Figure 1.

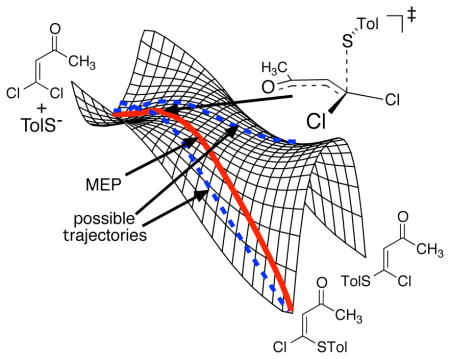
Qualitative energy surface for the reaction of 1 with sodium p-tolylthiolate.

These results are characteristic of an energy surface for the nucleophilic substitution reaction that resembles that shown in Figure 1. On this ‘bifurcating energy surface,’^5,6 the steepest-descent path passing through 5 leads only to 2, but trajectories passing through 5 could afford either 2 or 3. The adjacent TS 6 serves to define the “monkey-saddle” shape of the surface, but it is not involved in the reaction in a normal way in that trajectories approach it from higher energies.

Is this picture correct? The reliability of any simple calculational model, by itself, for a polar reaction in solution is intrinsically questionable. We sought to gauge the accuracy of the calculated surface by seeing if it could account for the experimental selectivity. For ordinary kinetic selectivity arising from two separate TSs leading to separate products, TST could be used to predict the selectivity for comparison with experiment. On bifurcating energy surfaces, it is usually, though not always,^7,22 necessary to employ trajectory calculations to predict the selectivity. Trajectory studies have been impressively successful at predicting product ratios,^{3b,4,5,6,7,8,23} but of course such success would be unlikely if the energy surface were qualitatively incorrect.

Toward that end, quasiclassical direct-dynamics trajectories²⁴ on a B3LYP/6-31+G**/PCM(ethanol) energy surface were initiated from the area of 5. Each normal mode of the TS was given its zero point energy plus a Boltzmann sampling of additional energy appropriate for 298.15 K, with a random phase and sign for its initial velocity. The mode associated with the imaginary frequency was given a Boltzmann sampling of energy “forward” over the col. A Verlet algorithm was employed to propagate the trajectories and 1-fs steps were taken until one of the products were formed or the starting materials were reformed. The median time for formation of products 2 and 3 was found to be 135 and 152 fs respectively. This is a short time that fits with the absence of an intermediate. TS recrossing was not a significant factor in this system, as only 12 out of 197 trajectories reformed the starting materials.

Of the 185 trajectories that formed products, 156 afforded 2 and 29 afforded 3. Within a 95% confidence range, the percentage of 2 in the mixture based on these trajectories would be 84 ± 5, which is in striking agreement with the experimental 81:19 ratio of products. This agreement supports the approximate accuracy of the bifurcating energy surface and role of dynamics in deciding the stereoselectivity.

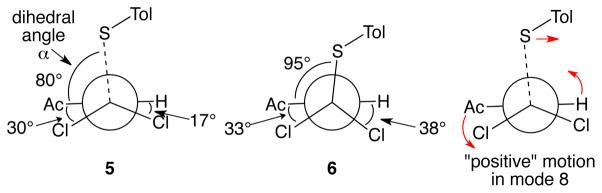
What is the origin of the selectivity for 2 over 3? Our results with Diels-Alder reactions of cyclopentadienones supported the importance of the shape of the potential energy surface as a control element for selectivity on bifurcating energy surfaces.⁶ However, later work with other Diels-Alder reactions and with [2 + 2] cycloadditions of ketenes has found that the choice of product is often controlled by the continuation of motion along a particular TS normal mode.^4,7,8 Such control by momentum through the TS is a form of “dynamic matching.” The two types of control elements are not mutually exclusive; the shape of the potential energy surface can control the overall odds of getting one product versus the other, while the motion in a mode at the TS controls what happens in a particular trajectory. In the current case, we expected that the selectivity for 2 versus 3 could be understood by simply considering the shape of the energy surface. In TS 5, the approach of the thiolate occurs at a dihedral angle versus the carbonyl carbon of the acyl group (dihedral angle “α”, Figure 2) that is acute (80°) versus the acyl group, while α in 6 is obtuse (95°). The acute angle in 5 may be viewed as resulting from a twisting that minimizes a Cl/acyl group repulsion in favor of a lesser Cl/H repulsion. TS 6 is the minimum-energy point on an energetic dividing line between 2 and 3, and continuation of C—S bond formation from 5 leads to a geometry that is on the “2-side” of 6. This general idea explains the preferred formation of 2. Our initial hypothesis was that product 3 would be formed only when the motion of the p-tolylthiolate in 5 quickly increases the α to greater than 95°.

Figure 2.

Relevant dihedral angles in 5 and 6, and motion associated with “mode 8” of 5.

Examination of the trajectories does not support such a simple picture. Starting from 5, it takes 50–100 fs (71 fs on average) for the C—S bond to form fully, defined by a C—S distance of less than 1.9 Å. At the point where the C—S distance passes 1.9 Å, 19 of the 29 trajectories leading to 3 have α’s less than 95° and seven have α’s less than 80°. Over 60% (98 out of 156) of the trajectories leading to 2 have α’s greater than 80° at this point. Neither α nor any other discernible geometrical parameter in the structures along the first 100 fs of the trajectories reliably predicts which product will be formed.

However, the direction of the motion through the TS is highly predictive. In particular, a low-energy (96 cm⁻¹) vibrational mode, (called here “mode 8” because it is the eighth lowest in energy) is a dominant controlling factor in deciding whether a trajectory may afford 3. Mode 8 is essentially a torsional mode that is twisting about the breaking carbon-carbon double bond. When the trajectories have an initial positive sign for the mode-8 velocity (defining positive as in Figure 2), then 29 out of 93 trajectories afford 3. When the mode-8 velocity is negative, however, 0 out of 92 trajectories afford 3. Mode 8 is equally likely to have a positive versus negative sign, and the overall selectivity results from a 50:50 mixture of the two. Despite the chaotic appearance of the trajectories in the first 100 fs after 5, the dynamic matching effect of the mode-8 motion imposes a hidden order on the system that completely predetermines whether a trajectory has the possibility of forming 3.

Recent work by Truhlar and coworkers has proposed an alternative model for understanding selectivity that occurs after dynamical bottlenecks as in the current reaction.²⁵ In the “canonical competitive nonstatistical model” (CCNM), the branching between products is divided into “indirect” and “direct” components, the former being predicted from TST and the later predicted from phase space theory. The absence of an intermediate leads the CCNM model to allocate 100% of the reaction to the indirect component, which is dominated by the stability of the initially formed conformers of the products. However, the initial conformer of 3 is 4.1 kcal/mol more stable than that for 2. The CCNM model thus predicts that 3 would be strongly favored and fails qualitatively in this case.

The consideration above of the shape of the energy surface and the motions along it in deciding the product mixture is intriguing because it is so foreign to the normal analyses of selectivity. TST is the underlying paradigm within which chemists understand selectivity, and it would normally be assumed, albeit implicitly, that TS energies were governing the stereoselectivity of a nucleophilic substitution. TST greatly simplifies the understanding of reactions, as it lets one ignore the actual motions of atoms and considers only the energies of single structures, but we are finding that TST is often inapplicable in ordinary organic reactions in solution. The example here adds to the growing list of classes of reactions that are most easily understood by consideration of dynamic effects.