Highlights
► Focal thinning of cortical bone in the proximal femur predisposes a hip to fracture. ► Thinning is difficult to detect in CT since the cortex may be narrower than the PSF. ► We present a model-fitting technique to estimate cortical thickness, density and mass. ► Evaluation on cadaveric femurs confirms accurate measurement of mass and peak density. ► Thickness errors do not exceed 20% and are confined to regions of thin cortex.
Keywords: Cortical bone, Osteoporosis, Hip fracture
Abstract
There is growing evidence that focal thinning of cortical bone in the proximal femur may predispose a hip to fracture. Detecting such defects in clinical CT is challenging, since cortices may be significantly thinner than the imaging system’s point spread function. We recently proposed a model-fitting technique to measure sub-millimetre cortices, an ill-posed problem which was regularized by assuming a specific, fixed value for the cortical density. In this paper, we develop the work further by proposing and evaluating a more rigorous method for estimating the constant cortical density, and extend the paradigm to encompass the mapping of cortical mass (mineral mg/cm2) in addition to thickness. Density, thickness and mass estimates are evaluated on sixteen cadaveric femurs, with high resolution measurements from a micro-CT scanner providing the gold standard. The results demonstrate robust, accurate measurement of peak cortical density and cortical mass. Cortical thickness errors are confined to regions of thin cortex and are bounded by the extent to which the local density deviates from the peak, averaging 20% for 0.5 mm cortex.
1. Introduction
Hip fractures are the most common cause for acute orthopaedic hospital admission in older people (Parker and Johansen, 2006), with their annual incidence projected to rise worldwide from 1.7 million in 1990 to 6.3 million in 2050 (Sambrook and Cooper, 2006). Bone mineral density (BMD) is currently the imaging biomarker of choice for assessing an individual’s fracture risk, but although it is specific (Johnell et al., 2005; Kanis et al., 2008) it lacks sensitivity (Kanis et al., 2008; Kaptoge et al., 2008; Sanders et al., 2006), missing the majority who go on to fracture. There is now growing evidence that focal, structural weaknesses may predispose a hip to fracture (Mayhew et al., 2005; Poole et al., 2010; de Bakker et al., 2009) and there is a consequent need to develop novel imaging methods capable of detecting such weaknesses, with multi-detector computed tomography (MDCT) the favoured modality (Bouxsein and Delmas, 2008).
While trabecular bone undoubtedly plays some role, it is the distribution of cortical bone that is believed to be critical in determining a femur’s resistance to fracture (Holzer et al., 2009; Verhulp et al., 2008). Compressive cracking of the cortex in the femoral neck or trochanter is often the first point of failure (de Bakker et al., 2009; Carpenter et al., 2005; Mayhew et al., 2005). Unfortunately, thin laminar structures such as the femoral cortex are not accurately depicted in clinical CT because of the images’ limited spatial resolution. Consequently, straightforward thickness estimation techniques, such as those based on thresholding (Buie et al., 2007; Hangartner, 2007) or some measure of full-width half-maximum (Prevrhal et al., 1999, 2003), are unreliable when the cortex is thin in relation to the imaging resolution. With normal bore, clinical CT scanners, such methods are increasingly inaccurate below around 2.5 mm (Dougherty and Newman, 1999; Hangartner and Gilsanz, 1996), with errors exceeding 100% for sub-millimetre cortices (Prevrhal et al., 2003).
We have recently proposed a more sophisticated technique that produces good estimates of cortical thickness down to 0.3 mm (Treece et al., 2010). In common with other attempts at deblurring medical images of laminar structures (Streekstra et al., 2007), we adopt restrictive models of both the object being scanned and the imaging system, and then attempt to fit these models to the observed data. This process is inevitably ill-posed, since a dense, thin, blurred cortex might appear identical to a less dense, less thin, blurred cortex. It is therefore necessary to incorporate some prior knowledge, and we found in Treece et al. (2010) that assuming a specific, fixed value for the density was more successful than assuming a constant blur. We subsequently applied this technique to show precisely, where in the proximal femur new bone is laid down following 2 years’ treatment with bone anabolic drugs (Poole et al., 2011).
1.1. Estimating cortical thickness in blurred data
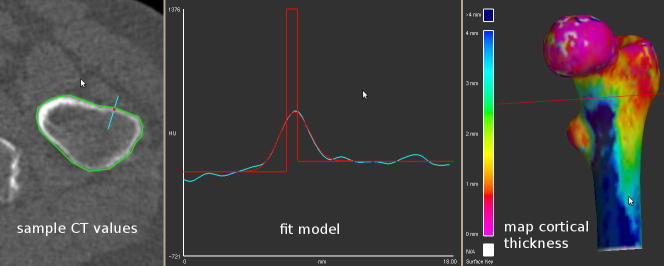
Cortical thickness is hard to define precisely, but we take as our gold standard the full-width half-maximum thickness that would be measured in a high resolution, unblurred CT scan, were such a scan possible. The aim here is to provide thickness estimates from a typical, blurred, low resolution clinical CT scan which are comparable with the idealized gold standard. Fig. 1 illustrates how this is currently achieved using the technique described in Treece et al. (2010) and implemented in our free-to-download Stradwin software.1 We here give a brief summary of the technique in order to provide the necessary theoretical background for the remainder of this paper.
Fig. 1.
Cortical thickness estimation from clinical CT data. Given a prior segmentation of the proximal femur (green contour, top left), CT values are examined along short lines (cyan, top left) that straddle the cortex and are perpendicular to it. The sampled CT values are shown in cyan in the bottom panel. Cortical thickness is estimated by assuming, in this example, a constant cortical density of 1611 HU. The Levenberg–Marquardt algorithm (More, 1977) is then used to find the imaging blur σ, tissue density , trabecular density and thickness tcd that best explain the data. The solution, and the idealised data yblur that it implies, are shown in red in the lower panel. By repeating this process at a large number of points, the cortical thickness can be mapped across the entire surface (top right).
Given a prior segmentation of the proximal femur, the CT data is sampled along short lines perpendicular to the femoral surface, at a large number of points on the surface. The lower panel in Fig. 1 shows the data from one such point (cyan), along with the model that best explains the data (red). In this model, the underlying density distribution y(x, t) along the line is assumed to be
| (1) |
where y0, y1 and y2 are the CT values in the surrounding tissue, cortex and trabecular bone respectively, H is the unit step function, t is the cortical thickness and x is measured from the centre of the cortex. The impulse response g(x) of the imaging system (image blur) is taken to be Gaussian with standard deviation σ
| (2) |
and hence the step response h(x) of the imaging system is
| (3) |
Combining Eqs. (3) and (1) gives the blurred cortex yblur(x, t) as
| (4) |
All that remains is to find the model parameters that minimize the sum of squared errors between yblur and the actual CT data. As mentioned previously, this is an ill-posed problem that requires regularization, and we have achieved good results by adopting a fixed value for the cortical density2 (Treece et al., 2010). The underlying assumption is that y1 does not vary significantly at different points on the proximal femur, at least in comparison with the much larger variation in cortical thickness. In all our work to date, we have estimated from regions of thick cortex, typically below the lesser trochanter on the femoral shaft, where the apparent peak density is not affected by the imaging blur.
1.2. Original contribution
There are three specific contributions. First, we develop and assess a more rigorous method for estimating using all the available data, not just a single measurement at a region of thick cortex. Unlike the original approach, the new technique furnishes 95% confidence intervals for , so unreliable data can be identified as such and excluded from further consideration.
Secondly, given that underestimating results in overestimating thickness t, we investigate whether we can measure cortical mass per unit area more accurately than thickness alone. A mass estimate of this nature is essentially the product of and t, though we additionally need to convert image density (HU) to mineral density (mg/cm3) using the calibration phantom included in every quantitative CT examination (Cann, 1988). Although the resulting measure has units mg/cm2, we shall refer to it loosely as “mass” in the remainder of this paper. (Dougherty and Newman, 1999) speak of cortical mass as a potentially useful indicator of regional bone strength.
Finally, we test the validity of the constant density assumption by measuring true density in high resolution (i.e. very low blur) CT scans of cadaveric femurs. While we have previously shown that cortical thickness estimates are relatively insensitive to the value of (Treece et al., 2010), it is nevertheless informative to examine how y1 varies with location on the proximal femur, and by how much.
1.3. Organization of the paper
The paper is organized as follows. In Section 2, we develop the theory that underpins the new density estimation method. In so doing, we discover an alternative technique for thickness estimation, and show how both variants may be trivially extended to measure cortical mass in addition to thickness. The methods are evaluated in Section 3 with the aid of sixteen cadaveric femurs which were imaged in a high resolution, peripheral quantitative CT (pQCT) system to establish ground truth thickness and mass. Section 3 also includes some simulations to confirm the causes of the subtle effects observed in the cadaveric studies, and we reprise a clinical case study to show the impact of these advances in practice. In Section 4, we discuss the relative merits of mass and thickness estimation, and how best to estimate density given the original and improved methods that we now have at our disposal. Finally, we draw some conclusions in Section 5.
2. Method
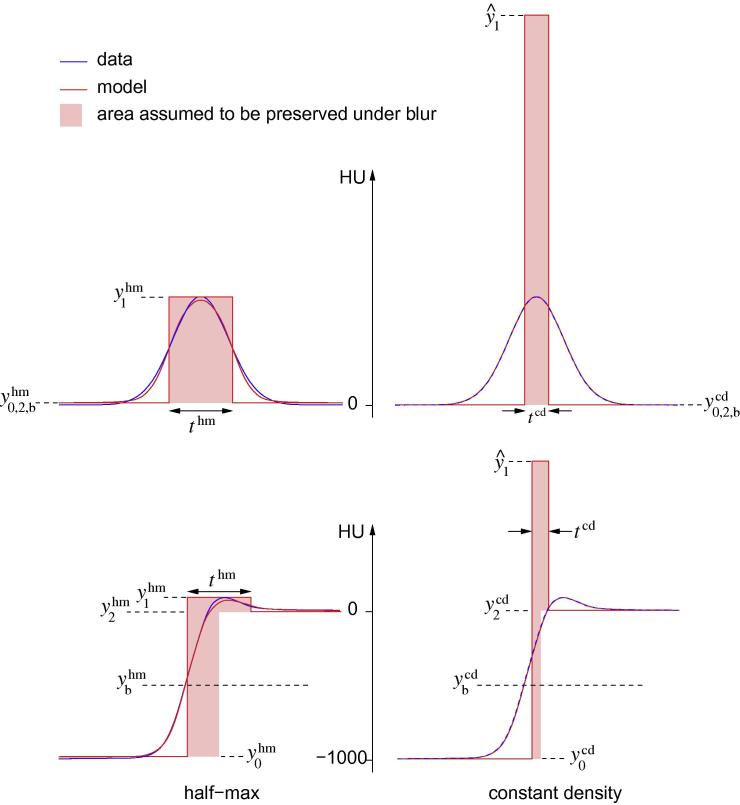
In the mathematical notation adopted throughout this paper, superscripts denote the estimation technique. Thus, tcd is the cortical thickness estimate obtained using the constant density technique, and is the corresponding mass estimate. As Fig. 2(right) shows, the fitted model also produces estimates of the tissue density , the trabecular density , and the average background density . For comparison, we also consider the full-width half-maximum measure of cortical thickness (Prevrhal et al., 1999, 2003), which we shall henceforth abbreviate to the “half-max” method.3 This estimates the thickness by looking at the half-way points between the apparent peak density and each of the background densities and . In practice, we estimate these parameters by optimizing a model fit, in exactly the same way as for constant density, except we fix y1 at the apparent peak density instead of : see Fig. 2(left).
Fig. 2.
The constant density and half-max estimation techniques. The upper two sub-figures illustrate the simple case, where y0 = y2, with a thin, dense cortex (red rectangle, top right) that appears less thin and less dense under image blur (blue). The constant density technique starts with an estimate of the true cortical density, and then finds the other model parameters that minimize the sum of squared errors between the data (blue) and yblur (red curve). Details of the optimization process can be found in Treece et al. (2010). In this case the fit is perfect, since the simulated data is a pure Gaussian, but see Fig. 1 for typical clinical data. The half-max technique uses a similar optimization process, except the true cortical density is assumed to be , the apparent peak density. The edges of the fitted cortex then coincide with the half-way points between and . The shaded areas are equivalent to the areas under the red Gaussians and are therefore approximately equal: the half-max area is actually around 6% smaller because the incorrect model does not precisely explain the data. This mass preservation property lies behind the hybrid constant density/half-max approach. When y0 < y2 (lower two sub-figures), the apparent density peak lies some distance to the right of the actual cortex. While the half-max model still fits well to produce the (incorrect) thm estimate, the red areas are no longer equivalent since the half-max area is predicated on a y0-y2 transition at the wrong location. This leads to significant overestimation of mass and thickness in the hybrid approach, by approximately 60% in this case. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
2.1. Cortical thickness through mass preservation
The half-max method is known to produce highly inaccurate thickness estimates when the cortex is thin, since even the narrowest density spike is blurred to the extent of g(x). For the straightforward case, where y0 = y2, it is trivial to deduce that thm → 2.35σ in the limit of small t. However, as previous studies have observed (Dougherty and Newman, 1999), the apparent extra mass of the cortex over and above the background is preserved under blur, and we might seek to exploit this property to improve the half-max estimate. For the simple case, where the background is constant, so y0 = y2 = yb (Fig. 2(top)), mass preservation implies
| (5) |
Given , and making the reasonable assumption that , we can therefore adjust the half-max thickness estimate and also obtain a mass estimate, resulting in a hybrid constant density/half max technique:
| (6) |
| (7) |
The situation is not so straightforward when y0 < y2. Applying Eq. (5) in this case is equivalent to preserving the areas shaded red in Fig. 2(bottom), but the half-max area is predicated on the cortex being centred at the apparent density peak, whereas the cortex is actually located a little to the left of this, as in Fig. 2(bottom right). By shifting the y0–y2 step in the half-max area to the left, we would obtain an area that is indeed preserved under blur, but we have no way of knowing the required correction a priori, since it depends on the true cortical thickness t. Eqs. (6) and (7) therefore represent a best guess, though they clearly overestimate mass and thickness in situations like Fig. 2(bottom).
2.2. Estimating cortical density in blurred data
The constant density and hybrid techniques require an estimate of the true cortical density y1. Our early approach was to sample the peak density at a region of thick cortex, but considering all the blurred data, and not just a single datum, should increase the accuracy and precision of the estimate. According to the model in Eq. (4), and noting that erf (x) = −erf (−x), the apparent density at the centre of the cortex is given by
| (8) |
Eq. (8) describes the expected distribution of apparent peak density ypeak with thickness t, given yb, y1 and σ. If we could plot the observed distribution, by measuring apparent peak density and thickness at each point on the surface, we could then estimate yb, y1 and σ by minimizing the differences between the two distributions. In contrast with our earlier approach, we would be making use of all the data and might expect a reasonable estimate even when there are no regions of cortex sufficiently thick to reveal the true density y1 in the blurred data.
The details of the algorithm are as follows. The first step is to use the half-max technique to measure apparent thickness thm, apparent peak density and background density at all points on the femoral surface. These observations are grouped into N bins indexed by the product , and the average value is recorded in each bin. Estimates and are then refined by minimizing the sum of the squared errors ϵ(i) between the observed and expected distributions at each bin i:
| (9) |
| (10) |
| (11) |
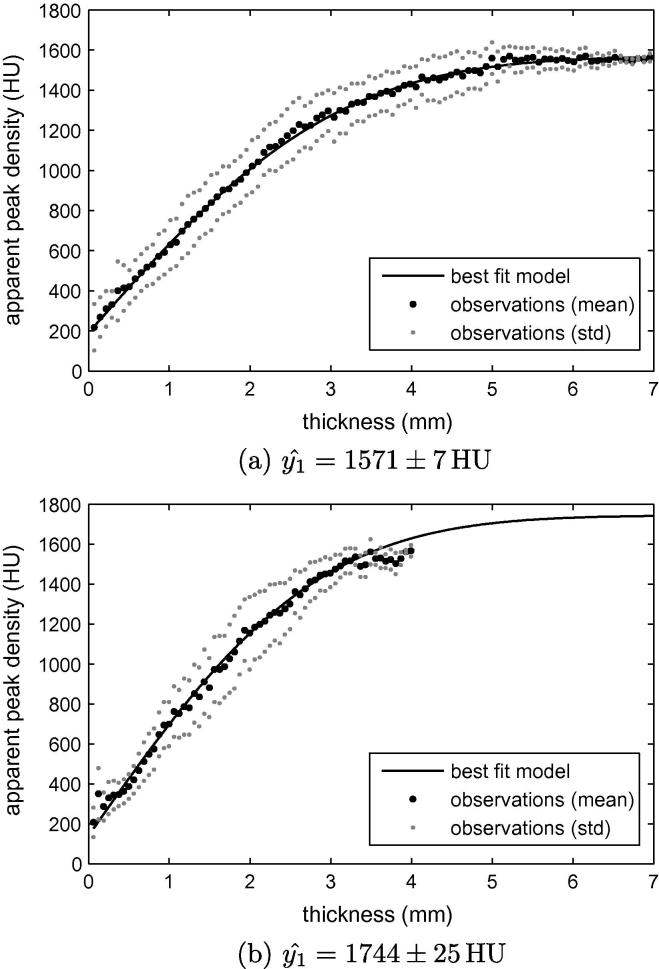
Eq. (9) converts the bin index p(i) into an estimate of true thickness t(i) using the hybrid technique of Eq. (6). Eq. (10) calculates the expected apparent peak density ypeak(i) for this thickness. Finally, Eq. (11) calculates the difference between the observed and expected peak densities. These three equations define the errors which we minimize by Levenberg–Marquardt optimization (More, 1977) to obtain optimal estimates and . A typical outcome is shown in Fig. 3a, indicating good agreement between the observations and the model. However, when the acquired data extends less far down the femur, or when the bone is osteoporotic, there may be insufficient thick cortex to fully constrain the model: such a case is shown in Fig. 3b. Scenarios (a) and (b) may be distinguished objectively by calculating the standard error of fit for the model parameter . In (a) , in (b) . The ranges are 95% confidence intervals, which are equal to twice the standard error of fit assuming the data is normally distributed and representative of the population (Press et al., 2002). It is, however, necessary to decide subjectively how much uncertainty to tolerate in any particular study. When the confidence intervals exceed this limit, the safest course of action is simply to exclude the scan from cortical thickness analysis.
Fig. 3.
Estimating the cortical density. For representative low resolution CT data sets, the graphs show the observed distribution of apparent peak density with thickness (dots), and the best fit model according to Eq. (8) (black line). For each bin, the mean (black dots) and ±1 standard deviation (grey dots) of the observations are displayed. The three model parameters are found by minimizing the sum of the squared differences between the mean observations and the model. (a) In this case, there is sufficient data to constrain the model parameters within a narrow range. (b) This scan did not extend far enough below the lesser trochanter to encounter thick cortical bone, so there is more uncertainty in the model parameters. The observations above 3 mm thickness are particularly unreliable since very little of the cortex was this thick.
3. Experiments and results
We present a series of experiments and results that: validate the derived distribution of apparent peak density with thickness across the femur; examine the accuracy of cortical density estimation using the new method, and compare with the accuracy of the original method; compare subsequent thickness and mass estimates from the various estimators; and correlate typical intra-subject cortical density variation with thickness estimation errors. Finally, we revisit our work (Poole et al., 2011) on cortical thickening following 2 years’ treatment with recombinant human parathyroid hormone, hPTH (1–34), to demonstrate the significance of these results in practice.
Some of the results are derived from observations across many different femurs but are best presented as colour maps on a representative (“canonical”) femur surface. To obtain these visualizations, each of the individual surfaces was first warped onto the canonical surface using a nonrigid, free form deformation. Having established a common morphology, the individual results could then be averaged to show typical distributions across the femoral surface.
3.1. High and low resolution cadaveric data for validation
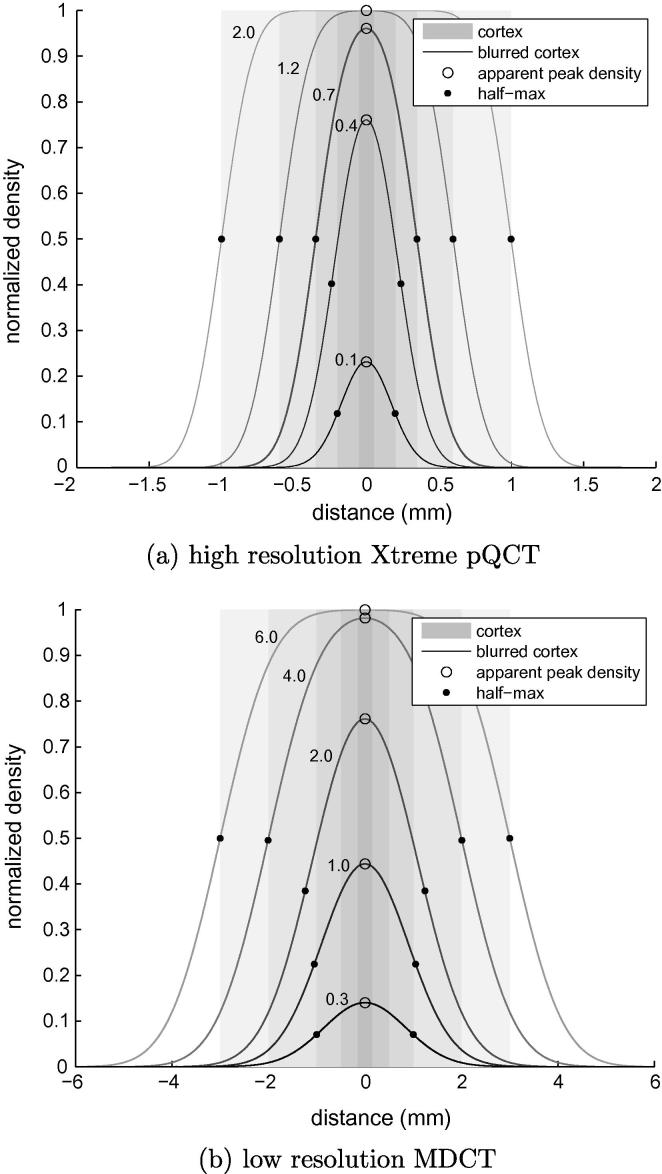
Sixteen cadaveric femurs were scanned in air at both high and low resolutions. The high resolution data was acquired on an Xtreme pQCT machine (Scanco Medical AG, Brüttisellen, Switzerland) at 82 μm/pixel in-plane resolution and 82 μm slice thickness. In these scans, the appearance of all but the thinnest cortices is largely unaffected by blur. We can therefore treat simple half-max thickness and density estimates, obtained from this high resolution data, as a gold standard. The half-max method is unbiased as long as the cortex is sufficiently wide compared with the imaging blur (Prevrhal et al., 1999), a condition that is satisfied down to around 0.4 mm thickness: see Fig. 4a. The low resolution data was acquired on a Siemens Somatom Sensation 64 MDCT machine (Siemens AG, Erlangen, Germany) at 589 μm/pixel in-plane resolution and 1 mm slice thickness. This is typical of clinical scanning conditions and serves as a test bed for the constant density and hybrid estimation methods. Image blur is far more severe, as shown in Fig. 4b.
Fig. 4.
High and low resolution data. For the straightforward case of uniform background (y0 = y2 = yb), these figures illustrate the expected effects of Gaussian blur on half-max thickness estimates and apparent peak density. (a) High resolution Xtreme pQCT. (b) Low resolution MDCT. Each curve is labelled with the corresponding true cortical thickness (mm). Note the different scales on the two distance axes.
Several precautions are necessary when comparing cortical measurements in corresponding high and low resolution data. First, the two femoral surfaces must be aligned using some sort of registration technique: we use the iterative closest point algorithm described in Treece et al. (2010). Thickness and mass estimates are made at every vertex of the low resolution surface mesh, using CT values sampled on 18 mm lines (the cyan lines in Fig. 1) oriented along the corresponding surface normals. These measurement locations and directions are then mapped onto the aligned high resolution surface, allowing us to compare the same number of thickness and mass estimates, taken at the same locations and using the same surface normals.
The next precaution concerns the spatial localization of the high and low resolution estimates. Fig. 5a and b show corresponding patches of cortex from high and low resolution scans respectively. High resolution thickness estimates would vary rapidly from the top to the bottom of the image, picking up every small detail of the irregular cortex. This detail is blurred out in the low resolution data: thickness estimates at any particular location, however well adjusted for trans-cortical blur, are always going to reflect the average cortical thickness in the vicinity of the estimation location, not the particular thickness at that location. We therefore blur the high resolution data in one dimension only, parallel to the cortex, as shown in Fig. 5c, before estimating thickness and mass. Note that this blur does not compromise estimation accuracy, only estimation localization, which is exactly what is required for a meaningful comparison between the high and low resolution data.
Fig. 5.
Blurring of high resolution data to match low resolution thickness localization. (a) High resolution data. (b) Corresponding low resolution data and (c) the blurred high resolution data used in the comparisons. The extent of the smoothing kernel is chosen to match the spatial resolution of the low resolution data.
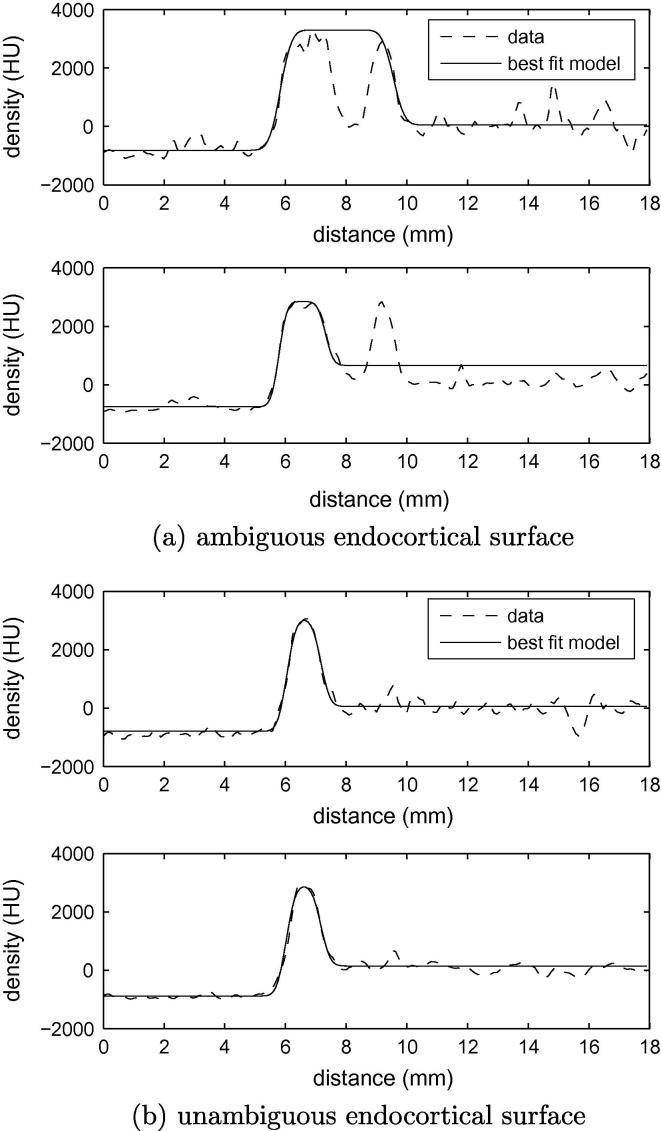
The final precaution concerns the sometimes ambiguous nature of the endocortical surface. Fig. 6a shows some high resolution data, where the location of the y1–y2 transition is far from clear. Is this a wide cortex encompassing a low density pore, or a narrow cortex with a nearby trabecular peak? For a fair comparison between the high and low resolution estimates, we must ensure that the two measurements opt for the same interpretation. We encourage this behaviour when fitting the model to the high resolution data, by blurring the error between the observed and modelled data within the Levenberg–Marquardt algorithm. Again, the extent of the blur is chosen to match the spatial resolution of the low resolution data. In the example in Fig. 6a, blurring the optimization error causes the algorithm to converge to the alternative solution, as it does with the low resolution data. There is little effect when the cortex is well defined, as in Fig. 6b.
Fig. 6.
Consistent interpretation of the endocortical boundary in high and low resolution data. By blurring the error when fitting a model to the high resolution data, we encourage the same interpretation of the endocortical boundary as with the low resolution data. (a) The top graph shows sample data through a cortex from a high resolution scan, along with the best fit half-max model without error blurring. The bottom graph shows the same data after blurring as in Fig. 5, and the best fit half-max model after blurring the optimization error. While the cortical extent is different, reflecting the alternative interpretation of the ambiguous data, the edge localization accuracy is unaffected. (b) When the cortex is well defined, neither of these blurring operations has a significant impact on the measured thickness.
What we have described is a refinement of the evaluation protocol in our earlier study (Treece et al., 2010), where we (correctly) attributed extreme errors to mismatched normals or different interpretations of the endocortical surface, and excluded outliers from the subsequent error analysis. With our new evaluation protocol, we no longer see extreme errors and outlier rejection is not required.
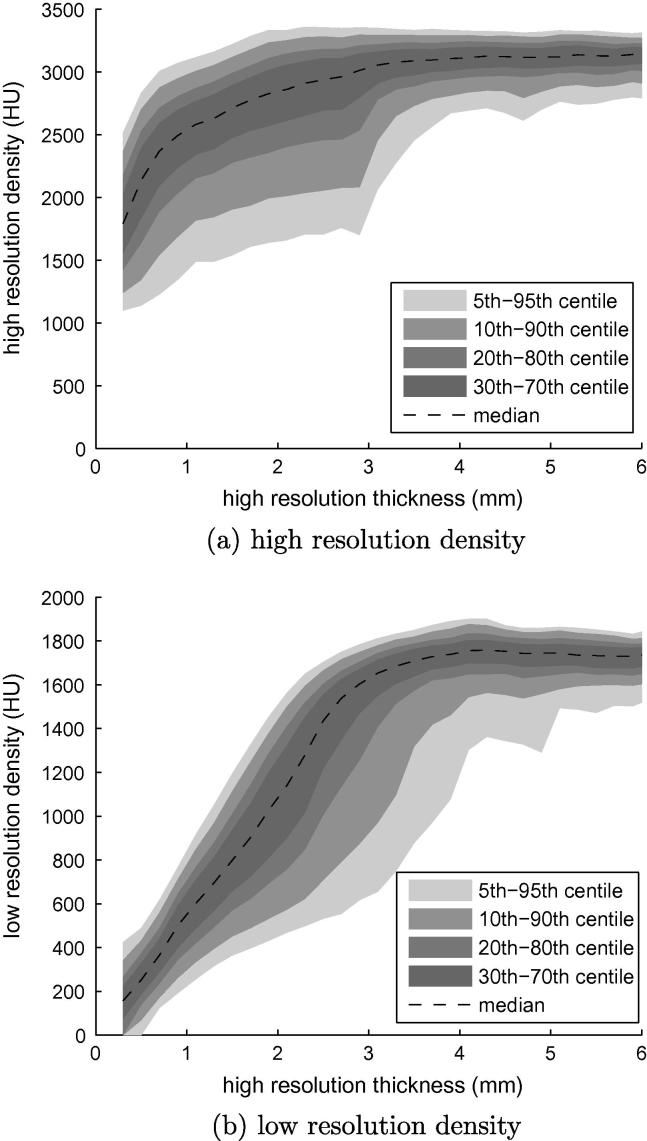
3.2. Validation of proposed method for estimating cortical density
Fig. 7a shows how cortical density varies with thickness in the sixteen cadaveric femurs. Since these measurements were made using the half-max method on the high resolution data, they can be trusted down to around 0.7 mm, beyond which Fig. 4a shows blur affecting the apparent peak density. The sharp density reduction at the far left of the distribution can therefore be attributed to measurement error. Above 0.7 mm, we observe fairly constant density, where the cortex is relatively thick, but some decline below 3 mm. This is not a measurement artefact but a feature of the bones. Fig. 7b shows a similar plot, but this time with the corresponding cortical densities observed in the low resolution data. As anticipated in Fig. 4b, image blur starts affecting the apparent peak density below around 3.5 mm, but the distribution appears to follow the form of Eq. (8) (c.f. Fig. 3), and we can therefore expect successful estimation of using the model-fitting approach of Section 2.2.
Fig. 7.
Distribution of apparent peak density with cortical thickness. All sixteen femurs contributed to the data in these graphs. (a) The high resolution distribution, with density and thickness estimated using the half-max method. (b) The y-axis now shows the corresponding peak CT values from the low resolution data.
This hypothesis is confirmed in Fig. 8, which shows the stability of the estimate as progressively more measurements, starting from the top of the femoral head, are fed into the model-fitting procedure. The estimates are highly variable when too few observations are used, but has converged to a stable value by the time measurements are incorporated from just above the lesser trochanter. For these sixteen femurs, adding yet more data from lower down the femoral shaft makes little difference to the estimation accuracy. Fig. 8c shows that, with marginally sufficient data, the model-fitting procedure tends to overestimate by a few percent — this is also apparent from the cyan band above the lesser trochanter in Fig. 8a. In contrast, the original density estimation technique tends to underestimate, and requires more data before approaching an acceptable value. While Fig. 8 reflects the healthy norm, osteoporotic specimens may need scanning a little lower before sufficiently thick cortex is encountered to fully constrain the model parameters. Unreliable solutions are not an undetectable hazard: on the contrary, they are readily identified by examining the confidence intervals, as demonstrated in Fig. 8b and c. The effects of on thickness and mass estimation are studied in Sections 3.4 and A: the latter is best read after Section 3.3.
Fig. 8.
Estimation of cortical density. The algorithm described in Section 2.2 was run repeatedly on all sixteen femurs, starting with just a little data from the top of the femoral head, then adding in progressively more data down to below the lesser trochanter. After each run, the estimate and the corresponding confidence interval were recorded, together with a second density estimate obtained using our original technique of sampling the peak density at the thickest region of cortex encountered thus far. The colour map in (a) shows the mean of for the new method, normalized by the true average value (derived from the high resolution data), mapped onto the canonical femur to show how much data contributed to the estimate. (b) shows the corresponding mean 95% confidence intervals, normalized by the final values obtained using all the available data. In (c), these estimates are plotted against depth down the femur, together with the estimate obtained using the original technique. For these sixteen femurs, the new estimate settles at around 4 cm, above the lesser trochanter, indicating that the femur must be scanned at least this far for reliable estimation of density. The 95% confidence interval is confirmed as a good indicator of estimation precision. Compared with the original method, the new technique is capable of more accurate estimation and achieves acceptable accuracy with less data. It does, however, tend to slightly overestimate the density. The original technique consistently underestimates.
3.3. Validation of proposed methods for estimating thickness and mass
3.3.1. Cadaveric data
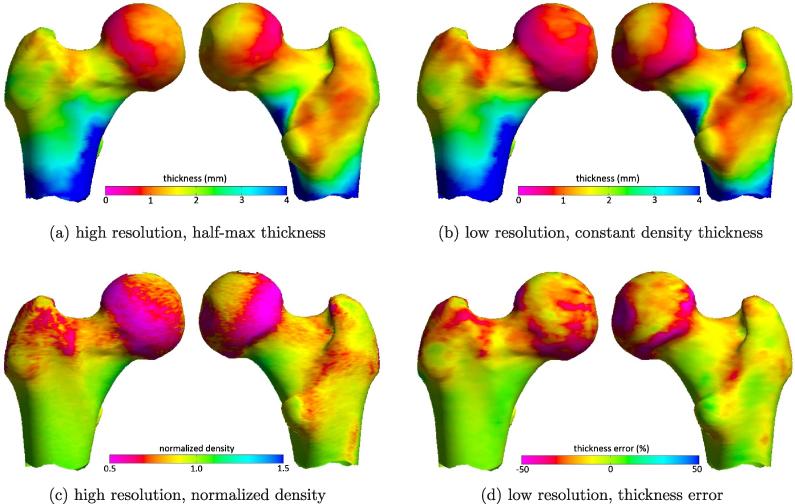
Having determined that the new density estimation method described in Section 2.2 provides a more accurate estimate of , we now revisit thickness estimation with the experimental refinements outlined in Section 3.1. Fig. 9 summarises the performance of the constant density thickness estimation technique incorporating the new estimate. It is apparent, at first sight, that the low resolution thickness estimates in (b) are good surrogates for the gold standard, high resolution measurements in (a). As expected, estimation errors (d) are correlated with true cortical density (c). We have already seen in Fig. 7a that the cortical density is not perfectly constant: at least in these sixteen femurs, it tends to drop off, where the cortex is thinner. We can now see in Fig. 9c, where these less dense regions of cortex are located. Furthermore, since Fig. 9c is normalized by the high resolution density that corresponds to , it appears that is biased towards the peak cortical density, which is a good estimate of the actual density at many locations on the femur but an overestimate at others. Fig. 9d confirms that overestimating y1 leads to underestimation of thickness by roughly the same factor. These errors are not very apparent in Fig. 9a and b because they are confined to regions of thin cortex. An error of, say, 20% in 1 mm cortex is fairly inconsequential in the context of the 0–4 mm dynamic range.
Fig. 9.
Illustrative results displayed on the canonical femur. Measurements on each of the sixteen femurs were expressed in the canonical morphology and then averaged. (a) Gold standard cortical thickness, calculated using the half-max method on the high resolution data. (b) Constant density thickness estimation from the low resolution data, with estimated using the method described in Section 2.2. (c) Cortical density in the high resolution data, normalized by the high resolution density that corresponds to . (d) The low resolution, constant density thickness estimation error, expressed as a percentage of the gold standard thickness.
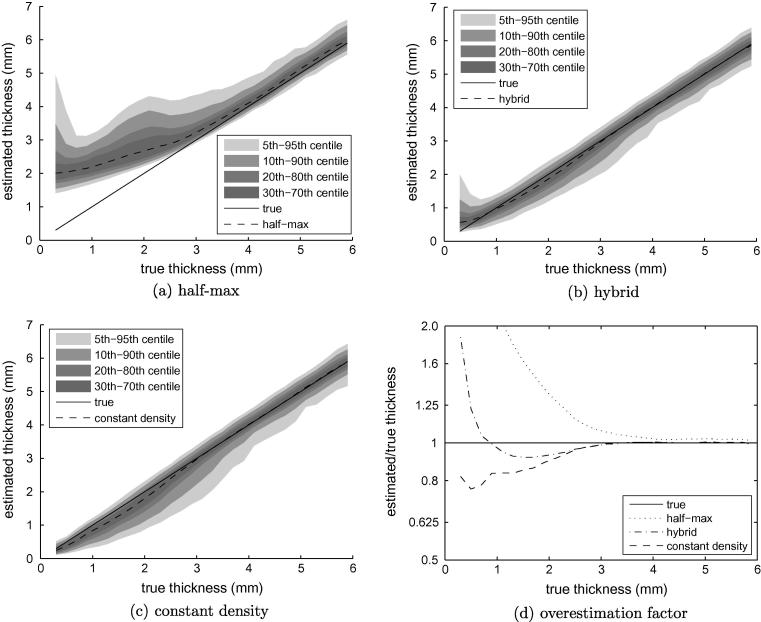
Fig. 10 compares the performance of the constant density approach with the half-max technique and the new hybrid approach described in Section 2.1. The shortcomings of the half-max method are clear in Fig. 10a, with increasingly inaccurate estimates below 2.5 mm. This is consistent with the performance anticipated in Fig. 4b, as is the asymptotic measurement of 2 mm for vanishingly thin cortex. In contrast, the constant density and hybrid methods perform relatively well. Fig. 10d indicates very little estimation error until 3 mm, where we know the constant density assumption starts to break down. From 3 mm down to 0.5 mm there is no catastrophic failure: median errors peak at around 20%, mirroring the 20% density reduction apparent in Fig. 7a. Below 0.5 mm, the pixel dimensions of the raw CT data approach the limit for effective sampling of the blurred cortex, with unavoidable consequences for the estimation error. The apparently superior performance of the hybrid method in the 0.5–3 mm range owes much to chance. The cadaveric femurs were scanned in air, with y0 ≪ y2. We have seen in Fig. 2(bottom) how the hybrid method is bound to overestimate thickness in such circumstances, and this fortuitously ameliorates the underestimation caused by too high a value of .
Fig. 10.
Cortical thickness estimation in low resolution data. Data from all sixteen femurs contributed to these graphs. True thickness was measured in the high resolution data using the half-max method.
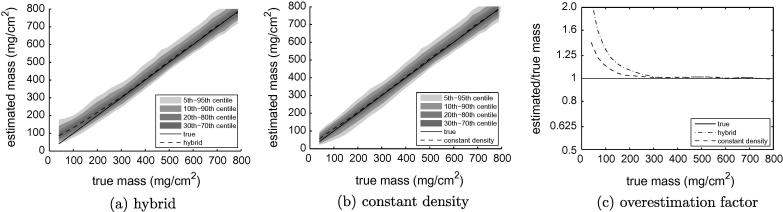
Fig. 11 shows how mass estimation is far less sensitive to any variation in the cortical density. Gaussian blurring is area preserving, so as long as the blurred y0–y1–y2 pulse fits the data well, the area under the pulse will be the same as the area under the data, providing a good mass estimate irrespective of the particular value of . When y0 ≠ y2, there is the added requirement that the fitted pulse coincide with the true location of the cortex, otherwise the mass estimate is corrupted by a y0–y2 transition at the wrong location. All these observations are borne out in Fig. 11, where we see mass estimation apparently unaffected by the variation in cortical density. The hybrid method overestimates mass for thin cortices, as predicted in Fig. 2(bottom, y0–y2 transition at the wrong location), and both techniques eventually fail when the cortex is undersampled.
Fig. 11.
Cortical mass estimation in low resolution data. Data from all sixteen femurs contributed to these graphs. True mass was measured in the high resolution data using the half-max method.
3.3.2. Simulated data
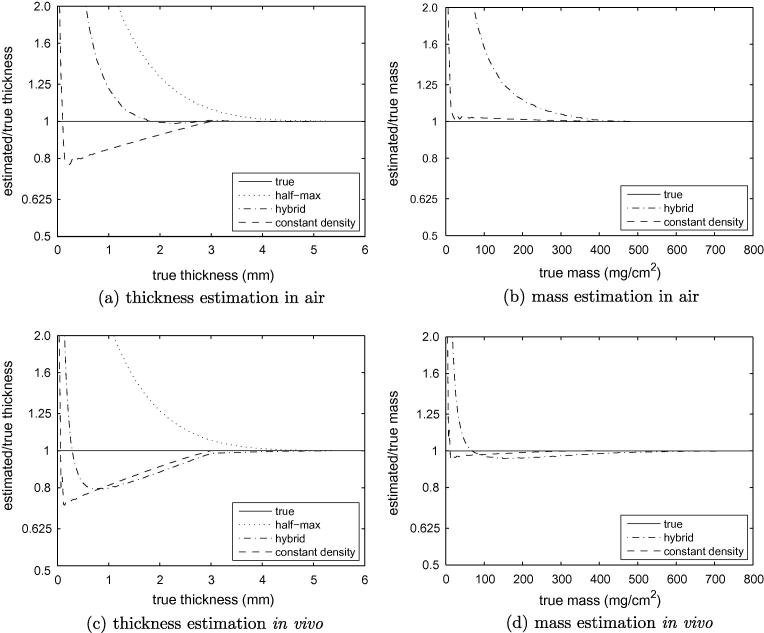
To validate the preceding claims of cause and effect, we simulated idealised cortical sections with a thickness-density relationship based on that observed in Fig. 7a, and two sets of y0/y2 values that simulate scanning in air and in vivo. Subsequent mass and thickness estimation results can be found in Fig. 12. Consistent with the observations in Fig. 2, the hybrid method produces larger estimates than the constant density method in air, but slightly smaller estimates in vivo. There is an excellent match between Fig. 12a and b and the experimental results in Figs. 10 and 11. Where there are discrepancies, they are easily explained. The low thickness sampling breakdown happens further to the left in the simulations, since these were conducted with a smaller pixel dimension. By increasing the pixel size we have observed the breakdown point moving to the right, and it is for this reason that we are confident that this is nothing more than a sampling effect. The actual hybrid results appear to lie somewhere between the air and in vivo simulations, but this is consistent with the cadaveric femurs not being perfectly clean. Any soft tissue attached to the periosteal surface will increase y0 above −1000 HU, closer to the assumed in vivo value of 0 HU.
Fig. 12.
Simulated thickness and mass measurements. To facilitate comparison of these simulations with Figs. 10d and 11c, the blur was set to approximate that of the low resolution scans (σ = 0.85 mm), as was the mapping from HU to mg/cm3. In all cases, the true cortical density y1 was modelled as varying linearly from 1300 HU at zero thickness to 1750 HU at 3 mm, thereafter remaining at 1750 HU. The various thickness and mass estimation techniques assumed . (a) and (b) simulate imaging in air, with y0 = −1000 HU and y2 = 300 HU. (c) and (d) simulate imaging in vivo, with y0 = 0 HU and y2 = 300 HU.
3.4. Clinical experiments
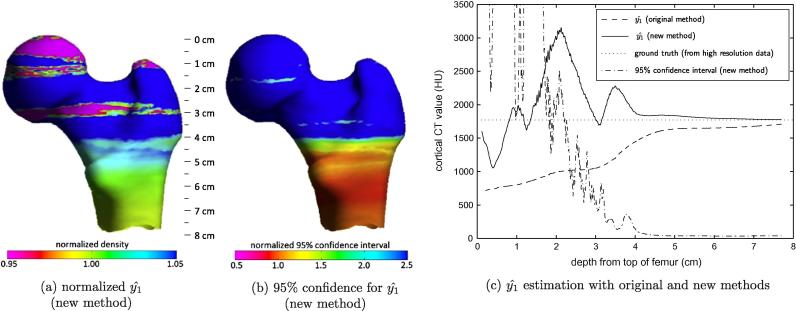
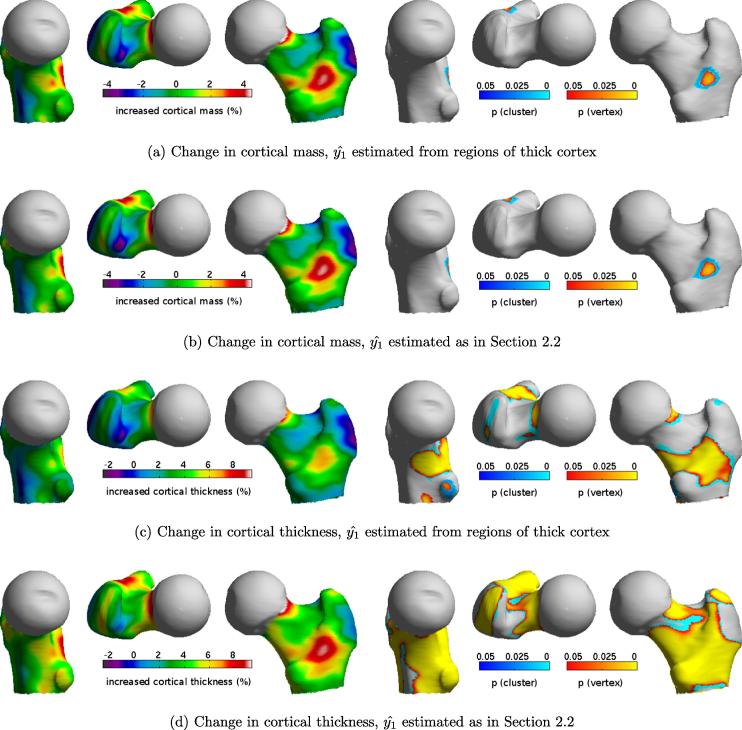
It remains to investigate, in the context of a clinical study, the relative merits of cortical mass and thickness estimation, and the practical consequences of estimating using the method described in Section 2.2. Hence, we here revisit our work on cortical thickening following 2 years’ treatment with recombinant human parathyroid hormone, hPTH (1–34). In Poole et al. (2011), CT scans of 65 osteoporotic women were analysed at baseline and 24 months, with cortical thickness estimated using the constant density technique and sampled from regions of thick cortex. All the resulting measurements were mapped onto the canonical femur for subsequent cohort analysis, producing the images in Fig. 13c.4 Statistically significant regions of thickened cortex were identified by statistical parametric mapping (SurfStat, Worsley et al., 2009). The resulting vertex p-maps (Fig. 13, yellow/orange) are sensitive to focal effects, while the cluster p-maps (cyan/blue) are sensitive to distributed effects. The reader is referred to Poole et al. (2011) for a full description of this work. Here, we augment the study with constant density cortical thickness maps based on the new method of estimating (Fig. 13d), as well as cortical mass maps using both density estimation methods (Fig. 13a and b).
Fig. 13.
Cortical mass and thickness effects following 2 years’ treatment with hPTH (1–34). Measurements from 65 subjects were mapped onto the canonical femur and averaged. The statistical parametric maps (right) indicate significant regions of mass increase (a and b) or thickening (c and d). Vertex effects are based on the magnitude of peaks corrected for multiple comparisons, while the cyan/blue areas are connected clusters of vertices exceeding an uncorrected p-value of 0.001.
4. Discussion
We have demonstrated in Section 3.2 that it is possible to estimate a single average value of cortical density from blurred clinical CT data, even in situations where the data does not extend below the lesser trochanter. Figs. 7 and 8 show that density does in fact vary with thickness and location, but that this variation is small relative to the variation in thickness. Thickness estimation accuracy is largely determined by the difference between actual local density and the presumed constant value.
Given the close agreement between the air simulation results in Fig. 12a and b, and the cadaveric results in Figs. 10 and 11, we have good reason to commend Fig. 12c and d as accurate predictors of likely in vivo performance. For cortical mass estimation, the constant density method outperforms the hybrid method since it is better able to model the observed data. In vivo the difference is relatively small, corresponding to the discrepancies between the red and blue curves in Fig. 2(top left). The story is much the same when estimating thickness, though both techniques are affected by an increasingly inappropriate value of below 3 mm. While it would be straightforward to correct the thickness estimates by exploiting prior knowledge of the thickness-density relationship, we have no evidence to suggest that the distribution observed in Fig. 7a generalises beyond the 16 specimens examined here. In the absence of any such evidence, we must accept thickness errors that are bounded by the extent to which the local density deviates from the peak density.
Although the hybrid method is slightly less accurate, it is significantly faster than the constant density approach. The former requires just one pass through the data to measure thm, and at all points on the femoral surface, and then calculate , as described in Section 2.2. The half-max estimates can then be corrected, immediately, using Eqs. (6) and (7). In contrast, the constant density approach requires a second pass through the data to estimate tcd and mcd using the just-calculated value of . To put this observation into perspective, it takes 10 s to map cortical thickness at 6500 locations (more than sufficient for a single femur) using a single core of a 2.67 GHz Intel Core i7 processor and the hybrid method, and twice as long for the constant density approach.
With reference to the practical application of these techniques in Section 3.4, the first point to note is the insensitivity of the cortical mass maps to the density estimate . This confirms the findings in Section 3.3.1 and reinforces the message that measuring cortical mass, using the various techniques described in this paper, is a relatively safe undertaking. However, there are some drawbacks. Firstly, it is necessary to know the calibration relating HU to mineral mg/cm3. There is also the danger of disregarding potentially significant density effects. For example, for the 65 individuals analysed here, baseline cortical density was 1185.1 ± 67.9 mg/cm3 (mean ±1 standard deviation), whereas at 24 months it was 1133.6 ± 78.1 mg/cm3. A paired t-test confirms that these densities are significantly different (p < 4.9 × 10−13). This is not surprising: hPTH (1–34) functions by increasing bone remodelling and hence porosity (Burr et al., 2001; Sato et al., 2004; Arlot et al., 2005). Consequently, in those regions, where the mass increases in Fig. 13a and b, it is reasonable to postulate a far more significant increase in thickness, since density has decreased. However, unlike the mass maps, the cortical thickness maps in Fig. 13c and d must be approached with some caution. There is the underlying assumption of constant cortical density: might a regionally fluctuating density undermine the apparent statistically significant results? Perhaps the regional mass increases correlate with density, not thickness? This seems unlikely: we know that average density has decreased, so we would be hypothesising a density increase in the regions most affected by hPTH (1–34), counteracted by an even greater decrease in the unaffected regions, in direct contradiction to how the drug is known to work. Nevertheless, Fig. 13c and d show changes in cortical thickness assuming constant density in any one scan, and must be interpreted as such.
A more subtle but equally important consideration is the possibility of measurement bias affecting the thickness maps. Fig. 13c and d differ because the new density estimates, obtained by model fitting, indicate around 2% more density reduction than the old estimates, obtained by sampling regions of thick cortex below the lesser trochanter. Might either or both of these methods be biased? Any systematic measurement bias that affects the baseline and 24 month density estimates to different degrees will manifest themselves as false thickness effects. So extreme care must be taken when interpreting any small, apparent thickness differences: bear in mind that a 10% thickness increase in 1 mm cortex is only 100 μm, and we are inferring this information from clinical CT scans with a point spread function of around 3 mm. In this instance, there is a known source of bias: the 24 month scans extended, on average, 4.5 mm lower down the femur than the baseline scans. This means that the baseline scans are more susceptible to imprecise estimates (caused by a lack of sufficiently thick cortical bone) than the 24 month scans. Referring to Fig. 8c, it is clear that sampling the thickest available cortex will tend to underestimate the true, peak cortical density: had there been more data, and the samples extended further to the right, we would have encountered higher density values. In contrast, the new model-fitting approach tends to overestimate when there is marginally sufficient data, as demonstrated clearly in Fig. 8c.
So Fig. 13c and d most likely represent lower and upper bounds on the true cortical thickness effect, though Fig. 8c suggests that the upper bound is likely to be closer to the truth. We are sanguine that the difference is only around 2%, despite the difficulties posed by this challenging study. Although all the scans extended below the lesser trochanter – some only just so – these were severely osteoporotic women with pathologically thin cortices. Furthermore, the point spread function of the CT system was around 3 mm, compared with 2 mm for the cadaveric studies. Nevertheless, the mean confidence interval for was ±14.8 HU and the worst case was ±38.0 HU: we therefore decided to include all 65 subjects in the cortical thickness analysis.
In summary, the merits of the new density estimation method are twofold. Compared with our previous approach of sampling the density in regions of supposedly thick cortex, the new technique makes use of all the available data. It can therefore produce estimates of that correctly exceed the peak density observed anywhere in the imaged cortex. When there is insufficient data to fully constrain the model, it does tend to overestimate density, though not as badly as the original technique underestimates. This brings us to the second advantage: the new method furnishes a confidence interval for , allowing objective inclusion or exclusion of particular scans. Our experience with the hPTH (1–34) study suggests that exclusion should rarely be necessary.
5. Conclusions
Cortical mass and thickness can be mapped across the proximal femur using either a constant density approach or a hybrid half-max/constant density approach. The former is more accurate but requires two passes through the data compared with a single pass for the latter. When a suitable calibration phantom is included in the scan, cortical mass can be measured in mg/cm2 to high accuracy. Cortical thickness estimation requires a good estimate of the cortical density, which is assumed to be constant at all points on the femur. While the model-fitting method presented in this paper estimates this density in a manner that can be considered optimal, in that it exploits all the available data, thickness estimates are nevertheless biased when there is any variation in the actual cortical density. In many studies, it may therefore be advisable to base any firm deductions on observations of cortical mass alone, unless the study involves comparison of two groups with different densities, in which case cortical thickness analysis, when applied with care, may well reveal more significant group-dependent effects.
Acknowledgments
Ken Poole is supported by Arthritis Research UK, the Evelyn Trust and the NIHR Cambridge Biomedical Research Centre. The cadaveric femurs were from the Melbourne Femur Collection Research Tissue Bank of the Victorian Institute of Forensic Medicine, with kind permission of Professor John Clement.
Footnotes
http://mi.eng.cam.ac.uk/˜rwp/stradwin.
Since cortical bone is an inhomogeneous material, we define as the CT value returned by cortical bone averaged over the scale of the imaging process.
The reader is referred to Treece et al. (2010) for further comparisons with the alternative thresholding approach (Buie et al., 2007; Hangartner, 2007), which is less precise than the half-max method when the cortex is thick, and increasingly prone to missing the cortex altogether when it is thin.
Fig. 13c is in fact slightly different from the corresponding figure in Poole et al. (2011), since we now use an improved smoothing algorithm when mapping onto the canonical femur.
Contributor Information
G.M. Treece, Email: gmt11@cam.ac.uk.
K.E.S. Poole, Email: kenpoole@doctors.org.uk.
A.H. Gee, Email: ahg@eng.cam.ac.uk.
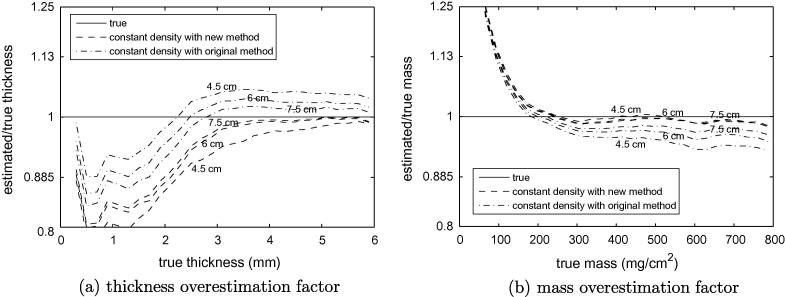
Appendix A. The effect of on thickness and mass estimation — cadaveric data
Fig. A.1a shows the results of constant density thickness estimation, with obtained using the method described in Section 2.2 (new method) and sampled from regions of thick cortex (original method). Recall from Fig. 8c how the new method tends to overestimate and hence underestimate thickness when there is marginally sufficient data, whereas the old method tends to underestimate and hence overestimate thickness, with the new method generally more accurate. This behaviour is apparent above 3 mm thickness in Fig. A.1a. Below 3 mm, we have seen in Fig. 7a how the constant density assumption starts to break down, and we therefore observe a predictable pattern of errors consistent with Fig. 10d.
Fig. A.1.
Cortical thickness and mass with different estimates. Data from all sixteen cadaveric femurs contributed to these graphs. Thickness (a) and mass (b) were estimated using the constant density technique and sampled from regions of thick cortex (original method) and using the technique described in Section 2.2 (new method). Results are shown with cortical density estimation based on data from progressively further down the femur (4.5 cm, 6 cm and 7.5 cm), as in Fig. 8. Regardless of the depth limit for density estimation, thickness and mass were estimated across the entire available femoral surface.
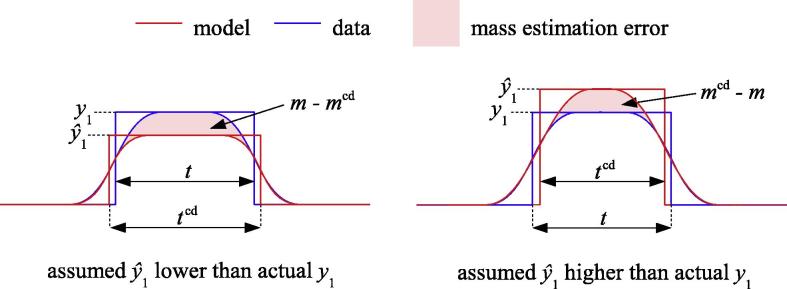
The corresponding mass results in Fig. A.1b are consistent with Fig. 11c. They confirm that is generally less critical when estimating mass, though there is some sensitivity for thick cortices. This is because the blurred y0––y2 pulse does not fit the data well when is incorrect and the cortex is thick: see Fig. A.2 and compare with the thin cortex case in Fig. 2. With this observation, we arrive at a more nuanced understanding of constant density mass estimation: for thin cortices, mass estimation is not sensitive to ; for thick cortices, there will be errors if does not correspond to the apparent density peak; and any errors will be less significant if is too high than if is too low, for reasons that are evident in Fig. A.2. For mass estimation, the new density estimation method therefore has two advantages over the original method: not only is it more accurate, but when there is marginally sufficient data it has the good fortune to overestimate .
Fig. A.2.
Constant density thickness and mass estimation for thick cortices. Both thickness (tcd) and mass (mcd) are sensitive to when the cortex is thick. Whereas thickness is affected equally whether is over- or underestimated, relative mass errors are greater when is underestimated.
It must be stressed that the scenarios studied in Figs. A.1 and A.2 are largely theoretical. They assume that is estimated from limited data devoid of regions of thick cortex, but is then used to estimate the thickness and mass of thick cortex regardless! In practice, cortical mass estimation remains a relatively safe undertaking. Either the scan includes sufficient thick cortex to arrive at a good estimate and therefore good mass estimates over the full range; or the scan includes only thin cortex, in which case Fig. 2 prevails and mass estimation is not particularly sensitive to .
References
- Arlot M., Meunier P.J., Boivin G., Haddock L., Tamayo J., Correa-Rotter R., Jasqui S., Donley D.W., Dalsky G.P., Martin J.S., Eriksen E.F. Differential effects of teriparatide and alendronate on bone remodeling in postmenopausal women assessed by histomorphometric parameters. J. Bone Miner. Res. 2005;20:1244–1253. doi: 10.1359/JBMR.050309. [DOI] [PubMed] [Google Scholar]
- Bouxsein M.L., Delmas P.D. Considerations for development of surrogate endpoints for antifracture efficacy of new treatments in osteoporosis: a perspective. J. Bone Miner. Res. 2008;23:1155–1167. doi: 10.1359/JBMR.080301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buie H.R., Campbell G.M., Klinck R.J., MacNeil J.A., Boyd S.K. Automatic segmentation of cortical and trabecular compartments based on a dual threshold technique for in vivo micro-CT bone analysis. Bone. 2007;41:505–515. doi: 10.1016/j.bone.2007.07.007. [DOI] [PubMed] [Google Scholar]
- Burr D.B., Hirano T., Turner C.H., Hotchkiss C., Brommage R., Hock J.M. Intermittently administered human parathyroid hormone (1–34) treatment increases intracortical bone turnover and porosity without reducing bone strength in the humerus of ovariectomized cynomolgus monkeys. J. Bone Miner. Res. 2001;16:157–165. doi: 10.1359/jbmr.2001.16.1.157. [DOI] [PubMed] [Google Scholar]
- Cann C.E. Quantitative CT for determination of bone mineral density: a review. Radiology. 1988;166:509–522. doi: 10.1148/radiology.166.2.3275985. < http://radiology.rsna.org/content/166/2/509.full.pdf+html>. [DOI] [PubMed] [Google Scholar]
- Carpenter R.D., Beaupre G.S., Lang T.F., Orwoll E.S., Carter D.R. New QCT analysis approach shows the importance of fall orientation on femoral neck strength. J. Bone Miner. Res. 2005;20:1533–1542. doi: 10.1359/JBMR.050510. [DOI] [PubMed] [Google Scholar]
- de Bakker P.M., Manske S.L., Ebacher V., Oxland T.R., Cripton P.A., Guy P. During sideways falls proximal femur fractures initiate in the superolateral cortex: evidence from high-speed video of simulated fractures. J. Biomech. 2009;42:1917–1925. doi: 10.1016/j.jbiomech.2009.05.001. [DOI] [PubMed] [Google Scholar]
- Dougherty G., Newman D. Measurement of thickness and density of thin structures by computed tomography. Med. Phys. 1999;26:1341–1348. doi: 10.1118/1.598629. [DOI] [PubMed] [Google Scholar]
- Hangartner T.N. Thresholding technique for accurate analysis of density and geometry in QCT, PQCT and μCT images. J. Musculoskelet. Neuronal. Interact. 2007;7:9–16. [PubMed] [Google Scholar]
- Hangartner T.N., Gilsanz V. Evaluation of cortical bone by computed tomography. J. Bone Miner. Res. 1996;11:1518–1525. doi: 10.1002/jbmr.5650111019. [DOI] [PubMed] [Google Scholar]
- Holzer G., von Skrbensky G., Holzer L.A., Pichl W. Hip fractures and the contribution of cortical versus trabecular bone to femoral neck strength. J. Bone Miner. Res. 2009;24:468–474. doi: 10.1359/jbmr.081108. [DOI] [PubMed] [Google Scholar]
- Johnell O., Kanis J.A., Oden A., Johansson H., Laet C.D., Delmas P., Eisman J.A., Fujiwara S., Kroger H., Mellstrom D., Meunier P.J., 3rd L.J.M., O’Neill T., Pols H., Reeve J., Silman A., Tenenhouse A. Predictive value of BMD for hip and other fractures. J. Bone Miner. Res. 2005;20:1185–1194. doi: 10.1359/JBMR.050304. [DOI] [PubMed] [Google Scholar]
- Kanis J.A., Burlet N., Cooper C., Delmas P.D., Reginster J.Y., Borgstrom F., Rizzoli R. European guidance for the diagnosis and management of osteoporosis in postmenopausal women. Osteoporosis. Int. 2008;19:399–428. doi: 10.1007/s00198-008-0560-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaptoge S., Beck T.J., Reeve J., Stone K.L., Hillier T.A., Cauley J.A., Cummings S.R. Prediction of incident hip fracture risk by femur geometry variables measured by hip structural analysis in the study of osteoporotic fractures. J. Bone Miner. Res. 2008;23:1892–1904. doi: 10.1359/JBMR.080802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayhew P.M., Thomas C.D., Clement J.G., Loveridge N., Beck T.J., Bonfield W., Burgoyne C.J., Reeve J. Relation between age, femoral neck cortical stability, and hip fracture risk. Lancet. 2005;366:129–135. doi: 10.1016/S0140-6736(05)66870-5. [DOI] [PubMed] [Google Scholar]
- More J.J. The Levenberg–Marquardt algorithm: implementation and theory. In: Watson A., editor. Vol. 630. Springer-Verlag; 1977. pp. 105–116. (Numerical Analysis. Lecture Notes in Mathematics). [Google Scholar]
- Parker M., Johansen A. Hip fracture. Brit. Med. J. 2006;333:27–30. doi: 10.1136/bmj.333.7557.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poole K.E., Mayhew P.M., Rose C.M., Brown J.K., Bearcroft P.J., Loveridge N., Reeve J. Changing structure of the femoral neck across the adult female lifespan. J. Bone Miner. Res. 2010;25:482–491. doi: 10.1359/jbmr.090734. [DOI] [PubMed] [Google Scholar]
- Poole K.E.S., Treece G.M., Ridgway G.R., Mayhew P.M., Borggrefe J., Gee A.H. Targeted regeneration of bone in the osteoporotic human femur. PLoS One. 2011;6:e16190. doi: 10.1371/journal.pone.0016190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press W.H., Teukolsky S.A., Vetterling W.T., Flannery B.P. second ed. Cambridge University Press; 2002. Numerical Recipes in C: The Art of Scientific Computing. [Google Scholar]
- Prevrhal S., Engelke K., Kalander W.A. Accuracy limits for the determination of cortical width and density: the influence of object size and CT imaging parameters. Phys. Med. Biol. 1999;44:751–764. doi: 10.1088/0031-9155/44/3/017. [DOI] [PubMed] [Google Scholar]
- Prevrhal S., Fox J.C., Shepherd J.A., Genant H.K. Accuracy of CT-based thickness measurement of thin structures: modeling of limited spatial resolution in all three dimensions. Med. Phys. 2003;30:1–8. doi: 10.1118/1.1521940. [DOI] [PubMed] [Google Scholar]
- Sambrook P., Cooper C. Osteoporosis. Lancet. 2006;367:2010–2018. doi: 10.1016/S0140-6736(06)68891-0. [DOI] [PubMed] [Google Scholar]
- Sanders K.M., Nicholson G.C., Watts J.J., Pasco J.A., Henry M.J., Kotowicz M.A., Seeman E. Half the burden of fragility fractures in the community occur in women without osteoporosis. When is fracture prevention cost-effective? Bone. 2006;38:694–700. doi: 10.1016/j.bone.2005.06.004. [DOI] [PubMed] [Google Scholar]
- Sato M., Westmore M., Ma Y.L., Schmidt A., Zeng Q.Q., Glass E.V., Vahle J., Brommage R., Jerome C.P., Turner C.H. Teriparatide [PTH(1–34)] strengthens the proximal femur of ovariectomized nonhuman primates despite increasing porosity. J. Bone Miner. Res. 2004;19:623–629. doi: 10.1359/JBMR.040112. [DOI] [PubMed] [Google Scholar]
- Streekstra G.J., Strackee S.D., Maas M., ter Wee R., Venema H.W. Model-based cartilage thickness measurement in the submillimeter range. Med. Phys. 2007;34:3562–3570. doi: 10.1118/1.2766759. [DOI] [PubMed] [Google Scholar]
- Treece G.M., Gee A.H., Mayhew P.M., Poole K.E.S. High resolution cortical bone thickness measurement from clinical CT data. Med. Image Anal. 2010;14:276–290. doi: 10.1016/j.media.2010.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verhulp E., van Rietbergen B., Huiskes R. Load distribution in the healthy and osteoporotic human proximal femur during a fall to the side. Bone. 2008;42:30–35. doi: 10.1016/j.bone.2007.08.039. [DOI] [PubMed] [Google Scholar]
- Worsley K., Taylor J., Carbonell F., Chung M., Duerden E., Bernhardt B., Lyttelton O., Boucher M., Evans A. Surfstat: a Matlab toolbox for the statistical analysis of univariate and multivariate surface and volumetric data using linear mixed effects models and random field theory. NeuroImage. 2009;47:S102. (Organization for Human Brain Mapping, 2009 Annual Meeting) [Google Scholar]