Polyamorphism in water

Abstract

Water, the most common and important liquid, has peculiar properties like the density maximum at 4 °C. Such properties are thought to stem from complex changes in the bonding-network structure of water molecules. And yet we cannot understand water. The discovery of the high-density amorphous ice (HDA) in 1984 and the discovery of the apparently discontinuous change in volume of amorphous ice in 1985 indicated experimentally clearly the existence of two kinds of disordered structure (polyamorphism) in a one-component condensed-matter system. This fact has changed our viewpoint concerning water and provided a basis for a new explanation; when cooled under pressure, water would separate into two liquids. The peculiar properties of water would be explained by the existence of the separation point: the liquid-liquid critical point (LLCP). Presently, accumulating evidences support this hypothesis. Here, I describe the process of my experimental studies from the discovery of HDA to the search for LLCP together with my thoughts which induced these experiments.

1. Introduction

In the 17th century, Galileo thought ice should be rarefied water. This stimulated the experimentalists of “Academie del Cimento”. They cooled water, measured its volume and observed the density maximum.¹⁾ In spite of the long history of the succeeding water researches, there has been no clear explanation for this peculiar behavior (Fig. 1). In comparison with gas and crystal, we should admit our poor understanding of liquid, especially water.

Fig. 1.

Ice water in a glass. Cold liquid water floats on warmer water, which represents water’s peculiar behavior.

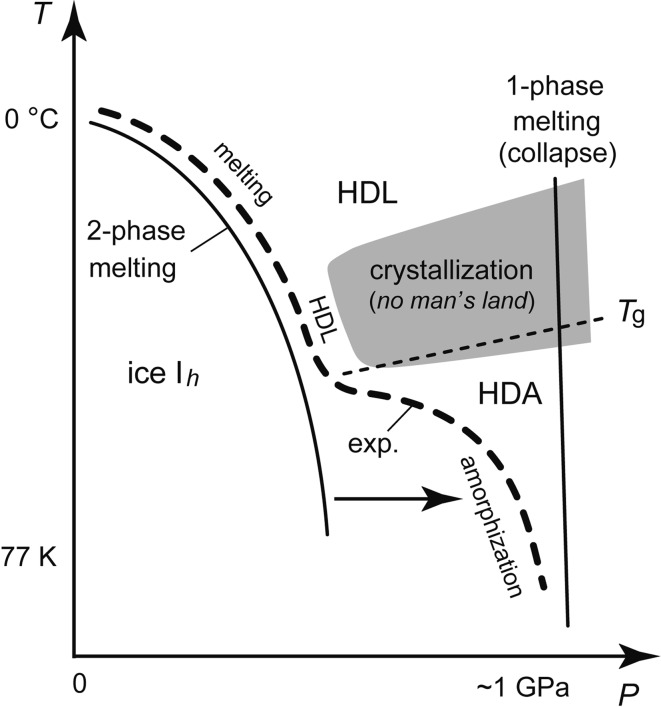
Water freezes to crystalline ice I_h below 0 °C, but water can also be supercooled, keeping the liquid state. The basic reason why water is difficult to understand is because the supercooled water crystallizes easily between ~150 K and ~235 K (Fig. 2). The temperature domain of the easy crystallization was named “no-man’s land” (NML). Consequently, measurement of the liquid water in this NML is technically difficult. When temperature is decreased from 4 °C, the volume of water increases from 1 cm³/g (or the density decreases from 1 g/cm³) and it shows the tendency to become infinite (or zero) at ~228 K in NML.²⁾ However, what really occurs in the liquid water of NML is unknowable.

Fig. 2.

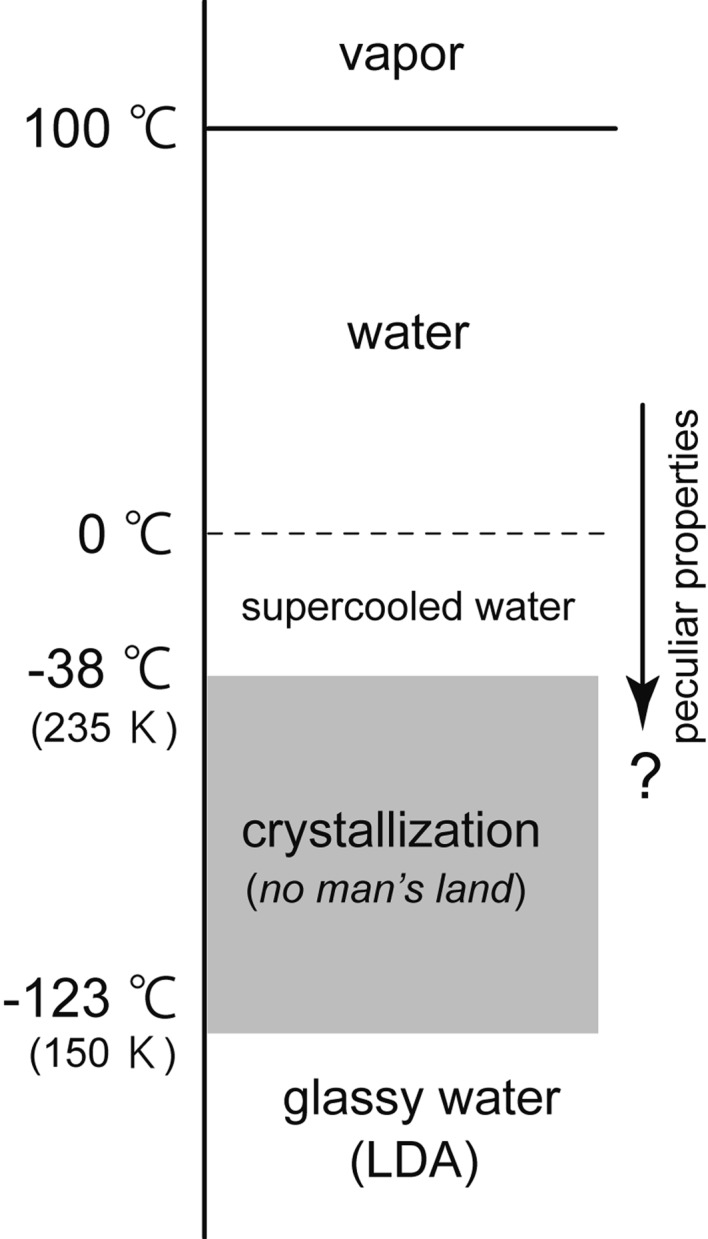
The amorphous forms of H₂O at one atmospheric pressure.

At temperatures lower than ~150 K, the existence of the low-density amorphous ice (LDA) has been known since 1935. LDA was made by the deposition of water vapor onto a cold substrate³⁾ or by the extremely rapid cooling, ~10⁶ K/s, of micrometer-size droplets of liquid water.⁴⁾ Water molecules of LDA were located disorderly like those of liquid water. However, LDA was solid, and its density, ~0.94 g/cm³, was as low as that of ice I_h. Although we might regard LDA as vitrified water,^5),6) the relationship between LDA and the high-temperature liquid water was unknown due to NML.

Incidentally, there was a natural expectation that the disordered structure of liquid, or glass, would change gradually when pressure and temperature were changed. In other words, it was commonly thought that the one-component material would have only one liquid phase. The possibility of a discontinuous change in volume of liquid was doubted and rarely discussed because there was no clear experimental evidence for the amorphous polymorphism (or polyamorphism).

As described below, the discovery of the high-density amorphous ice (HDA) at low-temperature and high-pressure conditions was the beginning of a novel and promising idea about the liquid state in NML.

2. Pressure-induced amorphization: the discovery of HDA

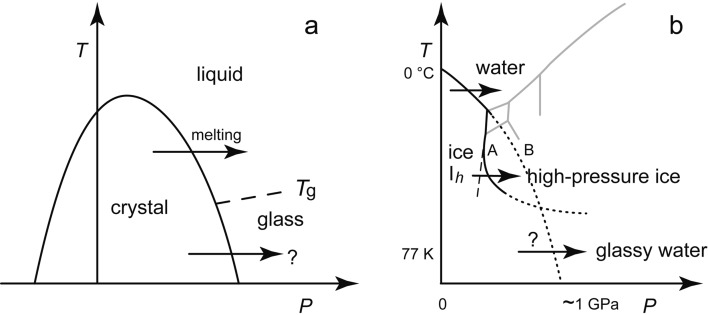
After Tammann reported in 1900 that the melting temperature of ice I_h decreased under pressure, the effect of pressure on melting interested the researchers of high-pressure phenomena of materials.^7),8) As shown in Fig. 3a, Naoto Kawai of Osaka University thought that the pressure (P)-temperature (T) line where a crystal would melt should continue to ~0 K if the crystal was not transformed to other crystalline structures.^9),10) I was a Kawai’s student and was interested in his idea. Later, in the compression experiment of ice I_h, we observed that the transition pressure to other high-pressure ices became higher at lower temperatures as shown by the line A in Fig. 3b.¹¹⁾ Then, I noticed that ice I_h might be compressed to its expected melting line (B in Fig. 3b) at adequately low temperatures. Usually, melting occurred easily on the melting line. The definition of melting was vague, and it had once been regarded as instability of a crystalline structure.¹²⁾ Consequently, it was considered that, even if temperature was low, ice I_h would do some kind of transition when it was compressed to its melting pressure. This speculation became gradually my motivation to compress ice I_h at the liquid-nitrogen temperature.

Fig. 3.

The low-temperature melting of a crystal. a: a hypothetical general melting line. b: the phase diagram of H₂O. A: the line of the compression-induced crystal-crystal transition. B: the extrapolated melting line. One atmospheric pressure is ~0.0001 GPa, or ~0.1 MPa.

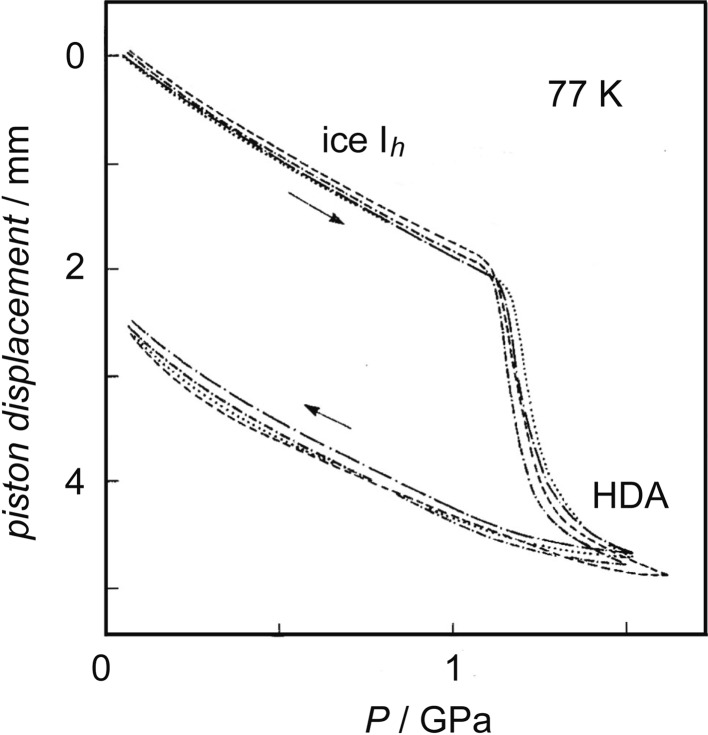
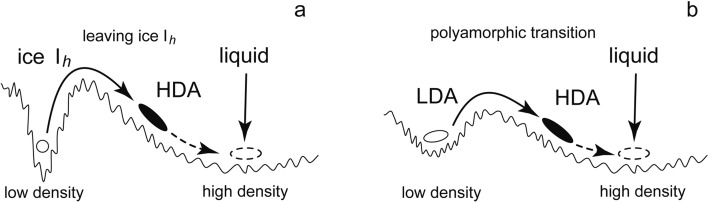
At National Research Council of Canada in Ottawa where I stayed for a few years as a postdoctoral fellow, my speculation about the low-temperature melting of ice I_h interested Whalley. We discussed ice I_h might become (‘melt’ into) a glass if temperature was lower than the glass-transition temperature (T_g) of liquid water. In order to examine this, I compressed ice I_h at 77 K by using a piston-cylinder apparatus. The volume (V) of ice I_h decreased rapidly by more than 20 % at ~1 GPa (Fig. 4).¹³⁾ When decompressed, the produced high-density sample was recovered at one atmospheric pressure and 77 K, and its density was ~1.17 g/cm³. The low-temperature X-ray measurement of the recovered solid sample by Calvert showed the halo diffraction ring, and this indicated the sample was apparently amorphous. The halo pattern resembled that of liquid water, which was consistent with the expectation of the pressure-induced ‘melting’. Relatively easy production of this high-density amorphous ice (HDA), together with its reproducibility, ensured its existence. The discovery of HDA was the discovery of a new method of making glass, and this initiated the research field of the pressure-induced amorphization of crystals. As shown in Fig 5a, I imagined the hypothetical potential surface from the Takeo Matsubara’s idea about the pressure-induced melting which was illustrated in the Kawai’s paper.¹⁰⁾ I speculated that the system ran out of the narrow hollow of ice I_h and that it immediately stopped due to both the roughness of the potential surface of the amorphous structure and the low temperature. I thought HDA was unstable and would relax toward the structure of the high-pressure liquid water.

Fig. 4.

The change in volume of ice I_h during the compression at 77 K.¹³⁾

Fig. 5.

The H₂O states on the supposed potential surface. a: the amorphization, or melting. b: the polyamorphic transition.

3. Transition between LDA and HDA: the discovery of apparent polyamorphism

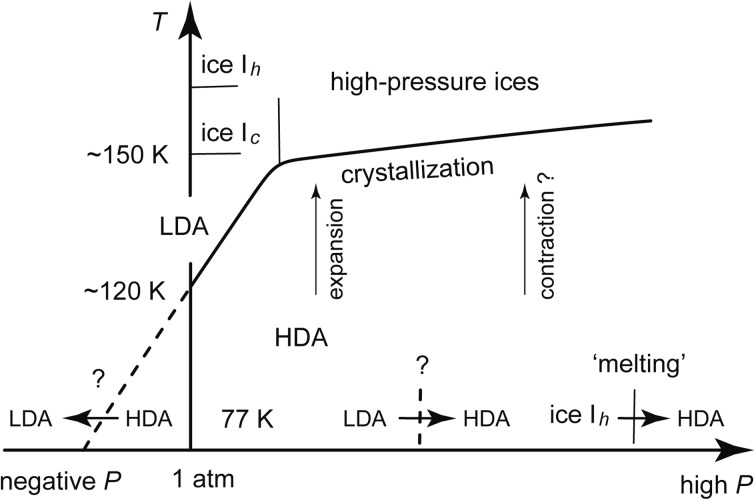
When HDA was heated at one atmospheric pressure, its structure relaxed gradually and HDA expanded slowly, and then, strangely, HDA quickly swelled by ~20 % at ~120 K and changed into LDA (Fig. 6). When heated further, LDA crystallized into ice I_c at ~150 K, and then ice I_c changed to ice I_h. When HDA was heated from 77 K at different pressures, it expanded gradually at low pressures and the expansion changed gradually toward contraction at high pressures (Fig. 6). On further heating under pressure, HDA crystallized into various high-pressure ices. Strictly speaking, the halo X-ray diffraction pattern of HDA indicated HDA was either truly amorphous or microcrystalline. However, I thought HDA was truly amorphous from this relaxation-crystallization manner.

Fig. 6.

The stability of HDA in the P-T diagram.

In this experiment, the temperature of the rapid HDA-to-LDA transition showed strong pressure dependence; the temperature decreased when the pressure decreased. From this noteworthy fact, I thought that HDA would change rapidly to LDA if it were decompressed to negative pressures at 77 K (Fig. 6). Moreover, I supposed by analogy that the LDA, made by the low-temperature decompression, would be truly amorphous because HDA, made by the 77 K compression, was likely truly amorphous. Further, I expected conversely that when LDA was compressed, it might change to HDA rapidly at a certain pressure. This rapid LDA-to-HDA transition was expected also because the structure of LDA seemed somewhat similar to the stable structure of ice I_h which showed the rapid change to HDA (Fig. 4). As shown in Fig. 5b, I imagined a basin of LDA and speculated that the system might run away out of the basin by compression. If so, there would be two amorphous phases of different disordered structures, and the transition between the two phases might occur discontinuously; the transition would be first-order. The desire to examine the possibility of the two amorphous phases became my motivation to compress LDA at a low temperature.

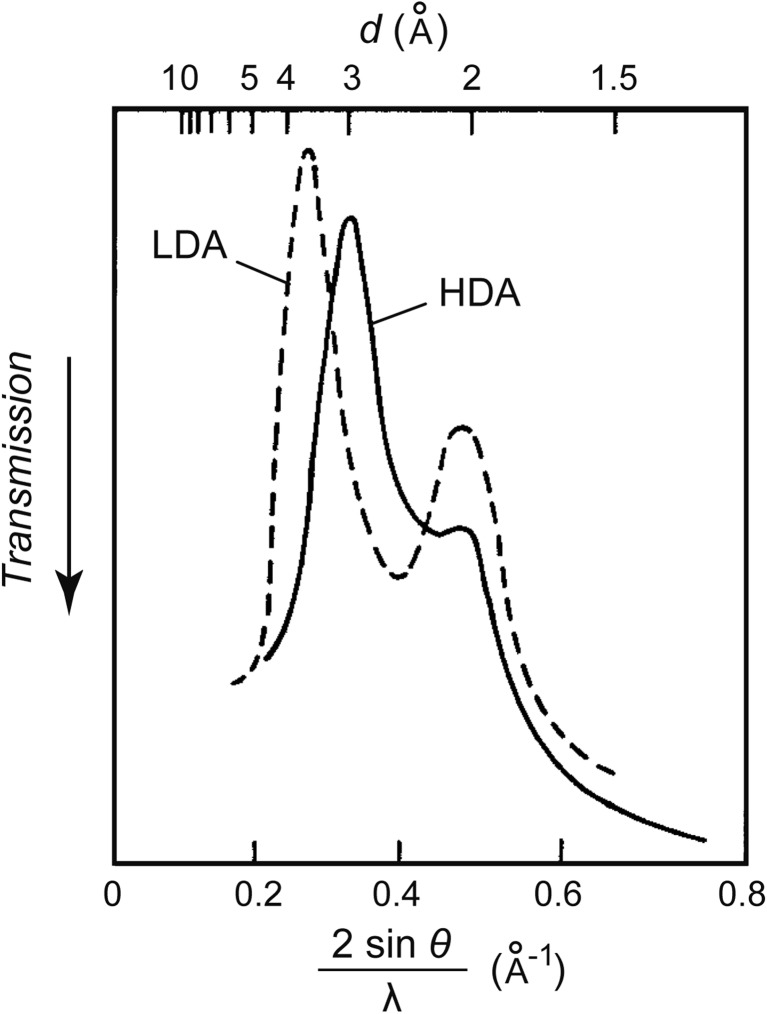
In July 1984, I compressed LDA at 77 K, and found that its volume decreased by ~20 % suddenly, rapidly and discontinuously at ~0.6 GPa (Fig. 7). The sharpness of the transition contrasted remarkably with the known dullness of the pressure-induced densification of general glasses.¹⁴⁾ The transition pressure of ~0.6 GPa was much lower than that of ~1 GPa of ice I_h, which hinted that LDA was truly amorphous. Then, the halo pattern of LDA before the transition and the halo pattern of HDA after the transition were confirmed by the x-ray measurements of the recovered samples (Fig. 8). This LDA-HDA transition was the first experimental example that clearly indicated the existence of polyamorphism. Whalley recognized the importance of this transition immediately, and we published it.¹⁵⁾

Fig. 7.

The change in volume of LDA during the compression at 77 K.¹⁵⁾

Fig. 8.

X-ray diffraction patterns (micrometer tracing) of LDA (the broken line) and HDA (the solid line) at one atmospheric pressure and ~95 K.¹⁵⁾ 2θ: the scattering angle. λ: the wavelength of the X-ray.

4. Water’s liquid-liquid transition and its liquid-liquid critical point

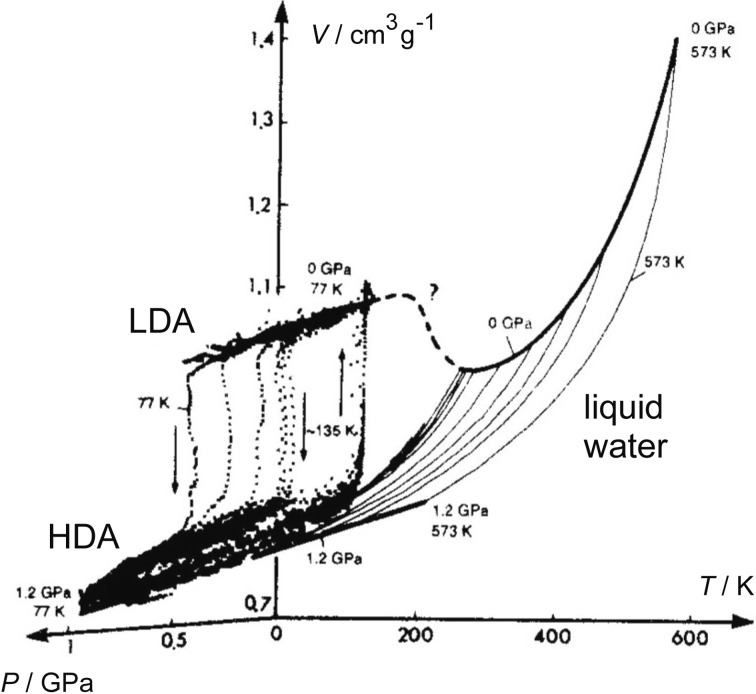
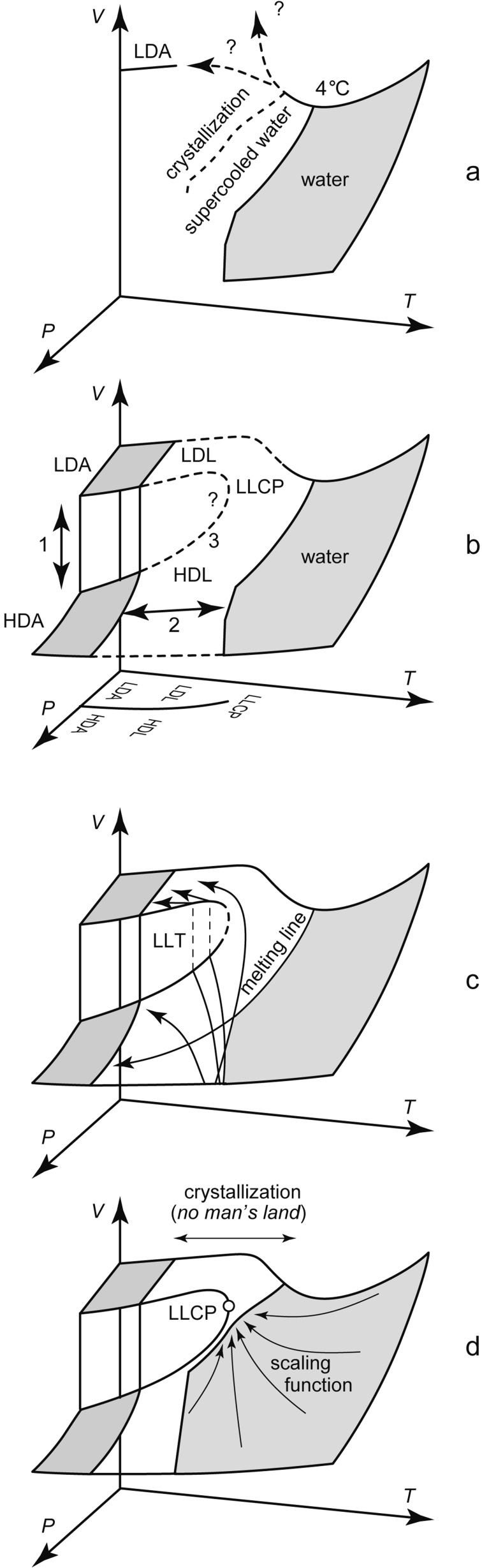
The discontinuous LDA-HDA transition implied the validity of the two-basin picture of Fig. 5b. Accordingly, if LDA and HDA were heated to temperatures higher than their T_gs, they were thought to relax into low-density liquid (LDL) and high-density liquid (HDL), respectively. Moreover, the discontinuous liquid-liquid transition (LLT) between LDL and HDL and the point where this LLT would disappear, the liquid-liquid critical point (LLCP), were imagined naturally. Liquid would change continuously at temperatures higher than the LLCP. On the other hand, at temperatures lower than the LLCP, hysteresis of the first-order transition between compression and decompression cycles was thought to occur; the hysteresis would be larger at lower temperatures. These were speculations, but in 1992, Poole et al. proposed this LLCP hypothesis concretely by the molecular-dynamics simulation of supercooled water and by taking the discontinuous LDA-HDA transition into account.¹⁶⁾ Both our experimental fact of polyamorphism and the theoretical prediction by Poole et al. have directed my interest toward the experimental identification of the LLCP.

4.1. Experimental problem

The difficulty of the experimental proof of the LLCP hypothesis, apart from the crystallization in NML, was that the amorphous ices were solid and not in the thermodynamical equilibrium. As for liquid, it was in the equilibrium and could be a sole state once pressure and temperature were fixed. Therefore, it would be possible to prove the discontinuity of the transition between two different liquids. However, regarding liquid water, LDL and HDL would crystallize immediately in NML, and we could not observe the LLT directly. In contrast, although we could observe the LDA-HDA transition, the non-equilibrium nature of LDA and HDA threw doubt on the discontinuity of the transition logically. That is, the existence of the barrier in Fig. 5b was doubted; the potential surface between LDA and HDA might be flat by nature. Then, the apparently discontinuous LDA-to-HDA transition (Fig. 7) might be, correctly, continuous or caused by unknown sticky relaxation of a non-equilibrium LDA state. If so, LLT of water would be continuous and LLCP would not exist.

Besides, because the analysis of HDA was in-sufficient, it was argued that HDA was microcrystalline or that HDA and liquid water possessed different structures and were not related each other.

I started studying the discontinuity of the LDA-HDA transition and the relationship between HDA and liquid water at National Institute for Researches in Inorganic Materials (now National Institute for Materials Science) in Tsukuba.

4.1.1. Discontinuity of the LDA-HDA transition

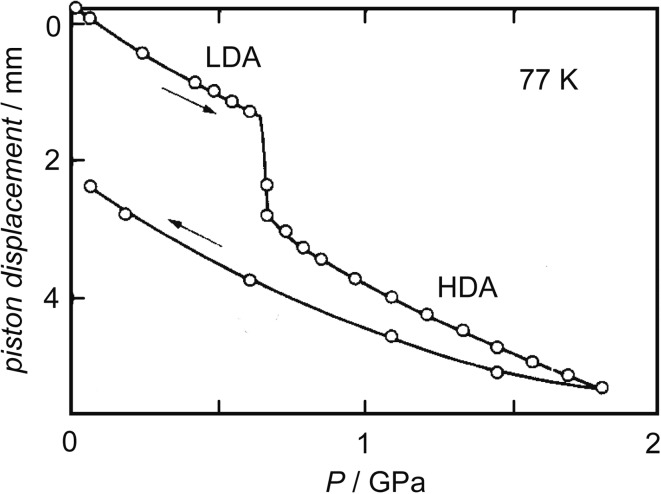
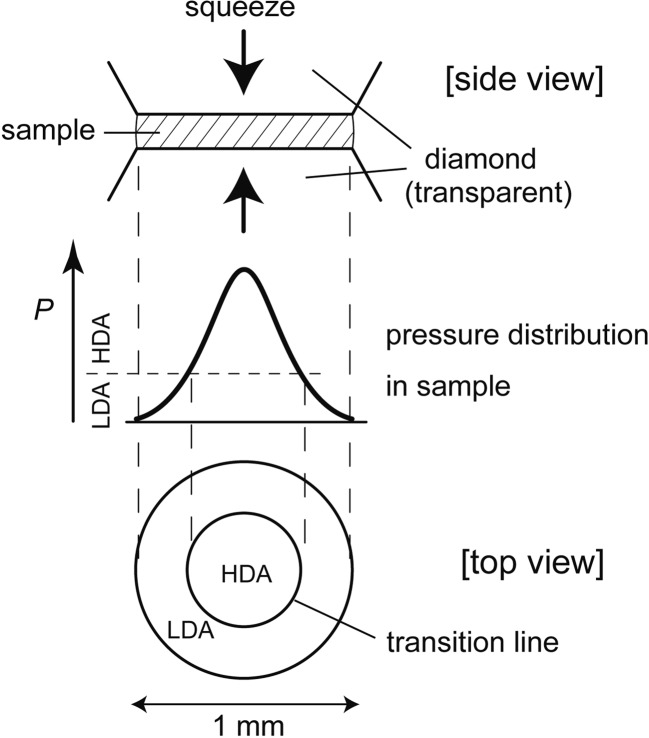
Slightly before the proposal of Poole et al., we squeezed directly LDA powder at 77 K between two diamonds of the so-called “diamond-anvil cell” (Fig. 9) and then heated the equipment from 77 K. We watched the sample under pressure during the heating and observed the transition line between the low-pressure LDA and the high-pressure HDA visually. The existence of the line meant the existence of a difference in their refractive index, or density. The line became gradually sharper and more distinct while the amorphous ices relaxed by the heating until their crystallization at ~150 K. This showed clearly the existence of two amorphous phases up to the crystallization temperature. From this observation, we mentioned the possibility of a large and rapid change in density of compressed liquid water near T_g.¹⁷⁾ In a different study using a piston-cylinder apparatus, I measured the volume of LDA and that of HDA at different pressures and temperatures, as shown in Fig. 10. I confirmed the LDA-HDA transition was reversible and it had hysteresis. These results were consistent with the discontinuity of the transition.¹⁸⁾ Later, we kept a lump of HDA at a fixed temperature at one atmospheric pressure and observed the temporal HDA-to-LDA transition. The HDA-LDA boundary region propagated in the sample, and the width of the boundary region appeared to narrow simultaneously.¹⁹⁾ This hinted that the transition occurred discontinuously by cooperative movement of molecules.

Fig. 9.

Schematic illustration of visual observation of the LDA-HDA transition in the diamond-anvil cell.

Fig. 10.

The volume of amorphous forms of H₂O at low temperatures.¹⁸⁾ The transitions between HDA and LDA are indicated by arrows.

4.1.2. Continuity between HDA and liquid water

As illustrated by the bold broken line of Fig. 11, the melting line of ice I_h became the amorphization line at low temperatures. Accordingly, HDL made by melting and HDA made by amorphization were thought to connect directly around the supposed T_g.²⁰⁾ Actually, this broken line was obtained by the compression of emulsified ice I_h, that was the micrometer-size crystalline ice dispersed in oil. This experiment started as follows. It was known that the emulsified liquid water, or micrometer-size droplets of water, when cooled below water’s freezing point, hardly changed into ice I_h. From this, I wondered if it was difficult for the emulsified ice I_h to change to other crystalline structures. In order to clarify this, I made the emulsified ice I_h by the crystallization of emulsified liquid water in NML and compressed it. It did not change to other crystalline phases on the line A of Fig. 3b, but it melted to the supercooled high-density liquid water (HDL) on the melting line B in the figure. Inside the NML, it was considered that the HDL, produced by the melting of ice I_h, crystallized to high-pressure ices immediately (Fig. 11). On the other hand, when compressed at 77 K, the emulsified ice I_h amorphized to HDA at the same pressure as the usual ice I_h amorphized. When the compression of the emulsified ice I_h was repeated at different temperatures, the melting line and the amorphization line were connected into one line. It was considered that the equilibrium “two-phase melting” between ice I_h and water changed continuously toward the “one-phase melting” (or collapse) of ice I_h at temperatures lower than T_g (the arrow in Fig. 11).

Fig. 11.

Illustration of the relationship between melting and amorphization of ice I_h.²⁰⁾ The bold broken line, exp., is the experimental data.

Later, we cooled the emulsified liquid water rapidly, ~10³ K/s, under pressure, vitrified it and decompressed the glassy water to one atmospheric pressure at 77 K. When heated, the glass changed to LDA, and this behavior was the same as that of HDA. This suggested HDA made by the pressure-induced amorphization resembled the vitrified HDL.²¹⁾ The existence of the glass transition from HDA to HDL was also hinted from the analogy of the glass transitions of dilute LiCl-aqueous solutions under pressure.²²⁾

4.1.3. My view on the problem

From these evidences, I believed the discontinuity of the LDA-HDA transition (the arrow-1 of Fig. 12b) and the thermodynamic connection between HDA and liquid water (the arrow-2 of Fig. 12b). This was the reason why I believed the LLCP hypothesis shown by the broken line-3 of Fig. 12b. The hypothesis seemed the simplest explanation for these experimental results. However, these evidences did not offer decisive proofs and, therefore, confusion of explanations existed. Although we could not affirm the discontinuity between LDA and HDA, and although some researchers suspected that HDA, the collapsed ice I_h, might be microcrystalline, I began the experiments of the supercooled liquid water in order to search for the hypothetical LLCP (or paradoxically for a clear disproof of LLCP). Here, I always used the emulsified sample to hinder both the crystallization of the liquid and the crystal-crystal transition. The surfactant of the emulsion hardly dissolved in water, and the thermodynamic data of the emulsified water were practically the same as those of pure water in the region of overlap.

Fig. 12.

The P-V-T relationship between liquid water and amorphous ices obtained by experiments (the lines and the gray regions). a: before our studies. b: this figure corresponds to Fig. 10. c: the arrows are the melting lines of crystalline ices, suggesting the existence of liquid water along the lines (see Figs. 11 and 14). d: estimation of the location of LLCP by adjusting the scaling function.

4.2. The location of LLT

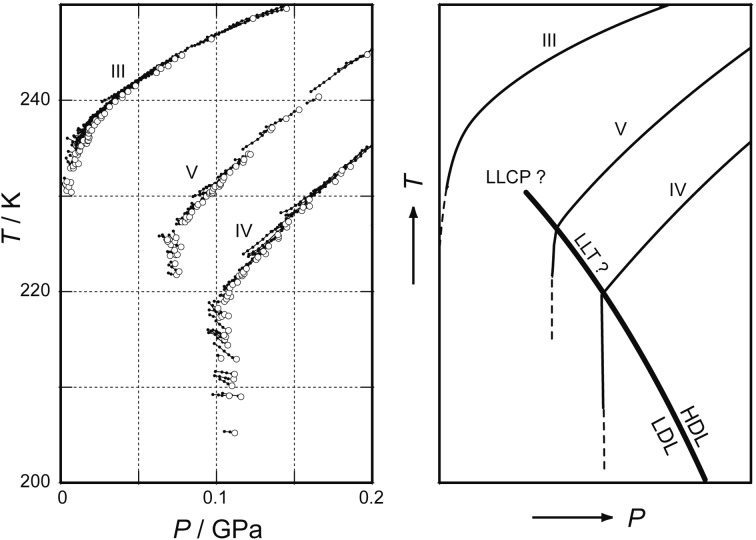
Although we could not study the supercooled water in NML directly, the low-temperature metastable melting lines of the micrometer-size crystalline ices could be measured as demonstrated in Fig. 11. As shown in Fig. 13, if LLT existed, and if the LLT line intersected with such a melting line, the slope of the melting line had to change discontinuously because the manner of melting would be different between LDL and HDL. Therefore, the metastable melting line of the emulsified ice IV, a high-pressure ice, was measured. It was found that the slope of its melting line was discontinuous at a point on the theoretically expected LLT line. Consequently, the existence of LLT, or the existence of the two liquid phases, was suggested indirectly.²³⁾ Meanwhile, Stanley invited me to write together a review article about the relationship between the liquid water and the two amorphous ices, and we co-authored it.²⁴⁾

Fig. 13.

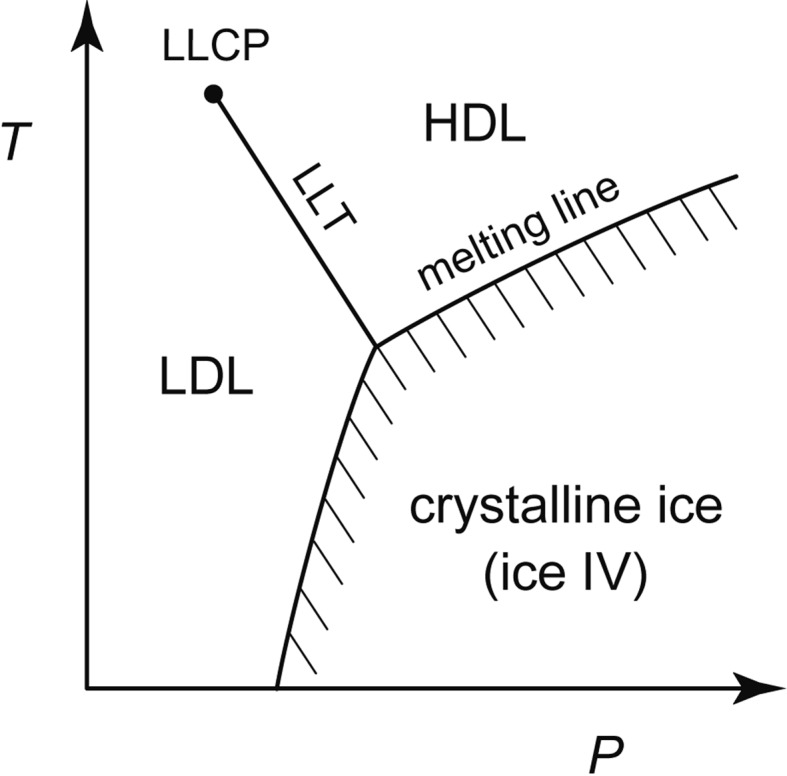
Illustration of the discontinuous change in the slope of a melting line.

4.3. The location of LLCP

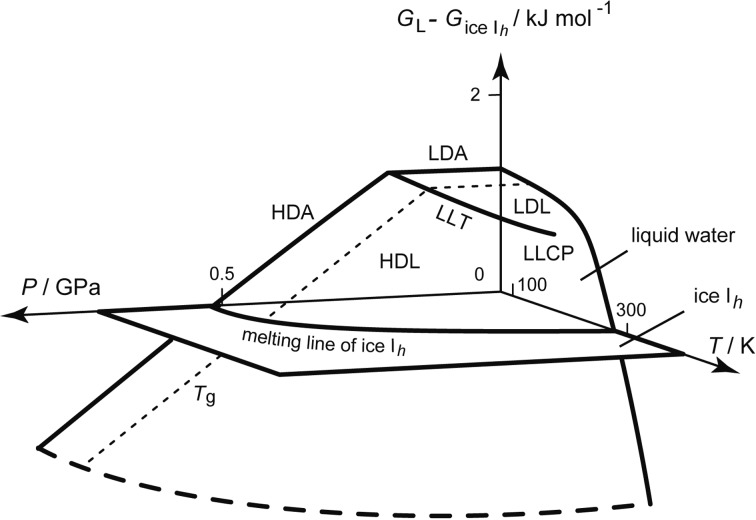
Contrarily, some researchers thought that the slope of the melting line of ice IV might curve strongly and continuously if the experiment were carried out much more precisely. Therefore, even if the change in the slope appeared experimentally discontinuous, the discontinuity was doubted logically because experimental errors were always inevitable. Nevertheless, I measured the melting lines of other high-pressure ices. Then, I hinted the location of LLCP experimentally (Fig. 12c). In Fig. 14 are shown the melting lines of D₂O ices. The melting lines of ice IV and ice V appeared to bend suddenly at ~220 K and ~225 K, respectively. In contrast, the melting line of ice III continued smoothly to low pressures. This suggested that LLT disappeared around ≈50 MPa and ≈230 K; the LLCP of D₂O might be located around here.²⁵⁾ Such melting lines were also used to estimate the water’s Gibbs-energy surface that had LLT and LLCP (Fig. 15).²³⁾

Fig. 14.

The melting lines of emulsified D₂O ices, III, IV and V.²⁵⁾ The almost vertical melting lines suggested small entropy of LDL.

Fig. 15.

The supposed difference between the Gibbs energy of liquid water, G_L(P, T), and that of ice I_h, G_{ice Ih}(P, T).²³⁾ The hypothetical LLT and LLCP are drawn. The surface near LLCP might be described by the scaling function.

Even though it seemed almost impossible to detect LLCP in NML directly by experiment, we might be able to suppose the location of LLCP by adjusting the scaling function, which described general critical phenomena, to supercooled water (Fig. 12d). A method for this was recently proposed,²⁶⁾ and I tried the method by using my new volumetric data of supercooled water. Then, the LLCP of H₂O was located around ≈50 MPa and ≈223 K (personal communications).

5. Conclusion

Our main results on water and amorphous ices are listed below and may be read in conjunction with Figs. 12b and 12c.

1. The discovery of HDA: the pressure-induced amorphization.¹³⁾

2. The discovery of apparently discontinuous LDA-HDA transition: polyamorphism.^{15),17)–19)}

3. The experimental results consistent with the connection between HDA and liquid water.^20)–22)

4. The experimental results consistent with LLT.²³⁾

5. The experimental results consistent with LLCP.²⁵⁾

Our discovery of the apparent polyamorphism in amorphous ice gradually and steadily inspired other researchers as if we have been awakened to the truth, and the polyamorphism formed a basis for the LLCP hypothesis. The hypothesis is strongly supported, but not proven, by the various evidences provided in these 25 years. The LLCP, if it exists, would affect the liquid state in a wide pressure-temperature region. As illustrated in Fig. 12, the minimum of volume (or the maximum of density) at 4 °C at one atmospheric pressure is explicable by the transformation of the high-temperature HDL toward the low-temperature LDL.

At least the following consensus seems emerging among water researchers. In the experimental aspect, the LDA-HDA transition is likely discontinuous, and the structure of HDA resembles that of our familiar liquid water (or HDL).^27),28) In the theoretical aspect, almost all studies of the simulations support the LLCP hypothesis.^29),30) The simulations can avoid the crystallization in NML and can provide information about the structure of liquid water. In addition, polyamorphism is found to arise generally from the ‘wavy’ pair potential between two model particles.^31),32) So far, the LLCP hypothesis has no serious defect although there are many unsolved questions such as the nucleation and growth of the LDA-HDA transition.

6. Implications

Polyamorphism is one of the basic concepts of the condensed-matter science. The polyamorphism in amorphous ice has stimulated the studies on the general polyamorphic transition, and these studies opened the broadened prospects on the researches of liquid and glass.^33)–35)

Needless to say, water is related to various research fields.³⁶⁾ If we understand how the polyamorphism of water is affected by solutes and by the electromagnetic field etc., its knowledge may be useful to understand the phenomena like photosynthesis.

Polyamorphism was already applied to the experimental studies of aqueous solutions, water in narrow pores,³⁷⁾ and water inside proteins.³⁸⁾ Because these conditions sometimes hindered the crystallization of water in NML, such studies were used to examine the LLCP hypothesis and then to support it. An example was the liquid-liquid immiscibility of the dilute salt water at low temperatures, which was suggested about 40 years ago.³⁹⁾ We presented evidences for the immiscibility by using LiCl-aqueous solutions and explained the immiscibility by the polyamorphism of pure water.^40)–42) As a result, LiCl was thought to dissolve in HDL than LDL. These studies would have implications for ice nucleation in clouds and in plants etc.,⁴³⁾ because the separated LDL readily crystallized.

Generally speaking, water represents liquid. Therefore, the understanding of water may be the understanding of liquid. The notion of polyamorphism certainly changed the previous understanding of water qualitatively. About 350 years has passed since the experiment of “Academie del Cimento”, and the existence of two kinds of liquid water, the secret behind the density-maximum phenomenon, is now gradually being revealed.

Abbreviations

LDA

low-density amorphous solid

HDA

high-density amorphous solid

LDL

low-density liquid

HDL

high-density liquid

LLT

liquid-liquid transition

LLCP

liquid-liquid critical point

NML

no-man’s land (the pressure-temperature domain of easy crystallization)

Profile

Osamu Mishima was born in Hiroshima in 1951. He learned the high-pressure science and technology at Faculty of Engineering Science, Osaka University, and studied the high-pressure phases of ice. He received his B. Eng., M. Eng., and Dr. Eng. from Osaka University in 1974, 1976, and 1979, respectively. After he served as an Assistant at the Osaka University Faculty of Engineering Science’s High-Pressure Laboratory, he became a Research Associate at National Research Council of Canada in Ottawa. He discovered both the pressure-induced amorphization of crystalline ice and the polyamorphism of amorphous ice with collaboration of Dr. E. Whalley and Dr. L. D. Calvert. These discoveries have started to change the view of water and to provide a much broader perspective on liquid and glass. He joined National Institute for Researches in Inorganic Materials (NIRIM) in Tsukuba in 1985. He continued the studies on the polyamorphism of water while he made at a high pressure the first primitive ultraviolet-light-emitting pn-junction diode of cubic-boron-nitride (cBN) semiconductor. At NIRIM, and at National Institute for Materials Science (NIMS) since 2001, he focused his studies on the water researches as an Independent Senior Researcher. He received the Nishina Memorial Prize in 2006, and was named NIMS Fellow in 2007. He received the Japan Society of High Pressure Science and Technology Award in 2002 and the Commendation for Science and Technology by the Minister of Education, Culture, Sports, Science and Technology (Prizes for Science and Technology, Research Category) in 2008.