Abstract
A new design of a system for preliminary detection of defective hearts is proposed which is composed of two subsystems, in which one is based on the relationship between the electrocardiogram (ECG) and phonocardiogram (PCG) signals. The relationship between both signals is determined as an impulse response (h(n)) of a system, where the decision is made based on the linear predictive coding coefficients of a heart’s impulse response. The other subsystem uses a phase space approach, in which the mean squared error between the distance vectors of the phase space of the normal heart and abnormal heart is judged by the likelihood ratio test (Λ) value, on which the decision is made. The advantage of the proposed system is that a heart’s diagnosis system based on the ECG and EPCG signals can lead to high performance heart diagnostics.
Keywords: signal transduction therapy, heart defect detection, electrocardiogram, envelop of phonocardiogram, phase space
Introduction
Heart disease includes any disorder that affects the heart’s ability to function normally. There are various forms of heart disease, for example, arrhythmias, prolapsed mitral valve, coronary artery disease, congenital heart disease, and so on. The most common cause of heart disease is a narrowing of the coronary arteries that supply blood to the heart muscle but some heart diseases are present at birth. In general, heart disease has been investigated by various methods,1–6 one of which is the noninvasive method, which has been widely used and recognized as the best method of investigation. In this work, we recommend using an electrocardiogram (ECG) signal for heart disease investigation,7–16 because it is a simple and noninvasive diagnostic tool. The signal can be easily obtained by placing the electrodes on the chest wall and limbs and hooking them to an ECG machine. Besides an ECG signal, a phonocardiogram (PCG) signal is also employed for heart disease diagnosis.17–21 In such a case, a PCG signal is the recorded heart sound using a microphone placed on the chest. Both ECG and PCG signals play important roles in heart abnormality detection; however, diagnosis based on ECG signal or PCG signal alone cannot detect all cases of heart symptoms. For example, an ECG signal can reveal various physiological and abnormal behaviors of the heart. But some symptoms such as heart murmurs often caused by defective heart valves cannot be detected from an ECG signal. Hence, some research has focused on diagnosing heart defects based on the relationship between ECG and PCG signals13–26 which can lead to high performance heart diagnostics.
Both ECG and PCG signals can thus be used together for early stage detection of heart disease. Early detection of heart disease is important because it can ease the treatment and also save people’s lives. In this work, an automated system for preliminary heart defect detection is proposed. The proposed system is composed of two decision-making subsystems. The first subsystem is based on the system’s impulse response and the other is based on phase space. The concept of the impulse response-based subsystem uses the relationship between an ECG signal and an envelope of a PCG signal (EPCG) of a heart. Since the PCG signal is easily corrupted by noises made by other organs,19–22 the envelope of a PCG signal is used instead of the PCG signal itself so as to avoid the effect of such interference noises. In this technique, a human heart is defined as a system that has an ECG signal and an EPCG signal as an input and an output, respectively. By considering a heart as a system, the impulse response h(n) of the system can be employed to indicate whether the heart is functioning normally. Hence, the ratio between discrete Fourier transform (DFT) of the ECG signal and DFT of the EPCG signal is determined where the inverse discrete Fourier transform (IDFT) of the result is the impulse response of the heart. In order to realize an automated system, a neural network is chosen for the learning/justifying scheme. However, rather than feeding the impulse response to a neural network, linear predictive coding (LPC) coefficients of h(n) are used instead. The trained neural network based on LPC coefficients representing a heart system can be employed for preliminary diagnosis of whether the heart is defective.
For the second subsystem, the chaos method is used as an additional decision-making technique. Basically, the chaos method is used to characterize the behavior of a physiological dynamic signal from a single experimental time series and has recently been applied to describe the behavior of ECG signals in27 and PCG signals in.28 In this paper, a phase portrait or a phase space of an ECG signal and of an EPCG signal is used to represent the behavior of an ECG signal and an EPCG signal. Mean squared error (MSE) between the distance vector of the objective ECG or EPCG signal and the distance vector of the reference signal is determined. It is noted that the distance vector is a vector whose element is the distance from an origin point to each point on the phase space. The statistical MSE data set of each case, normal or abnormal heart function, is applied to generate the probability density functions. The obtained MSE probability density functions are employed to determine a likelihood ratio test value (Λ). This value is a threshold for making a decision that the heart is either normal or abnormal.
Theoretical background
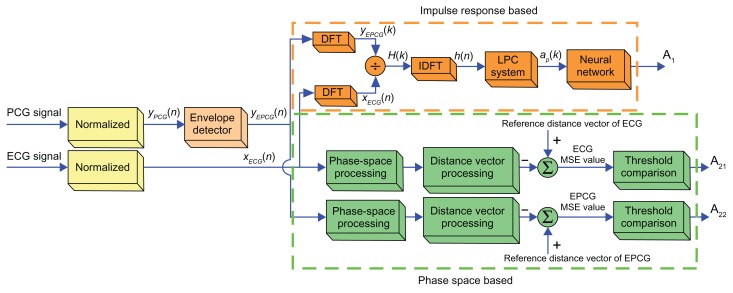
Generally, the ECG and PCG signals are concurrent phenomena, in which the former is the electrical signal while the latter is the mechanical signal. However, the phenomenon of ECG and PCG signals is related, because the PCG signal is obtained by the mechanical heart operation, which relies on the electrical heart operation. In order to activate the mechanical heart operation that generates the PCG signal, the ECG and PCG correlated signals are used. Based on the previous concept,26 the ECG and EPCG impulse response signals have shown a linear relationship and time-invariance. Thus, the human heart will be considered as a linear system in order to find the heart impulse response. The concept of the automated preliminary heart defects detection system can be illustrated as a block diagram (see Figure 1). There are two subsystems, the impulse response and the phase space subsystems. The details of each subsystem will be described later in this paper. However, it is worth noting that the ECG and EPCG signals employed in this research are normalized to be the signals at a standard heart rate, which for an adult whose heart is healthy (normal) in relaxing state is around 80 beats per minute. This pre-processing is needed because the recorded ECG/PCG signals of each person are derived from different heart rates. Even the signals recorded from the same person but at different times can be derived from different heart rates. Therefore, one period of different signals may have different numbers of signal samples. Thus, the signals processed in this work are pre-processed by frequency normalization. With this pre-processing, the signals will be the same during each period of data collection. Then the details of the impulse response and phase space subsystems are discussed.
Figure 1.
Block diagram of new automated preliminary heart defect detection.
Abbreviations: DFT, discrete Fourier transform; IDFT, indiscrete discrete Fourier transform; LPC, linear predictive coding; ECG, electrocardiogram; EPCG, envelope of a PCG signal; PCG, phonocardiogram.
Heart rate normalization
Let x(n) be a period, whose length is M samples, of an ECG/PCG signal of interest at an arbitrary heart rate. The discrete Fourier components of x(n) can be expressed as29
| (1) |
where k is the frequency index corresponding to digital frequency for 0 ≤ k ≤ M − 1.
This frequency index corresponds to kfs/M in Hertz (Hz) where fs is a sampling frequency. At a normal heart rate (80 beats per minute), a period is considered to be 0.75 seconds. If the sampling frequency fs is 8000 Hz, one period of 80 beats per minute heart rate ECG/PCG signal must contain 6000 samples (N). Since heart rate of the ECG/PCG signal at the recording time may not be at such rate, one period of the obtained signal (M) may be longer or shorter than 6000 samples. At this point, α is defined as the ratio of the standard length N and the obtained length M which are one period of ECG/PCG signal, at 80 beats per minute and arbitrary heart rates, respectively.
Now let us consider the parameter α. α > 1 implies that the heart rate of the interested ECG signal is higher than the standard rate. Contrarily, α < 1 implies it is lower than the standard rate. To normalize the length of the obtained signal to N samples in one period or to make α = 1, the obtained signal must be sampled by using a frequency lower or higher than 8000 Hz for α > 1 or α < 1, respectively. Since the signal has readily been obtained at fs = 8000 Hz, the alternative method can be achieved by synthesizing the normalized heart rate signal with the following relationship
| (2) |
where 0 ≤ n ≤ N − 1 and |X(k)|, ∠X(k) are magnitude and phase component of DFT coefficients X(k), respectively. In addition, k represents the frequency index corresponding to the highest digital frequency which occupies the spectrum of ECG and PCG bandwidth.
In this paper, the normalized heart rate technique for pre-processing is proposed. The parameter alpha is employed to adjust the time period scale, where we can choose any alpha value to obtain the normalized heart rate, which does not affect heart defect detection. Because of the normalized heart rate technique is employed to adjust time period scale (α) of the ECG and PCG signals but it is not used to adjust the waveform characteristics of the ECG and PCG signals. Therefore, the normalized heart rate technique does not affect heart defect detection, which is analyzed by using the waveform characteristics of the ECG and PCG signals. However, the signal scale is adjusted to be the same in each period of data length. Therefore, the parameter alpha value must be the same for each normalized heart rate.
Envelope detection of PCG signal
In this section, a technique for finding the envelope of a PCG signal is described. The concept is similar to the envelope detection used in amplitude demodulation.30 Envelope of a PCG signal is considered as information which is carried by the PCG carrier signal. To determine the envelop of a PCG signal the positive level of the PCG signal is first obtained, and then the signal is passed through a low pass filter to obtain the envelope.
Impulse response-based subsystem
The preliminary automated heart defect detection that is based on impulse response of a system can be depicted by a block diagram (Figure 1). In this work, a human heart will be considered as a linear system where an ECG signal (xECG(n)) and an EPCG signal (yEPCG(n)) are an input and an output of the system, respectively. With the linear property of a system, it can be shown that the output of the heart is determined by the convolution between the ECG input and the impulse response of the system (h(n)) as
| (3) |
By taking z-transform on both sides of equation (3), it thus yields
| (4) |
Hence, the transfer function of a system (H(z)) can be determined by
| (5) |
From equation (5), the DFT (H(k)) of the system is obtained by the following relationship
| (6) |
where YEPCG(k) and XECG(k) is the DFT of yEPCG(n) and xECG(n), respectively.
To obtain the impulse response (h(n)) of a system, the IDFT is applied on both sides of equation (6), which is
| (7) |
As shown in equation (7), the impulse response of a system can be determined by using the IDFT of the ratio between the DFT of an EPCG signal and the DFT of an ECG signal.
Linear predictive coding
The LPC technique is employed to extract the features of the impulse response in the form of LPC coefficients. The basic idea underlying LPC is that each signal sample x(n) is approximated as a linear combination of previous p samples as described in the following equation:
| (8) |
where x(n) is a signal sample, x′(n) is a predicted signal, p is the order of LPC and, ap(k) s are LPC coefficients.
By considering x(n) employed in equation (8) to be the impulse response (h(n)) of a heart system, an error between an original signal and an estimated signal is given by
| (9) |
The LPC coefficients (ak) are defined by minimizing the MSE. The procedure for minimizing the MSE is obtained by setting the partial differential MSE with respect to all of the parameters akto be zero. The LPC coefficients are found to be
| (10) |
where Rhh is a p × p autocorrelation matrix, rhh(m) is the autocorrelation of the sequence h(n), and ap is a p × 1 vector of model parameters.
The LPC coefficients ap(k) are employed to represent the feature of an impulse response of a system. In this research, two sets of the prototype LPC coefficients, one set for a normal heart system and another for an abnormal heart system, are fed to the input of an artificial neural network for learning and making decisions.
Decision making using a neural network
It has been shown that an artificial neural network (ANN) has often been employed in biomedical engineering research to classify the data.31,32 The ANN is inspired by the biological nervous systems and it is configured for a specific application, such as pattern recognition or data classification. In this research, an ANN is employed as a tool for distinguishing between a normal and an abnormal heart. In this study, the ANN used for heart pattern recognition is a feed-forward back propagation (BP) neural network. The BP algorithm is a supervised learning algorithm using feed-forward networks. It is basically a gradient descent method and its objective is to minimize the MSE between the target values and the actual output of the network.
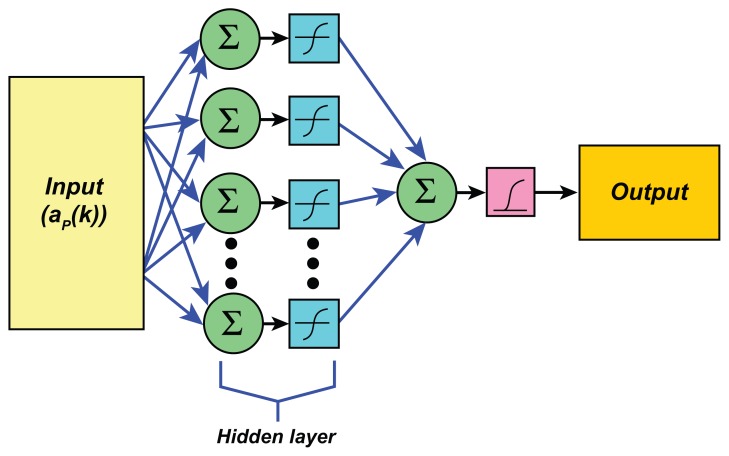
The ANN employed in this work is demonstrated in Figure 2. The ANN structure is composed of three layers, (i) the input layer, (ii) the hidden layer of neurons with a tangent sigmoid transfer function, and (iii) the output layer of neuron with linear transfer function. The signal fed to be the input for the input layer is the set of LPC coefficients that are impulse response signals of the heart system. The ANN output target values are 0 for an abnormal heart and 1 for a normal heart.
Figure 2.
Structure of the artificial neural network employed in this work.
The output obtained from the neural network can be one of four cases: TP, the value of true positive; FP, the value of false positive; TN, the value of true negative; and FN, the value of false negative. The decision on whether a heart is normal or abnormal is determined by positive predictive value (PPV) and negative predictive value (NPV), respectively. These values are evaluated, respectively, by
| (11) |
| (12) |
Phase space-based subsystem
Based on the concept of phase space, a data sequence measured in a time domain can be transformed into a geometric figure in space, which is called the phase space. Doing this can reveal some features that cannot be observed in a time domain. The phase space can be constructed by a procedure that starts from raw data and builds vector by iteration of time delay. In a discrete time signal, a scalar time s(n), n = 1,2,…, N can be extended in a multidimensional phase space using time delay coordinates. The delay coordinate construction approach, based on the Taken theorem, is applied to a series of data such as
| (13) |
Here, τ is a delay time, n is the number of sample used for phase space construction, m is the embedding dimension.
A reconstructed phase space matrix Y of dimension m and lag τ, called a trajectory matrix, is defined by
| (14) |
where row vectors S(n), with n = 1, 2,…, M represent individual points in the reconstructed phase space. The number of points is M = N − (m − 1)τ. The attributes of the constructed phase space plot depend on the choice of value for τ. The value of τ is typically chosen as the first minimum (τ = 1) in the graph. For a two-dimensional (m = 2) phase space, the trajectory matrix thus is
| (15) |
However, difficulty could be encountered in discriminating between normal and abnormal cases from the obtained phase spaces due to the similarity of spread characteristics of the curves. To improve the performance of classification, the phase space in this work is the plotting coordinates (s(n), s(n + 1)−s(n)), where s(n + 1)−s(n) is the tangent vector. The reconstructed phase space matrix employed in this research thus is given by
| (16) |
The block diagram of the subsystem for preliminary automated heart defect detection that is based on phase space of ECG and EPCG signals is shown in Figure 1.
Distance vector
The distance of the vector from the origin point (O) to the P point is equal to that of the displacement vector (⇉ ) which is determined by
| (17) |
By using the definition of the distance of the vector, the distance from the origin point to each point on the phase space is calculated in a form of vector. When the distance vector of the objective signal is determined the error between this vector and that of the reference normal heart is obtained. MSE of the error vector is then given by
| (18) |
Here, N is a number of samples, dref is a reference distance vector, either of ECG signal or EPCG signal, for a normal heart and dobj is a distance vector of the objective signal, either ECG signal or EPCG signal.
It should be mentioned that the reference distance vector is derived from the reference phase space of a normal heart. To obtain the reference phase space, many ECG/PCG data sequences from31,32 are employed to find their phase spaces. These results are averaged for a reference phase space of a normal heart for ECG signal and EPCG signal.
Likelihood ratio test
The MSE value as previously discussed can be used to make a decision about whether the objective signal is normal or abnormal. To achieve a definite decision, a threshold value of MSE must be defined. In this research, this threshold is obtained by using a likelihood ratio test (Λ).33 The likelihood ratio test is a statistical test of the goodness-of-fit between two models. It provides one objective criterion for selecting among possible models.
In general, the likelihood ratio test can be thought of as a reversed version of conditional probability. The conditional probability of x is P(ω|x) for a given parameter ω that is formalized in Bayes theorem.33 The likelihood ratio test is calculated to find the threshold value between probability density functions of MSE values derived by equation (18) for a normal case and an abnormal case through ECG signals or EPCG signals. The decision rule therefore is
| (19) |
Where P[ω1|x] is conditional probability of MSE values of a normal case and P[ω2|x] is conditional probability of MSE values of an abnormal case.
By applying Bayes theorem in equation (19), it is
| (20) |
From equation (20), P(x) does not affect the decision rule so it can be neglected. Hence, the likelihood ratio test Λ(x) is redefined as
| (21) |
where P[x|ω1] is a conditional probability density function (likelihood) of MSE values of a normal case, and P[x|ω2] is a conditional probability density function (likelihood) of MSE values of an abnormal case.
It is noted that P[x|ω1] and P[x|ω2] is defined by using a Gaussian distribution function as given by
| (22) |
where μ is the mean value of distribution and σ2 is the variance of distribution. In addition, the ratio P(ω2)/P(ω1), which is the maximum likelihood ratio test, is initially set to 1. The obtained likelihood ratio test is employed to make judgment on the given MSE value of the distance vector of the objective signal. As previously described, the proposed system is performed in a computer with the results of each subsystem discussed in the following sections.
Impulse response-based subsystem
Before the results are demonstrated, it should be noted that for the impulse response-based algorithm, it is important that the ECG signal and the PCG signal employed to determine the impulse response h(n) of a heart system must be recorded or measured at the same time. This restriction results in limited numbers of signal samples in the experiment. In this research, 80 sets of ECG signals and PCG signals measured at the same time from the voluntary patients are employed. Among these sets of signals, 40 sets were measured in normal cases and 40 sets in abnormal cases. In each case, 20 sets of data samples are used in the neural training process and 20 sets of data samples are used in the testing process.
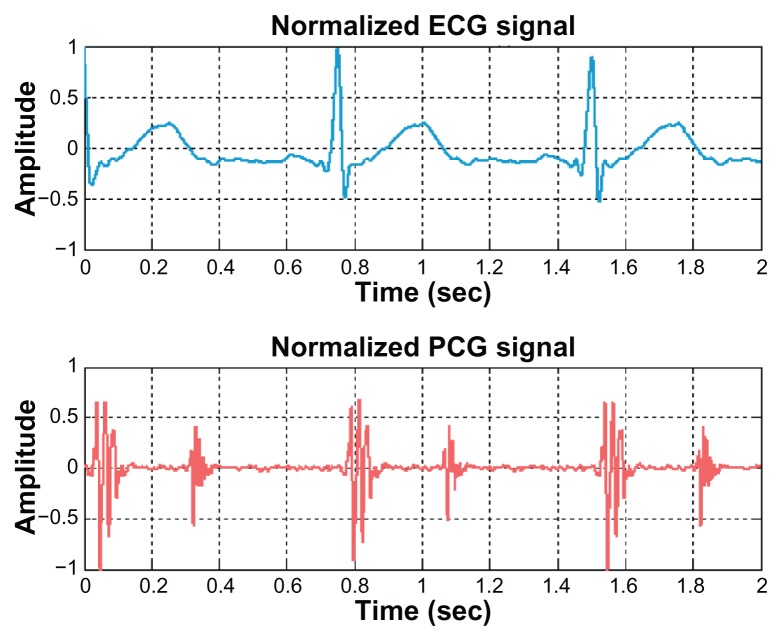
First, all signals (ECG and PCG signals) employed in this research are normalized to 80 beats per minute heart rate. In addition, the magnitude of these signals is normalized so that it is confined in the range −1 and 1. An example of the normalized ECG signal and the normalized PCG signal is demonstrated in Figure 3.
Figure 3.
Example of normalized ECG and PCG signals.
Abbreviations: ECG, electrocardiogram; PCG, phonocardiogram.
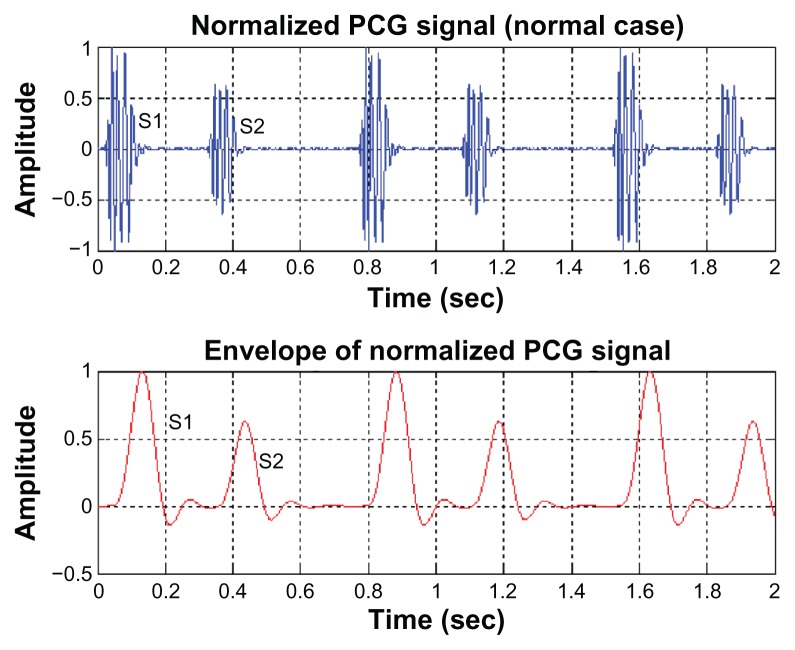
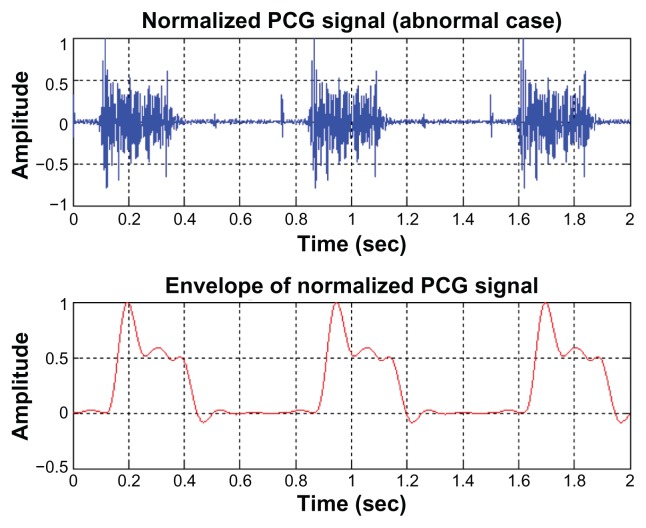
For PCG signals, the envelope of the signals is employed for the decision-making procedure. Examples of the envelope of the normalized PCG signals for normal cases and abnormal cases are illustrated in Figures 4 and 5, respectively. As can be seen, the first and second sounds clearly appeared in the normal cardiac sound (Figure 4, upper). But for abnormal mitral valve regurgitation case (Figure 5, upper), these sounds cannot be distinguished from each other.
Figure 4.
The envelope of a normal PCG signal.
Abbreviation: PCG, phonocardiogram.
Figure 5.
The envelope of an abnormal PCG signal.
Abbreviation: PCG, phonocardiogram.
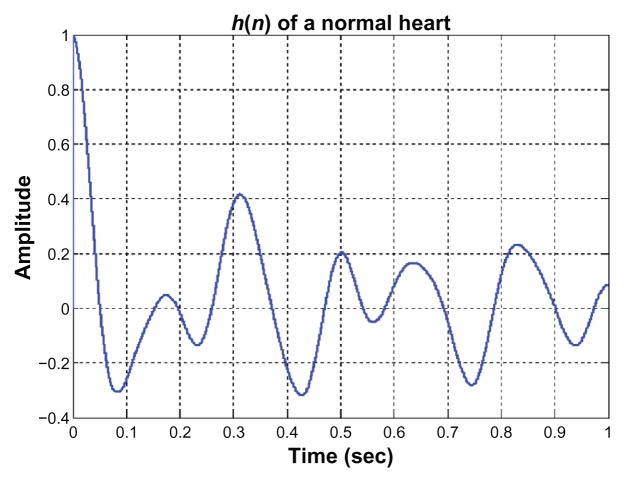
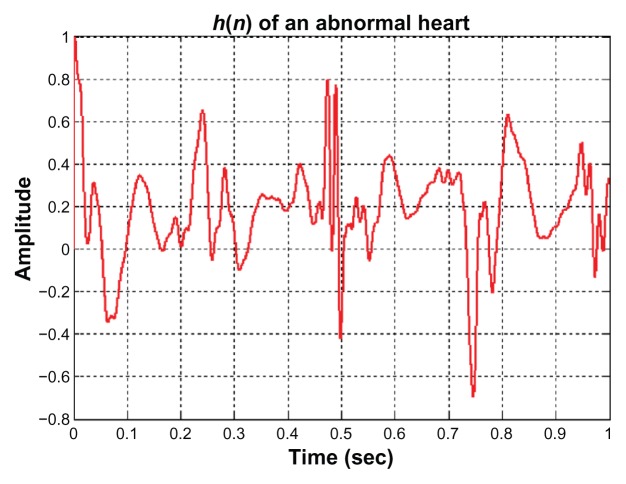
Once the ECG and PCG signals are normalized and the EPCG signals are obtained, the impulse response of a heart system is then determined. Examples of the impulse response of a normal heart system and of an abnormal heart system are illustrated in Figures 6 and 7, respectively. From 80 sets of ECG signals and PCG signals, 80 impulse response signals are obtained; 40 signals are of normal cases and 40 signals are of abnormal cases. Twenty signals of each case are fed to the input of the back propagation neural network for training process. After the learning process is completed, the other 20 signals of each case are tested by the trained neural system. The decision making by the neural network about whether a heart system is normal or abnormal depends on the output value (y) of the neural network. The decision will be normal if 0.9 < y < 1 and abnormal if y is <0.9. The results of neural training and testing processes are illustrated in Table 1. The results for PPV and NPV are approximately 85% and 90%, respectively. These numbers could be improved if the collected data samples are large. Because volunteer numbers were limited and because of the restriction that an ECG signal and a PCG signal must be measured at the same time and from the same person, the number of data samples used in this technique is not as high as desired.
Figure 6.
The impulse response of a normal heart system.
Figure 7.
The impulse response of an abnormal heart system.
Table 1.
Artificial neural network diagnosis results
| Cases | Diagnosis results (impulse response based) | ||||
|---|---|---|---|---|---|
|
|
|||||
| Normal | Abnormal | Accuracy (%) | |||
|
|
|||||
| PPV | NPV | ||||
| Training | |||||
| Normal | 20 | 20 | 0 | 100 | – |
| Abnormal | 20 | 0 | 20 | – | 100 |
| Testing | |||||
| Normal | 20 | 18 | 2 | 90 | – |
| Abnormal | 20 | 3 | 17 | – | 85 |
Abbreviations: PPV, positive predictive value; NPV, negative predictive value.
Phase space-based subsystem
For the phase space approach, the limitation on number of data samples (ECG and PCG signals) is not a problem, because the ECG and PCG signals employed in this method do not need to be measured at the same time and from the same patient. Hence, large samples can be obtained from online databases.31,32
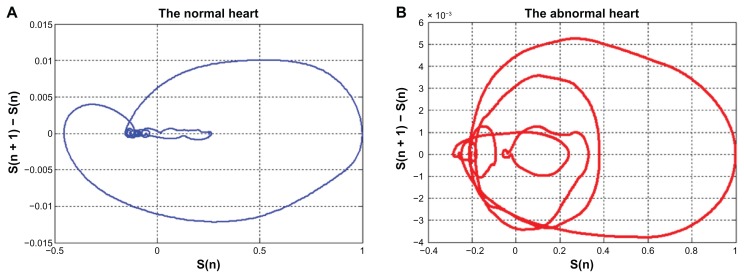
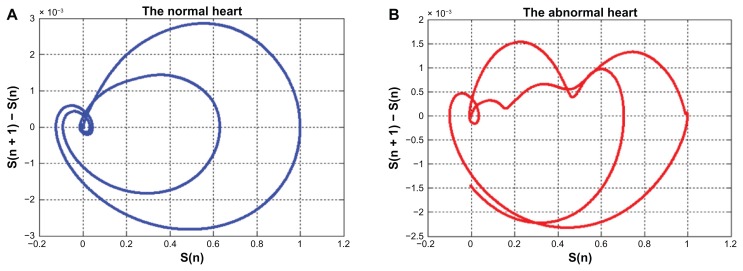
Examples of the two-dimensional phase space of the ECG and EPCG signals are demonstrated in Figures 8 and 9, respectively. By using phase space, the QRS complex as well as the P and T waves in a normal ECG signal can be observed clearly. Different patterns of the phase spaces of normal and abnormal cases can be seen in both ECG and EPCG signals.
Figure 8.
The phase space of ECG signals (A) normal case, (B) abnormal case.
Abbreviation: ECG, electrocardiogram.
Figure 9.
The phase space of EPCG signals (A) normal case, (B) abnormal case.
Abbreviation: EPCG, envelope of a PCG signal.
The obtained phase spaces of ECG and EPCG signals are then employed to determine their distance vectors. Each derived distance vector will be compared with a reference distance vector which is of the normal case to find the MSE value. It is noted that the reference ECG distance vector of the normal case and the reference EPCG distance vector of the normal case are obtained from averaging the phase space patterns of all normal ECG signals and normal PCG signals.
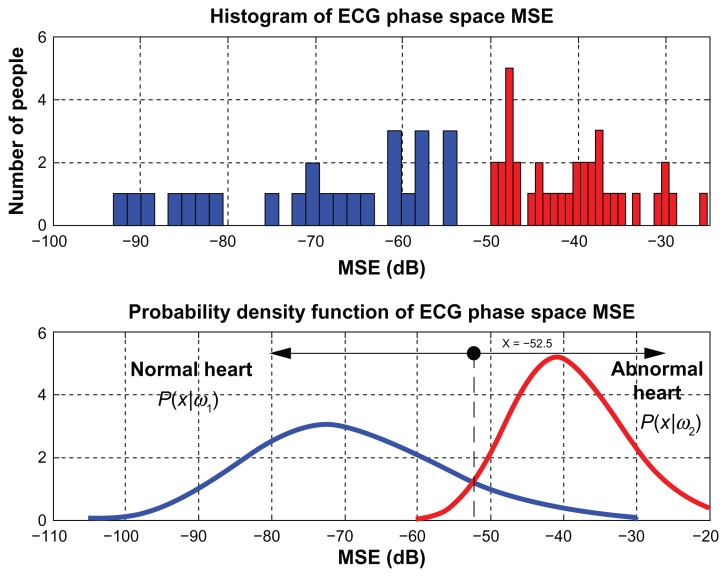
After the MSE values of normal heart and abnormal heart from the phase space of ECG signals and EPCG signals are obtained, mean and variance values are determined and applied to the Gaussian distribution function. For ECG signals, the probability density function of normal heart and abnormal heart are
| (23) |
| (24) |
Then, the likelihood ratio test (Λ(x)) for ECG can be calculated by
| (25) |
and found to be at x = −52.5. Figure 10 presents MSE values obtained from phase spaces of ECG signals (upper) and plots of probability density function of phase space MSE values of ECG signals (lower).
Figure 10.
The likelihood ratio test result of ECG phase space.
Abbreviations: ECG, electrocardiogram; MSE, mean square error.
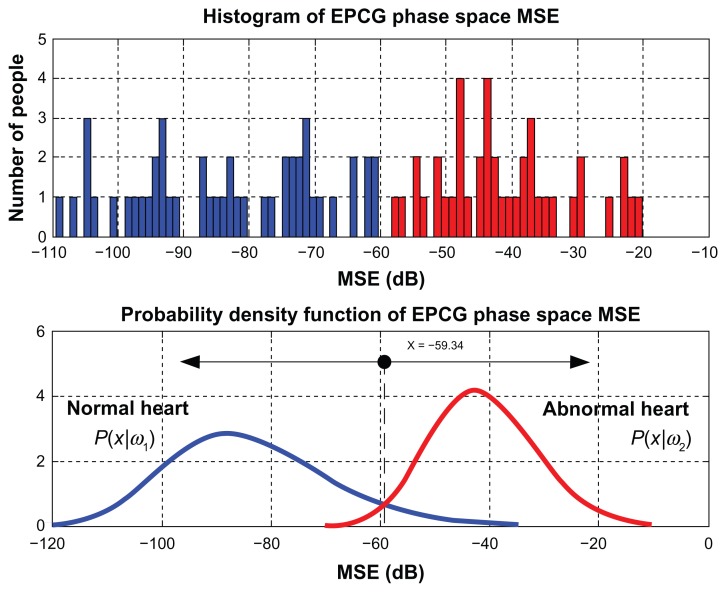
Similarly, mean and variance are determined from the MSE values of normal heart and abnormal heart of EPCG signals and applied to the Gaussian distribution function as following
| (26) |
| (27) |
The likelihood ratio test (Λ(x)) for EPCG is then defined by
| (28) |
and found to be at x = −59.34. MSE values obtained from phase spaces of EPCG signals are shown in Figure 11 (upper) and probability density function of phase space MSE values of EPCG signals are given in Figure 11 (lower).
Figure 11.
The likelihood ratio test result of EPCG phase space.
Abbreviations: EPCG, envelope of a PCG signal; MSE, mean square error.
The system of preliminary heart defect detection used indicates that the heart defect is caused by the abnormal ECG and/or abnormal PCG signals. To confirm the obtained likelihood ratio test, the 80 ECG and 80 EPCG signals used in the impulse response based technique were also tested by using the phase space approach (Tables 2 and 3, respectively). The results obtained show that the phase space-based approach provides 100% accuracy compared with the impulse response-based approach.
Table 2.
Phase space diagnosis results of ECG signals
| ECG signals | Diagnosis results (phase space based) | ||||
|---|---|---|---|---|---|
|
|
|||||
| Normal | Abnormal | Accuracy (%) | |||
|
|
|||||
| PPV | NPV | ||||
| Signal used in ANN training | |||||
| Normal | 20 | 20 | 0 | 100 | – |
| Abnormal | 20 | 0 | 20 | – | 100 |
| Signal used in ANN testing | |||||
| Normal | 20 | 20 | 0 | 100 | – |
| Abnormal | 20 | 0 | 20 | – | 100 |
Abbreviations: ANN, artificial neural network; PPV, positive predictive value; NPV, negative predictive value.
Table 3.
Phase space diagnosis results of EPCG signals
| EPCG signals | Diagnosis results (Phase space based) | ||||
|---|---|---|---|---|---|
|
|
|||||
| Normal | Abnormal | Accuracy (%) | |||
|
|
|||||
| PPV | NPV | ||||
| Signal used in ANN training | |||||
| Normal | 20 | 20 | 0 | 100 | – |
| Abnormal | 20 | 0 | 20 | – | 100 |
| Signal used in ANN testing | |||||
| Normal | 20 | 20 | 0 | 100 | – |
| Abnormal | 20 | 0 | 20 | – | 100 |
Abbreviations: ANN, artificial neural network; PPV, positive predictive value; NPV, negative predictive value.
Conclusion
In this paper, a non-invasive system for detecting heart malfunction is presented. The proposed system consists of two subsystems. One is based on the impulse response of a heart system derived from the relationship between an ECG signal and the envelope of a PCG signal (EPCG). The decision is made by the back propagation neural network from the impulse response signal. The percentage accuracy obtained was 90% and 85% for NPVs and PPVs, respectively. Increasing the size of the collected data samples can improve the accuracy. Because the restriction that there must be an ECG signal and a PCG signal measured at the same time and from the same person limited the number of volunteers, number of data samples used in this technique was not as high as desired. The other subsystem is based on phase space of the signal (ECG or EPCG). The MSE value obtained by comparing the distance vector of the testing signal with the reference distance vector is judged by the likelihood ratio test result. This technique provides 100% accuracy for decision making. The results from both techniques show that the impulse response-based method can be used primarily to detect a heart abnormality, whereas the phase space-based approach can be used to indicate whether the heart defect is caused from the abnormal ECG signal and/or abnormal PCG signal. This proposed preliminary automated heart defect detection technique can provide the opportunity to help patients in rural areas.
Acknowledgments
We would like to thank the King Mongkut’s Institute of Technology (KMITL), Thailand for providing the research facilities.
Footnotes
Disclosure
No conflicts of interest were declared in relation to this paper.
References
- 1.Smetana P, Batchvarov VN, Hnatkova K, Camm AJ, Malik M. Ventricular gradient and nondipolar repolarization components increase at higher heart rate. Am J Physiol Heart Circ Physiol. 2004;286:131–136. doi: 10.1152/ajpheart.00479.2003. [DOI] [PubMed] [Google Scholar]
- 2.Bollmann A, Kanuru NK, McTeague K, Walter PF, DeLurgio DB, Langberg JJ. Frequency analysis of human atrial fibrillation using the surface electrocardiogram and its response to ibutilide. Am J Cardiol. 1998;81:1439–1445. doi: 10.1016/s0002-9149(98)00210-0. [DOI] [PubMed] [Google Scholar]
- 3.Hirai T, Fujita M, Yoshida N, Yamanishi K, Inoko M, Miwa K. Importance of ischemic preconditioning and collateral circulation for left ventricular functional recovery in patients with successful intracoronary thrombolysis for acute myocardial infarction. Am Heart J. 1993;126:827–831. doi: 10.1016/0002-8703(93)90695-6. [DOI] [PubMed] [Google Scholar]
- 4.Mahdyoon H, Klein R, Eyler W. Radiographic pulmonary congestion in end-stage congestive heart failure. Am J Cardiol. 1989;63:625–627. doi: 10.1016/0002-9149(89)90912-0. [DOI] [PubMed] [Google Scholar]
- 5.Remes J, Miettinen H, Reunanen A. Validity of clinical diagnosis of heart failure in primary health care. Eur Heart J. 1991;12:315–321. doi: 10.1093/oxfordjournals.eurheartj.a059896. [DOI] [PubMed] [Google Scholar]
- 6.Matsuoka M, Oki T, Mishiro Y. Early systolic mitral annular motion velocities responses to dobutamine infusion predict myocardial viability in patients with previous myocardial infarction. Am Heart J. 2002;143:552–558. doi: 10.1067/mhj.2002.121266. [DOI] [PubMed] [Google Scholar]
- 7.Biel L, Pettersson O, Philipson L, Wide P. ECG analysis: a new approach in human identification. IEEE Trans Instrum Meas. 2001;50:808–812. [Google Scholar]
- 8.Kang-Ping Lin, Chang WH. QR feature extraction using Linear Prediction. IEEE Trans Biomed Eng. 1989;36:1050–1055. doi: 10.1109/10.40806. [DOI] [PubMed] [Google Scholar]
- 9.Ramakrishnan AG, Saha S. ECG Coding by wavelet-based linear prediction. IEEE Trans Biomed Eng. 1997;44:1253–1261. doi: 10.1109/10.649997. [DOI] [PubMed] [Google Scholar]
- 10.Polat K, Akdemir B, Günes S. Computer aided diagnosis of ECG data on the least square support vector machine. Digit Signal Process. 2008;18:25–32. [Google Scholar]
- 11.Gomis P, Jones DL, Caminal P, Berbari EJ, Lander P. Analysis of abnormal signal within the QRS complex of the high-resolution electrocardiogram. IEEE Trans Biomed Eng. 1997;49:681–693. doi: 10.1109/10.605425. [DOI] [PubMed] [Google Scholar]
- 12.Salleh SH. Different techniques and algorithms for biomedical signal processing. Malaysian Journal of Mathematical Sciences. 2008;2:133–145. [Google Scholar]
- 13.Dokur ZM, lmez TO, Yazgan E, Ersoy OK. Detection of ECG waveforms by neural networks. Med Eng Phys. 1997;19:738–741. doi: 10.1016/s1350-4533(97)00029-5. [DOI] [PubMed] [Google Scholar]
- 14.Özbay Y, Tezel G. A new method for classification of ECG arrhythmias using neural network with adaptive activation function. Digit Signal Process. 2010;20:1040–1049. [Google Scholar]
- 15.Silipo R, Marchesi C. Artificial neural networks for automatic ECG analysis. IEEE Trans Signal Processing. 1990;46:1417–1425. [Google Scholar]
- 16.Golden DP, Jr, Wolthuis RA, Hoffler GW. A spectral analysis of the normal resting electrocardiogram. IEEE Trans Biomed Eng. 1973;20:366–373. doi: 10.1109/TBME.1973.324231. [DOI] [PubMed] [Google Scholar]
- 17.Durand LG, Pibarot P. Digital signal processing of the Phonocardiogram: Review of the most recent advancements. Crit Rev Biomed Eng. 1995;1995;23:163–219. doi: 10.1615/critrevbiomedeng.v23.i3-4.10. [DOI] [PubMed] [Google Scholar]
- 18.Iwata A, Suzumura N, Ikegaya K. Pattern classification of the phonocardiogram using linear prediction analysis. Med Biol Eng Comput. 1977;15:407–412. doi: 10.1007/BF02457994. [DOI] [PubMed] [Google Scholar]
- 19.Gupta CN, Palaniappan R, Swaminathan S, Krishnan SM. Neural network classification of homomorphic segmented heart sounds. Applied Soft Computation. 2007;7:286–297. [Google Scholar]
- 20.Yan Z, Jiang Z, Miyamoto A, Wei Y. The moment segmentation analysis of heart sound pattern. Comput Methods Programs Biomed. 2010;98:140–150. doi: 10.1016/j.cmpb.2009.09.008. [DOI] [PubMed] [Google Scholar]
- 21.Karpman L, Cage J, Hill C, Forbes AD, Karpman V, Cohn K. Sound envelope averaging and the differential diagnosis of systolic murmurs. Am Heart J. 1975:600–606. doi: 10.1016/0002-8703(75)90224-0. [DOI] [PubMed] [Google Scholar]
- 22.Jasper J, Othman KR. Feature Extraction for human identification based on envelogram signal analysis of cardiac sounds in time-frequency domain. IEEE Conference of ICEIE. 2010;2:228–233. [Google Scholar]
- 23.Gang WJ, Bo SX, Ping W, Wei H, Lian DC. Remote heart sound monitoring system. Conf Proc IEEE Eng Med Biol Soc. 2005;27:2138–2140. doi: 10.1109/IEMBS.2005.1616883. [DOI] [PubMed] [Google Scholar]
- 24.Malarvili MB, Kamarulafizam I, Hussain S, Helmi D. Heart Sound segmentation algorithm based on instantaneous energy of electrocardiogram. Comput Cardiol. 2003;30:327–330. [Google Scholar]
- 25.Collins SP, Lindsell CJ, Peacock WF, Hedger VD, Storrow AB. The effect of treatment on the presence of abnormal heart sounds in emergency department patients with heart failure. Am J Emerg Med. 2006;24:25–32. doi: 10.1016/j.ajem.2005.06.005. [DOI] [PubMed] [Google Scholar]
- 26.Zhou P, Wang Z. A computer location algorithm for ECG, PCG and CAP. IEEE Trans Engineering in Medicine and Biology Society. 1998;20:220–222. [Google Scholar]
- 27.Srinivasan N, Wong T, Krishan M. A new phase space analysis algorithm for cardiac arrhythmia detection. IEEE Trans Engineering in Medicine and Biology Society. 2003;1:82–85. [Google Scholar]
- 28.Ahlstrom C. Heart sound cancellation from lung sound recordings using recurrence time statistic and nonlinear prediction. IEEE Trans Signal Processing Letter. 2005;12:812–815. [Google Scholar]
- 29.Lyons RG. Understanding Digital Signal Processing. Vol. 1. Reading, MA: Addison-Wesley Publishing Company; 1996. pp. 49–125. [Google Scholar]
- 30.Stremler FG. Introduction to Communication System. Philippines: Addison-Wesley Publishing Company; 1977. [Google Scholar]
- 31.Physiobank archives index. MIT–BIH database. [Accessed Jan 2010]. http://www.physionet.org/physiobank/database.
- 32.Physiobank archives index. [Accessed Jan 2010]. http://www.egeneralmedical.com/listohearmur.html.
- 33.Rangayyan RM. Biomedical Signal Analysis: A Case-Study Approach. Vol. 1. Hoboken, NJ: Wiley-IEEE Press; 2002. pp. 457–462. [Google Scholar]