Abstract
Pulse electron paramagnetic resonance (EPR) spectroscopy is employed at two very different excitation frequencies, 9.77 and 30.67 GHz, in the study of the nitrogen coordination environment of the Mn(III)Mn(IV) state of the dimanganese-containing catalases from Lactobacillus plantarum and Thermus thermophilus. Consistent with previous studies, the lower-frequency results reveal one unique histidine nitrogen-Mn cluster interaction. For the first time, a second, more strongly hyperfine-coupled 14N atom is unambiguously observed through the use of higher frequency/higher field EPR spectroscopy. The low excitation frequency spectral features are rationalized as arising from the interaction of a histidine nitrogen that is bound to the Mn(IV) ion, while the higher excitation frequency features are attributed to the histidine nitrogen bound to the Mn(III) ion. These results allow for the computation of intrinsic hyperfine coupling constants, which range from 2.2 to 2.9 MHz, for sp2-hybridized nitrogens coordinating equatorially to high-valent Mn ions. The relevance of these findings is discussed in the context of recent results from analogous higher frequency EPR studies of the Mn cluster in photosystem II and other exchange-coupled transition metal-containing systems.
Introduction
Dimanganese-containing catalases (MnCat) catalyze the disproportionation of hydrogen peroxide to water and molecular oxygen and are found in a wide range of mesophilic (e.g. Lactobacillus plantarum, LP)1 and thermophilic (e.g. Thermus thermophilus, TT) bacteria. Electronic absorption (abs), X-ray absorption (XAS)2,3 and electron paramagnetic resonance (EPR)4–6 spectroscopic investigations of MnCat have shown that the active site cycles between the Mn(II)Mn(II) and Mn(III)Mn(III) states during turnover. This “ping-pong” mechanism is described by the two half-reactions below.
| (1) |
| (2) |
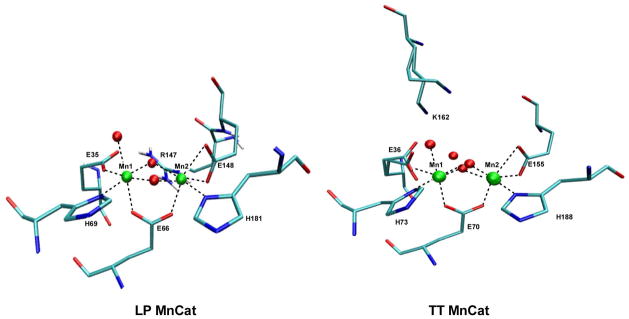
Results from X-ray crystallographic studies revealed that in its resting Mn(III)Mn(III) state, the active sites of LP MnCat (1.8 Å resolution)7 and TT MnCat (1.0 Å resolution)8 are quite similar (Figure 1). The Mn(III) ions are separated by 3.03 Å and bridged by two oxido (or hydroxido or aqua) groups and the carboxylate sidechain of a glutamate residue (Glu66 in LP; Glu70 in TT). Mn1 is coordinated in the equatorial plane in monodentate fashion by the carboxylate of another glutamate (Glu35 in LP; Glu36 in TT) and by the δ-N of a histidine residue (His69 in LP; His73 in TT). A solvent-derived ligand is present in the upper-axial position of Mn1 where substrate binding is presumed to occur. Mn2 is further coordinated by histidine (His181 in LP; His188 in TT) and glutamate (Glu148 in LP; Glu155 in TT).
Figure 1.
Structures of MnCat active sites for LP (left) and TT (right) derived from X-ray crystallographic data (PDB accession codes 1JKU and 2V8U, respectively). For TT MnCat, both orientations of Glu36 and Lys162 are shown (see Ref. 8,63).
Though not a participant in the disproportionation reaction mechanism, the “superoxidized” mixed-valence Mn(III)Mn(IV) state has been the subject of much study due to its having geometric and electronic structural features similar to those of the water-oxidizing tetranuclear Mn cluster found in photosystem II (PSII). These commonalities include the presence of high-valent exchange-coupled Mn centers; μ-oxido bridges between metal centers;9 protein-derived carboxylate ligands;10 and Mn ligation by the imidazole side-chain of histidine.11
Thus far, no X-ray crystal structure of superoxidized MnCat has been reported. However, EXAFS studies on the mixed-valence Mn(III)Mn(IV) form indicate that the Mn···Mn distance shortens to 2.70 Å upon one-electron oxidation, yet the Mn—N bond lengths remain at approximately 2.15 Å.3 The high-spin Mn ions (SMn(III) = 2 and SMn(IV) = 3/2) in MnCat couple antiferromagnetically to yield a net spin ST = 1/2 system. The corresponding X-band (9 GHz) continuous-wave (CW) EPR spectrum is characterized by 16 well-resolved peaks resulting from the hyperfine coupling of the electron spin with each I = 5/2 nuclear spin of the two 55Mn nuclei (100% natural abundance).4,5 This EPR spectrum resembles those observed for the S0 and S2 oxidation states of PSII.12 While there are further magnetic couplings between this electron spin and other neighboring nuclei such as 1H and 14N, such hyperfine splittings are not resolved in the CW EPR spectrum. However, advanced EPR methods such as electron nuclear double resonance (ENDOR) and electron spin echo envelope modulation (ESEEM) spectroscopies can detect these relatively small couplings. The hyperfine interaction (HFI) and nuclear quadrupole interaction (NQI) parameters deduced from such studies report on the distribution of unpaired electron spin density about the molecule, the distance between the nuclear and electron spins, and the chemical nature of the magnetically coupled nucleus.
Previous 9.5 GHz (330 mT) ESEEM spectroscopic studies of LP and TT MnCat in the Mn(III)Mn(IV) state13,14 showed deep modulations indicative of a hyperfine coupled 14N nucleus near the cancellation limit—i.e., with an isotropic HFI approximately twice the 14N Larmor frequency (Aiso ≈ 2.6 MHz, in this case).15,16 The corresponding HFI and NQI parameters were consistent with direct coordination of the imidazole N of one of the active-site histidines to Mn. There was no evidence for additional modulations from other nitrogenous ligands, and the possibility of multiple equivalent nitrogens was ruled out as no combination peaks were observed in the 3-pulse ESEEM spectra. Further, no resonances attributable to 14N were observed in CW ENDOR spectra.17 Generally, ENDOR spectroscopy is more sensitive than ESEEM spectroscopy to strongly coupled nitrogens. However, if significant hyperfine anisotropy and nuclear quadrupole interactions are present, the ENDOR resonances could be broadened beyond detection. Now, with the X-ray structures of MnCat in hand, we know that two histidine nitrogens are bound to the dinuclear Mn active site, yet so far only one is detected by magnetic resonance spectroscopy. Therefore, the electronic structure of one of the nitrogen nuclei bound the Mn cluster in MnCat remains unknown.
In this report, we present multifrequency ESEEM spectra (acquired at 9.77 and 30.67 GHz) of both LP and TT MnCat. These data afford, for the first time, quantitative bonding descriptions of metal ligand interactions for both metal sites of a mixed-valence exchange-coupled Mn dimer. The relevance of these findings is discussed in the context of recent results from higher frequency EPR studies of PSII and other exchange-coupled transition metal-containing systems.
Experimental Methods
Sample preparation
MnCat was isolated from Lactobacillus plantarum and Thermus thermophilus HB8 according to published procedures.1,5 The superoxidized Mn(III)Mn(IV) state of these proteins was prepared as previously described3,7 with minor modifications. LP MnCat was oxidized by redox cycling in the presence of hydrogen peroxide and hydroxylamine. Briefly, LP MnCat (0.1 mM active sites in 50 mM potassium phosphate buffer pH 7, containing 0.1 mM EDTA) was dialyzed against 1 L of 0.1 mM hydroxylamine and 0.1 mM H2O2 at 4°C for 4 hours. The protein was then transferred to 1 L of fresh 0.1 mM H2O2 solution (two changes) and finally dialyzed overnight against 50 mM potassium phosphate buffer pH 7 containing 0.1 mM EDTA. The superoxidized state of TT MnCat was prepared from the fully reduced Mn(II)Mn(II) form, obtained by anaerobic reduction with (NH2OH)2SO4 in 50 mM MOPS, pH 7. The colorless protein was anaerobically desalted on a Bio-Gel P-30 column (Bio-Rad Labs, Hercules, CA) equilibrated with 10 mM potassium phosphate pH 6.8 and 1.5 mL fractions collected under argon. Fractions were made 5 mM in sodium periodate (NaIO4) and the brown, superoxidized TT MnCat Mn(III)Mn(IV) samples were combined and concentrated. Protein solutions were loaded into 2.5 mm OD quartz tubes. The same samples were used for both X-band and Ka-band EPR experiments.
Spectroscopy
Electron spin-echo (ESE) detected EPR (π/2-τ-π-τ-echo), two-pulse ESEEM (π/2-τ-π-τ-echo), three-pulse ESEEM (π/2-τ-π/2-T-π/2-τ-echo), and hyperfine sublevel correlation (HYSCORE; π/2-τ-π/2-T1-π-T2-π/2-τ-echo) spectra were collected at 9.77 GHz (X-band) using a Bruker (Billerica, MA) EleXsys E-580 spectrometer equipped with a cylindrical dielectric cavity (MD5, Bruker). Pulse sequences were programmed with the PulseSPEL programmer via the XEPR interface. For HYSCORE spectroscopy, the inversion pulse width (tπ) was set equal to that for the π/2-pulse (tπ/2), 16 ns in all cases. A small but significant signal from adventitious Mn(II) was present in all field-swept ESE EPR spectra when short (tπ/2 < 20 ns) microwave pulses were employed. The use of longer (tπ/2 = 40 ns and tπ = 80 ns) microwave pulses temporally shifts—in the positive direction of the time-coordinate—the electron-spin echo of low-spin species relative to that of higher spin species.18,19 We were thus able to selectively acquire the EPR and ESEEM spectra of the S = 1/2 superoxidized Mn(III)Mn(IV) MnCat absent most of the S = 5/2 Mn(II) signal by integrating the intensity of only the latter half of the ESE (cf. Figure S1).
ESE EPR and two- and three-pulse ESEEM spectra were acquired at 30.67 GHz (Ka-band) using a home-built spectrometer.20 At this frequency, signals from the relatively small concentration of Mn(II) contaminant were dominant when employing short (tπ/2 ≈ 10 ns) microwave pulses. As described above, this unwanted contribution was mitigated using longer microwave pulses (tπ/2 = 30 ns and tπ = 60 ns) and collecting the latter half of the ESE.
Analysis of Magnetic Parameters
Frequencies contributing to observed modulation patterns were visualized using cosine-Fourier transforms back-filled with only the two highest frequency components of the spectrum.21 All spectral simulations were performed with the Matlab 7.5.0.342 (R2007b) software package (The Mathworks Inc., Natick, MA) using the EasySpin 3.1.0 toolbox.22,23
For exchange-coupled systems such as those encountered here, measured or effective metal HFI Aeff must be scaled by the appropriate projection factor matrix ci to achieve so-called intrinsic hyperfine coupling constants ai (i.e., Aeff = aici). These projection factors are computed by determining the expectation value of the local electron spin S⃗z,i projected onto the total electron spin of the molecule S⃗T24
| (3) |
and are dependent on the site spin Si, site-specific zero-field splitting parameters Di and Ei, and the isotropic Heisenberg exchange coupling parameter J.25 For MnCat, J is estimated to be relatively large (J = −100 to −175 cm−1)26–28 and thus dominates over contributions from zero-field splitting, which, for the metal centers, are likely not greater than 4 cm−1 and 1 cm−1 for the Mn(III) and Mn(IV) ions, respectively.29,30 In general, these properties simplify the projection factors to scalar quantities and thus are easily computed. For MnCat they are: cMn(III) = +2 and cMn(IV) = −1. Similarly, measured ligand HFI must be scaled by the projection factor corresponding to the metal to which it is bound.31 These intrinsic ligand HFI can be then interpreted in the usual terms of covalency and interspin distance. The isotropic part of the intrinsic HFI aiso is related to the population of unpaired electron spin at the nucleus (Fermi contact contribution, s-orbital population, fs) and the anisotropic part aaniso is a function of the electron-nuclear separation and asymmetric unpaired spin population in non-s-type orbitals.32
The properties of the NQI for the I = 1 nucleus of 14N, on the other hand, are not dependent on the electron spin—to first order—and can be evaluated without spin projection. The principal values of interest are e2Qq/h and η. In the first term, e is the electronic charge, h is Planck’s constant, Q is the nuclear quadrupole coupling constant of 14N, and q (qzz) is defined as the largest magnitude of the electric field gradient (EFG) at the nucleus, which is usually coincident with the direction of the dominant bonding interaction. The asymmetry parameter gives the deviation of the electric field gradient from axial symmetry (e.g., η can range from 0 to 1 describing an axially symmetric and rhombic EFG, respectively). The values for e2Qq/h and η of histidine can then be analyzed following the Townes-Dailey formalism33 implemented by Ashby et al. to give insight into charge donation from the nitrogen-centered lone pair to the metal center.34
Results
The ESE-detected field-swept EPR spectra of superoxidized LP and TT MnCat (collected at 9.77 GHz (X-band, left) and 30.67 GHz (Ka-band, right)) are shown at the top of Figures 2 and 4, respectively. These data are consistent with the 9.5 (continuous-wave (CW) and ESE-detected) and 34 GHz (CW) EPR data reported previously.13,35 However, the wings at the low- and high-field extrema of the X-band spectra disclose the presence of adventitiously-bound Mn(II)-containing species. As described in the Experimental Methods section, the microwave pulse parameters and data acquisition window were chosen to minimize contributions from these Mn(II) species to the ESEEM data (see Figure S1).18 The remaining pulse EPR data of LP and TT MnCat will be discussed in turn.
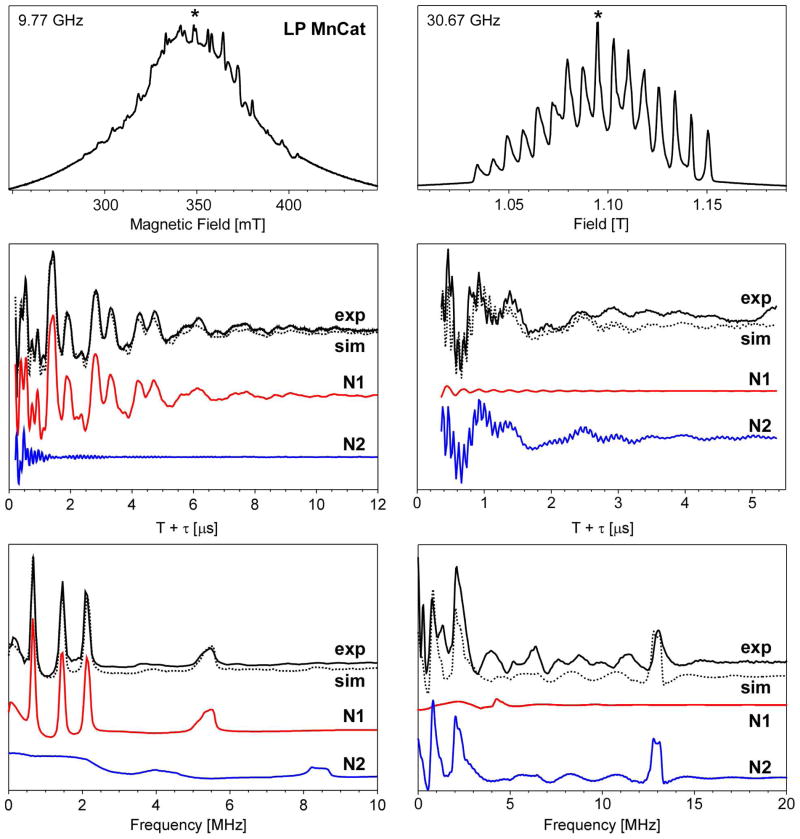
Figure 2.
Pulse EPR spectra of LP MnCat collected using 9.77 (left) and 30.67 GHz (right) microwave radiation. Top: ESE-detected field-swept EPR spectrum. Middle: 3-pulse ESEEM spectrum in resonance with g = 2.00 (348.7 mT at 9.77 GHz and 1.095 T at 30.67 GHz; see * symbol in top panels). Bottom: Cosine-backfilled Fourier transform of 3-pulse ESEEM data in middle panels. Combined (dotted) and individual simulations for two hyperfine-coupled 14N atoms are also shown: one weak (N1, red) and one strong (N2, blue).
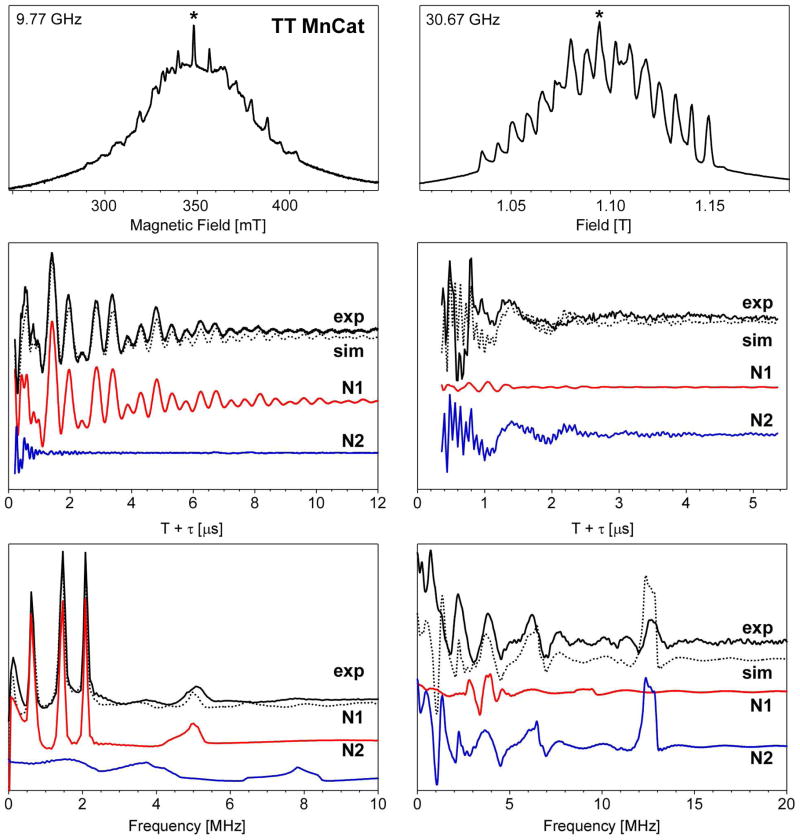
Figure 4.
Pulse EPR spectra of TT MnCat collected using 9.78 (left) and 30.67 GHz (right) microwave radiation. Top: ESE-detected field-swept EPR spectrum. Middle: 3-pulse ESEEM spectrum in resonance with g = 2.00 (348.2 mT at 9.78 GHz and 1.095 T at 30.67 GHz; see * symbol in top panels). Bottom: Cosine-backfilled Fourier transform of 3-pulse ESEEM data in middle panels. Combined (dotted) and individual simulations for two hyperfine-coupled 14N atoms are also shown: one weak (N1, red) and one strong (N2, blue).
Lactobacillus plantarum
Three-pulse ESEEM data were collected in resonance with the central feature of the 55Mn hyperfine-split EPR spectrum (348.7 mT at X-band and 1.095 T at Ka-band—designated by the * in Figures 2, top). The X-band data shown were acquired with τ = 128 ns to minimize contributions to the modulation pattern from weakly hyperfine-coupled protons. ESEEM spectra acquired using other values of τ are given in the Supporting Information (Figure S2). The X-band ESEEM data of LP MnCat (middle-left of Figure 2) are similar to those published by Stemmler et al.14 The corresponding FT (Figure 2, bottom-left) gives a set of sharp peaks at 0.67, 1.46, and 2.10 MHz resulting from transitions (ν0,A, ν−,A, and ν+,A) between (nearly) pure nuclear quadrupole states in one electron spin manifold (this electron spin manifold will be designated “A” for notational purposes), and a broader feature centered at 5.4 MHz that is assigned to the double quantum transition (νdq,B) in the opposite electron spin manifold, called “B”. These modulations are best-simulated assuming an isotropic g-tensor and using a single 14N atom (henceforth called N1) with effective HFC and NQI parameters as follows: Aiso = +2.67 MHz, Aaniso = [+0.41 +0.16 −0.57] MHz, e2Qq/h = 2.25 MHz and η = 0.58 with Euler angles for the NQI frame relative to the principal axes of the hyperfine tensor α = 110°, β = 15°, and γ = 85° (red lines in Figure 2). Our choice of sign for Aiso is arbitrary at this point.
In the present simulations, the quality of the fit of the anisotropic part of the hyperfine tensor was judged based on replication of the dampening behavior of the ESEEM modulation in the time domain as well as the width and shape of the νdq,B peak in the frequency spectrum. Specifically, we note that the doublet line-shape of the νdq peak can be modeled accurately only if significant anisotropic hyperfine contributions are included.36 A small, additional damping function (e−Γt, Γ = 0.2 μs−1) was applied to mimic the loss of nuclear coherence due to nuclear relaxation.
This Aiso = +2.67 MHz coupling is optimal for detecting ESEEM at X-band as the corresponding magnetic field at g = 2.0 (B0 ≈ 350 mT, see * in Figure 2, top, left) induces a magnetic field, due to the nuclear Zeeman effect, in one of the electron spin manifolds that nearly cancels the magnetic field caused by the hyperfine interaction. This “cancellation” condition leads to a coalescence—and thus heavy mixing—of nuclear spin levels in this manifold maximizing modulation depth (k) for the transition frequencies between these nuclear levels. We note that the above magnetic parameters produce simulations that are completely consistent with the previous higher frequency ESEEM data acquired at B0 = 400.2 and 477.1 mT.14 Furthermore, no clear peaks were observed that could be definitively ascribed to the other 14N ligand to the Mn active site. However, there does appear to be a broad feature at 3–4 MHz that Stemmler et al. noted could be due to a more strongly bound nitrogen.14
By going to an applied magnetic field of 1100 mT (corresponding to an excitation frequency at g = 2.0 of 30.1 GHz, Ka-band), we achieve the same near-cancellation conditions for this more strongly coupled 14N nucleus (designated N2). A representative Ka-band three-pulse ESEEM time trace (B0 = 1.095 T, τ = 210 ns) for LP MnCat (Figure 2, middle-right) shows rather deep modulations that completely damp out by 5 μs—much faster than observed in the X-band data—suggesting either a significant reduction in the longitudinal nuclear spin relaxation time (T1n) and/or greater anisotropy in the hyperfine coupling (cf. ESEEM data acquired with other values for with τ in Figures S4 and S5). The corresponding Fourier transform has features ca. 0.7, 1.4(sh), 2.1, 6.5, and 13.0 MHz.37 These features are assigned respectively to the three NQ transitions (ν0, ν−, and ν+) and the single and double quantum (νsq and νdq) transitions in the opposite spin manifold. These assignments are supported by the presence of negatively intense features in the two-pulse ESEEM spectrum that appear at frequencies that are combinations (sum and difference) of one of the NQ frequencies and νsq (see Figure S2).38 Notably, the frequencies of the NQ transitions here are nearly identical to those observed in X-band ESEEM spectra above, implying that the NQI parameters (e2Qq/h and η) for the corresponding nitrogens are similar. Indeed, the best simulation provides the following effective magnetic parameters for the nitrogen designated as N2: Aiso = −5.75 MHz, Aaniso = [−0.2 −0.6 0.8] MHz, e2qzzQ = 2.01 MHz and η = 0.79 with Euler angles for the NQI frame relative to the hyperfine tensor α = 75° β = 0° γ = −10° (blue lines in Figure 2). Our choice of the sign of Aiso is explained below. As the N2 Aaniso is approximately equal to that found for N1, the more rapid dampening of the nuclear modulations in the Ka-band data is modeled with a 50% greater Γ than was employed in simulating the X-band ESEEM spectra. If this nitrogen is bound to the Mn(III) ion, we posit that at least part of this increased rate of nuclear relaxation could be due to the greater local electron spin felt by N2 relative to N1 (SMn(III) = 2 vs. SMn(IV) = 3/2) and/or the Jahn-Teller distortion of the Mn(III) site leading to larger paramagnetic relaxation enhancement effects.39
Using the HFI and NQI parameters that best-fit the X-band data, the simulated spectrum of N1 at 1.095 T is shown in red on the right side of Figure 2. Its contribution to the Ka-band spectrum is small but nonetheless present, leading to weak features at 4 and 9 MHz arising from N1νdq,A and N1νdq,B, respectively. Likewise, 348 mT simulations for the more strongly hyperfine-coupled nitrogen N2 show a small contribution to the X-band ESEEM spectrum—broad low-intensity features centered at 4 and 8 MHz (blue line, left side of Figure 2). Upon inspection of the present X-band ESEEM spectra of LP MnCat and those given in previous publications, these additional features from the more strongly coupled 14N nucleus are indeed visible. Their diminished intensity relative to features arising from N1 is due to much smaller modulation depth parameters (k) for nuclear transition frequencies of N2 at 348 mT.38 These k’s are likely further attenuated because of cross-suppression effects with the strongly modulating N1.40
The combined (dotted line) simulations presented in Figure 2 employ magnetic parameters for two separate nitrogen nuclei coupled to the S = 1/2 electron spin and were achieved by simultaneous fitting of both X- and Ka-band data. The “individual” nitrogen ESEEM spectra in red and blue are presented to illustrate the dominance of spectral features from N1 to the X-band data and N2 to the Ka-band data. When multiple nuclei are magnetically coupled to the electron spin, the resulting three-pulse ESEEM modulation pattern is given by . The term describes the contribution to the modulation by nucleus i with orientation θ. The modulations from all like-oriented nuclei contributing via the same coherence transfer pathway (α or β) are multiplied according to the product rule; then the products from each coherence transfer pathway are added. Finally, this result is summed over all possible orientations to give the total observed echo envelope modulation. Thus the modulation pattern for multiple hyperfine-coupled nuclei is different from merely the sum of its individual parts as can be seen comparing the individual and combined spectra in Figure 2.
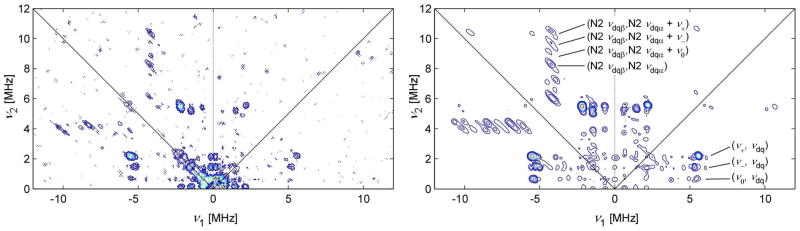
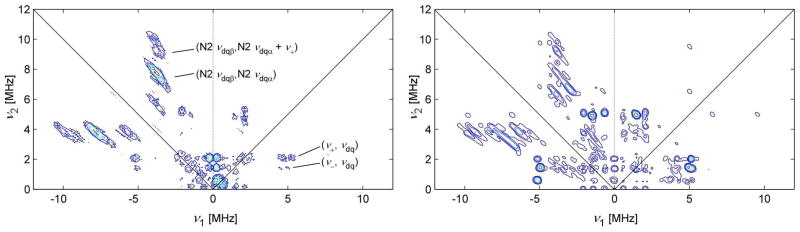
The X-band HYSCORE spectrum of LP MnCat is presented on the left side of Figure 3. The (NQ, N1νdq,A) cross-peaks for N1 are clearly visible in both quadrants. At much lower intensity, long correlation ridges are evident and are parallel to the antidiagonal in the (−,+) quadrant. These ridges are centered at (−4.2, +8.2) MHz and (−8.2, +4.2) MHz and, based on the one-dimensional ESEEM simulations described above, are assigned to the dq-dq correlated frequencies of N2 (N2νdq,A, N2νdq,B). The fact that these ridges are long, extending over 1 MHz, is diagnostic of a significant amount of anisotropy in the HFI of the corresponding nucleus. Accompanying the N2 dq-dq cross-peaks are similarly shaped cross peaks displaced along the ν1 and ν2 axes by approximately 0.7, 1.4, and 2.1 MHz (frequencies that correspond to the NQ transitions of N1). Such “shadow” peaks are diagnostic of multinuclear coherences wherein combinations (sums and differences) of nuclear transition frequencies in one electron spin manifold from different nuclei (e.g., N1ν+,A + N2νdq,A = +10.4 MHz) are correlated to a frequency in the opposite electron spin manifold (e.g., N2νdq,B = −4.2 MHz).40,41 From the direction of the shift, the relative sign of hyperfine interaction for the two nuclei can be deduced. Given the shift observed in this case, the effective hyperfine interactions for N1 and N2 must have opposite signs. This behavior is reproduced by the simulation of the HYSCORE spectrum (Figure 3, right).
Figure 3.
X-band HYSCORE spectrum of LP MnCat recorded at 348.7 mT (left) and corresponding simulation (right) using parameters given in Table 1. The spectrum is the sum of data collected using τ = 108 and 136 ns.
Thermus thermophilus
Qualitatively, the pulse EPR data for TT MnCat are quite similar to the corresponding data of LP MnCat (cf. Figures 2 and 4 and Figures 3 and 5). All spectral features are assigned identically, and only the specific frequencies are somewhat different. Thus the following analysis will be brief, emphasizing differences between the LP and TT MnCat spectra.
Figure 5.
X-band HYSCORE spectrum of TT MnCat recorded at 348.2 mT (left) and corresponding simulation (right) using parameters given in Table 1. The spectrum is the sum of data collected using τ = 92, 116 and 200 ns.
The FT of the X-band three-pulse ESEEM spectrum (τ = 128 ns) of TT MnCat (Figure 4, ESEEM spectra acquired with other τ-values are shown in Figure S6) is similar to that previously observed by Ivancich et al.,13 exhibiting sharp peaks at 0.65, 1.46, and 2.07 MHz as well as a broad feature centered at 5.2 MHz. The 5.2 MHz peak is at slightly lower frequency than its counterpart in the LP MnCat spectrum, suggesting a slightly smaller value of aiso for the former. The best simulation of the X-band data yielded the following effective magnetic coupling parameters: Aiso = +2.28 MHz, Aaniso = [+0.42 +0.28 −0.70] MHz, e2Qq/h = 2.29 MHz and η = 0.50 with Euler angles α = 0° β = 50° γ = 50°.
The Ka-band three-pulse ESEEM spectrum of TT MnCat (Figure 4, right-middle, and Figures S7 and S8) has considerably less modulation depth than is present in the corresponding data for LP MnCat. The NQ region of the frequency spectrum (Figure 4, right-bottom) is much less resolved, adding considerable uncertainty to our simulations. Nonetheless, the best simulation is achieved using Aiso = −5.2 MHz, Aaniso = [−0.3 −0.7 +1.0] MHz, e2Qq/h = 2.25 MHz and η = 0.65 with Euler angles α = 80° β = 80° γ = 40°. The reduction of Aiso relative to that for LP MnCat puts the TT MnCat N2 spin system further from the cancellation condition at this field (Acancellation = 6.74 MHz at 1095 mT). This has the effect of broadening the peaks that correspond to nuclear spin transitions within the B-electron spin manifold (nominally N2ν0, ν−, and ν+). While we are confident in our derived value for Aiso of N2, as this largely controls the position of the N2νdq,A peak seen clearly at 12.7 MHz, we will refrain from any in-depth analysis of the other magnetic parameters for this nucleus.
In the X-band HYSCORE spectrum of TT MnCat (Figure 5, right), long low-intensity correlation ridges are again apparent parallel to the diagonal in the (−,+) quadrant. These ridges centered at (−3.7, +7.8) MHz and (−7.8, +3.7) MHz are assigned as (N2νdq,A, N2νdq,B) and, as above, are accompanied by multinuclear coherences at (−10.0, +3.7) MHz and (−3.7, +10.0) MHz due to the combination of N1ν+,A with N2νdq,A.
Discussion
The Mn centers found in the active sites of arginase,42 MnCat,7,8 and PSII are predominantly coordinated by oxygen atoms—either in the form of solvent-derived ligands or carboxylate moieties from active-site amino-acid residues. Nitrogenous ligands are also employed, though much more sparingly. Each Mn ion in arginase and catalase is coordinated by the imidazole side-chain of a histidine, and results from X-ray diffraction and pulse EPR studies have shown that a single histidine is bound to one of the four Mn ions that compose the oxygen evolving complex (OEC) found in PSII.11,43–45 To better understand the role played by histidine in controlling the corresponding chemistries of these enzymes we must first generate quantitative bonding descriptions of the Mn—N unit. Analysis of 14N HFI and NQI parameters derived from magnetic resonance experiments provide a direct route to such descriptions.
Owing to the rules of vector addition for angular momenta, the measured ligand hyperfine interaction of a magnetic nucleus with the net unpaired electron spin of an exchange-coupled metal cluster must be scaled by the appropriate projection factor before being analyzed for geometric and electronic structure information (see Experimental Methods Section). This type of analysis has been employed in the exploration of histidine coordination to the dinuclear Fe active sites of Rieske [2Fe-2S] clusters, the hydroxylase domain of methane monooxygenase (MMOH),46–48 and hemerythrin (Hr).49 From these studies, approximate “intrinsic” hyperfine coupling parameters can be computed for the interaction of an imidazole nitrogen with a fictitious, isolated Fe(II) or Fe(III) ion (see Table S1). In the context of [2Fe-2S] clusters, the intrinsic aiso of the coordinating 14N atom is diagnostic of the of covalency of the bond to Fe(II);50,51 aaniso can reveal the protonation state of the distal, non-coordinating nitrogen of the imidazole ring;52 and the NQI parameters report on the orientation of the imidazole ring with respect to the FeS core.53 Equally, the 14N HFI measured in oxido-bridged Fe dimers is interpreted in terms of covalency; however, in these cases, the protonation state of the oxido bridge trans to the nitrogen ligand also influences the magnitude of hyperfine coupling.54
Unfortunately, the number of analogous studies targeting Mn—His interactions in exchange-coupled Mn clusters is comparatively limited. To begin to remedy this, we have performed pulse EPR studies at both X- and Ka-band microwave frequencies on the superoxidized Mn(III)Mn(IV) state of dimanganese catalase from both Lactobacillus plantarum and Thermus thermophilus. In the limit of strong exchange coupling, the projection factors are simply cMn(III) = +2 and cMn(IV) = −1. We can then compute general, intrinsic HFI for imidazole 14N atoms coupled to high-valent, high-spin Mn ions. Such intrinsic values can be used to determine the likely oxidation state of a Mn ion coordinated to a histidine when the isotropic contribution to the hyperfine interaction is known.
Structure of Superoxidized MnCat
The present and past advanced EPR studies performed at X-band microwave frequencies have measured nuclear transition frequencies for one of two active site histidines coordinated to the ST = 1/2 Mn cluster in superoxidized LP MnCat. For the first time, we have found conclusive spectroscopic evidence of the second histidine residue that is known from crystallographic studies to be coupled to the Mn active site. The ESEEM spectral features arising from both coordinating histidine nitrogens are well simulated at both X- and Ka-band excitation frequencies (magnetic parameters are given in Table 1). Notably, the NQI parameters for N2 are very similar to those for N1. Barring significant geometric rearrangements, these NQI are expected to be roughly equivalent as in both cases the imino nitrogen of a histidine is coordinated in an equatorial position of a pseudo-octahedral Mn ion. However, though the metal-based orbital participating in the Mn—N σ-antibonding interaction (3dx2-y2) is formally unoccupied in both sites, electronic effects could alter Mn—N bond covalency. The additional electron on the Mn(III) ion is formally placed in the 3dz2-based orbital, which, in low symmetry, could have some interactions with equatorial ligands through the doughnut-shaped charge in the xy-plane. Simultaneously, the familiar nephelauxetic effect of metal-centered oxidation should decrease the Racah B parameter and thus strengthen bonding. Indeed some changes are observed between the two Mn—N bonding interactions as, for LP MnCat, the N2 e2Qq/h parameter is reduced by 9% compared to that for N1 indicating increased charge donation of approximately 0.4% electrons from the N2-centered lone pair to the Mn ion. This modest increased covalency of the Mn—N2 bond relative to the Mn—N1 bond is also reflected in the analysis of the Fermi contact contribution to the hyperfine tensor given the Mn oxidation state assignments described below.
Table 1.
Measured and Computed HFI and NQI Parameters of 14N Atoms Coupled to Superoxidized MnCat and Relevant Model Complexes
| Species | assign.a | Aiso (MHz) | e2Qq/h (MHz) | η | Ref. |
|---|---|---|---|---|---|
| LP | N1 | 2.88 | 2.19 | 0.58 | 14 |
| LP + N3− | 3.34 | 1.97 | 0.74 | ||
| LP + CN− | 3.86 | 1.93 | 0.74 | ||
| LPmod1 | N1 | +1.98 | −2.40 | 0.71 | 28 |
| N2 | −3.27 | −2.44 | 0.70 | ||
| LPmod2 | N1 | +2.08 | −2.40 | 0.70 | |
| N2 | −4.04 | −2.38 | 0.72 | ||
| LPmod3 | N1 | +3.30 | +1.98 | 0.89 | |
| N2 | −6.62 | +2.02 | 0.93 | ||
| LPmod4 | N1 | −1.56 | +2.02 | 0.91 | |
| N2 | +4.73 | +1.90 | 0.49 | ||
| LP | N1 | +2.67 | 2.25 | 0.58 | this study |
| N2 | −5.75 | 2.01 | 0.79 | ||
| TT | N1 | 2.3 | 2.44 | 0.44 | 79 |
| TT | N1 | 2.45 | 2.34 | 0.51 | 13 |
| methylated TT | >4 | ||||
| TT | N1 | +2.28 | 2.29 | 0.50 | this study |
| N2 | −5.2 | 2.25 | 0.65 | ||
|
| |||||
| CYCLAMb | 2.70 | 3.06 | 0.39 | 80 | |
| Mn(III)ax | 9.23 | 2.98 | 71 | ||
| TMPAc | Mn(III)ax | 11.20 | 3.02 | 71 | |
| BIPYd | Mn(III)ax | 9.4 | 2.9 | 17 | |
| Mn(III)ax | 11.4 | 3.0 | 81 | ||
| Mn(III)ax | 11.3 | 63 | |||
| 2.78 | 2.42 | 0.14 | 80 | ||
| PHENe | 2.80 | 2.38 | 0.13 | 80 | |
| Mn(III)ax | 11.54 | 3.13 | 63 | ||
| TACNf | 2.73 | 3.06 | 0.36 | 80 | |
| BISPICENg | 2.51 | 2.87 | 0.54 | 80 | |
| Mn(III)ax | 12.1 | 2.3 | 63 | ||
| BPEAh | 3.04 | 2.86 | 0.20 | 80 | |
| TPENi | 2.51 | 2.73 | 0.15 | 80 | |
| DTNEj | Mn(III)ax | +12.0 | 72 | ||
| Mn(III)eq | −1.9 | ||||
| Mn(IV)ax | +1.9 | ||||
| Mn(IV)eq | +1.5 | 45 | |||
| PSII | H332 | 7.3 | 1.98 | 0.84 | |
Designations “ax” and “eq” refer to nitrogen coordination to a pseudo-octahedral metal ion in the axial and equatorial positions, respectively. For example, the designation “Mn(III)ax” refers to a nitrogen ligand bound along the local z-axis of a Mn(III) ion.
CYCLAM = 1,4,8,11-tetraazacyclotetradecane
TMPA = tris(2-methylpyridyl)amine
BIPY = 2,2′-bipyridine
PHEN = 1,10-phenanthroline
TACN = 1,4,7-triazacyclononane
BISPICEN = N,N′-bis(2-pyridylmethyl)ethane-1,2-diamine
BPEA = N,N-bis(2-pyridylmethyl)ethaneamine
TPEN = N,N,N′,N′-tetrakis(2-pyridylmethyl)-1,2-ethanediamine
DTNE = 1,2-bis(1,4,7-triazacyclonon-1-yl)ethane). These HFI were computed using the B3LYP hybrid density functional.
That Aiso for N2 is approximately twice that for N1 is traditionally understood in terms of the projection factors described above47 and indicates that N2 is bound to the Mn(III) ion whereas N1 is coordinated to Mn(IV). The fractional occupation of the s-orbitals (fs) on each nitrogen due to Fermi contact can be computed using the usual formula (we assume this contribution is exclusively due to N 2s-orbital, i.e. valence, occupation)32
| (4) |
where S is the local spin on the coordinating Mn ion and the HFI of one electron spin in a 14N 2s orbital, a2s0 = +1811 MHz.55 The measured site-specific aiso values for N1 and N2 in LP MnCat correspond to 0.44% and 0.64% unpaired spin in the ligand 2s orbital, respectively. For TT MnCat we similarly compute fs(N1) = 0.38% and fs(N2) = 0.57%. These values are noticeably smaller than the 1.4 to 2.0% range found for histidines coordinated to the high-spin tetrahedral Fe(II) site in Rieske-type [2Fe-2S] clusters56 in which the Fe—N bonds are at least partially coincident with lobes of the half-occupied Fe(II) t2g orbitals.51,57,58
It is possible that the effective HFI observed in our ESEEM studies could be assigned oppositely; namely, that N2 is coordinated to the Mn(IV) ion and N1 is bound to the Mn(III) ion. Projecting out the intrinsic HFI using these assignments and Equation (4) and the sets of magnetic parameters derived from our multifrequency LP MnCat spectra yield aiso(N2) = +5.75 MHz (fs = 0.95%) and aiso(N1) = −1.33 MHz (fs = 0.30%). If N2 were bound to the Mn(IV) ion, the large spin population computed above could be achieved through either (i) direct overlap of the nitrogen nucleus with a lobe of a half-occupied t2g orbital and/or (ii) a significant (>3-fold) increase in the covalency (assuming a linear correlation between unpaired spin in the N 2s orbital and covalency) of the bond. We disfavor this first case as it implies that N2 is strongly interacting with an unpaired electron on the Mn(IV) center on par with, for example, the strong interaction observed when nitrogen is coordinated in the axial position to a Mn(III) ion with a (t2g)3(3dz2)1 electron configuration (vide infra). This would require a significant departure from an idealized octahedral ligand field that already has the maximum possible ligand field stabilization energy −12 Dq (ligand-field splitting-energy parameter). Evidence for case (ii), an increase in M—N covalency due to metal-center oxidation, has been previously observed in an ENDOR study of the two histidine residues that interact with the dinuclear iron core of MMOH.47 The computed values for fs indicated a nearly two-fold increase in N 2s unpaired spin population for the Fe(III)—N unit compared to that found for the Fe(II)—N interaction. However, it is unclear what portion of this difference in fs is due to the change in oxidation state as there is also variance in the angle the imidazole plane forms with respect to the remaining equatorial Fe ligands.59
Furthermore, in the case of MnCat, the choice of projection factors could be a source of additional error. We, as others have, assume that since the exchange interaction between the two metal sites is much larger than the zero-field splitting interaction that the zero-order ground-state spin doublet is pure.26,60 However, this assumption may not be valid if there is significant delocalization of the net unpaired spin over both metal centers. In such a case, the site-specific spin expectation value (see Equation (3)) for each site would reduce for the nominally Mn(III) site and increase for the Mn(IV) site. Indeed such delocalization is suggested to explain shifts in the Mn L-edge X-ray absorption spectrum of superoxidized LP MnCat compared to Mn(III)Mn(IV) oxido bridged model compounds.61 Other possible explanations for the breaking of the nephelauxetic trend could be geometric differences between the two sites leading to increased covalency or more efficient exchange polarization and/or changes in the hydrogen bonding to the distal nitrogen of the imidazole ring.62 Importantly, we view the experimentally measured fs = 1.33% for the axial N—Mn(III) interaction in BISPICEN63 as a maximum and think it unlikely that a nitrogen atom bound to Mn(IV) would have unpaired spin in its 2s orbital approaching this value.
Ultimately, we can look to broken-symmetry density functional theory (BS DFT) calculations of magnetic parameters of superoxidized MnCat models to guide our analysis. Sinnecker et al. have computed 14N HFC parameters for the two coordinating imidazoles in LP MnCat.28 For their preferred model (see LPmod1, Table 1), the authors calculated the effective Aiso of the two coordinating nitrogen nuclei to be +1.98 MHz (fs = 0.33%) and −3.27 MHz (fs = 0.36%) for the nitrogen bound to the Mn(IV) and Mn(III) ions, respectively. The predicted NQI parameters for the nitrogens were also very similar to each other with e2Qq/h and η equal to −2.40 MHz and 0.71 (for N bound to Mn(IV)) and −2.44 MHz and 0.70 (for N bound to Mn(III)). This indicates that there are essentially no changes in the populations of the nitrogen 2 p-orbitals despite the fact that one would expect the Mn(IV) ion to be more oxidizing of the nitrogen lone-pair leading to a significant reduction of e2Qq/h.
More recent computations by Schnizel and Kaupp explored the density functional dependence of these magnetic parameters.64 Using B3LYP, their preferred functional, they predicted an effective Aiso of +2.7 MHz (fs = 0.45%) and −4.7 MHz (fs = 0.52%) for the nitrogen bound to the Mn(IV) and Mn(III) ions, respectively. We note that in both computational studies, 14N HFC parameters are predicted that are nearly identical to our spectroscopically determined values. Using these values and Equation (4) to compute fs leads to very similar unpaired spin densities on both nitrogen ligands, again, consistent with our experimental findings. Thus, in the absence of a more complete spectro-structural study on the correlation between nitrogen ligand HFI and bonding geometry in similar systems, we choose to continue our analysis using the assignments that N1 is bound to the Mn(IV) ion and N2 is bound to the Mn(III) ion.
The effective dipolar contributions to the HFI for each coordinating histidine nitrogen are computed using the point-dipole approximation for dinuclear exchange-coupled systems.65 Mn—N internuclear distances (r ≈ 2.05–2.12 Å) and Mn—Mn—N bond angles were taken from a combination of EXAFS results and the highest resolution X-ray crystallographic data available for each MnCat.7,8,14 For LP MnCat the two effective dipolar matrices are Adip = [+0.458, +0.578, −1.036] MHz and Adip = [−1.146, −1.091, +2.237] MHz for the 14N atom bound to the Mn(IV) and Mn(III) ion, respectively. We note that these contributions are very nearly axial indicating that the dipolar interaction with the bonding partner Mn ion is dominant. The total anisotropic HFI determined from our spectral fits is considerably more rhombic and therefore must be due to an asymmetric distribution of unpaired spin amongst the 14N 2 p-orbitals. This finding is supported by our measurement of a rhombic electric field gradient (η ≠ 0) at each nitrogen nucleus (Table 1).
The very short internuclear Mn(III)···Mn(IV) distance (2.70 Å) determined by EXAFS is interpreted as precluding protonation of the oxido bridges.3 However, the X-ray structure of LP MnCat in the resting Mn(III)Mn(III) (r = 3.03 Å) form suggests that the oxido bridge trans to the histidine ligands is protonated in this oxidation state.7 Studies of model systems have shown that the presence of the bridging glutamate or carboxylate bends the Mn2O2 core activating the oxido groups for protonation and exchange with solvent.66–68 The histidines in MnCat could be further contributing to this activation, labilizing the solvent bridge in order to accommodate the substrate hydrogen peroxide during the reduction step of the disproportionation.7,69,70
More evidence for the communication between the trans-oxido bridge and the active site histidines is afforded by X-band ESEEM results on reductively methylated TT MnCat.13 This study showed that methylation induces significant changes in the spectral features for what we have now assigned to the nitrogen bound to the Mn(IV) ion (N1). We suggest that it is lysine residue (Lys162) located in the second coordination sphere (Figure 1, right) that is reductively methylated, leading to the previously observed dramatic changes in the ESEEM spectrum. The X-ray crystal structure data also indicate that Lys162 is able to hydrogen bond directly with Glu36 that is bound to Mn1. Glu36 is postulated to be critical in proton transfer from bound hydrogen peroxide.8 Further, Lys162 appears to be hydrogen bonded through a water molecule to the μ-oxido bridge that is trans to the Mn-coordinating histidines. The loss of these interactions upon methylation of Lys162 would certainly disrupt the active site, potentially leading to a change in the coordination geometry of Mn1, protonation of the oxido bridge, and the observed larger value for Aiso for at least one of the nitrogenous ligands.
On a final note, the X-ray structure of Mn(III)Mn(III) LP MnCat with the competitive inhibitor azide bound to one of the Mn(III) ions reveals that the dimanganese oxido bridged core flattens somewhat, lengthening the inter-metal distance from 3.03 Å to 3.19 Å.7 This is consistent with the conclusions drawn in a pulse EPR study of azide-bound superoxidized LP MnCat,14 which suggested that the observed increase in 14N HFI for N1 (see Table 1)—and decrease in 55Mn HFI evident from the CW EPR spectrum—was attributable to an increase in the magnitude of the exchange interaction as the pseudo-octahedral Mn centers assumed a more co-planar geometry. Surprisingly, the authors did not see any X-band ESEEM features that could be assigned to the azide nitrogens. Assuming azide binds in a similar fashion in the superoxidized state to what was observed in the crystal structure of the Mn(III)Mn(III) state, we suggest that azide may be coordinating to the Mn(III) ion in the former. Based on our multifrequency ESEEM results as well as those from ENDOR studies of superoxidized MnCat and other Mn(III)Mn(IV) complexes, we would not expect to observe significant ESEEM modulations from the coordinating terminal nitrogen of azide (NA) if the anion was bound in the axial position of the Mn(III) ion. In such a case the hyperfine interaction would be far greater than the nuclear Zeeman term precluding efficient nuclear state mixing that is needed for ESEEM. This would suggest that the Mn(III) ion that azide is seen to bind in the crystal structure (Mn1, Figure 1, left), remains in the +3 oxidation state upon preparation of the superoxidized form of LP MnCat. Accordingly, this would implicate His69 in LP MnCat and His73 in TT MnCat as being responsible for the ESEEM signals we observe at Ka-band (Figures 2 and 4, right) whereas His181 in LP MnCat and His188 in TT MnCat must be giving rise to the X-band signals (Figure 2 and 4, left). That the other, presumably more weakly hyperfine-coupled, azide nitrogens (NB and NC) are also not detected via ESEEM spectroscopy could result from the geometric disorder of this ligand relative to the Mn cluster evinced by the relatively large Debye-Waller factors for the azide atoms in the X-ray structure (PDB accession code 1JKV).
Intrinsic HFI for 14N Atoms Bound to High-Valent Manganese Complexes
The central result of this study is that the magnitude of the intrinsic HFI of an 14N nucleus from histidine bound in the equatorial position to an octahedrally-coordinated Mn(III) or Mn(IV) ion is 2.2–2.9 MHz. The NQI parameters for these nitrogens analyzed using the Townes-Dailey formalism are completely consistent with the range of values for transition metal-bound imidazoles determined by Brown and coworkers.34 Computational results indicate that these magnetic parameters will be sensitive to the protonation state of the bridging oxido trans to the nitrogen, however to the best of our knowledge, no such experimental study of 14N HFI or NQI has been undertaken.28
A class of Mn—N coordination that is not present in MnCat is an N-donor binding in the axial position. Such interactions are found in some Mn(III)Mn(IV) model complexes and are characterized by very large HFI, Aeff ≈ 9.2–12.1 MHz, observed only via CW and pulse ENDOR experiments (see Table 1).63,71 DFT results confirm that such strong couplings arise from the interaction of the 14N nucleus with the unpaired electron in the 3dz2-orbital of the Mn(III) ion.72 Scaled by the projection factor, one computes an intrinsic aiso of 4.6–6.1 MHz for these nitrogens—much larger than the 2.3–2.9 MHz range for equatorial nitrogens ligands (see above)—due to the increase in the magnitude of the Fermi contact term with corresponding fs(Nax) = 1.0–1.3%.
No experimental study has conclusively determined what the intrinsic HFI might be for nitrogen bound in the axial position to a Mn(IV). However, Sinnecker et al. compute values of Aiso for such an axial interaction that are approximately equal to those calculated for the Mn(IV)—N interaction of equatorially liganding amides in the azanide complex [(DTNE)Mn(III)(μ-O)2(μ-OAc)Mn(IV)(DTNE)]2+ (see DTNE entry in Table 1).72
We now have in hand experimentally-verified classes of intrinsic HFI for 14N nuclei coordinated to exchange-coupled Mn dimers. The intrinsic hyperfine interactions of N-donor ligands in the equatorial plane of either an Mn(III) or Mn(IV) ion or bound in the axial position to a Mn(IV) ion are all approximately equal and centered at a value of 2.5 MHz. Under the condition of a pseudo-octahedral ligand field, only a nitrogen whose bond to Mn is coincident with a half-occupied metal centered orbital (e.g., axial ligand to a Mn(III) ion with one electron in the 3dz2 orbital) should fall outside this range.
Relevance to PSII
The Ka–band ESEEM spectra above illustrate the utility of mid-range microwave frequency spectrometers (30–35 GHz) for the quantitative determination of HFI and NQI parameters for 14N atoms that are strongly coupled to Mn ions (as well as to Fe ions). Such parameter determination has proven to be elusive in studies at the more common X-band frequency (though, the X-band HYSCORE results presented in Figures 3 and 5 suggest that, at a minimum, Aiso for strongly coupled 14N atoms can be estimated from the coordinates of the dq-dq cross peak). Going to these higher frequencies has already been shown to be of great use in identifying proteinaceous ligands to the OEC in PSII poised in the S2 state. In the S2 state, the Mn cluster is known to formally consist of three Mn(IV) ions and one Mn(III) ion.73 From analysis of the ESEEM spectrum of PSII in the S2 state, the following 14N magnetic parameters were determined: Aiso = 7.3 MHz, Aaniso = [+0.70 +0.70 −1.40] MHz, e2Qq/h = 1.98 MHz, η = 0.84.45 Just as was the case with MnCat, the NQI parameters are consistent with metal ion ligation by an imidazole nitrogen from histidine. Recent X-, Ka- and Q-band EPR studies of the H332E mutant of PSII from Synechocystis sp. PCC 6803 strongly suggest that His332 is the ligand to the Mn cluster.74,75 While certainly this coordination mode was suggested by recent X-ray crystallographic results of PSII,43,44 these structures are known to suffer from significant radiation damage leading to complete reduction of the metal centers and some alteration of the Mn—L geometries.76,77 Thus we must rely on nondestructive techniques such as EPR spectroscopy to definitively determine the native geometric structure of the OEC.
Using the intrinsic isotropic HFI for 14N atoms liganded to exchange coupled Mn clusters determined from our MnCat studies above, we can assess the likely oxidation state for the bonding partner of His332 in the S2 state of PSII. The isotropic component of projection factors for the Mn cluster of methanol-treated PSII have been estimated on the basis of 55Mn ENDOR results.78 These values depend on the pairwise exchange coupling scheme and oxidation state assignment of each ion within the tetranuclear Mn models explored. For our preferred model in which the lone Mn(III) ion is part of a trimeric cluster that is weakly exchange coupled to a fourth Mn ion, cMn(III) = 1.77 and cMn(IV) ranges from 1.00 to 1.27. Thus the intrinsic aiso HFI for the 14N nucleus of His332 with the OEC could range from 5.8–7.3 MHz if the coordinating ion is Mn(IV) or 4.1 MHz if the nitrogen is instead bound to the Mn(III) ion. These results clearly suggest that His332 is coordinated to the Mn(III) ion in the OEC. The computed intrinsic values for a His—Mn(IV) interaction are unrealistic as the largest site-specific aiso for an sp2 hybridized (i.e. histidine-like) nitrogen atom measured to date is 6.05 MHz for the pyridyl nitrogen atom axially coordinated to the Mn(III) ion in BISPICEN (see Table 1).63 That the 14N HFI found in studies of the OEC is so much larger than those measured for the equatorially liganded histidines in MnCat suggests that His332 is bound along an axis that contains a lobe of a half-occupied metal-centered orbital. If the Mn(III) site were octahedral in symmetry, the interacting orbital could be either 3dz2 or 3dx2-y2 depending on the nature of the Jahn-Teller distortion. However, if the Mn(III) is five-coordinate, trigonal bipyramidal, as has been suggested,78 then the nitrogen of His332 could be interacting with one of the half-occupied orbitals of the t2g set.
Supplementary Material
Acknowledgments
This research was supported by NIH grant GM-48242 to R.D.B. and NIH grant GM-42680 to J.W.W. The Ka-band spectrometer was funded by NIH grant GM-061211. The E580 spectrometer was funded by NIH grant S10-RR021075 and the University of California-Davis.
Footnotes
Comparison of ESE field-swept EPR spectra collected with soft and hard pulses. Three-pulse ESEEM data acquired using different values of τ and B0 along with corresponding simulations. Tabulation of nitrogen hyperfine coupling constants found for other exchange-coupled dinuclear biological metal clusters. This material is available free of charge via the Internet at http://pubs.acs.org
References
- 1.Kono Y, Fridovich I. J Biol Chem. 1983;258(10):6015–6019. [PubMed] [Google Scholar]
- 2.Waldo GS, Fronko RM, Penner-Hahn JE. Biochemistry. 1991;30(43):10486–10490. doi: 10.1021/bi00107a017. [DOI] [PubMed] [Google Scholar]
- 3.Waldo GS, Yu S, Penner-Hahn JE. J Am Chem Soc. 1992;114(14):5869–5870. [Google Scholar]
- 4.Khangulov SV, Barynin VV, Melik-Adamyan VR, Grebenko AI, Voevodskaya NV, Blyumenfel’d LA, Dobryakov SN, Il’yasova VB. Bioorg Khim. 1986;12(6):741–748. [Google Scholar]
- 5.Fronko RM, Penner-Hahn JE, Bender CJ. J Am Chem Soc. 1988;110(22):7554–7555. [Google Scholar]
- 6.Khangulov SV, Barynin VV, Voevodskaya NV, Grebenko AI. Biochim Biophys Acta, Bioenerg. 1990;1020(3):305–310. [Google Scholar]
- 7.Barynin VV, Whittaker MM, Antonyuk SV, Lamzin VS, Harrison PM, Artymiuk PJ, Whittaker JW. Structure. 2001;9(8):725–738. doi: 10.1016/s0969-2126(01)00628-1. [DOI] [PubMed] [Google Scholar]
- 8.Antonyuk SV, Melik-Adamyan VR, Popov AN, Lamzin VS, Hempstead PD, Harrison RM, Artymyuk PD, Barynin VV. Kristallografiya. 2000;45(1):111–122. [Google Scholar]
- 9.Yachandra VK, Guiles RD, McDermott A, Britt RD, Dexheimer SL, Sauer K, Klein MP. Biochim Biophys Acta Bioenerget. 1986;850(2):324–332. doi: 10.1016/0005-2728(87)90169-1. [DOI] [PubMed] [Google Scholar]
- 10.Debus RJ, Nguyen AP, Conway AB. Curr. Res. Photosynth., Proc. Int. Conf. Photosynth., 8th; 1990. pp. 829–832. [Google Scholar]
- 11.Tang XS, Diner BA, Larsen BS, Gilchrist ML, Jr, Lorigan GA, Britt RD. Proc Natl Acad Sci U S A. 1994;91(2):704–708. doi: 10.1073/pnas.91.2.704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Britt RD, Campbell KA, Peloquin JM, Gilchrist ML, Aznar CP, Dicus MM, Robblee J, Messinger J. Biochim Biophys Acta. 2004;1655(1–3):158–171. doi: 10.1016/j.bbabio.2003.11.009. [DOI] [PubMed] [Google Scholar]
- 13.Ivancich A, Barynin VV, Zimmermann JL. Biochemistry. 1995;34(20):6628–6639. doi: 10.1021/bi00020a008. [DOI] [PubMed] [Google Scholar]
- 14.Stemmler TL, Sturgeon BE, Randall DW, Britt RD, Penner-Hahn JE. J Am Chem Soc. 1997;119(39):9215–9225. [Google Scholar]
- 15.Flanagan HL, Gerfen GJ, Singel DJ. J Chem Phys. 1988;88(1):20–24. [Google Scholar]
- 16.Flanagan HL, Singel DJ. J Chem Phys. 1987;87(10):5606–5616. [Google Scholar]
- 17.Khangulov S, Sivaraja M, Barynin VV, Dismukes GC. Biochemistry. 1993;32(18):4912–4924. doi: 10.1021/bi00069a028. [DOI] [PubMed] [Google Scholar]
- 18.Hofbauer W, Bittl R. J Magn Reson. 2000;147(2):226–231. doi: 10.1006/jmre.2000.2202. [DOI] [PubMed] [Google Scholar]
- 19.Schäfer K-O. Exchange Coupled Manganese Complexes: Model Systems for the Active Centres of Redoxproteins Investigated with EPR Techniques. Technischen Universitat Berlin; Berlin: 2002. [Google Scholar]
- 20.Stich TA, Lahiri S, Yeagle G, Dicus M, Brynda M, Gunn A, Aznar C, DeRose VJ, Britt RD. Appl Magn Reson. 2007;31(1–2):321–341. doi: 10.1007/BF03166263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mims WB. J Magn Reson. 1984;59(2):291–306. [Google Scholar]
- 22.Stoll S, Schweiger A. J Magn Reson. 2006;178(1):42–55. doi: 10.1016/j.jmr.2005.08.013. [DOI] [PubMed] [Google Scholar]
- 23.Stoll S, Britt RD. Phys Chem Chem Phys. 2009;11:6614–6625. doi: 10.1039/b907277b. [DOI] [PubMed] [Google Scholar]
- 24.Orio M, Pantazis DA, Petrenko T, Neese F. Inorg Chem. 2009;48(15):7251–7260. doi: 10.1021/ic9005899. [DOI] [PubMed] [Google Scholar]
- 25.Bencini A, Gatteschi D. EPR of Exchange Coupled Systems. Verlag: 1990. [Google Scholar]
- 26.Zheng M, Khangulov SV, Dismukes GC, Barynin VV. Inorg Chem. 1994;33(2):382–387. [Google Scholar]
- 27.Michaud-Soret I, Jacquamet L, Debaecker-Petit N, Le Pape L, Barynin VV, Latour JM. Inorg Chem. 1998;37(15):3874–3876. doi: 10.1021/ic9712176. [DOI] [PubMed] [Google Scholar]
- 28.Sinnecker S, Neese F, Lubitz W. J Biol Inorg Chem. 2005;10(3):231–238. doi: 10.1007/s00775-005-0633-9. [DOI] [PubMed] [Google Scholar]
- 29.Andresen HG. Physical Review. 1960;120(5):1606–1611. [Google Scholar]
- 30.Gerritsen HJ, Sabisky ES. Physical Review. 1963;132(4):1507. [Google Scholar]
- 31.Sands RH, Dunham CM. Q Rev Biophys. 1975;7:443. doi: 10.1017/s0033583500001517. [DOI] [PubMed] [Google Scholar]
- 32.Owen J, Thornley JH. Rep Prog Phys. 1966;29:675. [Google Scholar]
- 33.Townes CH, Dailey BP. J Chem Phys. 1949;17(9):782–796. [Google Scholar]
- 34.Ashby CIH, Cheng CP, Brown TL. J Am Chem Soc. 1978;100(19):6057–6063. [Google Scholar]
- 35.Schäfer KO, Bittl R, Lendzian F, Barynin V, Weyhermüller T, Wieghardt K, Lubitz W. J Phys Chem B. 2003;107(5):1242–1250. [Google Scholar]
- 36.Benetis NP, Dikanov SA. J Magn Reson. 2005;175(1):124–145. doi: 10.1016/j.jmr.2005.03.012. [DOI] [PubMed] [Google Scholar]
- 37.The feature 6.5 MHz, though comparable in intensity to “baseline roll” features introduced by the cosine Fourier transform procedure, is present in all spectra for all values for τ (see Figure S4 in the Supporting Information) Similarly, this feature is broad and relatively intense in the corresponding magnitude transform of the ESEEM data (see Figures S5 and S8). Magnitude transforms do not suffer from deadtime-induced cosine-FT baseline distortions.
- 38.Mims WB. Physical Review B: Solid State. 1972;[3]5(7):2409–2419. [Google Scholar]
- 39.Poole CP, Farach HA. Relaxation in magnetic resonance; dielectric and mössbauer applications. Academic Press; New York: 1971. [Google Scholar]
- 40.Stoll S, Calle C, Mitrikas G, Schweiger A. J Magn Reson. 2005;177(1):93–101. doi: 10.1016/j.jmr.2005.07.012. [DOI] [PubMed] [Google Scholar]
- 41.Harmer J, Van Doorslaer S, Gromov I, Schweiger A. Chem Phys Lett. 2002;358(1,2):8–16. [Google Scholar]
- 42.Kanyo ZF, Scolnick LR, Ash DE, Christianson DW. Nature. 1996;383(6600):554–557. doi: 10.1038/383554a0. [DOI] [PubMed] [Google Scholar]
- 43.Ferreira KN, Iverson TM, Maghlaoui K, Barber J, Iwata S. Science. 2004;303(5665):1831–1838. doi: 10.1126/science.1093087. [DOI] [PubMed] [Google Scholar]
- 44.Loll B, Kern J, Saenger W, Zouni A, Biesiadka J. Nature. 2005;438(7070):1040–1044. doi: 10.1038/nature04224. [DOI] [PubMed] [Google Scholar]
- 45.Yeagle GJ, Gilchrist ML, McCarrick RM, Britt RD. Inorg Chem. 2008;47(6):1803–1814. doi: 10.1021/ic701680c. [DOI] [PubMed] [Google Scholar]
- 46.Hendrich MP, Fox BG, Andersson KK, Debrunner PG, Lipscomb JD. J Biol Chem. 1992;267(1):261–269. [PubMed] [Google Scholar]
- 47.DeRose VJ, Liu KE, Lippard SJ, Hoffman BM. J Am Chem Soc. 1996;118(1):121–134. [Google Scholar]
- 48.Bender CJ, Rosenzweig AC, Lippard SJ, Peisach J. J Biol Chem. 1994;269(23):15993–15998. [PubMed] [Google Scholar]
- 49.Dikanov SA, Davydov RM, Graslund A, Bowman MK. J Am Chem Soc. 1998;120(27):6797–6805. [Google Scholar]
- 50.Cline JF, Hoffman BM, Mims WB, Lahaie E, Ballou DP, Fee JA. J Biol Chem. 1985;260(6):3251–3254. [PubMed] [Google Scholar]
- 51.Gurbiel RJ, Batie CJ, Sivaraja M, True AE, Fee JA, Hoffman BM, Ballou DP. Biochemistry. 1989;28(11):4861–4871. doi: 10.1021/bi00437a051. [DOI] [PubMed] [Google Scholar]
- 52.Iwasaki T, Kounosu A, Samoilova RI, Dikanov SA. J Am Chem Soc. 2006;128(7):2170–2171. doi: 10.1021/ja0562393. [DOI] [PubMed] [Google Scholar]
- 53.Dikanov SA, Shubin AA, Kounosu A, Iwasaki T, Samoilova RI. J Biol Inorg Chem. 2004;9(6):753–767. doi: 10.1007/s00775-004-0571-y. [DOI] [PubMed] [Google Scholar]
- 54.Davydov R, Behrouzian B, Smoukov S, Stubbe J, Hoffman BM, Shanklin J. Biochemistry. 2005;44(4):1309–1315. doi: 10.1021/bi048599t. [DOI] [PubMed] [Google Scholar]
- 55.Morton JR, Preston KF. J Magn Reson. 1978;30(3):577–582. [Google Scholar]
- 56.The fs values mentioned here for nitrogens coordinating Rieske-type [2Fe-2S] clusters are recalculated from the reported isotropic 14N hyperfine coupling constants and a value of a2s0 = +1811 MHz. The original work employed a different value for a2s0 = 1163 MHz.
- 57.Gurbiel RJ, Doan PE, Gassner GT, Macke TJ, Case DA, Ohnishi T, Fee JA, Ballou DP, Hoffman BM. Biochemistry. 1996;35(24):7834–7845. doi: 10.1021/bi960380u. [DOI] [PubMed] [Google Scholar]
- 58.Gurbiel RJ, Ohnishi T, Robertson DE, Daldal F, Hoffman BM. Biochemistry. 1991;30(49):11579–11584. doi: 10.1021/bi00113a013. [DOI] [PubMed] [Google Scholar]
- 59.Rosenzweig AC, Nordlund P, Takahara PM, Frederick CA, Lippard SJ. Chem Biol. 1995;2(6):409–418. [PubMed] [Google Scholar]
- 60.Sage JT, Xia YM, Debrunner PG, Keough DT, Dejersey J, Zerner B. J Am Chem Soc. 1989;111(18):7239–7247. [Google Scholar]
- 61.Grush MM, Chen J, Stemmler TL, George SJ, Ralston CY, Stibrany RT, Gelasco A, Christou G, Gorun SM, Penner-Hahn James E, Cramer SP. J Am Chem Soc. 1996;118(1):65–69. [Google Scholar]
- 62.Rajendiran TM, Caudle MT, Kirk ML, Setyawati I, Kampf JW, Pecoraro VL. J Biol Inorg Chem. 2003;8(3):283–293. doi: 10.1007/s00775-002-0414-7. [DOI] [PubMed] [Google Scholar]
- 63.Randall DW. Pulsed EPR Studies of Tyrosine Radicals and Manganese Complexes: Insights into Photosynthetic Oxygen Evolution. University of California-Davis; Davis, CA: 1998. [Google Scholar]
- 64.Schinzel S, Kaupp M. Can J Chem. 2009;87(10):1521–1539. [Google Scholar]
- 65.Randall DW, Gelasco A, Caudle MT, Pecoraro VL, Britt RD. J Am Chem Soc. 1997;119(19):4481–4491. [Google Scholar]
- 66.Brunold TC, Gamelin DR, Solomon EI. J Am Chem Soc. 2000;122(35):8511–8523. [Google Scholar]
- 67.De Boer JW, Browne WR, Feringa BL, Hage R. C R Chim. 2007;10(4–5):341–354. [Google Scholar]
- 68.Dubois L, Pecaut J, Charlot MF, Baffert C, Collomb MN, Deronzier A, Latour JM. Chem--Eur J. 2008;14(10):3013–3025. doi: 10.1002/chem.200701253. [DOI] [PubMed] [Google Scholar]
- 69.Tagore R, Chen H, Crabtree RH, Brudvig GW. J Am Chem Soc. 2006;128(29):9457–9465. doi: 10.1021/ja061348i. [DOI] [PubMed] [Google Scholar]
- 70.Tagore R, Crabtree RH, Brudvig GW. Inorg Chem. 2007;46(6):2193–2203. doi: 10.1021/ic061968k. [DOI] [PubMed] [Google Scholar]
- 71.Tan XL, Gultneh Y, Sarneski JE, Scholes CP. J Am Chem Soc. 1991;113(21):7853–7858. [Google Scholar]
- 72.Sinnecker S, Neese F, Noodleman L, Lubitz W. J Am Chem Soc. 2004;126(8):2613–2622. doi: 10.1021/ja0390202. [DOI] [PubMed] [Google Scholar]
- 73.Roelofs TA, Liang W, Latimer MJ, Cinco RM, Rompel A, Andrews JC, Sauer K, Yachandra VK, Klein M. Proc Natl Acad Sci U S A. 1996;93(8):3335–3340. doi: 10.1073/pnas.93.8.3335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Debus RJ, Campbell KA, Gregor W, Li ZL, Burnap RL, Britt RD. Biochemistry. 2001;40(12):3690–3699. doi: 10.1021/bi002394c. [DOI] [PubMed] [Google Scholar]
- 75.Debus RJ, Campbell KA, Peloquin JM, Pham DP, Britt RD. Biochemistry. 2000;39(2):470–478. doi: 10.1021/bi9917737. [DOI] [PubMed] [Google Scholar]
- 76.Yano J, Kern J, Irrgang KD, Latimer MJ, Bergmann U, Glatzel P, Pushkar Y, Biesiadka J, Loll B, Sauer K, Messinger J, Zouni A, Yachandra VK. Proc Natl Acad Sci U S A. 2005;102(34):12047–12052. doi: 10.1073/pnas.0505207102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Dubois L, Jacquamet L, Pecaut J, Latour JM. Chemical Communications. 2006;43:4521–4523. doi: 10.1039/b609072a. [DOI] [PubMed] [Google Scholar]
- 78.Peloquin JM, Campbell KA, Randall DW, Evanchik MA, Pecoraro VL, Armstrong WH, Britt RD. J Am Chem Soc. 2000;122(44):10926–10942. [Google Scholar]
- 79.Dikanov SA, Tsvetkov YD, Khangulov SV, Goldfeld MG. Dokl Akad Nauk SSSR. 1988;302:1255–1257. [Google Scholar]
- 80.Sturgeon B. Electron Spin Echo Spectroscopy: Techniques and Applications to Manganese Systems. University of California-Davis; Davis, CA: 1994. [Google Scholar]
- 81.Tang XS, Sivaraja M, Dismukes GC. J Am Chem Soc. 1993;115(6):2382–2389. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.