A three-dimensional finite element analysis of finger joint stresses in the MCP joint while performing common tasks

Abstract

The goal of this study was to develop a three-dimensional finite element model of the metacarpophalangeal (MCP) joint to characterize joint contact stresses incurred during common daily activities. The metacarpal and proximal phalanx were modeled using a COMSOL-based finite element analysis. Muscle forces determined from a static force analysis of two common activities (pen grip and carrying a weight) were applied to the simulation to characterize the surface stress distributions at the MCP joint. The finite element analysis predicted that stresses as high as 1.9 MPa, similar in magnitude to stresses experienced at the hip, may be experienced by the subchondral bone in the MCP joint. The internal structure and material properties of the phalanges were found to play a significant role in both the magnitude and distribution of stresses, but the dependence on cancellous bone modulus was not as severe as predicted by previous two dimensional models.

Introduction

Rheumatoid arthritis [24] and osteoarthritis [5] are debilitating afflictions that have deleterious effects on the function of the hands. As hand function deteriorates over time due to age or complications from these forms of arthritis, total joint replacement may be performed in order to restore function, but such procedures have met with limited success [4,23] due to the complicated loading environment. Thus, understanding the stresses that occur during daily activities is critical to understanding the progression of joint deterioration and to the design of appropriate implants for finger joint arthroplasty.

While contact forces in the finger joints have been characterized over a range of postures [8,9,11,15,27,28], little has been done to examine the stresses within the joint. A previous study investigated the joint and muscle forces that develop within the hand for commonly performed tasks, with the results then applied to a two-dimensional finite element model that simulated stress distributions [6]. This study found stresses as high as 2 MPa which may arise in the subchondral bone of the metacarpophalangeal (MCP) joint for strenuous tasks, with the intrinsic properties of cancellous bone found to have a significant influence on the distribution and magnitude of stresses at the joint contact surface [6]. A two-dimensional model is somewhat limited, however, because it is not possible to account for the portion of cortical bone comprising the sides, which help to reinforce the structure. Consequently, the goal of this study was to characterize and model the joint contact stresses that occur within the finger during select daily tasks using finite element analysis (FEA) on a three-dimensional model of the MCP joint.

Methods

The joint and muscle forces used for this analysis are identical to those from a previous study which developed a two-dimensional finite element model to determine stresses at the MCP joint [6]. These forces were determined by treating the finger as a static system and simultaneously solving equilibrium force and moment equations with a custom code developed in MATLAB.

The two activities modeled here are the tasks of handwriting and carrying a weight, which were determined to have large, long enduring forces on the joints. Handwriting was chosen because it is a common “pinch” activity while carrying a weight was meant to simulate a common task that resulted in a distinctly different pattern of muscle forces [6]. For the handwriting activity, the external load was assumed to act at the fingertip (1.3 N), whereas for the weight-carrying activity, the load was assumed to act at the proximal interphalangeal joint with the load equally distributed on each side of the joint (45 N on the distal side of the metacarpal and 45 N on the proximal end of the proximal phalange) [6].

A number of assumptions were used in this analysis in order to simplify the indeterminate system to a solvable set of equations. For example, the extensor muscles of the finger were neglected as the activities were heavily dependent on the flexors to oppose the applied force and maintain equilibrium. As such, any influence of the extensors to help stabilize the joint was assumed to be negligible. In addition, the tension in the terminal extensor tendon (TE) was taken as the sum of the tensions in the radial band (RB) and ulnar band (UB), TE = RB + UB. The ulnar interosseous (UI) tension was assumed to act equally on the extensor slip (ES), ulnar band, and the proximal phalanx: , 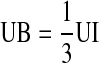. These assumptions also divide the lumbrical (LU) tension such that one third of the tension acts on the extensor slip and the remaining two thirds produces tension in the radial band, [27]. Finally, to simplify the equations to a solvable system, the intrinsic muscle tensions of the RI, UI, and LU were assumed to act together in proportion to the ratio of their physiological cross-sectional areas [8].

The stresses affecting the MCP joint were modeled using the Structural Mechanics module of COMSOL Multiphysics v3.2. A three-dimensional model of the proximal phalange and metacarpal system was developed with forces applied at appropriate points on the proximal phalange to simulate resultant muscle forces at the joint [6].

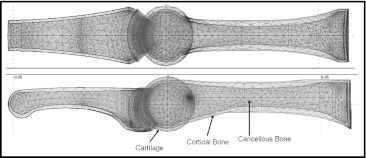
The direct (SPOOLES) linear system solver was used for this analysis. The geometry was meshed with linear Lagrange elements to the subdomain level with a maximum element size scaling factor of 1, element growth rate of 1.5, mesh curvature factor of 0.6, and mesh curvature cut off of 0.03 (Fig. 1). The size of the mesh was adjusted to determine if an increase in the number of elements had an effect on the generated solution.

Fig. 1.

Geometry and mesh used for the finite element analysis. The metacarpal and proximal phalanges were modeled as consisting of a thin outer cortical shell surrounding a cancellous bone interior

An overall metacarpal length of 69 mm and proximal phalange length of 46.5 mm were used for the model [27]. Geometry was approximated from X-ray images, with both the outer shell of the cortical bone and inner cancellous bone regions accounted for. Dimensions for the curvature of the joint heads were modeled as reported previously [2,25].

Cartilage at the joint interface was modeled as two layers, with one layer attached to each side of the joint and frictionless contact constraints between them. The layers completely encased the joint to ensure full cartilage contact regardless of the assumed finger posture, with a total joint gap width of 2 mm [13]. The Young’s moduli used for the cortical bone, cancellous bone, and cartilage were 18,600, 750, and 1.12 MPa, respectively [14,16,18]. The Poisson’s ratios were assumed to be 0.3 for both types of bone and 0.5 for the cartilage. The base of the metacarpal was constrained with boundary conditions prohibiting movement of the proximal end of the metacarpal, with the rest of the model being free to deform in response to the externally applied loads.

For the cases examined, von Mises stresses at the MCP joint were evaluated at the joint contact region on the surface of the metacarpal cortical bone and within the cartilage layer attached to the metacarpal. The mesh size was refined to determine what influence, if any, the number of mesh elements had on the generated solution. The final mesh utilized 82,031 elements with 48,897 degrees of freedom.

Because the mechanical properties of the cancellous bone vary considerably [17,19,20], the modulus was varied from 100 to 1,500 MPa [3,14,18]. The modulus of the cortical bone was varied from 16.5 to 20.5 GPa, and that of the cartilage was allowed to range from 0.5 to 2.0 MPa.

Results

The number of elements in the mesh was varied from 82,031 elements and 48,897 degrees of freedom (DOF) for the handwriting activity to meshes containing 41,657 elements (25,794 DOF) and 121,618 elements (70,647 DOF) in order to assess the convergence of the model. Similarly, the mesh for the weight-carrying activity was varied from the original mesh of 81,216 elements (48,405 DOF) to meshes containing 41,443 elements (25,728 DOF) and 117,510 elements (68,406 DOF). For both activities, the solution was found to vary by 5 % or less for each case.

The model exhibited significant surface stresses occurring at the MCP joint. An average von Mises stress of approximately 600 kPa in the subchondral bone was predicted for the handwriting activity, with a minimum bone stress of 110 kPa and a maximum bone stress of 1.4 MPa over the joint contact area. While the highest stresses at the metacarpal head were found throughout the stiff cortical bone, the cancellous bone region experienced stresses less than 75 kPa.

Significantly higher stresses were found at the MCP joint for the weight-carrying task. The FEA predicted average von Mises stresses of 1.88 MPa in the subchondral bone, with a minimum bone stress of 830 kPa and a peak bone stress of 3.6 MPa found at the joint (Table 1). The cartilage region experienced much lower overall stresses than the cortical bone, with an average stress of 126 kPa for the pen grip activity and 314 kPa for the weight-carrying activity (Fig. 2).

Table 1.

Comparison of stress results in the subchondral bone for two-dimensional and three-dimensional models [6]

Two-dimensional model			Three-dimensional model
	Handwriting (kPa)	Carrying a weight (kPa)		Handwriting (kPa)	Carrying a weight (kPa)
von Mises	630	2,510	von Mises	601	1,880
σ1	0	0	σ1	117	387
σ2	−113	−446	σ2	−222	−256
σ3	−679	−2700	σ3	−556	−1,180
τxy	−48.9	−641	τxy	−2.53	−22.6
			τyz	42.8	−312
			τxz	6.27	−18.0

Fig. 2.

FEA results for the weight-carrying activity. a Orientation of the metacarpal and proximal phalanges. b Close-up section of metacarpal cortical bone at the joint contact region. Peak stress was 3.6 MPa, with an average stress of 1.88 MPa across the joint contact area. c Cartilage stresses at the joint contact region. The average von Mises stress throughout this region was 314 kPa

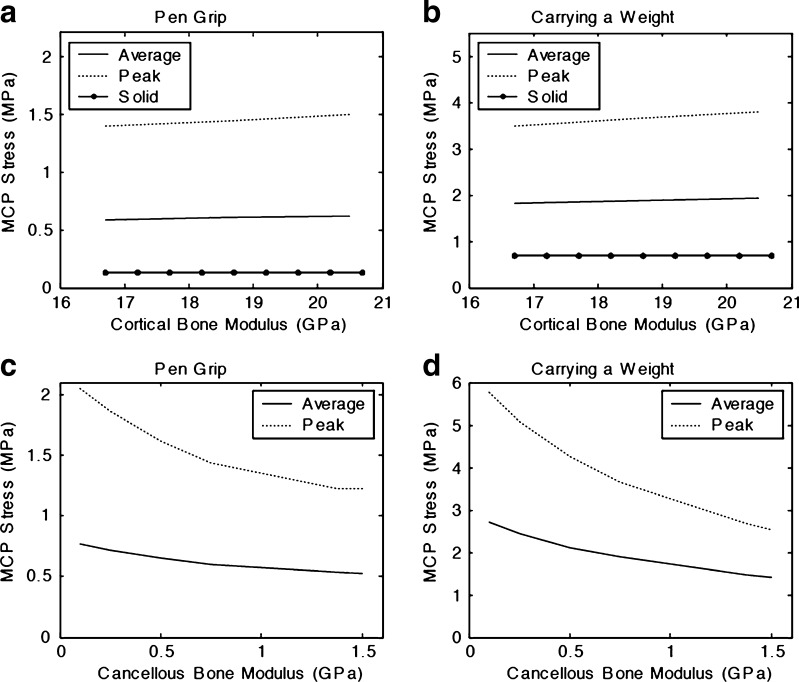
The model exhibited a high sensitivity to the material properties of cancellous bone, with the internal structure and composition of the phalanges playing a significant role on the stresses at the joint (Fig. 3). Very little change in stress results was observed from adjustments to the material properties of the cortical bone in the model. Similarly, stresses within the cartilage region showed little sensitivity to changes in modulus values, staying nearly constant across a range of input values.

Fig. 3.

Stresses within the subchondral region of the MCP joint showed little sensitivity to changes in cortical bone modulus for both activities (a, b), but were highly sensitive to variations in properties of cancellous bone (c, d). Average stresses predicted by the FEA for the subchondral region are represented by the solid line, with peak stresses shown by the dotted line. The dashed line in (a) and (b) represents joint stress predicted by the FEA for a solid bone geometry that does not account for the presence of cancellous bone. A linear relationship was found between the cortical bone modulus and MCP joint surface stress. In contrast, subchondral stresses indicated a high sensitivity to changes in Young's modulus of the cancellous bone as the modulus was varied across a wide range of physiologically relevant values

Discussion

As previously described [6], the forces predicted by the handwriting “pinch” model agreed well with those obtained by Chao et al. [9]. The highest predicted average stress of 1.88 MPa in the subchondral bone was similar to stresses experienced at other locations such as the hips and temporomandibular joints, where the bone stresses may range from 2 to 5 MPa [1,10]. As a comparison, the stresses reported at joints with more severe loading such as the knees or shoulders have been reported to experience stresses in the subchondral bone ranging from 10 to 20 MPa, or approximately an order of magnitude higher than those found at the finger in the current simulation [12,22].

The stresses found in this model are similar in scale, though smaller in magnitude, to those found in the previous two-dimensional analysis [6]. More importantly, the stresses in the subchondral bone varied by a factor of two over the expected range of cancellous bone moduli (100–1,500 MPa). For the same range, the two-dimensional model generated peak bone stresses that varied by a factor of 3.5 [6]. Taken together, this suggests that there is an important relationship between cancellous bone density and stresses in the MCP joint, but it is not as severe as predicted by the two-dimensional model. A two-dimensional model is prone to developing additional bending stresses within the cortical shell as it is not possible to account for the portion of cortical bone comprising the sides, which help to reinforce the structure. In contrast, a three-dimensional model is more able to distribute forces throughout the entire structure and provides a more realistic stress gradient across the joint contact surface. Likewise, stresses in the cartilage become more evenly distributed throughout a three-dimensional geometry, resulting in lower stresses in this region.

It should be noted that for this analysis, the properties of the cartilage were assumed to behave linearly. In reality, the differing instantaneous and equilibrium responses of cartilage result in the properties exhibiting a more complex behavior as it is compressed [16]. More importantly, the mechanical properties of the cartilage depend on chemical composition, age, and level of degeneration. Consequently, we varied the properties over a relatively large range to evaluate the sensitivity of the cartilage stiffness within the context of all the parameters that govern the behavior of the model. The model demonstrated that the results were considerably less sensitive to the cartilage modulus than the cancellous bone modulus. It is likely that the relative dependence of these parameters will be maintained regardless of the constitutive law used for the cartilage. Taken together, these data suggest that patients with low bone mass may exhibit accelerated cartilage wear when compared to patients with normal bone mass, providing an additional aspect to the clinical assessment and possibly additional treatment options. In particular, future work should examine the interactions between bone health and cartilage degeneration. Subsequent work on the role of fluid transport in the joint as a result of common loading activities and the finger joints may then provide a fruitful paradigm for evaluating the effects of loading on long-term cartilage damage and repair. Additional improvements to the model may include electromyographic data of muscle activation for various activities [9,26] or, where experimentally feasible, the use of magnetic resonance imaging-based characterization of local tissue deformations [7,21]. Ultimately, these results illustrate how common activities may have a highly strenuous effect on the hand and stresses at the joints and advance the work done in previous studies to describe how joint stresses distribute at the contact region.

These results may have implications for total joint replacement. There are two principle types of finger joint replacements, silicone and pyrocarbon, each of which fails in a different manner. Silicone implants typically fracture (approximately 25+ % over a 6-year follow-up) [23] while pyrocarbon implants dislocate or exhibit loosening and osteolysis (approximately 10 % of joints after even a short 19-month follow-up) [4]. Additionally, 50 % of silicone implants and 20 % of pyrocarbon implants demonstrated coronal plane abnormalities [4]. Fracture, dislocation, and coronal plane deformities are all likely a result of the loads applied to the joints and the quality of the surrounding bone. This may suggest that understanding the forces and stresses associated with daily activities is important to help design appropriate implants for finger joint arthroplasty.