Preserving the Accuracy and Resolution of the Sodium Bioscale from Quantitative Sodium MRI during Intra-Subject Alignment across Longitudinal Studies

Abstract

Emerging applications of sodium bioscales derived from quantitative sodium magnetic resonance (MR) imaging assess temporal changes in regional sodium concentration over intervals that vary from hours (monitoring tissue viability in stroke) to weeks (monitoring brain tumor treatment during radiation therapy) or even years (monitoring progression of neurodegenerative disease). Accurate interpretation of such quantitative data requires precise registration between MR imaging sessions to avoid session-to-session changes in partial volume effects between normal tissue (~38 mM sodium concentration), lesions (variable sodium concentration), and cerebrospinal fluid (~144 mM sodium concentration). The existing Automated Image Registration (AIR) algorithm is shown to be suitable for rapid, accurate, and precise determination of the transform that aligns sodium MR images. Implementation of this transform during image reconstruction from the k-space data is shown to produce smaller errors than conventional image-domain interpolation. Experimental results at 9.4 Tesla and 3.0 Tesla demonstrating this registration approach to sodium data illustrate preservation of quantification accuracy during alignment of sodium MR images acquired from the same subject during different imaging sessions.

Introduction

Quantitative sodium (²³Na) magnetic resonance (MR) imaging of the brain (1) measures the tissue sodium concentration (TSC) bioscale. This bioscale reflects the tightly regulated process of sodium ion homeostasis that is maintained by both systemic mechanisms and normal brain metabolism (2). The clinical potential for ²³Na neuroimaging was recognized (3) well before adequate technology for quantitative sodium MR imaging with acquisition times suitable for human subjects was available. Improvements in magnet and pulse sequence technology have led to quantitative (molar concentration values) and qualitative (arbitrary signal intensity values) sodium MR imaging of the human brain (1, 4-6) and body (7-9) at multiple institutions. The current generation of high- (10) and ultra-high field imaging systems (11) with efficient, ultra-short echo-time (UTE) pulse sequences (1, 12-14) enable acquisition times of 8-10 minutes to be used for sodium imaging of the human brain.

The TSC bioscale informs on diseases that disrupt sodium ion homeostasis (e.g., failure of metabolic energy production in stroke, (4)) and can be combined with a biochemical tissue model to compute the interstitial volume fraction (IVF) bioscale that provides insight into cell packing (15). Ongoing investigations of TSC and IVF suggest that these bioscales may reflect regional changes in sodium concentration in early neurodegenerative diseases (16,17) and enable non-invasive monitoring of the effectiveness of radio- and chemotherapy of brain tumors (15, 18).

Many of the emerging applications of sodium imaging and sodium bioscales call for the interpretation of regional changes in TSC and IVF from imaging sessions separated by weeks, months, or even years. As the resolution of quantitative sodium imaging that can be achieved within a practical imaging time is several cubic millimeters (19), single-voxel analysis is preferred over a region-of-interest (ROI) analysis, especially when the structures of interest are small (16). Meaningful interpretation of the temporal patterns of sodium bioscales, therefore, requires precise registration of datasets collected at different times from the same subject. Even with experienced operators and highly motivated subjects, session-to-session registration achieved by reproducing the head position of the subject is limited to a few millimeters of translation and a few degrees of rotation. This level of registration is insufficient for voxel-based analysis of quantitative sodium bioscales across different imaging sessions, as it would change partial volume averaging effects and thereby compromise the high precision available within an individual imaging examination (1). The large difference in sodium concentration between normal tissue and cerebrospinal fluid (CSF) means that even a small mis-registration can result in a significant compromise of TSC and IVF values of tissue close to CSF spaces. For example, if a nominal 5 mm isotropic voxel contains only brain tissue with a normal TSC of ~ 38 mM and the adjacent voxel contains only CSF with a TSC of ~ 144 mM, then a 0.5 mm translation between imaging sessions results in a voxel that is composed of 90% tissue and 10% CSF with a TSC of ~ 49 mM. Such a ~25% change from 38 mM to 49 mM between imaging sessions introduces by an uncorrected translation could disguise significant biological changes in TSC. For the typical nominal isotropic voxel size of 3-6 mm used for quantitative sodium MR imaging that results in a true isotropic resolution of ~6-9 mm based on the point spread function (19), an uncorrected translation of as small as 10% of a voxel dimension can cause significantly large inter-session errors near tissue-CSF boundaries. Uncorrected rotations can cause similar session-to-session changes to the voxel composition that result in large TSC errors. Such errors, if uncorrected, would defeat the purpose of high-precision quantification of parameters with small intrinsic biological variance.

We report on using the existing Automated Image Registration (AIR) alignment algorithm (20, 21) to determine the transform required to retrospectively align sodium MR datasets of the brain from the same subject independently acquired with the flexible twisted projection imaging (flexTPI) acquisition (1). The accuracy of applying this transform using conventional image-space resampling provided by AIR or directly in k-space with a subsequent image reconstruction is investigated in terms of the accuracy of the TSC bioscale obtained from the flexTPI acquisition.

Materials and Methods

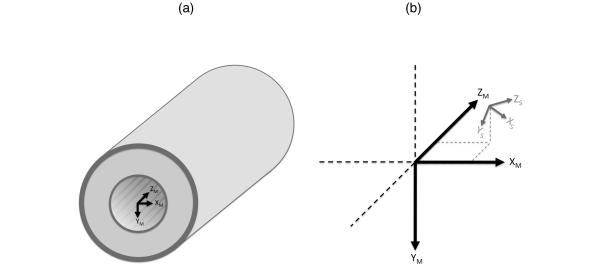
It is convenient to consider two coordinate systems (magnet and subject) when formulating the problem of MR image registration. For simplicity, and without loss of generality, only right-hand coordinate systems are used. The magnet coordinate system (denoted with subscript M) is defined as a y-down coordinate system with its origin located at the gradient isocenter and with the Z axis parallel to the main magnetic field and increasing in the direction of the service end of the magnet (see Figure 1.a). The magnet coordinate system is independent of the object being imaged and can be defined equivalently for any MR imaging device.

Figure 1.

Magnet coordinate system (subscript M) is defined relative to the gradient isocenter of the MR scanner (a). The subject coordinate system (subscript S) is defined relative to the subject anatomy. The subject coordinate system can be translated and rotated relative to the magnet coordinate system (b).

When a subject is placed in the MR scanner, the subject coordinate system (denoted with subscript S) is defined relative to the subject anatomy. In the subject coordinate system a point, p_S, is in the same anatomical location (e.g., center of left ventricle) regardless of head position or orientation. In contrast, a point in the magnet coordinate system, p_M, corresponds to different anatomical locations depending on head position but maps to the same physical location inside the MR scanner. The patient and magnet coordinate systems generally have different origins (translation) and orientations (rotation). Using homogenous coordinate notation (22), if p_M is a length-four column vector¹ of defining a point in the magnet coordinate system, it can be converted to the corresponding point in the subject coordinate system through the 4 × 4 homogenous transform T_M → S that performs the translation and rotation necessary to move from magnet to subject coordinates:

$$p_S=T_{M\to S}\cdot p_M$$ (1)

The low sensitivity and rapid transverse relaxation of the sodium MR signal dictates that 3-D UTE projection-based imaging be used to maximize the SNR and achievable resolution (19). The flexTPI acquisition sequence combines non-selective excitation with center-out, non-Cartesian k-space trajectories to collect data in the magnet coordinate system over a field-of-view that is symmetric about the gradient isocenter (1). Other 3-D UTE imaging techniques well-suited to sodium imaging often use similar geometries (12,14,23).

Mal-alignment of data from the same subject occurs between imaging sessions when the participant head position is not exactly reproduced and within the same imaging session due to head motion between scans. In both cases, there are different subject coordinate systems for each dataset even though the magnet coordinate systems are identical. When the data are reconstructed and displayed in the magnet coordinate system, the resulting images are not aligned.

Registration of two datasets is achieved by aligning the subject coordinate systems for the two acquisitions. Mathematically, this requires finding the transform that maps all points in the subject coordinate system of the second acquisition (denoted with subscript S₂) to the subject coordinate system of the first acquisition (denoted with subscript S₁):

$$T_{S_2\to S_1}=T_{M\to S_1}{T}_{S_2\to M}$$ (2)

Once this transformation is known, it can be applied to the second dataset to transform it into the same subject coordinate system as the first dataset. Since both datasets are of the same subject, and can be considered rigid, only translations and rotations need to be considered. The non-linear image warping that would be necessary to register data from different subjects is unnecessary provided any regions of change in the time between the acquisition of the two datasets (e.g., progressive pathological processes over time) are excluded when determining T_S2 → S₁ . It is also assumed that the properties and performance of the scanner are stable over the same time interval.

The rotation and translation described by T_S2 → S₁ can be applied in either image space or k-space. In image space, interpolation is performed using an interpolation kernel and the coordinate transform defined by T_S2 → S₁ (20). Popular interpolation kernels for MR image data include tri-linear (default of the AIR software package), windowed sinc, and chirp-z. Image-domain interpolation will often result in some loss of spatial resolution due to the use of a finite-length interpolation kernel (24).

The rotation and translation described by T_S2 → S₁ can also be applied directly in k-space using basic properties of the Fourier transform. First, T_S2 → S₁ is decomposed into rotation and translation components:

$$T_{S_2\to S_1}=R_{T_{S_2\to S_1}}{T}_{T_{S_2\to S_1}}$$ (3)

where R_TS2 → S₁ is a pure 3-D rotation transform (no translation) and T_TS2 → S₁ is a pure 3-D translation transform (no rotation). In Equation {3}, translation is applied before rotation. The opposite (rotation then translation) decomposition is also possible, but the resulting rotation and translation transforms will be different since in general $T_{S_2\to S_1}\ne T_{S_1\to S_2}^{-1}$.

Rotation and translation can be performed in k-space by modifying the complex data values and the known k-space sampling locations. Let s_S2 and k_S2 denote a complex-valued k-space sample and the k-space location of that sample in the second dataset that is to be reconstructed so it is aligned to the first dataset. Rotation of the final image data is implemented by rotating the k-space locations

$$k_A=R_{T_{S_2\to S_1}}\cdot K_{S_2}$$ (4)

to yield the k-space coordinates for the second dataset aligned to the subject coordinate system of the first data. Translation is performed through a phase shift of the k-space data

$$S_A=S_{S_2}\cdot e^{-j2\pi \left(B\cdot T_{S_2\to S_1}\cdot k_{S_2}\right)}$$ (5)

where the vector B=[1 1 1 0] performs the necessary summation over the three physical dimensions to produce a scalar result. Alignment is performed by applying equations {4} and {5} to every k-space value and k-space location pair in the second dataset.

Since flexTPI is reconstructed with a gridding-based (25) reconstruction, Equations {4} and {5} can be easily incorporated into the overall reconstruction with minimal additional computational complexity by simply using k_A for gridding rather than k_S2 and gridding the values s_A rather than s_S2 . In contrast, Fourier-based acquisitions that sample k-space on a Cartesian grid require rotating the entire 3-D Fourier data using a resampling approach and adjusting the phase of the data or using a specialized reconstruction (26, 27).

Finding the transform T_S2 → S₁ , or equivalently the translation and rotation between the two datasets, is a well-researched topic for MR imaging data (20, 28,29). Sodium MR image data imposes the constraints of lower resolution and signal-to-noise ratio than the traditional proton anatomical data for which MR image registration is typically considered. The Automatic Image Registration (AIR) algorithm performs well for rigid alignment and was originally designed for low-resolution positron emission tomography (30), making it well suited to registration of sodium MR data from the same subject. AIR has since been enhanced (version 5.3.0 was used in this work) for MR image data and offers a mature algorithm with many alignment options (20).

Accuracy and Precision of AIR in Determining the Alignment Transform

The accuracy and precision of T_S2 → S₁ determined by AIR was investigated with simulations based on experimental human data acquired from a custom-built 9.4 Tesla (11) MR scanner and a clinical 3.0 Tesla MR scanner (HDx, GE Healthcare, Wisconsin). Flexible TPI was performed at 9.4 Tesla (F_R=0.201, T_R=160ms, T_E=260us, G_MAX=5.47 mT/m, FOV=22 cm, matrix=76, 10 minute total acquisition time) and 3.0 Tesla (F_R=0.25, T_R=160ms, T_E=360us, G_MAX=4 mT/m, FOV=22 cm, matrix=50, 4 averages, 17 minute total acquisition time) on healthy volunteers using protocols approved by the Institutional Review Board under an investigational device exemption (IDE) from the Food and Drug Administration. Eddy currents and system delays were corrected using existing methods (1, 31) so as to minimize image distortions due to gradient and k-space infidelities. Typical quantitative sodium imaging on humans is performed with scan durations of 8-10 minutes, but the increased signal averaging at 3 Tesla was used to improve the signal-to-noise ratio (SNR) of the experimental data so that simulated data could be generated at an SNR equivalent to the 2 averages used for routine imaging. At 9.4 Tesla, there is sufficient SNR that this averaging is not necessary.

The experimental data were used to generate 100 synthetic human datasets with known random translations (uniformly distributed ±5 cm translations in the X, Y, and Z directions) and rotations (uniformly distributed ±15 degree rotation about X, Y, and Z axes). For each synthetic dataset, S₁ was taken as the subject coordinate system of the original experimental data and S₂ as the subject coordinate system that resulted from the random rotation followed by translation. T_S2 → S₁ was computed using the known rotation and translation values and the synthetic dataset was generated by applying k-space domain rotation and translation described by $T_{S_2\to S_1}^{-1}$ $}. As Equations {4} and {5} and AIR perform translation before rotation, the synthetic datasets were generated with rotation applied before translation so that the negative translation distances and rotation angles exactly recover the original location and orientation when translation is performed before rotation. Complex Gaussian noise was added to the k-space data to reduce the SNR to a level below that typically achieved for a 10-minute acquisition. The resultant SNR, estimated as signal mean divided by signal standard deviation from a homogenous region of white matter, after adding the complex Gaussian noise was ~7:1 for the 3.0T data (4.4 mm isotropic voxels) and ~5:1 for the 9.4T data (2.9 mm isotropic voxels). This ensured that the noise in each synthetic dataset was at a level higher than typical human sodium images and independent so that it did not provide features that could be exploited by the alignment algorithm when estimating T_S2 → S₁ .

The translations and rotations for each synthetic dataset were then determined using AIR to align the randomly transformed image to the original orientation. Because both datasets had the same contrast and were of the same subject, a rigid-body six-parameter model was used with a least-square cost function. AIR was initialized with zero rotation and the translation estimated from the centroid of each dataset. Three-dimensional spatial filtering with a full-width at half-max equal to the voxel size was specified for both datasets being aligned. Background voxels in both datasets were suppressed by a threshold set equal to three times the noise level estimated from a background region.

The complete processing was performed for images reconstructed with voxel sizes equal to 2.89 mm (9.4 Tesla only), 4.4 mm, 5.9 mm, and 8.8 mm isotropic, respectively. For each voxel size, the synthetic datasets were generated with and without a Blackman k-space filter. Such filtering of k-space reduces the Gibbs artifacts that result from finite k-space sampling at the expense of spatial resolution. Both filtered and unfiltered k-space cases were evaluated to determine whether the inclusion of this k-space filter impacts the estimation of T_S2 → S₁ . In total, the alignment was performed on 800 9.4 Tesla datasets (four different voxel sizes, each with and without k-space filtering) and 600 3.0 Tesla datasets (three different voxel sizes, each with and without k-space filtering) with random translations and rotations and unique noise. In each case, the rotation and translation determined by AIR were recorded for comparison to the known values used to produce the rotation and translation. The average times required to compute the alignments were also recorded.

Simulation of Applying the Alignment Transform in Image-space and k-space

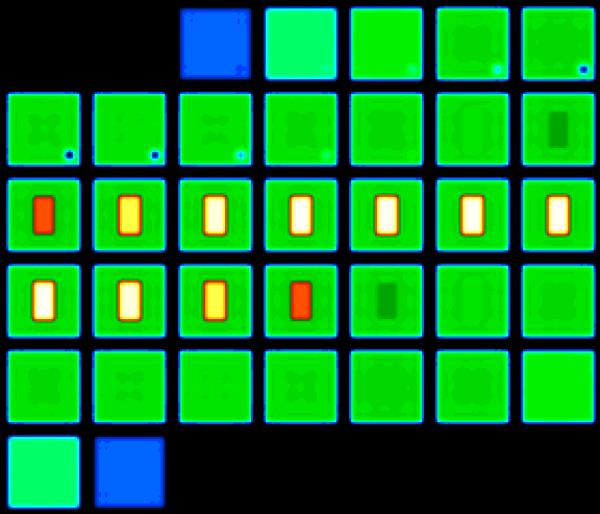
The impact of applying the alignment transform with either image-space resampling or k-space manipulation, as described by Equations {4} and {5}, was investigated using a simulated phantom. The numerical phantom, with axial partitions shown tiled in Figure 2, has a rectangular compartment (2.605 × 4.921 × 2.605 cm³) of CSF (144 mM concentration, T₂ = 55 ms) surrounded by a compartment (10 × 10 × 10 cm³) of tissue (38 mM, biexponential T₂ of 60% 2.5 ms and 40% 14 ms). These concentrations and relaxation characteristics were selected to match experimental values for the human brain (1, 5, 6, 15, 32, 33). A small (1.15 cm isotropic) void (0 mM) was also present in the numerical phantom to produce an asymmetrical phantom without 180° rotational symmetry. Although the compartments of the phantom were simulated with sharp boundaries, the reconstructed image data shown in Figure 2 had smooth transitions and some Gibbs artifacts (particularly along the edges of the CSF compartment) as expected due to the short transverse relaxation rate of the sodium signal and flexTPI sampling scheme (19).

Figure 2.

Simulation phantom (shown reconstructed with a Blackman k-space filter) used to compare the impact of applying the ideal transform in image-space and k-space. The phantom was simulated to have sodium characteristics matching brain parenchyma (38 mM concentration, biexponential relaxation: 60% T₂=2.5 ms, 40% T₂=14ms, green) and CSF (144 mM concentration, T₂=55 ms, white). The small signal void that appears as low concentration (blue) removed any orientation ambiguity. Thirty-five axial partitions are shown. The color scale (right) is the sodium concentration in mM.

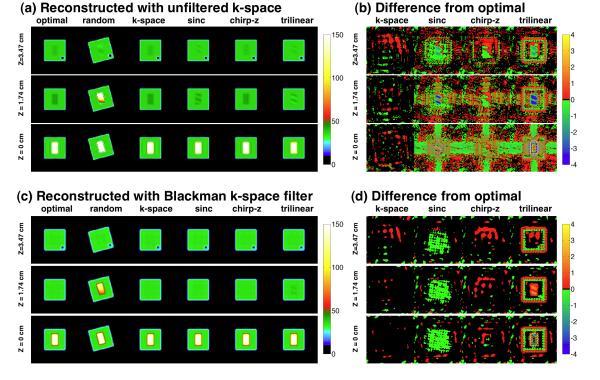
The k-space data for the phantom was simulated for flexTPI acquisitions optimized for resolution (F_R=0.201, T_R=160ms, T_E=260us, G_MAX=5.47 mT/m, FOV=22 cm, matrix=76) (19). This best resolution achievable within a practical imaging time was used to investigate the impact of applying the alignment transform in the most sensitive case. Data were generated for 50 random translations (uniformly distributed ±5 cm translations in the X, Y, and Z directions) and rotations (uniformly distributed ±15 degree rotation about X, Y, and Z axes). For each simulated phantom, the data were transformed back to the original orientation using image-space interpolation with tri-linear, chirp-z, and windowed sinc (+/− 5 sidelobes) and the exact T_S2 → S₁ . The aligned data were also reconstructed directly using the simulated k-space data and Equations {4} and {5}. Each aligned result was compared to the original data reconstructed with no translation or rotation. This comparison dataset represented the best possible reconstruction for the data and was used as the gold standard. The simulation was performed with both unfiltered k-space data and with a Blackman k-space filter to reduce Gibbs ringing. The performance was measured in terms of the maximum error in mM, the average error in mM computed for voxels in the original dataset with a concentration of at least 1 mM, and the total resampling time.

Alignment of Human ²³Na Data

Sodium MR imaging was performed at 9.4 Tesla (11) and 3.0 Tesla on healthy volunteers using protocols approved by the Institutional Review Board under an IDE from the Food and Drug Administration. FlexTPI imaging was performed at 9.4 Tesla using a custom-built quadrature-birdcage radiofrequency (RF) coil tuned to 105.92 MHz. Two imaging sessions were completed using the flexTPI acquisition with parameters optimized for resolution (19) with a 10-minute acquisition time (F_R=0.201, T_R=160ms, T_E=260us, G_MAX=5.47 mT/m, FOV=22 cm, matrix=76). Shimming to maximize the B₀ homogeneity was performed at the sodium frequency at the beginning of each imaging session. Two sodium acquisitions were then performed with different echo times to enable B₀-corrected image reconstruction to further minimize B₀ inhomogeneities.

FlexTPI imaging was performed at 3.0 Tesla using a custom-built quadrature-birdcage radiofrequency (RF) coil tuned to 33.80 MHz. Two imaging sessions were completed using flexTPI with the same parameters (1) and an 8.5-minute acquisition time (F_R=0.25, T_R=160ms, T_E=350us, G_MAX=4 mT/m, FOV=22 cm, matrix=50). Shimming and B₀ mapping were performed at the proton frequency as previously described (1).

For the 9.4 Tesla and 3.0 Tesla data collection, the subject was removed from the scanner and RF coil between imaging sessions. Although the operator attempted to replicate head position and orientation in the two acquisitions as would be done for clinical imaging, exact replication of head position was unlikely to be achieved. The data from these two imaging sessions were reconstructed with B₀ correction. Eddy currents and system delays were corrected using existing methods (1, 31) so as to minimize image distortions due to gradient and k-space infidelities. The image data were then aligned using AIR to determine the transform necessary to match the subject coordinate system of session 2 to the subject coordinate system of session 1. The determined transform was applied in k-space using Equations {4} and {5} to produce the B₀-corrected session 2 image aligned to that of session 1. This alignment and processing represented the standard case of the same subject being imaged on the same MR scanner at different times.

Results

Accuracy and Precision of AIR in Determining the Alignment Transform

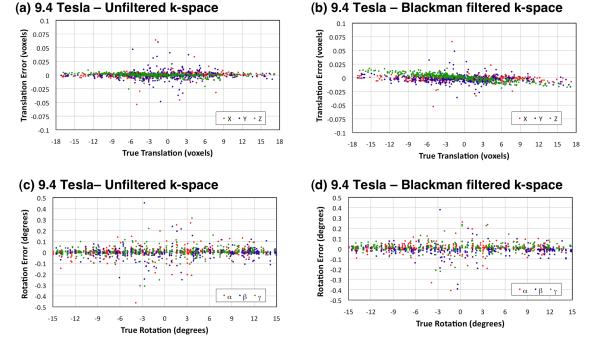
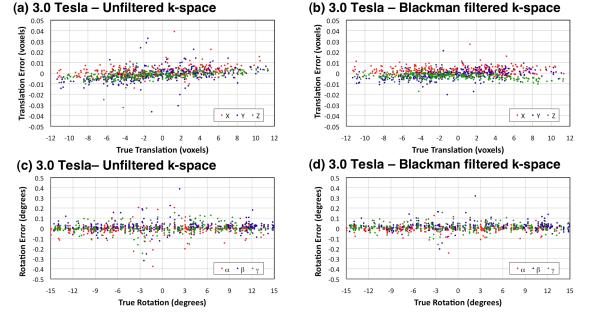
Figures 3 and 4 show scatter plots of the errors in alignment obtained with AIR for the human brain images at 9.4 Tesla and 3.0 Tesla, respectively. Regardless of whether k-space filtering was used during image reconstruction, translation and rotation errors were small. Tables 1 and 2 summarize the processing time and errors of determining the alignment transform by AIR for sodium MR brain images at isotropic voxels dimensions of 2.9 mm (9.4 Tesla only), 4.4 mm, 5.9 mm, and 8.8 mm, respectively, both with and without Blackman k-space filtering during image reconstruction. All alignment transforms were computed within a very acceptable time (less than one second on a commercial consumer-grade Apple MacBook Pro laptop computer with a 2.2 GHz Intel Core i7 processor and 8 GB of 1333 MHz DDR3 memory).

Figure 3.

Error in determining random translations (a,b) and rotations (c,d) of ²³Na human brain images with 2.9 mm, 4.4 mm, 5.9 mm, and 8.8 mm isotropic voxels at 9.4 Tesla. Each plot includes all 400 results (100 random translations and rotations for each voxel size). Table 1 details the translation and rotation errors for individual voxel sizes.

Figure 4.

Error in determining random translations (a,b) and rotations (c,d) of ²³Na human brain images with 4.4 mm, 5.9 mm, and 8.8 mm isotropic voxels at 3.0 Tesla. Each plot includes 300 results (100 random translations and rotations for each voxel size). Table 2 details the translation and rotation errors for individual voxel sizes.

Table 1.

Processing time and errors in translation and rotation for AIR in determining the alignment transform for simulated 9.4 Tesla 23Na images of the same brain.

Voxel Size (mm)	Alignment Time2 (s)	Absolute Translation Error (mm)			Absolute Rotation3 Error (degrees)
		X	Y	Z	α	β	γ
2.9	0.978 ± 0.382	0.005 ± 0.004	0.005 ± 0.004	0.006 ± 0.004	0.006 ± 0.007	0.006 ± 0.008	0.005 ± 0.005
2.9+B1	0.820 ± 0.307	0.009 ± 0.014	0.014 ± 0.010	0.022 ± 0.004	0.013 ± 0.009	0.014 ± 0.009	0.011 ± 0.009
4.4	0.625 ± 0.222	0.013 ± 0.012	0.016 ± 0.022	0.009 ± 0.006	0.012 ± 0.014	0.012 ± 0.012	0.009 ± 0.007
4.4+B 1	0.590 ± 0.241	0.012 ± 0.009	0.017 ± 0.016	0.018 ± 0.012	0.013 ± 0.012	0.013 ± 0.010	0.012 ± 0.008
5.9	0.461 ± 0.165	0.029 ± 0.041	0.027 ± 0.030	0.024 ± 0.023	0.022 ± 0.025	0.028 ± 0.044	0.022 ± 0.022
5.9+B1	0.439 ± 0.154	0.023 ± 0.031	0.026 ± 0.026	0.034 ± 0.023	0.022 ± 0.022	0.023 ± 0.033	0.019 ± 0.016
8.8	0.270 ± 0.061	0.069± 0.070	0.080 ± 0.070	0.039 ± 0.056	0.070 ± 0.082	0.070 ± 0.090	0.066 ± 0.061
8.8+B1	0.269 ± 0.057	0.054± 0.072	0.064 ± 0.071	0.040 ± 0.033	0.066 ± 0.063	0.065 ± 0.041	0.050 ± 0.045

¹Image data reconstructed with a Blackman k-space filter

²Processing was performed on an Apple Macbook Pro with a 2.2 GHz Intel Core i7 and 8 GB of random access memory.

³Rotations around the X, Y, and Z axes are denoted α, β, and γ, respectively.

Table 2.

Processing time and errors in translation and rotation for AIR in determining the alignment transform for simulated 3.0 Tesla 23Na images of the same brain.

Voxel Size (mm)	Alignment Time2 (s)	Absolute Translation Error (mm)			Absolute Rotation3 Error (degrees)
		X	Y	Z	α	β	γ
4.4	0.53 ± 0.11	0.013 ± 0.011	0.020 ± 0.017	0.012 ± 0.009	0.010 ± 0.011	0.013 ± 0.012	0.011 ± 0.009
4.4+B 1	0.50 ± 0.19	0.015 ± 0.011	0.016 ± 0.012	0.017 ± 0.010	0.010 ± 0.008	0.017 ± 0.012	0.010 ± 0.008
5.9	0.35 ± 0.07	0.020 ± 0.016	0.025 ± 0.026	0.018 ± 0.018	0.023 ± 0.025	0.030 ± 0.024	0.017 ± 0.016
5.9+B1	0.35 ± 0.09	0.017 ± 0.012	0.019 ± 0.016	0.019 ± 0.012	0.015 ± 0.012	0.024 ± 0.016	0.015 ± 0.012
8.8	0.25 ± 0.04	0.040 ± 0.046	0.049 ± 0.055	0.028 ± 0.033	0.056 ± 0.060	0.058 ± 0.065	0.058 ± 0.045
8.8+B1	0.23 ± 0.03	0.034 ± 0.032	0.030 ± 0.032	0.020 ± 0.019	0.036 ± 0.037	0.048 ± 0.049	0.046 ± 0.033

¹Image data reconstructed with a Blackman k-space filter

²Processing was performed on an Apple Macbook Pro with a 2.2 GHz Intel Core i7 and 8 GB of random access memory.

³Rotations around the X, Y, and Z axes are denoted α, β, and γ, respectively.

Simulation of Applying the Alignment Transform in Image-space and k-space

Table 3 summarizes the results from the simulation of applying the alignment transform either in the image domain by conventional image-space interpolation or during image reconstruction by modifying the k-space data using Equations {4} and {5}. The max error (mM), average error (mM), and processing time (s) varied significantly among the alignment methods with the k-space based alignment producing smaller errors than any of the image domain based alignment methods. Figure 5 shows selected images from the simulated phantom shown in Figure 2 for three representative slices at different locations along the Z-axis. For each Z-axis location, the optimal (no translation or rotation) and randomly rotated and translated images are shown with the aligned images that resulted from applying T_S2 → S₁ in k-space during image reconstruction or directly in image space using one of three AIR interpolation methods (sinc, chirp-z, tri-linear) without and with the Blackman k-space filter (Figures 5.a and 5.c, respectively). The differences between aligned and optimal magnitude images for each of alignment implementation strategy, shown for the k-space and image space application of the aligning transform without and with the Blackman k-space filter (Figures 5.b and 5.d), emphasize the magnitude of the errors that result from each alignment implementation method. Application of the alignment transform in k-space improves the fidelity of the aligned image and minimizes the differences from the reference image. The Blackman filter further improves this result. Although the geometric features are retained by all methods, the difference images clearly demonstrate the distortions in signal intensity that represent the loss of quantification. This disturbance was lowest in the k-space alignment with use of the Blackman k-space filter.

Table 3.

Errors in quantification of TSC and the processing time for the simulation phantom (Figure 2) when the alignment transform is applied directly in k-space during image reconstruction or in image space (sinc, chirp-z, trilinear).

	Reconstructed with unfiltered k-space				Reconstructed with Blackman filtered k-space
	k-space	sinc	chirp-z	trilinear	k-space	sinc	chirp-z	trilinear
Maximum error (mM)	0.180 ± 0.015	5.209 ± 0.576	1.392 ± 0.133	34.704 ± 3.019	0.125 ± 0.015	0.552 ± 0.036	0.158 ± 0.022	6.826 ± 0.288
Average1 error (mM)	0.034 ± 0.003	0.338 ± 0.020	0.154 ± 0.010	0.874 ± 0.010	0.027 ± 0.003	0.068 ± 0.001	0.028 ± 0.003	0.293 ± 0.001
Time1 (s)	17.311 ± 1.156	28.183 ± 1.771	1.713 ± 0.154	0.059 ± 0.014	16.311 ± 1.670	26.395 ±1.789	1.581 ± 0.174	0.060 ± 0.028

¹Average error computed over all voxels with a TSC of at least 1 mM.

²Processing was performed on an Apple Macbook Pro with a 2.2 GHz Intel Core i7 and 8 GB of random access memory.

Figure 5.

Results for three axial partitions (top, middle, bottom) through a simulation phantom (shown in Figure 2) for representative phantom alignments without k-space filtering (a,b) and with (c,d) Blackman k-space filtering. The “optimal” (original simulation reference image with no translation or rotation), “random” (representative simulation image with a random rotation and translation) and images aligned to “optimal” image applying the alignment transform in “k-space” or in image space using AIR “sinc”, “chirp-z” or “trilinear” interpolations are shown. The image intensities are quantified in units of millimolar sodium concentration shown on color scale at right of each part of the figure. The differences (b,d) between the “optimal” and aligned data are also shown in the same units of millimolar of sodium concentration. The three image-domain resampling methods result in larger errors than the k-space alignment implementation. These visual results are tabulated numerically in Table 3.

Alignment of Human ²³Na Data

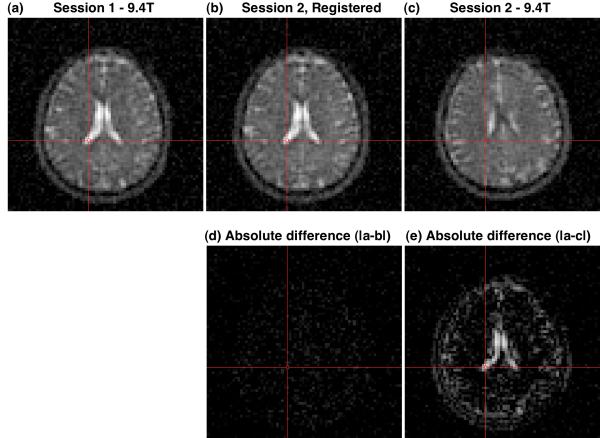
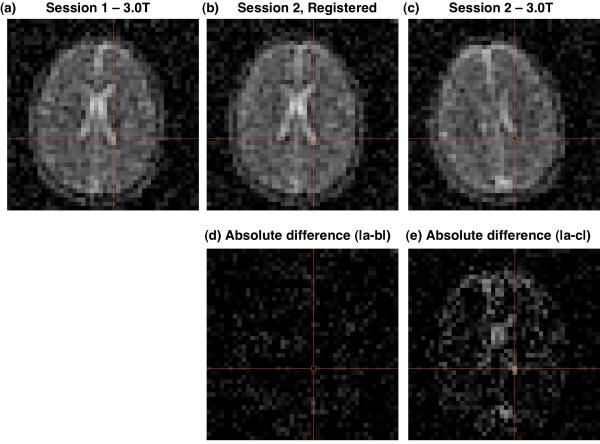
Figure 6 shows selected axial images from the same Z-location in the magnet coordinate system for the first and second 9.4T imaging sessions (Figures 6.a and 6.c, respectively), along with the resultant aligned image after finding the alignment transform using AIR and applying the resultant alignment transform to the k-space data during reconstruction (Figure 6.b). The fidelity of the alignment for both resolution and quantification is demonstrated by the absence of significant signal intensity or features in the absolute difference image (Figure 5.d) calculated from k-space aligned images 6.a and 6.b when compared to the significant non-zero signal intensity and imaging features for the absolute difference image for the non-aligned images 6.a and 5.c (Figure 6.e). Figure 7 shows selected 3.0T ²³Na axial images before (Figures 7.a and 7.c, respectively) and after (Figure 7.b) alignment. Similar to the 9.4T results of Figure 6, there is an absence of significant signal intensity or features in the absolute difference image (Figure 7.d) computed from the aligned images 7.a and 7.b when compared the absolute differences image computed from the non-aligned images 7.a and 7.c.

Figure 6.

Example of registration of 9.4 T sodium ²³Na images (a,c) from different imaging sessions (1,2) of the same subject. The images from the session 1 (a) and session 2 (c) have different subject coordinate systems because of different head positions for the two sessions. After determining the alignment transform using AIR in the image domain, the images from session 2 were aligned to the images from session 1 by applying the transform in the k-space domain and then reconstructing these session 2 data in the session 1 subject coordinate system. The features of the resultant image (b) match those in session 1 (a) as demonstrated by the near zero absolute difference image (d). By comparison, the absolute difference image for the unaligned images (a and c) shows significant non-zero features (e). The absolute difference images (d and e) are shown on the same gray scale as (a and c).

Figure 7.

Example of registration of 3.0 T sodium ²³Na images (a,c) from different imaging sessions (1,2) of the same subject. The images from the session 1 (a) and session 2 (c) have different subject coordinate systems because of different head positions for the two sessions. After determining the alignment transform using AIR in the image domain, the images from session 2 were aligned to the images from session 1 by applying the transform in the k-space domain and then reconstructing these session 2 data in the session 1 subject coordinate system. The features of the resultant image (b) match those in session 1 (a) as demonstrated by the near zero absolute difference image (d). By comparison, the absolute difference image for the unaligned images (a and c) shows significant non-zero features (e). The absolute difference images (d and e) are shown on the same gray scale as (a and c).

Discussion and Conclusion

Translation and rotation of sodium MR imaging data can be determined rapidly, accurately, and precisely using the existing AIR algorithm. Maximum translation errors of 0.006±0.004 mm and 0.080±0.070 mm were achieved for smallest (2.9 mm isotropic) and largest (8.8 mm isotropic) voxel sizes tested for sodium imaging reconstructed without k-space filtering. Both are below 1% of the voxel dimension. This error would not be significant for proton imaging where resolution is much greater than sodium imaging. Rotations were detected by the AIR algorithm with excellent accuracy and precision. Worst-case errors of 0.006 ± 0.008 degrees and 0.070 ± 0.082 degrees were achieved for 2.9 mm and 8.8 mm voxels and unfiltered k-space reconstruction, respectively. Inclusion of k-space filtering did not have a significant impact on the accuracy at which data translations and rotations could be determined for sodium MR data. AIR provided excellent registration of sodium MR image data at all combinations of voxel size and k-space filtering evaluated for both data representative of 9.4 T and 3.0 T sodium MR imaging performed in less than 10 minutes. With the improved spatial resolution and SNR available through longer acquisitions or higher static magnetic field strength, these alignment errors are expected to be maintained or possibly reduced. The time required to perform each alignment was less than one second on a standard consumer laptop computer. The only notable limitation of the AIR implementation is that it does not natively support data stored as DICOM image files. This means the two datasets must be converted to an AIR supported format prior to finding T_S2 → S₁ . Although this conversion is straightforward, it does represent an additional processing step.

The analysis did assume that the head was a rigid body and that rotations and translations of the participant’s head resulted in pure translations and rotations in the image domain. This assumption may be violated for areas of non-ideal imaging due to B₀ and B₁ inhomogenities that result in image artifacts that do not translate and rotate with head position. The rigid-body assumption may be violated in the setting of changing anatomy or sodium concentration due to disease or treatment response. In such cases, the area of change should be excluded when determining the transform to align the two imaging sessions. In addition, gradient imperfections, such as non-linear gradients near the edge of the field-of-view, that cause geometric distortions cannot be corrected by rigid alignment using only translation and rotation. Likewise, any temporal instability of the imaging system (e.g., gradient heating) or hardware changes may reduce the effectiveness of rigid alignment. However, quality assurance and consistent operator performance should minimize these effects to acceptable levels.

The transform describing the rotation and translation can be applied in image-space using conventional image resampling or directly in k-space during image reconstruction. Performing the translation and rotation in k-space produced lower maximum and average alignment errors than applying the same transform in image space. This was true for final images generated with and without k-space filtering. While image-space interpolation was generally faster than using Equations {4} and {5} to apply the transform in k-space, unacceptably high errors, especially near high-contrast borders, can occur. Longer processing time did not necessarily translate to better performance. For example, the windowed sinc interpolation required approximately 50% more processing time than applying T_S2 → S₁ in k-space, but it still had worse maximum error (5.209 ± 0.576 mM vs. 00.180 ± 0.015 mM for unfiltered k-space data) and average error (0.338 ± 0.020 mM vs. 0.034 ± 0.003 mM for unfiltered k-space data). The chirp-z and tri-linear (the default in AIR) interpolations were much faster than performing the translation and rotation in k-space, but both had higher maximum and average errors. In practice, the average errors for all methods are likely to be acceptable as the worst average error was 0.874 ± 0.010 mM (trilinear image-space interpolation of image data reconstructed without k-space filtering). This is within the single voxel variation of ~ ±2 mM for normal tissue and ~ ±7.5 mM for CSF expected for an SNR of 20:1 (an achievable SNR in human imaging with a practical acquisition time of less than 10 minutes). The maximum errors, however, were much higher for the image-space interpolation methods, reaching as high as 34.704 ± 3.019 mM (tril-inear image-space interpolation of image data reconstructed without k-space filtering). The k-space implementation of the required translation and rotation produced a far more acceptable error of 0.180 ± 0.015 mM, lower than all image-space interpolation methods tested. Among the image-domain methods tested, the chirp-z interpolation performed best by a significant margin and approached the performance of the k-space implementation for reconstructions with k-space filtering.

Although the errors for image-space rotation and translation can theoretically be reduced by using a larger interpolation kernel, the computational time will grow rapidly as the resampling must be done in three-dimensions. Perfect image-domain resampling of the data would require interpolating the complex image data rather than the magnitude data as is commonly done. Applying the rotation and translation in k-space avoided these problems as the solution corresponded to using an unwindowed sinc interpolation kernel on the complex data.

The maximum and average errors due to applying T_S2 → S₁ were lower for both k-space and image-space implementations when the image data were reconstructed with a Blackman k-space filter. This was likely because that k-space filtering reduces the spatial resolution of the final images, making slight mis-registrations less significant in terms of TSC error.

For gridding-based reconstructions that are common for the projection-based acquisitions used for sodium MR imaging, translations and rotations are easily incorporated into the reconstruction process. In addition, since flexTPI samples a sphere of k-space rotations and translations implemented in k-space will not modify the point-spread function. Unlike image-domain interpolation, this means that applying T_S2 → S₁ in k-space will preserve the spatial resolution of the sodium MR data. This is an important feature for quantification of bioscales as changes in spatial resolution can complicate quantitative single-voxel or small ROI analysis due to partial volume effects. A limitation of including the transformation in the reconstruction is that if a time-consuming reconstruction is required (e.g., multi-frequency reconstruction for B₀-inhomgeneity correction) it must be completely repeated once the alignment transform coefficients are determined from the image data sets. Image space resampling operates directly on the image-domain data thereby avoiding this requirement, but at the cost of higher resampling errors with loss of quantification accuracy.

Alignment of human sodium neuroimaging data from separate imaging sessions has been demonstrated using experimental data from both 9.4 T and 3.0 T. Subtraction of the aligned datasets showed excellent agreement with no features identifiable in the difference image. The preservation of image intensity and spatial resolution indicates that the accuracy of the bioscale can be maintained with alignment of images across different examinations.

In addition to the session-to-session registration challenge that motivated this work, the results may also improve intra-session registration when multiple sodium datasets are acquired to compute B₀- and B₁-inhomogenity corrections (1) with the assumption that identical head position has been maintained throughout the total examination time.

In conclusion, sodium MR imaging data of the human brain can be aligned accurately and precisely to enable single voxel comparison of quantitative bioscales across longitudinal studies.