Network-assisted Causal Gene Detection in Genome-wide Association Studies: An Improved Module Search Algorithm

Abstract

The recent success of genome-wide association (GWA) studies has greatly expanded our understanding of many complex diseases by delivering previously unknown loci and genes. A large number of GWAS datasets have already been made available, with more being generated. To explore the underlying moderate and weak signals, we recently developed a network-based dense module search (DMS) method for identification of disease candidate genes from GWAS datasets, leveraging on the joint effect of multiple genes. DMS is designed to dynamically search for the best nodes in a step-wise fashion and, thus, could overcome the limitation of pre-defined gene sets. Here, we propose an improved version of DMS, the topologically-adjusted DMS, to facilitate the analysis of complex diseases. Building on the previous version of DMS, we improved the randomization process by taking into account the topological character, aiming to adjust the bias potentially caused by high-degree nodes in the whole network. We demonstrated the topologically-adjusted DMS algorithm in a GWAS dataset for schizophrenia. We found the improved DMS strategy could effectively identify candidate genes while reducing the burden of high-degree nodes. In our evaluation, we found more candidate genes identified by the topologically-adjusted DMS algorithm have been reported in the previous association studies, suggesting this new algorithm has better performance than the unweighted DMS algorithm. Finally, our functional analysis of the top module genes revealed that they are enriched in immune-related pathways.

1 Introduction

Building on the "common-disease-common-variant (CDCV)" hypothesis, genome-wide association (GWA) studies have been popular during the past several years to identify disease associated markers and genes. So far, more than 200 diseases or traits have been studied by GWAS, and more than 4500 markers have been identified for disease association [1]. Despite the success of GWA studies, these findings only represent a small proportion of the genetic factors involved in complex diseases, while a great number of disease-associated markers and their interactions have not been discovered yet. There are many explanations of the possible missingness or lack of power, such as rare variations and epigenetic factors that are difficult to detect in GWA studies, either because of the GWAS design (i.e., common variants) or the limitation of computation power in genome-wide SNP interactions. Among these explanations, one important factor is that most genome-wide significant markers identified so far are observed to have modest effects on individual odds ratios that are typically less than 1.2 [2]. To overcome this limitation (i.e., no strong genetic effect of the markers), gene-set based methods have recently been proposed to investigate the joint effect of multiple functionally related genes [3–5]. It has been implicated that these methods could have improved power in uncovering a set of genes significantly enriched with association signals, and such genes could exist in the same pathway or functional group [4].

We recently developed a network-based algorithm, the dense module search (DMS), to identify subnetworks significantly enriched with association signals from GWAS dataset(s) for a specific disease/trait [6]. DMS could overcome the disadvantages of pre-defined pathways, which are limited to a priori knowledge and only include approximately 30% of human genes, a problem frequently observed in standard gene-set based analysis. DMS allows a dynamic search of de novo gene sets consisting of genes interconnected in the context of a protein-protein interaction (PPI) network. Our previous applications of DMS to GWAS datasets for breast cancer and pancreatic cancer have demonstrated that DMS could successfully identify a set of genes in the form of subnetworks, which are significantly enriched and associated with the diseases. We also showed that DMS could greatly improve power when we compared the performance with other methods such as Gene Set Enrichment Analysis (GSEA), which is currently the major algorithm for gene-set based analysis of GWAS datasets [7].

Here, we proposed topologically-matched normalization strategy in the DMS method to substantially improve the DMS algorithm. The major aim is to adjust the potential bias when applying network-based methods. For example, it has been found cancer proteins have more interactors because of their functional importance [8–9]. Correspondingly, high-degree proteins would have more chance to be selected in network analysis, especially when performing step-wise searching and expanding strategies in DMS. Consequently, cancer genes have often been observed in candidate gene prioritization studies when investigators studied other diseases such as psychiatric disorders. In this study, we demonstrated that our topologically-adjusted DMS method could efficiently reduce the bias caused by the degree and, thus, substantially improve the power to detect true candidate genes in a psychiatric disorder.

II. Material and Methods

A. The CATIE GWAS Dataset

The Clinical Antipsychotic Trial of Intervention Effectiveness (CATIE) project is a multiphase randomized controlled trial. It was genotyped by Perlegen Sciences using the Affymetrix 500K and Perlegen’s custom 164K chip. A detailed description of the samples can be found in reference [10]. We accessed this dataset (Distribution 7.0) from http://www.nimhgenetics.org/ through NIMH approval. Only the Causation samples were used. The pipeline of quality control, including the selection of samples and markers, was described in references [6, 11–12]. In summary, a total of 738 schizophrenia patients and 733 controls, and 446,225 SNPs were used in this study.

To facilitate the network-based strategy, SNP markers were further mapped to genes based on their genomic coordinates. Because some SNPs may execute their function through regulation or other functional effects, we included an extended region of 20kb both upstream and downstream of each gene. Finally, gene-wise P values were computed using the SNP with the smallest P value among all the SNPs mapped to a gene. This approach resulted in a total of 19,310 genes.

We used a comprehensive human PPI network downloaded from the Protein Interaction Network Analysis (PINA) platform [13] (March 4, 2010). Six public PPI databases have been collected in this dataset (MINT, IntAct, DIP, BioGRID, HPRD, and MIPS/MPact). After overlaying the GWAS data onto this network, we removed the nodes (genes) that were not genotyped or failed to be mapped to human protein coding genes or the edges indicating self-interaction. We had 9,227 nodes and 43,869 edges.

B. Weighted DMS

We overlay the GWAS data onto the PPI network by assigning each node a z-score based on the P value of its encoding gene, i.e., z_i = Φ⁻¹ (1 − P_i) for the i^th node, where Φ⁻¹ is the inverse normal cumulative density function and P_i is the corresponding gene-wise P value from the GWAS dataset.

To adjust the bias caused by nodes with many interactors, we proposed the topologically-matched randomization method in comparison to the previous regular randomization. We used the parameter of degree to describe the topological characteristics of the network, defined as the number of interactors for each node in the overall network. After examining the degree distribution of the working interactome, we categorized the nodes into four groups according to their degrees: group A with degree range between 0–2², group B 2²–2⁴, group C 2⁴–2⁶, and group D >2⁶.

The detailed module search strategy can be referred to in our previous work [6]. Briefly, the strategy has the following steps.

Step 1. Candidate module construction. Each node in the network is used as the seed to search for a local highest-scored module. During the module expansion, the neighborhood nodes with ≤ 2 steps away from the seed module are iteratively evaluated, and the node with the maximum score increase is selected. The module expansion is terminated when no neighborhood node can increase the module score by Z_(m+1) ≥ Z_m × (1 + r), where r = 0.1 is used in this work and can be adjusted appropriately in different DMS applications.

Step 2. Module normalization. To determine whether the module score is higher than expected by chance, a total of 1,000 topologically-matched random networks are generated. More specifically, for each module, we first counted the number of nodes in each of the four degree groups as defined above, and then randomly selected the same number of nodes for each group from the working interactome, resulting in a topologically-matched random module. In each random process, module scores are computed for all the candidate modules generated in step 1. Finally, a normalized score is computed for each module by $Z_N=\frac{Z_m-\mathit{\text{mean}}(Z_m(\pi ))}{\mathit{\text{sd}}(Z_m(\pi ))}$, where Z_m (π) is the score of the π^th randomization, and Z_m is the observed module score.

Step 3. Module selection. We select the modules that are scored within the top 1% quantile of the module score distribution and merge them to construct a disease-specific subnetwork. This subnetwork is enriched with association signals from the GWAS dataset used.

We named this improved version of the DMS algorithm “topo-adjusted DMS” for search disease-specific modules and subnetworks from GWAS dataset(s).

III. Results

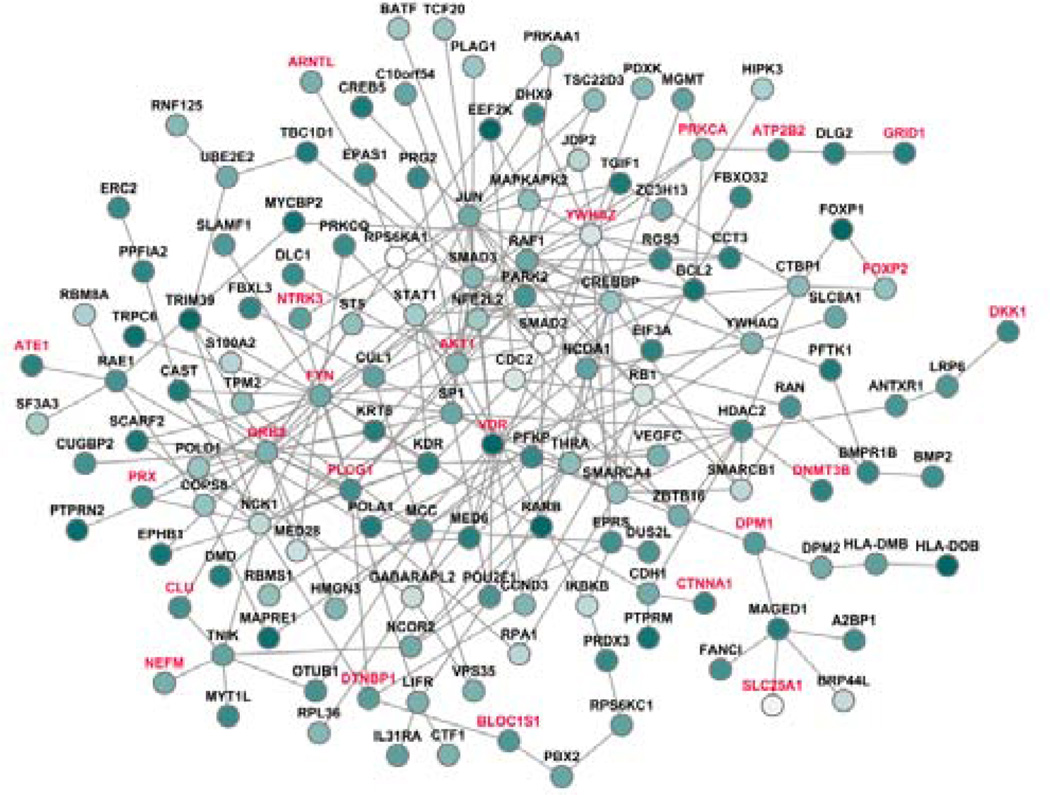
We applied the topo-adjusted DMS algorithm to the CATIE GWAS dataset for schizophrenia. We obtained a total of 8,545 modules and, based on that, selected the top 86 modules (1% of all modules) according to their score Z_N values. By combining these modules, we first constructed a subnetwork including 179 nodes (genes) in the 86 modules. Visual examination of this network showed that two genes, PTP4A3 and IKBKE, showed extremely high degree and betweenness values, another topological character defined as the number of shortest path going through a node. Each of these two genes introduced many nodes that are weakly connected to the network by only one edge (PPI). Thus, these two genes, as well as those connected to the subnetwork only through these two genes, were manually removed from the subsequent analysis, as they are likely false positive nodes that escaped the topo-adjusted randomization process. As a result, a total of 143 nodes were included in the final subnetwork, and we denoted it as the schizophrenia-specific subnetwork (Figure 1).

Figure 1.

Module gene based subnetwork for schizophrenia. Nodes in red are szgenes. The node darkness is proportinal to the z-score.

To demonstrate the improvement of the weighted DMS method, we applied the previous unweighted DMS method to the same GWAS dataset. It generated a subnetwork with 86 modules and 173 genes. To evaluate their performance, we downloaded schizophrenia candidate genes from the SZGene database [14] (as of January 26, 2011). This database manually collected genes that have been studied for association with schizophrenia through traditional association studies as well as GWA studies. These genes (we denoted as “szgenes”) can serve as gold positives. We found a total of 23 szgenes were included in the weighted DMS results (16.08%), while only 20 szgenes were included in the unweighted DMS results (11.56%) (Table I). The result indicates that the topo-adjusted DMS could greatly improve the proportion of known candidate genes for schizophrenia; thus, it has high sensitivity in searching for candidate genes.

TABLE I.

Summary of DMS Results

	Unweighted DMS	Topo-adjusted DMS
# modules	86	86
# module genes	173	143
# szgenes in modules	20	23
Proporntion of szgenes	11.56%	16.08%

Further examination of the module genes showed that a total of 114 genes (79.72%) had P values < 0.05. The remaining "non-significant" genes were recruited mainly because they were located in a low-P-value environment and they interacted with genes with small P values. For example, the genes NCK1 and MED28 did not show significant association with schizophrenia individually; however, each of them was observed to interact with the protein products of other important genes for schizophrenia. NCK1 interacts with four proteins encoded by szgenes, DTNBP1, FYN, PLCG1, and PRX, and MED28 interacts with two such proteins encoded by FYN and GRB2. This further demonstrated the capability of DMS to identify joint effect of multiple genes, despite that they may not be significantly associated with the disease on their own. More importantly, selection of these genes did not rely on their pre-defined pathways.

As shown in Figure 1, the resultant subnetwork includes many interesting genes related to schizophrenia. The nodes labeled in red are those that have been studied in previous association studies or recent GWA studies. The genes AKT1 [15], DTNBP1 [16], DLG2 [17], GRID1 [18], NTRK3 [19] and YWHAZ [20] have been well-studied in schizophrenia, most of which have positive associations.

We then examined the pathways that are significantly enriched with the subnetwork genes by using the Ingenuity Pathway Analysis (IPA) system [21]. For the canonical pathways, the most significantly enriched ones include TGF-β Signaling, RAR Activation, 14-3-3-mediated Signaling, Neurotrophin/TRK Signaling, and PPARα/RXRα Activation (Table II), most of which are related to immune and inflammation system, supporting the immune-involved hypothesis of schizophrenia.

TABLE II.

Significantly Enriched Pathways in the Subnetwork

Ingenuity Canonical Pathways	PBHa	Ob
TGF-β signaling	1.95×10−8	11
RAR activation	1.95×10−8	14
Molecular mechanisms of cancer	2.88×10−8	18
Prolactin signaling	2.88×10−8	10
Glucocorticoid receptor signaling	2.45×10−7	15
14-3-3-mediated signaling	1.91×10−6	10
Neurotrophin/TRK signaling	3.80×10−6	8
PPARα/RXRα activation	5.37×10−6	11
Pancreatic adenocarcinoma signaling	6.92×10−6	9
Regulation of IL-2 expression in activated and anergic T lymphocytes	7.76×10−6	8
Thrombopoietin signaling	8.13×10−6	7

^aBH: multiple testing correction by Benjamini & Hochberg (1995).

^bObserved number of module genes in the category.

IV. Discussion

In this study, we present an improved network-assisted algorithm to identify candidate genes from GWAS dataset through an optimization towards the maximum joint effects of a set of genes. Compared to standard gene-set based analysis, the dense module search method introduces flexibility through a dynamic search of the best node in each step, and, thus, it is granted the opportunity to identify de novo gene sets (i.e., modules) in the context of the whole human interactome. The proposed randomization process in this study takes topological characteristics into account and further improves its sensitivity to search for weak to moderate genes. Our application of the topo-adjusted DMS to the schizophrenia CATIE GWAS dataset successfully demonstrated the superiority of our topo-adjusted DMS method, as the module genes are more likely to have positive association signals from previous studies.

As shown in Table I, the weighted DMS method greatly increased the coverage rate of szgenes from 11.56% to 16.08%. At the molecular level, the weighted DMS method successfully recovered several well-studied genes for schizophrenia and other psychiatric disorders, including AKT1, DTNBP1, GRID1, and NTRK3. Interestingly, gene GRB2 was also found in the top list. We have recently identified GRB2 as a candidate gene for schizophrenia by using a completely different network approach [12, 22] and have successfully validated several SNPs located in GRB2 to be positively associated with schizophrenia patients in the Irish Case Control Study of Schizophrenia (ICCSS) sample [23]. Here, using an independent GWAS dataset, we recovered GRB2 as a strong schizophrenia candidate gene again. Furthermore, as shown in Figure 1, GRB2 functions as a "hub" node by interacting with several proteins that are encoded by strong schizophrenia candidate genes like PLCG1 [24] and FYN [25]. Due to space limitations, we are unable to discuss more details of these genes, or other promising genes in this schizophrenia-specific subnetwork. However, the wealth of information included in the subnetwork provided valuable insights for interpretation of previous identified genes as well as a promising list for future validation.

In summary, we proposed an effective network-based algorithm to identify candidate genes from GWAS datasets and demonstrated it in a schizophrenia GWAS dataset. The R package of the DMS method, dmGWAS, can be found on our website (http://bioinfo.mc.vanderbilt.edu/dmGWAS.html). The user may utilize it for the analysis of other GWAS datasets.